(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
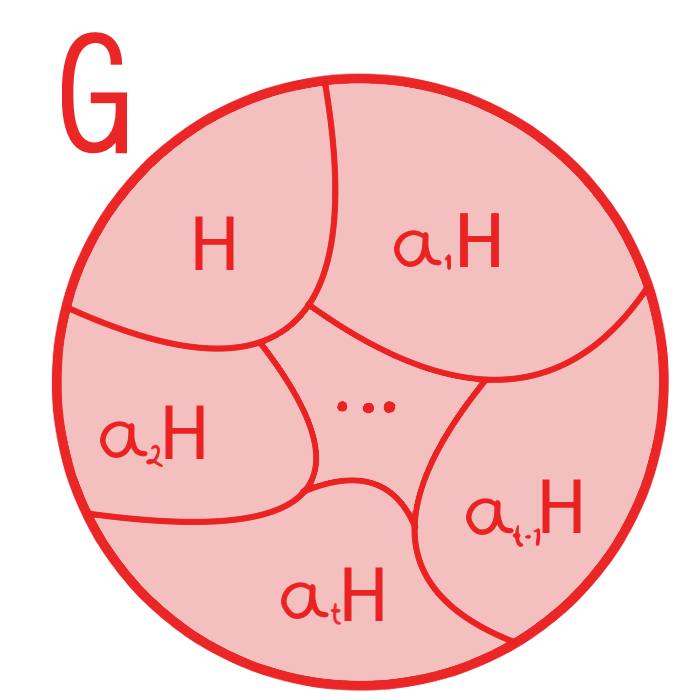
En la entrada anterior vimos que si tenemos un grupo $G$ y nos agarramos un subgrupo $H$, obtenemos una partición $H, a_1H, a_2H, a_3H, \dots, a_tH$ donde
\begin{align*}
|H| = \#a_2 H = \#a_3 H = \cdots = a_t H.
\end{align*}
Recuerda que $|G|$ se refiere al orden de un grupo y $\#a_iH$ es el orden de un conjunto que no es necesariamente un grupo. Esto quiere decir que el orden de $G$ es un $t$ veces del orden de $H$, en decir $|G| = t|H|.$ Este resultado sencillo pero importante es conocido como el Teorema de Lagrange, aunque en esta entrada, lo definimos en términos del índice de $H$ en $G$, $[G:H]$.
Joseph-Louis Lagrange, conocido simplemente como Lagrange, nació en 1739 y falleció en 1813.
A pesar de que vivió antes de que la teoría de conjuntos se desarrollara en el siglo XIX, su trabajo fue muy importante para ella. Por eso este teorema tiene su nombre.
Ingredientes para la demostración
Lema. Sea $G$ un grupo, $H$ un subgrupo de $G$, $a\in G$. Entonces $$\# aH = |H|.$$
Demostración. Sean $G$ un grupo, $H\leq G$ y $a \in G$.
Consideremos $\varphi : H \to a \, H$, tal que $h \mapsto ah$.
Veamos que $\varphi$ es inyectiva ya que si tomamos $h, \bar{h} \in H$ son tales que $\varphi(h) = \varphi(\bar{h})$ entonces $ah = a \varphi$ y por cancelación, $h = (\bar h)$.
Además, $\varphi$ es suprayectiva ya que dado $ah \in aH$ con $h\in H$ tenemos
$$ ah = \varphi(h) \in \text{Im}\varphi. $$
Donde $\text{Im}\varphi$ es la imagen de $\varphi$.
Por lo tanto $|H| = \# a H$.
$\blacksquare$
Señoras y señores, les presento a Lagrange
Ahora ya tenemos todos los ingredientes para demostrar el teorema de Lagrange.
Teorema. (Teorema de Lagrange) Sea $G$ un grupo finito, $H$ subgrupo de $G$. Entonces $|H|$ divide al orden de $G$ y
$$[ G:H ] = \frac{|G|}{|H|}.$$
Demostración. Sea $G$ un grupo finito, $H\leq G$. Como $G$ es finito debe haber una cantidad finita de clases laterales izquierdas de $G$ en $G$, notemos que cada una es no vacía con al menos un elemento.
Sean $a_1, \dots , a_t \in G$ representantes de las distintas clases laterales izquierdas de $H$ en $G$, con $t = [ G : H ]$. Sabemos que $\displaystyle G = \bigcup^{t}_{i=1} a_i H$. Como $a_iH \cap a_jH = \emptyset$ para $i\neq j$, con $i,j\in\{1,\dots, t\}$, entonces la unión, es una unión disjunta. Así podemos hacer,
\begin{align*}
|G| = \left| \bigcup^{t}_{i=1} a_i H\right| &= \sum^{t}_{i=1} \#a_iH \\
&= \sum^{t}_{i = 1} |H| &\text{Lema anterior} \\
&= t|H| = [ G:H ] |H|
\end{align*}
Así $|G| = [ G : H ] |H|$, enconces $|H|\Big| |G|$ y $\displaystyle [ G : H ] = \frac{|G|}{|H|}$.
$\blacksquare$
Consecuencias del teorema
Corolario 1. Sea $G$ un grupo finito, $a\in G$. Entonces $o(a) \Big| |G|$. Así $a^{|G|} = e$.
Demostración. Sea $G$ un grupo finito, $a\in G$. Consideremos $\left< a \right> \leq G$. Por el teorema de Lagrange:
$$ o(a) = |\left< a \right>|\Big| |G| \Rightarrow o(a)\Big| |G|.$$
Así $|G| = o(a)q$, para algún $q \in \z$,
$$a^{|G|} = a^{o(a)q} = \left( a^{o(a)}\right)^q = e^q = e.$$
$\blacksquare$
Corolario 2. Todo grupo finito de orden primo es cíclico.
Demostración. Sea $G$ un grupo finito, $|G| = p$ con $p$ primo.
Como $|G| > 1$ sea $a \in G \setminus \{e\}$. Por el corolario 1,
$$1 < o(a) \Big| |G| = p.$$
Entonces $o(a) = p$. Así $\left< a \right> = G$ y $G$ es cíclico.
$\blacksquare$
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sea $G$ un grupo finito, $H$ y $K$ subgrupos de $G$ con $K\subseteq H$. En cada inciso (son los ejercicios 2 y 3 de la entrada anterior) justifica usando el teorema de Lagrange ¿cómo es $[G:K]$ en términos de $[G:H]$ y $[H_K]$?
- $G = Q$ los cuaternios, $H = \left<i\right>$ y $K = \{\pm 1\}$.
- $G = S_4$, $H = A_4$ y $K = \left<(1\;2\;3)\right>$.
- Encuentra todos los subgrupos del grupo de los cuaternios y de $\z_8$ ¿de qué orden son? ¿cuántos hay del mismo orden?
- Revisa el video de la Sorbona: Lagrange-Universidad de la Sorbona. Se puede poner poner subtítulos en español.
Más adelante…
El teorema de Lagrange es uno de los resultados más importantes del curso. Se usará multiples veces. Por lo pronto, en la siguiente entrada, revisitaremos los grupos cíclicos y usaremos el teorema de Lagrange para probar una caracterización de esos grupos.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Relación de equivalencia dada por un subgrupo e índice de $H$ en $G$.
- Siguiente entrada del curso: Caracterización de grupos cíclicos.
- Resto de cursos: Cursos.

Por favor, puedes explicar sobre el teorema de Lagrange en grupos infinitos?
Hola Wendys. Cuando el grupo es infinito, en vez de poner el teorema como un cociente, se despeja |G| y se pone como el siguiente producto: |G|=|H|[G:H]. Para entender qué está diciendo, hay que entender un poco de cardinalidades infinitas, pues en la derecha hay un producto de cardinales. Si te interesa conocer un poco más de arimética cardinal, puedes echarle un ojo a nuestro curso de Teoría de Conjuntos: https://blog.nekomath.com/tc1.