Archivo de la etiqueta: Conjuntos numerables

Teoría de los Conjuntos I: Conjuntos numerables (parte II)

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

En la entrada anterior hemos mostrado algunos ejemplos de conjuntos equipotentes al conjunto de los números naturales. En algunos casos exhibimos funciones biyectivas del conjunto de los números naturales en cada uno de los respectivos conjuntos. Sin embargo, esta labor puede resultar complicada, en muchas ocasiones exhibir funciones biyectivas de un conjunto en otro presenta diversas dificultades. Debido a esto, en varias situaciones resulta muy útil aplicar el teorema de Cantor-Schröder-Bernstein para mostrar que dos conjuntos son equipotentes sin necesidad de proporcionar una biyección. En esta entrada añadiremos otro par de ejemplos de conjuntos equipotentes al conjunto de los números naturales, pero haremos uso del teorema de Cantor-Schröder-Bernstein para mostrar tal equipotencia.

Conjuntos numerables.

En el siguiente ejemplo aparece un conjunto que ya conocíamos y que de hecho se encuentra en la entrada anterior, se trata del conjunto de números racionales, para el cual dimos dos maneras de mostrar que es numerable.

Ejemplo.

$\mathbb{Q}$ es numerable, es decir, equipotente a $\mathbb{N}$.

Lo que haremos será mostrar que $\mathbb{Q}^{+}\cup\{0\}$ y $\mathbb{N}$ son equipotentes con ayuda del teorema de Cantor-Schröder-Bernstein. Luego, como $\mathbb{Q}^{-}$ y $\mathbb{Q}^{+}$ son equipotentes podremos concluir que $\mathbb{Q}$ es la unión de dos conjuntos ajenos numerables y, por tanto, que $\mathbb{Q}$ es numerable.

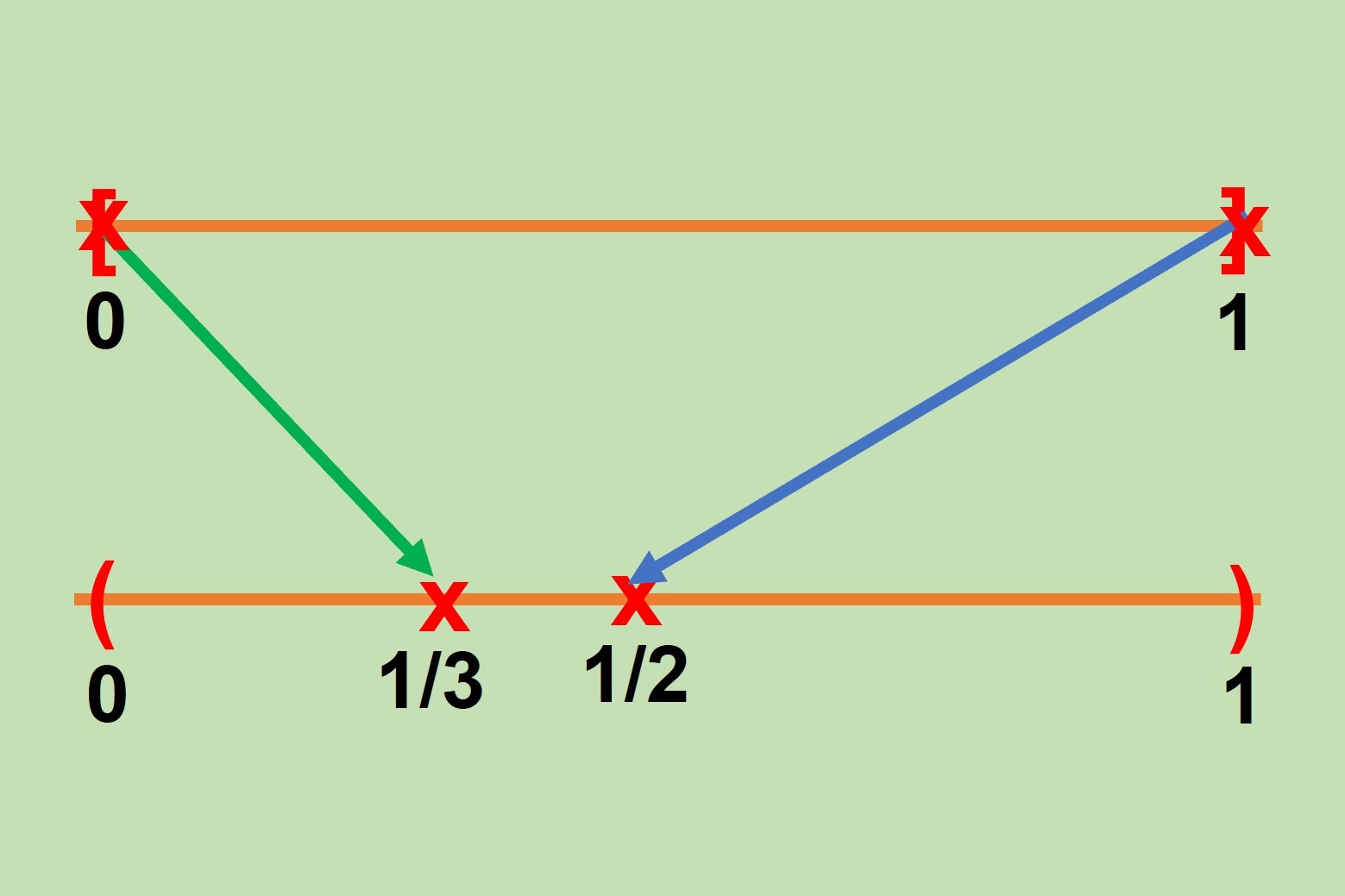
Ante un claro abuso de notación en lo que sigue, definamos $f:\mathbb{N}\to\mathbb{Q}^{+}\cup\{0\}$ por medio de $f(n)=\frac{n}{1}$. Luego, $f$ es una función ineyctiva de $\mathbb{N}$ en $\mathbb{Q}^{+}\cup\{0\}$, pues si $f(n)=f(m)$, entonces, $\frac{n}{1}=\frac{m}{1}$ lo cual implica que $n\cdot 1=m\cdot1$, es decir, $n=m$. Ahora, tenemos que exhibir una función inyectiva de $\mathbb{Q}^{+}\cup\{0\}$ en $\mathbb{N}$. Definamos $g:\mathbb{Q}^{+}\cup\{0\}\to\mathbb{N}\times\mathbb{N}$ por medio de $$g\left(\frac{p}{q}\right)=\left\{\begin{array}{lcc}
(p,q) & \textnormal{si}\ \frac{p}{q}\in\mathbb{Q}^{+}\ \textnormal{y}\ p\ \textnormal{y}\ q\ \textnormal{son primos relativos}\\
(0,0) & \textnormal{si}\ \frac{p}{q}=0
\end{array}
\right.$$

Debido a que cada racional en $\mathbb{Q}^{+}$ tiene una expresión única de la forma $\frac{p}{q}$ con $p$ y $q$ primos relativos, entonces, $g$ está bien definida. Veamos que $g$ es inyectiva. Supongamos que $\frac{p}{q},\frac{s}{t}\in\mathbb{Q}^{+}\cup\{0\}$ son tales que $g(\frac{p}{q})=g(\frac{s}{t})$. Si $\frac{p}{q}=0$, entonces, $g(\frac{p}{q})=(0,0)$ y así $g(\frac{s}{t})=(0,0)$; luego, $\frac{s}{t}=0$, pues en caso contrario, podríamos asumir que $s$ y $t$ son primos relativos y por tanto $g(\frac{s}{t})=(s,t)\not=(0,0)$ ya que $s\not=0$. Así pues, si $\frac{p}{q}=0$, entonces, $\frac{s}{t}=0$. Análogamente, si $\frac{s}{t}=0$, entonces, $\frac{p}{q}=0$. Supongamos ahora que $\frac{p}{q}\not=0\not=\frac{s}{t}$ y que tanto $p$ y $q$ como $s$ y $t$, son primos relativos. Así, $g(\frac{p}{q})=(p,q)$ y $g(\frac{s}{t})=(s,t)$ y por consiguiente, $(p,q)=(s,t)$, de modo que $s=p$ y $q=t$, lo que demuestra que $\frac{p}{q}=\frac{s}{t}$. Por tanto, $g$ es una función inyectiva. Finalmente, si consideramos la función inyectiva $h:\mathbb{N}\times\mathbb{N}\to\mathbb{N}$ definida por medio de $h(n,m)=2^n(2m+1)$, la cual aparece en los ejercicios de la sección anterior, tendremos que $h\circ g:\mathbb{Q}^{+}\cup\{0\}\to\mathbb{N}$ es una función inyectiva. Por el teorema de Cantor-Schröder-Bernstein concluimos que $\mathbb{Q}^{+}\cup\{0\}$ es numerable y, consecuentemente, $\mathbb{Q}$ es numerable.

$\square$

El siguiente ejemplo también aparece en la entrada anterior, pero ahora utilizaremos el teorema de Cantor-Schröder-Bernstein. Como bien lo vimos, dicho ejemplo nos proporciona una gran cantidad de conjuntos numerables y, al mismo tiempo, muestra una propiedad interesante del conjunto de números naturales.

Ejemplo.

Si $A\subseteq\mathbb{N}$ es un conjunto infinito, entonces, $A$ es numerable.

Demostración.

Sea $A\subseteq\mathbb{N}$ un conjunto infinito. La función $\iota:A\to\mathbb{N}$ definida por medio de $\iota(n)=n$ para cada $n\in\mathbb{N}$ es una función inyectiva. Ahora vamos a exhibir una función inyectiva de $\mathbb{N}$ en $A$.
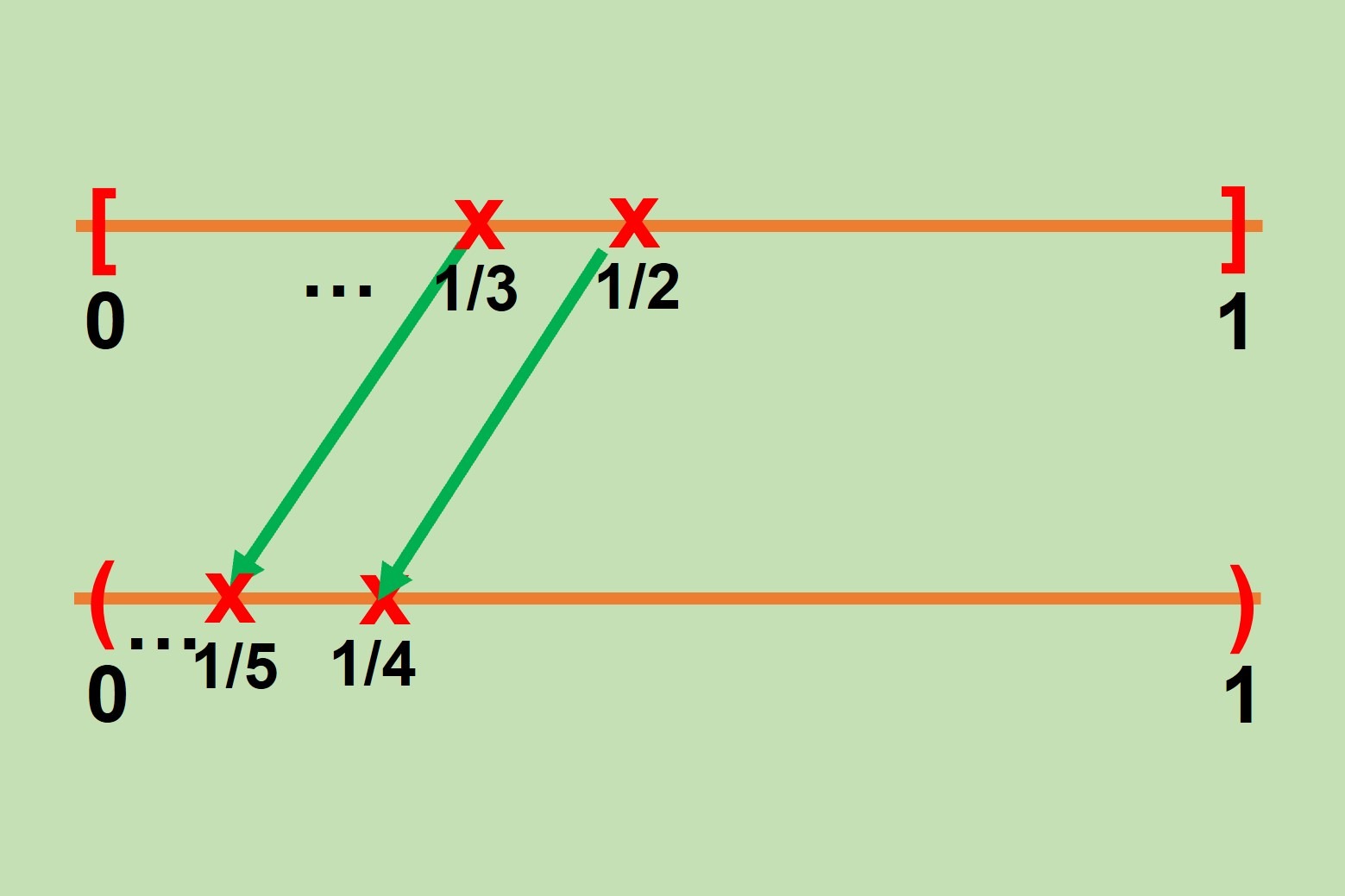
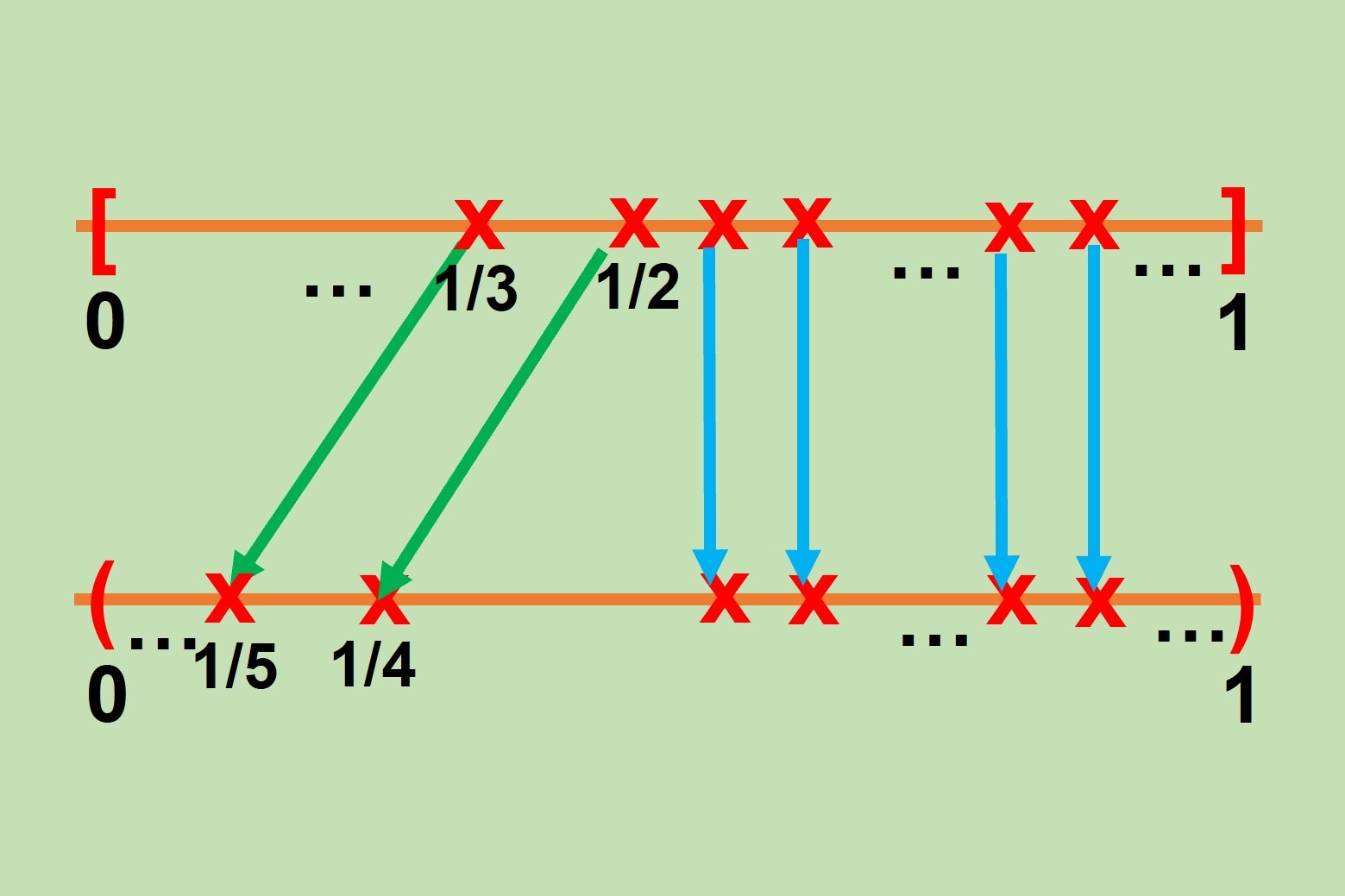
Para cada $n\in A$ definamos $n^{\uparrow}:=\{m\in A:n<m\}$. Notemos que para cada $n\in A$, $n^{\uparrow}\not=\emptyset$, pues en caso contrario existiría $n\in A$ tal que para cada $m\in A$, $m\leq n$ y en consecuencia, $A\subseteq s(n)=n\cup\{n\}$, lo cual implicaría que $A$ es finito, contradiciendo la hipótesis sobre $A$. Así pues, por el buen orden de $\mathbb{N}$, para cada $n\in A$ existe $min(n^{\uparrow})$. Una vez hecho lo anterior elijamos $n_0=min(A)$ y definamos $g:A\to A$ por medio de $g(n)=min(n^{\uparrow})$. Por el teorema de recursión, existe una única función $f:\mathbb{N}\to A$ tal que $f(0)=n_0$ y $f(n+1)=g(f(n))$ para cada $n\in\mathbb{N}$. Veamos que $f$ es una función inyectiva. Para ello, veamos que $f(n)<f(n+1)$ para cada $n\in\mathbb{N}$. Sea $n\in\mathbb{N}$. Luego, $f(n+1)=g(f(n))=min(f(n)^{\uparrow})$ por lo que $f(n+1)\in f(n)^{\uparrow}$ y así $f(n)<f(n+1)$. Por lo tanto $f$ es una función inyectiva de $\mathbb{N}$ en $A$. Por el teorema de Cantor-Schröder-Bernstein podemos concluir que $\mathbb{N}$ y $A$ son equipotentes.

$\square$

Como probarás en los ejercicios de esta entrada, la función $f:\mathbb{N}\to A$ que aparece en el ejemplo precedente es de hecho biyectiva. Por otro lado, como lo habíamos mencionado previo al ejemplo, éste nos proporciona una gran cantidad de conjuntos numerables; por mencionar algunos tenemos los conjuntos $A_n:=\{m\in\mathbb{N}:n<m\}$ para cada $n\in\mathbb{N}$, o también algunos que ya conocíamos como el conjunto de números pares $\{2k:k\in\mathbb{N}\}$, el cual ya sabíamos que era equipotente a $\mathbb{N}$, y algunos otros más interesantes, como el conjunto de números primos pues dicho conjunto es infinito. Para conocer la definición de número primo puedes consultar el siguiente enlace Álgebra Superior II: Números primos y sus propiedades.
Otra consecuencia del ejemplo anterior es el siguiente corolario.

Corolario. Si $B$ es un conjunto numerable y $A\subseteq B$ es un conjunto inifinito, entonces, $A$ es un conjunto numerable.

Demostración.

Dado que $B$ es numerable, existe una función biyectiva $g:B\to\mathbb{N}$. Luego, la restricción de $g$ al conjunto $A$, $g\upharpoonright_{A}:A\to\mathbb{N}$, es una función inyectiva y, más aún, es una biyección entre $A$ y $g[A]\subseteq\mathbb{N}$. Dado que $A$ es infinito, también lo es $g[A]$, pero por el ejemplo anterior sabemos que $g[A]$ es numerable y, en consecuencia, $A$ es numerable.

$\square$

Hasta ahora, en los dos ejemplos que hemos visto, si bien hicimos uso del teorema de Cantor-Schröder-Bernstein y nos facilitó probar la equipotencia de tales conjuntos con $\mathbb{N}$, también es factible exhibir o mostrar directamente la existencia de una función biyectiva. En los ejemplos subsecuentes será más clara la utilidad e importancia del teorema de Cantro-Schröder-Bernstein, y además un tanto más interesantes, pues sin dicho teorema probar la equipotencia con $\mathbb{N}$ es bastante más complicado.

Para introducir el siguiente ejemplo es necesario mencionar un resultado importante del conjunto de números enteros, conocido como el teorema fundamental de la aritmética. Tal teorema asegura que dado cualquier número entero positivo mayor a 1, éste tiene una expresión única como producto de números primos, es decir, si $z\in\mathbb{Z}^{+}$ es cualquier entero positivo mayor a 1, existen únicos números primos $p_1,\ldots,p_n$ y únicos números naturales distintos de cero $\alpha_1,\ldots,\alpha_n$ tales que $z=p_1^{\alpha_1}\cdots p_n^{\alpha_n}=\Pi_{i=1}^{n}p_i^{\alpha_i}$. Puedes consultar el teorema fundamental de la aritmética y su prueba en el siguiente enlace Álgebra Superior II: Teorema fundamental de la aritmética e infinidad de números primos; más aún, en dicho enlace puedes encontrar la prueba de que el conjunto de números primos es inifinito y, de acuerdo al último ejemplo que enunciamos, éste conjunto es numerable.

Ejemplo.

$[\mathbb{N}]^{<\mathbb{N}}:=\{A\subseteq\mathbb{N}:A\ \textnormal{es finito}\}$ es numerable.

Demostración.

Notemos que la función $f:\mathbb{N}\to[\mathbb{N}]^{<\mathbb{N}}$ definida por medio de $f(n)=\{n\}$ es una función inyectiva, de modo que para aplicar el teorema de Cantor-Schröder-Bernstein hace falta exhibir una función inyectiva de $[\mathbb{N}]^{<\mathbb{N}}$ en $\mathbb{N}$.
Para construir tal función inyectiva, consideremos en primer lugar al conjunto de números primos $\mathbb{P}:=\{p\in\mathbb{Z}^{+}:p\ \textnormal{es primo}\}$. Dado que $\mathbb{P}$ puede ser visto como un subconjunto de $\mathbb{N}$, sabemos, por el ejemplo anterior, que existe una función (biyectiva) $f:\mathbb{N}\to \mathbb{P}$ tal que $f(0)=min(\mathbb{P})$ y tal que $f(n)<f(n+1)$ para cada $n\in\mathbb{N}$. Así, si denotamos como $p_n:=f(n)$ para cada $n\in\mathbb{N}$, podemos escribir $\mathbb{P}=\{p_n:n\in\mathbb{N}\}$ y se satisface que $p_n<p_{n+1}$ para cada $n\in\mathbb{N}$. Vamos a considerar para el resto de la prueba que $\mathbb{P}$ está enumerado de esta manera.
Ahora bien, si $A\subseteq\mathbb{N}$ es un conjunto finito y no vacío, digamos $|A|=n+1$ con $n\in\mathbb{N}$, entonces, $A$ puede ser enumerado de manera similar a como lo hicimos con $\mathbb{P}$; esto es, existe una función biyectiva (de hecho única) $f_A:n+1\to A$ tal que $f_A(0)=min(A)$ y $f_A(k)<f_A(m)$ si y sólo si $k<m$. Así, si denotamos como $a_k:=f_A(k)$ para cada $k\in n+1$, tenemos que $A=\{a_k:k\in n+1\}$ y que $a_k<a_m$ si y sólo si $k<m$. Para el resto de la prueba utilizaremos estas enumeraciones con cualquier subconjunto finito no vacío de $\mathbb{N}$, es decir, dado $A\subseteq\mathbb{N}$ no vacío, con $|A|=n+1$, escribiremos $A=\{a_k:k\in n+1\}$ y se entenderá que $a_k<a_m$ si y sólo si $k<m$.

Una vez mencionado lo anterior definamos $F:[\mathbb{N}]^{<\mathbb{N}}\setminus\{\emptyset\}\to\mathbb{Z}^{+}$ por medio de $F(A)=\Pi_{k=0}^{n}p_k^{a_k}$ si $A=\{a_k:k\in n+1\}$, para cada $A\in[\mathbb{N}]^{<\mathbb{N}}\setminus\{\emptyset\}$. Veamos que tal función es inyectiva. Supongamos que $A,B\in[\mathbb{N}]^{<\mathbb{N}}\setminus\{\emptyset\}$ son conjuntos tales que $F(A)=F(B)$. Si $|A|=n+1$ y $|B|=m+1$ con $n,m\in\mathbb{N}$, y además $A=\{a_k:k\in n+1\}$ y $B=\{b_k:k\in m+1\}$, entonces, $F(A)=\Pi_{k=0}^{n}p_k^{a_k}$ mientras que $F(B)=\Pi_{k=0}^{m}p_k^{b_k}$; luego, como $\Pi_{k=0}^{n}p_k^{a_k}=\Pi_{k=0}^{m}p_k^{b_k}$ se tiene $n=m$, pues si $n<m$, entonces, $m>0$ y $b_m>0$, ya que $b_m>b_0$ y $b_0\geq0$, por lo que $p_m^{b_m}$ es una potencia positiva del primo $p_m$ que no aparece en el producto $\Pi_{k=0}^{n}p_k^{a_k}$, pero que sí aparece en el producto $\Pi_{k=0}^{m}p_k^{b_k}$, lo cual contradice el teorema fundamental de la aritmética. Análogamente, no puede ocurrir que $m<n$. Por tanto, $n=m$ y, por consiguiente, $a_k=b_k$ para cada $k\in n+1$. En consecuencia, $A=B$. Por tanto, $F$ es una función inyectiva. Finalmente, como $\mathbb{Z}^{+}$ es numerable, existe $G:\mathbb{Z}^{+}\to\mathbb{N}\setminus\set{0}$ función biyectiva y así $G\circ F:[\mathbb{N}]^{<\mathbb{N}}\setminus\set{\emptyset}\to\mathbb{N}\setminus\set{0}$ es una función inyectiva. Por consiguiente, la función $\tilde{F}:[\mathbb{N}]^{<\mathbb{N}}\to\mathbb{N}$ definida por medio de $$\tilde{F}(A)=\left\{ \begin{array}{lcc}
0 & \textnormal{si}\ A=\emptyset \\
(G\circ F)(A) & \textnormal{si}\ A\not=\emptyset
\end{array}
\right.$$

es inyectiva. El teorema de Cantor-Schröder-Bernstein nos permite concluir que $[\mathbb{N}]^{<\mathbb{N}}$ es numerable.

$\square$

Para el último ejemplo que trataremos en esta entrada vamos a definir lo que es una sucesión.

Definición. Si $A$ es un conjunto y $f:\mathbb{N}\to A$ es una función, diremos que $f$ es una sucesión en $A$. Por otro lado, si $n\in\mathbb{N}$ y $g:n\to A$ es una función, diremos que $g$ es una sucesión finita de longitud $n$ en $A$.

Dado un conjunto $A$ vamos a denotar como $^nA$ al conjunto de todas las sucesiones finitas de longitud $n$ en $A$.

Ejemplo.

El conjunto $\mathbb{N}^{<\mathbb{N}}:=\cup_{n\in \mathbb{N}}\ ^n\mathbb{N}$ es numerable.

Demostración.

Primero vamos a dar una función inyectiva de $\mathbb{N}$ en $\mathbb{N}^{<\mathbb{N}}$. Para cada $n\in\mathbb{N}\setminus\{0\}$ definamos $x_n:1\to\mathbb{N}$ como $x_n(0)=n$. Si $n\in\mathbb{N}\setminus\{0\}$, $x_n$ es una sucesión finita de longitud $1$ en $\mathbb{N}$, es decir, $x_n\in{^1\mathbb{N}}$. Ahora, para $n=0$ definamos $x_0:=\emptyset:0\to\mathbb{N}$ la función vacía, es decir, la única sucesión finita de longitud $0$ en $\mathbb{N}$, de modo que $x_0\in{^0\mathbb{N}}$. Una vez definidas estas sucesiones finitas vamos a considerar la función $f:\mathbb{N}\to\mathbb{N}^{<\mathbb{N}}$ dada por $f(n)=x_n$ para cada $n\in\mathbb{N}$. Notemos que $f$ es inyectiva, pues si $n,m\in\mathbb{N}$ son naturales distintos podemos suponer que $n<m$; luego, si $n=0$, entonces $f(n)=f(0)=x_0=\emptyset$ mientras que $m>0$ y $f(m)=x_m=\{(0,m)\}$, de modo que $f(n)\not=f(m)$. Si ahora $0<n$, entonces también $0<m$ y $f(n)=x_n=\{(0,n)\}$ mientras que $f(m)=x_m=\{(0,m)\}$, pero dado que $(0,n)\not=(0,m)$ pues $n\not=m$, concluimos que $f(n)\not=f(m)$. Por tanto $f$ es inyectiva.

Ahora vamos a dar una función inyectiva de $\mathbb{N}^{<\mathbb{N}}$ en $\mathbb{N}$. En el penúltimo ejemplo consideramos al conjunto de números primos enumerado como $\mathbb{P}=\{p_n:n\in\mathbb{N}\}$ de tal manera que $p_n<p_{n+1}$ para cada $n\in\mathbb{N}$. Retomando dicha enumeración del conjunto de números primos definamos $g:\mathbb{N}^{<\mathbb{N}}\to\mathbb{N}\times\mathbb{Z}$ por medio de $$g(x)=\left\{\begin{array}{lcc}
(n+1,\Pi_{k=0}^{n}p_k^{x(k)}) & \textnormal{si}\ x\in{^{n+1}\mathbb{N}} \\
(0,0) & \textnormal{si}\ x=\emptyset
\end{array}
\right.
$$

Probar que la función $g$ es inyectiva requiere, esencialmente, del teorema fundamental de la aritmética; si $x\in{^{n+1}\mathbb{N}}$ y $y\in{^{m+1}\mathbb{N}}$ con $n\not=m$, entonces, $n+1\not=m+1$ y por ende $g(x)=(n+1,\Pi_{k=0}^{n}p_k^{x(k)})\not=(m+1,\Pi_{k=0}^{m}p_k^{y(k)})=g(y)$. Si $x=\emptyset$ y $y\in{^{n+1}\mathbb{N}}$ con $n\in\mathbb{N}$, entonces $g(y)=(n+1,\Pi_{k=0}^{n}p_k^{y(k)})\not=(0,0)=g(x)$. Por tanto, para concluir que $g$ es inyectiva, basta comprobar que si $n\in\mathbb{N}$ y $x,y\in{^{n+1}\mathbb{N}}$ son elementos distintos, entonces $g(x)\not=g(y)$, lo cual dejamos como un ejercicio al final de esta entrada.

Por el teorema de Cantor-Schröder-Bernstein, $\mathbb{N}^{<\mathbb{N}}$ es numerable.

$\square$

Tarea moral

  • Sea $A\subseteq\mathbb{N}$ conjunto inifinito. Para cada $n\in A$ definimos $n^{\uparrow}:=\{m\in A:n<m\}$. Definimos $g:A\to A$ por medio de $g(n)=\textnormal{min}(n^{\uparrow})$ y consideremos la única función $f:\mathbb{N}\to A$ tal que $f(0)=\textnormal{min}(A)$ y $f(n+1)=g(f(n))$ para cada $n\in\mathbb{N}$. Demuestra que $f$ es una biyección.
  • Prueba que la función $g:\mathbb{N}^{<\mathbb{N}}\to\mathbb{N}\times\mathbb{Z}$ definida por medio de $g(x)=\left\{\begin{array}{lcc} (n+1,\Pi_{k=0}^{n}p_k^{x(k)}) & \textnormal{si}\ x\in^{n+1}\mathbb{N} \\ (0,0) & \textnormal{si}\ x=\emptyset
    \end{array}
    \right.$ es inyectiva.
  • Demuestra lo siguiente:
    $(a)$ Si $A\subseteq\mathbb{N}$ es un conjunto finito no vacío con $|A|=n+1$, $n\in\mathbb{N}$, existe una única función biyectiva $f_A:n+1\to A$ tal que $f_A(0)=\textnormal{min}(A)$ y que $f_A(m)<f_A(k)$ si y sólo si $m<k$ para cualesquiera $m,k\in n+1$.
    $(b)$ Utilizando el hecho de que $\mathbb{N}^{<\mathbb{N}}$ es numerable muestra que $[\mathbb{N}]^{<\mathbb{N}}$ es numerable. Puede que te ayude de algo el inciso $(a)$.
  • Demuestra que si $B\subseteq A$ son conjuntos tales que $B$ es numerable pero $A$ no, entonces, $A\setminus B$ no es numerable.
  • Diremos que una sucesión $x$ en $\mathbb{N}$ es semiconstante si existe $n_0\in\mathbb{N}$ tal que para cada $n\geq n_0$, $x(n)=x(n_0)$. Demuestra que si $\mathcal{S}$ es el conjunto de todas las sucesiones semiconstantes en $\mathbb{N}$, entonces $\mathcal{S}$ es numerable.

Más adelante…

En la siguiente entrada concluiremos el contenido acerca de conjuntos infinitos y veremos ejemplos de conjuntos no numerables.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Teoría de los Conjuntos I: Conjuntos numerables

Por Gabriela Hernández Aguilar

2 respuestas

Introducción

Ahora que hemos desarrollado una herramienta para comparar conjuntos que tienen más elementos que otros y hemos trabajado con conjuntos finitos e infinitos, hablaremos un poco más acerca de estos últimos, en especifico de aquellos que tienen la misma cantidad de elementos que el conjunto de los números naturales. En esta entrada nos enfocaremos principalmente en exhibir un par de ejemplos de conjuntos numerables dando una función biyectiva explícita en cada caso.

Conjuntos numerables

Definición. Sea $A$ un conjunto, decimos que $A$ es numerable si es equipotente a $\mathbb{N}$, es decir, si existe una función biyectiva $f:\mathbb{N}\to A$. De ser así, lo denotaremos con $|A|=|\mathbb{N}|$.

Ejemplo.

En la entrada de equipotencia vimos que existe una función biyectiva entre el conjunto de los números pares y los números naturales, por lo que podemos concluir que $$|\{2k:k\in \mathbb{N}\}|=|\mathbb{N}|.$$

$\square$

Ejemplo.

El conjunto $\mathbb{Z}$ de los números enteros es un conjunto numberable. (Puedes revisar la construcción del conjunto de los números enteros en el siguiente enlace: Álgebra Superior II: Construcción de los enteros y su suma).

Consideremos $f:\mathbb{N}\to \mathbb{Z}$ dada por:

$f(n)= \left\{ \begin{array}{lcc}
             \overline{(k,0)} &   si  & n=2k\ \text{para algún}\ k\in \mathbb{N} \\
             \\ \overline{(0,k+1)} &  si & n=2k+1\ \text{para algún}\ k\in\mathbb{N}
             \end{array}
   \right.$

Resulta que $f$ es biyectiva. En efecto, veamos primero que $f$ es inyectiva.

Sean $x_1, x_2\in \mathbb{N}$ tales que $f(x_1)=f(x_2)$. Tenemos los siguientes casos:

Caso 1. Si $x_1=2k$ y $x_2=2m$ para algunos $k,m\in \mathbb{N}$, entonces $f(x_1)=\overline{(k,0)}$ y $f(x_2)=\overline{(m,0)}$ y así, $\overline{(k,0)}=\overline{(m,0)}$, por lo que $k+0=m+0$, es decir, $k=m$ y por lo tanto, $x_1=2k=2m=x_2$.

Caso 2. Si $x_1=2k+1$ y $x_2=2m+1$ para algunos $k,m\in \mathbb{N}$, entonces $f(x_1)=\overline{(0,k+1)}$ y $f(x_2)=\overline{(0,m+1)}$ y así, $\overline{(0,k+1)}=\overline{(0,m+1)}$, por lo que $0+(m+1)=0+(k+1)$ y así $m=k$. Por tanto, $x_1=2k+1=2m+1=x_2$.

El caso en el que $x_1=2k$ y $x_2=2m+1$ no puede ocurrir, pues de lo contrario se tendría que $\overline{(k,0)}=\overline{(0,m+1)}$ por lo que $k+(m+1)=0+0=0$, lo cual es imposible. De manera análoga, no puede ocurrir que $x_1=2m+1$ y $x_2=2k$ para algunos $m,k\in\mathbb{N}$.

Por lo tanto, $f$ es inyectiva.

Ahora veamos que $f$ es suprayectiva. Sea $y\in \mathbb{Z}$, tenemos los siguientes casos:

Caso 1. Si $y\in \mathbb{Z}^+\cup\set{\overline{(0,0)}}$, entonces $y=\overline{(k,0)}$ para algún $k\in\mathbb{N}$. Así, para $x=2k\in\mathbb{N}$ se tiene $f(x)=y$.

Caso 2: Si $y\in \mathbb{Z}^{-}$, entonces $y=\overline{(0,k)}$ para algún $k\in\mathbb{N}\setminus\{0\}$. Luego, existe $k’\in\mathbb{N}$ tal que $s(k’)=k$, es decir, $k’+1=k$. Luego, tomando $x=2k’+1$ se tiene $f(x)=\overline{(0,k’+1)}=\overline{(0,k)}=y$.

Concluimos que $f$ es suprayectiva.

Por lo tanto $f$ es biyectiva y así, $|\mathbb{N}|=|\mathbb{Z}|$.

$\square$

Antes de pasar al siguiente ejemplo vale la pena introducir la siguiente proposición que nos da una condición suficiente para que un conjunto sea numerable.

Proposición. Sea $A$ un conjunto. Si $f:\mathbb{N}\to A$ es una función sobreyectiva, entonces, $A$ es finito o numerable.

Demostración.

Sea $f:\mathbb{N}\to A$ una función sobreyectiva. Supongamos que $A$ no es finito y veamos que entonces debe ser numerable. Para cada $n\in\mathbb{N}$ definamos el conjunto $A_n:=\{k\in\mathbb{N}:f(k)\not=f(m)\ \textnormal{para cada}\ m\leq n\}$. Dado que $A$ no es finito, $A_n\not=\emptyset$ para cada $n\in\mathbb{N}$ y, por tanto, existe $\textnormal{min}(A_n)$. Definamos $g:\mathbb{N}\to\mathbb{N}$ por medio de $g(n)=\textnormal{min}(A_n)$. Por el teorema de recursión, existe una única función $h:\mathbb{N}\to\mathbb{N}$ tal que $h(0)=0$ y $h(n+1)=g(h(n))$ para cada $n\in\mathbb{N}$. Lo que vamos a probar ahora es que $F:=f\circ h:\mathbb{N}\to A$ es una biyección. Para ello notemos primero que $h(n)<h(n+1)$ para cada $n\in\mathbb{N}$. En efecto, si $n\in\mathbb{N}$, entonces, $h(n+1)=g(h(n))=\textnormal{min}(A_{h(n)})$ y así, en particular, $h(n+1)\in A_{h(n)}=\{k\in\mathbb{N}:f(k)\not=f(m)\ \textnormal{para cada}\ m\leq h(n)\}$, por lo que $h(n)<h(n+1)$. Consecuentemente, $h(m)<h(n)$ si y sólo si $m<n$. Esto último trae como consecuencia también que $n\leq h(n)$ para cada $n\in\mathbb{N}$ y se puede dar una prueba de ello por inducción, pues para $n=0$ se tiene que $h(0)=0\geq0$ y si suponemos que $h(n)\geq n$ para algún $n\in\mathbb{N}$, entonces, $h(n+1)>h(n)\geq n$ y así $h(n+1)\geq n+1$, pues de lo contrario tendríamos que $n+1>h(n+1)>n$ lo cual es imposible.
Una vez mencionado esto, veamos que $F$ es inyectiva. Para ello es suficiente mostrar que para cada $n\in\mathbb{N}$, $F(n+1)\not=F(k)$ para cada $k\leq n$. En efecto, si probamos esto último, y $m,n\in\mathbb{N}$ son naturales tales que $F(n)=F(m)$, entonces, $n=m$, ya que de lo contrario podemos suponer que $m<n$ y así $0<n$ por lo que existe un único $k\in\mathbb{N}$ tal que $k+1=n$; luego, $m\leq k$ y dado que $F(n)=F(k+1)\not=F(s)$ para cada $s\leq k$, en particular $F(n)\not=F(m)$ lo cual contradice la hipótesis de que $F(n)=F(m)$. Por tanto $F$ es inyectiva.
Sea pues $n\in\mathbb{N}$ y veamos que $F(n+1)\not=F(k)$ para cada $k\in\mathbb{N}$ tal que $k\leq n$. Por lo que hemos probado, si $k\leq n$, entonces $h(k)\leq h(n)$. Luego, como $h(n+1)=g(h(n))=\textnormal{min}(A_{h(n)})$, entonces, $f(h(n+1))\not=f(k)$ para cada $k\leq h(n)$; en particular, $f(h(n+1))\not=f(h(k))$ para cada $k\leq n$, es decir, $F(n+1)\not=F(k)$ para cada $k\leq n$. Lo anterior, como lo habíamos mencionado, nos permite concluir que $F$ es inyectiva.

Resta mostrar que $F$ es sobreyectiva. Para ello, veamos por inducción que para cada $n\in\mathbb{N}$ existe $k_n\in\mathbb{N}$ tal que $F(k_n)=f(n)$. Si $n=0$, entonces, para $k_0=0$ tenemos que $F(k_0)=f(0)$. Supongamos que para cada $m\leq n$, con $n\in\mathbb{N}$, existe $k_m\in\mathbb{N}$ tal que $F(k_m)=f(m)$. Veamos que para $n+1$ existe $k_{n+1}\in\mathbb{N}$ tal que $F(k_{n+1})=f(n+1)$. Si $f(n+1)=f(m)$ para algún $m\leq n$, entonces, por hipótesis, $f(n+1)=f(m)=F(k_m)$ para algún $k_m\in\mathbb{N}$. Supongamos ahora que $f(n+1)\not=f(k)$ para cada $k\leq n$. Dado que $n+1\leq h(n+1)$, podemos asegurar que el conjunto $B=\{k\in\mathbb{N}:n+1\leq h(k)\}$ es no vacío y, por consiguiente, existe $m=\textnormal{min}(B)$. Más aún, como $n+1\in B$ tenemos que $m\leq n+1$. Si $n+1=h(m)$, entonces, $F(m)=f(h(m))=f(n+1)$. Supongamos ahora que $n+1<h(m)$. Observemos que esta última desigualdad implica que $m\not=0$, de modo que existe $s\in\mathbb{N}$ tal que $s+1=m$ y dado que $m\leq n+1$, se sigue que $s\leq n$. Ahora bien, por la minimalidad de $m$ en el conjunto $B$, debe ocurrir que $h(s)<n+1$ y por ende $h(s)\leq n$. Finalmente, como $n+1<h(m)$ y $h(m)=h(s+1)=g(h(s))=\textnormal{min}(A_{h(s)})$, donde recordemos que $A_{h(s)}=\{k\in\mathbb{N}:f(k)\not=f(t)\ \textnormal{para cada}\ t\leq h(s)\}$, entonces, existe $t\leq h(s)$ tal que $f(t)=f(n+1)$. Esto muestra que existe $t\leq n$, ya que $t\leq h(s)\leq n$, tal que $f(t)=f(n+1)$ pero esto contradice que $f(n+1)\not=f(t)$ para cada $t\leq n$. De modo que necesariamente debe ocurrir que $n+1=h(m)$. Por tanto, para cada $n\in\mathbb{N}$ existe $k_n\in\mathbb{N}$ tal que $F(k_n)=f(n)$. Como $f$ es sobreyectiva se sigue que $F$ es sobreyectiva.
Por lo tanto, $F$ es una función biyectiva y, consecuentemente, $A$ es numerable.

$\square$

La proposición anterior, además de ser una propiedad interesante de los conjuntos numerables, nos ayuda a obtener una gran cantidad de este tipo de conjuntos. Por ejemplo, si $A\subseteq\mathbb{N}$ es cualquier conjunto infinito, entonces, podemos denotar $a_0=\textnormal{min}(A)$ y definir $g:\mathbb{N}\to A$ por medio de la siguiente regla \[g(n)=\left\{\begin{array}{lcc}
n & \textnormal{si}\ n\in A\\
n_0 & \textnormal{si}\ n\notin A
\end{array}
\right.\]

Ciertamente la función anterior es sobreyectiva y, por tanto, debido a que $A$ no es finito, $A$ es numerable. Más adelante daremos otra prueba de este hecho utilizando resultados distintos.
Otro ejemplo interesante de conjunto numerable que podemos obtener con la proposición anterior lo veremos después de la siguientes observaciones.

En los ejercicios de esta entrada mostrarás que el conjunto $\mathbb{N}\times\mathbb{N}$ es numerable dando una función biyectiva explícita entre $\mathbb{N}\times\mathbb{N}$ y $\mathbb{N}$. Utilizando este hecho y que $\mathbb{Z}$ es numerable, lo cual probamos en el ejemplo precedente, podemos concluir que $\mathbb{Z}\times\mathbb{Z}$ es numerable. En efecto, si $f:\mathbb{N}\to\mathbb{Z}$ es la biyección que dimos en el ejemplo anterior, entonces, $F:\mathbb{N}\times\mathbb{N}\to\mathbb{Z}\times\mathbb{Z}$ definida por medio de $F(n,m)=(f(n),f(m))$ es una biyección y, por tanto, $\mathbb{Z}\times\mathbb{Z}$ es numerable. Este último hecho puede ser generalizado, es decir, es posible demostrar que si $A$ y $B$ son conjuntos numerables, entonces, $A\times B$ es numerable. Tendrás oportunidad de demostrar esto en los ejercicios de esta sección. Una vez mencionado esto pasamos al siguiente ejemplo.

Ejemplo.

El conjunto de números racionales $\mathbb{Q}$ es numerable.

Demostración.

Puedes revisar la construcción del conjunto de los números racionales en el siguiente enlace: Álgebra Superior II: Esbozo de construcción de los números racionales y reales. Como podemos observar en dicho enlace, los números racionales se definen como el conjunto de clases de equivalencia de una relación de equivalencia, $\sim$, definida sobre el conjunto $\mathbb{Z}\times(\mathbb{Z}\setminus\{0\})$, y sus elementos son de la forma $\overline{(a,b)}$ con $a\in\mathbb{Z}$ y $b\in\mathbb{Z}\setminus\{0\}$. Tal relación se define como sigue: diremos que $(a,b)\sim(c,d)$ si y sólo si $a\cdot d=c\cdot b$, donde este último producto es el producto de los números enteros. Así, $\mathbb{Q}=\{\overline{(a,b)}:a\in\mathbb{Z},b\in\mathbb{Z}\setminus\{0\}\}$ donde $\overline{(a,b)}=\{(c,d)\in\mathbb{Z}\times(\mathbb{Z}\setminus\{0\}):(c,d)\sim(a,b)\}$. Observemos que $\mathbb{Q}$ no es finito, pues contiene al conjunto $\{\overline{(z,1)}:z\in\mathbb{Z}\}$, el cual es infinito.

Para mostrar que $\mathbb{Q}$ es numerable definamos $g:\mathbb{Z}\times(\mathbb{Z}\setminus\{0\})\to\mathbb{Q}$ por medio de $g(a,b)=\overline{(a,b)}$. La función $g$ es sobreyectiva. Luego, como $\mathbb{Z}\times(\mathbb{Z}\setminus\{0\})$ es numerable, existe una función biyectiva $h:\mathbb{N}\to\mathbb{Z}\times(\mathbb{Z}\setminus\{0\})$ y así $g\circ h:\mathbb{N}\to \mathbb{Q}$ es una función sobreyectiva y por tanto como $\mathbb{Q}$ no es finito debe ser numerable.

$\square$

Si bien hemos mostrado que $\mathbb{Q}$ es numerable, no tenemos aún una función biyectiva explícita de $\mathbb{N}$ en $\mathbb{Q}$. Lo que haremos para finalizar con esta entrada es intentar determinar una función biyectiva explícita entre $\mathbb{N}$ y $\mathbb{Q}$.

A continuación añadiremos un par de definiciones que involucran el concepto de multiplicación de naturales que vimos en la entrada Teoría de los Conjuntos I: Producto en los naturales.

Definición. Dados dos naturales $n$ y $m$, diremos que $m$ divide a $n$ si existe $k\in\mathbb{N}$ tal que $m\cdot k=n$ y lo denotaremos por $m\mid n$.

El algoritmo de la división en $\mathbb{Z}$, cuyo enunciado y demostración se puede consultar en el enlace: Álgebra Superior II: Algoritmo de la división en los enteros, nos permite concluir que, para cualesquiera naturales $n$ y $m$, con $m\not=0$, existen únicos naturales $q$ y $r$ tales que $n=mq+r$, con $0\leq r<m$. Este hecho será utilizado más adelante para probar la sobreyectividad de una función que va de $(\mathbb{N}\setminus\{0\})\times\mathbb{N}$ a un subconjunto de los números racionales.

Definición. Dados dos naturales $n$ y $m$, no ambos cero, diremos que el natural $d$ es máximo común divisor de $n$ y $m$ si se satisface lo siguiente:

  1. $d\mid n$ y $d\mid m$.
  2. si $d’$ es otro natural tal que $d’\mid n$ y $d’\mid m$, entonces, $d’\leq d$.

Para una prueba de que el máximo común divisor de dos naturales $n$ y $m$, no ambos cero, siempre existe y además es único, puede consultar el enlace Álgebra Superior II: Máximo común divisor. Debido a esto, es posible otorgar una notación al máximo común divisor de dos naturales $n$ y $m$; tal notación será la siguiente, si $d$ es el máximo común divisor de $n$ y $m$, escribiremos $d:=(n,m)$. Diremos además que $n,m\in\mathbb{N}$ son primos relativos si $(n,m)=1$.

Para finalizar con esta serie de definiciones y observaciones añadimos lo siguiente:

Notación. Dado un natural $n$ distinto de $0$, denotaremos por $E_n$ al conjunto $\{m\in\mathbb{N}:m\leq n\ y\ (m,n)=1\}$. Observemos que dicho conjunto es un subconjunto del número natural $s(n)=n+1$ y, por tanto, es finito, es decir, existe un único natural, que denotaremos por $\varphi(n)$, tal que $E_n\sim\varphi(n)$. Además, para cada $n\in\mathbb{N}$, con $n\not=0$, se tiene que $E_n\not=\emptyset$ pues $1\in E_n$, de modo que $\varphi(n)\not=0$.

Ahora bien, debido al buen orden de los números naturales, nos es posible dar una enumeración fija a cada conjunto $E_n$, es decir, podemos escribir $E_n=\{n_1,n_2,\ldots,n_{\varphi(n)}\}$ de tal forma que $n_1<n_2<\ldots<n_{\varphi(n)}$. No está de más recordar cómo se define el orden en $\mathbb{N}$, por lo que agregamos el siguiente enlace para que pueda ser consultado: Teoría de los Conjuntos I: Principio de inducción. Así, siempre que escribamos $E_n=\{n_1,n_2,\ldots,n_{\varphi(n)}\}$ supondremos que se cumple $n_1<n_2<\ldots<n_{\varphi(n)}$.

Una vez mencionado esto pasamos a dar otra prueba de que $\mathbb{Q}$ es numerable.

Ejemplo.

$\mathbb{Q}$ es numerable.

Por comodidad, en lo siguiente denotaremos al elemento $\overline{(a,b)}\in\mathbb{Q}$ simplemente como $\frac{a}{b}$.

Lo que haremos será exhibir una función biyectiva del conjunto $(\mathbb{N}\setminus\{0\})\times\mathbb{N}$ en el conjunto $\mathbb{Q}^{+}\cup\{\frac{0}{1}\}$, donde $\mathbb{Q}^{+}$ se puede describir como el conjunto $\mathbb{Q}^{+}=\{\frac{a}{b}:a,b\in\mathbb{Z}^{+}\}$. Si además abusamos de la notación escribiendo $0=\frac{0}{1}$ y $\mathbb{N}\setminus\{0\}=\mathbb{Z}^{+}$ (pues podemos identificar a los números naturales distintos de cero con los enteros positivos mediante la función biyectiva que envía el natural $n$ al entero $\overline{(n,0)}$), podemos escribir $\mathbb{Q}^{+}\cup\{\frac{0}{1}\}=\{\frac{a}{b}:a,b\in\mathbb{N}\setminus\{0\}\}\cup\{0\}$. Además, dado un natural $k\in\mathbb{N}\setminus\{0\}$ escribiremos $k-1$ para denotar al único natural que satisface $s(k-1)=k$.

En los ejercicios de esta sección probarás que para todo natural $n\in\mathbb{N}\setminus\{0,1\}$ existen únicos $k\in\mathbb{N}\setminus\{0,1\}$ e $i\in\{1,\ldots,\varphi(k)\}$ tales que $n=\sum_{t=1}^{k-1}\varphi(t)+i$. Una vez dicho esto definamos $F^{+}:(\mathbb{N}\setminus\set{0})\times\mathbb{N}\to\mathbb{Q}^{+}\cup\{0\}$ por medio de la siguiente regla:

$F^{+}(n,m)= \left\{ \begin{array}{lcc}
             0 &   si  & n=1,\ m=0 \\
\frac{1}{m} &  si & n=1,\ m\not=0 \\
\frac{k}{km+k_i} & si & n=\sum_{t=1}^{k-1}\varphi(t)+i
             \end{array}
   \right.$

donde en el último renglón, $k$ e $i$ son los únicos naturales que satisfacen la igualdad $n=\sum_{t=1}^{k-1}\varphi(t)+i$, con $i\in\{1,\ldots,\varphi(k)\}$, y $k_i$ es el $i-$ésimo elemento que aparece en la enumeración del conjunto $E_{k}=\{k_1,\ldots,k_i,\ldots,k_{\varphi(k)}\}$, enumeración que acordamos satisface $k_1<k_2<\ldots<k_{\varphi(k)}$.
Debido a la únicidad de los naturales $k$ e $i$ para cada $n\in\mathbb{N}\setminus\{0,1\}$, $F^{+}$ es una función bien definida. Veamos que es biyectiva.

Comprobaremos en primer lugar la inyectividad. Sean $(n,m),(n’,m’)\in(\mathbb{N}\setminus\{0\})\times\mathbb{N}$ elementos distintos. Distinguiremos los siguientes casos:

Caso 1. $n=n’$. Dado que $(n,m)\not=(n’,m’)$ pero $n=n’$, entonces, $m\not=m’$. Sin perder generalidad podemos suponer que $m<m’$. Ahora, podemos considerar los siguientes dos subcasos.
Subcaso 1. $n=1$. Si $m=0$, entonces, $0<m’$ y así $F^{+}(n,m)=0$ mientras que $F^{+}(n’,m’)=\frac{1}{m’}$, por lo que $F^{+}(n,m)\not=F^{+}(n’,m’)$. Si ahora $m\not=0$, entonces, $m’\not=0$ y tenemos que $F^{+}(n,m)=\frac{1}{m}$ y $F^{+}(n’,m’)=\frac{1}{m’}$; luego, $\frac{1}{m}\not=\frac{1}{m’}$, pues $m=1\cdot m\not=1\cdot m’=m’$, de modo que $F^{+}(n,m)\not=F^{+}(n’,m’)$.
Subcaso 2. $n>1$. Sean $k\in\mathbb{N}\setminus\{0,1\}$ e $i\in\{1,\ldots,\varphi(k)\}$ tales que $n’=n=\sum_{t=1}^{k-1}\varphi(t)+i$. Luego, $F^{+}(n,m)=\frac{k}{km+k_i}$ y $F^{+}(n’,m’)=\frac{k}{km’+k_i}$ y como $km’+k_i\not=km+k_i$, pues de lo contrario obtendríamos que $m=m’$, se sigue que $k\cdot(km’+k_i)\not=k\cdot(km+k_i)$, es decir, $F^{+}(n,m)=\frac{k}{km+k_i}\not=\frac{k}{km’+k_i}=F^{+}(n’,m’)$.

Caso 2. $n\not=n’$. Sin pérdida de generalidad podemos suponer $n<n’$. Si $n=1$, entonces, o bien $F^{+}(n,m)=0$ o bien $F^{+}(n,m)=\frac{1}{m}$; por otro lado, como $n’>n=1$, entonces podemos elegir $k\in\mathbb{N}\setminus\set{0,1}$ e $i\in\{1,\ldots,\varphi(k)\}$ tales que $n’=\sum_{t=1}^{k-1}\varphi(t)+i$ y así $F^{+}(n’,m’)=\frac{k}{km’+k_i}$. Luego entonces, $F^{+}(n,m)\not=F^{+}(n’,m’)$ ya que claramente $\frac{k}{km’+k_i}\not=0$, pero también $\frac{k}{km’+k_i}\not=\frac{1}{m}$ pues de darse la igualdad se tendría que $m\cdot k=1\cdot(km’+k_i)$, lo cual implicaría que $k$ divide a $k_i$ y eso es imposible, pues $k>1$ y $(k,k_i)=1$.
Si ahora $n>1$, podemos fijar $k’\in\mathbb{N}\setminus\{0,1\}$ y $j\in\{1,\ldots,\varphi(k’)\}$ tales que $n=\sum_{t=1}^{k’-1}\varphi(t)+j$. Luego, suponiendo también, como en el párrafo anterior, $n’=\sum_{t=1}^{k-1}\varphi(t)+i$, tenemos que $F^{+}(n,m)=\frac{k’}{k’m+k’_j}$ y $F^{+}(n’,m’)=\frac{k}{km’+k_i}$. Si $k=k’$, entonces, $j<i$, pues de lo contrario tendríamos que $\sum_{t=1}^{k-1}\varphi(t)+i=n’\leq\sum_{t=1}^{k-1}\varphi(t)+j=\sum_{t=1}^{k’-1}\varphi(t)+j=n$, lo cual es una contradicción; en consecuencia, $k’_j=k_j<k_i$ y, más aún, $\frac{k’}{k’m+k’_j}=\frac{k}{km+k_j}\not=\frac{k}{km’+k_i}$, pues en caso contrario se seguiría que $k\cdot(km’+k_i)=k\cdot(km+k_j)$ y, por tanto, que $km’+k_i=km+k_j$ lo cual es imposible pues se seguiría que, en $\mathbb{Z}$, $k$ divide a $k_i-k_j$ el cual es un entero que satisface $0<k_i-k_j<k$.
Para concluir el caso $2$ supongamos que $k\not=k’$. Dado que $(k’,k’m+k’_j)=1=(k,km’+k_i)$, pues de lo contrario $k’$ no sería primo relativo con $k’_j$ así como $k$ no lo sería con $k_i$, entonces, $\frac{k’}{k’m+k’_j}\not=\frac{k}{km’+k_i}$, es decir, $F^{+}(n,m)\not=F^{+}(n’,m’)$. Esto demuestra que $F^{+}$ es una función inyectiva.

Probemos ahora que $F^{+}$ es sobreyectiva. Sea $\frac{p}{q}\in\mathbb{Q}^{+}\cup\{0\}$. Si $\frac{p}{q}=0$, entonces, $\frac{p}{q}=F^{+}(1,0)$. Si $\frac{p}{q}=\frac{1}{m}$, entonces, $\frac{p}{q}=F^{+}(1,m)$. Supongamos ahora que $\frac{p}{q}\not=0$ y que $\frac{p}{q}\not=\frac{1}{m}$ para cada $m\in\mathbb{N}\setminus\set{0}$. Podemos suponer que $(p,q)=1$. Luego, existen únicos naturales $m$ y $r$ tales que $q=pm+r$ con $0\leq r<p$. Nótese que $r\not=0$, pues en caso contrario se tendría que $p$ divide a $q$, pero como $(p,q)=1$ se seguiría que $p=1$, lo cual contradice que $\frac{p}{q}\not=\frac{1}{m}$ para cada $m\in\mathbb{N}\setminus\set{0}$. Así pues, $1\leq r<p$. Ahora bien, $(r,p)=1$, pues de lo contrario, $p$ y $q=pm+r$ compartirían un factor distinto de $1$; es decir, existiría un natural $k$ mayor a $1$ tal que $k$ divide a $p$ y $q$, lo cual contradice que $(p,q)=1$. Por tanto, $(r,p)=1$ y, en consecuencia, $r\in E_p=\{p_1,\ldots,p_{\varphi(p)}\}$. Sea $i\in\{1,\ldots,\varphi(p)\}$ tal que $r=p_i$. Luego, $F^{+}(\sum_{t=1}^{p-1}\varphi(t)+i,m)=\frac{p}{pm+p_i}=\frac{p}{pm+r}=\frac{p}{q}$. Por tanto, $F^{+}$ es sobreyectiva.

Lo anterior prueba que $F^{+}$ es una biyección de $(\mathbb{N}\setminus\{0\})\times\mathbb{N}$ en $\mathbb{Q}^{+}\cup\{0\}$. Luego, como la función $f:\mathbb{N}\times\mathbb{N}\to(\mathbb{N}\setminus\set{0})\times\mathbb{N}$ definida por medio de $f(n,m)=(s(n),m)$ es una biyección entre estos conjuntos, y existe $g:\mathbb{N}\to\mathbb{N}\times\mathbb{N}$ función biyectiva (como lo comprobarás en los ejercicios de esta sección), concluimos que $F^{+}\circ f\circ g:\mathbb{N}\to\mathbb{Q}^{+}\cup\{0\}$ es una biyección de $\mathbb{N}$ en $\mathbb{Q}^{+}$. Finalmente, como $\mathbb{Q}=\mathbb{Q}^{+}\cup\set{0}\cup\mathbb{Q}^{-}$, donde $\mathbb{Q}^{-}$ puede ser descrito por el conjunto $\{\frac{a}{b}:a\in\mathbb{Z}^{-},b\in\mathbb{Z}^{+}\}$, y $\mathbb{Q}^{-}$ es equipotente a $\mathbb{Q}^{+}$, entonces, $\mathbb{Q}$ es la unión ajena de dos conjuntos numerables; luego, como probarás en los ejercicios de esta entrada, se sigue que $\mathbb{Q}$ es numerable. Por tanto, $\mathbb{N}$ es equipotente a $\mathbb{Q}$.

$\square$

Aún cuando la función biyectiva que dimos en el último ejemplo no posee una regla de correspondencia agradable, sí es explícita, aunque resulte todavía complicado en la práctica calcular la imagen de la mayoría de los números naturales bajo dicha función.

Tarea moral

La siguiente lista de ejercicios te permitirá reforzar el contenido visto en esta entrada.

  1. Si un conjunto $A$ es numerable y $x\in A$ es un elemento arbitrario, ¿será cierto que $A\setminus\set{x}$ es también numerable?
  2. Sea $\mathbb{N}_0:=\mathbb{N}\setminus\set{0}$. Muestra que $f:\mathbb{N}\times\mathbb{N}\to\mathbb{N}_0$ dada por $f(n,m)=2^n(2m+1)$ es una función biyectiva.
  3. Utilizando el ejercicio anterior, muestra que si $A$ y $B$ son conjuntos numerables, entonces $A\times B$ también es numerable.
  4. Sean $A$ y $B$ conjuntos ajenos y numerables. Muestra que $A\cup B$ es numerable . ¿Y si los conjuntos $A$ y $B$ no son ajenos?
  5. Demuestra que para cada $n\in\mathbb{N}\setminus\set{0,1}$, existen únicos $k\in\mathbb{N}\setminus\{0,1\}$ e $i\in\{1,\ldots,\varphi(k)\}$ tales que $n=\sum_{t=1}^{k-1}\varphi(t)+i$.

Más adelante…

En la siguiente entrada continuaremos el contenido acerca de conjuntos numerables.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Cálculo Diferencial e Integral I: Conjuntos infinitos (Adicional)

Por Karen González Cárdenas

Deja un comentario

Introducción

En esta última entrada de la unidad veremos un poco sobre la cardinalidad de un conjunto, un par de definiciones para decir cuando un conjunto es infinito o finito y algunos teoremas útiles. Dado que se trata de un tema adicional varios de los teoremas y resultados sólo serán enunciados.

Cardinalidad de un conjunto

Definición (Cardinalidad): Sea $A$ un conjunto. Definimos a la cardinalidad de $|A|$ como una medida que indica el número de elementos en dicho conjunto $A$ y la denotaremos como:
$$|A|.$$

Ejemplo: Sea $A= \left\{ 1,2,3,g,y,b \right\}$ así tenemos que su cardinalidad sería:
$$|A|=6.$$

Definición: Decimos que $|A| \leq |B|$ si existe una función $f: A \rightarrow B$ inyectiva.

Misma cardinalidad

Definición: Sean $A,B$ conjuntos. Decimos que $A$ y $B$ tienen la misma cardinalidad $$|A|=|B|,$$ si existe una función $f: A \leftrightarrow B$ biyectiva.

Para los fines de esta entrada, daremos la definición de función biyectiva. Revisaremos esta definición con mayor detenimiento en la unidad 3, dedicada a las funciones, como parte de este curso.

Definición: Sea $f: A \rightarrow B$ una función. Decimos que $f$ es biyectiva si cumple con ser inyectiva y sobreyectiva.

Ejemplo: Si consideramos los intervalos $[0,1]$ y $(0,1)$. Vemos que:
$$|[0,1]| = |(0,1)|.$$
Primero tomamos los valores $0$ y $1$ en el intervalo $[0,1]$ y los enviamos a los valores $\frac{1}{3}$ y $\frac{1}{2}$ respectivamente en el intervalo $(0,1)$.

Ahora consideramos los valores de la forma $\frac{1}{n}$ con $n \in \mathbb{N}\setminus \left\{0\right\}$ y $n \geq 2$. A estos valores los enviaremos a los de la forma $\frac{1}{n+2}$. De este modo lo que haremos será enviarlos al $(0,1)$ como en el ejemplo de la siguiente imagen:

Y por último, a los valores restantes los enviamos a ellos mismos en el intervalo $(0,1)$.

Así la función biyectiva sería $f: [0,1] \leftrightarrow (0,1)$:
\begin{equation*}
f(x)=
\begin{cases}
x &\text{si $x \neq 0,1,\frac{1}{n}$ con $n\geq 2$}\\
\frac{1}{2} & \text{si $x= 1$}\\
\frac{1}{3} &\text{si $x=0$}\\
\frac{1}{x+2} &\text{si $x = \frac{1}{n}$ con $n\geq 2$}\\
\end{cases}
\end{equation*}

Conjuntos finitos e infinitos

Definición (1): Sea $A$ un conjunto.

  • $A$ es finito si existe una función biyectiva $f: A \leftrightarrow \left\{1,2, \cdots , N \right\}$ para algún $N \in \mathbb{N}\setminus \left\{0\right\}$.
  • $A$ es infinito si no es finito.

Definición (2): Sea $A$ un conjunto.

  • $A$ es infinito si existe $A’ \subset A$ subconjunto propio de A y una función biyectiva $f: A’ \leftrightarrow A$.
  • $A$ es finito si no es infinito.

Teorema: Sean $A,B$ conjuntos no vacíos. Si $A \subseteq B$ entonces
$$|A| \leq |B|.$$
Demostración: Proponemos a la función $f: A \rightarrow B$ como $f(x)=x$. Observamos que $f$ es inyectiva y cumple que para todo $x \in A$ se sigue que $x \in B$. Por definición se sigue que $|A| \leq |B|.$

$\square$

Observación: Si $A,B$ son conjuntos infinitos puede ocurrir que $A \subset B$ y que $|A|=|B|.$

Teorema: Sean $A,B$ conjuntos finitos.

  • Si $A \cap B = \emptyset$ entonces:
    $|A \cup B|= |A|+|B|.$
  • Si $A \cap B \neq \emptyset$ entonces:
    $|A \cup B|= |A|+|B|-|A \cap B|.$

Definición (3): Un conjunto $A$ es infinito si existe $B \subseteq A$ tal que
$$|B|=|\mathbb{N}|.$$

Conjuntos numerables

Definición: Sea $A$ un conjunto no vacío. Decimos que $A$ es numerable si $|A|=|\mathbb{N}|$ es decir si existe una función biyectiva:
$$f: A \rightarrow \mathbb{N}.$$

Teorema: Sean $A,B$ conjuntos. Si $A$ es finito y $B$ es infinito numerable entonces $A \cup B$ es numerable.
Demostración: Como $A$ es finito consideremos que tiene $m$ elementos.
$$A = \left\{ a_{1}, a_{2}, \cdots , a_{m} \right\}.$$
Y como $B$ es infinito y numerable entonces es de la forma:
$$B = \left\{ b_{1}, b_{2}, \cdots , b_{n}, \cdots \right\}.$$
Así al considerar la unión $A \cup B$ tendríamos:
$$A \cup B = \left\{ a_{1}, a_{2}, \cdots , a_{m}, b_{1}, b_{2}, \cdots , b_{n}, \cdots \right\}.$$
Tenemos los siguientes dos casos:

  • Si $A\cap B = \emptyset$ y consideramos la siguiente indización:
    $$A \cup B = \left\{ a_{1}, a_{2}, \cdots , a_{m}, b_{m+1}, b_{m+2}, \cdots , b_{m+n}, b_{m+n+1}, \cdots \right\}.$$
    Vemos $|A \cup B|=|\mathbb{N}|.$
  • Si $A\cap B \neq \emptyset$. Supongamos que tenemos $k$ elementos en la intersección, es decir:
    $$a_{1}= b_{1}, a_{2}= b_{2}, \cdots , a_{k}= b_{k}$$
    $$A = \left\{ a_{1}, a_{2}, \cdots ,a_{k}, a_{k+1}, \cdots, a_{m} \right\}.$$
    Así consideramos la siguiente indización para la unión:
    $$A \cup B = \left\{ a_{k+1}, a_{k+2}, \cdots , a_{m}, b_{1}, b_{2}, \cdots , b_{n}, \cdots \right\}.$$
    Observamos que $|A \cup B|=|\mathbb{N}|.$

$\square$

Teorema: Si $A$ y $B$ son conjuntos infinitos y numerables entonces $A \cup B$ es infinito y numerable.
Demostración: Primero vemos que $A \cup B$ es infinito ya que al ocurrir que:

  • $A \subseteq A \cup B$ con $A$ infinito y numerable.
  • $B \subseteq A \cup B$ con $B$ infinito y numerable.

por definición (3) concluimos que $A \cup B$ es infinito.

Nos falta ver qué $A \cup B$ es numerable, ya que $A$ es numerable podemos escribirlo de la siguiente manera:
$$A = \left\{ a_{1}, a_{2}, \cdots \right\}.$$
Análogamente para $B$:
$$B = \left\{ b_{1}, b_{2}, \cdots \right\},$$
por lo que la unión se vería como:
$$A \cup B= \left\{ a_{1}, b_{1},a_{2}, b_{2},a_{3},b_{3} \cdots, a_{n}, b_{n}, \cdots \right\}.$$
Observemos que si consideramos la siguiente indización:
$$A \cup B= \left\{ a_{1}, b_{2},a_{3}, b_{4},a_{5},b_{6} \cdots, a_{2n-1}, b_{2n}, \cdots \right\},$$

el conjunto tiene una relación biunívoca con el conjunto de los naturales.
Veamos qué sucede en los siguientes casos:

  • Si $A \cap B = \emptyset \Rightarrow |A \cup B|=|\mathbb{N}|.$
  • Si $A \cap B \neq \emptyset$. Consideremos que existen k elementos en la intersección, por lo que serían de la forma:
    $$a_{1}= b_{1}, a_{2}= b_{2}, \cdots , a_{k}= b_{k}.$$
    Por lo que ahora la unión se vería como:
    $$A \cup B= \left\{ a_{1}, a_{2}, a_{3}, \cdots,a_{k}, a_{k+1}, b_{k+1},a_{k+2}, b_{k+2} \cdots, a_{k+n}, b_{k+n}, \cdots \right\}$$
    y si consideramos la siguiente nueva indización:
    $$A \cup B= \left\{ a_{1}, a_{2}, a_{3}, \cdots,a_{k}, a_{k+1}, b_{k+2},a_{k+3}, b_{k+4} \cdots, a_{k+(2n-1)}, b_{k+2n}, \cdots \right\},$$
    tenemos que tiene una relación biunívoca con $\mathbb{N}$ por lo que también se cumple que $|A \cup B|=|\mathbb{N}|$.

$\square$

A continuación enunciaremos un teorema que generaliza el resultado sobre conjuntos numerables ya visto.

Teorema: Sean $A_{1}, A_{2}, \cdots, A_{N}, \cdots $ conjuntos no vacíos.

  • Si $A_{1}, A_{2}, \cdots, A_{N}$ son numerables $\Rightarrow \begin{multline*} \bigcup_{i=1}^{N} A_{i} \end{multline*}$ es numerable.
  • Si $A_{1}, A_{2}, \cdots$ son numerables $\Rightarrow \begin{multline*} \bigcup_{i=1}^{\infty} A_{i} \end{multline*}$ es numerable.

Más adelante

Ahora que hemos concluido con la unidad relacionada a los Números reales, en la próxima iniciaremos el tema de funciones definiendo qué es el dominio, rango y regla de correspondencia de una función.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»