Introducción

En esta entrada hablaremos acerca del principio de inducción. Será de gran importancia pues una vez que lo demostremos, se podrá utilizar como método de demostración para proposiciones cuyo enunciado depende de un número natural. En otras palabras, el principio de inducción nos ayudará a demostrar que ciertas proposiciones o propiedades se cumplen para cualquier natural $n$.

Principio de inducción¹

El principio de inducción dice lo siguiente.

Teorema. Sea $P(n)$ una proposición (como las que se vieron en la primera unidad) que depende de un número natural $n$. Supongamos que las siguientes dos cosas son ciertas.

1. $P(0)$ se cumple.
2. Para cualquier $n\in \mathbb{N}$, si $P(n)$ es verdadero, entonces $P(s(n))$ también es verdadero.

Entonces, $\set{n\in \mathbb{N}:P(n)}=\mathbb{N}$, es decir, la proposición es cierta para cualquier número natural $n$.

Demostración.

Tomemos $P(n)$ una propiedad. Si se cumplen 1) y 2), entonces

$A=\set{n\in \mathbb{N}: P(n)}$

es un conjunto inductivo.

En la entrada anterior probamos que cualquier conjunto inductivo contiene a los naturales. Así, $\mathbb{N}\subseteq A$.

Además, $A\subseteq \mathbb{N}$ pues para cualquier $n\in A$, $n\in \mathbb{N}$ y por lo tanto, $A=\mathbb{N}$.

$\square$

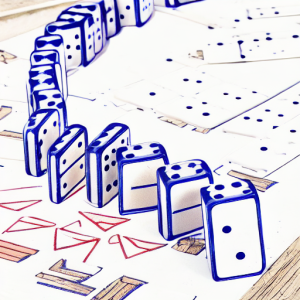
Para entender este teorema, podemos imaginar una fila con tantas fichas de dominó como números naturales, como en la imagen. Hay una primera ficha. Para cualquier ficha hay una siguiente. ¿Qué necesitamos para garantizar que se caigan todas las fichas mediante el «efecto dominó»?

Podemos interpretar al teorema como sigue. Tomemos informalmente la proposición $P(n):$»el dominó $n$ cae». Lo que nos diría el punto 1) del principio de inducción es que la ficha correspondiente a cero. Lo que nos diría el punto 2) del principio de inducción es que tenemos la garantía de que para cualquier natural $n$ «si el dominó $n$ se cae, entonces el dominó $n+1$ también», por ejemplo, porque el dominó $n$ y $n+1$ están suficientemente cerca como para que el dominó $n$ empuje al $n+1$ al caer. Lo que garantizaría el principio de inducción es que todas las fichas caerán.

Orden de los naturales

A continuación definiremos una relación en el conjunto de números naturales, la cual resultará ser una relación de orden, pero esto último lo probaremos en la próxima entrada.

Definición. Sean $n,m\in \mathbb{N}$. Decimos que $n\leq m$ si y sólo si $n\in m$ o $n=m$.

Ejemplos.

• $0=\emptyset$ y $1=\set{\emptyset}$ son números naturales. Luego, $0\leq 1$ pues $\emptyset\in \set{\emptyset}$.
• $0=\emptyset$ y $2=\set{\emptyset, \set{\emptyset}}$ son números naturales. Luego, $0\leq 2$ pues $\emptyset\in \set{\emptyset, \set{\emptyset}}$.
• $1=\set{\emptyset}$ y $2=\set{\emptyset, \set{\emptyset}}$ son números naturales. Luego, $1\leq 2$ pues $\set{\emptyset}\in \set{\emptyset, \set{\emptyset}}$.

$\square$

A continuación veremos un ejercicio en el que usaremos la relación que definimos arriba y el principio de inducción.

Proposición. $0\leq m$ para cualquier $m\in \mathbb{N}$.

Demostración.

Debemos probar que $\set{m\in \mathbb{N}: 0\leq m}=\mathbb{N}$. Procederemos usando el principio de inducción.

• $0\leq 0$ pues $0=0$.
• Ahora, si $0\leq m$ para algún $m\in \mathbb{N}$, veamos que $0\leq s(m)$. Dado que $0\leq m$, $0=m$ ó $0\in m$. Consecuentemente, $0\in s(m)$, es decir, $0\leq s(m)$.

Por lo tanto, $\set{m\in\mathbb{N}:0\leq m}=\mathbb{N}$.

$\square$

Tarea moral

1. Demuestra que la relación $\leq$ que definimos en esta entrada es un orden parcial.
2. Demuestra que cualesquiera naturales $n$ y $m$ son $\leq$-comparables, aplicando inducción sobre $n$. ¿Puedes dar una demostración alternativa que use un resultado de la entrada?
3. Demuestra que para todo natural $n\not=0$, existe un natural $k$ tal que $n=s(k)$.
4. Demuestra que para cualquier $n\in \mathbb{N}\setminus \set{0,1}$, existe $k\in \mathbb{N}$ tal que $n=s(s(k))$.
5. Muestra que $\mathbb{N}$ no tiene máximo con el orden $\leq$ que hemos definido.

Más adelante…

En la siguiente entrada probaremos que el conjunto de los naturales con el orden que hemos definido en esta entrada es un buen orden.

Entradas relacionadas

• Entrada relacionada: Álgebra Superior II: Principio de inducción y teoremas de recursión
• Ir a Teoría de los Conjuntos I
• Entrada anterior: Teoría de los Conjuntos I: Conjuntos inductivos y axioma del infinito
• Siguiente entrada: Teoría de los Conjuntos I: Buen orden en los naturales

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

1. Puedes consultar más contenido acerca del principio de inducción en el siguiente libro: Hrbacek, Karel y Jech, Thomas, Introduction to Set Theory, Marcel Dekker Inc. 1984, p. 42-44. ↩︎