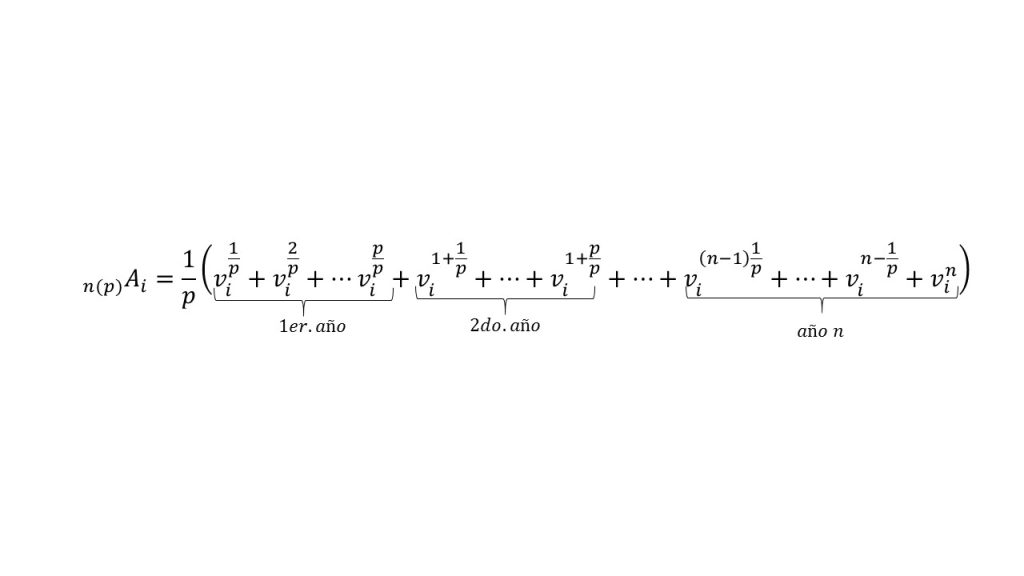
Matemáticas Financieras: Anualidades continuas

Por Erick de la Rosa

Introducción

En el tema anterior, se logró obtener las herramientas necesarias para estar en condiciones, de poder evaluar un proyecto de inversión. Para poder estudiar este tipo de anualidades, se hará uso de algunas herramientas de cálculo diferencial e integral, ya que se pretende abordar dicho tema, desde un enfoque infinitesimal con la finalidad de poder calcular las tasas instantáneas de interés (fuerza de interés).

Descripción y valor presente

Este tipo de anualidades, sólo se usan para mostrar el comportamiento de un crédito en cada instante, ya que como se ha mostrado en las anualidades que hasta este momento se han estudiado, mantiene tiene su relación con el concepto de amortización el cual va ligado con cierta periodicidad. Cabe hacer mención que, como su nombre lo indica, este tipo de anualidad se caracteriza por realizar los pagos a cada «instante», motivo por el cual este tipo de anualidad no tienen aplicación en la vida real.

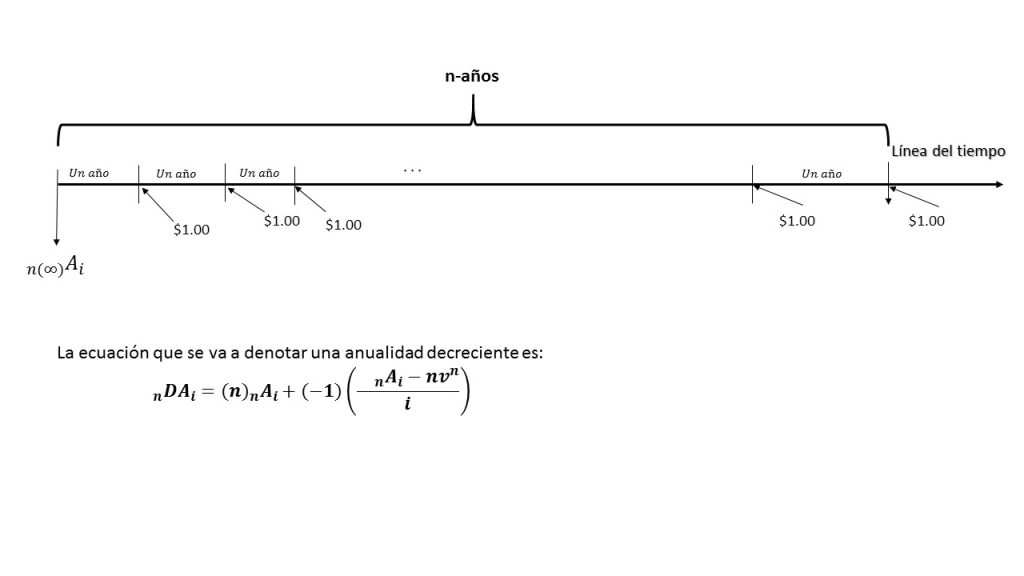
Elaboración propia, basado en Matemáticas Financieras, fundamentos y aplicaciones, Cánovas T., Ed. Trillas, pag. 180.

En la imagen anterior, se muestra gráficamente el comportamiento que tiene una anualidad continua, en la que se observa los pagos que la caracterizan, ya que por ser una línea recta, ésta cuenta con una infinidad de puntos, que a su vez representan un número infinito de pagos que serán efectuados cuando haya transcurrido un cierto lapso de tiempo. De cierta forma, éste tipo de anualidad tiene similitud con el tema anterior (anualidades pagaderas p veces al año), ya que ésta se calcularía igual, con la diferencia que sería pagadera un número infinito de veces al año. Bajo ésta idea, es como se va a desarrollar el modelo para representar una anualidad continua.

El valor presente de ésta anualidad queda denotado por la siguiente expresión:

$$\prescript{}{n(\infty)}{\mathbf{A}}_i=\int_0^n v^t dt.$$

Ahora si multiplicamos por un uno especial, es decir, multiplicamos por:

$$\prescript{}{n(\infty)}{\mathbf{A}}_i=\int_0^n \frac{ln v}{ln v} v^t dt=\frac{1}{ln v}\int_0^n (ln v) (v^t) dt.$$

Recordemos que: $$d ln U=\frac{dU}{U}$$

luego: $$\int_0^n d ln U U=\int_0^n dU=U|_0^n.$$

Entonces, la ecuación en la que se estaba trabajando antes del recordatorio queda de la siguiente forma:

$$\prescript{}{n(\infty)}{\mathbf{A}}_i=\frac{1}{ln v}v^t\Big\rvert_0^n=\frac{1}{ln v}(v^n-v^0)=\frac{v^n-1}{ln v}.$$

Haciendo otro recordatorio; a partir de la triple igualdad se tiene $v^t=e^{-\delta t}$, despejando a $\delta$ para obtener $ln v=-\delta$. Luego sustituyendo éste valor en la ecuación y multiplicando por menos uno nos queda la ecuación que se venía trabajando en:

$$\prescript{}{n(\infty)}{\mathbf{A}}_i=\frac{1-v^n}{\delta}$$

ahora multiplicando $i$ ésta ecuación, se tiene:

$$\prescript{}{n(\infty)}{\mathbf{A}}_i=\frac{i}{i}\frac{1-v^n}{\delta}=\frac{i}{\delta}\frac{1-v^n}{i}.$$

Por otra parte, es necesario recordar: $$\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$$

entonces: $$\prescript{}{n(\infty)}{\mathbf{A}}_i=\frac{i}{\delta}\prescript{}{n}{\mathbf{A}}_i.$$

De ésta ecuación, se va a calcular el valor presente para una anualidad continua a $n$ año, con un capital de un peso pagadero anualmente un número infinito de veces. Una observación que es importante resaltar, es que tiene mucha similitud con la anualidad pagadera $p$ veces al año, con una tasa de interés efectiva anual:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{i}{i^{(p)}}\prescript{}{n}{\mathbf{A}}_i.$$

Esta ocurre, porque el valor de una tasa nominal tiende a $\delta$ cuando $m$ tiende a $\infty$, ahora, si la anualidad cambiamos el capital de un peso por un capital con valor $X$, entonces la expresión para obtener el valor presente queda expresada como:

$$V=X\prescript{}{n(\infty)}{\mathbf{A}}_i=\frac{Xi}{\delta}\prescript{}{n}{\mathbf{A}}_i.$$

Monto

Para calcular el monto de una anualidad continua, se seguirá calculando en primera instancia con un peso como capital, a fin de simplificar los cálculos.

Partiendo de la siguiente ecuación:

$$\prescript{}{n(\infty)}{\mathbf{A}}_i=\frac{i}{\delta}\prescript{}{n}{\mathbf{A}}_i.$$

Se tiene que el monto de una anualidad continua, con un capital de un peso anual convertible infinitamente al año, durante $n$ años, a una tasa efectiva anual, queda denotado por la expresión:

$$\prescript{}{n(\infty)}{\mathbf{S}}_i=\frac{i}{\delta}\prescript{}{n}{\mathbf{A}}_i(1+i)^n.$$

Cambiando dicha expresión, obtenido con un peso, a un capital $X$, la expresión queda como sigue:

$$M=X\prescript{}{n(\infty)}{\mathbf{S}}_i=\frac{Xi}{\delta}\prescript{}{n}{\mathbf{A}}_i(1+i)^n.$$

Aunque las anualidades continuas, no tienen aplicación o uso en la vida real, es importante señalar que; en la anualidad continúa el pago se hace un número infinito de veces, esto no quiere decir que el monto acumulado después de un tiempo será infinito, porque el pago anual se va a dividir entre infinito para poder obtener dichos pagos, luego entonces, una cualquier cantidad dividida, entre infinito, el resultado es una cantidad que prácticamente sea cero. Por ésa razón este tipo de anualidad será omitido el calificativo de pagadera un número infinito de veces al año, ya que no es posible calcular dichos pagos, sólo se puede calcular las anualidades con capital de un peso o capital $X$, así como sólo se puede calcular su monto y su valor presente.

Ejercicios resueltos

Ejercicio. Calcular el valor presente de la siguiente anualidad continua a 5 años, de un peso, con una tasa de interés del 5% anual.

Solución

Para resolver éste ejercicio se necesitará la siguiente ecuación:

$$\prescript{}{n(\infty)}{\mathbf{A}}_i=\frac{i}{\delta}\prescript{}{n}{\mathbf{A}}_i$$

Primero recordemos que:

$\delta$ se obtiene de la expresión $e^{\delta}=ln(1+i)$, por lo que al aplicar logaritmo se tiene: $\delta=ln (1+i)$
$$V=\frac{1}{(1+i)^n}$$
$$\prescript{}{n}{\mathbf{A}}_i=\left(\frac{1-V_i^n}{i}\right)$$

Luego entonces:

$$V=\frac{0.05}{ln(1+.05)}\prescript{}{5}{\mathbf{A}}_{0.05}$$

$$=\frac{0.05}{0.0487902}\left(\frac{1-V_{0.05}^5}{0.05}\right)=(1.024796)(4.3294767)=4.4368304$$

Ejercicio. Calcule el monto de una anualidad continua a 5 años, con un capital de \$3 mil pesos, con una tasa del 4% anual

Solución

Para resolverlo, se utilizará la siguiente ecuación:

$$M=X\prescript{}{n(\infty)}{\mathbf{S}}_i=\frac{Xi}{\delta}\prescript{}{n}{\mathbf{A}}_i(1+i)^n$$

$$=3,000\prescript{}{5}{\mathbf{S}}_{0.04}=\frac{3,000(0.04)}{0.0392207}\prescript{}{5}{\mathbf{A}}_{0.04}(1+0.04)^5$$

$$=(3059.608829)(4.4518223)(1.2166529)=16,571.82821$$

Más adelante…

Hasta este momento, ya se cuenta con herramientas suficiente para poder hacer operaciones más complejas, como lo es evaluar un proyecto de inversión, tema que será estudiado un poco más adelante, antes se abordaran algunos temas como el de amortización que nos permitirá facilitar ciertas operaciones que son muy útiles en la práctica.

Ir a Matemáticas Financieras
Entrada anterior
Entrada siguiente

Estadística No Paramétrica: Pruebas para proporciones

Por Alondra Sierra

Deja un comentario

Introducción

Las pruebas binomiales se caracterizan porque la distribución de la estadística de prueba tiene una distribución binomial, de la cual solo se conoce el tener “éxito” o “fracaso” en cada observación.

En esta unidad veremos distintos tipos de pruebas binomiales, así como sus aplicaciones con diferentes ejercicios. Comenzaremos en esta entrada hablando de pruebas para proporciones.

1.1 Pruebas para proporciones

Usaremos la prueba de proporciones cuando, dada una población, nos interese conocer la proporción de elementos de la población que posee cierta característica, o bien, evaluar las afirmaciones con respecto a una proporción de la población.

Partimos de una muestra aleatoria $X_1,X_2, …, X_n$ la cual clasificaremos en dos categorías, $C_1$ y $C_2$. La observación $X_i$ podría estar en $C_1$ o en $C_2$.

El número de observaciones en $C_1$ es denotado como $O_1$, mientras que para $C_2$ es $n-O_1$.

La hipótesis nula siempre será:

$H_0: p=p^*$

(En donde, $p^*$ de población es igual a alguna proporción de población $p^*$)

La hipótesis alternativa toma alguna de las siguientes formas dependiendo del problema en cuestión:

A. $H_1: p≠p^* $ (Prueba de dos colas)

B. $H_1: p < p^*$ (Prueba de cola inferior o derecha)

C. $H_1: p > p^*$ (Prueba de cola superior o izquierda)

De acuerdo a la metodología usada en (Conover, 1999), para el caso A, la región de rechazo es de tamaño $\alpha$ y corresponde a la suma de las dos colas de la distribución nula del estadístico $T$; $\alpha_1$ (cola inferior) y $\alpha_2$ (cola superior).

El estadístico de prueba $T$ será la proporción de la población que se estará evaluando, en donde, su distribución nula es la distribución binomial con parámetros $p = p^*$ la probabilidad especificada en la hipótesis nula y $n$ el tamaño de la muestra.

$T =$ Número de observaciones en $C_1$

Cuando $n \leq 20$ utilizamos el estadístico:

$T \sim Bin(n,p^*)$

donde $T$ se obtiene de la Tabla de Distribución Binomial (A1).

Cuando $n > 20$ utilizamos la aproximación normal y en este caso se utilizan los cuantiles aproximados $X_q$ para obtener el estadístico $T$.

$X_q = np + Z_q \sqrt{np(1 – p)}$

donde $Z_q$ se obtiene de la Tabla de Distribución Normal (A2).

Buscamos los cuantiles $t_1$ y $t_2$ como:

$P[Y \leq t_1] = \alpha_1$

$P[Y \leq t_2] = 1 – \alpha_2$ ó $P[Y> t_2] = \alpha_2$

$Y \sim Bin(n, p^*)$ ó $ Y \sim X_q $

según sea el caso.

Si $T \sim X_q $, aproximamos:

$t_1$, el cuantil $q_1 = \frac{⍺}{2}$
$t_2$, el cuantil $ q_2 = 1- \frac{⍺}{2}$

Rechazamos $H_0$ sí:

$T \leq t_1$ o $T> t_2$

Al tener un valor de $T$ mayor o menor que estos cuantiles, los valores se encuentran alejados por la derecha e izquierda de la media, y por lo tanto están dentro de la región de rechazo. Por este motivo no aceptaríamos la hipótesis nula.

Para calcular el $p-value$ usamos la siguiente fórmula:

$p-value = 2 * min\{ P [ Y \leq T ], P [Y \geq T] \}$,

Si $n\leq20$ buscamos $T$ en la tabla A1

En otro caso, el $p-value$ puede obtenerse como:

$P[Y\leq t] \cong P(Z \leq \frac{t -np^* + 0.5}{\sqrt{np^*(1-p^*)}})$

y $P[Y\geq t]\cong 1-P(Z \leq\frac{t -np^* – 0.5}{\sqrt{np^*(1-p^*)}})$

donde $t$ se encuentra en la tabla A2, siendo $t$ el valor observado de $T$.

En ambos casos, si el $p-value \leq \alpha$, rechazamos la hipótesis nula con un nivel de significancia $\alpha$.

Para el caso de la cola inferior y superior, se utiliza el mismo procedimiento correspondientemente.

Ejemplos

Veamos algunos ejemplos de cómo se utiliza la prueba anterior.

Problema 1. De acuerdo a la base de datos del Sector Salud, se cree que 30% de pacientes adultos mayores ya tienen aplicada la 4ta dosis de vacunación contra COVID. El mismo Sector Salud decide investigar a sus pacientes y preguntar sobre la aplicación de la vacuna. Se seleccionan aleatoriamente a 1400 pacientes adultos mayores, de los cuales 360 confirmaron haberse aplicado la dosis. Prueba usando $\alpha = 0.05$

Solución.

PRUEBA DE DOS COLAS

HIPÓTESIS:

$H_0: p = 30$%

v.s.

$H_1:p \neq 30$%

ESTADÍSTICO DE PRUEBA:

Corresponde a las 360 personas que confirmaron haberse aplicado la dosis.

$T = 360$

como el tamaño de muestra $n > 20 $

$T \sim X_q $

CUANTILES:

Buscamos $t_1$ y $t_2$ tal que:

$P[Y \leq t_1] = P[Y \leq t_\alpha] = \alpha_1$

$P[Y \geq t_2] = P[Y \geq t_1-\frac{\alpha}{2}] = \alpha_2$

con $\alpha = 0.05$ buscamos $\frac{\alpha}{2}$ y $1-\frac{\alpha}{2}$ en T2

$\frac{\alpha}{2} = \frac{0.05}{2} = 0.025 \Rightarrow z =-1.96$

$1-\frac{\alpha}{2} = 1 – \frac{0.05}{2} = 0.975 \Rightarrow z =1.96$

Sustituyendo en $X_q$ para cada cuantil tenemos :

$t_1 = (1400)(0.3) -1.96 \sqrt{(1400)(0.3)(1 – 0.3)} = 386.39$

$t_2 = (1400)(0.3) +1.96 \sqrt{(1400)(0.3)(1 – 0.3)} = 453.60$

$\therefore t_1 = 386$ y $t_2 = 453$

REGIÓN DE RECHAZO:

Rechazamos $H_0$ sí $T\leq t_1$ ó $T > t_2$

$T =360 \leq t_1 =386$ ó $T =360 \ngtr t_2= 454$

como se cumple la primera condición, $T\leq t_1$ entonces Rechazamos $H_0$.

P-VALUE:

Rechazamos $H_0$ sí $p-value \leq \alpha$

$p-value = 2 * min\{ P [ Y \leq T ], P [Y \geq T] \}$

Este cálculo lo realizaremos con ayuda del software de R:

Ejemplo del cálculo en código de R

#1. Dos colas
T = 360; #Estadistico de prueba
alpha = 0.05; 
n = 1400 #Tamanio muestra
p = 0.3; #probabilidad

# cuantil t = qbinom(alpha,n,p*);
t = qbinom(alpha,n,p);

# p_value = 2*min(c(pbinom(T,n,p*), pbinom(T,n,p*,lower.tail = F)));
p_value = 2*min(c(pbinom(T,n,p), pbinom(T,n,p,lower.tail = F)));
#p_value = 2*pbinom(t,n,p);

# Rechazo H0 si p_value < alpha
if (p_value <= alpha){print("rechazo H0")
}else{print("No rechazo H0")}

El resultado de esto es:

» Rechazo $H_0$ «.

$\blacksquare$

Nota. Otra forma de validar en R, es con la función de proporciones que tiene R:

# Prueba de Proporciones en R
prop.test(T, n, p, alternative = c("two.sided"), conf.level = 1-alpha)

Esto da como resultado la siguiente información:

	1-sample proportions test with
	continuity correction

data:  T out of n, null probability p
X-squared = 12.042, df = 1,
p-value = 0.0005202
alternative hypothesis: true p is not equal to 0.3
95 percent confidence interval:
 0.2345892 0.2810463
sample estimates:
        p 
0.2571429

donde tenemos que el $p-value = 0.0005202$, y con el cual podemos seguir Rechazando $H_0$

CONCLUSIÓN:

Como se rechazó $H_0$, podemos decir que hay información suficiente para afirmar que el 30% de los pacientes adultos mayores no tienen aplicada la 4ta dosis de vacunación contra COVID.

Problema 2. Un docente del CONAMAT, afirma que solo el 5% de sus alumnos de un grupo de 18, no pasan la prueba COMIPEMS. La dirección solicita el resultado de los 18 alumnos y solamente 3 de ellos no logran pasar el examen. Si el docente cree que la proporción de alumnos que no pasaron es mayor al número de alumnos que ya confirmaron no pasar, ¿Se puede rechazar $H_0:p=0.05$ con $alpha$ = 0.05?

Solución.

PRUEBA DE COLA SUPERIOR

HIPÓTESIS:

$H_0: p \leq 0.05$

v.s.

$H_1: p > 0.05$

ESTADÍSTICO DE PRUEBA:

Corresponde a los 3 alumnos que no lograron pasar el examen.

$T = 3$

como el tamaño de muestra $n \leq 20 $

$T \sim bin(18,0.05) $

CUANTILES:

Buscamos $t_2$ en T1 con:

$n = 18 , T=Y =3$ y $p = 0.05$

obtenemos $t_2 = 0.9891$

REGIÓN DE RECHAZO:

Rechazamos $H_0$ sí $T > t_2$

$T = 3 > t_2= 0.9891$

como sí se cumple la condición entonces Rechazamos $H_0$.

P-VALUE:

Rechazamos $H_0$ sí $p-value \leq \alpha$

Cálculo en código R

#2. Cola superior
T = 3; #Estadistico de prueba
alpha = 0.05; 
n = 18 #Tamanio muestra
p = 0.05; #probabilidad

# cuantil t = qbinom(1-alpha,n,p*);
alpha_2 =1-alpha;
t = qbinom(alpha_2,n,p);

# p_value = 1- pbinom(T,n,p*);
p_value = 1-pbinom(T,n,p);

# Rechazo H0 si p_value < alpha
if (p_value <= alpha){print("rechazo H0")
}else{print("No rechazo H0")}

El resultado de esto es:

» Rechazo $H_0$ «

$\blacksquare$

CONCLUSIÓN:

Como rechazamos $H_0$, existe evidencia suficiente para afirmar lo que señala el docente.

Problema 3. La cafetería «Fast-Coffee» asegura que el 95% de sus clientes son despachados en menos de 10 minutos una vez comandada su orden. Al finalizar el día, durante el corte, se toman aleatoriamente 9 comandas de las cuáles 8 órdenes fueron entregadas en menos de 10 min. ¿Puede concluirse $\alpha$= 5% que menos del 95% de los clientes se les entregó su orden dentro del lapso señalado?

Solución.

PRUEBA DE COLA INFERIOR

HIPÓTESIS:

$H_0: p \geq 95$%

v.s.

$H_1: p < 95$%

ESTADÍSTICO DE PRUEBA:

Corresponde a las 8 órdenes entregadas en menos de 10 min.

$T = 8$

como el tamaño de muestra $n \leq 20 $

$T \sim bin(9,0.95) $

CUANTILES:

Buscamos $t_1$ en T1 con:

$n = 9 , T=Y =8$ y $p = 0.95$

obtenemos $t = 0.3698$

REGIÓN DE RECHAZO:

Rechazamos $H_0$ sí $T \leq t_1$

$T = 8 \nless t_1= 0.3698$

como no se cumple la condición entonces No Rechazamos $H_0$.

P-VALUE:

Rechazamos $H_0$ sí $p-value \leq \alpha = 0.05$

Cálculo en código R

#3. Cola inferior
T = 8; #Estadistico de prueba
alpha = 0.05; 
n = 9 #Tamanio muestra
p = 0.95; #probabilidad

# cuantil t = qbinom(alpha,n,p*);
t = qbinom(alpha,n,p);

# p_value = pbinom(T,n,p*);
p_value = pbinom(T,n,p);

# Rechazo H0 si p_value < alpha
if (p_value <= alpha){print("rechazo H0")
}else{print("No rechazo H0")}

El resultado de esto es:

«No rechazo $H_0$ «

$\blacksquare$

CONCLUSIÓN:

No existe evidencia suficiente para asegurar que el 95% de los clientes son despachados en menos de 10 minutos una vez comandada su orden.

Más adelante…

En la siguiente entrada veremos otro tipo de prueba binomial: la prueba de cuantiles. Esta prueba se utilizará cuando nos interese hacer inferencia sobre un cuantil específico de alguna distribución.

Ejercicios

En un rancho donde se crían vacas para producir leche, se utilizó un nuevo alimento para ver si mejora la cantidad de leche producida. Se quiere verificar si la cantidad producida de leche es mayor al 15% contra la producción del mes anterior. Se toma una muestra de 200 vacas, donde solo 35 vacas fallan con la producción esperada. ¿Es posible comprobar la hipótesis con $\alpha$=0.01 ?
Una empresa de salto en paracaídas asegura que el 90% de los grupos de salida a la avioneta para realizar el salto es en menos de 10 min entre cada grupo. De 25 grupos, 12 de estos salieron dentro del lapso de tiempo estimado anteriormente. ¿Se puede concluir con $\alpha$ = 0.05, que menos del 90% de las salidas entre cada grupo se hacen en 10 minutos?
Una farmacéutica desarrolló una vacuna contra la Leucemia y quiere saber si tiene una efectividad mayor al 85% contra dicha enfermedad. Se toma una muestra de 100 personas a las que se les aplica dicha vacuna, de las cuales 65 personas mostraron resultados positivos contra la enfermedad. ¿Se puede concluir que la vacuna tiene una efectividad mayor al 85%? Prueba usando $\alpha$ = 0.10

Enlaces relacionados

A1: Tabla de distribución Binomial
A2: Tabla de distribución Normal
Conover, W. J. (1999). Practical Nonparametric statistics (3ª ed.). Second Edition. USA. Wiley & Sons

Entradas relacionadas

Ir a: Estadística no paramétrica
Entrada anterior del curso:
Siguiente entrada del curso: Estadística No Paramétrica: Pruebas para cuantiles

Matemáticas Financieras: Anualidades pagaderas P veces al año

Por Erick de la Rosa

Deja un comentario

Introducción

En este apartado se abordará uno de los temas más típicos que nos podemos encontrar dentro de las matemáticas financieras, y se caracteriza por ser uno de los temas que comienzan a combinar las reglas, en el sentido de que vamos a utilizar variantes que hasta el momento no se habían utilizado, como lo es que la periodicidad de la tasa de interés no va a coincidir con la que se está manejando en el tipo de pagos, motivo por el que se tendrá que utilizar un tipo de tasa equivalente. Sin embargo, como se verá más adelante, siempre va a ser posible encontrar una tasa efectiva que logre resolver éste problema. Uno de los principales objetivos de este tipo de anualidad es explicar de forma sencilla la forma en que se puede amortizar un crédito.

Descripción general

Este tipo de anualidad tiene como punto de partida una cantidad que debe de cubrirse durante justamente un año, dicha cantidad deberá de ser la misma durante los años que siguen, hasta que se haya pagado la totalidad de la deuda que se haya adquirido. Su principal característica consiste en que se defina el número de veces $p$ en que serán realizados los pagos durante el año, lo anterior quiere decir que dicha cantidad anual será dividida entre $p$ para obtener la cifra que será pagada cada p-ésimo año. Por ejemplo, si un contrato de crédito estipula que la deuda será pagada con anualidades de \$24,000 pagaderos mensualmente, esto significa que cada mes se realizará un pago de \$2,000 durante los 12 meses que tiene dicho año. Este tipo de anualidades son muy parecidas al tema de tasas nominales, las cuales coinciden con la misma característica de ser pagaderas $m$ veces al año.

Vale la pena recordar que las tasas nominales, se obtienen de dividir una tasa nominal entre $m$. Por lo que de forma similar se pueden calcular este tipo de anualidades, sólo que la cantidad que se pretende pagar durante el año, es una referencia y cada uno de los $p$-ésimos es la cantidad real que se va a pagar, además de que serán estás cantidades la que se utilizarán cuando se quiera calcular su valor presente.

Al hacer uso de este tipo de anualidades se pueden tener las siguientes variaciones:

Del tipo de anualidad en el que la periodicidad de la tasa sea menor a la del periodo de cada pago.
Cuando el periodo del pago sea igual al de la tasa.
Cuando la periodicidad de la tasa sea mayor que la del pago.

La siguiente gráfica nos muestra el comportamiento de este tipo de anualidad:

Elaboración propia, basado en Matemáticas financieras, fundamentos y aplicaciones, Cánovas T. Ed. Trillas, pag. 172.

La imagen muestra el comportamiento de una anualidad pagadera p veces al año, la cual será denotada por:

$$\prescript{}{n(p)}{\mathbf{A}}_i$$

donde:

$n$ es la cantidad de años que se pactó, en los cuales se va a realizar el pago del crédito.
$p$ es la cantidad de veces que la anualidad será pagadera en un año.
$i$ es la cantidad de interés, que en particular para este tipo de anualidades, no será precisamente efectiva por $p$-ésimo cada periodo.

Valor presente con tasa de interés efectiva anual

Para obtener el valor presente de este tipo de anualidades, haciendo los cálculos con un capital de \$1 peso, a una tasa de interés efectiva anual $i$, se hace lo siguiente:

Reduciendo términos nos queda:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(v_i^{\frac{1}{p}}+v_i^{\frac{2}{p}}+…+v_i^{\frac{p}{p}}+v_i^{1+\frac{1}{p}}+…+v_i^2+…+v_i^{(n-1)+\frac{1}{p}}+…+v_i^{n-\frac{1}{p}}+v_i^n\right).$$

Como el resultado que se acaba de obtener. está siendo multiplicado por una progresión geométrica entonces:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{v_i^{\frac{1}{p}}-v_i^nv_i^{\frac{1}{p}}}{1-v_i^{\frac{1}{p}}}\right)$$

luego factorizando a $v_i^{\frac{1}{p}}$:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{v_i^{\frac{1}{p}}(1-v_i^n)}{1-v_i^{\frac{1}{p}}}\right).$$

Ahora multiplicando por el número 1, pero expresado como $\frac{(1+i)^{\frac{1}{p}}}{(1+i)^{\frac{1}{p}}}$ se obtiene:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{(1+i)^{\frac{1}{p}}v_i^{\frac{1}{p}}(1+v_i^n)}{(1+i)^{\frac{1}{p}}(1-v_i^{\frac{1}{p}})}\right).$$

Nótese que $v=\frac{1}{1+i}$, luego entonces:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{(1-v_i^n)}{(1+i)^{\frac{1}{p}}-1}\right).$$

Luego, por la triple igualdad se tiene:

$$(1+i)^{\frac{1}{p}}=\left(1+\frac{i^{(p)}}{p}\right)^1.$$

Sustituyendo dicha expresión se tiene:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{(1-v_i^n)}{\left(1+\frac{1^{(p)}}{p})\right)-1}\right)$$

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1-v_i^n}{p+i^{(p)}-p}.$$

Reduciendo la expresión queda:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1-v_i^n}{i^{(p)}}$$

ésta expresión puede escribirse en términos de $\prescript{}{n}{\mathbf{A}}_i$ al mulitplicar el lado derecho por $\frac{i}{i}$:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{i}{i^{(p)}}\left(\frac{1-v_i^n}{i}\right)$$

recordando que $\prescript{}{n}{\mathbf{A}}_i=\left(\frac{1-v_i^n}{i}\right)$ se obtiene:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{i}{i^{(p)}}\prescript{}{n}{\mathbf{A}}_i.$$

Por otra parte, para obtener el valor presente de ésta anualidad, es necesario calcular una tasa efectiva por $p$-ésimo, así como una $i’$, que sea equivalente efectiva anual, para lograrlo se hace lo siguiente:

$$(1+i)^{\frac{1}{p}}=\left(1+\frac{i^{(p)}}{p}\right)^1=(1+i’)$$

$$i’=\frac{i^{(p)}}{p}=(1+i)^{\frac{1}{p}}-1.$$

Usando la tasa que se acaba de obtener, se puede calcular la anualidad a $n$ años, pagadera $p$ veces al año, como una anualidad vencida de $np$ pagos de $1/p$ (que significa $p$ pagos al año, aplicados por $n$ años). El valor presente de dicha anualidad queda denotado por la expresión:

$$\prescript{}{n(p)}{\mathbf{A}}_{i’}=\frac{1}{p}\prescript{}{n+p}{\mathbf{A}}_{i’}.$$

Como $\prescript{}{n}{\mathbf{A}}_i=\frac{1-v_i^n}{i}$ se tiene:

$$\prescript{}{n(p)}{\mathbf{A}}_{i’}=\frac{1}{p}\prescript{}{n+p}{\mathbf{A}}_{i’}=\frac{1}{p}\left(\frac{1-v_{i’}^{np}}{i’}\right).$$

Observación, para el cálculo de todas éstas expresiones se utilizó un capital de \$1 peso, entonces al cambiar dicho valor por uno $X$, la expresión obtenida del valor presente queda como:

$$V=X\prescript{}{n(p)}{\mathbf{A}}_{i’}=\frac{X}{p}\prescript{}{np}{\mathbf{A}}_{i’}.$$

Otro método para encontrar el valor presente de una anualidad pagadera $p$ veces al año con una tasa de interés efectiva anual, es calculando el monto al final del año, y de los pagos $p$, $1/p$ que se realizan durante dicho año.

Lo anterior se traduce en la siguiente expresión:

$$X=\frac{1}{p}\left((1+i)^{1-\frac{1}{p}}+(1+i)^{1-\frac{2}{p}}+…+(1+i)^{\frac{1}{p}}+1\right).$$

Reduciendo términos al efectuar las sumas, se obtiene:

$$X=\frac{1}{p}\left(\frac{1-(1+i)^{1-\frac{1}{p}}(1+i)^{\frac{1}{p}}}{1-(1-i)^{\frac{1}{p}}}\right)=\frac{1}{p}\left(\frac{1-(1+i)^1}{1-(1+i)^{\frac{1}{p}}}\right).$$

Como $(1+i)^{\frac{1}{p}}=\left(1+\frac{i^{(p)}}{p}\right)^1$

luego entonces:

$$X=\frac{1}{p}\left(\frac{1-(1+i)^1}{1-\left(1+\frac{i^{(p)}}{p}\right)}\right)=\frac{1}{p}\left(\frac{1-(1+i)}{\frac{i^{(p)}}{p}}\right)=\frac{p}{p}\left(\frac{1-(1+i)}{i^{(p)}}\right)=\frac{i}{i^{(p)}}.$$

Lo que se acaba de obtener nos dice que el pago anual es equivalente a la suma de los $p$ pagos de $1/p$, que se realizan en el año, los cuales son acumulados con una tasa de interés efectiva anual, observe que la suma aritmética de cada uno de ellos es igual a uno.

Finalmente, la expresión del valor presente de una anualidad pagadera p veces al año es:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{i}{i^{(p)}\prescript{}{n}{\mathbf{A}}_i}$$

El resultado que es igual al que previamente se había obtenido previamente con el otro método.

Por último, se va a cambiar el capital de \$1 peso, por un capital$X$, y la expresión queda:

$$V=X\prescript{}{n(p)}{\mathbf{A}}_i=X\frac{i}{i^{(p)}\prescript{}{n}{\mathbf{A}}_i}.$$

Las anualidades pagaderas $p$ veces al año, se resuelven calculando una tasa efectiva equivalente por periodo de pago, aplicando el modelo de anualidades vencidas, considerando que los pagos se realizan $p$ veces de $1/p$ cada año.

Observación: para calcular una anualidad pagadera $p$ veces al año, con una tasa nominal de interés, sólo es necesario calcular la tasa equivalente por periodo de pago, haciendo uso del modelo de anualidades vencidas, tomando en consideración que realizan $p$ pagos de $1/p$ de forma anual.

Monto

Para calcular el monto de este tipo de anualidades, se va a obtener partiendo de un capital de \$1 peso, para luego obtener su valor presente por $n$ periodos con una tasa efectiva anual, o durante $np$ periodos en el caso de que la tasa sea efectiva por cada periodo de pago.

Para el primer supuesto, se utiliza la siguiente ecuación:

$${\prescript{}{(n)(p)}{\mathbf{S}}_{i}}=\frac{i}{i^{(p)}}{\prescript{}{n}{\mathbf{A}}_{i}}(1+i)^n.$$

Para el segundo supuesto, se utilizará:

$${\prescript{}{(n)(p)}{\mathbf{S}}_{i’}}=\frac{1}{p}{\prescript{}{(n)}{\mathbf{A}}_{i’}}(1+i)^{n*p}.$$

Por último, se realizará el cambio del capital que fue de un peso por el monto \$X, lo que hace que las dos ecuaciones queden de la siguiente forma:

$$M=X\prescript{}{n(p)}{\mathbf{S}}_i=X\frac{i}{i^{(p)}}\prescript{}{n}{\mathbf{A}}_i(1+i)^n$$

$$M=X\prescript{}{n(p)}{\mathbf{S}}_{i’}=\frac{X}{p}\prescript{}{n+p}{\mathbf{A}}_{i’}(1+i’)^{n+p}$$

Ejercicios resueltos

Ejercicio. Una empresa de mantenimiento de maquinaria pesada para la construcción, necesita un crédito para modernizar su planta, por una cantidad de \$120 mil. El banco con el que está realizando dicho préstamo, le ofrece que lo pague en dos años, con pagos semanales a una tasa de interés efectiva anual del 15%. Se necesita saber ¿cuánto se pagara cada semana?

Solución

Para este caso, como el pago va a ser semanal, se tiene una tasa pagadera 52 veces al año, con una tasa de interés efectiva anual, lo cual implica que se necesita una tasa que sea equivalente efectiva semanal, la cual se obtiene de la siguiente forma:

$$1+i’=(1+0.15)^{\frac{1}{52}}$$

de donde $i=.002691$

Luego la ecuación que se va a utilizar es la siguiente:

$$120,000=X{\prescript{}{(2)(52)}{\mathbf{A}}_{0.002691}}$$

despejando a $X$ se tiene:

$$X=\frac{120,000}{\prescript{}{104}{\mathbf{A}}_{0.002691}}=\frac{120,000}{90.6091738}=1324.3692$$

Por lo tanto, el pago semanal que se tiene que realizar es de: \$1324.37.

Ejercicio. La empresa COPPEL vende articulos para el hogar, entre los que destacan electrodomésticos, ropa, muebles, etc. Una familia desea adquirir una sala, el valor de ésta asciende a \$40,000, si al solicitar el crédito aportan un enganche de \$10 mil pesos, y el resto lo pagan a crédito. ¿Cuánto es lo que deben de pagar cada mes, si la tasa de interés que les están cobrando es del 35% pagadero mensual.

Solución

En este ejemplo se presenta el caso en el que el plazo de la tasa de interés coincide con la temporalidad de los pagos, esto es, m=p. En tal situación la ecuación que se va a utilizar para resolverlo es la siguiente:

$$40,000=10,000+X{\prescript{}{(1)(12)}{\mathbf{A}}_{0.02916}}$$

$$=\frac{40,000-10,000}{\frac{1-v_{0.029}^{12}}{0.029}}$$

$$=\frac{30,000}{10.005989}=\$2998.2041$$

Más adelante…

Hasta este momento se han estado analizando varios tipos de anualidades, y como bien se podrá observar, las combinaciones entre ellas cada vez es mayor, lo que implica con ello, un mayor grado de dificultad, sobre todo cuando se esté trabajando con tasas equivalentes, en las que muchas veces sólo se deja indicada la operación, sin embargo es necesario tener muy en cuenta que ésos cálculos no deben de ser olvidados. En los temas siguientes se irán abordando más tipos de anualidades, en particular las que son del tipo continuas.

Entradas relacionadas

Ir a Matemáticas Financieras
Entrada anterior
Entrada siguiente

Matemáticas Financieras: Anualidades decrecientes

Por Erick de la Rosa

Deja un comentario

Introducción

En éste apartado, se abordarán las anualidades opuestas a las que acabamos de revisar, las anualidades decrecientes, las cuales como su nombre lo indica su principal característica es que conforme avanza el tiempo van disminuyendo. Su uso se presenta en los casos en los que se otorga un préstamo, un crédito, en el que el bien adquirido con el paso del tiempo se va deteriorando, es decir, cuando están nuevos y recién adquiridos requieren un mantenimiento mínimo, sin embargo con el paso del tiempo y el uso, van necesitando cada vez mantenimientos más costosos, y si a ello se le agrega que aún no se terminan de pagar, pues este tipo de anualidad se amolda muy bien a ésta situación, en la que el deudor le conviene bastante que en el momento en el que se requieran servicios más costosos, se pague cada vez menos a la deuda adquirida, sin que por ello se omita o incumpla alguna obligación. Todo este acuerdo, se pacta desde un inicio entre las partes involucradas.

Descripción y valor presente

Una anualidad decreciente, es aquella que conforme avanza el tiempo, los pagos que se van realizando cada vez son menores, el objetivo de este tipo de anualidad es que la persona deudora este en las condiciones de poder cumplir cómodamente con sus obligaciones, al mismo tiempo que la institución que otorga el crédito o préstamo no vea afectado la recuperación de sus recursos ni asuma un riesgo mayor.

Éste tipo de anualidad, tiene como característica principal que cada pago realizado es igual al anterior menos una cierta cantidad. Otra característica importante es que comienza con un pago de cierto valor, llamémoslo $n$ y los pagos siguientes van a ir disminuyendo una cierta cantidad, hasta llegar al último pago con valor igual a un peso.

Elaboración propia, basada en Matemáticas Financieras, fundamentos y aplicaciones, Cánovas T. Ed. Trillas, pag. 166

El valor presente de esta anualidad se denota por:

$$\prescript{}{n}{\mathbf{(DA)}}_i$$

donde:

$D$ hace referencia a la palabra decreasing (decreciente).
$n$ es el número de pagos que se van a realizar.
$i$ continúa representando la tasa de interés efectiva por periodo.

Para obtener el valor presente de dicha anualidad, se partirá de la siguiente expresión:

$$\prescript{}{n}{\mathbf{(DA)}}_i=(n)\prescript{}{n}{\mathbf{A}}_i+(-1)\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$

Luego:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{in\prescript{}{n}{\mathbf{A}}_i-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$

Recordando, que $\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$, la expresión anterior se convierte en:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{in\left(\frac{1-v^n}{i}\right)-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$

Luego, cancelando las $i$ del numerador y multiplicando por $n$ la expresión que está entre paréntesis, se obtiene:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{n(1-v^n)-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}=\frac{n-nv^n-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$

Por último, reducimos términos:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{n-\prescript{}{n}{\mathbf{A}}_i}{i}.$$

Para generalizar la expresión, se toma como primer pago a $P$ y los pagos siguientes disminuyen una cantidad $Q$, pero se debe de tener cuidado con el último pago, $P-(n-1)Q$, sea positivo; esto es que $P$ debe ser mayor a $(n-1)Q.$

Entonces, la ecuación para calcular el valor presente seria:

$$V=P\prescript{}{n}{\mathbf{A}}_i-Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$

Monto

El monto de una anualidad decreciente, con $n$ pagos que se aportarán durante $n$ periodos, fijando el primer pago $n$ y los pagos siguientes irán disminuyendo en una unidad, se calcula de forma similar a los crecientes, y es denotada por:

$$\prescript{}{n}{\mathbf{SD}}_i=\frac{n-\prescript{}{n}{\mathbf{A}}_i}{i}(1+i)^n.$$

En este tipo de anualidad decreciente, el primer pago será $P$ mientras que los pagos siguientes serán disminuidos por una cantidad $-Q$, la expresión queda denotada por:

$$V=P\prescript{}{n}{\mathbf{A}}_i(1+i)^n-Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right)(1+i)^n.$$

Por último, el monto de una anualidad geométrica decreciente con razón $(1-K)$ es:

$$V=X\left(1-\frac{(1-k)^n}{(1+i)^n}\right)\left(\frac{(1+i)^n}{1+k}\right).$$

Ejercicios resueltos

Ejercicio. Una empresa de aeronaves, necesitan refacciones para sus aviones, sus socios desean adquirir un crédito para ello, y planean pagarlo con aportaciones decrecientes, las cuales están basadas en su experiencia de ingresos. Al hacer sus cálculos, llegan a la conclusión de que cada uno de sus socios pueden realizar aportaciones mensuales de forma vencida, comenzando con un adelanto de \$6 mil pesos, disminuyendo los siguientes pagos en \$250, hasta llegar a mensualidades de \$2 mil. Pretenden, además, negociar, para que el banco les otorgue un plazo para pagar su crédito de 2 años, a una tasa de interés del 10.5% pagadero mensual el banco les otorga una plazo de año y medio. ¿Se necesita saber qué cantidad es la que el banco puede prestar a cada uno de sus socios?

Solución

Para resolver éste problema, lo que se necesita es hacer uso del concepto de valor presente de una anualidad decreciente, el cual, va a ser más el valor presente de una anualidad vencida de pagos iguales por la cantidad de \$2,000.

La anualidad decreciente consistirá en:

$$\frac{6,000-2,000}{250}+1=16$$

de esta forma se obtiene el número de pagos por el que se encuentra formada nuestra anualidad decreciente, siendo el primer pago de \$6,000 y el último de \$2,000.

Tomando en cuenta, que el plazo total que se les ha otorgado es de año y medio, eso implica que habrá 2 mensualidades adicionales de \$2,000 cada una. De esta forma, la ecuación que se va a utilizar para resolver éste problema es:

$$V=6,000\prescript{}{16}{\mathbf{A}}_{0.0125}-250\left(\frac{\prescript{}{16}{\mathbf{A}}_{0.0125}-16v_{0.0125}^{16}}{0.0125}\right)+250\prescript{}{2}{\mathbf{A}}_{0.0125}v_{0.0125}^{16}$$

$$=6,000(14.4202)-250\left(\frac{(14.4202)-16(0.8197463)}{0.0125}\right)+250(1.9631)(0.9754611)$$

$$=86,521.2-250(104.3407360)+478.731921$$

$$=86,521.2-26085.184+478.731921=60914.74792$$

La cantidad que se les podría otorgar a los socios es: \$60,914.74792

Ejercicio. Una empresa de restaurantes, desea abrir una sucursal en el pueblito abc, para llevarlo a cabo ha considerado una inversión de \$250 mil pesos. El dueño en base a su experiencia, aspira a tener ingresos de la siguiente forma:

Considera poder hacerse de clientes durante los primeros 2 años, por lo que calcula tener ingresos en el primer mes de cada periodo de \$3000 pesos, los cuales irán incrementando \$800 pesos cada periodo durante los meses restantes (23 meses).
Espera que las ventas se mantengan estables en los 2 años que siguen, ingresos de \$6 mil
En el último año considera tener ingresos de \$7 mil pesos, con una posible caída de ventas de \$200 pesos mensuales hasta el término de dicho año.

Si el dueño de ése restaurante, espera recuperar su inversión de \$250 mil pesos valuados a la fecha de apertura, así como tener una ganancia de 25% anual. ¿Se necesita saber si con los datos que él dueño planeó, es suficiente para alcanzar sus metas, sobre todo si se propone tener ganancias netas del 35%.

Solución

Para poder resolver éste ejercicio, hay que hacer lo siguiente:

Traer a valor presente la cantidad de ingresos que planea obtener, durante los 5 años, a la tasa de rendimiento que el dueño pronostica.
Restar la cantidad que se obtenga en el primer paso, a los costos que consumió el restaurante para poder abrir, esto es el 70%, con esto se obtiene el valor actual de las utilidades esperadas
Por último, se necesita comparar la inversión realizada. Si el valor presente de las utilidades netas es igual a la inversión realizada, entonces significa que el dueño si pudo recuperar su inversión y que además su restaurante habrá tenido el rendimiento que él consideró tener el cual era de 25% anual.

La tasa de rendimiento esperada es del 25% anual, la cual tiene una tasa equivalente mensual del 0.0187693. Este dato se obtiene de la triple igualdad

$$(1+i)=(1.025)^{\frac{1}{12}}$$

de donde se obtiene $i=0.0187693.$

Ahora, la ecuación de valor que se necesita para resolver este problema es:

$$V=3,000\prescript{}{24}{\mathbf{A}}_{0.0187693}+800\left(\frac{\prescript{}{24}{\mathbf{A}}_{0.0187693}-24v_{0.0187693}^{24}}{0.0187693}\right)$$

$$+6,000\prescript{}{24}{\mathbf{A}}_{0.0187693}
v_{0.0187693}^{24}$$

$$+\left(7,000\prescript{}{12}{\mathbf{A}}_{0.0187693}-200\left(\frac{\prescript{}{12}{\mathbf{A}}_{0.0187693}-12v_{0.0187693^{12}}}{0.0187693}\right)\right)v_{0.0187693}^{48}.$$

Esta ecuación tiene 3 secciones:

La primera, representa el valor presente de la anualidad creciente de los 2 primero años, mientras que la segunda, representa el presupuesto de ventas (\$7000 mensuales) para el tercer y cuarto año.

La última sección pertenece a la anualidad decreciente que conforma el presupuesto de ventas para el quinto año y que se lleva, también, hasta la fecha de valuación multiplicándolo por $v_0.01715^{48}$.

$$v=300,000(19.539037)+80,000(208.82239)+1,400 000(19.539037)(0.6649055)$$

$$+[1,200,000(10.762845)-50,000(57.016793)(0.4420993)$$

$$v=5,861,711.10+16,705,791+27,354,651+4,449,541.50$$

$$v=\$54,371,694.60.$$

Del valor obtenido, aún falta por restarle el \$70% por concepto de costo de ventas, lo que equivale a \38,060,185.40, para obtener el valor presente de los flujos de utilidades netas que brinda el proyecto. De esta forma tenemos la siguiente ecuación:

$$U=54,371,694.6-38,060,185.4=\$16,311,509.2.$$

El resultado obtenido, significa que la inversión si podrá ser recuperada, y que además tendrá un rendimiento mayor al esperado de 23.144% toda vez que el valor presente de las utilidades netas futuras es mayor a la inversión original.

_{*Éste ejercicio fue basado del libro Matemáticas Financieras, fundamentos y aplicaciones, Cánovas T. Ed. Trillas, pag. 168.}

Más adelante…

Se abordarán las anualidades pagaderas p veces al año, las cuales son de gran utilidad cuando se tiene casos en los que lo que se pretende es dar una expresión clara de cómo se puede ir pagando un crédito, conociendo la cantidad que se debe de pagar en cada periodo. Con este tema terminamos de adquirir las herramientas necesarias para poder evaluar proyectos de inversión.

Entradas relacionadas

Ir a Matemáticas Financieras
Entrada anterior
Entrada siguiente

Álgebra Moderna I: Clases de Conjugación, Centro de $G$, Ecuación de Clase y $p$-Grupo

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Esta entrada es una caja de herramientas. Continuamos sobre la línea de estudiar las propiedades de una órbita y de su orden. Primero, nos vamos a enfocar en grupos actuando sobre sí mismos, a partir de esto definiremos un nuevo conjunto al que llamamos el centro de $G$ y daremos algunas observaciones al respecto.

El segundo bloque importante de la entrada es probar la llamada ecuación de clase, una ecuación que nos permite calcular el orden de un $G$-conjunto usando otros conjuntos relacionados. Uno de estos conjuntos lo definiremos como $X_G$, el conjunto de todos los elementos de $X$ que quedan fijos sin importar el elemento de $G$ que actúa sobre ellos. Volveremos a encontrar a la órbita de los elementos en la demostración de esta ecuación.

Por último, comenzaremos a trabajar con $p$-grupos, es decir grupos de orden una potencia de un número primo y usaremos la ecuación de clase para demostrar una propiedad de los $p$-grupos.

Decimos que esta entrada es una caja de herramientas, porque no estamos introduciendo temas que vayamos a estudiar a profundidad, más bien son conceptos que nos ayudarán a llegar al tema principal de esta unidad: los Teoremas de Sylow.

Clases de conjugación, centralizadores y centro de $G$

La acción de un grupo actuando en sí mismo por conjugación es muy importante y debido a ello daremos nombres y notaciones específicas para las órbitas y estabilizadores correspondientes (que fueron estudiados de manera general en la entrada Órbita de $x$ y tipos de acciones).

Definición. Sea $G$ es un grupo actuando en sí mismo por conjugación, es decir $g\cdot x = g x g^{-1}$ para todos $g,x\in G$. Dado $x\in G$ la órbita del elemento $x$ bajo esta acción se llama la clase de conjugación de $x$ y se denota por $x^G$, esto es:
\begin{align*}
x^G=\mathcal{O}(x) &= \{g\cdot x | g\in G \} = \{gxg^{-1} | g\in G\}.
\end{align*}

Por otro lado el estabilizador de $x$ se llama el centralizador de $x$ en $G$ y se denota por $C_G(x)$, es decir:

\begin{align*}
C_G(x)=G_x &= \{g\in G|g\cdot x = x\} = \{g\in G | gxg^{-1} = x\}\\
&= \{g\in G | gx = xg\}.
\end{align*}

Siendo entonces el conjunto de todos los elementos del grupo que conmutan con $x$.

Otra colección que resultará clave en el material que desarrollaremos más adelante es el llamado centro de un grupo:

Definición. Sea $G$ un grupo. El centro de $G$, denotado por $Z(G)$, es
\begin{align*}
Z(G) = \{x\in G | xg = gx \quad \forall g\in G\}.
\end{align*}

Es decir, el centro es la colección de todos los elementos de $G$ que conmutan con todos los demás.

Observación 1. $Z(G)$ es un subgrupo normal de $G$.

Demostración.
Primero, tomemos el neutro $e\in G$ y veamos que está en $Z(G)$. Como estamos hablando del neutro, se cumple que $eg = g = ge$ para toda $g\in G$, entonces $e\in Z(G)$.

Ahora, tomamos $x\in Z(G)$ entonces $xg = gx$ para toda $g\in G$. Así $g=x^{-1}gx$ para toda $g\in G$, lo que implica que $gx^{-1} = x^{-1}g$ para toda $g\in G$ por lo que $x^{-1} \in Z(G)$.

Luego, si tomamos $x,y\in Z(G)$, se tienen las siguientes igualdades por la definición del centro $(xy)g = x(yg) = x(gy) = (xg)y = (gx)y = g(xy)$ para todo $g\in G$. Así, $xy \in Z(G)$.

Concluimos que el centro es un subgrupo.

Por último, probemos que es un subgrupo normal. Sean $x\in Z(G)$ y $g\in G$. Al conjugar $x$ con $g$ podemos usar la asociatividad y la definición de centro para concluir que

\begin{align*}
gxg^{-1} &= (gx)g^{-1} &\text{Agrupamos}\\
&= (xg)g^{-1} &\text{Porque }x, g \in Z(G)\\
&= x(gg^{-1}) &\text{Agrupamos} \\
&= xe &\text{Inverso}\\
&= x \in Z(G).
\end{align*}

Por lo tanto $Z(G)\unlhd G$.

$\blacksquare$

Observación 2. Sean $G$ un grupo y $x\in G$. Entonces $x\in Z(G)$ si y sólo si $x^G = \{x\}$.

Demostración. Sean $G$ un grupo y $x\in G$. Tenemos que
\begin{align*}
x^G = \{x\} &\Leftrightarrow gxg^{-1} = x \quad \forall g\in G &\\
&\Leftrightarrow gx = xg &\text{Multiplicamos por $g$ a la derecha}\\
&\Leftrightarrow x\in Z(G).
\end{align*}

$\blacksquare$

La observación anterior nos dice entonces que los elementos del centro son precisamente aquellos cuya clase de conjugación es trivial.

Ecuación de Clase

Para poder enunciar la ecuación de clase, que describe la carnalidad de un $G$-conjunto $X$ en términos de los índices de ciertos estabilizadores, definamos primero un cierto subconjunto de $X$:

Definición. Sean $G$ un grupo y $X$ un $G$-conjunto finito. Definimos,
\begin{align*}
X_G = \{x\in X | g\cdot x = x \; \forall g\in G\}.
\end{align*}

Es decir, $X_G$ es el conjunto de elementos de $X$ que quedan fijos sin importar qué elemento de $G$ actúe sobre ellos.

Nota: Es posible que te encuentres con otra notación $X^G$ para este mismo conjunto. En general, si $H$ es un subgrupo de $G$, el conjunto de puntos fijos por $H$ se denota por $X^H$. Pero en este curso usaremos la notación ya dada, es decir, $X_G$.

Notemos que dado $x\in X$ se tiene que $x\in X_G$ si y sólo si $g\cdot x = x$ para toda $g\in G$ y esto sucede si y sólo si $\mathcal{O}(x) = \{x\}.$ Entonces se cumple lo siguiente:

Observación 3. $x\in X_G$ si y sólo si $\mathcal{O}(x) = \{x\}.$

Así, el conjunto $X_G$ consiste de los elementos cuya órbita es trivial.

Proposición. (Ecuación de Clase)
Sean $G$ un grupo y $X$ un $G$-conjunto finito. Tenemos que
\begin{align*}
\#X = \#X_G + \sum_{j=1}^k [ G : G_{x_j}]
\end{align*}
con $x_1, \cdots x_k$ representantes de las distintas órbitas con más de un elemento.

En particular, si $G$ es finito y actúa en $G$ por conjugación
\begin{align*}
|G| = |Z(G)| + \sum_{j= i}^{k} [ G: C_G(x_j) ]
\end{align*}
con $x_1,\cdots x_k$ representantes de las distintas clases de conjugación con más de un elemento.

Demostración.
Sean $G$ un grupo y $X$ un $G$-conjunto finito.

Sabemos que las órbitas son una partición de $X$. Sean $x_1,\cdots,x_k, x_{k+1},\cdots, x_t$ representantes de las distintas órbitas, donde $\#\mathcal(x_j) > 1$ si $j\in \{1,\cdots, k \}$ y $\#\mathcal{O}(x_j) = 1$ si $j\in \{k+1,\cdots , t\}.$ Entonces por un lado tenemos a las órbitas que tienen un sólo elemento y, por otro lado, las demás.

Por la observación 3, $X_G = \{x\in X| \# \mathcal{O}(x) = 1\} = \{x_{k+1},\cdots, x_t\}$.

Así,
\begin{align*}
\# X &= \sum_{j=1}^t \#\mathcal{O}(x_j) \\
&= \sum_{j= 1}^k \#\mathcal{O}(x_j) + \sum_{j= k+1}^t \#\mathcal{O}(x_j) &\text{Separamos la suma}\\
&= \sum_{j= 1}^k \#\mathcal{O}(x_j) + \sum_{j = k+1}^t 1 & \#\mathcal{O}(x_j) = 1 \text{ para } j \geq k+1\\
&= \sum_{j= 1}^k [ G : G_{x_j} ] + \# X_G & \text{Por la observación 3.}
\end{align*}

Si $G$ es finito y actúa en $G$ por conjugación, $X_G = Z(G)$, $\mathcal{O}(x_j) = x_j^G$ son las clases de conjugación y $G_{x_j} = C_G(x_j)$. Así
\begin{align*}
|G| = \sum_{j= 1}^k \lceil G: C_G(x_j) \rceil + |Z(G)|.
\end{align*}

$\blacksquare$

$p$-grupo

Hemos tratado con grupos finitos de orden primo, de ellos sabemos propiedades importantes como el hecho de que son cíclicos. El siguiente paso en nuestro estudio, es enfocarnos en los grupos cuyo orden es una potencia de algún primo. No todos los grupos finitos cumplen esta característica, pero los que sí, nos permiten entender a los demás.

Definición. Sean $G$ un grupo y $p\in\z^+$ un primo. Decimos que $G$ es un $p$-grupo si $|G| = p^t$ para alguna $t\in \n$.

Teorema. Sean $p\in \z^+$ un primo, $G$ un $p$-grupo y $X$ un $G$-conjunto finito. Entonces $$\#X \equiv \# X_G ( \text{mód } p).$$

Demostración.
Sean $p\in \z^+$ un primo, $G$ un $p$-grupo y $X$ un $G$-conjunto finito. Por la ecuación de clase,
\begin{align*}
\#X = \#X_G + \sum_{j=1}^k [G: G_{x_j} ]
\end{align*}
con $x_1,\cdots, x_k$ representantes de las distintas órbitas con más de un elemento. Como $G$ es un $p$-grupo, $|G| = p^t$ con $t\in \n$. Dado que el orden de los estabilizadores divide al orden de $G$ tenemos que $|G_{x_j}| \mid p^t$ y por lo tanto $|G_{x_j}| = p^{m_j}$ con $m_j\in \n, m_j \leq t.$

Entonces

\begin{align*}
1< \# \mathcal{O}(x_j) &= [G: G_{x_j} ] & \text{Por lo visto anteriormente}\\
&= \frac{|G|}{|G_{x_j}|} & \text{Propiedad del índice}\\
&= \frac{p^t}{p^{m_j}} & \text{Consecuencia de la hipótesis}\\
&= p^{t-m_j}.
\end{align*}

Así, $p$ divide a $[G: G_{x_j}]$ para toda $j\in \{1,\cdots, k\}.$ Por lo que

\begin{align*}
p \text{ divide a } \sum_{j=1}^k [G:G_{x_j}].
\end{align*}

Pero por la ecuación de clase $ \displaystyle \sum_{j=1}^k [G:G_{x_j}]= \# X – \# X_G.$

Entonces
\begin{align*}
p \text{ divide a } \# X – \# X_G.
\end{align*}

En consecuencia $\# X \equiv \#X_G( \text{mód } p).$

$\blacksquare$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Considera el grupo $S_4$ actuando sobre sí mismo por conjugación.
- Determina las clases de conjugación de $S_4$.
- Escribe la ecuación de clase de $S_4$.
- Deduce el orden de cada uno de los estabilizadores $G_x$, donde $x\in S_4$.
Encuentra todos los $p$-subgrupos de $S_4$.
Sean $X = \{H \,|\, H \leq D_{2(4)}\}$ y $G = \left< a \right>$ con $a$ la rotación de $\displaystyle \frac{\pi}{2}$. Considera la acción de $G$ en $X$ dada por $g \cdot H = gHg^{-1}$ para todo $g\in G$, $H \in X$. Encuentra $X_G$ y verifica que $\#X \equiv \# X_G (\text{mód }2)$.

Más adelante…

Ahora nuestro interés está puesto en los números primos o más bien, en la relación de los números primos con el orden de los grupos. Esta entrada te da lo que tienes que saber de $p$-grupos y más adelante veremos cómo mediante ellos se pueden estudiar otros grupos. Además, eventualmente veremos un caso especial de los $p$-grupos, llamados $p$-subgrupos de Sylow, que nos llevará (para sorpresa de nadie) a los Teoremas de Sylow.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Tamaño de una órbita y de un estabilizador.
Siguiente entrada del curso: Teorema de Cauchy.
Resto de cursos: Cursos.