Archivo de la categoría: Matemáticas

Posts de matemáticas, la ciencia más cercana a las artes.

Álgebra Superior I: Los espacios vectoriales $\mathbb{R}^2$ y $\mathbb{R}^3$

Por Eduardo García Caballero

Introducción

A lo largo de esta unidad nos hemos enfocado en estudiar los vectores, las operaciones entre estos y sus propiedades. Sin embargo, hasta ahora solo hemos ocupado una definición provisional de vectores —listas ordenadas con entradas reales—, pero no hemos dado una definición formal de estos. En esta entrada definiremos qué es un espacio vectorial y exploraremos algunas de las propiedades de dos ejemplos importantes de espacios vectoriales: $\mathbb{R}^2$ y $\mathbb{R}^3$-

Las propiedades de espacio vectorial

En entradas anteriores demostramos que los pares ordenados con entradas reales (es decir, los elementos de $\mathbb{R}^2$), en conjunto con la suma entrada a entrada y el producto escalar, cumplen las siguientes propiedades:

1. La suma es asociativa:
\begin{align*}
(u+v)+w &= ((u_1,u_2) + (v_1,v_2)) + (w_1,w_2) \\
&= (u_1,u_2) + ((v_1,v_2) + (w_1,w_2)) \\
&= u+(v+w).\end{align*}

2. La suma es conmutativa:
\begin{align*}u+v &= (u_1,u_2) + (v_1,v_2) \\&= (v_1,v_2) + (u_1,u_2) \\&= v+u.\end{align*}

3. Existe un elemento neutro para la suma:
\begin{align*}
u + 0 &= (u_1,u_2) + (0,0) \\&= (0,0) + (u_1,u_2) \\&= (u_1,u_2) \\&= u.
\end{align*}

4. Para cada par ordenado existe un elemento inverso:
\begin{align*}
u + (-u) &= (u_1,u_2) + (-u_1,-u_2) \\&= (-u_1,-u_2) + (u_1,u_2) \\&= (0,0) \\&= 0.
\end{align*}

5. La suma escalar se distribuye bajo el producto:
\begin{align*}
(r+s)u &= (r+s)(u_1,u_2) \\&= r(u_1,u_2) + s(u_1,u_2) \\&= ru + su.
\end{align*}

6. La suma de pares ordenados se distribuye bajo el producto escalar:
\begin{align*}
r(u + v) &= r((u_1,u_2) + (v_1,v_2)) \\&= r(u_1,u_2) + r(v_1,v_2) \\&= ru + rv.
\end{align*}

7. El producto escalar es compatible con el producto de reales:
\[
(rs)u = (rs)(u_1,u_2) = r(s(u_1,u_2)) = r(su).
\]

8. Existe un elemento neutro para el producto escalar, que justo es el neutro del producto de reales:
\[
1u = 1(u_1,u_2) = (u_1,u_2) = u.
\]

Cuando una colección de objetos matemáticos, en conjunto con una operación de suma y otra operación de producto, cumple las ocho propiedades anteriormente mencionadas, decimos que dicha colección forma un espacio vectorial. Teniendo esto en consideración, los objetos matemáticos que pertenecen a la colección que forma el espacio vectorial los llamaremos vectores.

Así, podemos ver que los pares ordenados con entradas reales, en conjunto con la suma entrada a entrada y el producto escalar, forman un espacio vectorial, al cual solemos denominar $\mathbb{R}^2$. De este modo, los vectores del espacio vectorial $\mathbb{R}^2$ son exactamente los pares ordenados con entradas reales.

Como recordarás, anteriormente también demostramos que las ternas ordenadas con entradas reales, en conjunto con su respectiva suma entrada a entrada y producto escalar, cumplen las ocho propiedades antes mencionadas (¿puedes verificarlo?). Esto nos indica que $\mathbb{R}^3$ también es un espacio vectorial, y sus vectores son las ternas ordenadas con entradas reales. En general, el que un objeto matemático se pueda considerar o no como vector dependerá de si este es elemento de un espacio vectorial.

Como seguramente sospecharás, para valores de $n$ distintos de 2 y de 3 también se cumple que $\mathbb{R}^n$ forma un espacio vectorial. Sin embargo los espacios $\mathbb{R}^2$ y $\mathbb{R}^3$ son muy importantes pues podemos visualizarlos como el plano y el espacio, logrando así describir muchas de sus propiedades. Por esta razón, en esta entrada exploraremos algunas de las principales propiedades de $\mathbb{R}^2$ y $\mathbb{R}^3$.

Observación. Basándonos en la definición, el hecho de que una colección de elementos se pueda considerar o no como espacio vectorial depende también a las operaciones de suma y producto. Por esta razón, es común (y probablemente más conveniente) encontrar denotado el espacio vectorial $\mathbb{R}^2$ como $(\mathbb{R}^2,+,\cdot)$. Más aún, a veces será importante destacar a los elementos escalares y neutros, encontrando el mismo espacio denotado como $(\mathbb{R}^2, \mathbb{R}, +, \cdot, 0, 1)$. Esto lo veremos de manera más frecuente cuando trabajamos con más de un espacio vectorial, sin embargo, cuando el contexto nos permite saber con qué operaciones (y elementos) se está trabajando, podemos omitir ser explícitos y denotar el espacio vectorial simplemente como $\mathbb{R}^2$ o $\mathbb{R}^3$.

Combinaciones lineales

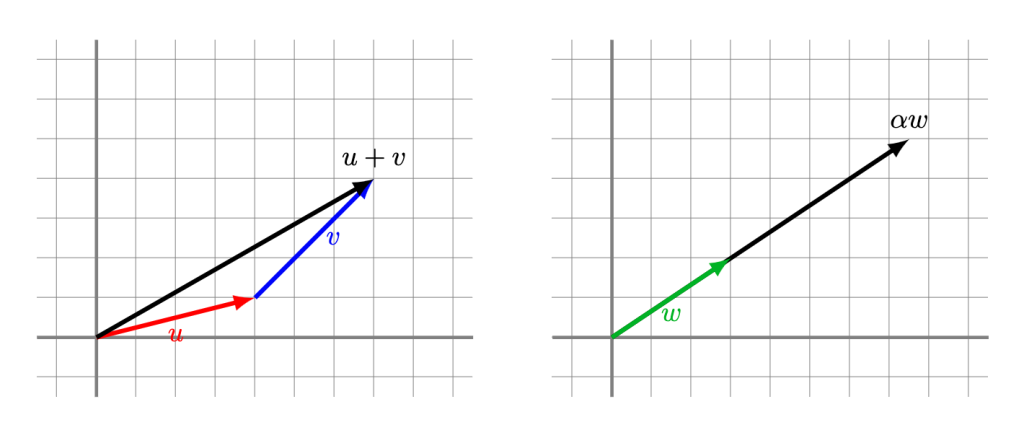
Como vimos en entradas anteriores, la suma de vectores en $\mathbb{R}^2$ la podemos visualizar en el plano como el resultado de poner una flecha seguida de otra, mientras que el producto escalar lo podemos ver como redimensionar y/o cambiar de dirección una flecha.

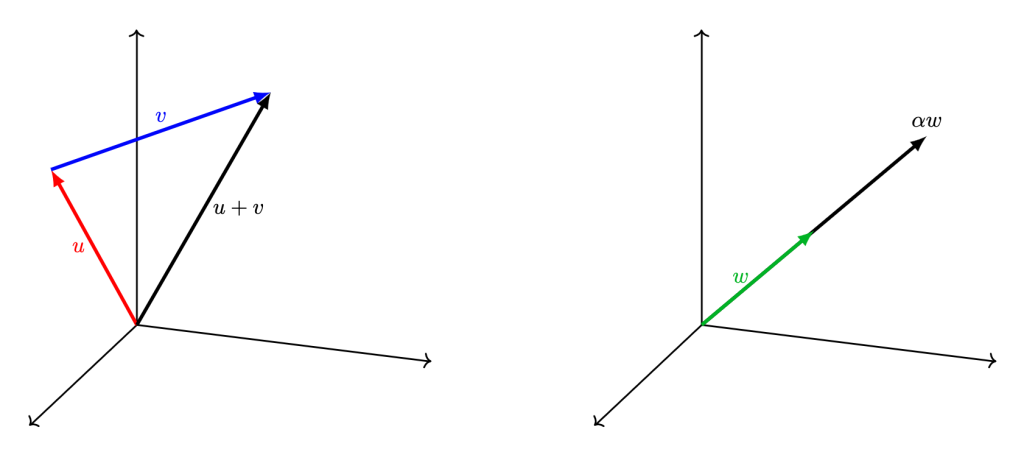
En el caso de $\mathbb{R}^3$, la intuición es la misma, pero esta vez en el espacio.

Si tenemos varios vectores, podemos sumar múltiplos escalares de ellos para obtener otros vectores. Esto nos lleva a la siguiente definición.

Definición. Dado un conjunto de $n$ vectores $v_1, \ldots, v_n$ en $\mathbb{R}^2$ o ($\mathbb{R}^3$), definimos una combinación lineal de estos vectores como el resultado de la operación
\[
r_1v_1 + r_2v_2 + \cdots + r_nv_n,
\]
donde $r_1, \ldots, r_n$ son escalares.

Ejemplo. En $\mathbb{R}^2$, las siguientes son combinaciones lineales:
\begin{align*}
4(9,-5) + 7(-1,0) + 3(-4,2) &= (17,-14), \\[10pt]
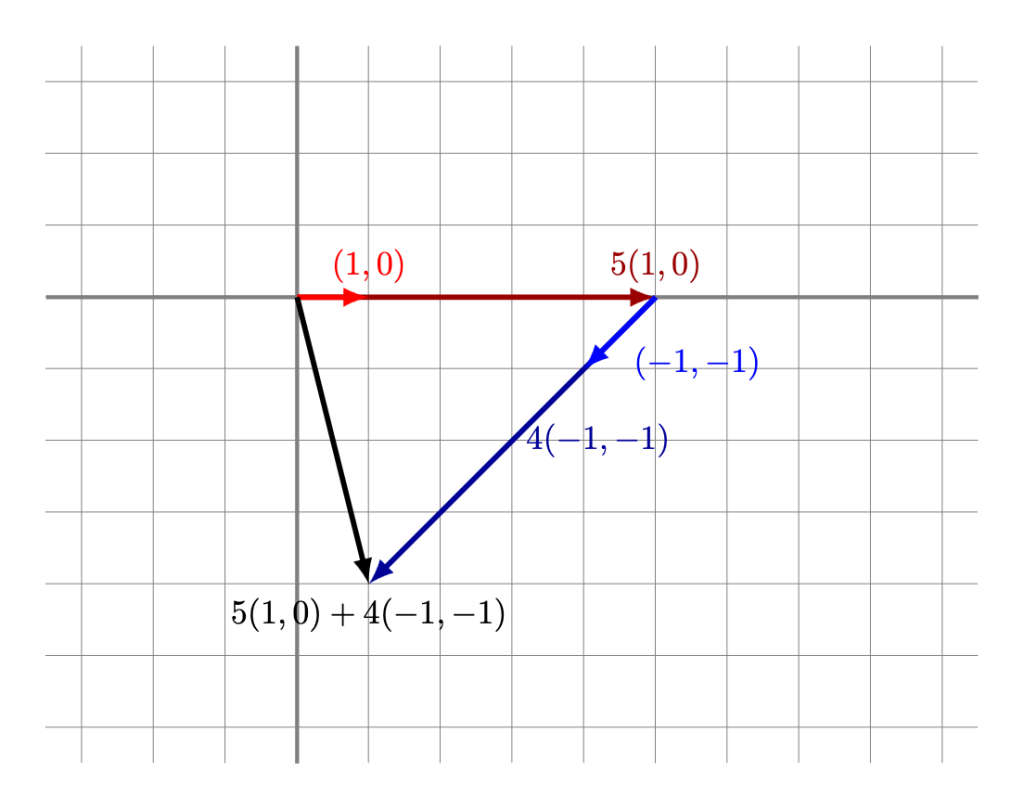
5(1,0) + 4(-1,-1) &= (1,-4), \\[10pt]
-1(1,0) + 0(-1,-1) &= (-1,0), \\[10pt]
5(3,2) &= (15,10).
\end{align*}
De este modo podemos decir que $(17,-14)$ es combinación lineal de los vectores $(9,-5)$, $(-1,0)$ y $(-4,2)$; los vectores $(1,-4)$ y $(-1,0)$ son ambos combinación lineal de los vectores $(1,0)$ y $(-1,-1)$; y $(15,10)$ es combinación lineal de $(3,2)$.

Las combinaciones lineales también tienen un significado geométrico. Por ejemplo, la siguiente figura muestra cómo se vería que $(1,-4)$ es combinación lineal de $(1,0)$ y $(-1,-1)$:

$\triangle$

Ejemplo. En el caso de $\mathbb{R}^3$, observamos que $(7,13,-22)$ es combinación lineal de los vectores $(8,1,-5)$, $(1,0,2)$ y $(9,-3,2)$, pues
\[
4(8,1,-5) + 2(1,0,2) + (-3)(9,-3,2) = (7,13,-22).
\]

$\triangle$

Espacio generado

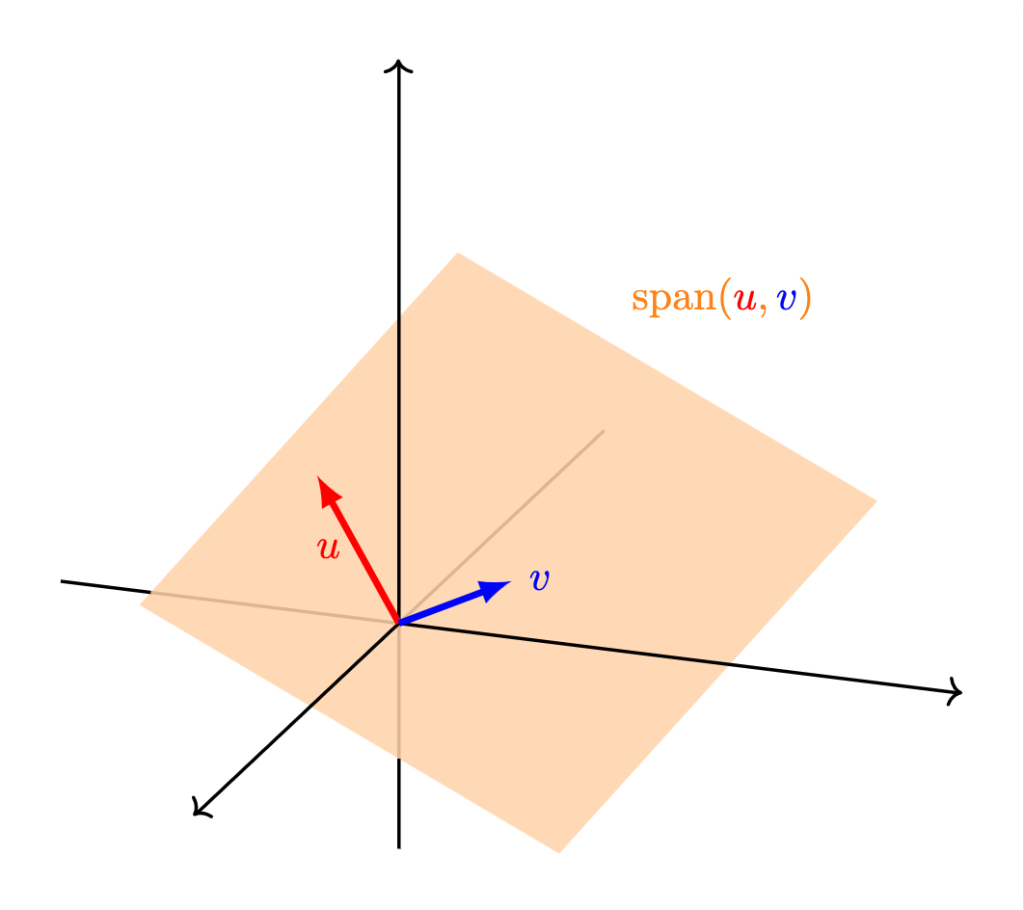
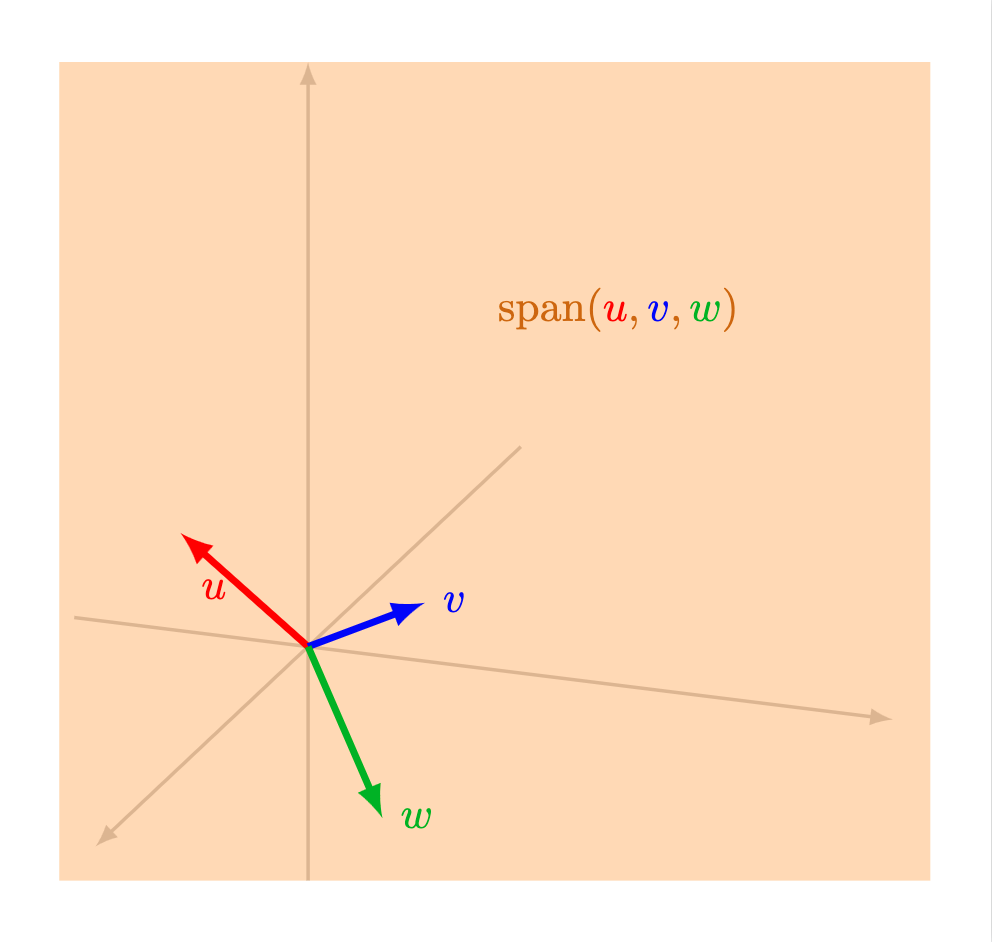
La figura de la sección anterior nos sugiere cómo entender a una combinación lineal de ciertos vectores dados. Sin embargo, una pregunta natural que surge de esto es cómo se ve la colección de todas las posibles combinaciones lineales de una colección de vectores dados.

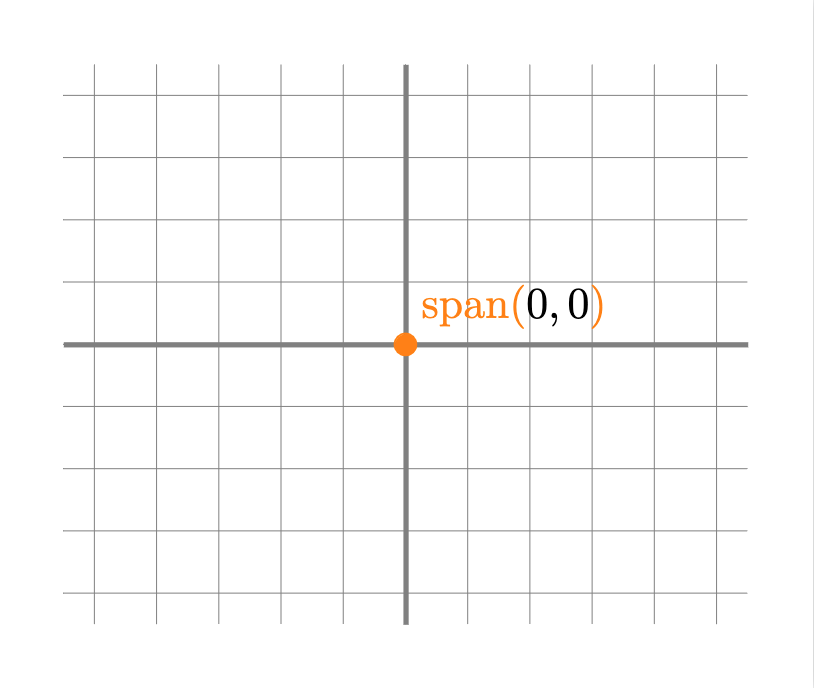
Definición. Dado un conjunto de $n$ vectores $v_1, \ldots, v_n$ en $\mathbb{R}^2$ o ($\mathbb{R}^3$), definimos al espacio generado por ellos como el conjunto de todas sus posibles combinaciones lineales. Al espacio generado por estos vectores podemos encontrarlo denotado como $\operatorname{span}(v_1, \ldots, v_n)$ o $\langle v_1, \ldots, v_n \rangle$ (aunque esta última notación a veces se suele dejar para otra operación del álgebra lineal).

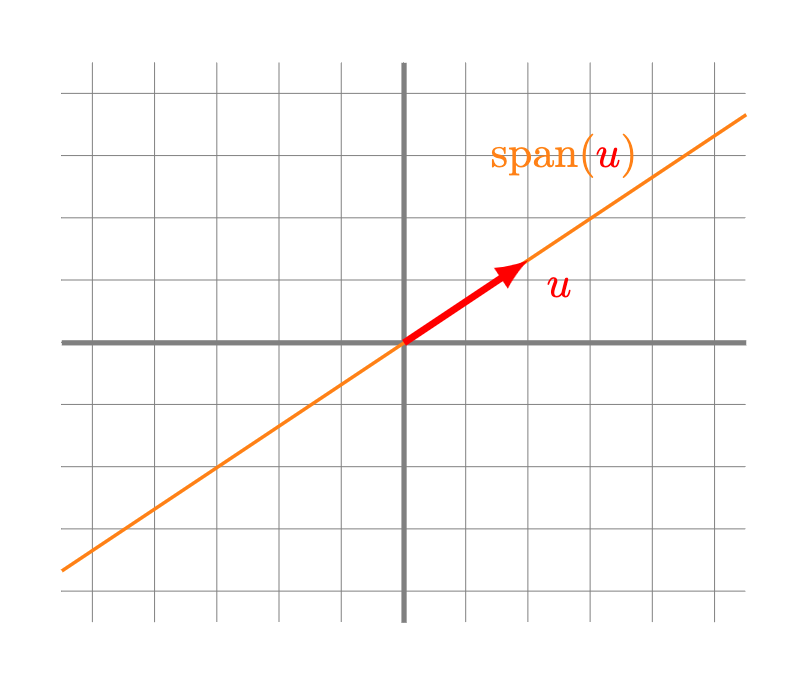
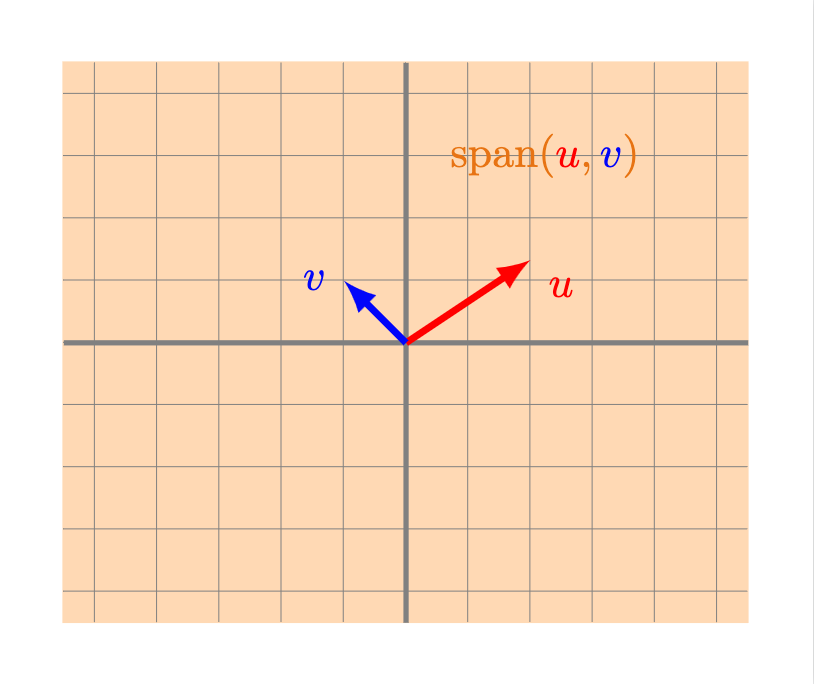
¿Cómo puede verse el espacio generado por algunos vectores? Puede demostrarse que en el caso de $\mathbb{R}^2$ tenemos los siguientes casos.

Un punto: esto sucede si y sólo si todos los vectores del conjunto son iguales al vector $0$.

Una recta: esto sucede si al menos un vector $u$ es distinto de 0 y todos los vectores se encuentran alineados. La recta será precisamente aquella formada por los múltiplos escalares de $u$.

Todo $\mathbb{R}^2$: esto sucede si al menos dos vectores $u$ y $v$ de nuestro conjunto no son cero y además no están alineados. Intenta convencerte que en efecto en este caso puedes llegar a cualquier vector del plano sumando un múltiplo de $u$ y uno de $v$.

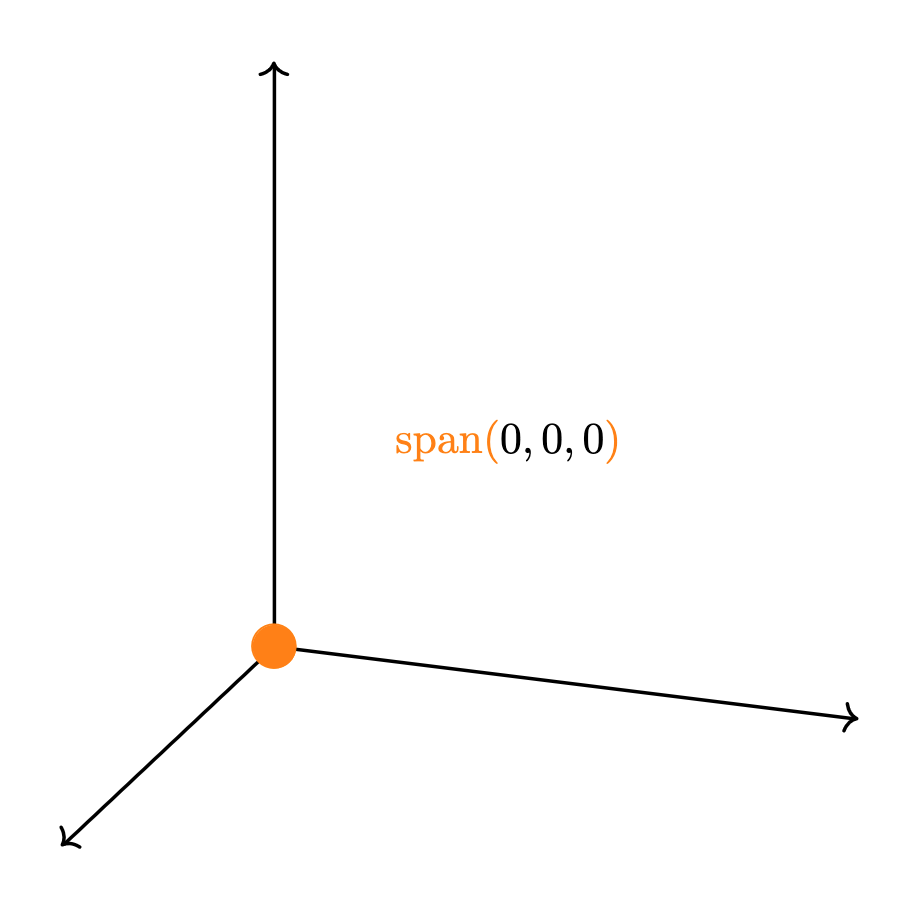
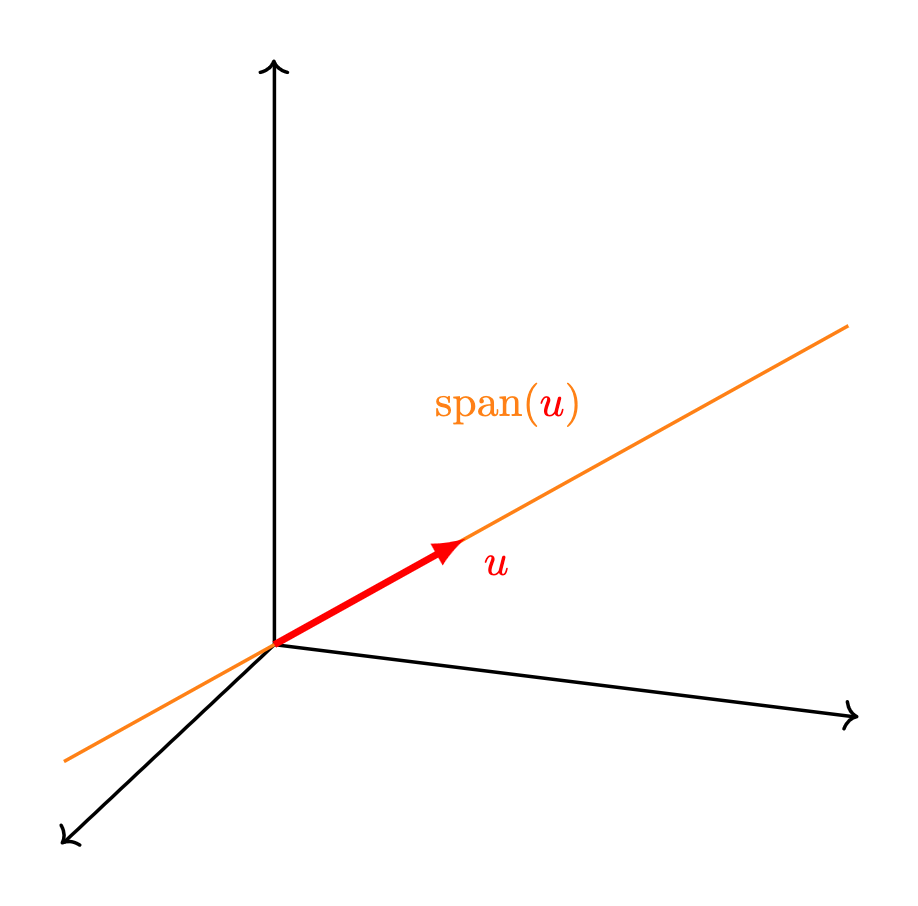
En $\mathbb{R}^3$, puede mostrarse que el espacio generado se ve como alguna de las siguientes posibilidades:

Un punto: esto sucede si y sólo si todos los vectores del conjunto son iguales al vector $0$.

Una recta: esto sucede si al menos un vector $u$ es distinto de $0$ y todos los vectores se encuentran alineados con $u$. La recta consiste precisamente de los reescalamientos de $u$.

Un plano: esto sucede si al menos dos vectores $u$ y $v$ no son cero y no están alineados, y además todos los demás están en el plano generado por $u$ y $v$ estos dos vectores.

Todo $\mathbb{R}^3$: esto sucede si hay tres vectores $u$, $v$ y $w$ que cumplan que ninguno es el vector cero, no hay dos de ellos alineados, y además el tercero no está en el plano generado por los otros dos.

Muchas veces no sólo nos interesa conocer la forma del espacio generado, sino también obtener una expresión que nos permita conocer qué vectores pertenecen a este. Una forma en la que podemos hacer esto es mediante ecuaciones.

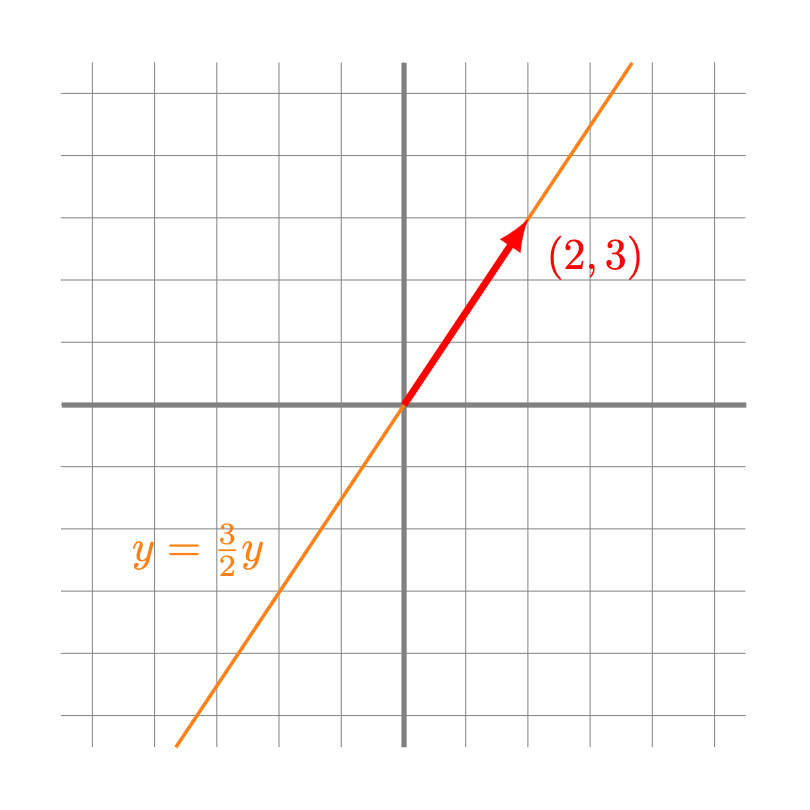
Ejemplo. Por ejemplo, observemos que el espacio generado el vector $(3,2)$ en $\mathbb{R}^2$ corresponde a los vectores $(x,y)$ que son de la forma
\[
(x,y) = r(2,3),
\]
donde $r \in \mathbb{R}$ es algún escalar. Esto se cumple si y sólo si
\[
(x,y) = (2r,3r),
\]
lo cual a su vez se cumple si y sólo si $x$ y $y$ satisfacen el sistema de ecuaciones
\[
\begin{cases}
x = 2r \\
y = 3r
\end{cases}.
\]
Si despejamos $r$ en ambas ecuaciones y las igualamos, llegamos a que
\[
\frac{x}{2} = \frac{y}{3},
\]
de donde podemos expresar la ecuación de la recta en su forma homogénea:
\[
\frac{1}{2}x – \frac{1}{3}y = 0;
\]
o bien en como función de $y$:
\[
y = \frac{3}{2}x.
\]

$\triangle$

La estrategia anterior no funciona para todos los casos, y tenemos que ser un poco más cuidadosos.

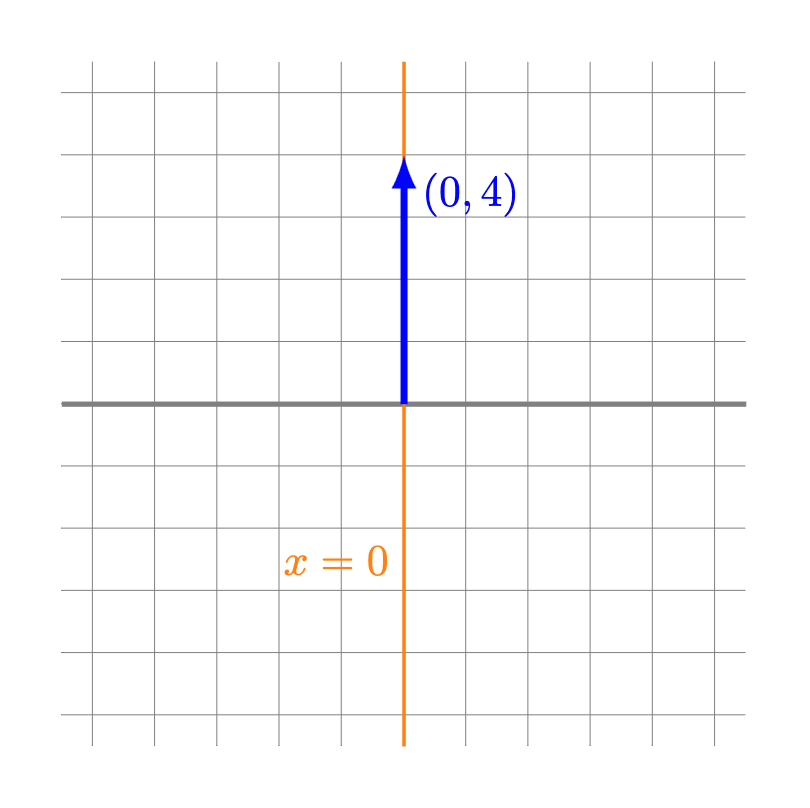
Ejemplo. El espacio generado por $(0,4)$ corresponde a todos los vectores $(x,y)$ tales que existe $r \in \mathbb{R}$ que cumple
\begin{align*}
(x,y) &= r(0,4) \\
(x,y) &= (0,4r),
\end{align*}
es decir,
\[
\begin{cases}
x = 0 \\
y = 4r
\end{cases}.
\]
En este caso, la única recta que satisface ambas ecuaciones es la recta $x = 0$, la cual no podemos expresar como función de $y$.

En la siguiente entrada veremos otras estrategias para describir de manera analítica el espacio generado.

$\triangle$

El saber si un vector está o no en el espacio generado por otros es una pregunta que se puede resolver con un sistema de ecuaciones lineales.

Ejemplo. ¿Será que el vector $(4,1,2)$ está en el espacio generado por los vectores $(2,3,1)$ y $(1,1,1)$? Para que esto suceda, necesitamos que existan reales $r$ y $s$ tales que $r(2,3,1)+s(1,1,1)=(4,1,2)$. Haciendo las operaciones vectoriales, esto quiere decir que $(2r+s,3r+s,r+s)=(4,1,2)$, de donde tenemos el siguiente sistema de ecuaciones:

$$\left\{\begin{matrix} 2r+s &=4 \\ 3r+s&=1 \\ r+s &= 2.\end{matrix}\right.$$

Este sistema no tiene solución. Veamos por qué. Restando la primera igualdad a la segunda, obtendríamos $r=1-4=-3$. Restando la tercera igualdad a la primera, obtendríamos $r=2-4=-2$. Así, si hubiera solución tendríamos la contradicción $-2=r=-3$. De este modo no hay solución.

Así, el vector $(4,1,2)$ no está en el espacio generado por los vectores $(2,3,1)$ y $(1,1,1)$. Geométricamente, $(4,1,2)$ no está en el plano en $\mathbb{R}^3$ generado por los vectores $(2,3,1)$ y $(1,1,1)$.

$\triangle$

Si las preguntas de espacio generado tienen que ver con sistemas de ecuaciones lineales, entonces seguramente estarás pensando que todo lo que hemos aprendido de sistemas de ecuaciones lineales nos servirá. Tienes toda la razón. Veamos un ejemplo importante.

Ejemplo. Mostraremos que cualquier vector en $\mathbb{R}^2$ está en el espacio generado por los vectores $(1,2)$ y $(3,-1)$. Para ello, tomemos el vector $(x,y)$ que nosotros querramos. Nos gustaría (fijando $x$ y $y$) poder encontrar reales $r$ y $s$ tales que $r(1,2)+s(3,-1)=(x,y)$. Esto se traduce al sistema de ecuaciones

$$\left \{ \begin{matrix} r+3s&=x\\2r-s&=y. \end{matrix} \right.$$

En forma matricial, este sistema es $$\begin{pmatrix} 1 & 3 \\ 2 & -1 \end{pmatrix} \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix}.$$

Como la matriz $\begin{pmatrix} 1 & 3 \\ 2 & -1 \end{pmatrix}$ tiene determinante $1(-1)-(3)(2)=-7$, entonces es invertible. ¡Entonces el sistema siempre tiene solución única en $r$ y $s$ sin importar el valor de $x$ y $y$! Hemos con ello demostrado que cualquier vector $(x,y)$ es combinación lineal de $(1,2)$ y $(3,-1)$ y que entonces el espacio generado por ambos es todo $\mathbb{R}^2$.

$\triangle$

Independencia lineal

Mientras platicábamos en la sección anterior de las posibilidades que podía tener el espcio generado de un conjunto de vectores en $\mathbb{R}^2$ y $\mathbb{R}^3$, fuimos haciendo ciertas precisiones: «que ningún vector sea cero», «que nos vectores no estén alineados», «que ningún vector esté en los planos por los otros dos», etc. La intuición es que si pasaba lo contrario a alguna de estas cosas, entonces los vectores no podían generar «todo lo posible». Si sí se cumplían esas restricciones, entonces cierta cantidad de vectores sí tenía un espacio generado de la dimensión correspondiente (por ejemplo, $2$ vectores de $\mathbb{R}^3$ no cero y no alineados sí generan un plano, algo de dimensión $2$). Resulta que todas estas restricciones se pueden resumir en una definición muy importante.

Definición. Dado un conjunto de $n$ vectores $v_1, \ldots, v_n$ en $\mathbb{R}^2$ o ($\mathbb{R}^3$), diremos que son linealmente independientes si es imposible escribir al vector $0$ como combinación lineal de ellos, a menos que todos los coeficientes de la combinación lineal sean iguales a $0$. En otras palabras, si sucede que $$r_1v_1 + r_2v_2 + \cdots + r_nv_n=0,$$ entonces forzosamente fue porque $r_1=r_2=\ldots=r_n=0$.

Puede mostrarse que si un conjunto de vectores es linealmente independiente, entonces ninguno de ellos se puede escribir como combinación lineal del resto de vectores en el conjunto. Así, la intuición de que «generan todo lo que pueden generar» se puede justificar como sigue: como el primero no es cero, genera una línea. Luego, como el segundo no es múltiplo del primero, entre los dos generarán un plano. Y si estamos en $\mathbb{R}^3$, un tercer vector quedará fuera de ese plano (por no ser combinación lineal de los anteriores) y entonces generarán entre los tres a todo el espacio.

La independencia lineal también se puede estudiar mediante sistemas de ecuaciones lineales.

Ejemplo. ¿Serán los vectores $(3,-1,-1)$, $(4,2,1)$ y $(0,-10,-7)$ linealmente independientes? Para determinar esto, queremos saber si existen escalares $r,s,t$ tales que $r(3,-1,-1)+s(4,2,1)+t(0,-10,-7)=(0,0,0)$ en donde al menos alguno de ellos no es el cero. Esto se traduce a entender las soluciones del siguiente sistema de ecuaciones:

$$\left\{ \begin{array} 33r + 4s &= 0 \\ -r +2s -10t &= 0 \\ -r + s -7t &= 0.\end{array} \right. $$

Podemos entender todas las soluciones usando reducción Gaussiana en la siguiente matriz:

$$\begin{pmatrix} 3 & 4 & 0 & 0 \\ -1 & 2 & -10 & 0 \\ -1 & 1 & -7 & 0 \end{pmatrix}.$$

Tras hacer esto, obtenemos la siguiente matriz:

$$\begin{pmatrix}1 & 0 & 4 & 0\\0 & 1 & -3 & 0\\0 & 0 & 0 & 0 \end{pmatrix}.$$

Así, este sistema de ecuaciones tiene a $t$ como variable libre, que puede valer lo que sea. De aquí, $s=3t$ y $r=-4t$ nos dan una solución. Así, este sistema tiene una infinidad de soluciones. Tomando por ejemplo $t=1$, tenemos $s=3$ y $r=-4$. Entonces hemos encontrado una combinación lineal de los vectores que nos da el vector $(0,0,0)$. Puedes verificar que, en efecto, $$(-4)(3,-1,-1)+3(4,2,1)+(0,-10,-7)=(0,0,0).$$

Concluimos que los vectores no son linealmente independientes.

$\triangle$

Si la única solución que hubiéramos obtenido es la $r=s=t=0$, entonces la conclusión hubiera sido que sí, que los vectores son linealmente independientes. También podemos usar lo que hemos aprendido de matrices y determinantes en algunos casos para poder decir cosas sobre la independencia lineal.

Ejemplo. Mostraremos que los vectores $(2,3,1)$, $(0,5,2)$ y $(0,0,1)$ son linealmente independientes. ¿Qué sucede si una combinación lineal de ellos fuera el vector cero? Tendríamos que $r(2,3,1)+s(0,5,2)+t(0,0,1)=(0,0,0)$, que se traduce en el sistema de ecuaciones $$\left\{ \begin{array} 2r &= 0 \\ 3r + 5s &= 0 \\ r + 2s + t &= 0. \end{array}\right.$$

La matriz asociada a este sistema de ecuaciones es $\begin{pmatrix} 2 & 0 & 0 \\ 3 & 5 & 0 \\ 1 & 2 & 1 \end{pmatrix}$, que por ser triangular inferior tiene determinante $2\cdot 5 \cdot 1 = 10\neq 0$. Así, es una matriz invertible, de modo que el sistema de ecuaciones tiene una única solución. Como $r=s=t$ sí es una solución, esta debe ser la única posible. Así, los vectores $(2,3,1)$, $(0,5,2)$ y $(0,0,1)$ son linealmente independientes. Geométricamente, ninguno de ellos está en el plano hecho por los otros dos.

$\triangle$

Bases

Como vimos anteriormente, existen casos en los que el espacio generado por vectores en $\mathbb{R}^2$ (o $\mathbb{R}^3$) no genera a todo el plano (o al espacio). Por ejemplo, en ambos espacios vectoriales, el espacio generado por únicamente un vector es una recta. Esto también puede pasar aunque tengamos muchos vectores. Si todos ellos están alineados con el vector $0$, entonces su espacio generado sigue siendo una recta también. En la sección anterior platicamos que intuitivamente el problema es que los vectores no son linealmente independientes. Así, a veces unos vectores no generan todo el espacio que pueden generar.

Hay otras ocasiones en las que unos vectores sí generan todo el espacio que pueden generar, pero lo hacen de «manera redundante», en el sentido de que uno o más vectores se pueden poner de más de una forma como combinación lineal de los vectores dados.

Ejemplo. Si consideramos los vectores $(2,1)$, $(1,0)$ y $(2,3)$, observamos que el vector $(2,3)$ se puede escribir como
\[
0(2,1)+3(1,0) + 2(2,3) = (7,6)
\]
o
\[
3(2,2) + 1(1,0) + 0(2,3)= (7,6),
\]
siendo ambas combinaciones lineales del mismo conjunto de vectores.

$\triangle$

Uno de los tipos de conjuntos de vectores más importantes en el álgebra lineal son aquellos conocidos como bases, que evitan los dos problemas de arriba. Por un lado, sí generan a todo el espacio. Por otro lado, lo hacen sin tener redundancias.

Definición. Diremos que un conjunto de vectores es base de $\mathbb{R}^2$ (resp. $\mathbb{R}^3$) si su espacio generado es todo $\mathbb{R}^2$ (resp. $\mathbb{R}^3$) y además son linealmente independientes.

El ejemplo de base más inmediato es el conocido como base canónica.

Ejemplo. En el caso de $\mathbb{R}^2$, la base canónica es $(1,0)$ y $(0,1)$. En \mathbb{R}^3$ la base canónica es $(1,0,0)$, $(0,1,0)$ y $(0,0,1)$.

Partiendo de las definiciones dadas anteriormente, vamos que cualquier vector $(a,b)$ en $\mathbb{R}$ se puede escribir como $a(1,0) + b(0,1)$; y cualquier vector $(a,b,c)$ en $\mathbb{R}^3$ se puede escribir como $a(1,0,0) + b(0,1,0) + c(0,0,1)$.

Más aún, es claro que los vectores $(1,0)$ y $(0,1)$ no están alineados con el origen. Y también es claro que $(1,0,0),(0,1,0),(0,0,1)$ son linealmente idependientes, pues la combinación lineal $r(1,0,0)+s(0,1,0)+t(0,0,1)=(0,0,0)$ implica directamente $r=s=t=0$.

$\triangle$

Veamos otros ejemplos.

Ejemplo. Se tiene lo siguiente:

Los vectores $(3,4)$ y $(-2,0)$ son base de $\mathbb{R}^2$ pues son linealmente independientes y su espacio generado es todo $\mathbb{R}^2$.
Los vectores $(8,5,-1)$, $(2,2,7)$ y $(-1,0,9)$ son base de $\mathbb{R}^3$ pues son linealmente independientes y su espacio generado es todo $\mathbb{R}^3$.

¡Ya tienes todo lo necesario para demostrar las afirmaciones anteriores! Inténtalo y haz dibujos en $\mathbb{R}^2$ y $\mathbb{R}^3$ de dónde se encuentran estos vectores.

$\triangle$

Como podemos observar, las bases de un espacio vectorial no son únicas, sin embargo, las bases que mencionamos para $\mathbb{R}^2$ coinciden en tener dos vectores, mientras que las bases para $\mathbb{R}^3$ coinciden en tener tres vectores. ¿Será cierto que todas las bases para un mismo espacio vectorial tienen la misma cantidad de vectores?

Más adelante…

En esta entrada revisamos qué propiedades debe cumplir una colección de objetos matemáticos para que sea considerado un espacio vectorial, además de que analizamos con más detalle los espacios vectoriales $\mathbb{R}^2$ y $\mathbb{R}^3$.

Como seguramente sospecharás, para otros valores de $n$ también se cumple que $\mathbb{R}^n$, en conjunto con sus respectivas suma entrada a entrada y producto escalar, forman un espacio vectorial. Sin embargo, en contraste con los espacios $\mathbb{R}^2$ y $\mathbb{R}^3$, este espacio es más difícil de visualizar. En la siguiente entrada generalizaremos para $\mathbb{R}^n$ varias de las propiedades que aprendimos en esta entrada.

Tarea moral

Realiza lo siguiente:
- De entre los siguientes vectores, encuentra dos que sean linealmente independientes: $(10,16),(-5,-8),(24,15),(10,16),(15,24),(-20,-32)$.
- Encuentra un vector de $\mathbb{R}^2$ que genere a la recta $2x+3y=0$.
- Determina qué es el espacio generado por los vectores $(1,2,3)$ y $(3,2,1)$ de $\mathbb{R}^3$.
- Da un vector $(x,y,z)$ tal que $(4,0,1)$, $(2,1,0)$ y $(x,y,z)$ sean una base de $\mathbb{R}^3$.
Demuestra que $(0,0)$ es el único vector $w$ en $\mathbb{R}^2$ tal que para todo vector $v$ de $\mathbb{R}^2$ se cumple que $v+w=v=w+v$.
Prueba las siguientes dos afirmaciones:
- Tres o más vectores en $\mathbb{R}^2$ nunca son linealmente independientes.
- Dos o menos vectores en $\mathbb{R}^3$ nunca son un conjunto generador.
Sean $u$ y $v$ vectores en $\mathbb{R}^2$ distintos del vector cero. Demuestra que $u$ y $v$ son linealmente independientes si y sólo si $v$ no está en la línea generada por $u$.
Encuentra todas las bases de $\mathbb{R}^3$ en donde las entradas de cada uno de los vectores de cada base sean iguales a $0$ ó a $1$.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Cálculo de determinantes
Entrada siguiente del curso: El espacio vectorial $\mathbb{R}^n$

Álgebra Superior I: Introducción a vectores y matrices con entradas reales

Por Eduardo García Caballero

Deja un comentario

Introducción

Los vectores y las matrices son algunos de los objetos matemáticos que nos encontraremos con mayor frecuencia durante nuestra formación matemática. Esto se debe a que nos permiten abordar con sencillez varios problemas de distintas áreas de las matemáticas, como lo son la geometría analítica y la teoría de gráficas. Además, nos ayudan a modelar con gran precisión fenómenos de otras disciplinas, como de la mecánica clásica, gráficos por computadora, circuitos eléctricos, robótica, entre otras.

A pesar de que el estudio a profundidad de los vectores y matrices lo realizaremos en los cursos de Álgebra Lineal I y Álgebra Lineal II, esto no es un impedimento para que nos familiaricemos con varios de los conceptos, técnicas y algoritmos que nos permitirán sacar provecho a esta maravillosa área de las matemáticas.

¿Qué son los vectores?

Dependiendo del área que estudiemos, nos podríamos encontrar con distintas definiciones de vectores. Por ejemplo, en la mecánica clásica se visualiza a los vectores como flechas en el plano o en el espacio, ancladas en un «origen» o en cualquier otro punto del plano. En ciencias de la computación, entenderemos que un vector consiste en un arreglo en el que todas sus entradas son datos del mismo tipo. Como veremos más adelante, las distintas formas de visualizar los vectores son equivalentes.

En este curso trabajaremos con un tipo específico de vectores: los vectores cuyas entradas son números reales. ¿Números reales? Sí. Aquí el temario de la asignatura de un brinco un poco grande. Hasta ahora, hemos intentado construir las matemáticas desde sus fundamentos: lógica, conjuntos, funciones, números naturales, etc. Sin embargo, ahora trabajaremos con el conjunto $\mathbb{R}$ de números reales.

Ya platicamos de que el conjunto de naturales $\mathbb{N}$ se puede pensar desde un sistema axiomático y que de hecho podemos «construir» a los naturales a partir de nociones de teoría de conjuntos. En el curso de Álgebra Superior 2 se platica de cómo construir al conjunto $\mathbb{Z}$ de enteros a partir de $\mathbb{N}$, al conjunto $\mathbb{Q}$ de racionales a partir de $\mathbb{Z}$ y finalmente de cómo construir a $\mathbb{R}$ desde $\mathbb{Q}$. Pero por ahora supondremos la existencia de $\mathbb{R}$ y que cumple todos los axiomas que se tratan por ejemplo en un curso de Cálculo Diferencial e Integral I.

Vectores con entradas reales

Un vector con entradas reales lo podemos entender como una lista ordenada de uno o más números (también conocida como tupla) en la que todos sus valores son números reales. Aquí «lista ordenada» lo pensamos no en el sentido de que sus entradas «van creciendo o decreciendo en orden», sino en el sentido «ordenado» como de parejas ordenadas de la segunda unidad de estas notas. Es decir, no nos importan no sólo los números usados, sino también en qué lugar quedaron.

Un ejemplo que seguramente ya has visto en tus clases de geometría analítica son los vectores en el plano o en el espacio. Recordemos que el vector $(5, \pi)$ determina una única posición en el plano, mientras que $\left(8, \sqrt{2}, \tfrac{4}{3}\right)$ determina una única posición en el espacio. Como ambas tuplas están formadas únicamente por números reales, podemos decir que son vectores con entradas reales. A cada uno de los números que aparecen en la lista le llamaremos entrada, y nos podemos referir a la posición de la entrada para decir cuál es su valor; por ejemplo, la primera entrada de $(5, \pi)$ es $5$, mientras que la tercera entrada de $\left(8, \sqrt{2}, \tfrac{4}{3}\right)$ es $\tfrac{4}{3}$.

Como recordarás, decimos que estos vectores se encuentran en $\mathbb{R}^2$ y $\mathbb{R}^3$, respectivamente. Analizando los ejemplos, te darás cuenta de que el número que acompaña a $\mathbb{R}$ se refiere a la cantidad de números reales que están enlistados en cada vector. Entonces, probablemente te preguntarás qué pasa con listas de más números. Aunque quizá sean más difíciles de visualizar (¡aunque no imposibles!), también existen vectores con cuatro, cinco o incluso más entradas. Esto nos lleva a la siguiente definición.

Definición. Para un número entero positivo $n$, un vector con $n$ entradas reales es una lista ordenada de $n$ elementos, el cual escribiremos $(x_1,x_2,\ldots,x_n)$. El conjunto $\mathbb{R}^n$ consiste de todos los vectores con $n$ entradas reales.

Así, podemos ver que tenemos que $(1,-3.5,e,1)$ es un vector en $\mathbb{R}^4$, mientras que $(1,1,2,3,5,7,13)$ es un vector en $\mathbb{R}^7$. En notación de conjuntos, $(1,-3.5,e,1)\in\mathbb{R}^4$ y $(1,1,2,3,5,7,13)\in\mathbb{R}^7$.

Una forma de empezar a ver cómo los vectores se relacionan entre ellos es preguntándonos cuándo estos son iguales. La primera condición que seguramente se nos vendrá a la mente es que los dos vectores deben tener la misma longitud; de este modo, podemos inmediatamente descartar que $(5, \pi)$ y $(8, \sqrt{2}, \tfrac{4}{3})$ sean iguales.

Otra condición que seguramente consideraremos es que todas sus entradas deben ser iguales. Así, podemos también descartar que $(5, \pi)$ y $(4, 8)$ sean iguales. Sin embargo, ¿son $(5,\pi)$ y $(\pi, 5)$ iguales? Como recordarás, los vectores son listas ordenadas, por lo que no sólo es importante que tengan las mismas entradas, sino que también aparezcan en el mismo orden. Así, podemos también descartar que $(5,\pi)$ y $(\pi, 5)$ sean iguales: basta ver con que la primera entrada del $(5,\pi)$ es $5$, mientras que la primera entrada de $(\pi,5)$ es $\pi$, y claramente $5\ne\pi$. Así mismo, $(1,5,8,1,3)$ es distinto de $(1,5,8,1,4)$ pues aunque compartan muchos elementos en varias de sus posiciones, en el primer vector la última entrada es $3$ y el el segundo la última entrada es $4$.

Definición. Diremos que dos vectores $(x_1,\ldots,x_n)$ y $(y_1,\ldots,y_n)$ de $\mathbb{R}^n$ son iguales si para toda $i=1,\ldots,n$ se tiene que $x_i=y_i$

Por otra parte, antes dijimos que los vectores tienen varias formas de ser representados. Como ejemplo de esto, podemos ver que el vector $(1,-3.5,e,1)$ puede ser representado como

\[
\begin{pmatrix}
1 \\
-3.5 \\
e \\
1
\end{pmatrix}
\qquad
\text{y}
\qquad
\begin{pmatrix}
1 & -3.5 & e & 1
\end{pmatrix}.
\]

Al formato de la izquierda se le conoce como vector vertical o vector columna, mientras que al formato de la derecha se le conoce como vector horizontal o vector fila. Dependiendo del contexto, en ocasiones nos encontraremos con estas representaciones en vez de la que mostramos inicialmente, aunque es importante recordar que siguen siendo vectores con entradas reales, pues son listas ordenadas de números reales.

Matrices con entradas reales

Otro objeto matemático en el que también se enlistan varios números reales se conoce como matriz, con la diferencia de que esta lista tiene forma de arreglo rectangular.

Definición. Una matriz con entradas reales es un arreglo rectangular en donde en cada una de sus posiciones se coloca un número real.

Por ejemplo, las siguientes son matrices con entradas reales:

\[
\begin{pmatrix}
0 & 8 & -4.5 \\
2 & 9 & 0 \\
1 & \pi & 5
\end{pmatrix},
\qquad
\begin{pmatrix}
0 & -3 & 9 & 4.25 \\
100 & 0.1 & -2 & \sqrt{2}
\end{pmatrix}.
\]
Como podrás ver, para poder identificar a una entrada de una matriz debemos de hacer referencia a dos propiedades: el número de fila y el número de columna en el que se encuentra. Las filas se cuentan de arriba hacia abajo, y las columnas de izquierda a derecha. Así, vemos que la entrada que se encuentra en la fila 3 y columna 2 de la primera matriz es $\pi$. A cada entrada le asignamos una coordenada $(i,j)$, donde $i$ es el número de fila y $j$ es el número de columna. Así, $\pi$ se encuentra en la posición $(3,2)$ de la primera matriz.

Por convención, cuando mencionamos el tamaño de una matriz, primero se especifica el número de filas y posteriormente el número de columnas. Así, la primera matriz es de tamaño $3\times 3$, mientras que la segunda es de tamaño $2 \times 4$. Ya que elegimos el tamaño de una matriz, podemos considerar a todas las matrices de ese tamaño.

Definición. El conjunto $M_{m,n}(\mathbb{R})$ consiste de todas las matrices de $m$ filas, $n$ columnas y en donde cada entrada es un número real.

En el caso de que la cantidad de filas y de columnas de la matriz sean el mismo, diremos que se trata de una matriz cuadrada. De nuestros ejemplos anteriores, la primera sí es una matriz cuadrada, pero la segunda no. Para simplificar un poco la notación, introducimos lo siguiente.

Definición. El conjunto $M_n(\mathbb{R})$ consiste de todas las matrices de $n$ filas, $n$ columnas y en donde cada entrada es un número real.

Es decir, simplemente $M_n(\mathbb{R})=M_{n,n}(\mathbb{R})$.

Al igual que pasa con los vectores, podemos comparar dos matrices para saber si estas son iguales. Como te podrás imaginar, hay algunas condiciones que dos matrices deben cumplir para ser iguales: en primera, ambas deben de tener el mismo tamaño; es decir, sus números de filas deben de ser iguales y sus números de columnas deben de ser iguales. Por lo tanto, vemos que las matrices mostradas anteriormente son diferentes. Además, sus correspondientes entradas deben de ser iguales. Podemos escribir esto en una definición como sigue.

Definición. Sean $A$ y $B$ matrices en $M_{m,n}(\mathbb{R})$. Diremos que estas matrices son iguales si para cada $i\in \{1,\ldots,m\}$ y cada $j\in \{1,\ldots,n\}$ se cumple que la entrada $(i,j)$ de $A$ es la misma que la entrada $(i,j)$ de $B$.

¿Puedes decir por qué las siguientes matrices son diferentes?
\[
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{pmatrix}
\ne
\begin{pmatrix}
1 & 4 & 7 \\
2 & 5 & 8 \\
3 & 6 & 9
\end{pmatrix}.
\]

Notación y algunos vectores y matrices especiales

En matemáticas, es usual que denotemos los vectores con letras minúsculas (siendo las más comunes la $u$, $v$ y $w$) aunque muchas veces te podrás encontrar con notaciones especiales que los hacen más fáciles de distinguir, por ejemplo, $\overrightarrow{a}$ o $\mathbf{a}$. Nosotros no haremos esta distinción y usaremos simplemente letras minúsculas. Por ejemplo podríamos tomar al vector $u=(1,2,3)$ de $\mathbb{R}^3$.

Por su parte, las matrices las solemos representar con letras mayúsculas (generalmente las primeras del abecedario: $A$, $B$, $C$). Si la entrada que se encuentra en la fila $i$ y colmuna $j$ de la matriz se le denota como con la correspondiente letra minúscula y con subíndices la posición de su entrada: $a_{ij}$. Así, tendríamos que en
\[
A=
\begin{pmatrix}
0 & 8 & -4.5 \\
2 & 9 & 0 \\
1 & \pi & 5
\end{pmatrix}
\]
la entrada $a_{13} = -4.5$ y la entrada $a_{31} = 1$. ¿Cuál es la entrada $a_{23}$?

Además, existen algunos vectores y matrices con entradas reales que nos encontraremos con bastante frecuencia, y por esta razón reciben nombres especiales:

El vector en el que todas sus entradas son el número cero se conoce como vector cero o vector nulo. Por ejemplo, el vector nulo en $\mathbb{R}^2$ es $ (0,0)$ mientras que el nulo en $\mathbb{R}^3$ es $(0,0,0)$. Generalmente, denotamos este vector como $0$ (o, en ocasiones, como $\overrightarrow{0}$ o $\mathbf{0}$) .Es importante observar que se usa el mismo símbolo para representar a los vectores nulos con números distintos de entradas (de modo que podremos encontrar que $0=(0,0)$, en el caso de $\mathbb{R}^2$, o que $0=(0,0,0)$, en el caso de $\mathbb{R}^3$). Esto es algo que debemos tener en cuenta, aunque no suele representar mayores complicaciones, pues el contexto nos dirá 1) Si el símbolo $0$ se usa para el real cero o el vector cero y 2) Con cuántas entradas estamos trabajando.
La matriz en el que todas sus entradas son cero se conoce como matriz cero o matriz nula. Ejemplos de matrices nulas son
\[
\begin{pmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}
\qquad
\text{y}
\qquad
\begin{pmatrix}
0 & 0 \\
0 & 0
\end{pmatrix}.
\]
Estas matrices se suelen denotar con el símbolo $\mathcal{O}$, aunque en el caso de las matrices sí es común especificar las dimensiones de la matriz, de modo que la primera matriz escrita en este inciso se denota como $\mathcal{O}_{3\times 4}$ mientras que una matriz cuadrada, como la segunda de este inciso, se denota como $\mathcal{O}_2$.

El vector en $\mathbb{R}^n$ cuya $i$-ésima entrada es $1$ y el resto de sus entradas es $0$ se conoce como vector canónico, y se denota $\mathrm{e}_i$. Por ejemplo, el vector canónico $\mathrm{e}_3$ en $\mathbb{R}^4$ es $(0,0,1,0)$.
Además, al conjunto de todos los posibles vectores canónicos en $\mathbb{R}^n$ se conoce como la base canónica de $\mathbb{R}^n$; así, la base canónica de $\mathbb{R}^4$ es
\[
\{(1,0,0,0), \ (0,1,0,0), \ (0,0,1,0), (0,0,0,1)\} = \{\mathrm{e}_1, \mathrm{e}_2, \mathrm{e}_3, \mathrm{e}_4\}.
\]
Llamamos diagonal de una matriz cuadrada a las componentes cuyos número de fila y número de columna coinciden. Además, diremos que una matriz es una matriz diagonal si es una matriz cuadrada en la que todas sus entradas que no están en la diagonal (es decir, que su número de fila es distinto a su número de columna) son cero. Ejemplos de matrices diagonales son
\[
\begin{pmatrix}
5 & 0 & 0 \\
0 & 8 & 0 \\
0 & 0 & \pi
\end{pmatrix}
\qquad
\text{y}
\qquad
\begin{pmatrix}
6 & 0 & 0 & 0 \\
0 & 7 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 9
\end{pmatrix}
\]
(Observemos que aquellas entradas que se encuentran sobre su diagonal también pueden ser cero, aquí no tenemos ninguna restricción).
La matriz diagonal en la que todas sus entradas sobre la diagonal son 1 se conoce como matriz identidad. Ejemplos de matrices identidad son
\[
\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}
\qquad
\text{y} \\
\qquad
\begin{pmatrix}
1
\end{pmatrix}.
\]
A esta matriz la denotamos por $\mathcal{I}$ y especificamos su tamaño como subíndice. Así, las matrices anteriores son ${I}_3$ e $\mathcal{I}_1$.

Más adelante…

En esta entrada vimos las definiciones de vectores y matrices con entradas reales que usaremos para trabajar en este curso. También revisamos cuándo dos vectores (o matrices) son iguales. Además, vimos algunos ejemplos de vectores y matrices que nos encontraremos con bastante frecuencia en las matemáticas.

En las siguientes entradas veremos que también se pueden hacer operaciones entre vectores y matrices, aunque necesitaremos que se cumplan algunas condiciones especiales.

Tarea moral

Basándonos en la definiciones, verifica las siguientes igualdades:
- El vector $(4-4,1,3)$ es igual al vector $(0,2-1,2+1)$.
- La matriz $A=\begin{pmatrix} 1 & 2 \\ 2 & 4\end{pmatrix}$ es igual a la matriz $B$ de $2\times 2$ cuyas entradas están dadas por $b_{ij}=i\cdot j$.
Encuentra todos los posibles vectores que hay en $\mathbb{R}^3$ cuyas entradas sean únicamente los números $1$ y $2$. ¿Cuántos deben de ser?
Seguramente algunos los nombres de los vectores y matrices especiales te recuerdan a algún tipo de operación. ¿Qué operaciones crees que podamos hacer con los vectores y/o matrices, y qué comportamiento tendrían aquellos que reciben un nombre especial?
¿Por qué podemos decir que una matriz nula cuadrada cumple con ser una matriz diagonal?
Escribe todos los elementos de la base canónica de $\mathbb{R}^6$.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Problemas de triángulo de Pascal y binomio de Newton
Entrada siguiente del curso: Operaciones de suma y producto escalar con vectores y matrices

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Espacios de funciones

Por Lizbeth Fernández Villegas

Deja un comentario

$ \textit{ MATERIAL EN REVISIÓN}$

Introducción

En las entradas anteriores hablamos de métricas definidas en distintos conjuntos. Trabajamos a partir de las distancias entre elementos representados como puntos. La mayoría de estos ejemplos fueron sobre el conjunto $\mathbb{R}^n$ pero, ¿será posible considerar como elementos objetos, aparentemente más complejos? Observemos ahora conjuntos de funciones y veamos si es posible definir una métrica entre ellas.

Considera el conjunto $C^0[a,b]$, que es el conjunto de funciones continuas que van del intervalo $[a,b] \subset \mathbb{R} \to \mathbb{R}$. Sean $f,g \in C^0[a,b]$. La suma de funciones y el producto de una función por un escalar para $\lambda \in \mathbb{R}$ están definidos como:

\begin{align*}
(f+g)(x)&:= f(x)+g(x)\\
(\lambda f)(x)&:= \lambda f(x)
\end{align*}

Estas operaciones nos permiten considerar $C^0[a,b]$ como un espacio vectorial. Las normas comúnmente usadas en este espacio son:

$$\norm{f}_p:= \left(\int_{a}^{b} |f(x)|^p \,dx \right)^{1/p} , \text{si } p \in [1,\infty),$$

$$\norm{f}_\infty:= \underset{a \leq x \leq b}{max}\, |f(x)|$$

En la sección de Espacios normados pudimos observar que una norma induce una métrica en un espacio vectorial. Es importante observar que la distancia entre funciones puede ser diferente según la métrica que se considere. Como ejemplo, para cada $k \in \mathbb{N}, \,$ consideremos las funciones en $C^0[0,1]$ definidas como:

\begin{align*}
f_k(x) &:= \left\{ \begin{array}{lcc}
1-kx & si & 0\leq x \leq \frac{1}{k}\\
0 & si & \frac{1}{k} \leq x \leq 1
\end{array}
\right.\\
g(x)&:= 0, \forall x \in [0,1]
\end{align*}

A continuación visualizamos el comportamiento de $f_k(x)$ para $k=1,2,3.$

Mientras que la función $g$ permanece sobre el eje horizontal.

Si calculamos la distancia entre $f_k(x)$ y $g(x)$ inducida por la norma $||\cdot||_\infty$, podemos ver que $\forall \, k \geq 1$

\begin{align*}
||f_k(x)-g(x)||_\infty &= \underset{0\leq x \leq 1}{max} \, |f_k(x)-g(x)|\\
&= \underset{0\leq x \leq \frac{1}{k}}{max} \, |1-kx-0| \\
&= \underset{0\leq x \leq \frac{1}{k}}{max} \, |1-kx|\\
&= 1
\end{align*}

La distancia es la línea más grande entre $f_k$ y el eje horizontal.

Pero si consideramos $||\cdot||_p$ para $p=1$
\begin{align*}
\norm{f_k(x)-g(x)}_1&=\norm{f_k(x)-0}_1\\
&=\norm{f_k(x)}_1\\
&= \int_{0}^{1} |f(x)| \,dx\\
&= \int_{0}^{1/k}1-kx\\
&=\dfrac{1}{2k}
\end{align*}

De modo que cuando $k \to \infty, \norm{f_k(x)-g(x)}_1 \to 0$

La distancia es el área bajo la curva $f_k.$

Esto muestra que la distancia entre dos funciones puede variar, considerablemente, al variar también la métrica usada.

Comentarios antes de la proposición

Nota que en el ejemplo anterior las funciones son acotadas, como lo son en general las funciones de $C^0[a,b]$, pues son continuas en un intervalo cerrado en $\mathbb{R}$. ¿Qué pasa si alguna de las funciones no es acotada?

Sean $f:[0,1] \to \mathbb{R} \text{ y } g:[0,1] \to \mathbb{R}$ definidas como:
\begin{align*}
f(x) &:= \left\{ \begin{array}{lcc}
1/x & si & 0 < x \leq 1\\
0 & si & x = 0
\end{array}
\right.\\
g(x)&:= 0
\end{align*}
Entonces para todo $ x \in [0,1]$
$|f(x)-g(x)|=|f(x)-0|=|f(x)|=f(x)$
Como $f$ no es acotada en $[0,1]$ no podemos hablar del valor del supremo por lo que la métrica inducida por $\norm{ \cdot }_\infty$ no está definida en este caso.

¿Qué pasa si $f \text{ y }g$ son acotadas pero no necesariamente son continuas?
Sean $f:[a,b] \to \mathbb{R}$ y $g:[a,b] \to \mathbb{R}$ tales que para todo $ \, x\in [a,b], |f(x)|\leq M_f \text{ y } |g(x)| \leq M_g$ para $M_f, M_g \in \mathbb{R}$ Entonces:
\begin{align*}
|f(x)-g(x)|&=|f(x)+(-g(x))|\\
&\leq|f(x)|+|g(x)|\\
&\leq M_f + M_g
\end{align*}

Se concluye que el conjunto $\{|f(x)-g(x)|: x \in [a,b]|\}$ es acotado y por tanto aquí sí podemos hablar del supremo.

Recordemos que en la entrada Espacios métricos mostramos esta distancia para el conjunto $\mathcal{B}(A,\mathbb{R})$ (el conjunto de funciones acotadas con dominio $A$ y contradominio $\mathbb{R}.$ Puedes verificar que $f$ y $g$ satisfacen ser acotadas bajo la definición en esa sección.

Podemos pensar que, para generalizar esta distancia entre funciones cuyo contradominio sea cualquier espacio métrico, basta con que esa distancia esté acotada. Veamos lo siguiente:

Definición. Función acotada. Sea $S$ un conjunto no vacío y $X=(X,d)$ un espacio métrico. Decimos que una función $f:S \to X$ es acotada si existe $M \in \mathbb{R}$ y $x_0 \in X$ tales que para todo $ \, y \in S$ ocurre que $d(f(y),x_0) \leq M$. El conjunto de funciones acotadas de $S$ en $X$ se denota como:
$$\mathcal{B}(S,X):= \{ f:S \to X:f \text{ es acotada}\}$$.

La bola $B(x_0,M)$ contiene al conjunto $f(S).$

Proposición. La métrica $d$ en $X$ induce una métrica en $\mathcal{B}(S,X)$ dada por:
$$d_\infty (f,g):= \underset{z\in S}{sup}\, \,d(f(z),g(z))$$
Y recibe el nombre de métrica uniforme.
Demostración:
Sean $f,g,h \in \mathcal{B}$ entonces:
1) \begin{align*} d_\infty(f,g)&=0 \\
\Leftrightarrow \underset{z\in S}{sup}\,d(f(z),g(z))&=0 \\
\Leftrightarrow \forall \, z \in S, d(f(z),g(z))&=0 \\
\Leftrightarrow \forall \, z \in S, f(z)&=g(z) \\
\Leftrightarrow f&=g. \\
\text{Por lo tanto: } d_\infty (f,g)=0 &\Leftrightarrow f=g
\end{align*}

2) \begin{align*}
d_\infty (f,g)&=\underset{z\in S}{sup}\,d(f(z),g(z))\\
&=\underset{z\in S}{sup}\,d(g(z),f(z)) \\
&=d_\infty(g,f).\\
\text{Por lo tanto: } d_\infty(f,g)&=d_\infty(g,f)
\end{align*}

3) \begin{align*}
d_\infty(f,g)&=\underset{z\in S}{sup}\,d(f(z),g(z))\\
&\leq \underset{z\in S}{sup}\,\{d(f(z),h(z))+d(h(z),g(z))\}\\
&\leq \underset{z\in S}{sup}\,d(f(z),h(z)) + \underset{z\in S}{sup}\,d(h(z),g(z))\\
&\leq d_\infty(f,h)+d_\infty(h,g)\\
\text{Por lo tanto: }d_\infty(f,g)&\leq d_\infty(f,h)+d_\infty(h,g).
\end{align*}

Ejemplos de espacios de funciones

Veamos ejemplos de espacios de funciones y analicemos la cercanía entre ellas. Recordemos que esto lo hacemos a través de las bolas abiertas con centro en un elemento del espacio métrico. En este caso, el centro es una función.

Funciones continuas del intervalo $[0,1]$ en $\mathbb{R}$

Si consideramos a $C^0 [0,1]$ podemos observar que la bola abierta con centro en $f=0$ y radio $1$ está dado por $\{h: |h(x)|<1,x \in [0,1]\}$. Entonces, una función $h$ que esté en $B(f=0,1)$ debe satisfacer que para todo $ x \in [0,1], \, -1<h(x)<1$.

Representación de una función $h$ cuya distancia a la función $0$ es menor que $1.$

En consecuencia, la bola abierta queda representada por curvas cuyos puntos se encuentren entre las rectas $y=-1$ y $y=1$.

Representación de funciones cuya distancia a la función $0$ es menor que $1$.

Por otro lado, si consideramos como centro la función identidad $I$ donde para cada $x \in [0,1],$ $I(x):=x, \,$ la bola de radio $1$ está dada por $\{h:|h(x)-x|<1,x \in [0,1]\}$. Entonces, una gráfica $h$ que esté en $B(I,1)$ debe satisfacer que para todo $ x \in [0,1], \, -1<h(x)-x<1$ es decir para todo $ x \in [0,1], \, x-1<h(x)<x+1.$

Representación de una función $h$ cuya distancia a la identidad es menor que $1$.

Entonces, la bola abierta queda representada por curvas cuyos puntos se encuentren entre las rectas $y=x-1$ y $y=x+1$.

Representación de funciones cuya distancia a la función identidad es menor que $1$.

De manera general si consideramos como centro una función $f$ la bola de radio $1$ está dada por $\{h: |h(x)-f(x)|<1,x \in [0,1]\}$. Entonces, una gráfica $h$ que esté en $B(f,1)$ debe satisfacer que para todo $ x \in [0,1], -1<h(x)-f(x)<1$ es decir para todo $ x \in [0,1], f(x)-1<h(x)<f(x)+1$.

Representación de una función continua $f: [0,1] \to \mathbb{R},$ el centro de la bola abierta.

Representación de una función $h$ cuya distancia a la función $f$ es menor que $1.$

Entonces, la bola abierta queda representada por curvas cuyos puntos se encuentren entre las curvas de $f(x)-1$ y $f(x)+1$.

Representación de funciones cuya distancia a la función $f$ es menor que $1$.

Funciones continuas del intervalo $[0,1]$ en $\mathbb{R}^2$
Consideremos a $\mathbb{R}^2$ con la métrica euclidiana y al conjunto
$$C([0,1], \mathbb{R}^2) := \{f:[0,1] \to \mathbb{R}^2 \, | \, f \text{ es continua}\}.$$
Una función en este conjunto se representa como una curva continua en $\mathbb{R}^2$

Representación de una función $h:[0,1] \to \mathbb{R}^2.$

Entonces, una función $h$ que esté en la bola abierta con centro en $f=0$ y radio $1$ debe satisfacer $\{ h: \norm{h(x)-0}<1,x \in [0,1]\}$. Por tal motivo, su representación debe estar dentro de la bola de radio $1$ con centro en $0$.

La distancia entre la función $h$ y $0$ es menor que $1$.

Concluimos que $B(f=0,1)=\{ h: \norm{h(x)}<1, x \in [0,1], \}$. Dicho conjunto puede representarse de esta forma:

Funciones cuya distancia a la función $0$ es menor que $1$.

Funciones continuas de $[0,1]^2$ en $\mathbb{R}$

Ahora identifiquemos el conjunto $B(f=0,1)$ en el espacio
$$C([0,1]^2, \mathbb{R}) := \{f:[0,1]^2 \to \mathbb{R} \, | \, f \text{ es continua}\}.$$
El cuadrado $[0,1]^2$ visualizado en el plano $x_1 \, x_2$ se muestra como una sábana continua y representa la función $f(x)=0, \, x \in [0,1]^2.$

Si $h$ está en $B(f=0,1)$ entonces $|h(x)-0|<1,x \in [0,1]^2$, es decir, para todo $x \in [0,1]^2, -1<h(x)<1$. De modo que su gráfica será una sábana que esté entre las gráficas de $f_1(x)=-1 \, y\, f_2(x)=1$.

La $B(f=0,1)$ será la colección de todas las sábanas que cumplan esas condiciones:

Ahora considera como centro la función $f(x_1,x_2)=x_1$. Observemos el conjunto $B(f,1)$ en el espacio $C([0,1]^2, \mathbb{R}).$
La gráfica de $f$ se muestra a continuación.

Representación de una función $f:[0,1]^2 \to \mathbb{R}$.

Si $h$ está en $B(f,1)$ entonces $|h(x)-f(x)|<1,x \in [0,1]^2$, es decir, para todo $x \in [0,1]^2, x_{1}-1<h(x_1,x_2)<x_{2}+1$. De modo que su gráfica será una sábana que esté entre las gráficas de $f_1(x_1,x_2)=x_{1}-1\,$ y $\, f_2(x_1,x_2)=x_{1}+1$.

La distancia entre la función $h$ y $f$ es menor que $1$.

La $B(f,1)$ será la colección de todas las sábanas que cumplan esas condiciones:

Queda como ejercicio al lector hacer el análisis corresponiente para una bola abierta con centro en una función arbitraria.

Representación de una función $h:[0,1]^2 \to \mathbb{R}^2$

Funciones continuas de $[0,1]^2$ en $\mathbb{R}^2$

Considera $h$ una función en
$$C([0,1]^2, \mathbb{R}^2) := \{f:[0,1]^2 \to \mathbb{R}^2 \, | \, f \text{ es continua}\}.$$
Bajo esa función, el cuadrado $[0,1]^2$ es transformado en una superficie como las mostradas en la imagen.

Si buscamos funciones que estén en la bola con centro en la función $0$ y radio $1$, demuestra que las figuras que representan la imagen de estas funciones estarán dentro del círculo unitario.

Representación de una función $h_1:[0,1]^2 \to \mathbb{R}^2$

Representación de una función $h_2:[0,1]^2 \to \mathbb{R}^2$

Representación de una función $h_3:[0,1]^2 \to \mathbb{R}^2$

Más adelante…

Aprenderemos cómo identificar objetos que se aproximan entre sí y las condiciones que debe haber para que esto ocurra. Conoceremos el concepto de sucesión convergente en espacios métricos y descubriremos más particularidades que en el espacio euclidiano no ocurren pero en otros espacios sí.

Tarea moral

Describe una representación de la bola abierta en el espacio $C([0,1], \mathbb{R}^2)$ con un centro en una función distinta a la función cero.
Describe una representación de la bola abierta con centro en una función arbitraria en el espacio de funciones $C([0,1]^2, \mathbb{R}).$
En el espacio de funciones $C([0,1]^2, \mathbb{R}^2)$ buscamos funciones que estén en la bola con centro en la función $0$ y radio $1$. Demuestra que las figuras que representan la imagen de estas funciones estarán dentro del círculo unitario.

Bibliografía

Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 17-22.

Enlaces

Nociones topológicas básicas en espacios métricos

Por Lizbeth Fernández Villegas

4 respuestas

$ \textit{ MATERIAL EN REVISIÓN}$

Introducción

Ya que hemos visto cómo son las bolas abiertas en diferentes métricas, procederemos a analizar cómo son cuando las comparamos con un conjunto $A \subset X$. Como recurso, usaremos imágenes representativas con la intención de ayudar en la abstracción de los conceptos que a continuación se anuncian. Aunque las bolas no necesariamente se representan siempre como circunferencias (métrica del taxista), o como objetos con bordes punteados (como el segmento vertical que forma parte de la bola abierta en la métrica del ascensor), para fines gráficos rescataremos la idea de usar líneas punteadas para hacer alusión al «borde» de una bola abierta, sugiriendo que son puntos en el conjunto $X$ que no están en ella. Por el contrario, representaremos con lineas continuas a los puntos que sí formen parte de un conjunto dado.

Unas breves comparaciones entre subconjuntos y puntos

Para iniciar, pensemos en un espacio métrico $(X,d)$:

Representación de un espacio métrico $X.$

Y en un conjunto $A$ contenido en $X$:

Representación de un conjunto $A$ contenido en un espacio métrico $X.$

Identifiquemos puntos arbitrarios en $X$:

Representación de puntos en el espacio métrico $X.$

Entonces un punto $x \in X$ puede pertenecer o no al conjunto $A$.
Si $x \in A$, entonces una bola abierta con centro en $x$ podría tener puntos tanto en $A$ como en $X \setminus A$.

Representación de una bola abierta con centro en $A$ y con puntos «dentro» y «fuera» del conjunto $A.$

Representación de otra bola abierta con centro en $A$ y con puntos «dentro» y «fuera» del conjunto $A.$

o bien, puede tener todos sus puntos en $A$

Representación de una bola abierta con centro en $A$ y con todos sus puntos en $A.$

¿Puede haber una bola con centro en un punto en $A$ que esté totalmente contenida en el conjunto $X \setminus A$?

Por otro lado, si consideramos ahora $x \notin A$ , una bola abierta con centro en $x$ podría tener puntos tanto en $A$ como en $X \setminus A$.

Representación de una bola abierta con centro en $X \setminus A$ y con puntos «dentro» y «fuera» del conjunto $A.$

Representación de otra bola abierta con centro en $X \setminus A$ y con puntos «dentro» y «fuera» del conjunto $A.$

O bien, puede solo tener puntos en $X \setminus A$

Representación de una bola abierta con centro en $X \setminus A$ y con todos sus puntos en $X \setminus A.$

¿Es posible que una bola con centro en un punto en $X \setminus A$ esté totalmente contenida en $A$?.

Habiendo hecho estos comentarios generales, asignemos términos a los puntos de $X$ según las condiciones que cumplan las bolas abiertas asociadas.

Conceptos topológicos en un espacio métrico

Definición. Punto interior de un conjunto. Sea $A$ un subconjunto del espacio métrico $(X,d)$ y sea $x \in X$. Decimos que $x$ es punto interior de $A$ en $(X,d)$ si existe $\varepsilon > 0$ tal que $B(x,\varepsilon) \subset A$.

Representación de una bola abierta con centro en $x$ contenida en $A.$

Aunque $x$ pueda tener alguna bola abierta que no esté «totalmente» contenida en $A$, basta con que exista una que sí lo esté para que a $x$ se le considere un punto interior.

Representación de bolas abiertas con centro en un punto interior $x.$ Existe una contenida en $A.$

De acuerdo con la definición, un punto $x \in X$ no será punto interior de $A$ cuando para todo $ \varepsilon >0, B(x,\varepsilon)$ tiene puntos en $X \setminus A$. Los siguientes esquemas muestran puntos que no son puntos interiores del conjunto $A$ (tal vez sí lo sean de otro conjunto).

Representación de las bolas abiertas con centro en un punto que no es punto interior de $A.$

Definición. Interior de un conjunto. El conjunto formado por todos los puntos interiores de $A$ se denomina interior de $A$ en $(X,d)$ y se denota como:
$$Int (A) := \{x \in X|x \text{ es punto interior de A}\}$$

Representación de puntos que tienen una bola abierta contenida en $A.$

El conjunto $Int(A)$ se representa de la siguiente manera:

Representación de todos los puntos interiores de $A.$

Definición. Conjunto abierto. Diremos que $A \subset X$ es un conjunto abierto en $(X,d)$ si $A=Int(A)$.

Nota que en la definición de punto interior, no hemos pedido, explícitamente, que el punto en cuestión pertenezca a $A,$ pero si pruebas que para todo $A \subset X$ se cumple que $Int(A) \subset A$ notarás que un conjunto $A$ es abierto cuando todos sus puntos son puntos interiores, es decir, cuando también $A \subset Int(A)$. El conjunto $A$ que estamos considerando en nuestros dibujos no es abierto, pues tiene puntos que no son puntos interiores.

Representación de un punto de $A$ que no tiene una bola abierta contenida en $A.$

Pero si tomamos un conjunto $A$ de la siguiente forma, sí coincide con su interior y por lo tanto, es abierto.

Representación de un conjunto $A$ donde todos sus puntos son puntos interiores de $A.$

Definición. Punto de contacto o punto de adherencia. Sea $A$ un subconjunto del espacio métrico $(X,d)$ y sea $x \in X$. Se dice que $x$ es punto de contacto (o de adherencia) de $A$ en $(X,d)$ si para todo $\varepsilon >0$ se cumple que $B(x,\varepsilon) \cap A \neq \emptyset$.

Representación de un punto de contacto de $A.$

Incluso un punto que no esté en $A$ podría ser punto de contacto de $A$.

Representación de un punto de contacto de $A$ que no está en $A.$

Pero si existe una bola abierta con centro en $x$ que no interseca al conjunto $A,$ $x$ no será punto de contacto, incluso si sí tuviera alguna bola que sí interseca al conjunto $A.$

Representación de un punto de $X$ que no es punto de contacto de $A.$

Definición. Cerradura o adherencia de un conjunto. El conjunto formado por todos los puntos de contacto es denominado la cerradura de $A$ en $(X,d)$, y se denota como:

$$ \overline {A} := \{x \in X| x \text{ es punto de contacto de A}\}$$

Representación de puntos de contacto del conjunto $A.$

Todos los puntos de contacto de $A$.

Definición. Conjunto cerrado. Diremos que un conjunto $A \subset X$ es un conjunto cerrado en $(X,d)$ si $A=\overline{A}$.
Si pruebas que para todo $A \subset X$ se satisface que $A \subset \overline{A}$ notarás que un conjunto $A$ es cerrado cuando todos sus puntos de contacto están en $A$, es decir, cuando $\overline{A} \subset A$. En el ejemplo que estamos manejando, $A$ no es cerrado, pues tiene puntos de contacto que no están en $A$:

Pero si $A$ fuera considerado inicialmente de esta forma, sí coincide con su cerradura y por tanto, es cerrado:

Representación de un conjunto que tiene como elementos a todos sus puntos de contacto.

Al final de esta sección se te propondrá como ejercicio demostrar que $A \subset X$ es un conjunto cerrado en $(X,d)$ si y solo sí su complemento $X \setminus A$ es un conjunto abierto en $(X,d)$.

Representación de un conjunto $A$ cerrado y su complemento abierto.

Definición. Bola cerrada. Sea $(X,d)$ un espacio métrico. Considera un punto $x \in X$ y $\varepsilon \in \mathbb {R}, \, \varepsilon>0$. La bola cerrada con centro en $x$ y radio $\varepsilon$ se define como el conjunto de puntos en $X$ tales que el valor de su distancia al punto $x$ es menor o igual que $\varepsilon$. Se denota como:

$$\overline{B}(x,\varepsilon) := \{y \in X | d(x,y) \leq \varepsilon \}$$

Nota: A diferencia de la bola abierta, la bola cerrada sí incluye a los puntos cuya distancia al centro es exactamente $\varepsilon$.

Antes de poner un círculo «cerrado» como representación de una bola cerrada, enunciemos la siguiente:

Proposición. La cerradura de una bola abierta $B(x,\varepsilon)$ (denotado como $\overline{B(x,\varepsilon)}$) no coincide, necesariamente con la bola cerrada $\overline{B}(x,\varepsilon)$. Veamos un contraejemplo con la métrica discreta en $\mathbb{R}^2$ y con $\varepsilon=1$.

Dado un punto $x$ en $\mathbb{R}^2$, según la definición, la bola cerrada de radio $1$ con centro en $x$ es el conjunto:

\begin{align*}
\overline{B}(x,1) :&= \{y \in \mathbb{R}^2 | d(x,y) \leq 1\}\\
&= \mathbb{R}^2
\end{align*}

Pues la distancia entre dos puntos en la métrica discreta solo puede ser $0$ o $1$.

Representación de una bola cerrada de radio $1$ en $\mathbb{R}^2$ con la métrica discreta.

Pero si consideramos que para todos los puntos $y$ de $\mathbb{R}^2$ la bola abierta $B(y,1)= \{y\}$, (pues la distancia entre $y$ y el resto de los puntos en $\mathbb{R}^2$ no es menor que $1$), veremos que todos los puntos en $\mathbb{R}^2$ que son distintos de $x$ tienen una bola abierta que no interseca a $B(x,1)$, por lo tanto no hay ningún punto de $\mathbb{R}^2$ diferente de $x$ que esté en la cerradura de $B(x,1)= \{x\}$. En conclusión $\overline{B(x,1)}=\{x\}$.

Representación de la cerradura de una bola abierta de radio $1$ en $\mathbb{R}^2$ con la métrica discreta.

Proposición. En espacios normados la cerradura de una bola abierta sí es la bola cerrada. Es decir $\overline{B(x,\varepsilon)} = \overline{B}(x,\varepsilon)$. La demostración se propone como ejercicio.

Definición. Punto de acumulación. Sea $A$ un subconjunto de un espacio métrico $(X,d)$ y sea $x \in X$. Decimos que $x$ es punto de acumulación de $A$ en $(X,d)$ si para todo $ \varepsilon >0$ se cumple que $(B(x,\varepsilon) \setminus \{ x \}) \cap A \neq \emptyset$. Nota que a diferencia del punto de contacto, el punto de acumulación se descarta de la intersección entre las bolas abiertas y $A$.

Representación de bolas abiertas que intersecan al conjunto $A$ incluso quitando el centro.

¿Es un punto de contacto también un punto de acumulación en cualquier métrica?

Proposición. Toda bola abierta que tiene un punto de acumulación de $A$, tiene también una cantidad infinita de puntos en $A.$

Demostración:
Supón que $x \in X$ es un punto de acumulación de $A$ y que $x \in B(y,\varepsilon), y \in X, \varepsilon>0$.

Representación de un punto de acumulación $x$ como elemento de una bola abierta con centro en $y.$

Supón también que, contrario a lo que se quiere demostrar, esta bola abierta tiene una cantidad finita de puntos en $A$, digamos $\{x_1,x_2,…,x_n\}$ distintos de $x$.

Representación de la cantidad finita de puntos que suponemos pertenecen a la bola abierta con centro en $y.$

Considera $\varepsilon_{i}:=d(x,x_i), \, i=1,2,…,n \,$ la distancia entre cada uno de ellos a $x$. Sea $\varepsilon_0>0$ tal que $B(x,\varepsilon_0) \subset B(y,\varepsilon).$ Esta $\varepsilon_0$ existe porque $x$ es elemento de $B(y,\varepsilon) \, $ y toda bola abierta es un conjunto abierto en el espacio métrico (se dejará como ejercicio al final de esta sección).
Sea $\varepsilon_{m}= min\{\varepsilon_{i}|i=0,…,n\}$. Entonces el conjunto $B(x,\varepsilon_{m})\setminus \{x\}$ deja fuera todos los puntos de $A$, pues para todo $ \, x_i, i=1,…,n$ pertenecientes a $A \cap B(y,\varepsilon), \varepsilon_{m} \leq d(x,x_i)$, por lo tanto existe una bola abierta que, al quitarle el punto $x$ no interseca a $A$.

Representación de una bola abierta con centro en $x$ que es punto de acumulación, pero al «quitar» $x$ no interseca al conjunto $A.$

Entonces $x$ no es un punto de acumulación de $A$, lo cual es una contradición a la hipótesis. Por lo tanto una bola abierta que tenga un punto de acumulación de $A$, tiene también una cantidad infinita de puntos en $A$.

Nota: Se puede concluir también que un conjunto finito no tiene puntos de acumulación.

Definición. Punto frontera de un conjunto. Sea $A$ un subconjunto del espacio métrico $(X,d)$ y sea $x \in X$. Decimos que $x$ es punto frontera de $A$ en $(X,d)$ si para toda $\varepsilon > 0$ se cumple que $B(x,\varepsilon) \cap A \neq \emptyset$ y también $B(x,\varepsilon) \cap (X/A) \neq \emptyset$ .

Representación de bolas abiertas que tienen puntos tanto «dentro» como «fuera» del conjunto $A.$

Definición. Conjunto frontera de un conjunto. El conjunto formado por todos los puntos frontera es denominado la frontera de $A$ en $(X,d)$, y se denota como:

$$\partial A := \{x \in X| x \text{ es punto frontera de A}\}$$

Proposición. Prueba que $\partial A := \overline{A} \setminus Int(A)$. La demostración se propone como ejercicio.

La Topología es un área de las Matemáticas que generaliza estos conceptos del espacio métrico. Estudia familias de subconjuntos de un conjunto $X$ donde los elementos, (que son subconjuntos de $X),$ se denominan abiertos en $X.$ Si esta familia $\tau \subset \mathcal{P}(X) \,$ de abiertos satisface que tiene al conjunto $X$ y al conjunto $\emptyset$ como elementos, que la unión arbitraria de abiertos es también un abierto y que la intersección de dos conjuntos abiertos es un conjunto abierto, decimos que $\tau$ es una topología, o un espacio topológico en $X.$ (Para saber más ver Antonyan, S., Curso de Topología. Facultad de Ciencias, UNAM). Para finalizar con esta sección, veamos por qué un espacio métrico es un espacio topológico:

Proposición. Sea $(X,d)$ un espacio métrico. Entonces cumple con los siguientes axiomas:

1. Los conjuntos $X$ y $\emptyset$ son abiertos en $(X,d)$.
2. Si $\{U_i\}:i \in \mathcal{I}$ es una colección de conjuntos abiertos de $X$ entonces la unión $\cup_{i\in \mathcal{I}} \, U_i$ es un conjunto abierto.
3. Si $U$ y $V$ son subconjuntos abiertos de $X$ entonces la intersección $U \cap V$ es un conjunto abierto en $X$.

Demostración:
Para demostrar que $X$ es abierto, demostraremos que cada punto en $X$ es un punto interior de $X$. Sea $x \in X$ y $\varepsilon>0$, por definición $B(x,\varepsilon)= \{y \in X|d(x,y)<\varepsilon \} \subset X. \,$ Por lo tanto para todo $\, x\in X, \, x \in Int(X)$. Se concluye que $X$ es abierto. La propiedad para el conjunto $\emptyset$ se cumple por vacuidad.

Representación de una bola abierta con centro en $x$ contenida en $X.$

Sea $x \in \cup_{i\in \mathcal{I}} \, U_i \,$ entonces $x \in U_{i_0}$ para algún $i_0 \in \mathcal{I}$. Como particularmente $U_{i_0}$ es un conjunto abierto, entonces existe $\varepsilon>0$ tal que$ B(x,\varepsilon) \subset U_{i_0} \subset \cup_{i\in \mathcal{I}} \, U_i$. Por lo tanto para todo $ \, x\in \cup_{i\in \mathcal{I}} \, U_i$ se cumple que $x \in Int(\cup_{i\in \mathcal{I}} \, U_i)$, en consecuencia $\cup_{i\in \mathcal{I}} \, U_i$ es un conjunto abierto en $X$.

Representación de una bola abierta con centro en $x$ contenida en la unión de abiertos.

Si $x \in U \cap V$ para $U,V$ abiertos en $X$, entonces $x \in U$ y $x \in V$ de modo que existen $\varepsilon_1 >0$ y $\varepsilon_2 >0$ tales que $B(x,\varepsilon_1) \subset U$ y $B(x,\varepsilon_2) \subset V$. Sea $\varepsilon= min \{\varepsilon_1,\varepsilon_2\}$ entonces $B(x,\varepsilon) \subset B(x,\varepsilon_1) \subset U$ y $B(x,\varepsilon) \subset B(x,\varepsilon_2) \subset V$. Así, $B(x,\varepsilon) \subset U \cap V$, probando así que para todo $\, x \in U \cap V, x \in Int(U \cap V)$. Por lo tanto $U \cap V$ es un conjunto abierto en $X.$

Representación de una bola abierta con centro en $x$ contenida en la intersección de dos abiertos.

Más adelante…

Pondremos en práctica las nociones aquí aprendidas para analizar espacios métricos de funciones. Una vez conocido mejor ese espacio, continuaremos con la generalización de definiciones vistas en los cursos de cálculo y hablaremos de convergencia de sucesiones, límite y continuidad en espacios métricos.

Tarea moral

Sea $X$ un espacio métrico y $A \subset X$. Demuestra que se cumplen las siguientes afirmaciones:

Una bola abierta en $X$ es un conjunto abierto.
El conjunto $Int(A)$ es abierto.
Para todo $A \subset X$, $Int(A) \subset A$.
Una bola cerrada en $X$ es un conjunto cerrado.
El conjunto $\overline{A}$ es cerrado.
$A$ es un conjunto cerrado en $(X,d)$ si y solo sí su complemento $X \setminus A$ es un conjunto abierto.
La frontera de $A$ es un conjunto cerrado.
Si $A$ es finito, entonces es cerrado.
En espacios normados la cerradura de una bola abierta sí es la bola cerrada. Es decir $\overline{B(x,r)} = \overline{B}(x,r)$.
¿Es siempre la frontera de una bola abierta $B(x,d)$ el mismo conjunto de puntos $y \in X$ donde se cumple la igualdad $d(x,y)=\varepsilon? \,$ Demuestra que en espacios normados sí ocurre.
$\partial A = \overline{A} \setminus Int(A)$.

Bibliografía

Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 60-66 y 74-77.
Bartle, R.G., The Elements of Real Analysis. New York: J. Wiley, 1964.Págs: 69-74.
Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 37-43.
Jost, J., Postmodern Analysis (3rd ed.). New York: Springer-Verlag, 2005. Págs: 84-87.
Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 60-62 y 64-66.
Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Págs: 32-35.

Enlaces

La bola abierta en un espacio métrico

Por Lizbeth Fernández Villegas

Deja un comentario

$ \textit{ MATERIAL EN REVISIÓN}$

Introducción

Probablemente recuerdes que en los cursos de Cálculo Diferencial e Integral se habló de bolas de radio $\varepsilon>0$ con centro en un punto $x$. Había otros conjuntos, como los conjuntos abiertos y cerrados, de los que habrás visto representaciones gráficas, (puedes consultar la entrada $\mathbb{R}^n$ como espacio Topológico para tener presente los conceptos en la métrica usual). Estas ideas pueden generalizarse a otros espacios con métrica distinta a la euclidiana. En la sección que aquí se presenta visualizaremos algunos ejemplos y comprobarás que conjuntos como la bola abierta, quedan representados por figuras diferentes a las ya conocidas (no siempre se trata de círculos o esferas). Observarás los cambios que las métricas pueden generar, incluso cuando también se trata de distancias en el conjunto $\mathbb {R}^n$.
Comencemos por identificar puntos que estén “cerca” entre sí, aquellos cuya distancia no exceda cierta cantidad. Para eso tenemos la siguiente:

Definición. Bola abierta. Sea $(X,d)$ un espacio métrico. Considera un punto $x \in X$ y $\varepsilon \in \mathbb {R}$ tal que $\varepsilon>0$. La bola abierta con centro en $x$ y radio $\varepsilon$ se define como el conjunto de puntos en $X$ tales que el valor de su distancia al punto $x$ es menor que $\varepsilon$. Se denota como:

$$B(x,\varepsilon) := \{y \in X | d(x,y) < \varepsilon\}$$

Representación de bola abierta con centro en $x.$ Los puntos en verde tienen distancia a $x$ menor que $\varepsilon,$ contrario a los puntos rojos.

Nota que si $x$ es el centro, entonces siempre está en la bola abierta sin importar el valor de $\varepsilon > 0$, pues precisamente, $d(x,x)=0<\varepsilon$

Ejemplos de bolas abiertas en espacios métricos

La bola abierta en la métrica discreta

Recordemos que en la métrica discreta, la distancia entre dos puntos diferentes siempre es $1$. Entonces, si $0<\varepsilon<1$ la bola abierta solo tendrá como elemento al centro.

Representación de $B(x, \varepsilon ),$ con $0 < \varepsilon<1 $ en la métrica discreta.

Por el contrario, si $\varepsilon>1$ la bola abierta tendrá como elementos a todos los elementos del espacio métrico.

Representación de $B(x, \varepsilon ),$ con $\varepsilon > 1 $ en la métrica discreta.

La bola abierta en $\mathbb{R}$ con la métrica euclidiana

Considera el conjunto $\mathbb{R}$ con la métrica usual.
\[
d(x,y) := |x-y| := \left\{ \begin{array}{lcc}
x-y & si & x \geq y \\
\\ y-x & si & x < y
\end{array}
\right.
\]
Para $x,y \in \mathbb{R}$

Entonces para un punto $x_{0} \in \mathbb{R}$ y $\varepsilon>0$, la bola abierta $B(x_0,\varepsilon)$ está dada por el intervalo abierto $(x_{0}-\varepsilon,x_{0}+\varepsilon)$.

Representación de $B(x_0,\varepsilon) = (x_{0}-\varepsilon,x_{0}+\varepsilon).$

Más específicamente, la bola abierta con centro en $0$ y radio $3$ es el intervalo $(-3,3)$.

Mientras que la bola abierta con centro en $2$ y radio $3$ es el intervalo $(-1,5)$.

La bola abierta en $\mathbb{R}^2$ con la métrica euclidiana

Considera ahora $\mathbb{R}^2$ y la métrica euclidiana definida por:
$$d(x,y) := \sqrt{(x_{1}-y_{1})^2+(x_{2}-y_{2})^2}$$
con $x=(x_{1},x_{2})$ y $y=(y_{1},y_{2}) \in \mathbb{R}^2$.

Entonces para un punto $x_{0}=(x_{0_1},x_{0_2}) \in \mathbb{R}^2$ y $\varepsilon>0$, la bola abierta $B(x_0,\varepsilon)$ está dada por el conjunto de puntos que están «dentro de la circunferencia» con centro en $x_0$ y radio $\varepsilon$.

Representación de $B(x_0, \varepsilon)$ en $\mathbb{R}^2$ con la métrica usual.

Representación de $B((2,3),4)$ en $\mathbb{R}^2$ con la métrica usual.

Por ejemplo, si $x_0=(2,3)$ y $\varepsilon=4$ la bola abierta $B((2,3),4)$ está formada por los puntos dentro de la circunferencia con centro en $(2,3)$ y radio $4$.

La bola abierta en $\mathbb{R}^3$ con la métrica euclidiana

Si pensamos en $\mathbb{R}^3$ y la métrica euclidiana definida por:
$$d(x,y) := \sqrt{(x_{1}-y_{1})^2+(x_{2}-y_{2})^2+(x_{3}-y_{3})^2}$$
con $x=(x_{1},x_{2},x_{3})$ y $y=(y_{1},y_{2},y_{3}) \in \mathbb{R}^3$.

Entonces para un punto $x_0=(x_{0_1},x_{0_2},x_{0_3}) \in \mathbb{R}^3$ y $\varepsilon>0$, la bola abierta $B(x_0,\varepsilon)$ está dada por el conjunto de puntos que están «dentro de la esfera» con centro en $x_0$ y radio $\varepsilon$.

Representación de $B(x_0, \varepsilon)$ en $\mathbb{R}^3$ con la métrica usual.

Representación de $B((3,2,1),3)$ en $\mathbb{R}^3$ con la métrica usual.

Por ejemplo, si $x_0=(3,2,1)$ y $\varepsilon=3$, la bola abierta $B((3,2,1),3)$ está formada por los puntos “dentro de la esfera” con centro en $(3,2,1)$ y radio $3$.

La bola abierta en la métrica del taxista
En la sección Otros ejemplos de espacios métricos definimos esta métrica en el conjunto $\mathbb{R}^2$ como:
$$d(x,y) :=|y_1-x_1|+|y_2-x_2| $$
para $x=(x_{1},x_{2})$ y $y=(y_{1},y_{2}) \in \mathbb{R}^2$.
Entonces para un punto $x_{0}=(x_{0_1},x_{0_2}) \in \mathbb{R}^2$ y $\varepsilon >0$, la bola abierta $B(x_{0},\varepsilon )$ está dado por el conjunto de puntos $y=(y_{1},y_{2}) \in \mathbb{R}^2$ que satisfacen:
\begin{align*}
d(x_{0},y)=|y_1-x_{0_1}|+|y_2-x_{0_2}|&< \varepsilon \\
\Leftrightarrow |y_2-x_{0_2}|&< \varepsilon -|y_1-x_{0_1}| \\
\Leftrightarrow – \varepsilon +|y_1-x_{0_1}|< y_2-x_{0_2}&< \varepsilon -|y_1-x_{0_1}|
\end{align*}
Esto quiere decir que el conjunto buscado está delimitado por las rectas:
\begin{align}
y_{2}-x_{0_2}&= \varepsilon -(y_1-x_{0_1})\\
y_{2}-x_{0_2}&= \varepsilon +(y_1-x_{0_1})\\
y_{2}-x_{0_2}&= – \varepsilon -(y_1-x_{0_1})\\
y_{2}-x_{0_2}&= – \varepsilon +(y_1-x_{0_1})
\end{align}
Que son representadas a continuación:

Como la desigualdad es estricta concluimos que la bola abierta será un «rombo abierto» cuyas diagonales tienen longitud $2\varepsilon$ con centro en el punto $x_{0}=(x_{0_1},x_{0_2})$.

Representación de $B(x_0, \varepsilon)$ en $\mathbb{R}^2$ con la métrica del taxista.

Como ejemplo considera la bola abierta con centro en $(-3,2)$ y de radio $2$. El conjunto $B((-3,2),2)$ se muestra en la siguiente imagen.

Representación de $B((-3,2),2)$ en $\mathbb{R}^2$ con la métrica del taxista.

La bola abierta en la métrica del ascensor

Recordemos que el desplazamiento entre dos pisos de edificios iguales o diferentes motiva una métrica en $\mathbb{R}^2$. (Ver Otros ejemplos de espacios métricos). Si estamos en el piso marcado con el punto $x_{0}=(x_{0_1},x_{0_2}) \in \mathbb{R}^2$ y tenemos $\varepsilon>0$ como límite de distancia, procedamos a identificar los puntos a los que podemos llegar:

Estando en el mismo edificio, el ascensor puede llevarnos hasta una distancia menor que $\varepsilon$ hacia arriba, o bien, una distancia menor que $\varepsilon$ hacia abajo.

Representación de $B((x_{0_1},x_{0_2}), \varepsilon)$ en $\mathbb{R}^2$ con la métrica del ascensor cuando $|x_{0_2}|> \varepsilon$.

Como la planta baja está a distancia $\varepsilon_1:=|x_{0_2}|$ entonces si $\varepsilon_1> \varepsilon$, nuestro ascensor no llega hasta ahí.

En contraparte, si $\varepsilon_1 \leq \varepsilon$, entonces sí podemos llegar a la planta baja y, quizá también, a otros niveles del «sótano».

En este caso, aún nos podemos desplazar hasta una distancia $\varepsilon-\varepsilon_1$, primero sobre el eje $x$ y luego sobre el eje $y$ a modo de la métrica del taxista. En consecuencia, la bola abierta está conformado por una linea vertical de longitud $2\varepsilon$, sin los extremos, que tiene centro en el punto $x_{0}=(x_{0_1},x_{0_2})$. Si $\varepsilon_1 < \varepsilon$, se agrega también a la bola abierta, un «rombo abierto» con centro en el punto $(x_{0_1},0)$ cuyas diagonales miden $2(\varepsilon-\varepsilon_1)$. Esto se representa en la siguiente imagen:

Representación de $B((x_{0_1},x_{0_2}), \varepsilon)$ en $\mathbb{R}^2$ con la métrica del ascensor cuando $|x_{0_2}|\leq \varepsilon$.

Como ejemplo, la bola con centro en $(-2,1)$ y radio $3$ tendrá la siguiente representación:

Representación de $B((-2,1), 3)$ en $\mathbb{R}^2$ con la métrica del ascensor.

La bola abierta en el tablero de ajedrez.
Hemos visto que en un conjunto dado por las casillas del tablero de ajedrez se pueden definir métricas de acuerdo al movimiento de cada pieza. Como ejemplo, considera el movimiento permitido para la reina. Sea $x_0$ la casilla donde se encuentra. En cada turno, esta pieza se puede mover en cualquier dirección y cualquier cantidad de casillas. Como la distancia entre dos casillas se define como el mínimo de movimientos necesarios para que la pieza llegue de una casilla a la otra, entonces tenemos las siguientes bolas abiertas para distintos valores de $\varepsilon$:

Si $0<\varepsilon \leq 1$ entonces la distancia entre dos casillas debe ser menor que $1$. En consecuencia buscamos señalar las casillas a las que se puede desplazar la reina en $0$ movimientos que es, únicamente, la casilla en la que está posicionada.

Representación de $B(x_0, \varepsilon)$ con $0<\varepsilon \leq 1$ en el tablero de ajedrez con la métrica de la reina.

Si $1<\varepsilon \leq 2$ entonces se permite hacer a lo más un movimiento. Las casillas a las que se puede desplazar la reina están señaladas en tonos amarillos, pues puede elegir cualquier dirección y elegir también, detenerse en cualquiera de ellas.

Representación de $B(x_0, \varepsilon)$ con $1<\varepsilon \leq 2$ en el tablero de ajedrez con la métrica de la reina.

Si $2<\varepsilon$ entonces ya se permiten hacer 2 movimientos. En la figura anterior podemos visualizar casillas no sombreadas en amarillo. No obstante a cualquiera de ellas se puede llegar desde alguna de las casillas iluminadas. En consecuencia, con dos movimientos es posible que la reina llegue a cualquier casilla del tablero.

Representación de $B(x_0, \varepsilon)$ con $2<\varepsilon$ en el tablero de ajedrez con la métrica de la reina.

En contraparte el rey, que también se puede mover en cualquier dirección, no puede avanzar más que una casilla por turno. Esto origina las siguientes representaciones de bolas abiertas:

Para $\varepsilon \leq 1$ el rey no puede hacer ningún movimento y permanece en la casilla donde esté ubicado.

Representación de $B(x_0, \varepsilon)$ con $0 < \varepsilon \leq 1$ en el tablero de ajedrez con la métrica del rey.

Para $1 <\varepsilon \leq 2$ el rey puede hacer un movimiento y acceder así, a las casillas adyacentes a su posición.

Representación de $B(x_0, \varepsilon)$ con $1 <\varepsilon \leq 2$ en el tablero de ajedrez con la métrica del rey.

Para $2 <\varepsilon \leq 3$ el rey puede avanzar hasta dos casillas, lo que se representa iluminando las casillas vecinas con respecto a la imagen anterior.

Representación de $B(x_0, \varepsilon)$ con $2 <\varepsilon \leq 3$ en el tablero de ajedrez con la métrica del rey.

Para $3 <\varepsilon \leq 4$ una nueva familia de casillas vecinas se agrega a la bola abierta. ¿Puedes decir entonces, cuál es la distancia más grande entre dos casillas con la métrica del rey? ¿Y con la de la reina?

Representación de $B(x_0, \varepsilon)$ con $3 <\varepsilon \leq 4$ en el tablero de ajedrez con la métrica del rey.

Más adelante

Retomaremos los conceptos de interior, cerradura o frontera de un conjunto, así como de conjunto abierto y cerrado vistos en los cursos de Cálculo pero ahora generalizados en cualquier espacio métrico.

Tarea moral

Representa las bolas abiertas en la métrica del ajedrez con otras piezas.
Muestra un ejemplo de bola abierta en la métrica del ascensor en el que el centro esté fuera del rombo, uno donde esté dentro y uno más donde el centro esté sobre el vértice.
Da un ejemplo de espacio métrico y dos bolas $B(x,\varepsilon_1)$ y $B(y,\varepsilon_2)$ tales que $\varepsilon_1>\varepsilon_2$ pero $B(x,\varepsilon_1) \subset B(y,\varepsilon_2)$.