Introducción
En las entradas anteriores hablamos de métricas definidas en distintos conjuntos. Trabajamos a partir de las distancias entre elementos representados como puntos. La mayoría de estos ejemplos fueron sobre el conjunto $\mathbb{R}^n$ pero, ¿será posible considerar como elementos objetos, aparentemente más complejos? Observemos ahora conjuntos de funciones y veamos si es posible definir una métrica entre ellas.
Considera el conjunto $C^0[a,b]$, que es el conjunto de funciones continuas que van del intervalo $[a,b] \subset \mathbb{R} \to \mathbb{R}$. Sean $f,g \in C^0[a,b]$. La suma de funciones y el producto de una función por un escalar para $\lambda \in \mathbb{R}$ definidos como:
\begin{align*}
(f+g)(x)&:= f(x)+g(x)\\
(\lambda f)(x)&:= \lambda f(x)
\end{align*}
Nos permiten considerar $C^0[a,b]$ como un espacio vectorial. Presentamos algunas normas para este espacio:
$$\norm{f}_p:= (\int_{a}^{b} |f(x)|^p \,dx)^{1/p} , \text{si } p \in [1,\infty),$$
$$\norm{f}_\infty:= máx\{|f(x)|:a\leq x \leq b \}.$$
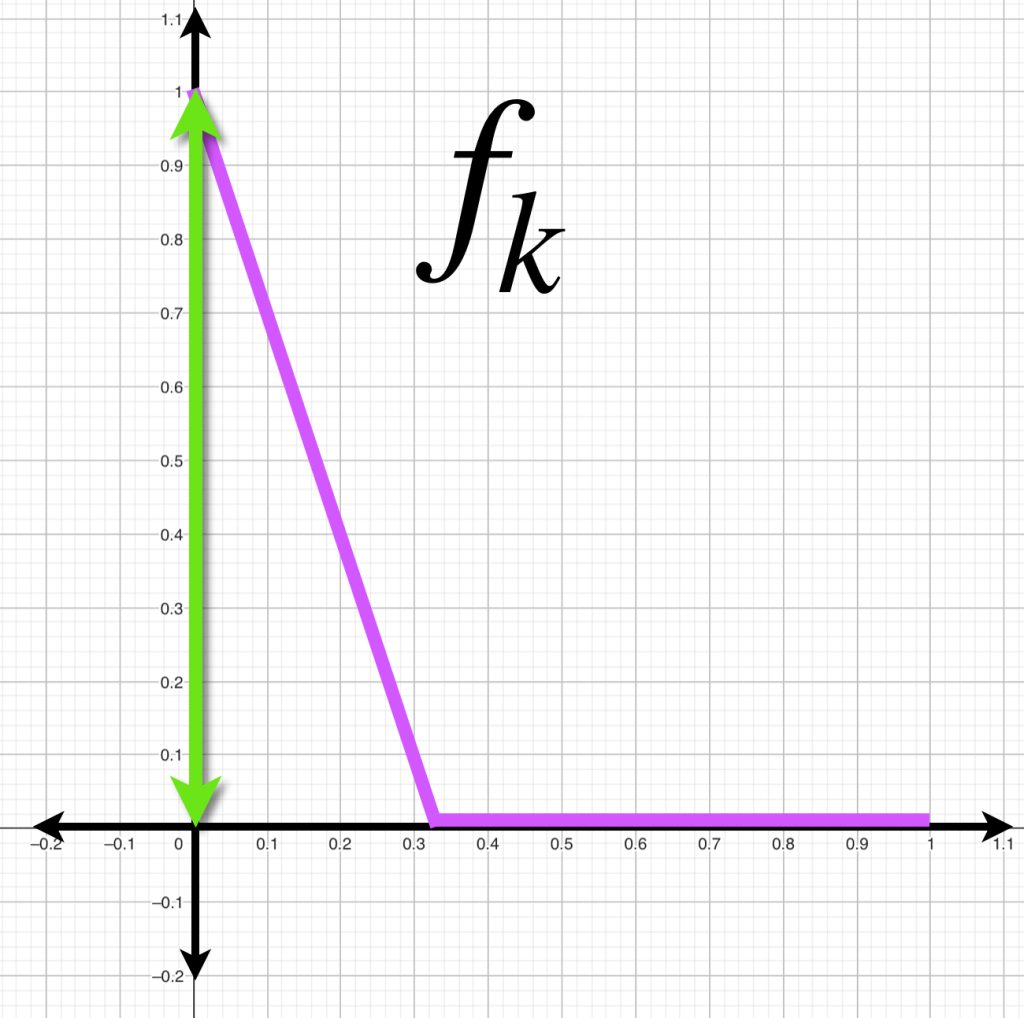
En la sección de Espacios normados pudimos observar que una norma induce una métrica en un espacio vectorial. Es importante observar que la distancia entre funciones puede ser diferente según la métrica que se considere. Como ejemplo, consideremos las funciones en $C^0[0,1]$ definidas como:
\begin{align*}
f_k(x) &= \left\{ \begin{array}{lcc}
1-kx & si & 0\leq x \leq \frac{1}{k}\\
0 & si & \frac{1}{k} \leq x \leq 1
\end{array}
\right.\\
g(x)&= 0, \forall x \in [0,1]
\end{align*}
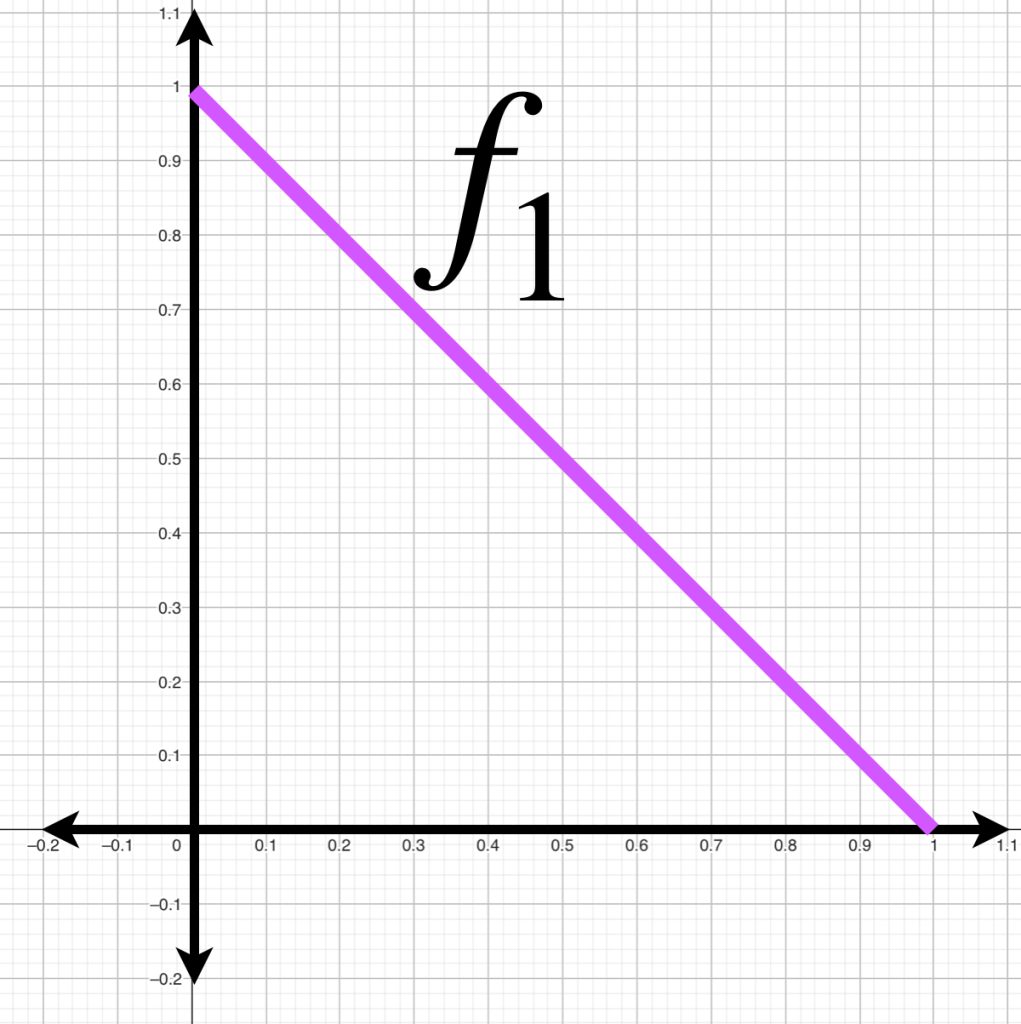
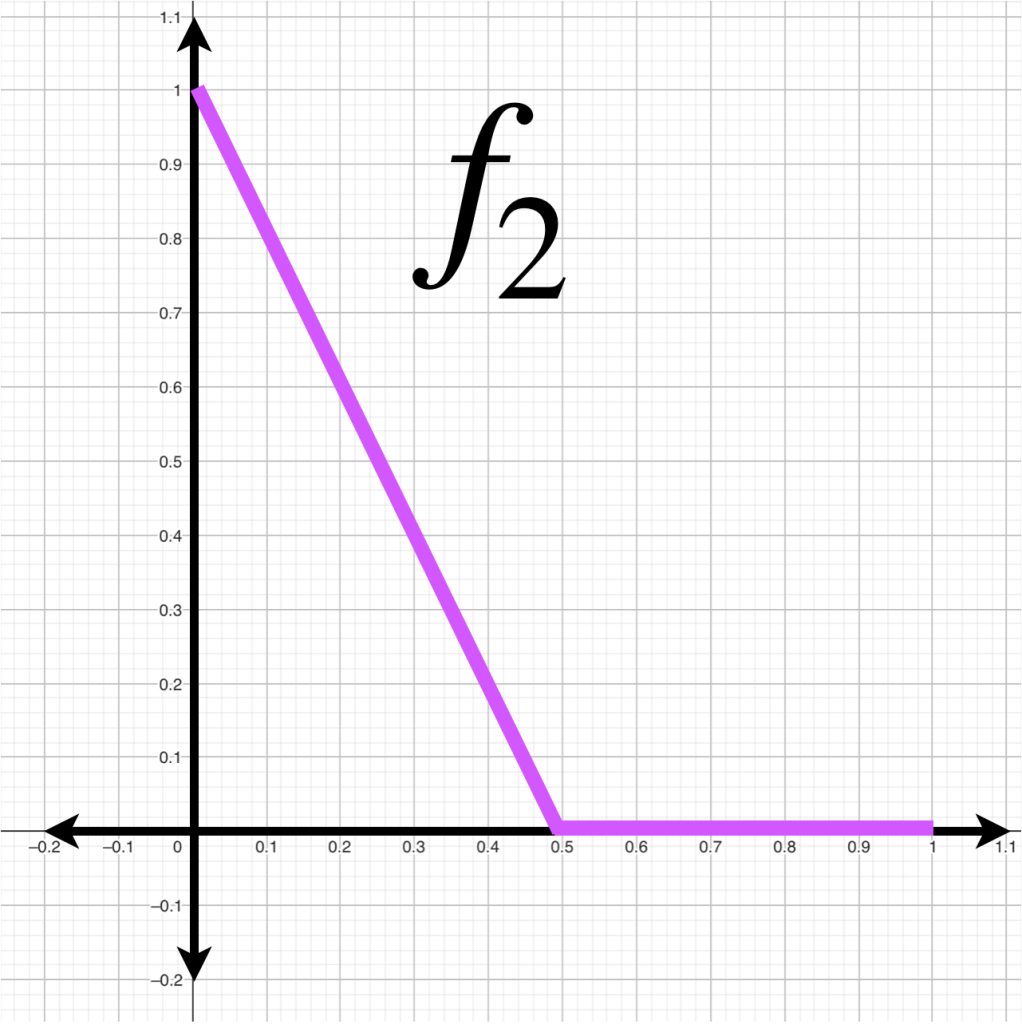
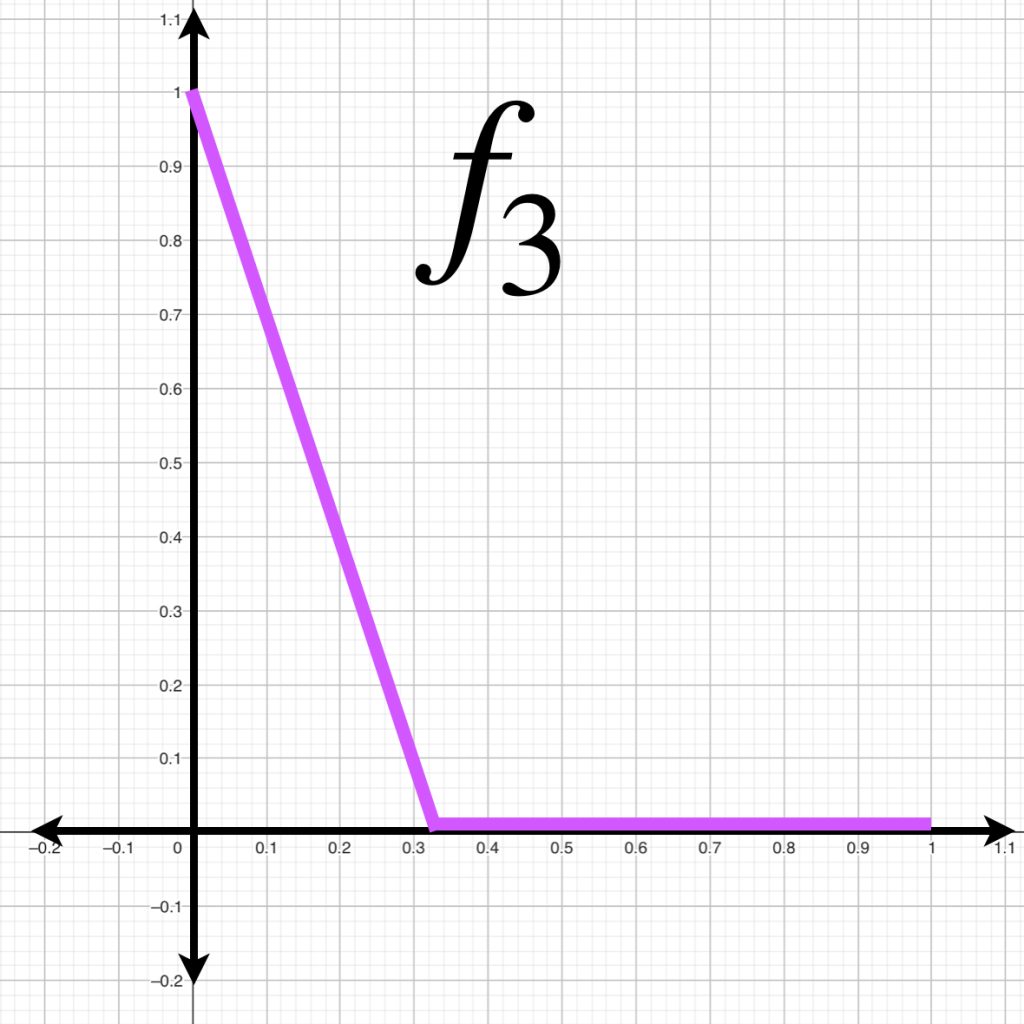
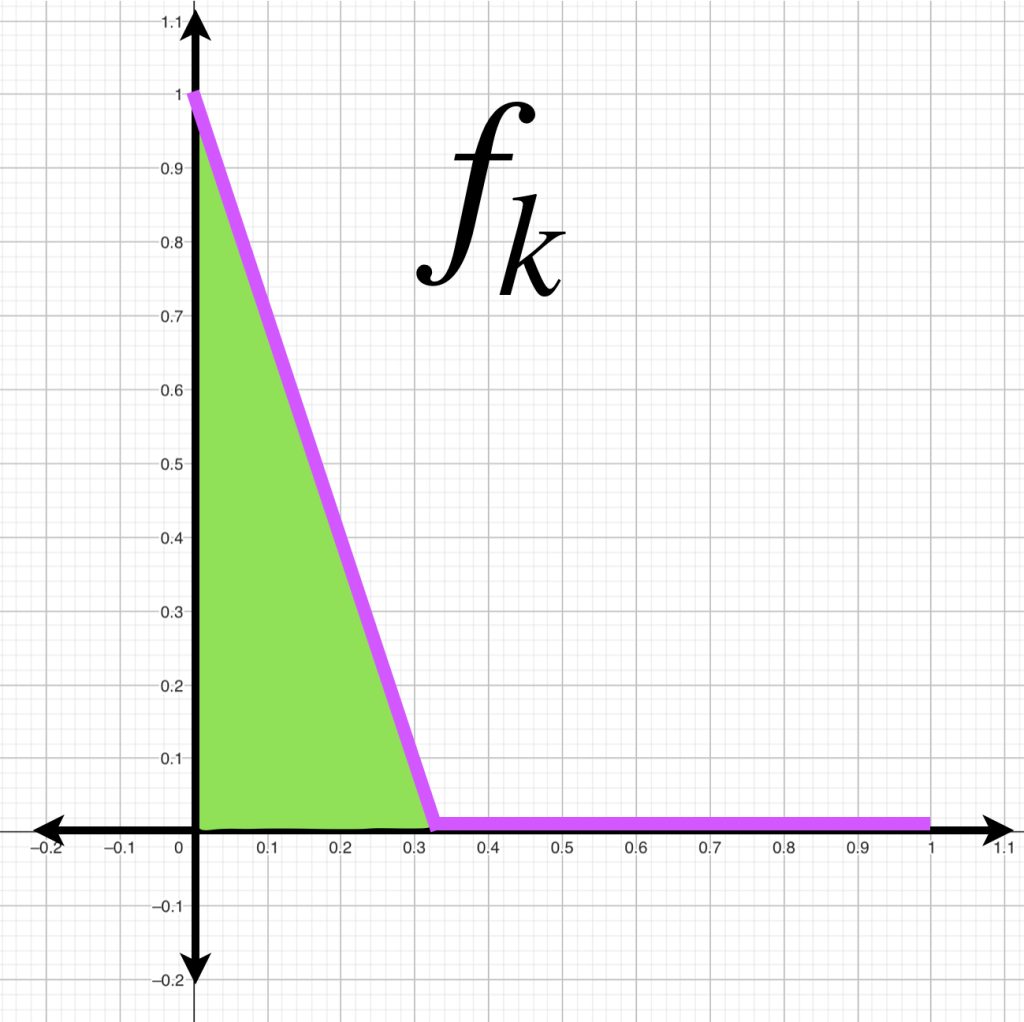
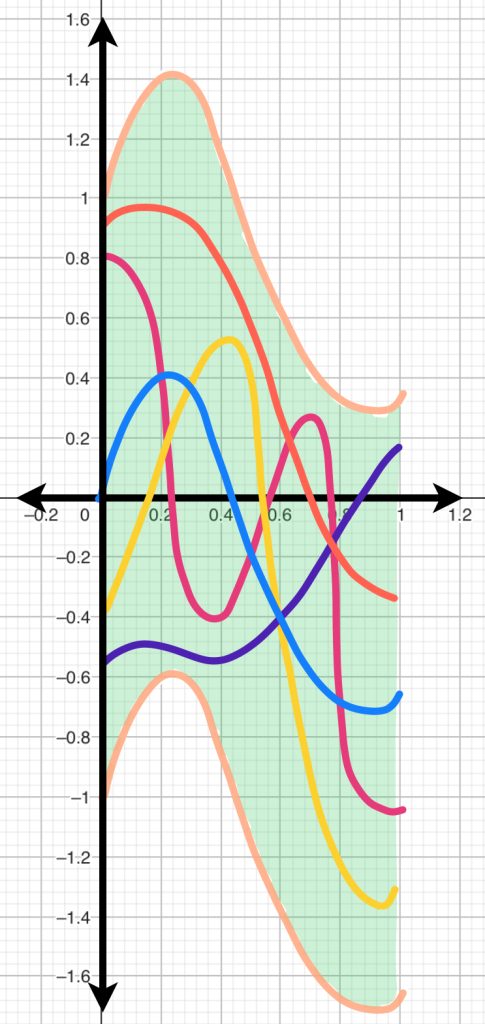
A continuación visualizamos el comportamiento de $f_k(x)$ para $k=1,2,3.$
Mientras que la función $g$ permanece sobre el eje horizontal.
Si calculamos la distancia entre $f_k(x)$ y $g(x)$ con la norma $||\cdot||_\infty$, podemos ver que $\forall \, k \geq 1$
\begin{align*}
||f_k(x)-g(x)||_\infty &= máx\{|f_k(x)-g(x)|:0\leq x \leq 1 \}\\
&= máx\{|1-kx-0|: 0\leq x \leq \frac{1}{k} \}\\
&= máx\{|1-kx|:0\leq x \leq \frac{1}{k} \}\\
&= 1
\end{align*}
Pero si consideramos $||\cdot||_p$ para $p=1$
\begin{align*}
\norm{f_k(x)-g(x)}_1&=\norm{f_k(x)-0}_1\\
&=\norm{f_k(x)}_1\\
&= \int_{0}^{1} |f(x)| \,dx)\\
&= \int_{0}^{1/k}1-kx\\
&=\dfrac{1}{2k}
\end{align*}
De modo que cuando $k \to \infty, \norm{f_k(x)-g(x)}_1 \to 0$
Esto muestra que la distancia entre dos funciones puede variar, considerablemente, al variar también la métrica usada.
Comentarios antes de la proposición
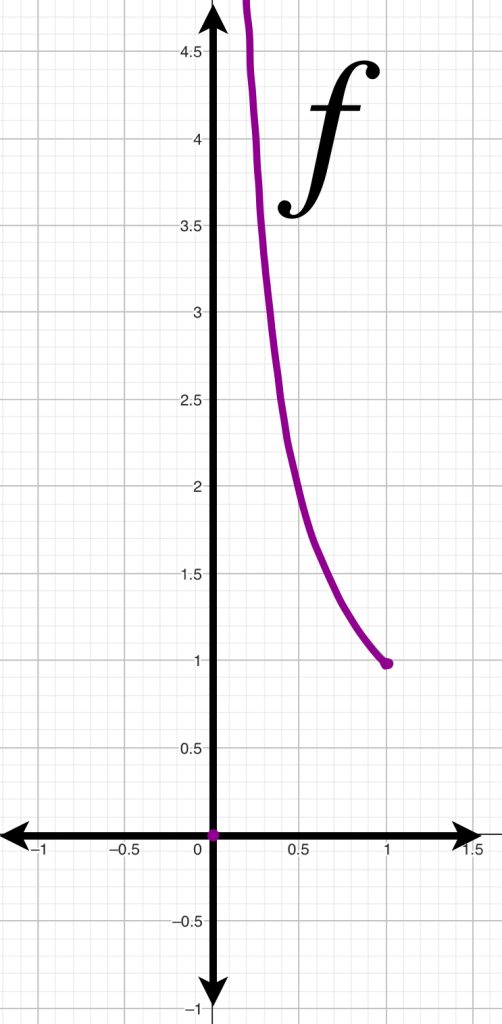
Nota que en el ejemplo anterior las funciones son acotadas, como lo son en general las funciones de $C^0[a,b]$, pues son continuas en un conjunto compacto en $\mathbb{R}$. ¿Qué pasa si alguna de las funciones no es acotada?
Sean $f:[0,1] \to \mathbb{R} \text{ y } g:[0,1] \to \mathbb{R}$ definidas como:
\begin{align*}
f(x) &= \left\{ \begin{array}{lcc}
1/x & si & 0 < x \leq 1\\
0 & si & x = 0
\end{array}
\right.\\
g(x)&= 0
\end{align*}
Entonces $\forall x \in [0,1]$
$|f(x)-g(x)|=|f(x)-0|=|f(x)|=f(x)$
Como $f$ no es acotada en $[0,1]$ no podemos hablar del valor del supremo por lo que la métrica inducida por $\norm{.}_\infty$ no está definida en este caso.
¿Qué pasa si $f \text{ y }g$ son acotadas pero no necesariamente son continuas?
Sean $f:[a,b] \to \mathbb{R}$ y $g:[a,b] \to \mathbb{R}$ tales que $\forall \, x\in [a,b], |f(x)|\leq M_f \text{ y } |g(x)| \leq M_g$ para $M_f, M_g \in \mathbb{R}$ Entonces:
\begin{align*}
|f(x)-g(x)|&=|f(x)+(-g(x))|\\
&\leq|f(x)|+|g(x)|\\
&\leq M_f + M_g
\end{align*}
Se concluye que el conjunto $\{|f(x)-g(x)|: x \in [a,b]|\}$ es acotado y por tanto aquí sí podemos hablar del supremo.
Podemos pensar que para generalizar esta distancia entre funciones, basta con que esa distancia esté acotada. Veamos lo siguiente:
Definición función acotada: Sea $S$ un conjunto y $X=(X,d)$ un espacio métrico. Decimos que una función $f:S \to X$ es acotada si existe $M \in \mathbb{R}$ y $x_0 \in X$ tales que $\forall \, y \in S$ ocurre que $d(f(y),x_0) \leq M$. El conjunto de funciones acotadas de $f$ en $X$ se denota como:
$$\mathcal{B}(S,X):= \{ f:S \to X:f \text{ es acotada}\}$$.
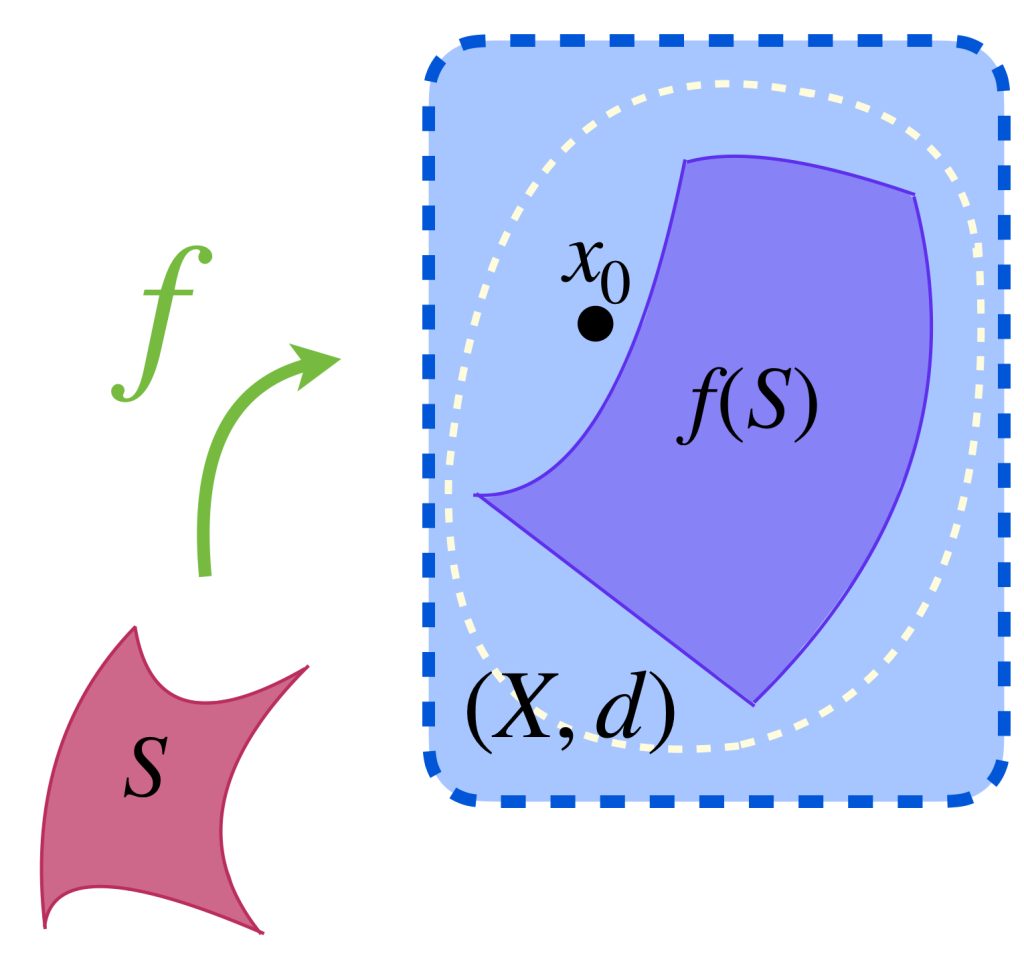
Proposición: La métrica $d$ en $X$ induce una métrica en $\mathcal{B}(S,X)$ dada por:
$$d_\infty (f,g):= \underset{z\in S}{sup}\,d(f(z),g(z))$$
Y recibe el nombre de métrica uniforme.
Demostración:
Sean $f,g,h \in \mathcal{B}$ entonces:
1) \begin{align*} d_\infty(f,g)&=0 \\
\Leftrightarrow \underset{z\in S}{sup}\,d(f(z),g(z))&=0 \\
\Leftrightarrow \forall \, z \in S, d(f(z),g(z))&=0 \\
\Leftrightarrow \forall \, z \in S, f(z)&=g(z) \\
\Leftrightarrow f&=g. \\
\text{Por lo tanto: } d_\infty (f,g)=0 &\Leftrightarrow f=g
\end{align*}
2) \begin{align*}
d_\infty (f,g)&=\underset{z\in S}{sup}\,d(f(z),g(z))\\
&=\underset{z\in S}{sup}\,d(g(z),f(z)) \\
&=d_\infty(g,f).\\
\text{Por lo tanto: } d_\infty(f,g)&=d_\infty(g,f)
\end{align*}
3) \begin{align*}
d_\infty(f,g)&=\underset{z\in S}{sup}\,d(f(z),g(z))\\
&\leq \underset{z\in S}{sup}\,\{d(f(z),h(z))+d(h(z),g(z))\}\\
&\leq \underset{z\in S}{sup}\,d(f(z),h(z)) + \underset{z\in S}{sup}\,d(h(z),g(z))\\
&\leq d_\infty(f,h)+d_\infty(h,g)\\
\text{Por lo tanto: }d_\infty(f,g)&\leq d_\infty(f,h)+d_\infty(h,g)
\end{align*}
Ejemplos de espacios de funciones
Veamos ejemplos de espacios de funciones y analicemos la cercanía entre ellas. Recordemos que esto lo hacemos a través de las bolas abiertas con centro en un elemento del espacio métrico. En este caso, el centro es una función.
Funciones continuas del intervalo $[0,1]$ en $\mathbb{R}$
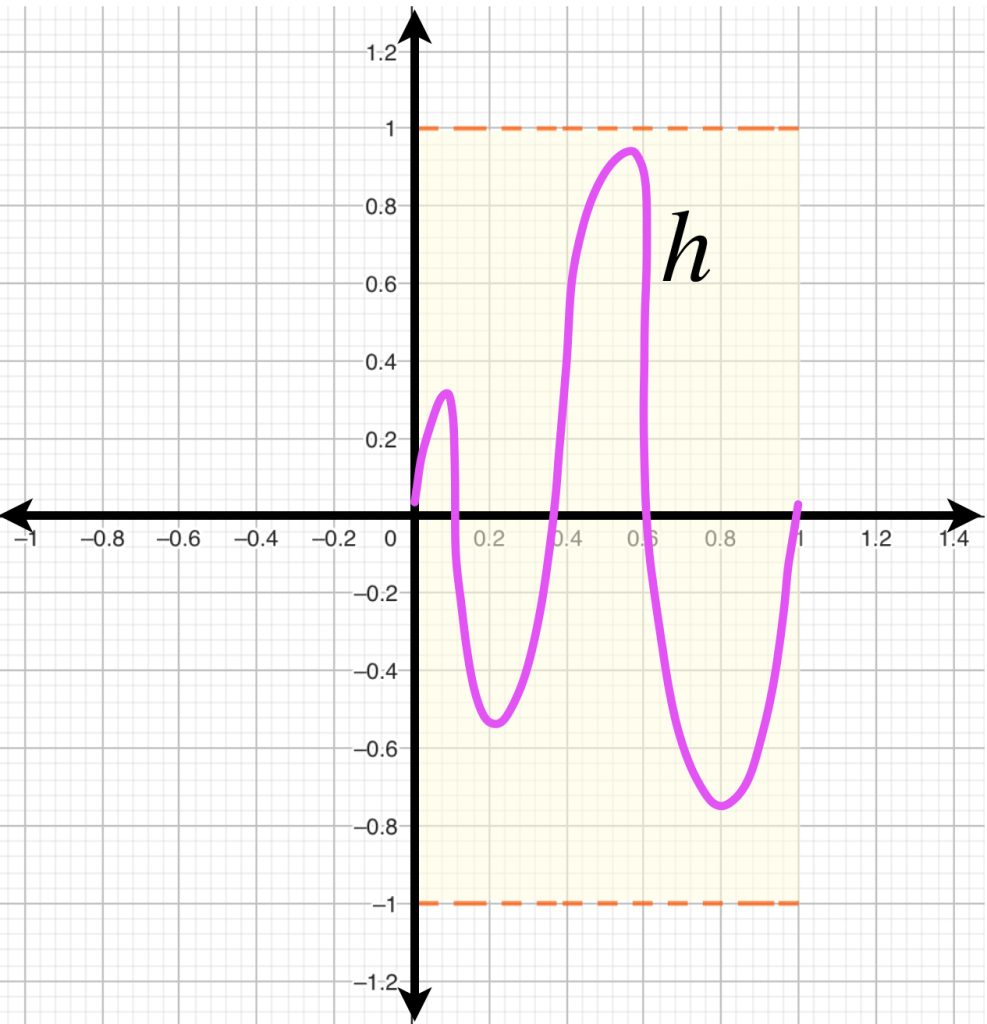
Si consideramos a $C[0,1]$ podemos observar que la bola abierta con centro en $f=0$ y radio $1$ está dado por $\{h: |h(x)|<1,x \in [0,1]\}$. Entonces, una función $h$ que esté en $B(f=0,1)$ debe satisfacer que $\forall x \in [0,1], -1<h(x)<1$.
En consecuencia, la bola abierta queda representada por curvas cuyos puntos se encuentren entre las rectas $y=-1$ y $y=1$.
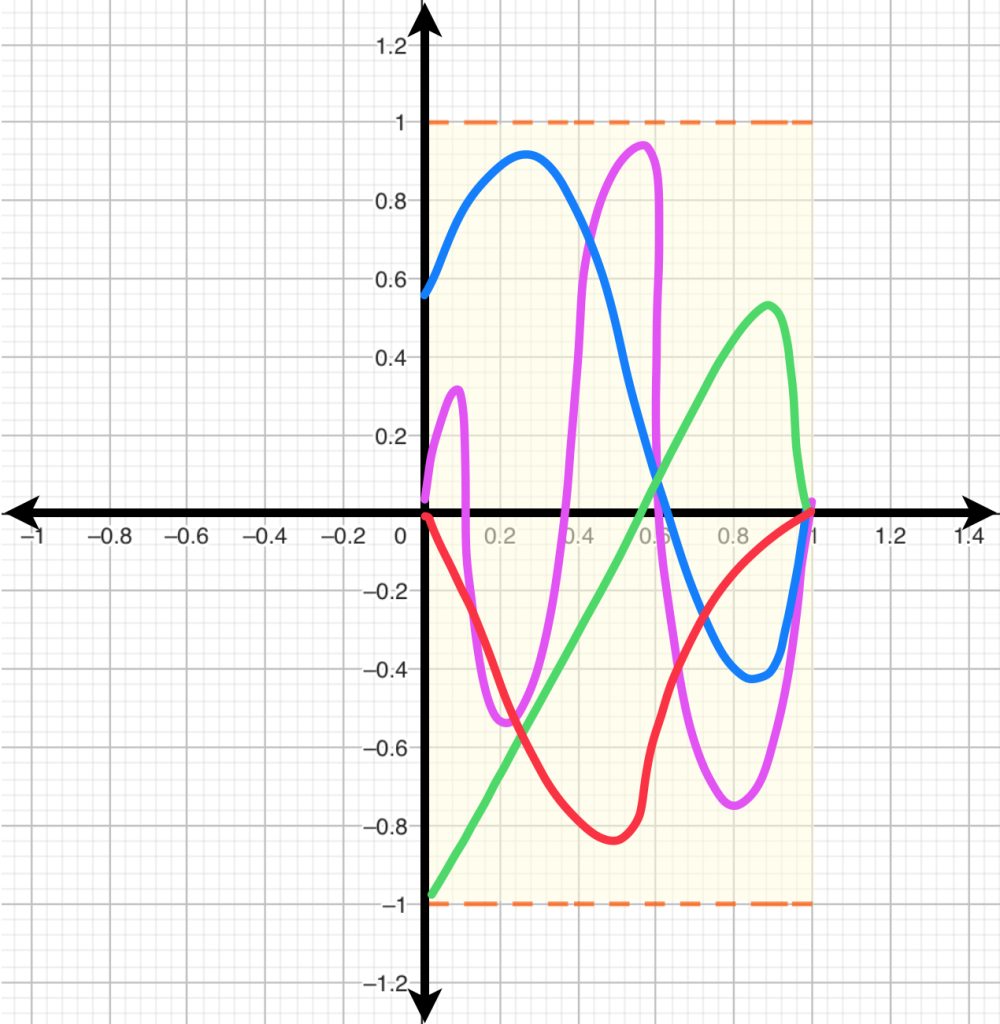
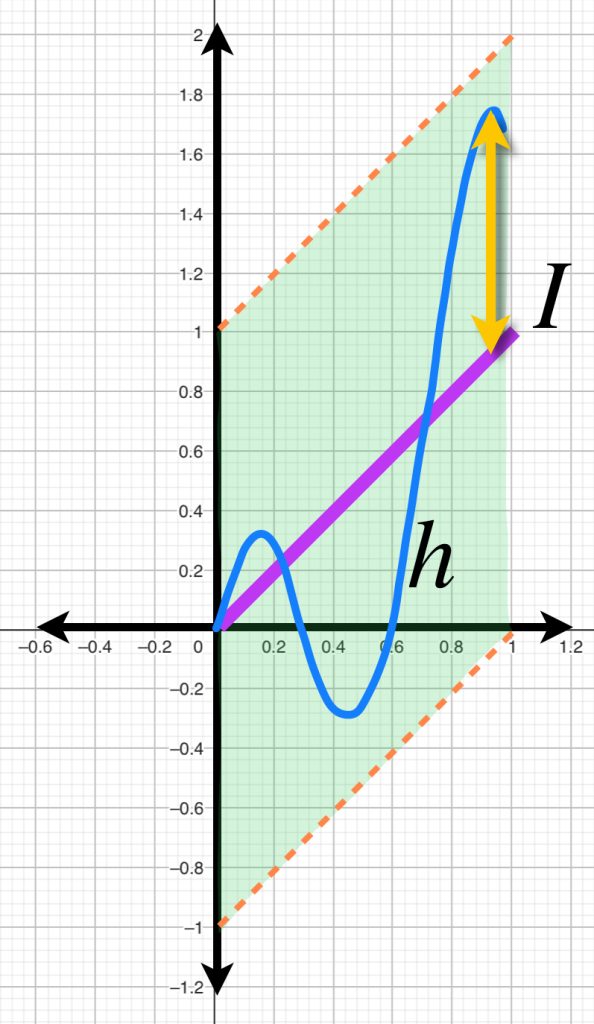
Por otro lado, si consideramos como centro la función identidad $I(x)=x$ la bola de radio $1$ está dada por $\{h:|h(x)-x|<1,x \in [0,1]\}$. Entonces, una gráfica $h$ que esté en $B(I,1)$ debe satisfacer que $\forall x \in [0,1], -1<h(x)-x<1$ es decir $\forall x \in [0,1], x-1<h(x)<x+1$.
Entonces, la bola abierta queda representada por curvas cuyos puntos se encuentren entre las rectas $y=x-1$ y $y=x+1$.
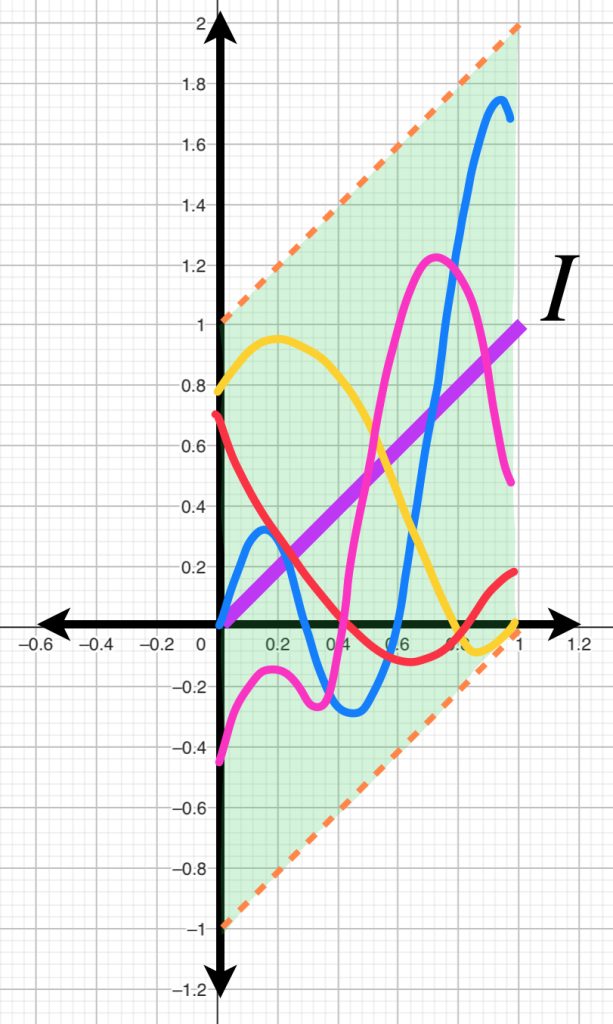
De manera general si consideramos como centro una función $f(x)$ la bola de radio $1$ está dada por $\{h: |h(x)-f(x)|<1,x \in [0,1]\}$. Entonces, una gráfica $h$ que esté en $B(f,1)$ debe satisfacer que $\forall x \in [0,1], -1<h(x)-f(x)<1$ es decir $\forall x \in [0,1], f(x)-1<h(x)<f(x)+1$.
Funciones continuas del intervalo $[0,1]$ en $\mathbb{R}^2$
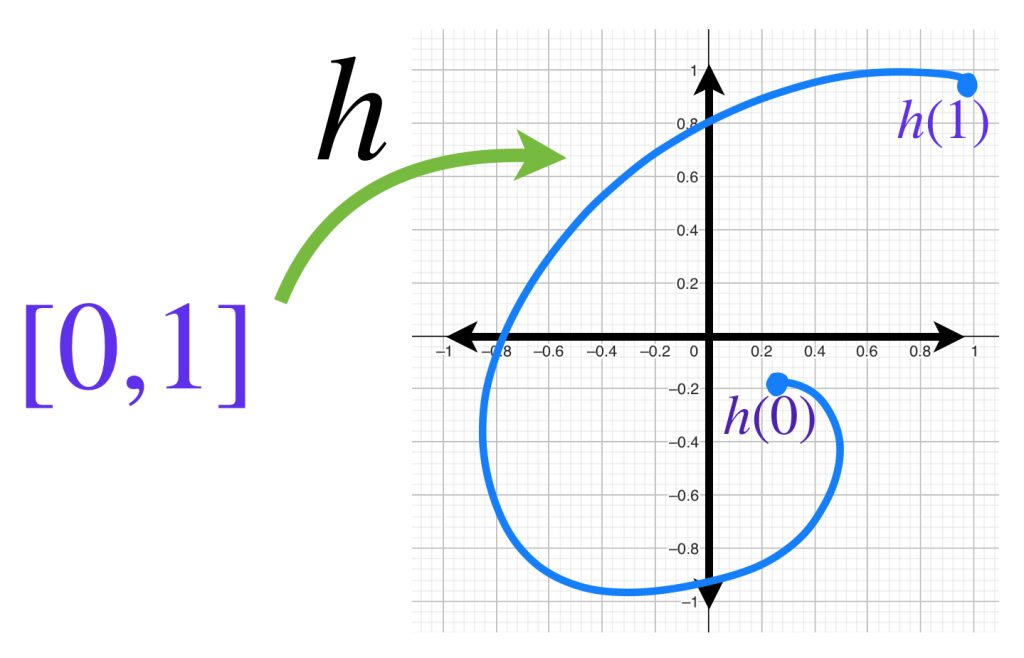
Consideremos a $\mathbb{R}^2$ con la métrica euclideana y a $C[0,1] \to \mathbb{R}^2$ el conjunto de funciones continuas. Una función en este conjunto se representa como una curva continua en $\mathbb{R}^2$
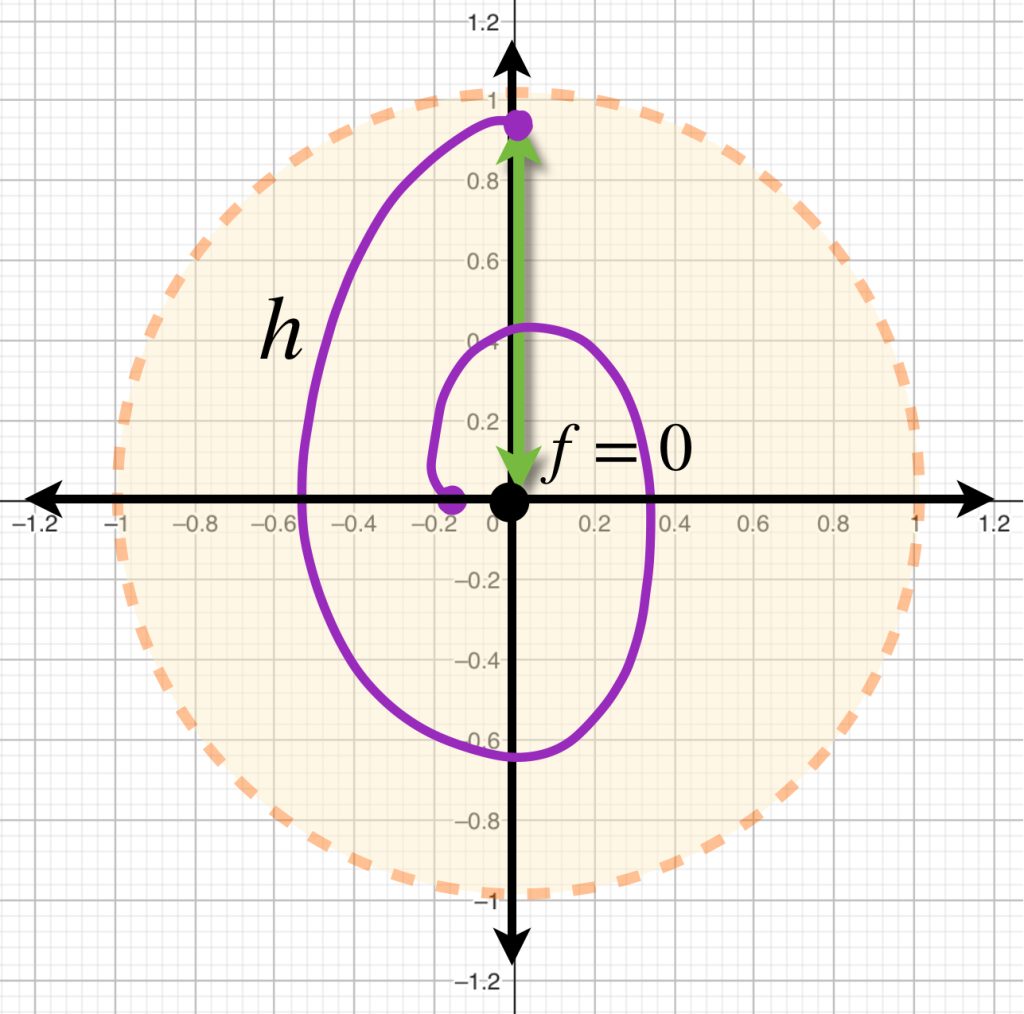
Entonces, una función $h$ que esté en la bola abierta con centro en $f=0$ y radio $1$ debe satisfacer $\{ h: \norm{h(x)-0}<1,x \in [0,1]\}$. Entonces su representación debe estar dentro de la bola de radio $1$ con centro en $0$.
Concluimos que $B(f=0,1)=\{ h: \norm{h(x)}<1, x \in [0,1], \}$. Dicho conjunto puede representarse de esta forma:
Funciones continuas de $[0,1]^2$ en $\mathbb{R}$
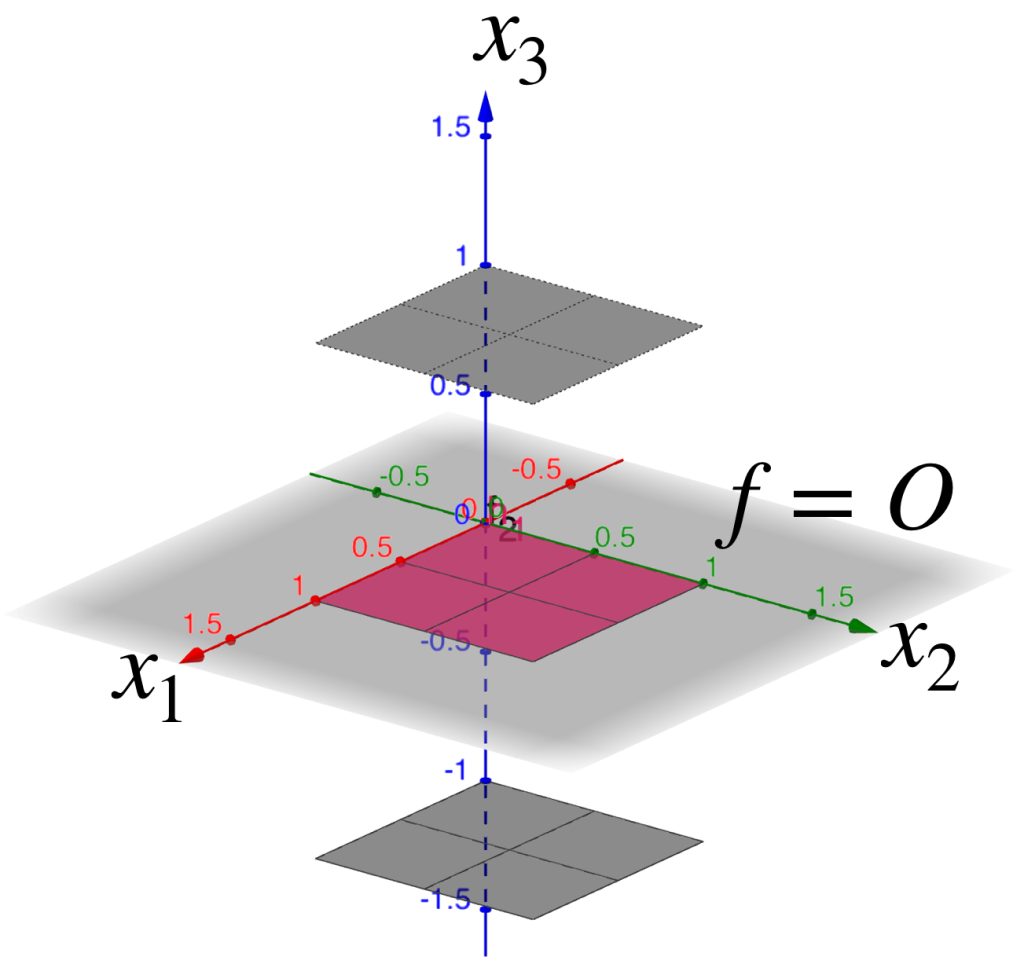
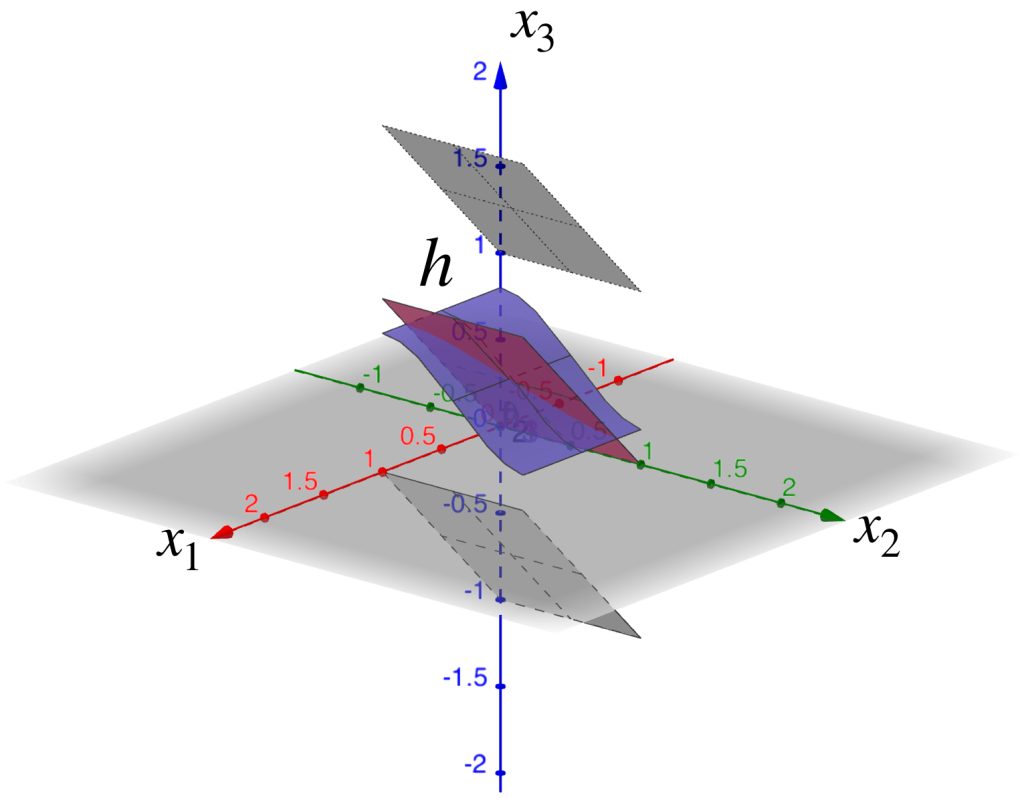
Ahora identifiquemos el conjunto $B(f=0,1)$ en el espacio $C^0[0,1]^2 \to \mathbb{R}$
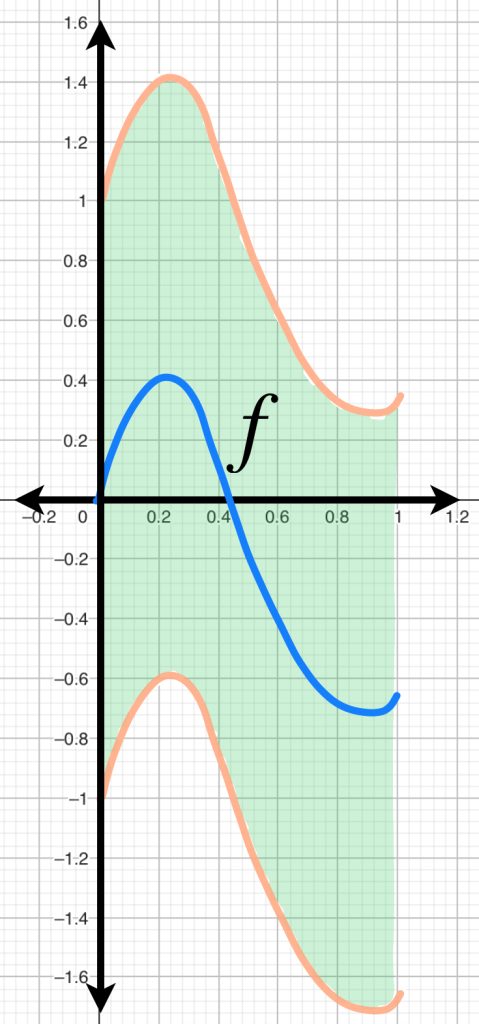
El cuadrado $[0,1]^2$ visualizado en el plano $x_1 \, x_2$ se muestra como una sábana continua y representa la función $f(x)=0, x \in [0,1]^2$.
Si $h$ está en $B(f=0,1)$ entonces $|h(x)-0|<1,x \in [0,1]^2$, es decir, para todo $x \in [0,1]^2, -1<h(x)<1$. De modo que su gráfica será una sábana que esté entre las gráficas de $f_1(x)=-1 \, y\, f_2(x)=1$.
La $B(f=0,1)$ será la colección de todas las sábanas que cumplan esas condiciones:
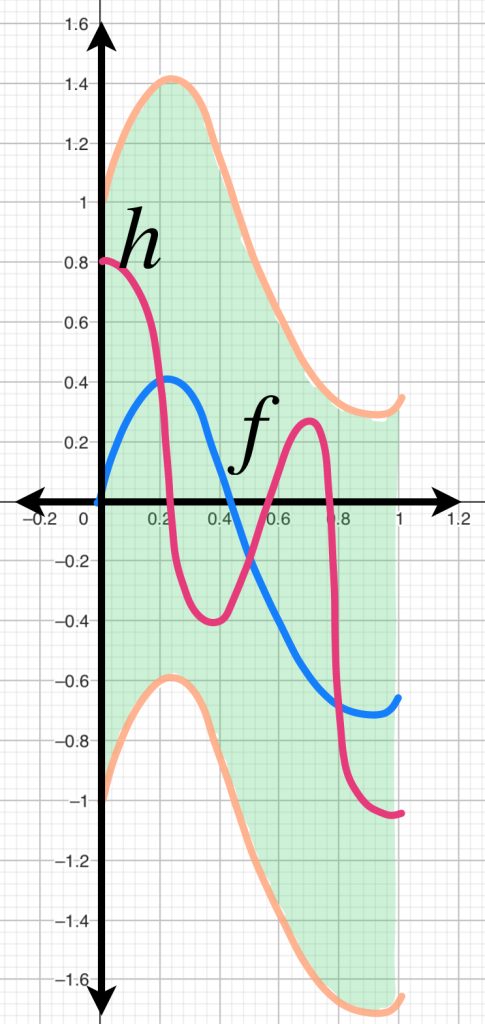
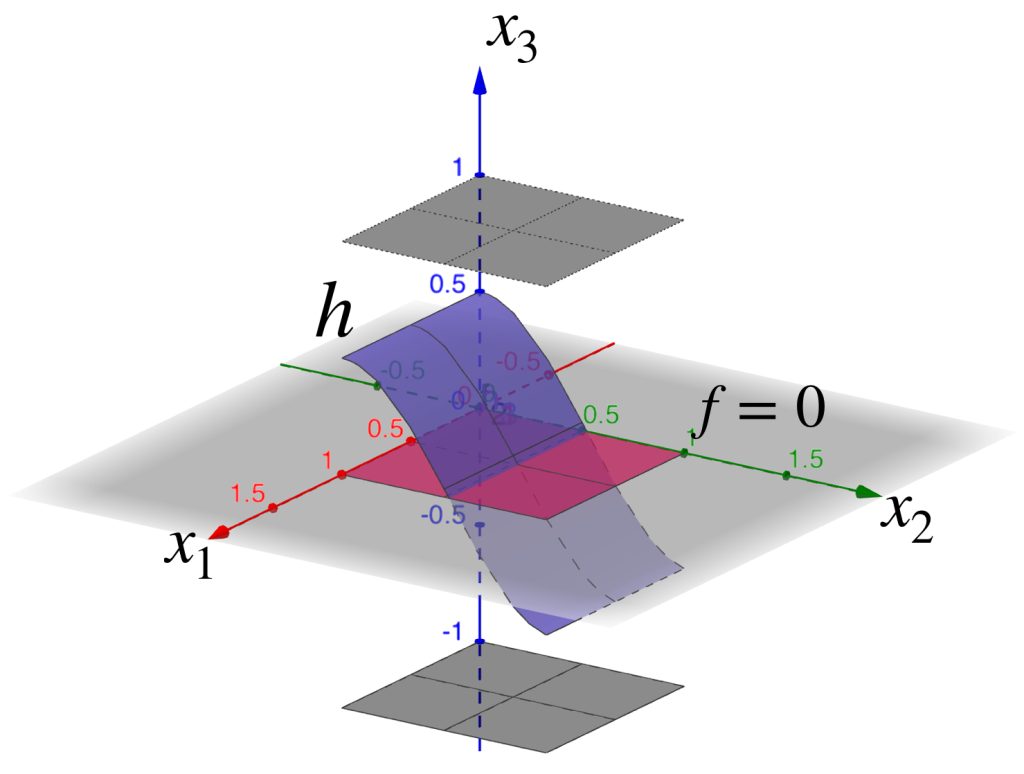
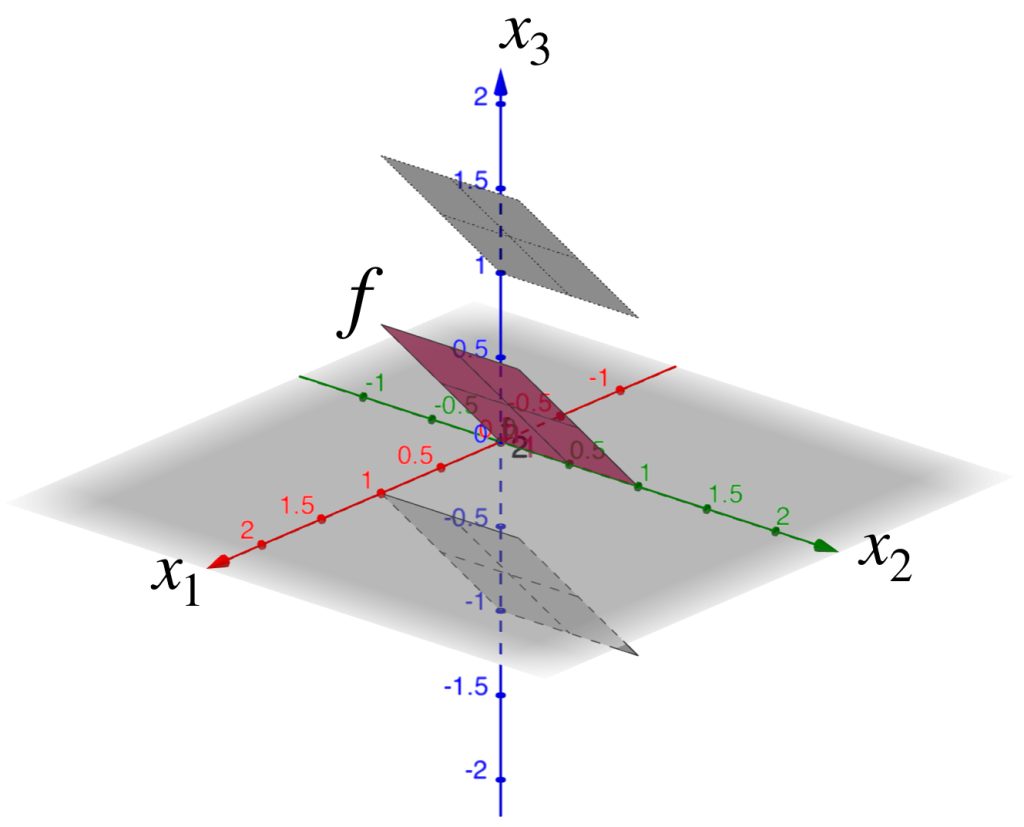
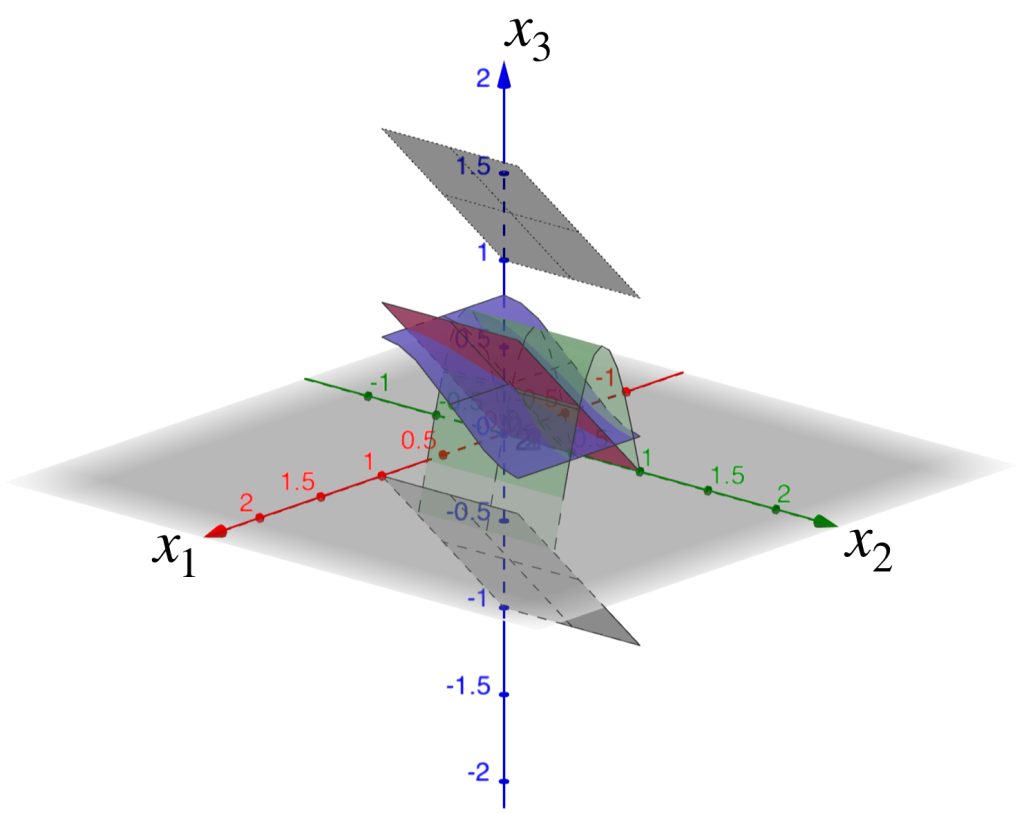
Ahora considera como centro la función $f(x_1,x_2)=x_1$. Observemos el conjunto $B(f,1)$ en el espacio $C^0[0,1]^2 \to \mathbb{R}$.
La gráfica de $f$ se muestra a continuación.
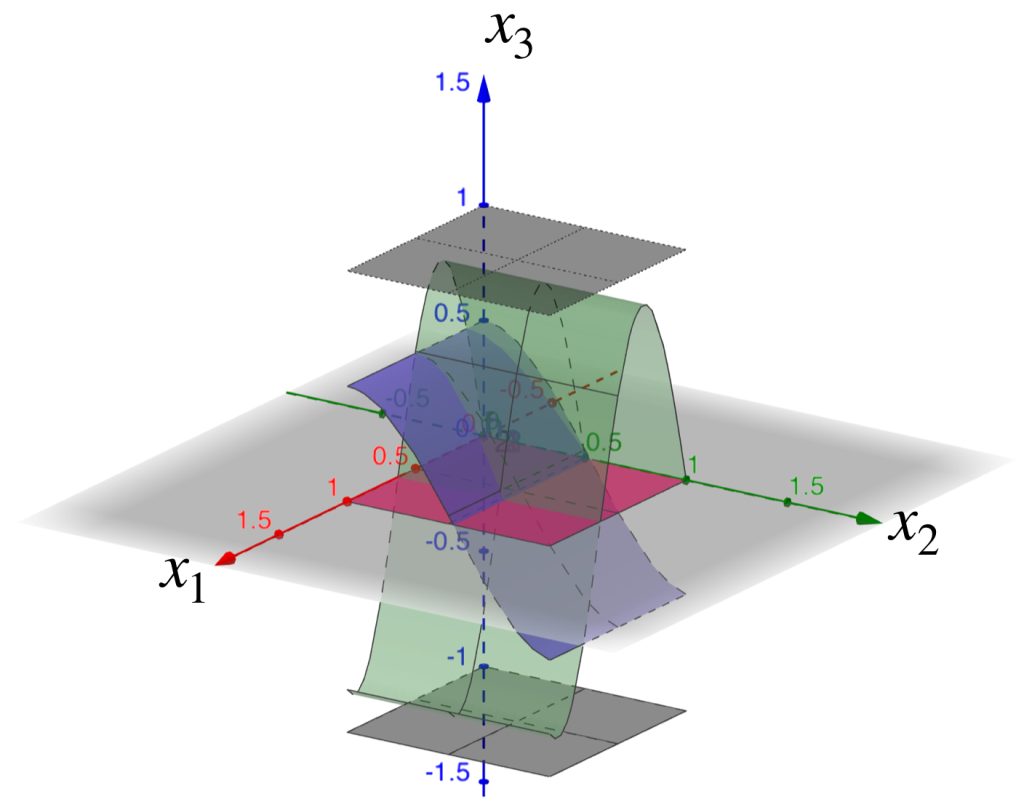
Si $h$ está en $B(f,1)$ entonces $|h(x)-f(x)|<1,x \in [0,1]^2$, es decir, para todo $x \in [0,1]^2, x_{1}-1<h(x_1,x_2)<x_{2}+1$. De modo que su gráfica será una sábana que esté entre las gráficas de $f_1(x_1,x_2)=x_{1}-1\, y \, f_2(x_1,x_2)=x_{1}+1$.
La $B(f,1)$ será la colección de todas las sábanas que cumplan esas condiciones:
Queda como ejercicio al lector hacer el análisis corresponiente para una bola abierta con centro en una función arbitraria.
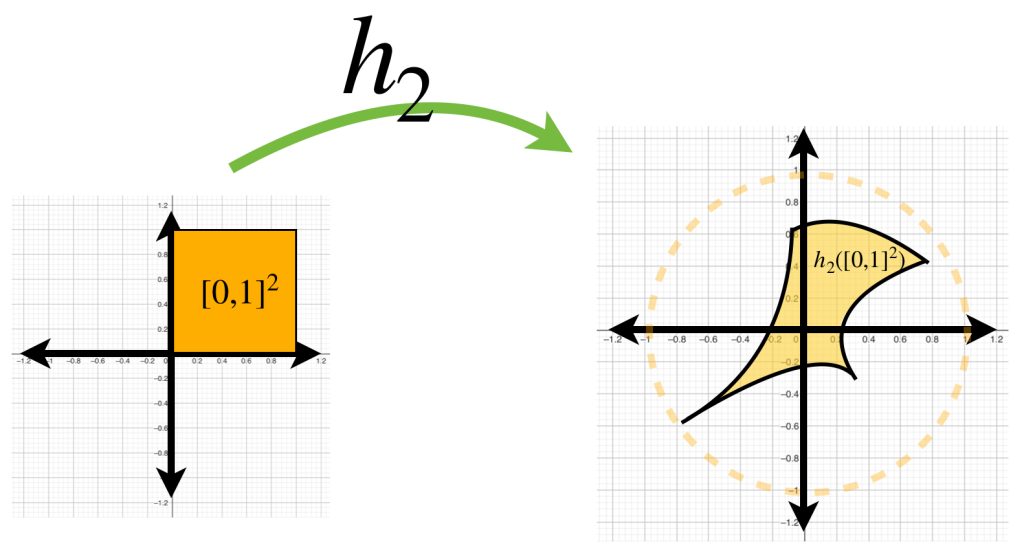
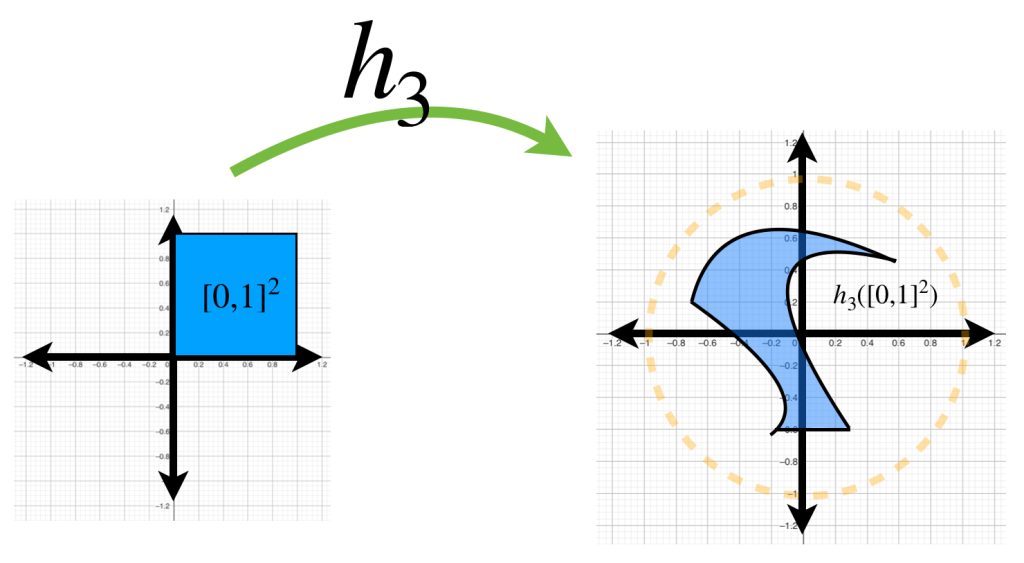
Funciones continuas de $[0,1]^2$ en $\mathbb{R}^2$
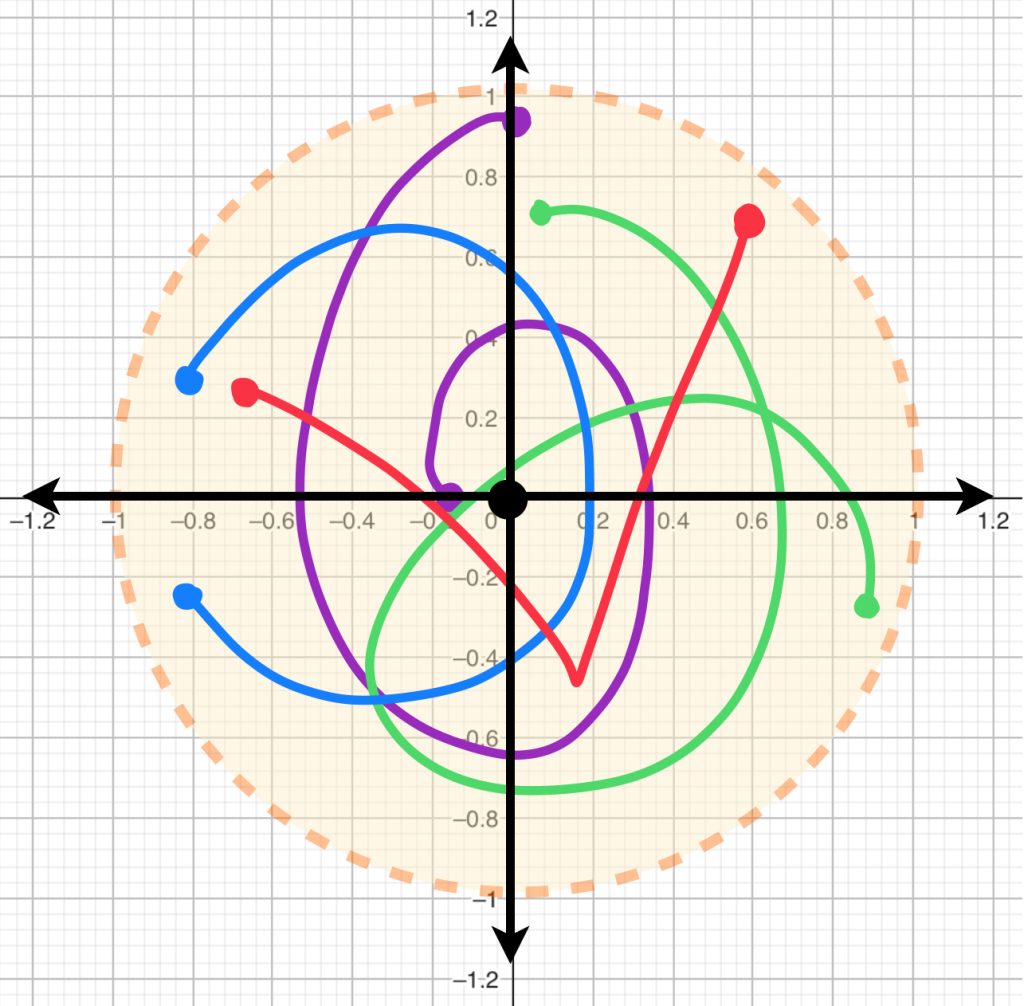
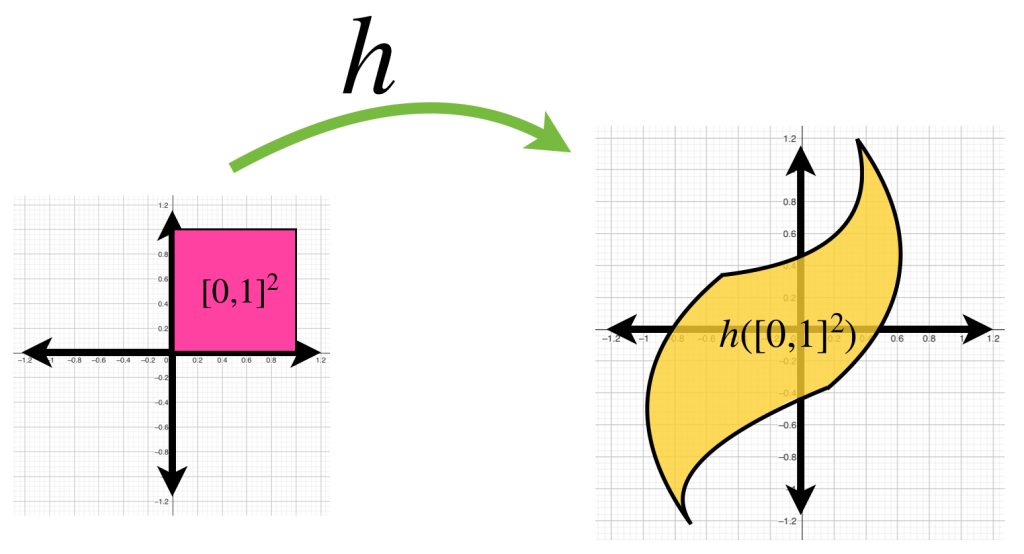
Considera $h$ una función en $C^0[0,1]^2 \to \mathbb{R}^2$. Bajo esa función, el cuadrado $[0,1]^2$ es transformado en una superficie como las mostradas en la imagen.
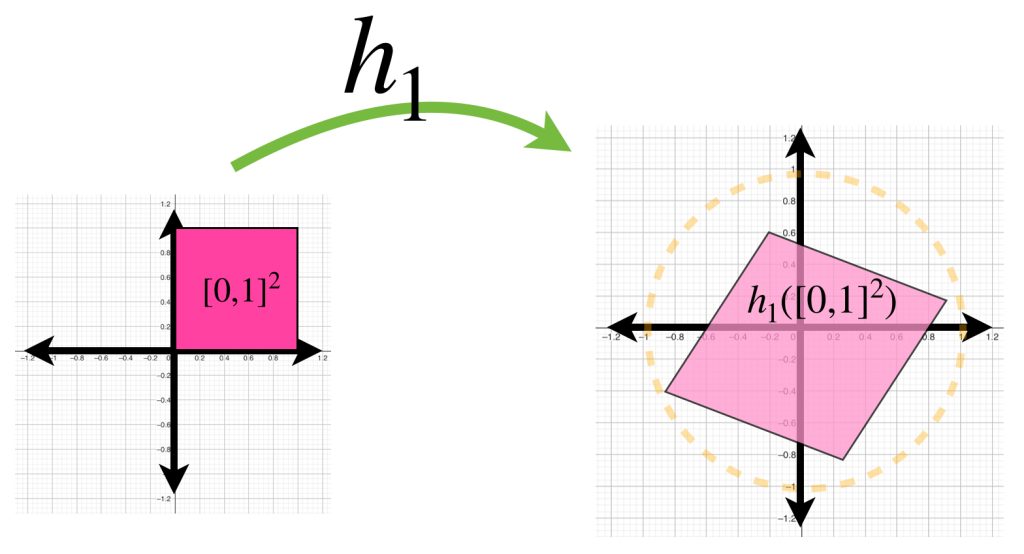
Si buscamos funciones que estén en la bola con centro en la función $0$ y radio $1$, demuestra que las figuras que representan la imagen de estas funciones estarán dentro del círculo unitario.
Más adelante…
Aprenderemos cómo identificar objetos que se aproximan entre sí y las condiciones que debe haber para que esto ocurra. Conoceremos el concepto de sucesión convergente en espacios métricos y descubriremos más particularidades que en el espacio euclideano no ocurren pero en otros espacios sí.
Tarea moral
- Describe una representación de la bola abierta en $\mathbb{R}^2$ con un centro en una función distinta a la función cero.
- Describe una representación de la bola abierta con centro en una función arbitraria en el espacio de funciones continuas de $\mathbb{R}^2$ en $\mathbb{R}$.
- En el espacio de funciones continuas de $[0,1]^2$ en $\mathbb{R}^2$ buscamos funciones que estén en la bola con centro en la función $0$ y radio $1$. Demuestra que las figuras que representan la imagen de estas funciones estarán dentro del círculo unitario.