Introducción
«Desde un punto de vista intuitivo, un espacio métrico es, simplemente, un conjunto en donde podemos hablar de la distancia entre sus elementos, lo que nos permitirá precisar la noción de «proximidad», una idea que está presente implícitamente en todos los conceptos fundamentales de la Topología y el Análisis.
Como estructura matemática abstracta, el concepto de espacio métrico fue introducido inicialmente por el matemático francés M.Fréchet en 1906. Probó que las ideas de Cantor de subconjuntos abiertos y cerrados podían extenderse de manera natural a los espacios métricos. Más tarde, el concepto fue desarrollado por F. Hasdorff en su Mengenlehre. En parte, su importancia radica en que constituye una interesante generalización de los espacios normados, cuya teoría fue básicamente desarrollada por Stephan Banach como cimiento del Análisis Funcional. El desarrollo posterior de las investigaciones sobre topología métrica ha puesto de manifiesto su extraordinario poder para unificar una amplia variedad de teorías hasta entonces dispersas y aparentemente independientes». (Diaz, 1998).
¿Qué es un espacio métrico?
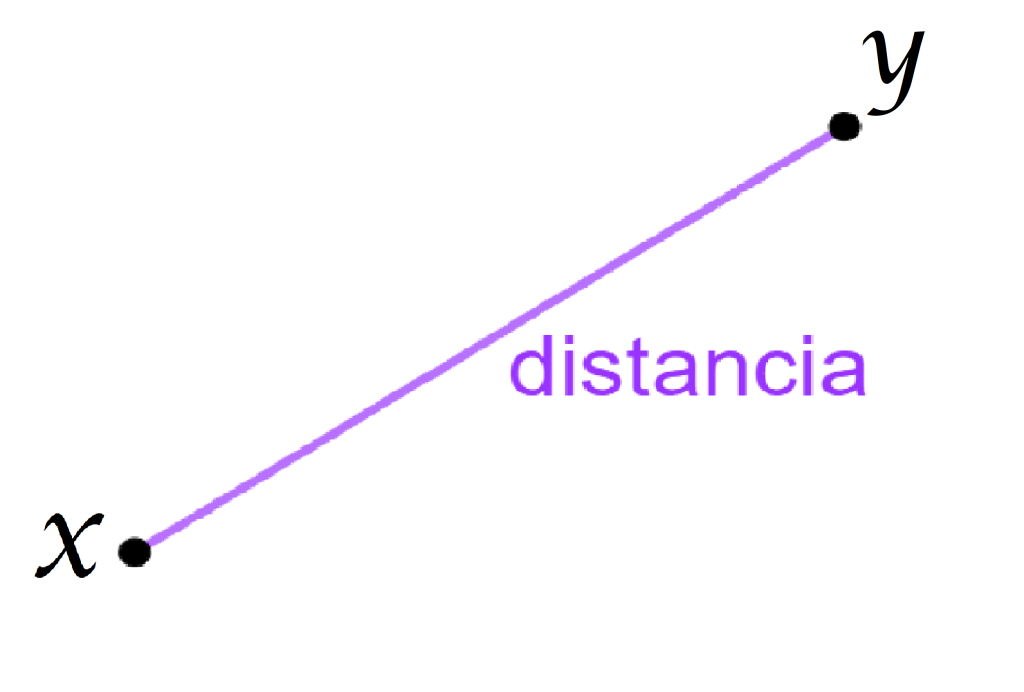
Pensemos en un conjunto de elementos que representamos como puntos. Si para cada par de puntos especificamos qué distancia hay entre ellos entonces tenemos un espacio métrico (cuando se cumplen ciertas condiciones).
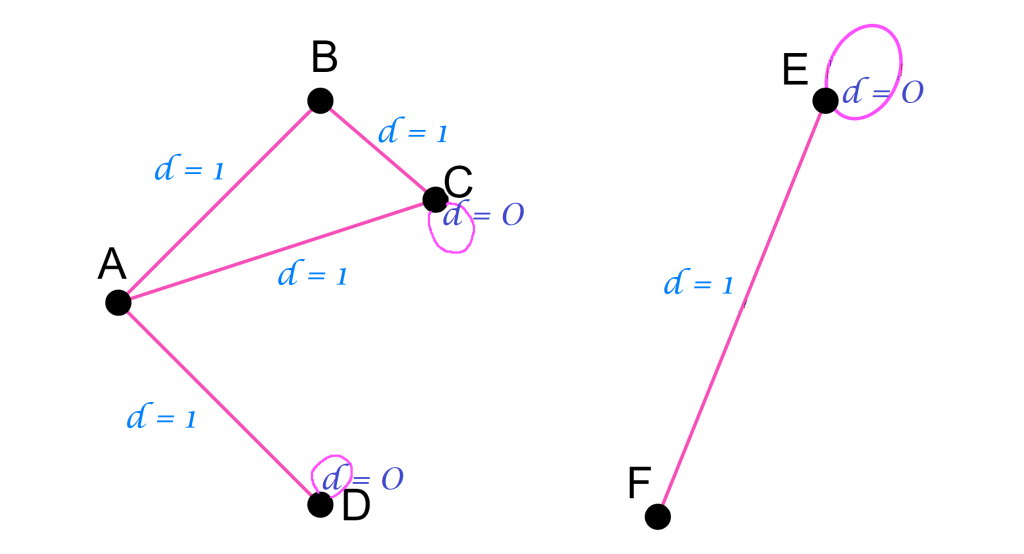
En el siguiente esquema se muestran solo algunas de las distancias entre dos puntos. Nota que la distancia del punto $E$ a sí mismo es $0$. Así lo será también la distancia de cualquier punto a sí mismo.
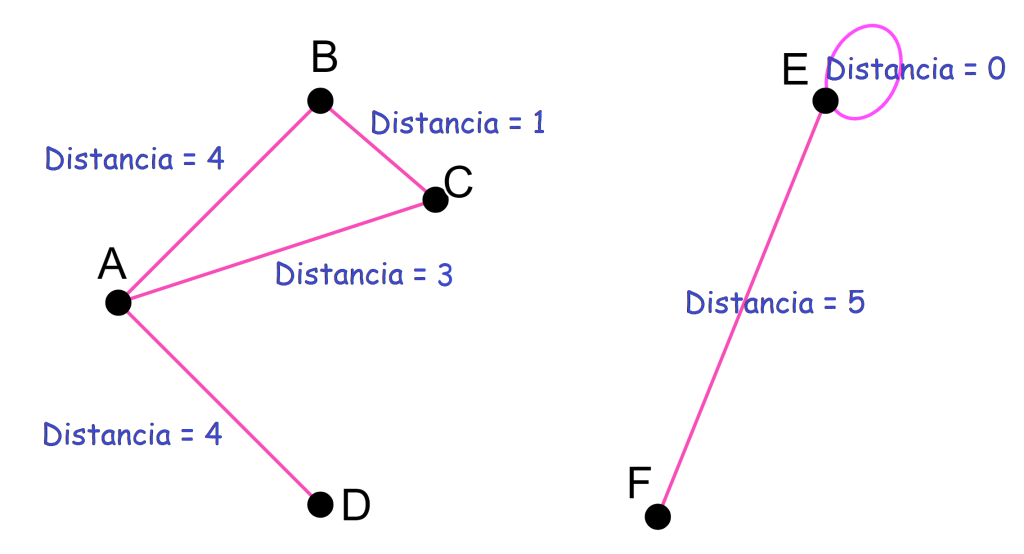
La distancia cumplirá lo siguiente:
- La distancia de un punto a sí mismo será $0$. La distancia entre puntos distintos será distinta de $0$.
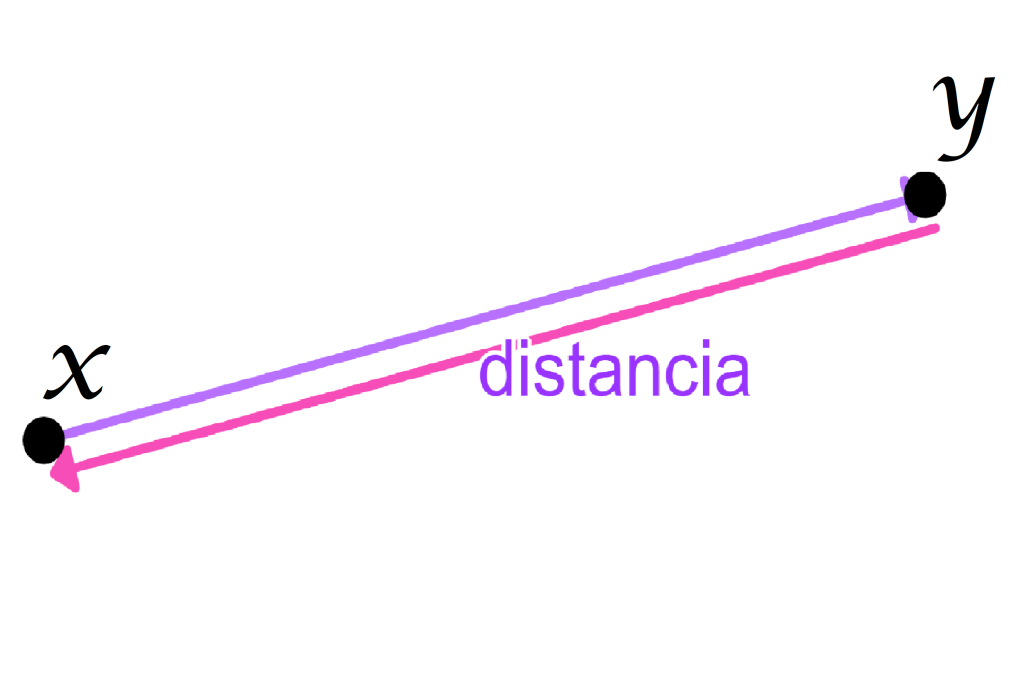
- En un espacio métrico la distancia entre dos puntos es simétrica. La distancia entre el punto $x$ y $y$ coincide con la distancia entre el punto $y$ y $x$. ¿Puedes mencionar un ejemplo en tu vida cotidiana en el que tu recorrido de ida no coincida con el de regreso? Donde cambie la longitud del camino, el tiempo, el costo económico o algún otro factor.
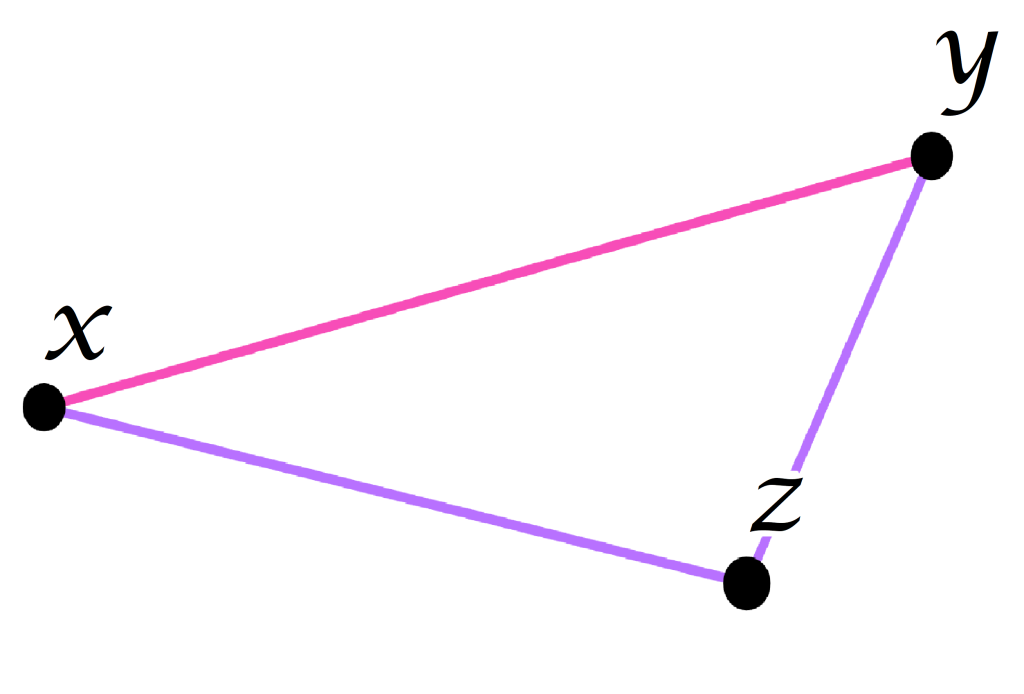
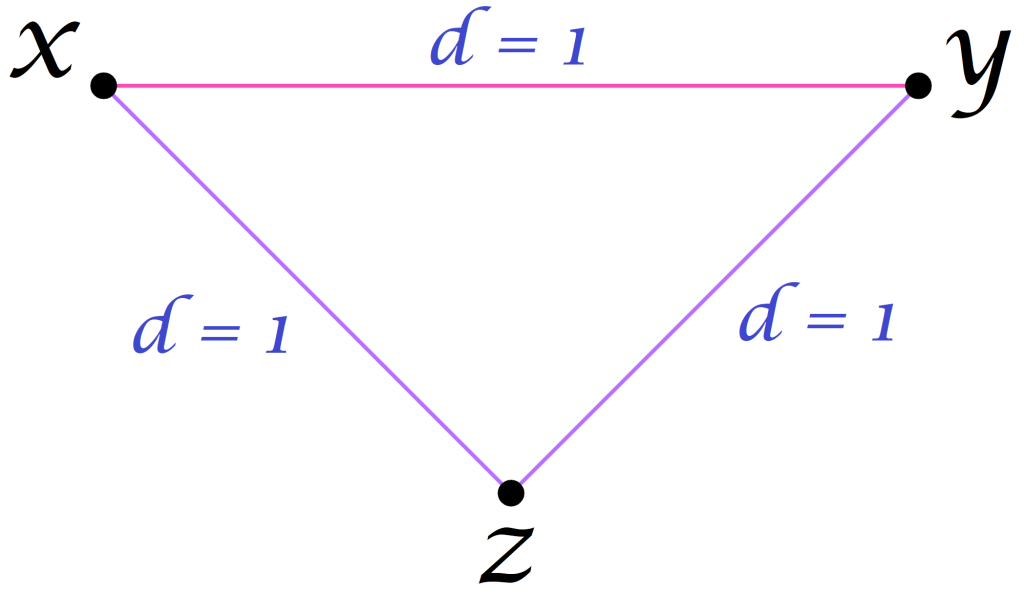
- Entre tres puntos se satisface la desigualdad del triángulo. La suma de dos de las distancias entre los vértices de un triángulo es mayor o igual que la distancia restante.
De manera formal, tenemos lo siguiente:
Definición espacio métrico. Un espacio métrico $(X,d)$ es un par ordenado donde $X$ es un conjunto no vacío, (cuyos elementos llamaremos puntos) y $d$ es la métrica asociada a este.
Definición métrica. Llamaremos métrica o distancia en $X$ a una relación $d: X \times X \to \mathbb{R}$ que satisface que para cualesquiera $x$, $y$, $z$ $\in X$:
\[
\begin{align}
& d(x,y)=0 \quad\text{si y solo si}\quad x = y \\
& d(x,y) = d(y,x) \\
& d(x,y) \leq d(x,z) + d(z,y)
\end{align}
\]
Nota: La distancia nunca es negativa. De estos axiomas se deduce que si $x \neq y$ entonces $0<d(x,y)$ pues:
\begin{align*}
0 &= d(x,x)\\
&\leq d(x,y) + d(y,x)\\
&= d(x,y) + d(x,y)\\
&= 2d(x,y)
\end{align*}
Luego de multiplicar por $\dfrac{1}{2}$ ambos lados, se deduce que $0 \leq d(x,y)$. Como $x \neq y$ concluimos a partir del axioma $(1)$ que $0<d(x,y)$.
Ejemplos de espacios métricos
La métrica discreta.
Sea $X$ un conjunto no vacío. Para todo $x, y \in X$ definimos $d:X \times X \to \mathbb{R}$ como:
\[
d(x,y)= \left\{\begin{array}{lcc}
0 & si & x = y \\
\\ 1 & si & x \neq y
\end {array}
\right.
\]
En este caso $(X,d)$ recibe el nombre de espacio discreto.
Demostración: Sean $x, y, z \in X$. El axioma $(1)$ se cumple por definición.
Para demostrar el axioma $(2)$ veamos que si $x = y$ entonces $d(x,y) = 0 = d(y,x)$. Por otro lado, si $x \neq y$ entonces $d(x,y) = 1 = d(y,x)$. En cualquier caso $d(x,y) = d(y,x)$.
Para demostrar $(3)$ veamos que si $x=y$ entonces $d(x,y)=0$. Como las distancias siempre son mayores o iguales a cero se sigue que $d(x,y) \leq d(x,z)+d(z,y)$.
Por otro lado, si $x \neq y$ entonces $d(x,y) = 1$ y tenemos los siguientes casos:
Notemos que $d(x,z) = 1$ o $d(z,y) = 1$, pues de lo contrario tendríamos que $d(x,z) = 0$ y $d(z,y)=0$, lo cual implica que $x = z = y$. Por lo tanto $x = y$, lo cual es una contradicción. De lo anterior se concluye que $d(x,y)=1 \leq d(x,z) + d(z,y)$.
El conjunto de los números reales $\mathbb{R}$ con la métrica usual
Sean $x,y \in \mathbb{R}$. Se define:
\[
d(x,y) = |x-y| = \left\{ \begin{array}{lcc}
x-y & si & x \geq y \\
\\ y-x & si & x < y
\end{array}
\right.
\]
Demostración: $(1)$ Sean $x,y,z \in \mathbb{R}$ entonces $d(x,y)=0 \text{ si y solo si } |x-y|=0 \text{ si y solo si } x=y$.
$(2)$ $d(x,y)=|x-y|=|y-x|=d(y,x)$.
$(3)$ $d(x,y)=|x-y|=|x-z+z-y|\leq|x-z|+|z-y|=d(x,z)+d(z,y)$.
El conjunto $\mathbb R^n$ con la métrica usual:
Si $x,y,z \in \mathbb R^n$, con $x=(x_{1},…,x_{n})$, $y=(y_{1},…,y_{n})$ y $z=(z_{1},…,z_{n})$ se define:
$d(x,y) = \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}$
Demostración:
$(1)$
\begin{align*}
d(x,y) = 0
&\iff \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2} = 0 \\
&\iff \forall i=1,…,n, (x_{i}-y_{i})^2 = 0 \\
&\iff\forall i=1,…,n, x_{i}=y_{i} \\
&\iff x=y
\end{align*}
$(2)$
$\forall i=1,…,n, (x_{i}-y_{i})^2= (y_{i}-x_{i})^2$ entonces:
\begin{align*}
\sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}&=\sqrt{(y_{1}-x_{1})^2+…+(y_{n}-x_{n})^2}\\
\text{ Por lo tanto } \quad d(x,y)&=d(y,x)
\end{align*}
$(3)$
\begin{align*}
d(x,y) &= \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}\\
&= \sqrt{(x_{1}-z_{1}+z_{1}-y_{1})^2+…+(x_{n}-z_{n}+z_{n}-y_{n})^2}\\
&\leq \sqrt{(x_{1}-z_{1})^2+…+(x_{n}-z_{n})^2} + \sqrt{(z_{1}-y_{1})^2+…+(z_{n}-y_{n})^2}\\
&=d(x,z)+d(z,y)
\end{align*}
Este espacio métrico es llamado el «espacio aritmético euclídeo de $n$ dimensiones $\mathbb R^n$»
El conjunto $C_{[a,b]}:=\{f:[a,b] \to \mathbb R: \quad\text{f es función continua}\}$
Considera $f,g \in C_{[a,b]}$. Para cada $t \in [a,b]$ identifiquemos la medida del segmento que une a los puntos$ (t,f(t))$ y $(t,g(t))$. El segmento más grande representará la distancia entre ambas funciones.
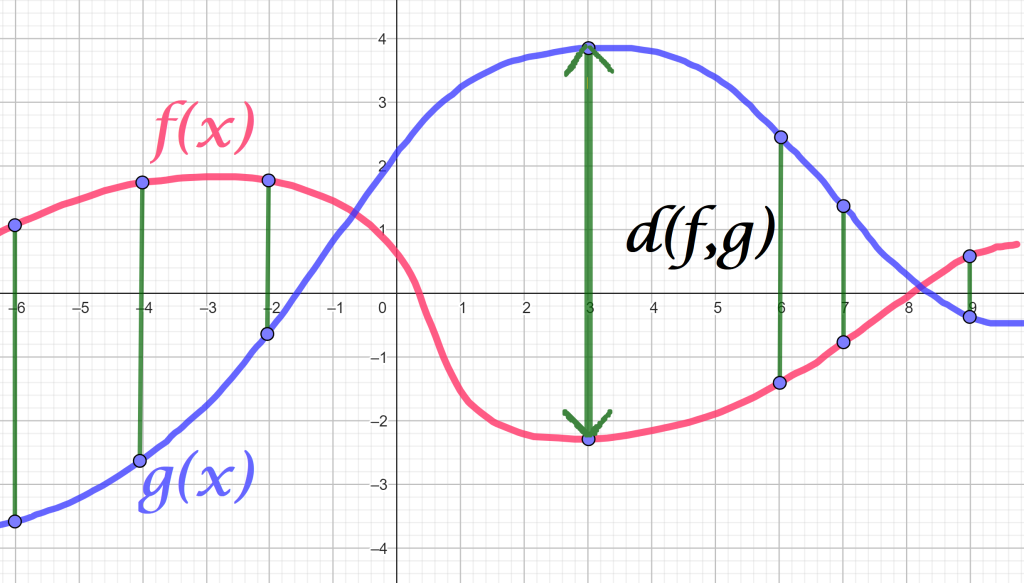
Definimos:
$$d(f,g) = \underset{a \leq t \leq b}{max}\, |f(t)-g(t)|$$
Recordemos que este máximo existe, pues al ser $f$ y $g$ funciones continuas, también lo es $|f-g|$ lo que le permite alcanzar su máximo en el compacto [a,b].
Demostración: Sean $f, g \in C_{[a,b]}$
$(1)$ \begin{align*} d(f,g) = 0 &\iff 0 = \underset{a \leq t \leq b}{max}\, |f(t)-g(t)|\\
&\iff \forall t \in [a,b], |f(t)-g(t)| =0\\
&\iff \forall t \in [a,b], f(t) = g(t)\\
&\iff f=g
\end{align*}
$(2)$
Como $\forall t \in [a,b], f(t)$ y $g(t) \in \mathbb{R} $, entonces $|f(t)-g(t)| = |g(t)-f(t)|$. Así:
\begin{align*}
d(f,g) &= \underset{a \leq t \leq b}{max}\, |f(t)-g(t)|\\
&= \underset{a \leq t \leq b}{max}\, |g(t)-f(t)|\\
&= d(g,f)\\
\text{Por lo tanto }\quad d(f,g) &= d(g,f).
\end{align*}
$(3)$
Como $f$ y $g$ son funciones continuas en un conjunto compacto entonces la función $f-g$ también es continua en el compacto $[a,b]$ y alcanza su máximo: $\underset{a \leq t \leq b}{max}\,|f(t)-g(t)| = |f(t_{1}) – g(t_{1})|$ para algún $t_{1} \in [a,b]$
Como
\begin{align*}|f(t_{1}) – g(t_{1})| &= |f(t_{1})-h(t_{1})+h(t_{1})-g(t_{1})|\\
&\leq |f(t_{1}) – h(t_{1})| + |h(t_{1} – g(t_{1}))|\\
& \leq \underset{a \leq t \leq b}{max}\, |f(t)-h(t)| + \underset{a \leq t \leq b}{max}\, |h(t)-g(t)|
\end{align*}
concluimos $d(f,g) \leq d(f,h) + d(h,g)$.
El conjunto $\mathcal{B}(A,\mathbb{R}):= \{ f:A \to \mathbb{R}: f\text{ es acotada}\}$
Definición función acotada. Sea A un conjunto. Decimos que una función $f:A \to \mathbb{R}$ es acotada si existe $M \in \mathbb{R}$ y $x_0 \in \mathbb{R}$ tales que $\forall \, a \in A$ ocurre que $|x_0-f(a)| \leq M$.
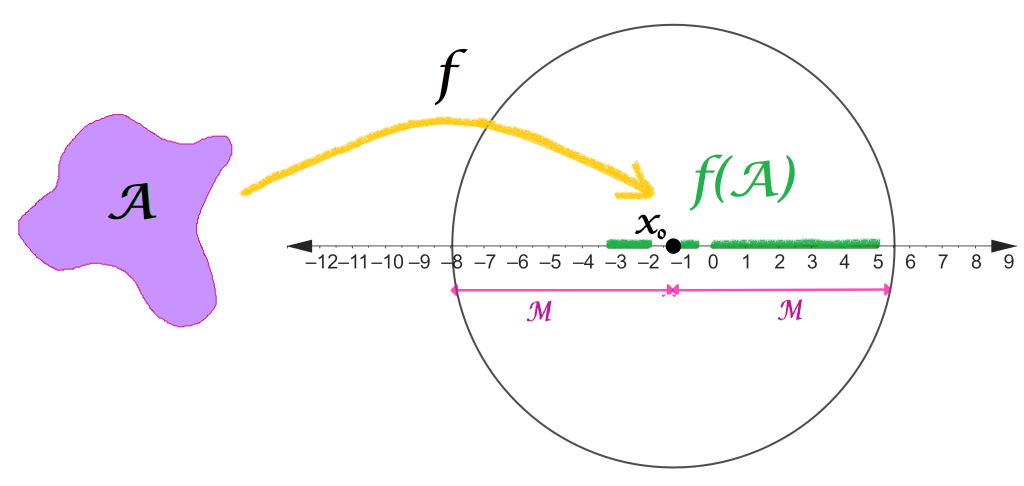
Definición espacio de funciones acotadas. El conjunto $$\mathcal{B}(A,\mathbb{R}):= \{ f:A \to \mathbb{R}: f\text{ es acotada}\}$$ es un espacio métrico pues si dos funciones $f,g \in \mathcal{B}(A, \mathbb{R})$ entonces la función $f-g$ también es acotada, por lo tanto existe el $\underset{z\in A}{sup}\,|f(z)-g(z)|$. Esto permite definir la distancia entre ellas como: $$d_\infty (f,g):= \underset{z\in A}{sup}\,|f(z)-g(z)|$$ Y recibe el nombre de métrica uniforme.
Demostración: Sean $f,g,h \in \mathcal{B}$ entonces:
$(1)$ \begin{align*}
d_\infty(f,g)&=0 \\
\Leftrightarrow \underset{z\in A}{sup}\,|(f(z)-g(z)|&=0 \\
\Leftrightarrow \forall \, z \in A, |f(z)-g(z)|&=0 \\
\Leftrightarrow \forall \, z \in A, f(z)&=g(z) \\
\Leftrightarrow f&=g. \\
\text{Por lo tanto: } d_\infty (f,g)=0 &\Leftrightarrow f=g
\end{align*}
$(2)$ \begin{align*}
d_\infty (f,g)&=\underset{z\in A}{sup}\,|f(z)-g(z)|\\
&=\underset{z\in A}{sup}\,|g(z)-f(z)| \\
&=d_\infty(g,f).\\
\text{Por lo tanto: } d_\infty(f,g)&=d_\infty(g,f)
\end{align*}
$(3)$ \begin{align*}
d_\infty(f,g)&=\underset{z\in A}{sup}\,|f(z)-g(z)|\\
&\leq \underset{z\in A}{sup}\,\{|f(z)-h(z)|+|h(z)-g(z)|\}\\
&\leq \underset{z\in A}{sup}\,|f(z)-h(z)| + \underset{z\in A}{sup}\,|h(z)-g(z)|\\
&\leq d_\infty(f,h)+d_\infty(h,g)\\
\text{Por lo tanto: }d_\infty(f,g)&\leq d_\infty(f,h)+d_\infty(h,g)
\end{align*}
Más adelante
Ya que conocemos la definición de espacio métrico y que hemos visto cómo demostrar que satisfacen los axiomas de la métrica, conoceremos otros ejemplos más que nos permitirán notar, otras distancias que ya están incluso, en nuestra vida cotidiana.
Tarea moral
¡Es tu turno de practicar! Demuestra para $x,y \in \mathbb R^2$ con $x=(x_{1},x_{2})$ y $y=(y_{1},y_{2})$ que son métricas para $\mathbb R^2$:
- $d(x,y) = \sqrt{(x_{1}-y_{1})^2 + 4(x_{2}-y_{2})^2}$
- $d(x,y) = |x_{1}-y_{1}|+…+|x_{n}-y_{n}|$
- $d(x,y) = max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\}$
Enlaces
- Análisis Matemático.
- Enlace a entrada anterior.
- Enlace a entrada siguiente.




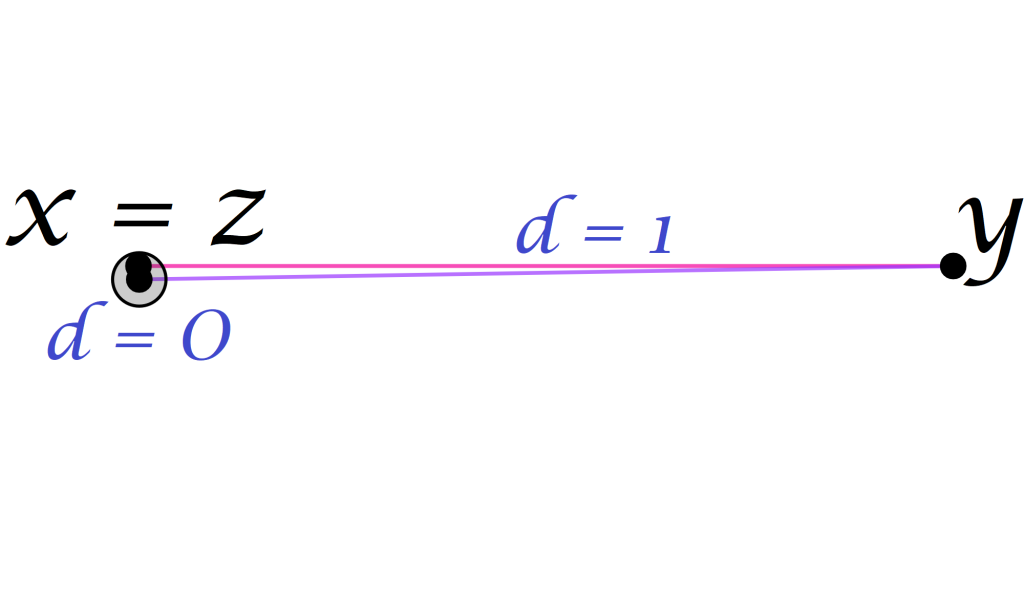
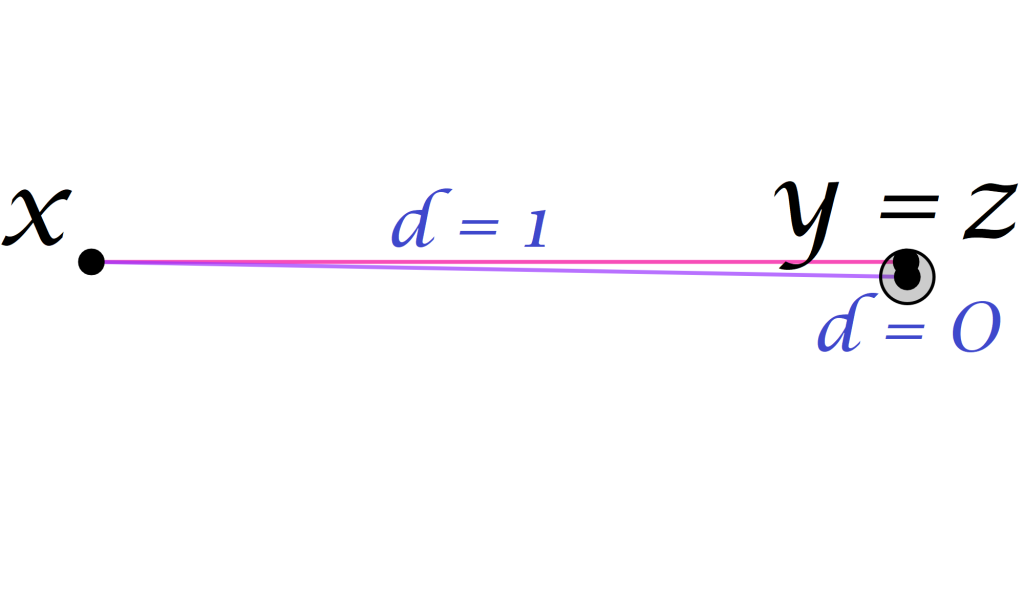
En la tarea moral inciso 3) falta ponerle los corchetes a la métrica para indicar de qué conjunto será el máximo
Gracias por la observación.