Introducción
Al estudiar matemáticas un concepto que no puede pasar desapercibido es el del infinito. Intuitivamente cuando pensamos en el infinito estamos considerando a algo que no tiene fin, algo sin límites. Aunque dicho concepto aparece en diversas ramas de las matemáticas como el cálculo, el análisis, la geometría, la teoría de conjuntos, entre otras, es claro que la idea que tenemos sobre él es equivalente entre todas estas ramas y su importancia radica en que nos permite entender y describir mejor alguna problemática puntual. Por ejemplo cuando queremos hablar sobre el comportamiento de una sucesión conforme ésta crece cada vez más y más hacemos uso del límite al infinito de nuestra variable, o cuando hablamos de la cardinalidad de un conjunto que tiene una cantidad de elementos numerable, intuitivamente pensamos en que dicho conjunto tiene una infinidad de elementos.
Lo anterior no es la excepción al estudiar Variable Compleja. Dado que el campo de los números complejos $\mathbb{C}$ no puede ordenarse bajo la relación de ser positivo, la idea de que un número complejo $z = a + ib$ crezca o decrezca no tiene sentido. Sin embargo podemos preguntarnos en qué sucede con su módulo $|\,z\,|$, ya que conforme crece $|\,z\,|$ de manera arbitraria tendremos que el número complejo $z$ se alejará más del origen. Entonces, al pensar en que $z \rightarrow \infty$ no tendremos que distinguir entre las direcciones de los ejes, sino simplemente recordar que estamos pensando en que el módulo $|\,z\,|$ crece sin límite a lo largo de los ejes real e imaginario, por lo que la notación $|\,z\,| \rightarrow \infty$ será lo mismo que $a^2+b^2 \rightarrow \infty$.
En su momento veremos que es necesario estudiar funciones de variable compleja para las que el módulo de la variable crezca de manera arbitraria, por lo que resulta conveniente agregar al plano complejo un punto ideal, llamado el punto al infinito, denotado por $\infty$.
Definición 11.1. (El plano complejo extendido.)
Se define al plano complejo extendido como el conjunto dotado con el punto $z_\infty=\infty$ como: \begin{equation*}
\mathbb{C}_{\infty} := \mathbb{C}\cup \{\infty\}.
\end{equation*}
Observación 11.1.
Es claro que en el plano complejo $\mathbb{C}$ no existe un lugar destinado para el punto al infinito. Sin embargo, ¿qué pasa con aquellos puntos $z\in\mathbb{C}$ tales que $|\,z\,|>\frac{1}{\varepsilon}$ para todo $\varepsilon>0$ suficientemente pequeño? El punto al infinito nos permite responder esta pregunta, ya que a los puntos con dicha propiedad los podemos pensar como un $\varepsilon$-vecindario del punto al infinito.
Primeramente debemos establecer las siguientes reglas aritméticas para poder operar con este nuevo punto del plano complejo extendido: \begin{align*}
z \pm \infty = \infty \pm z = \infty, \quad \forall z \in \mathbb{C}.\\
z \cdot \infty = \infty \cdot z = \infty, \quad \text{si}\,\,\, z \neq 0.\\
\frac{z}{0} = \infty, \quad \text{si}\,\,\, z \neq 0.\\
\frac{z}{\infty} = 0, \quad \text{si}\,\,\, z \neq \infty.\
\end{align*}
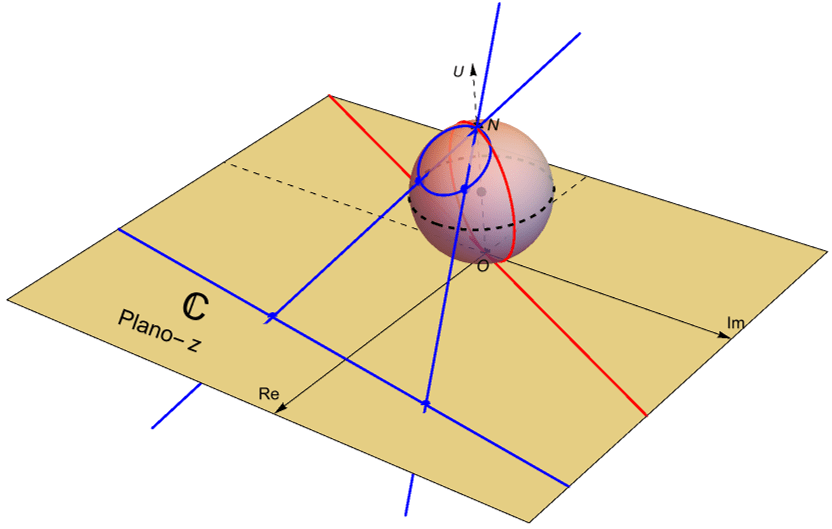
Un módelo que nos permite representar al plano complejo extendido es la esfera unitaria en $\mathbb{R}^3$, cuyo centro es el punto $(0,0,1)$, situada sobre el plano complejo $\mathbb{C}$, figura 52, es decir el conjunto: \begin{equation*}
\mathbb{S} = \{ (x,y,u) \in \mathbb{R}^3 \, : \, x^2 + y^2 + (u-1)^2 = 1 \},
\end{equation*} dotada con los puntos $N=(0,0,2)$, llamado el polo norte o el punto al infinito y $O=(0,0,0)$ llamado el polo sur o el origen. A dicho modelo se le denomina la esfera de Riemann.
Es posible identificar a $\mathbb{S}\setminus\{N\}$ con el plano complejo si consideramos a $\mathbb{C}$ como el plano: \begin{equation*}
\Pi = \{(a,b,0)\in\mathbb{R}^3 \, : \, a,b \in \mathbb{R}\}, \tag{11.1}
\end{equation*} y al punto $N$ con el punto al infinito.
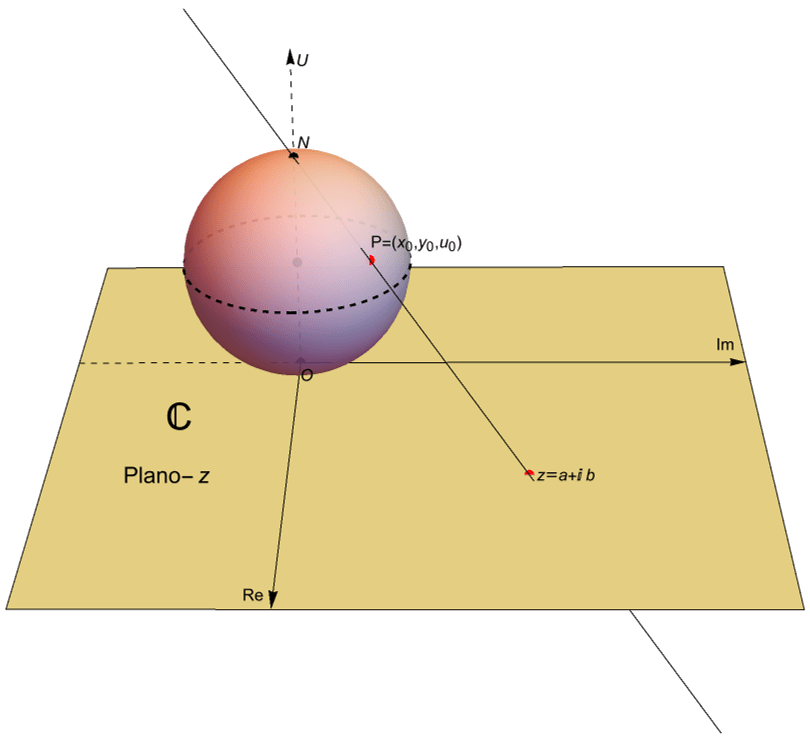
De acuerdo con la gráfica, tenemos que un número complejo $z=a+ib$ con un módulo demasiado grande se aleja del origen $(0,0,0)$ conforme el punto $P=(x_0,y_0,u_0)$ está más cerca del punto al infinito $N$.
Notemos que si trazamos una recta desde $N$ hasta el número complejo $z=a+ib$ en el plano complejo, al cual le corresponde el punto $(a,b,0)$ en $\mathbb{R}^3$, entonces existe un único punto $P=(x_0, y_0, u_0)$ en la esfera de Riemann tal que pertenece a dicha recta. Por otra parte, para un punto $P=(x_0, y_0, u_0)\in\mathbb{S}$, distinto de $N$, es posible extender el segmento de recta que une a $N$ con dicho punto $P$ hasta intersecar al plano complejo $\mathbb{C}$ en un único punto $z=a+ib$, figura 52.
Lo anterior nos deja ver que existe una relación biunívoca entre $\mathbb{S}\setminus\{N\}$ y $\mathbb{C}$, pensado como el plano (11.1), descrita a continuación.
Podemos escribir a la recta que pasa por los puntos $N=(0,0,2)$ y $P=(x_0,y_0,u_0)$ en su forma paramétrica como:
\begin{equation*}
N + (P-N)t, \quad t\in\mathbb{R}.
\tag{11.2} \end{equation*} Dado que la recta (11.2) interseca al plano $\mathbb{C}$, dado por (11.1), en el número complejo $z=a+ib$, es decir el punto $(a,b,0)$, entonces se tiene que para algún $t\in\mathbb{R}$: \begin{align*}
(a,b,0) &= N + (P-N)t\\
& = (tx_0,ty_0, 2 + t(u_0-2)).
\end{align*} De lo anterior tenemos el siguiente sistema de ecuaciones: \begin{align*}
a = t x_0,\tag{11.3.1} \\
b = t y_0,\tag{11.3.2} \\
2(t-1) = t u_0. \tag{11.3.3}
\end{align*} Además de (11.3.3) es claro que: \begin{equation*}
t = \frac{2}{2-u_0}. \tag{11.3.4}
\end{equation*} Sustituyendo (11.3.4) en (11.3.1) y (11.3.2) tenemos: \begin{align*}
a = \frac{2x_0}{2-u_0},\\
b = \frac{2y_0}{2-u_0}. \tag{11.4}
\end{align*}
Por otra parte, sabemos que $P=(x_0,y_0,u_0) \in \mathbb{S}$, por lo que satisface: \begin{equation*}
x_0^2 + y_0^2 + (u_0 – 1)^2 = 1.
\end{equation*}
Multiplicando ésta última expresión por $t^2$ obtenemos: \begin{align*}(tx_0)^2 + (ty_0)^2 + (tu_0 -t)^2 = t^2\\
\\
\Longrightarrow \quad (tx_0)^2 + (ty_0)^2 + (tu_0)^2 = 2t^2 u_0. \tag{11.5.1} \end{align*}
Dado que $z=a+ib\in\mathbb{C}$, sabemos que $|\,z\,|^2 = a^2 + b^2 $, por lo que sustituyendo (11.3.1), (11.3.2) y (11.3.3) en (11.5.1) tenemos:
\begin{align*}
a^2 + b^2 + 4(t-1)^2 = 4t(t-1).\\
\\
\Longrightarrow \quad t = \frac{|\,z\,|^2 + 4}{4}\tag{11.5.2}
\end{align*}
De (11.3.1), (11.3.2), (11.3.3) y (11.5.2) se sigue que: \begin{align*}
x_0 = \frac{a}{t} = \frac{4a}{|\,z\,|^2 + 4},\\
y_0 = \frac{b}{t} = \frac{4b}{|\,z\,|^2 + 4}, \tag{11.6}
\end{align*} \begin{equation*}
u_0 = \frac{2(t-1)}{t} = \frac{2\,|\,z\,|^2}{|\,z\,|^2 + 4}.
\end{equation*}
Esta forma de asociar o hacer corresponder a los puntos $z$ de $\mathbb{C}$ con la esfera de Riemann $\mathbb{S}$, dotada con $N=(0,0,2)$ y $O=(0,0,0)$, se le conoce como la proyección estereográfica.
Definición 11.2. (La proyección estereográfica.)
Definimos a la proyección estereográfica como la función $\varphi:\mathbb{S} \to \mathbb{C}_{\infty}$ tal que para $P=(x,y,u)\in \mathbb{S}$: \begin{equation*}
\varphi(P) = \left\{\begin{array}{lcc}
\infty, & \text{si} & P=N=(0,0,2),\\
\\ z= a+ib, & \text{si} & P \neq N,
\end{array}
\right.
\end{equation*} donde $z=a+ib\in\mathbb{C}$ representa al punto $(a,b,0)$ de $\mathbb{R}^3$ tal que $a = \dfrac{2x}{2-u}$, $b=\dfrac{2y}{2-u}$.
Proposición 11.1.
Sea $\mathbb{S}^* = \mathbb{S}\setminus{N}$. La proyección estereográfica es un homeomorfismo entre $(\mathbb{S}^*,d_{\mathbb{R}^3})$ y $(\mathbb{C},d)$, donde $d_{\mathbb{R}^3}$ es la distancia usual de $\mathbb{R}^3$ y $d$ la métrica euclidiana en $\mathbb{C}$.
Demostración. Veamos que está función es biyectiva. Es claro que si $P,Q\in\mathbb{S}^*$, entonces para algún $z_1, z_2 \in \mathbb{C}$ se tiene:
\begin{align*}
\varphi(P) = \varphi(Q) \quad & \Longrightarrow \quad z_1 = z_2\\
& \Longrightarrow \quad \operatorname{Re}(z_1) = \operatorname{Re}(z_2)\\
& \quad \quad \quad \, \operatorname{Im}(z_1) =\operatorname{Im}(z_2)\\
& \quad \quad \quad \, \, \text{y} \,\, |\,z_1\,| = |\,z_2\,|. \end{align*} Por lo que $P=Q$, entonces $\varphi$ es inyectiva.
Consideremos a $z=a+ib \in\mathbb{C}$, notemos que si $P=(x_0,y_0,u_0)\in\mathbb{S}^*$, con $x_0$, $y_0$ y $u_0$ dados como en (11.6) entonces: \begin{align*}
\varphi(P) & = \varphi\left(\frac{4a}{|\,z\,|^2+4}, \frac{4b}{|\,z\,|^2+4}, \frac{2\,|\,z\,|^2}{|\,z\,|^2+4}\right)\\
& = \frac{2\left(\frac{4a}{|\,z\,|^2+4}\right)}{2-\frac{2\,|\,z\,|^2}{|\,z\,|^2+4}} + i\, \frac{2\left(\frac{4b}{|\,z\,|^2+4}\right)}{2-\frac{2\,|\,z\,|^2}{|\,z\,|^2+4}}\\
& = a + ib\\
& = z.
\end{align*} Por lo tanto, como $z\in\mathbb{C}$ era arbitrario se sigue que para todo número complejo $z$ existe un punto $P\in\mathbb{S}^*$ tal que $\varphi(P) = z$. Por lo tanto $\varphi$ es sobreyectiva.
Dado que la proyección estereográfica es una función biyectiva, entonces existe la función inversa de $\varphi$, digamos $\varphi^{-1}$, la cual es una función que va de $\mathbb{C}_\infty$ a $\mathbb{S}$ tal que para $z\in\mathbb{C}_\infty$: \begin{equation*}
\varphi^{-1}(z) = \left\{\begin{array}{lll}
N=(0,0,2), & \text{si} & z = \infty,\\
P= \left( \dfrac{4a}{|\,z\,|^2 + 4}, \dfrac{4b}{|\,z\,|^2 + 4}, \dfrac{2\,|\,z\,|^2}{|\,z\,|^2 + 4}\right), & \text{si} & z = a+ib \in\mathbb{C}.
\end{array}
\right.
\end{equation*}
Considerando las ecuaciones que definen a las funciones $\varphi$ y $\varphi^{-1}$, dadas en (11.4) y en (11.6), no es difícil verificar que ambas funciones son continuas en su respectivo dominio, por lo que se deja como ejercicio.
$\blacksquare$
Observación 11.2.
Consideremos la ecuación general de un plano, es decir: \begin{equation*}
Ax+By+Cu+D=0.
\end{equation*} Si dicho plano pasa por el centro de la esfera $\mathbb{S}$, es decir por el punto $(0,0,1)$, entonces dicho plano es de la forma: \begin{equation*}
Ax+By+C(u-1)=0. \tag{11.7}
\end{equation*} Más aún, al intersecar a la esfera $\mathbb{S}$ con un plano de la forma (11.7) se obtiene una circunferencia máxima.
Observación 11.3.
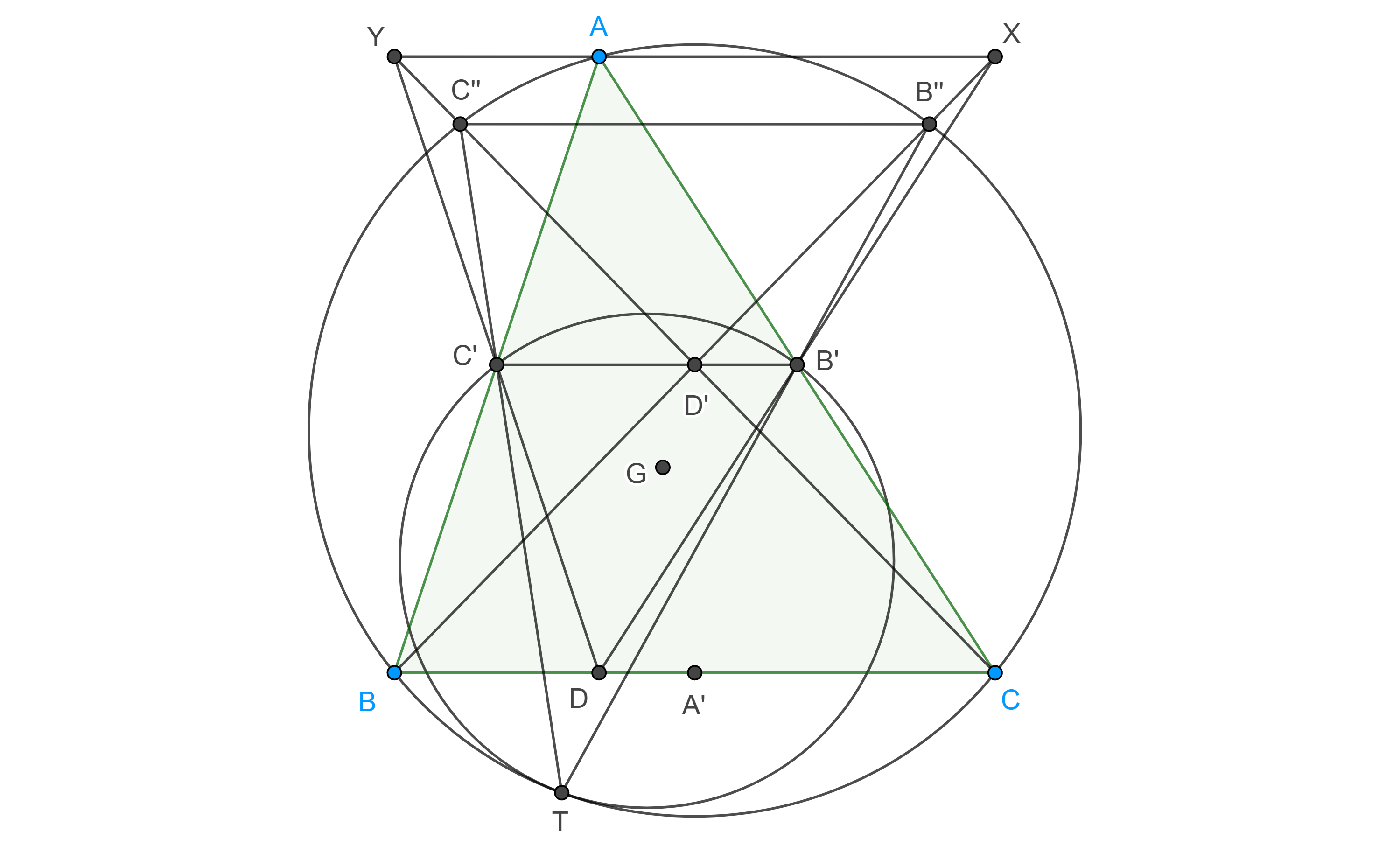
Notemos que bajo la proyección estereográfica los lugares geométricos del plano complejo $\mathbb{C}$ corresponden con lugares geométricos de la esfera de Riemann $\mathbb{S}$ y viceversa. Es importante recordar que no existe un punto en el plano complejo destinado para el punto al infinito, sin embargo no es difícil observar de manera geométrica que líneas longitudinales que pasan por el polo norte $N$, como el meridiano 0 o meridiano de Greenwich, corresponden con rectas en el plano complejo $\mathbb{C}$ que pasan por el origen $z=0$. Por otra parte, en la esfera de Riemann las líneas de latitud, como el ecuador, corresponden con circunferencias en el plano complejo $\mathbb{C}$ centradas en el origen $z=0$, mientras que una circunferencia arbitraria en la esfera de Riemann, que no pase por el polo norte $N$, corresponde con una circunferencia en el plano complejo $\mathbb{C}$. No debe ser difícil notar que conforme el radio de las circunferencias tiende a infinito, las líneas de latitud en la esfera tienden al polo norte $N$ que corresponde con el punto al infinito.

Proposición 11.2.
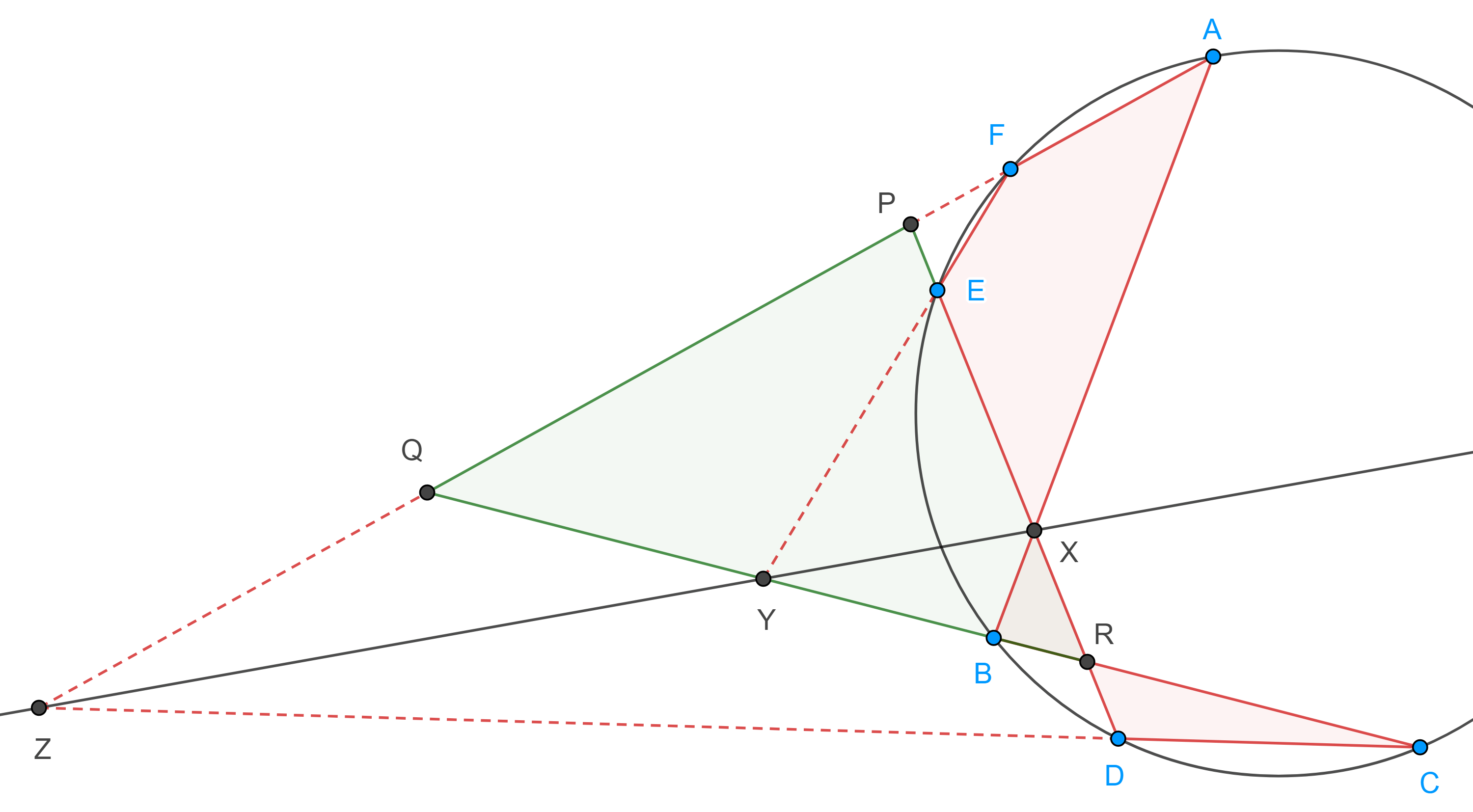
Bajo la proyección esterográfica, circunferencias en la esfera de Riemann, $\mathbb{S}$, corresponden con circunferencias o rectas en el plano complejo $\mathbb{C}$, figuras 53 y 54.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Observación 11.4.
De nuestros cursos de Geometría Analítica y Cálculo sabemos que una trayectoria o camino en $\mathbb{R}^n$ es una función continua $\gamma:(c,d)\rightarrow \mathbb{R}^n$, y al conjunto $\Gamma = \{ \gamma(t) \, : \, t\in(c,d)\}$ lo llamamos la curva descrita por $\gamma$. Además sabemos que podemos expresar a una trayectoria $\gamma$ por medio de sus funciones componentes, por ejemplo en $\mathbb{R}^3$ tenemos que $\gamma(t) = \left(x(t),y(t),z(t)\right)$ donde $x(t),y(t),z(t)$ son funciones reales continuas llamadas las componentes de $\gamma$. Por otra parte, decimos que una curva es suave en $(c,d)$ si es diferenciable en $(c,d)$, es decir si sus funciones componentes son derivables en $(c,d)$ y sus derivadas no se anulan simultáneamente en $(c,d)$, excepto quizás en $c$ o $d$.
Observación 11.5.
Por otra parte, sabemos que el ángulo $\theta$ entre dos vectores $u,v$ en $\mathbb{R}^2$ o $\mathbb{R}^3$ se puede obtener mediante: \begin{equation*}
\operatorname{cos}(\theta) = \frac{u \cdot v}{\left\lVert u \right\rVert \left\lVert v \right\rVert},
\end{equation*} donde «$\cdot$» representa el producto interior entre $u$ y $v$, mientras que $\left\lVert \cdot \right\rVert$ la norma de cada vector.
Dadas dos curvas suaves, descritas por $\gamma_1$ y $\gamma_2$, podemos definir el ángulo entre ellas como el ángulo que se forma entre las rectas tangentes a cada curva en un punto de intersección. Es claro que dadas dos rectas tangentes, que se intersecan entre sí, se obtienen dos ángulos distintos, digamos $\theta_1$ y $\theta_2$ cuya relación entre ellos está dada por $\theta_1 + \theta_2 = \pi$, por lo que para evitar confusión sobre cuál de los dos ángulos obtenidos se está considerando, diremos que el ángulo $\theta$ que se forma entre dos curvas suaves será tal que $\theta\in(0,\pi/2)$. Con esta consideración tenemos que $\operatorname{cos}(\theta)>0$.
Una pregunta interesante que podemos hacernos es ¿qué pasa con los ángulos entre cualesquiera dos curvas suaves en el plano complejo $\mathbb{C}$ o en la esfera de Riemann $\mathbb{S}$?, es decir, ¿bajo la proyección estereográfica se conserva el ángulo entre dos curvas suaves? Para responder esta pregunta primeramente podemos realizar un análisis geométrico.
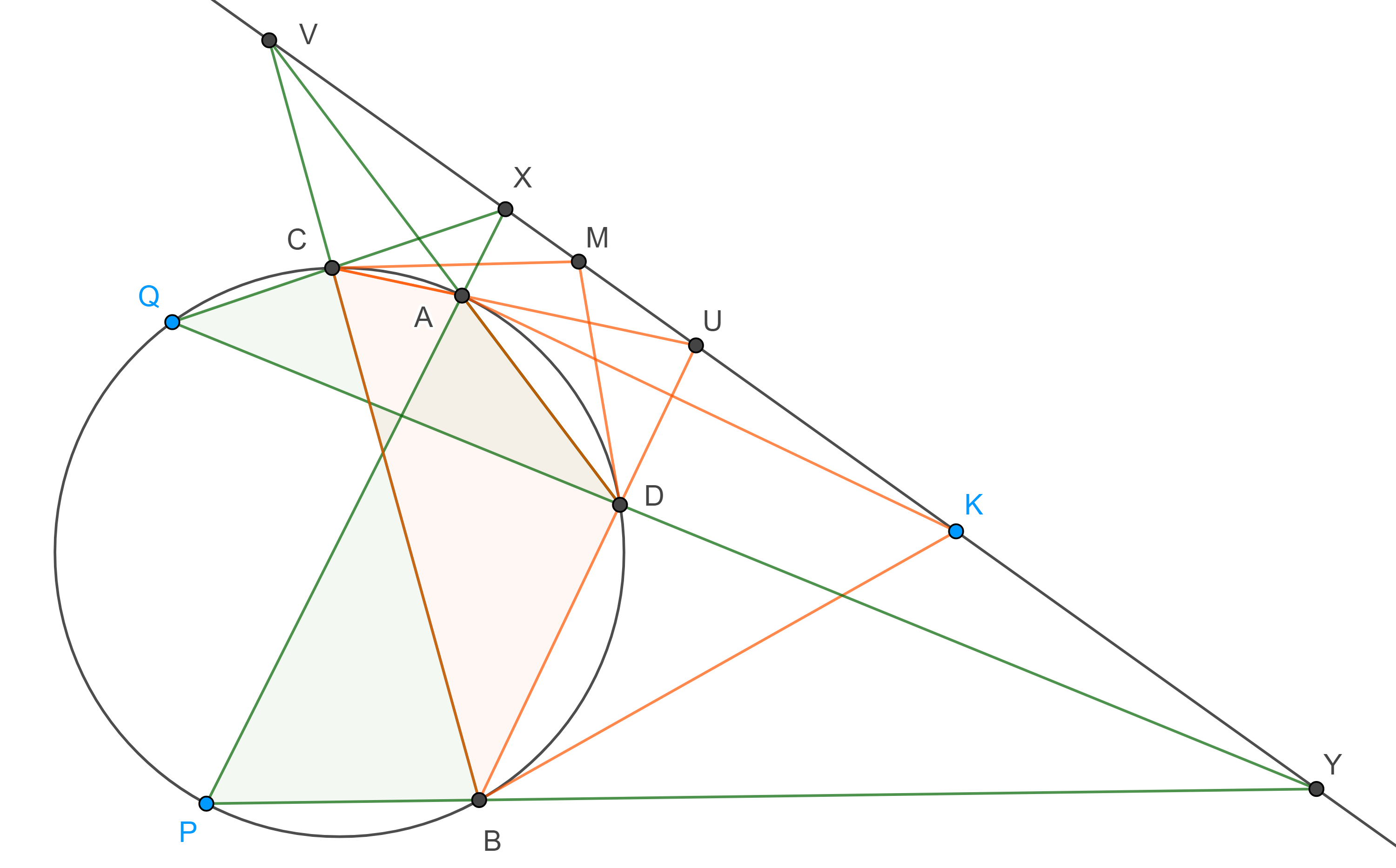
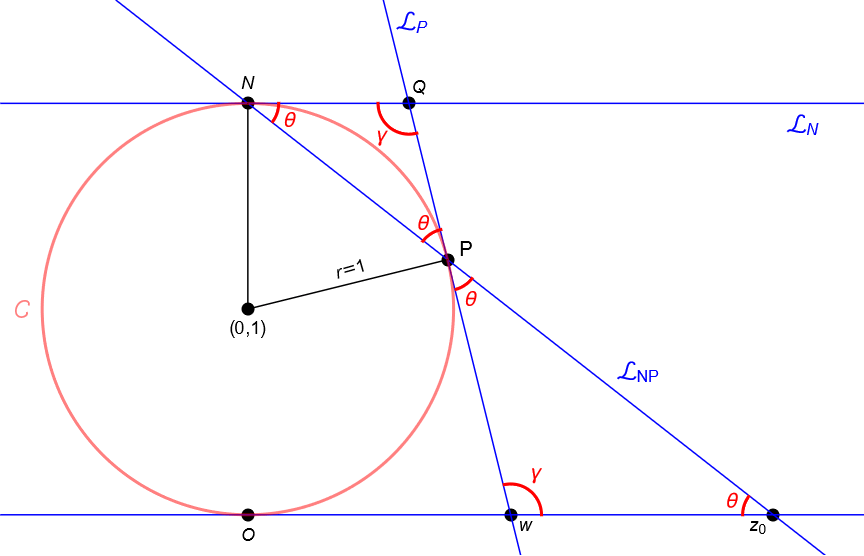
De acuerdo con nuestros cursos de Cálculo y Geometría sabemos que es posible encontrar el plano tangente a la esfera $\mathbb{S}$ en el punto $P$, digamos $\Pi_P$. Consideremos al plano $u=2$, es decir el plano tangente a $\mathbb{S}$ en el polo norte $N$, digamos $\Pi_N$ y consideremos al plano que pasa por el centro de $\mathbb{S}$, por el polo norte $N$ y por el punto $P$, digamos $\Pi_{CNP}$. No es difícil convencerse de que la intersección de dicho plano con la esfera $\mathbb{S}$ determina una circunferencia máxima, digamos $\mathcal{C}$, además la intersección del plano $\Pi_{CNP}$ con los planos $\Pi_P$, $\Pi_N$ y $\mathbb{C}$ determina tres rectas, digamos $\mathcal{L}_P$, $\mathcal{L}_N$ y $\mathcal{L}_O$, la primera recta es tangente a $\mathcal{C}$ en $P$ y la segunda recta es tangente a $\mathcal{C}$ en $N$, mientras que la tercera recta es tangente a $\mathbb{S}$ en el origen y pasa por el punto $z_0=\varphi(P)$. Notemos que $\mathcal{L}_P$ y $\mathcal{L}_N$ se intersecan en un punto $Q\in\mathbb{R}^3$ y las rectas $\mathcal{L}_P$ y $\mathcal{L}_O$ se intersecan en un punto $w\in\mathbb{C}$. Por otra parte la intersección de los planos $\Pi_N$ y $\mathbb{C}$ con el plano $\Pi_P$ determinan otras dos rectas, digamos $\mathcal{L}_Q$ y $\mathcal{L}_w$, la primera pasa por $Q$ y la segunda pasa por $w$. Por construcción es claro que la recta $\mathcal{L}_N$ pasa por el punto $Q$, figura 55.
Dada la perfecta simetría de la esfera, es fácil concluir que los planos $\Pi_N$ y $\Pi_P$ forman los mismos ángulos con la recta que pasa por $N$ y $P$, digamos $\mathcal{L}_{NP}$, y que la recta $\mathcal{L}_Q$ es perpendicular a la recta $\mathcal{L}_{NP}$. Para ver esto más claro consideremos el corte transversal hecho sobre la esfera $\mathbb{S}$ con el plano $\Pi_{CNP}$. Más aún, como el plano $\Pi_N$ es paralelo al plano complejo $\mathbb{C}$, es claro que los planos $\Pi_P$ y $\mathbb{C}$ forman los mismos ángulos con la recta $\mathcal{L}_{NP}$ en el punto $z_0\in\mathbb{C}$ dado por la proyección estereográfica, figura 55. De acuerdo con la figura 56 es claro que los triángulos $NQP$ y $Pwz_0$ son semejantes.
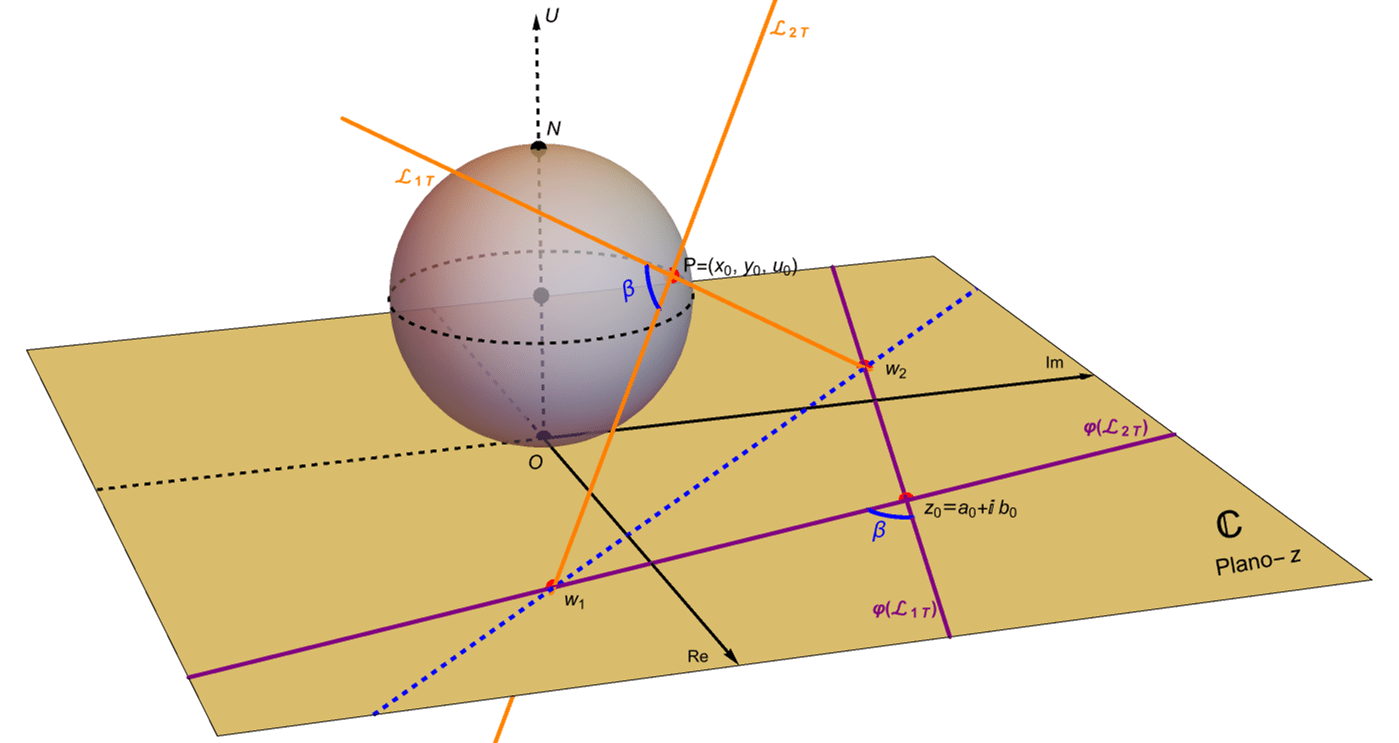
Supongamos que dos curvas suaves en $\mathbb{S}$, digamos $\Gamma_1$ y $\Gamma_2$, se intersecan en un punto $P\in\mathbb{S}$ con $P\neq N$. Sean $\mathcal{L}_{1T}$ y $\mathcal{L}_{2T}$ las respectivas rectas tangentes a las curvas $\Gamma_1$ y $\Gamma_2$ en el punto $P$ y sea $\beta$ el ángulo entre ellas, es decir $\beta\in(0,\pi/2)$.
Sin perder generalidad consideremos a la recta tangente $\mathcal{L}_{2T}$ en el punto $P\in\mathbb{S}$. Es fácil convencerse que la recta tangente bajo la proyección estereográfica en el punto $z_0=\varphi(P)\in\mathbb{C}$, digamos $\varphi\left(\mathcal{L}_{2T}\right)$, está dada por la intersección de un plano que contiene a $\mathcal{L}_{2T}$ y $\mathcal{L}_{NP}$, digamos $\pi$, con el plano complejo $\mathbb{C}$. Considerando lo anterior tenemos que las rectas tangentes $\mathcal{L}_{2T}$ y $\varphi\left(\mathcal{L}_{2T}\right)$ forman los mismos ángulos con $\mathcal{L}_{NP}$. Más aún, dado que la intersección del plano $\Pi_P$ con $\mathbb{C}$ determina a la recta $\mathcal{L}_w$ entonces es fácil concluir que las rectas tangentes $\mathcal{L}_{2T}$ y $\varphi\left(\mathcal{L}_{2T}\right)$ forman los mismos ángulos con $\mathcal{L}_w$, figura 57.
Haciendo lo mismo con la recta tangente $\mathcal{L}_{1T}$ concluimos que los ángulos que forman las dos rectas tangentes a las curvas $\Gamma_1$ y $\Gamma_2$ en el punto de intersección $P\in\mathbb{S}$, es decir $\mathcal{L}_{1T}$ y $\mathcal{L}_{2T}$ forman los mismos ángulos que las rectas tangentes a las imágenes de las curvas, digamos $\varphi\left(\Gamma_1\right)$ y $\varphi\left(\Gamma_2\right)$, dadas por la proyección estereográfica en el punto de intersección $z_0=\varphi(P)\in\mathbb{C}$, figura 58.


Hasta ahora hemos argumentado de manera geométrica que bajo la proyección estereográfica el ángulo que se forma entre dos curvas suaves $\Gamma_1$ y $\Gamma_2$ se conserva, ahora haremos una prueba analítica de esta propiedad, para ello consideremos lo siguiente.
Observación 11.6.
Notemos que para cualesquiera dos curvas suaves en la esfera de Riemann $\mathbb{S}$, al hablar del ángulo $\alpha$ que se forma entre ellas en un punto de intersección $P\in\mathbb{S}$ necesitamos pensar en el ángulo $0<\theta<\pi/2$ que se forma entre sus rectas tangentes en dicho punto, pero ¿cómo obtenemos una recta tangente a una curva suave en un punto $P\in\mathbb{S}$? Supongamos que una curva suave en $\mathbb{S}$ está descrita por la trayectoria $\gamma:(c,d)\rightarrow\mathbb{S}\subset\mathbb{R}^3$ cuyas funciones componentes son $x(t)$, $y(t)$ y $z(t)$, es decir $\gamma(t) = (x(t), y(t), z(t))$. Dado que la curva es suave en $(c,d)$ tenemos que existe $\gamma'(t)=(x'(t), y'(t), z'(t)) \neq 0$ para toda $t\in(c,d)$. Considerando que la curva descrita por $\gamma$ pasa por el punto $P=(x_0,y_0,u_0)\in\mathbb{S}$, entonces para algún $t_0\in(c,d)$ se cumple que $\gamma(t_0) = P$, por lo que podemos determinar a la recta tangente a dicha curva en el punto $P$, digamos $\mathcal{L}_{T}$, de forma paramétrica como: \begin{equation*}
\mathcal{L}_T: \quad P + \gamma'(t_0) \lambda, \quad \lambda\in\mathbb{R}.
\end{equation*}
Observación 11.7.
De manera geométrica es claro que $\mathcal{L}_T$ se puede obtener mediante la intersección de un plano tangente a la esfera $\mathbb{S}$ en el punto $P$, digamos $\Pi_T$, y un plano que pasa por el centro de la esfera y por $P$, digamos $\Pi_{CP}$. Considerando el plano $\Pi_{CP}$, por la observación 11.2 tenemos que existe una circunferencia máxima que que cae en dicho plano y que además pasa por el punto $P\in\mathbb{S}$. Entonces podemos concluir que para una recta tangente a la esfera en un punto $P$ existe una circunferencia máxima que pasa por dicho punto y que cae en el plano $\Pi_{CP}$.
De acuerdo con lo anterior, ver qué pasa con el ángulo $0<\theta<\pi/2$ que forman las rectas tangentes a dos curvas suaves en un punto de intersección $P\in\mathbb{S}$ bajo la proyección estereográfica, es equivalente a ver qué sucede con el ángulo que se forma entre dos circunferencias máximas de la esfera $\mathbb{S}$ bajo la proyección estereográfica, el cual está dado por el ángulo que se forma entre los planos en los que caen dichas circunferencias.
Proposición 11.3.
La proyección estereográfica es conforme o isogonal, es decir preserva ángulos.
Este resultado nos dice que el ángulo $\theta\in(0,\pi/2)$ que forman dos curvas suaves en la esfera $\mathbb{S}$, en un punto de intersección $P\in\mathbb{S}$, se preserva bajo la proyección estereográfica, es decir que en el plano complejo $\mathbb{C}$ las rectas tangentes de las imágenes de dichas curvas bajo la proyección estereográfica, en la imagen del punto de intersección, formarán nuevamente un ángulo $\theta$.
Recíprocamente para dos curvas suaves que se intersecan en el plano complejo $\mathbb{C}$, es decir en el plano $\Pi$ dado por (11.1), el ángulo $\theta\in(0,\pi/2)$ formado por sus rectas tangentes en el punto de intersección se preserva bajo la proyección estereográfica.

Demostración. Sean $\Gamma_1$ y $\Gamma_2$ dos curvas suaves en $\mathbb{S}$, descritas por $\gamma_1:(c,d)\rightarrow\mathbb{R}^3$ y $\gamma_2:(e,f)\rightarrow\mathbb{R}^3$, las cuales se pueden escribir considerando sus funciones componentes como: \begin{align*}
\gamma_1(t) = (x_1(t),y_1(t),u_1(t)),\\
\gamma_2(t) = (x_2(t),y_2(t),u_2(t)).
\end{align*} Para probar este resultado consideremos los siguientes casos:
- El ángulo $\theta\in(0,\pi/2)$ que se forma entre $\Gamma_1$ y $\Gamma_2$ que se intersecan en el polo norte $N$ (o en el polo sur $O$) se preserva bajo la proyección estereográfica.
- El ángulo $\theta\in(0,\pi/2)$ que se forma entre $\Gamma_1$ y $\Gamma_2$ que se intersecan en un punto $P\neq N$ se preserva bajo la proyección estereográfica.
Caso 1. Dado que el polo norte $N$ y el polo sur $O$ son puntos antipodales en $\mathbb{S}$, una circunferencia máxima que pase por el polo norte también pasa por el polo sur. Entonces, considerando la observación 11.7, tenemos que es indistinto si las dos curvas $\Gamma_1$ y $\Gamma_2$ se intersecan en el polo norte o en el polo sur, pues el ángulo que forman sus rectas tangentes en cualquiera de dichos puntos será el mismo que forman las dos circunferencias máximas que pasan por dichos puntos, es decir, el ángulo que se forma entre los dos planos que contienen a cada una de las circunferencias máximas.
Entonces, sin pérdida de generalidad supongamos que $\Gamma_1$ y $\Gamma_2$ se intersecan en el polo norte $N=(0,0,2)$. Por la observación 11.7 sabemos que cada recta tangente a cada curva, en el punto $N=(0,0,2)$, se obtiene mediante la intersección de un plano tangente a la esfera $\mathbb{S}$ en el polo norte, es decir el plano $u=2$, y un plano que pasa por el centro de la esfera y por el punto $N=(0,0,2)$, digamos $\Pi_{CN}$. De acuerdo con la observación 11.2 dichos planos son de la forma: \begin{align*}
\Pi_{1CN}: \quad A_1x+B_1y=0,\\
\Pi_{2CN}: \quad A_2x+B_2y=0.
\end{align*} Más aún, sabemos que en cada uno de estos planos cae una circunferencia máxima que pasa por $N=(0,0,2)$ y por $O=(0,0,0)$. Por lo que considerando las observaciones 11.5 y 11.7 tenemos que el ángulo $0<\theta<\pi/2$ que forman dichas circunferencias es tal que: \begin{align*}
\operatorname{cos}(\theta) & = \frac{(A_1,B_1,0) \cdot (A_2,B_2,0)}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}\\
& = \frac{A_1 A_2 + B_1 B_2}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}.
\end{align*} De acuerdo con la proposición 11.1, tenemos que bajo la proyección estereográfica las dos circunferencias máximas en la esfera $\mathbb{S}$, que pasan por el polo norte $N$, corresponden con dos rectas en el plano complejo $\mathbb{C}$ que pasan por el origen (¿por qué?), cuyas ecuaciones están dadas por: \begin{align*}
A_1x + B_1y =0, \quad u=0,\\
A_2x + B_2y =0,\quad u=0.
\end{align*} Es claro que el ángulo $0<\beta<\pi/2$ que forman estas rectas tangentes a las imágenes de las curvas $\Gamma_1$ y $\Gamma_2$ bajo la proyección estereográfica, en el punto de intersección $z=0$, es tal que: \begin{align*}
\operatorname{cos}(\beta) & = \frac{(A_1,B_1,0) \cdot (A_2,B_2,0)}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}\\
& = \frac{A_1 A_2 + B_1 B_2}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}.
\end{align*} Por lo que, el ángulo $\alpha$ que forman las curvas $\Gamma_1$ y $\Gamma_2$ en el polo norte o en el polo sur se conserva bajo la proyección estereográfica.
Caso 2. Supongamos que $\Gamma_1$ y $\Gamma_2$ se intersecan en un punto $P\in\mathbb{S}$ con $P=(x_0,y_0,u_0)\neq N$.
Dado que dichas curvas se intersecan en el punto $P=(x_0,y_0,u_0)\in\mathbb{S}\setminus\{N\}$, entonces existen $t_0\in(c,d)$ y $t_0^*\in(e,f)$ tales que: \begin{align*}
\gamma_1(t_0) = (x_1(t_0),y_1(t_0),u_1(t_0)) = P,\\
\gamma_2(t_0^*) = (x_2(t_0^*),y_2(t_0^*),u_2(t_0^*)) = P. \tag{11.8.1}
\end{align*} Como $\Gamma_1$ y $\Gamma_2$ son suaves, tenemos que $\gamma_1$ es diferenciable en $(c,d)$ y $\gamma_2$ es diferenciable en $(e,f)$, por lo que: \begin{align*}
\gamma_1′(t_0) \neq 0,\quad \text{para}\,\, t_0\in(c,d),\\
\gamma_2′(t_0^*) \neq 0, \quad \text{para}\,\, t_0^*\in(e,f). \tag{11.8.2} \end{align*} Así, por la observación 11.6, las rectas tangentes a cada curva son respectivamente: \begin{align*}
\mathcal{L}_{1T}: \quad P + \gamma_1′(t_0) \lambda_1, \quad \lambda_1\in\mathbb{R},\\
\mathcal{L}_{2T}: \quad P + \gamma_2′(t_0^*) \lambda_2, \quad \lambda_2\in\mathbb{R}.
\end{align*} Entonces, considerando la observación 11.5, tenemos que el ángulo $0<\theta<\pi/2$ que se forma entre $\mathcal{L}_{1T}$ y $\mathcal{L}_{2T}$ en el punto de intersección $P\in\mathbb{S}$ es tal que: \begin{align*}
\operatorname{cos}(\theta) & = \frac{\gamma_1′(t_0) \cdot \gamma_2′(t_0^*)}{\left\lVert\gamma_1′(t_0)\right\rVert\left\lVert\gamma_2′(t_0^*) \right\rVert}\\
&=\frac{x_1′(t_0)\,x_2′(t_0^*) + y_1′(t_0)\,y_2′(t_0^*) + u_1′(t_0)\,u_2′(t_0^*)}{\sqrt{x_1′(t_0)^2 + y_1′(t_0)^2 + u_1′(t_0)^2} \sqrt{x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2}}. \tag{11.9}
\end{align*} Dado que las curvas $\Gamma_1$ y $\Gamma_2$ están en $\mathbb{S}$ se cumple que: \begin{align*}
x_1(t)^2 + y_1(t)^2 + (u_1(t)-1)^2 = 1, \quad \forall t\in(c,d),\\
x_2(t)^2 + y_2(t)^2 + (u_2(t)-1)^2 = 1, \quad \forall t\in(e,f). \tag{11.10.1} \end{align*} Y considerando (11.8.1) tenemos que: \begin{align*}
x_1′(t)^2 + y_1′(t)^2 + u_1′(t)^2 \neq 0, \quad \forall t\in(c,d),\\
x_2′(t)^2 + y_2′(t)^2 + u_2′(t)^2 \neq 0, \quad \forall t\in(e,f). \tag{11.10.2}
\end{align*}
Por otra parte, el punto de intersección $P\in\mathbb{S}\setminus\{N\}$ de las curvas $\Gamma_1$ y $\Gamma_2$ bajo la proyección estreográfica corresponde con el punto $z_0=a_0+ib_0\in\mathbb{C}$, donde: \begin{align*}
a_0 = \frac{2x_0}{2-u_0},\\
b_0 = \frac{2y_0}{2-u_0}.
\end{align*} Considerando a $\mathbb{C}$ como el plano dado por (11.1), tenemos que dicho punto $z_0$ lo podemos asociar con el punto $(a_0,b_0,0)$ de $\mathbb{R}^3$.
Mientras que bajo la proyección estereográfica las imágenes de las curvas $\Gamma_1$ y $\Gamma_2$, digamos $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$, están descritas por las funciones $\alpha_1:(c,d)\to\mathbb{R}^3$ y $\alpha_2:(e,f)\to\mathbb{R}^3$ en el plano complejo $\mathbb{C}$ y se pueden escribir considerando sus funciones componentes como: \begin{align*}
\alpha_1(t) = (a_1(t),b_1(t),0),\\
\alpha_2(t) = (a_2(t),b_2(t),0),
\end{align*} donde para cada $i=1,2$ se tiene que: \begin{align*}
a_i(t) = \frac{2x_i(t)}{2-u_i(t)},\\
b_i(t) = \frac{2y_i(t)}{2-u_i(t)}. \tag{11.11}
\end{align*}
De acuerdo con lo anterior, es claro que las curvas $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$ obtenidas bajo la proyección estereográfica son también curvas suaves en sus respectivos dominios $(c,d)$ y $(e,f)$, por lo que considerando el punto de intersección $z_0$ tenemos que para los valores $t_0\in(c,d)$ y $t_0^*\in(e,f)$ dados se cumple que: \begin{align*}
\alpha_1(t_0) = (a_1(t_0),b_1(t_0),0) = z_0,\\
\alpha_2(t_0^*) = (a_2(t_0^*),b_2(t_0^*),0) = z_0. \tag{11.12.1}
\end{align*} Más aún, como las funciones $\alpha_1$ y $\alpha_2$ son diferenciables en $(c,d)$ y $(e,f)$ respectivamente, entonces tenemos que para $t_0\in(c,d)$ y $t_0^*\in(e,f)$ se cumple: \begin{align*}
\alpha_1′(t_0) = (a_1′(t_0),b_1′(t_0),0) \neq 0,\\
\alpha_2′(t_0^*) = (a_2′(t_0^*),b_2′(t_0^*),0) \neq 0. \tag{11.12.2}
\end{align*} Por lo que las rectas tangentes a las curvas $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$ en el punto de intersección $z_0$ tienen como ecuaciones: \begin{align*}
\ell_{1T}: \quad z_0 + \alpha_1′(t_0) \delta_1, \quad \delta_1\in\mathbb{R},\\ \ell_{2T}: \quad z_0 + \alpha_2′(t_0^*) \delta_2, \quad \delta_2\in\mathbb{R}.
\end{align*} Entonces, considerando la observación 11.5, tenemos que el ángulo $0<\beta<\pi/2$ que se forma entre $\ell_{1T}$ y $\ell_{2T}$ en el punto de intersección $z_0\in\mathbb{C}$ es tal que: \begin{align*}
\operatorname{cos}(\beta) & = \frac{ \alpha_1′(t_0) \cdot \alpha_2′(t_0^*)}{\left\lVert \alpha_1′(t_0) \right\rVert \left\lVert \alpha_2′(t_0^*) \right\rVert}\\
& = \frac{a_1′(t_0) \, a_2′(t_0^*) + b_1′(t_0)\,b_2′(t_0^*)}{\sqrt{a_1′(t_0)^2 + b_1′(t_0)^2} \sqrt{a_2′(t_0^*)^2 + b_2′(t_0^*)^2}}.\tag{11.13}
\end{align*}
Para probar que el ángulo $\theta$, que forman las curvas $\Gamma_1$ y $\Gamma_2$ en el punto de intersección $P\in\mathbb{S}\setminus\{N\}$, se preserva bajo la proyección estereográfica veamos que las ecuaciones (11.9) y (11.13) son iguales.
Derivando las ecuaciones dadas en (11.11) tenemos para cada $i=1,2$ que: \begin{align*}
a_i'(t) = \frac{2}{(2-u_i(t))^2}\left[u_i'(t)\,x_i(t)+x_i'(t)\,(2-u_i(t))\right],\\
b_i'(t) = \frac{2}{(2-u_i(t))^2}\left[u_i'(t)\,y_i(t)+y_i'(t)\,(2-u_i(t))\right]. \tag{11.14}
\end{align*} Considerando las ecuaciones dadas en (11.6), obtenemos la relación inversa entre las curvas suaves $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$ en el plano complejo $\mathbb{C}$ con las curvas suaves $\Gamma_1$ y $\Gamma_2$ en la esfera $\mathbb{S}$. Considerando dicha relación es fácil verificar que para $i=1,2$ se cumple: \begin{equation*}
x_i'(t) \, x_i(t) + y_i'(t)\,y_i(t) + u_i'(t)\left[u_i(t)-1\right] = 0. \tag{11.15}
\end{equation*}
Considerando (11.8.1), (11.10.1), (11.12.1), (11.14) y (11.15) es fácil verificar que para $t_0\in(c,d)$ y para $t_0^*\in(e,f)$ se cumple respectivamente: \begin{align*}
a_1′(t_0)^2 &+ b_1′(t_0)^2\\
&=\frac{4}{(2-u_1(t_0))^4}\Bigg(\left[x_1′(t_0)^2+y_1′(t_0)^2+u_1′(t_0)^2\right](2-u_1(t_0))^2\Bigg),\\
&=\frac{4}{(2-u_0)^4}\Bigg(\left[x_1′(t_0)^2+y_1′(t_0)^2+u_1′(t_0)^2\right](2-u_0)^2\Bigg), \tag{11.16.1}
\end{align*} \begin{align*}
a_2′(t_0^*)^2 &+ b_2′(t_0^*)^2\\
&=\frac{4}{(2-u_2(t_0^*))^4} \Bigg( \left[x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2\right] (2-u_2(t_0^*))^2 \Bigg),\\
&=\frac{4}{(2-u_0)^4} \Bigg( \left[x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2\right] (2-u_0)^2 \Bigg). \tag{11.16.2}
\end{align*} Dado que el punto $P=(x_0,y_0,u_0)\neq N$, entonces $u_0 \neq 2$, por lo que podemos simplificar (11.16.1) y (11.16.2) como: \begin{equation*}
a_1′(t_0)^2 + b_1′(t_0)^2 = \frac{4}{(2-u_0)^2} \Bigg( x_1′(t_0)^2 + y_1′(t_0)^2 + + u_1′(t_0)^2 \Bigg), \tag{11.17.1}
\end{equation*} \begin{equation*}
a_2′(t_0^*)^2 + b_2′(t_0^*)^2 = \frac{4}{(2-u_0)^2} \Bigg(x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2 \Bigg). \tag{11.17.2}
\end{equation*} Además como $P\in\mathbb{S}$ se cumple que: \begin{equation*}
x_0^2+y_0^2=u_0(2-u_0). \tag{11.18}
\end{equation*}
Considerando (11.12.2), (11.14), (11.15), (11.18) y que $u_0\neq2$ es fácil verificar que: \begin{align*}
\alpha_1′(t_0) \cdot \alpha_2′(t_0^*) & = a_1′(t_0)\,a_2′(t_0^*) + b_1′(t_0)\,b_2′(t_0^*)\\
& = \frac{4}{(2-u_0)^2}\Bigg(x_1′(t_0)\,x_2′(t_0^*) + y_1′(t_0)\,y_2′(t_0^*) + u_1′(t_0)\,u_2′(t_0^*)\Bigg) \tag{11.19}
\end{align*}
Sustituyendo (11.17.1), (11.17.2) y (11.19) en (11.13) tenemos que: \begin{align*}
\operatorname{cos}(\beta) & = \frac{x_1′(t_0)\,x_2′(t_0^*) + y_1′(t_0)\,y_2′(t_0^*) + u_1′(t_0)\,u_2′(t_0^*)}{\sqrt{x_1′(t_0)^2 + y_1′(t_0)^2 + u_1′(t_0)^2} \sqrt{x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2}}\\
& = \operatorname{cos}(\theta).
\end{align*}
Por lo tanto el ángulo $\theta$ que se forma entre las curvas $\Gamma_1$ y $\Gamma_2$ en un punto de intersección $P\in\mathbb{S}$, distinto del polo norte (o del polo sur), se preserva bajo la proyección estereográfica.
$\blacksquare$
Del mismo modo en que introducimos una métrica en $\mathbb{C}$, es posible definir una métrica en $\mathbb{C}_\infty$, la cual nos permitirá caracterizar y analizar las propiedades de este nuevo conjunto.
Dados dos puntos $z,w\in\mathbb{C}_\infty$ debemos definir una forma de medir distancia entre ellos, es decir una métrica $d:\mathbb{C}_\infty \times \mathbb{C}_\infty \to [0, \infty)$. Desde que la proyección estereográfica nos da una biyección entre el plano complejo extendido $\mathbb{C}_\infty$ y la esfera de Riemann $\mathbb{S}$, podemos definir la métrica de $\mathbb{C}_\infty$ considerando la distancia usual entre dos puntos $P,Q\in\mathbb{R}^3$, es decir la métrica euclidiana de $\mathbb{R}^3$. Tenemos que si $P=(x_1,y_1,u_1)$ y $Q=(x_2,y_2,u_2)$ son dos puntos de $\mathbb{R}^3$ entonces: \begin{equation*}
d_{\mathbb{R}^3}(P,Q) = \sqrt{(x_1 \,-\, x_2)^2 + (y_1 \,-\, y_2)^2 + (u_1 \,-\, u_2)^2}. \tag{11.20}
\end{equation*}
Considerando la proyección estereográfica, podemos hacer corresponder los puntos $z=a+ib$ y $w=\alpha+i\beta$ en $\mathbb{C}_\infty$ con los puntos $P,Q\in\mathbb{S}$ respectivamente, entonces de acuerdo con (11.20) podemos definir la distancia entre $z$ y $w$ como: \begin{equation*} \chi(z,w) = \sqrt{(x_1 \,-\, x_2)^2 + (y_1 \,-\, y_2)^2 + (u_1 \,-\, u_2)^2}. \tag{11.21} \end{equation*}
Dado que $P$ y $Q$ son puntos de $\mathbb{S}$, entonces se cumple que: \begin{align*}
x_1^2 + y_1^2 +(u_1 -1)^2 = 1,\\
x_2^2 + y_2^2 +(u_2 -1)^2 = 1. \tag{11.22}
\end{align*} De acuerdo con (11.22) y considerando (11.8), es fácil ver que:
\begin{align*}
(x_1 \,-\, x_2)^2 + (y_1 \,-\, y_2)^2 + (u_1 \,-\, u_2)^2 & = 2\left(u_1 + u_2 \,-\, x_1 x_2 \,-\, y_1 y_2 \,-\, u_1 u_2\right)\\
& = \frac{16 |\, z \,-\, w \,|^2}{\left(|\,z\,|^2 + 4\right)\left(|\,w\,|^2 + 4\right)}. \tag{11.23}
\end{align*} Entonces por (11.21) y (11.23) tenemos que: \begin{equation*}
\chi(z,w) = \frac{4 |\, z \,-\, w \,|}{\sqrt{\left(|\,z\,|^2 + 4\right)\left(|\,w\,|^2 + 4\right)}}. \tag{11.24}
\end{equation*}
Notemos que los puntos $z\neq \infty$ y $w=\infty$ de $\mathbb{C}_\infty$ corresponden con los puntos $P=(x,y,u)$ y $N=(0,0,2)$ de $\mathbb{S} \subset \mathbb{R}^3$, por lo que considerando (11.20) es fácil ver que: \begin{equation*}
\chi(z,\infty) = \frac{4}{\sqrt{|\,z\,|^2 + 4}}. \tag{11.25}
\end{equation*}
Considerando (11.24) y (11.25) tenemos que: \begin{equation*}
\chi(z,w)= \left\{ \begin{array}{lcc}
\dfrac{4 |\, z \,-\, w \,|}{\sqrt{|\,z\,|^2 + 4} \,\sqrt{|\,w\,|^2 + 4}}, & \text{si} & z,w\in\mathbb{C}\\
\dfrac{4}{\sqrt{|\,z\,|^2 + 4}}, & \text{si} & z\in\mathbb{C}, w=\infty,\\
0, & \text{si} & z=\infty, w=\infty.\\
\end{array}
\right.
\end{equation*}
A esta métrica en $\mathbb{C}_\infty$, inducida por la métrica euclidiana de $\mathbb{R}^3$, se le conoce como la métrica cordal.
Notemos que $\mathbb{C}_\infty$ dotado con la métrica cordal forman un espacio métrico, ver ejercicio 4. Considerando la entrada anterior podemos verificar algunas propiedades para este espacio métrico.
Primeramente, dado que la métrica cordal es inducida por la distancia usual de $\mathbb{R}^3$, debe ser claro que si $z,w\in\mathbb{C}_\infty$, entonces: \begin{equation*}
\chi(z,w) \leq 2,
\end{equation*} ya que 2 es el diámetro de $\mathbb{S}\subset\mathbb{R}^3$. Por lo que la métrica cordal es acotada.
Proposición 11.4.
El espacio métrico $(\mathbb{C}_\infty, d)$, donde $d$ es la métrica cordal, es compacto.
Demostración. Dado que $\mathbb{S} \subset \mathbb{R}^3$ es cerrado y acotado, tenemos por el teorema de Heine – Borel que $\mathbb{S}$ es compacto en $\mathbb{R}^3$. Dado que la proyección estereográfica $\varphi$ define un homeomorfismo de $\mathbb{S}$ en $\mathbb{C}_\infty$, entonces se sigue que $\mathbb{C}_\infty$ es también compacto.
$\blacksquare$
Proposición 11.5.
El espacio métrico $(\mathbb{C}_\infty, d)$, donde $d$ es la métrica cordal, es completo.
Demostración. Ejercicio.
$\blacksquare$
Tarea moral
- Considera la proposición 11.1. Argumenta porqué la proyección estereográfica y su inversa, es decir las funciones $\varphi$ y $\varphi^{-1}$ son continuas. Hint: Consulta la entrada 9.
- Demuestra la proposición 11.2. Hint: Utiliza la observación 11.2.
- ¿Por qué una circunferencia en $\mathbb{S}$ que pasa por $N=(0,0,2)$ y por $O=(0,0,0)$ corresponde a una recta que pasa por el origen en el plano complejo $\mathbb{C}$?
- Muestra que las igualdades del caso 2 de la proposición 11.2 son ciertas. Argumenta tus desarrollos.
- Verifica que la igualdad dada por (11.23) es cierta.
- Demuestra que la métrica cordal satisface las condiciones de métrica, es decir, demuestra que para cualesquiera $z_1, z_2, z_3\in\mathbb{C}_\infty$ se cumple:
i) $\chi(z_2, z_1) \geq 0$.
ii) $\chi(z_2, z_1) = 0$ si y solo si $z_1=z_2$.
iii) Simetría: $\chi(z_1, z_2) = \chi(z_2, z_1)$.
iv) Desigualdad del triángulo: $\chi(z_2, z_1) \leq \chi(z_2, z_3) + \chi(z_3, z_1)$. Hint: Utiliza los ejercicios 8 y 9 de la entrada 3, sección de tarea moral, para probar la desigualdad del triángulo. - Considera a la función: \begin{equation*}
\chi(z,w) = \frac{4 \, |\,z\,-\,w\,|}{\sqrt{|\,z\,|^2 + 4} \, \sqrt{|\,w\,|^2 + 4}}, \quad \forall z,w\in\mathbb{C},
\end{equation*} de acuerdo con el ejercicio anterior es claro que dicha función es un métrica en $\mathbb{C}$. Prueba que dicha métrica $\chi$ y la métrica euclidiana $d(z,w) = |\,z\,-\,w\,|$ son equivalentes. - De acuerdo con la entrada anterior, sea $z_0\in\mathbb{C}_\infty$ y sea $d$ la métrica cordal, una pregunta que puede resultar es, dado $\rho>0$, ¿cómo se define un $\rho$-vecindario de $z_0$ en $\mathbb{C}_\infty$? Describe a dicho conjunto.
- Demuestra la proposición 11.5.
Más adelante…
En esta entrada hemos hecho una compactificación del plano complejo agregándole un punto ideal, llamado el punto al infinito, obteniendo así el plano complejo extendido $\mathbb{C}_\infty$ el cual representamos mediante el módelo de la esfera de Riemann.
Hemos visto que existe una relación biunívoca entre el plano complejo extendido y la esfera de Riemann dada por la proyección estreográfica, la cual resulto tener propiedades interesantes que aparecerán más adelante para caracterizar a algunas funciones.
Además dotamos al plano complejo extendido con una métrica, llamada la métrica cordal, la cual nos permite tratar a $\mathbb{C}_\infty$ como un espacio métrico, por lo que podemos considerar algunas propiedades de la entrada anterior para caracterizar la topología de este espacio métrico.
La importancia de trabajar con esta extensión se verá a lo largo del curso cuando requiramos trabajar con funciones complejas para las cuales el módulo de la variable crezca de manera arbitraria.
Con esta entrada finalizamos la primera unidad de este curso: Introducción y preliminares. La siguiente entrada comenzaremos la segunda unidad titulada: Analicidad y funciones de variable compleja.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Conexidad y compacidad en un espacio métrico.
- Siguiente entrada del curso: Funciones de variable compleja. Definiciones y preliminares.