Introducción
En esta entrada presentamos los conceptos de segmento dirigido, razón en la que un punto divide a un segmento y punto al infinito, que nos serán de ayuda en los próximos temas, además demostramos el teorema de Stewart, el cual nos sirve para calcular el valor de cualquier ceviana en un triángulo.
Segmento dirigido
Para un segmento $AB$ hasta ahora solo habíamos considerado su magnitud, la cual siempre es positiva o $0$ si $A = B$, ahora también consideraremos el sentido en el que recorremos el segmento es decir de $A$ a $B$ o de $B$ a $A$, lo que nos permitirá asignarles un signo.
Si hacemos el recorrido $AB$ y luego el recorrido $BA$ entonces terminaremos en $A$ que es donde empezamos, por lo que podemos decir que:
$\begin{equation} AB + BA = 0 \Leftrightarrow BA = – AB \Leftrightarrow AB = – BA. \end{equation}$
Igualmente, si tenemos tres puntos colineales $A$, $B$ y $C$, y hacemos el recorrido $AB$, luego $BC$ y al final $CA$, regresaremos al punto inicial, es decir:
$\begin{equation} AB + BC + CA = 0 \Leftrightarrow AB + BC = – CA = AC. \end{equation}$
donde la última igualdad se da por la ecuación $(1)$.
Teorema 1, de Euler. Para cualesquiera cuatro puntos colineales $A$, $B$, $C$ y $D$ tenemos lo siguiente: $AB \times CD + AC \times DB + AD \times BC = 0$.
Demostración. Por las ecuaciones $(1)$ y $(2)$ tenemos
$CD = CA + AD = – AC + AD$,
$DB = DA + AB = – AD + AB$,
$BC = BA + AC = – AB + AC$.
Entonces,
$AB \times CD + AC \times DB + AD \times BC$
$= AB(- AC + AD) + AC(- AD + AB) + AD(- AB + AC)$
$= – (AB \times AC) + (AB \times AD) – (AC \times AD) + (AC \times AB) – (AD \times AB) + (AD \times AC)$
$ = 0$.
$\blacksquare$
División de un segmento en una razón dada
Definición 1. Sean $AB$ un segmento y $P$ un punto en la recta $AB$ definimos la razón en que $P$ divide al segmento $AB$ como $\dfrac{AP}{PB}$.
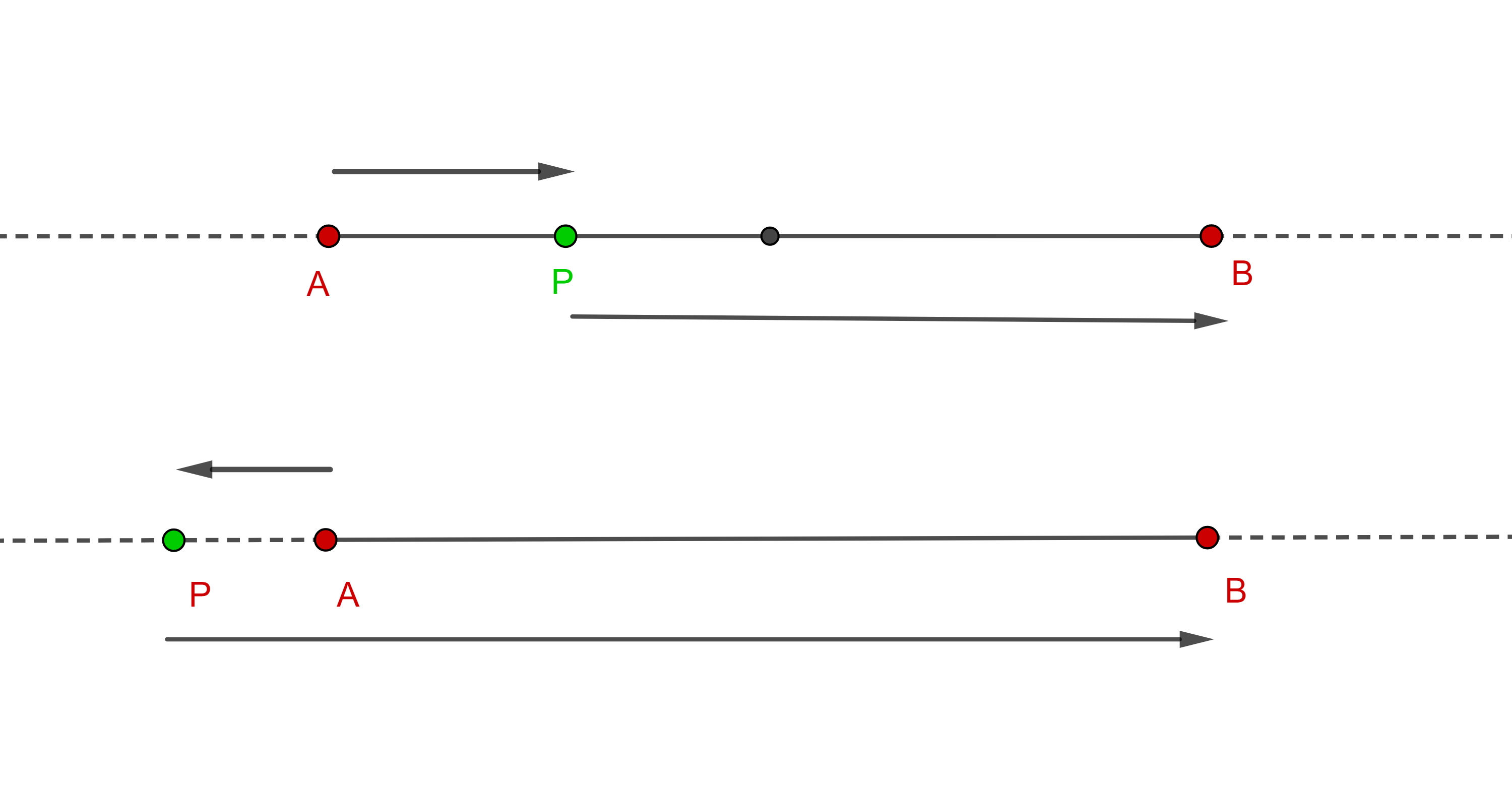
Si $P$ esta entre $A$ y $B$ decimos que la división es interna y entonces $AP$ y $PB$ tienen el mismo sentido, por lo que la razón será positiva, si $P = A$ la razón será $0$ e ira creciendo hasta llegar a $1$ en el punto medio de $AB$ y continuará creciendo positivamente tanto como queramos mientras $P$ se acerque más a $B$ pero sin llegar a ser $B$.
Si $P$ esta fuera del segmento $AB$ la división es externa, en tal caso $AP$ y $PB$ tienen sentidos opuestos, por lo tanto, la razón será negativa, para valores del lado opuesto a $B$ respecto de $A$, $|AP| < |PB|$, por lo tanto, la razón será mayor a $- 1$ y menor que $0$, si $P$ está en el lado opuesto a $A$ respecto de $B$ entonces $|AP| > |PB|$, por lo tanto, la razón será menor que $- 1$.
Teorema 2. Sean $A$ y $B$ dos puntos fijos entonces para todo número real $\lambda$ diferente de $- 1$, existe un único punto $P$ en la recta que pasa por $A$ y $B$ tal que la razón $\dfrac{AP}{PB} = \lambda$.
Demostración. Sean $AB = a$ y $AP = x$, por la ecuación $(2)$,
$PB = PA + AB = – AP + AB = – x + a$.
Por lo tanto, $\dfrac{x}{a – x} = \dfrac{AP}{PB} = \lambda$.
Resolviendo para $x$ obtenemos
$PA = x = \dfrac{a \lambda}{1 + \lambda}$.
Ahora supongamos que $\lambda > 0$ y que existen $P$ y $P’$ tal que $\dfrac{AP}{PB} = \lambda = \dfrac{AP’}{P’B}$.
Por la observación hecha en la definición 1, $P$ y $P’$ están dentro del segmento $AB$, además $AP = \dfrac{a \lambda}{1 + \lambda} = AP’$.
Por lo tanto, $P = P’$.
Similarmente, en caso de que $\lambda < 0$ vemos que $P = P’$, solo hay que considerar dos subcasos, $\lambda > – 1$ y $\lambda < – 1$.
$\blacksquare$
Punto al infinito
Ahora consideremos una recta fija $AB$ y un punto fijo $Q$ fuera de la recta y consideremos el conjunto de todas las rectas que pasan por $Q$ e intersecan a $AB$, a cada recta que pasa por $Q$ le podemos asociar el punto $P$ de intersección con $AB$, notemos que cuanto más se aleja $P$ de $A$ y de $B$, $\dfrac{AP}{PB}$ se aproxima más a $- 1$, esto pasa en ambos sentidos, pero al mismo tiempo la rectas se parecen más a la paralela a $AB$ por $Q$.
Esto motiva la siguiente definición.
Definición 2. Decimos que dos rectas paralelas se intersecan en el punto al infinito, o punto ideal, el cual cumple lo siguiente.
- Para cada recta en el plano, existe solo un punto ideal.
- El conjunto de todos los puntos ideales se encuentran en una recta, llamada recta al infinito o recta ideal.
- Si $P$ es el punto ideal de la recta $AB$ entonces $\dfrac{AP}{PB} = – 1$.
Teorema de Stewart
Teorema 3, de Stewart. Si $A$, $B$, $C$ son tres puntos colineales y $P$ cualquier otro punto en el plano entonces:
$PA^2 \times BC + PB^2 \times CA + PC^2 \times AB + AB \times BC \times CA = 0$.
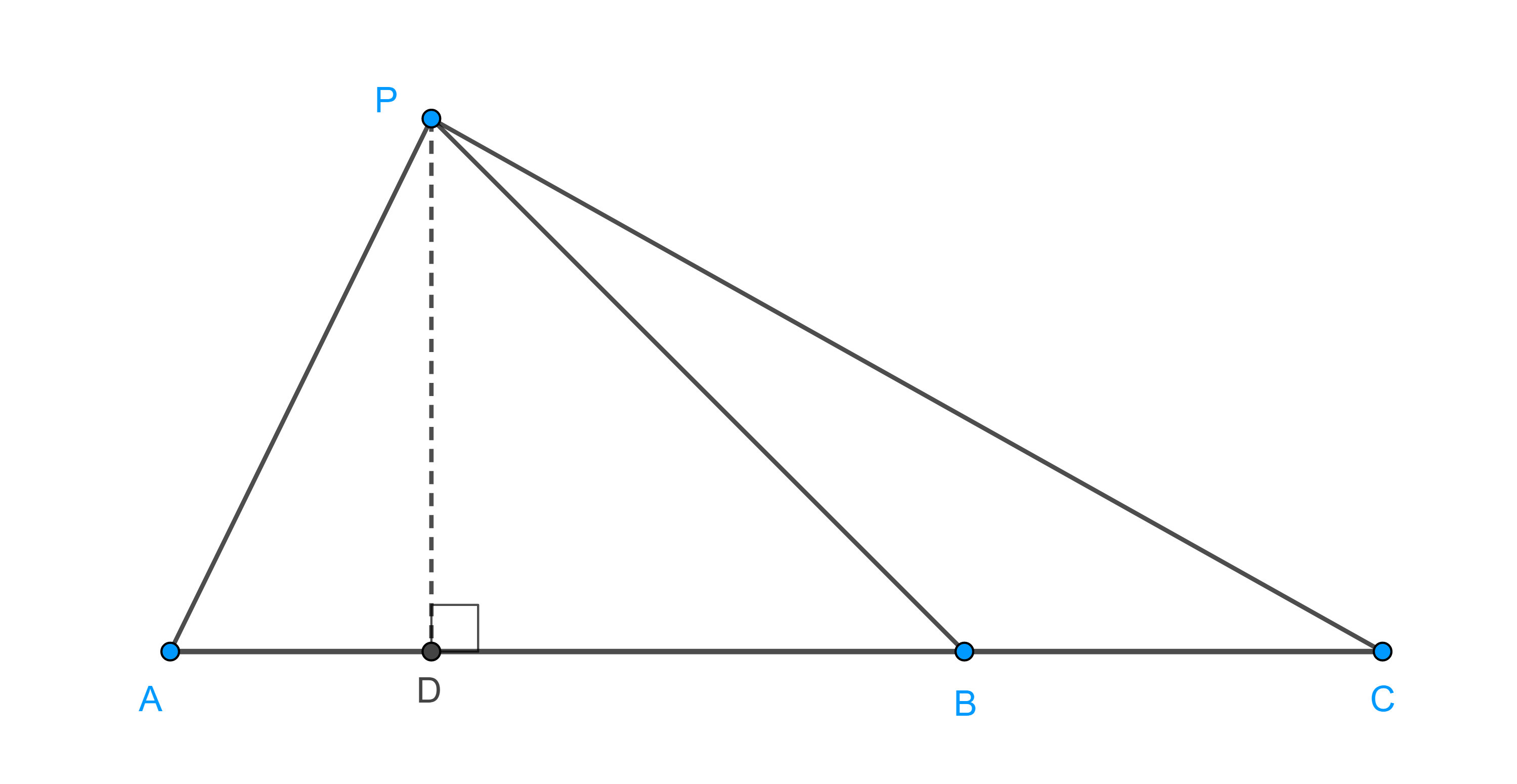
Demostración. Supongamos que $P$ no pertenece a la recta $ABC$, sea $D$ la proyección de $P$ en $ABC$, por el teorema de Pitágoras y las ecuación $(1)$ y $(2)$ tenemos:
$PC^2 = PD^2 + CD^2$,
$PA^2 = PD^2 + AD^2 = PD^2 + (AC + CD)^2 = PD^2 + AC^2 + 2AC \times CD + CD^2$
$= PC^2 + AC^2 – 2CA \times CE$,
$PB^2 = PD^2 + BD^2 = PD^2 + (BC + CD)^2 = PD^2 + BC^2 + 2BC \times CD + CD^2$
$= PC^2 + BC^2 + 2BC \times CE$.
Multiplicamos $PA^2$ por $BC$ y $PA^2$ por $CA$, luego sumamos,
$PA^2 \times BC = PC^2 \times BC + AC^2 \times BC – 2CA \times CE \times BC$,
$PB^2 \times CA = PC^2 \times CA + BC^2 \times CA + 2BC \times CE \times CA$.
$PA^2 \times BC + PB^2 \times CA$
$= PC^2(BC + CA) + AC^2 \times BC – BC^2 \times AC$
$= PC^2 \times BA + AC \times BC(AC – BC)$
$= – PC^2 \times AB – CA \times BC(AC + CB)$.
Como resultado,
$PA^2 \times BC + PB^2 \times CA + PC^2 \times AB + AB \times BC \times CA = 0$.
Ahora supongamos que $P$ pertenece a la recta $ABC$, sea $Q$ un punto en la perpendicular a $ABC$ por $P$, por Pitágoras y el resultado anterior tenemos,
$QA^2 = QP^2 + PA^2, QB^2 = QP^2 + PB^2, QC^2 = QP^2 + PC^2$.
$\Rightarrow$
$0 = QA^2 \times BC + QB^2 \times CA + QC^2 \times AB + AB \times BC \times CA$
$= PA^2\times BC + PB^2\times CA + PC^2 \times AB + AB \times BC \times CA + QP^2(BC + CA + AB)$.
Como, $BC + CA + AB = 0$, por la ecuación $(2)$, se tiene el resultado esperado.
$\blacksquare$
Ejemplo
Problema. Muestra que si $A$, $B$ y $O$ son tres puntos colineales entonces
$OA^2 + OB^2 = AB^2 + 2OA \times OB$.
Solución. Por la ecuacion $(1)$, $AB = AO + OB$.
Entonces,
$AB^2 = AO^2 + 2AO \times OB + OB^2 = OA^2 – 2OA \times OB + OB^2$.
Por lo tanto,
$OA^2 + OB^2 = AB^2 + 2OA \times OB$.
$\blacksquare$
Más adelante…
En la siguiente entrada estudiaremos los puntos notables del triángulo que resultan de la intersección de las mediatrices, las bisectrices, las medianas y las alturas del triángulo.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sean $A$, $B$ y $O$ tres puntos colineales, considera $M$, el punto medio de $AB$, muestra que $PM = \dfrac{PA + PB}{2}$.
- Si $P$, $O$, $A$, $B$ y $C$ son colineales y $OA + OB + OC = 0$, muestra que $PA + PB + PC = 3PO$.
- Muestra que si en la misma recta sucede que $OA + OB + OC = 0$ y $O’A’ + O’B’ + O’C’ = 0,$ entonces $AA’ + BB’ + CC’ = 3OO’$.
- ¿Qué nos dice el teorema de la bisectriz si el triángulo es isósceles o equilátero?
- Usando el teorema de Stewart, demuestra que en cualquier triángulo el cuadrado de la bisectriz interna de uno de los ángulos es igual al producto de los lados que forman dicho ángulo menos el producto de los segmentos en los cuales el lado opuesto es dividido por la bisectriz.
- Prueba que la suma de los cuadrados de las distancias desde el vértice del ángulo recto en un triángulo rectángulo a los puntos de trisección de la hipotenusa es igual a $\dfrac{5}{9}$ por el cuadrado de la hipotenusa.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Semejanza de triángulos.
- Siguiente entrada del curso: Puntos notables del triángulo.
- Otros cursos.
Fuentes
- Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 2-8.
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 151-153.
- Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 45-47.
- Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 13-15, 154.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»