Introducción
En esta entrada mostraremos el teorema de Desargues que nos habla sobre triángulos en perspectiva, también mostraremos los teoremas de Pascal y de Pappus, estos nos dicen cuando los lados opuestos de un hexágono se intersecan en puntos colineales.
Definición. Dos triángulos $\triangle ABC$ y $\triangle A’B’C’$ están en perspectiva desde una recta si los lados correspondientes $AB$, $A’B’$; $BC$, $B’C’$ y $CA$, $C’A’$ se intersecan en puntos colineales, a dicha recta se le conoce como eje de perspectiva.
Dos triángulos $\triangle ABC$ y $\triangle A’B’C’$ están en perspectiva desde un punto si las rectas que unen vértices correspondientes $AA’$, $BB’$ y $CC’$ son concurrentes, a dicho punto se le conoce como centro de perspectiva.
Observación. Notemos que ya hemos trabajado con un tipo especial de perspectiva, la homotecia, donde los vértices correspondientes son concurrentes pero los lados correspondientes son paralelos.
En este caso el centro de perspectiva es el centro de homotecia y como las rectas paralelas se intersecan en el punto al infinito entonces la recta al infinito es el eje de perspectiva.
El siguiente teorema generaliza esta dualidad eje-centro de perspectiva.
Teorema de Desargues
Teorema 1, de Desargues. Dos triángulos tienen un centro de perspectiva si y solo si tienen un eje de perspectiva.
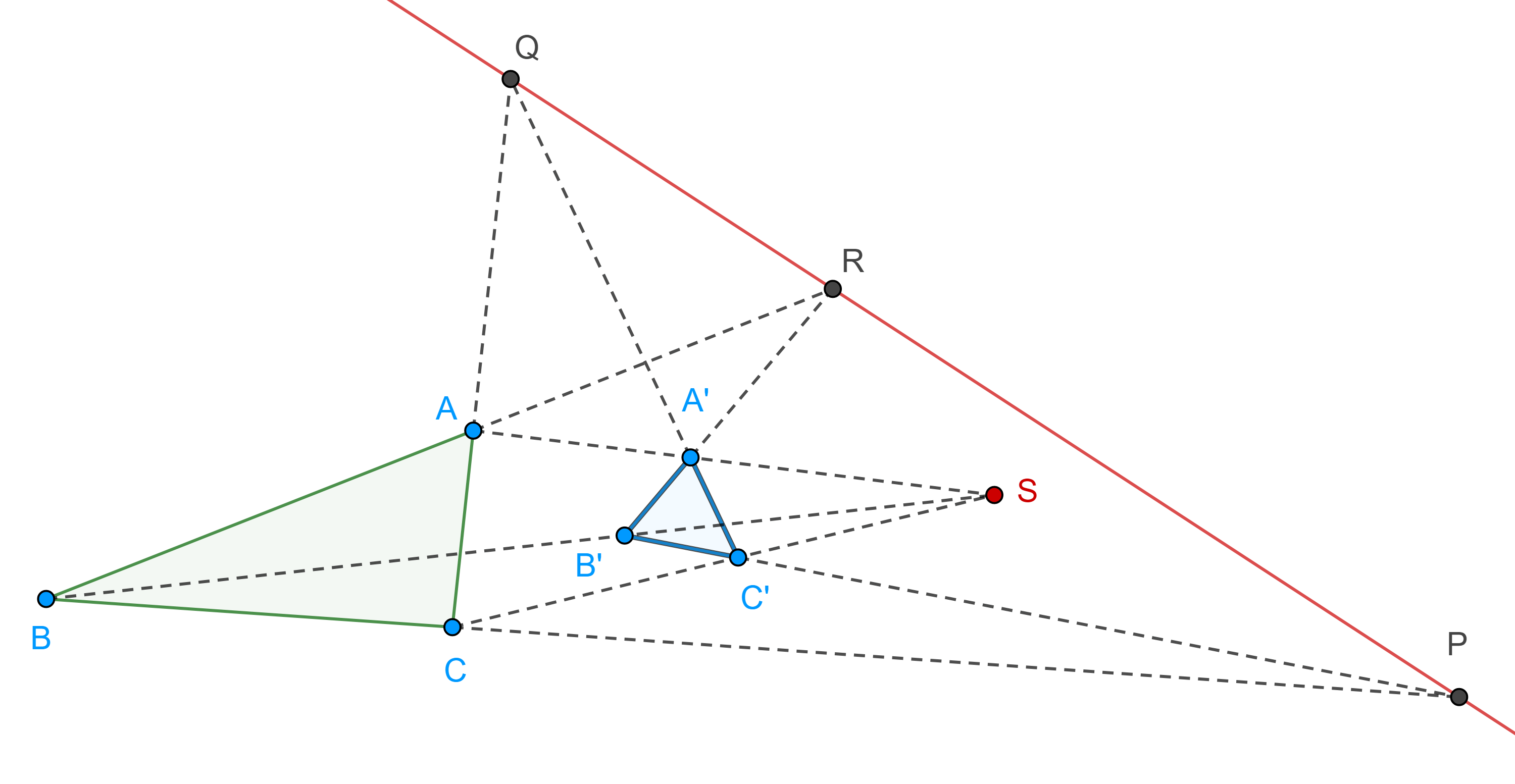
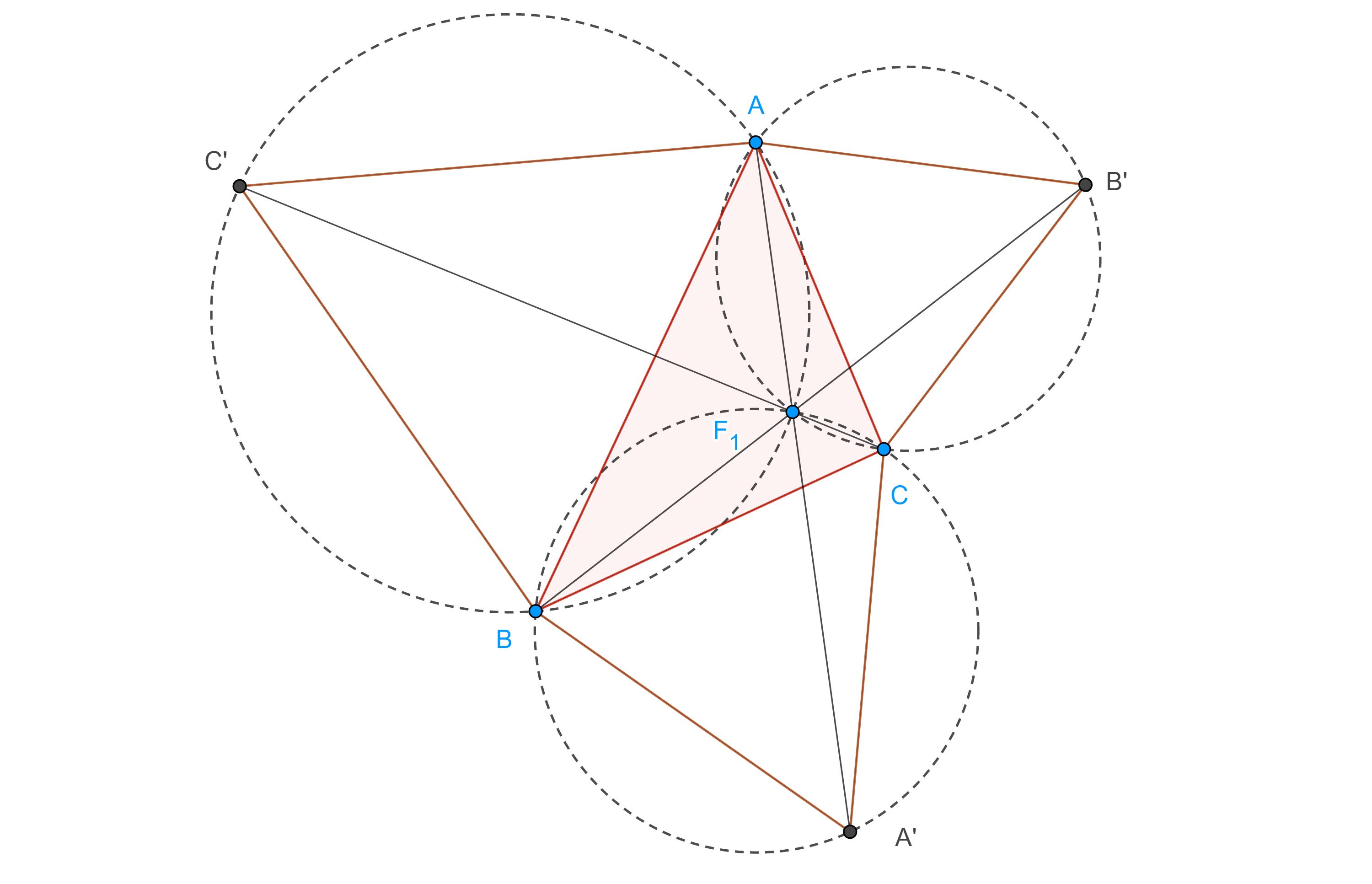
Demostración. Consideremos dos triángulos, $\triangle ABC$ y $\triangle A’B’C’$,
sean $R = AB \cap A’B’$, $P = BC \cap B’C’$ y $Q = CA \cap C’A’$.
Supongamos que $AA’$, $BB’$ y $CC’$ concurren en $S$, aplicamos el teorema de Menelao a $\triangle SAB$, $\triangle SAC$ y $\triangle SBC$ con sus respectivas transversales $B’A’R$, $C’A’Q$ y $B’C’P$.
$\begin{equation} \dfrac{SA’}{A’A} \dfrac{AR}{RB} \dfrac{BB’}{B’S} = -1, \end{equation}$
$\begin{equation} \dfrac{SA’}{A’A} \dfrac{AQ}{QC} \dfrac{CC’}{C’S} = -1, \end{equation}$
$ \begin{equation} \dfrac{SB’}{B’B} \dfrac{BP}{PC} \dfrac{CC’}{C’S} = -1. \end{equation}$
Hacemos el cociente de $(1)$ entre $(2)$ y obtenemos
$\begin{equation} \dfrac{AR}{RB} \dfrac{BB’}{B’S} \dfrac{QC}{AQ} \dfrac{C’S}{CC’} = 1. \end{equation}$
Multiplicamos $(3)$ por $(4)$ y obtenemos
$\dfrac{AR}{RB} \dfrac{BP}{PC} \dfrac{QC}{AQ} = – 1$.
Por lo tanto, por el teorema de Menelao, $P$, $Q$ y $R$ son colineales.
$\blacksquare$
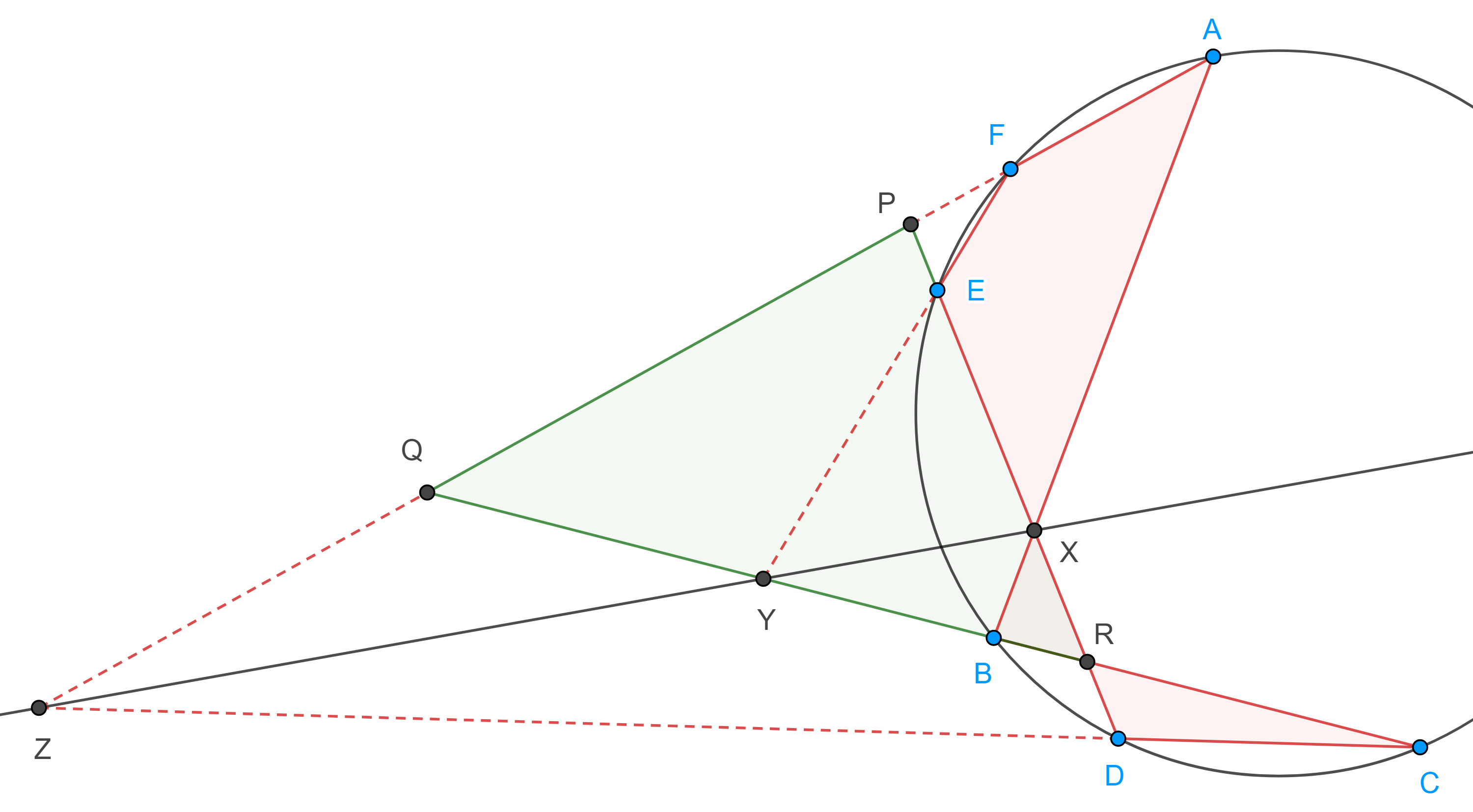
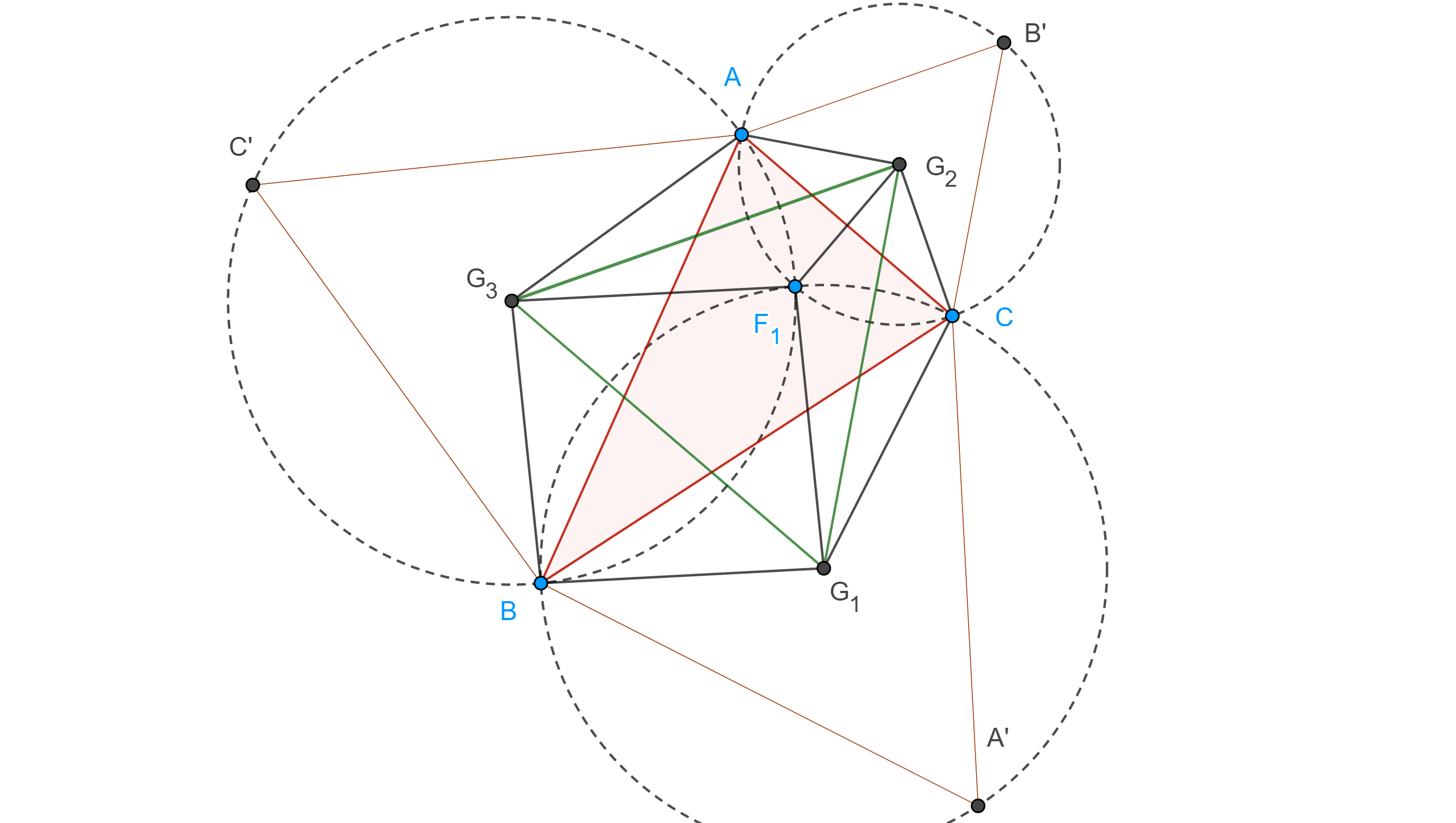
Conversamente, supongamos que $RPQ$ es una recta y sea $S = BB’ \cap CC’$.
Notemos que $QR$, $CB$ y $C’B$ concurren en $P$ (figura 1), por lo tanto, $\triangle QCC’$ y $\triangle RBB’$ están en perspectiva desde $P$, por la implicación que ya probamos los puntos $A = QC \cap RB$, $A’ = QC’ \cap RB’$ y $S = BB’ \cap CC’$, son colineales.
Por lo tanto, $AA’$, $BB’$ y $CC’$ concurren en $S$.
$\blacksquare$
Punto de Gergonne
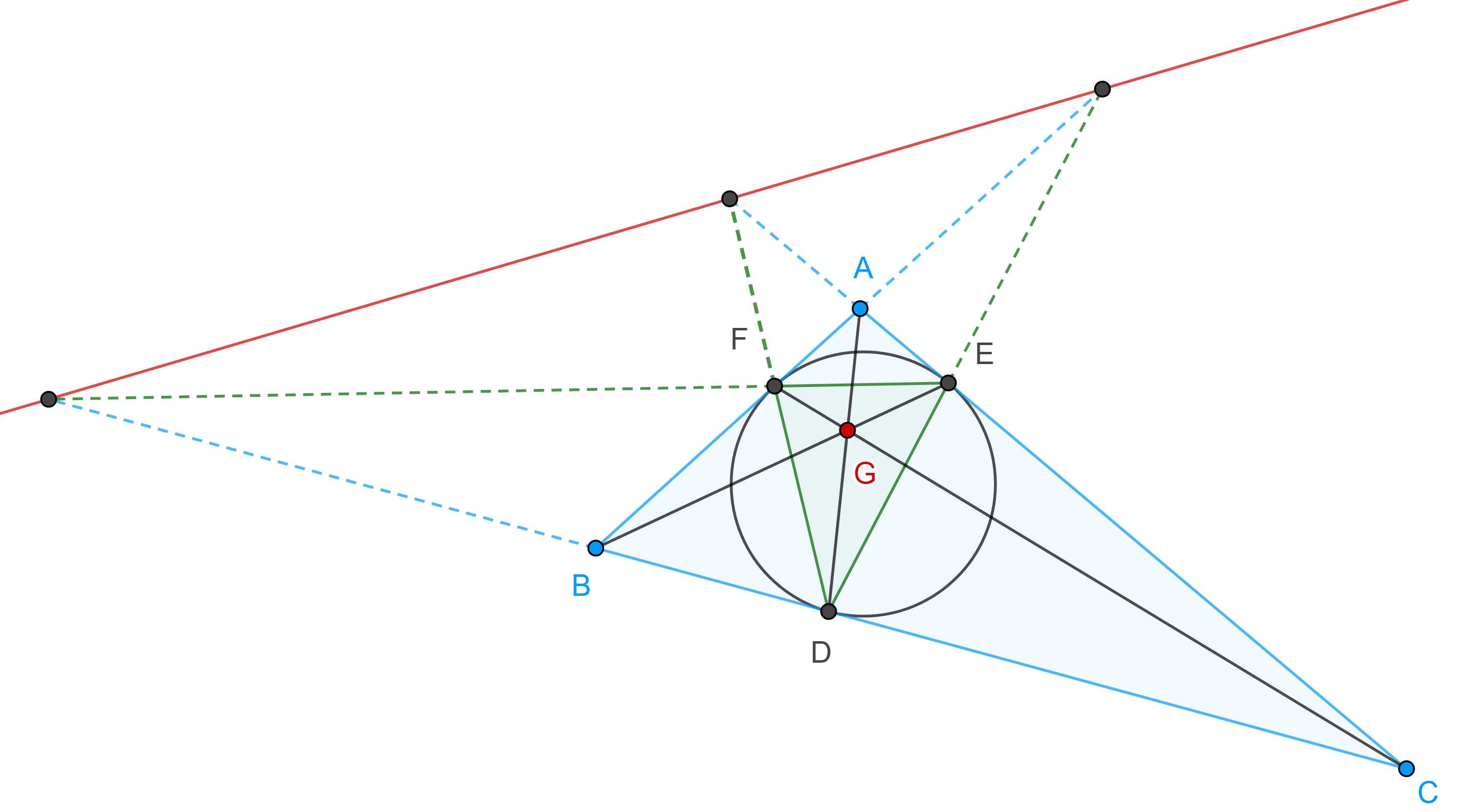
Proposición. Considera un triángulo $\triangle ABC$ y su incírculo $\Gamma$, sean $D$, $E$ y $F$ los puntos de tangencia de $\Gamma$ con los lados $BC$, $CA$ y $AB$ respectivamente, entonces $AD$, $BE$ y $CF$ son concurrentes, en un punto conocido como punto de Gergonne.
Demostración. En la entrada anterior demostramos que los triángulos $\triangle ABC$ y $\triangle DEF$ están en perspectiva desde la recta de Gergonne de $\triangle ABC$, es decir, $AB$, $DE$; $BC$, $EF$ y $CA$, $FD$ se intersecan en tres puntos colineales.
Por lo tanto, por el teorema de Desargues $AD$, $BE$ y $CF$ son concurrentes
$\blacksquare$
Triángulos con dos ejes de perspectiva
Teorema 2. Si dos triángulos tienen dos ejes de perspectiva entonces tienen tres ejes de perspectiva.
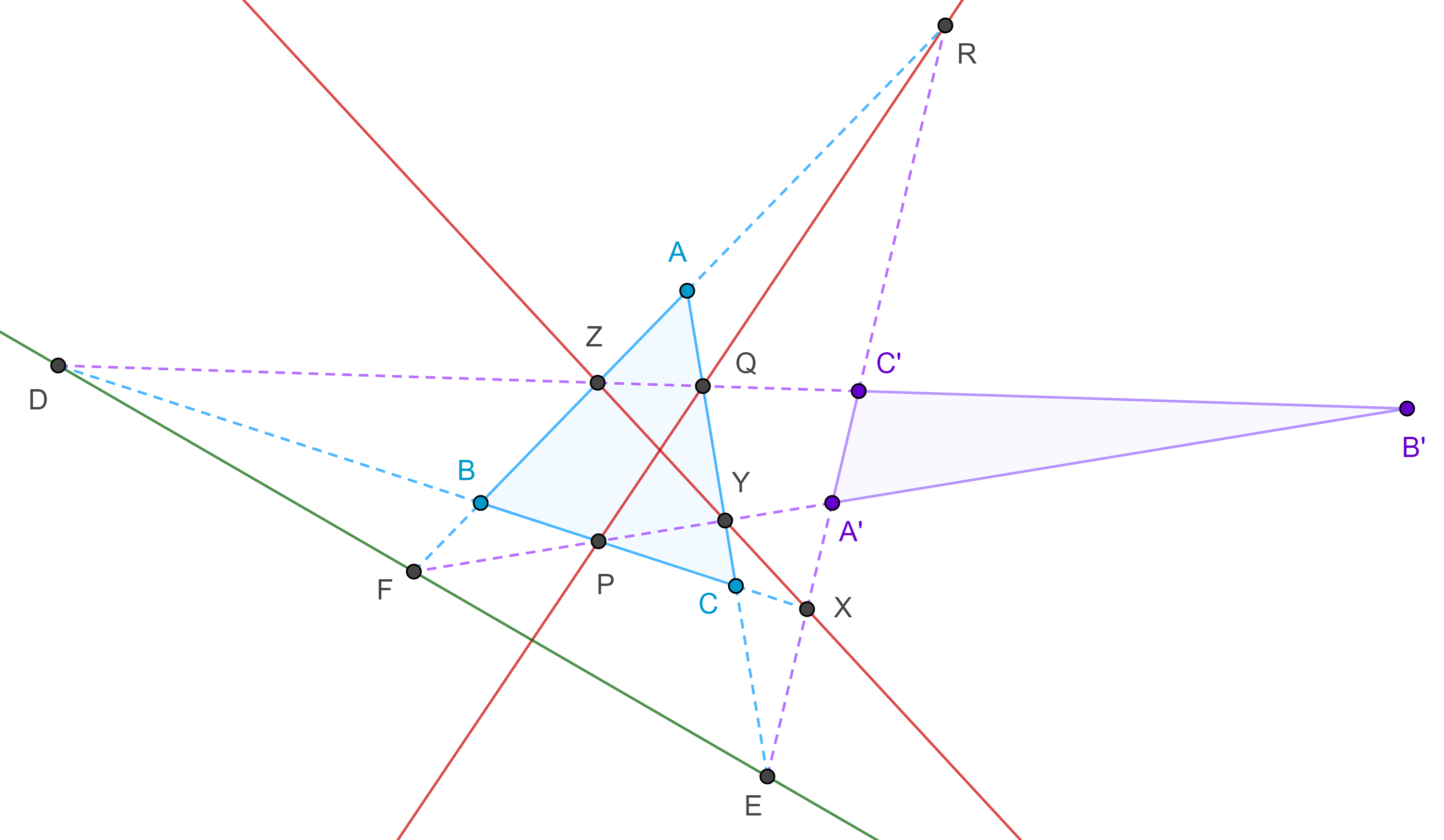
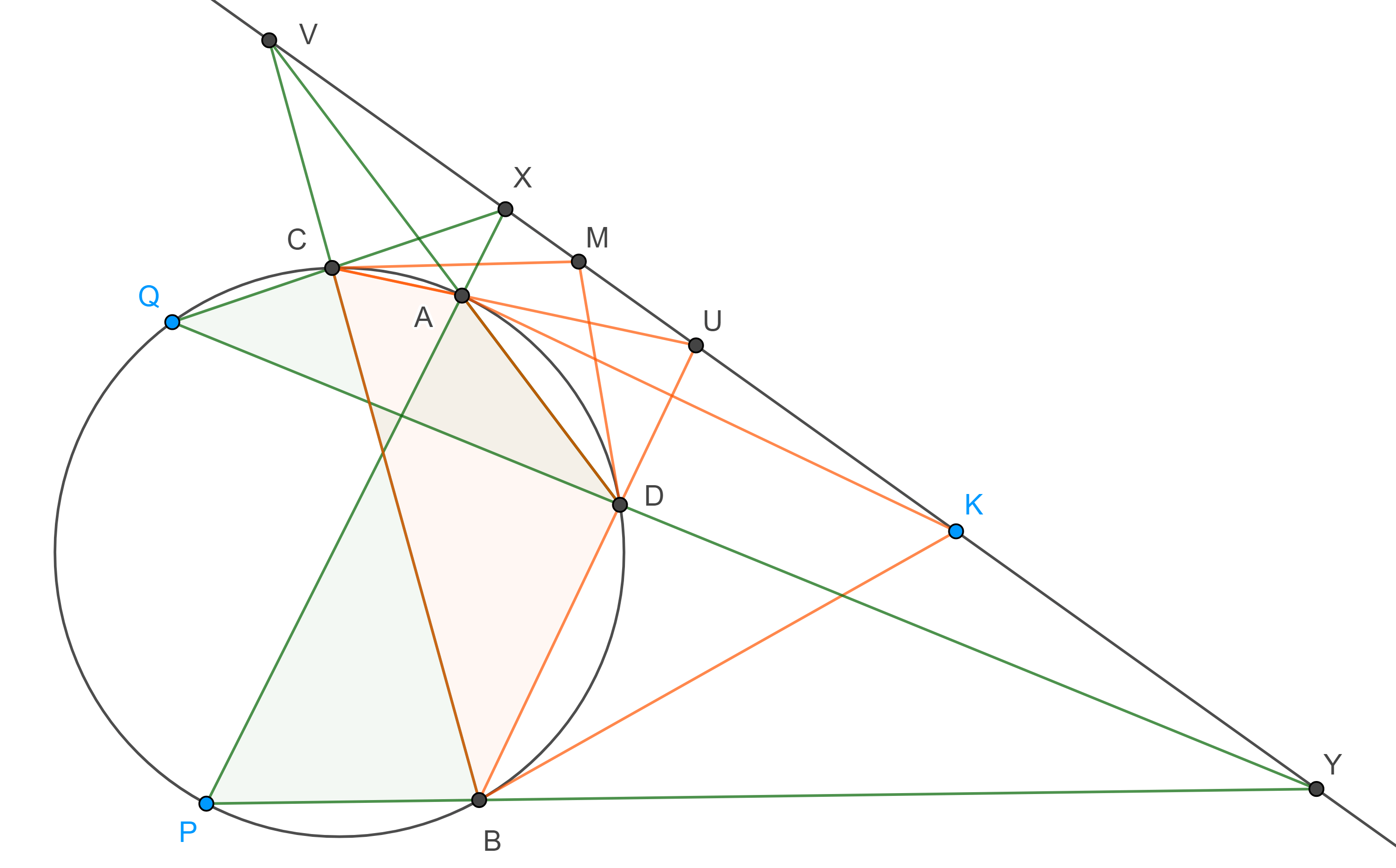
Demostración. Supongamos que los triángulos $\triangle ABC$ y $\triangle A’B’C’$ están en perspectiva desde dos rectas, es decir, los puntos, $Z = AB \cap B’C’$, $X = BC \cap C’A’$ y $Y = CA \cap A’B’$ son colineales y los puntos $R = AB \cap C’A’$, $P = BC \cap A’B’$ y $Q = CA \cap B’C’$ son colineales.
Sean $F = AB \cap A’B’$, $D = BC \cap B’C’$ y $E = CA \cap C’A’$, aplicamos el teorema Menelao a $\triangle ABC$ y las transversales $DZQ$, $FPY$ y $EXR$.
$\dfrac{AZ}{ZB} \dfrac{BD}{DC} \dfrac{CQ}{QA} = -1$,
$\dfrac{AF}{FB} \dfrac{BP}{PC} \dfrac{CY}{YA} = -1$,
$\dfrac{AR}{RB} \dfrac{BX}{XC} \dfrac{CE}{EA} = -1$.
Multiplicamos estas tres igualdades y reordenamos
$\dfrac{AF}{FB} \dfrac{BD}{DC} \dfrac{CE}{EA} (\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA}) (\dfrac{AR}{RB} \dfrac{BP}{PC} \dfrac{CQ}{QA}) = – 1$.
Recordemos que como $X$, $Y$, $Z$ y $P$, $Q$, $R$ son colineales entonces
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = – 1$,
$\dfrac{AR}{RB} \dfrac{BP}{PC} \dfrac{CQ}{QA} = – 1$.
Por lo tanto
$\dfrac{AF}{FB} \dfrac{BD}{DC} \dfrac{CE}{EA} = -1$.
Y por el teorema de Menelao $D$, $E$ y $F$ son colineales.
$\blacksquare$
Corolario. Si dos triángulos tienen dos centros de perspectiva entonces tienen tres centros de perspectiva.
Demostración. Por el teorema de Desargues, si dos triángulos tienen dos centros de perspectiva entonces tienen dos ejes de perspectiva.
Por el teorema anterior, existe un tercer eje de perspectiva.
Nuevamente por el teorema de Desargues, existe un tercer centro de perspectiva.
$\blacksquare$
Teorema de Pappus
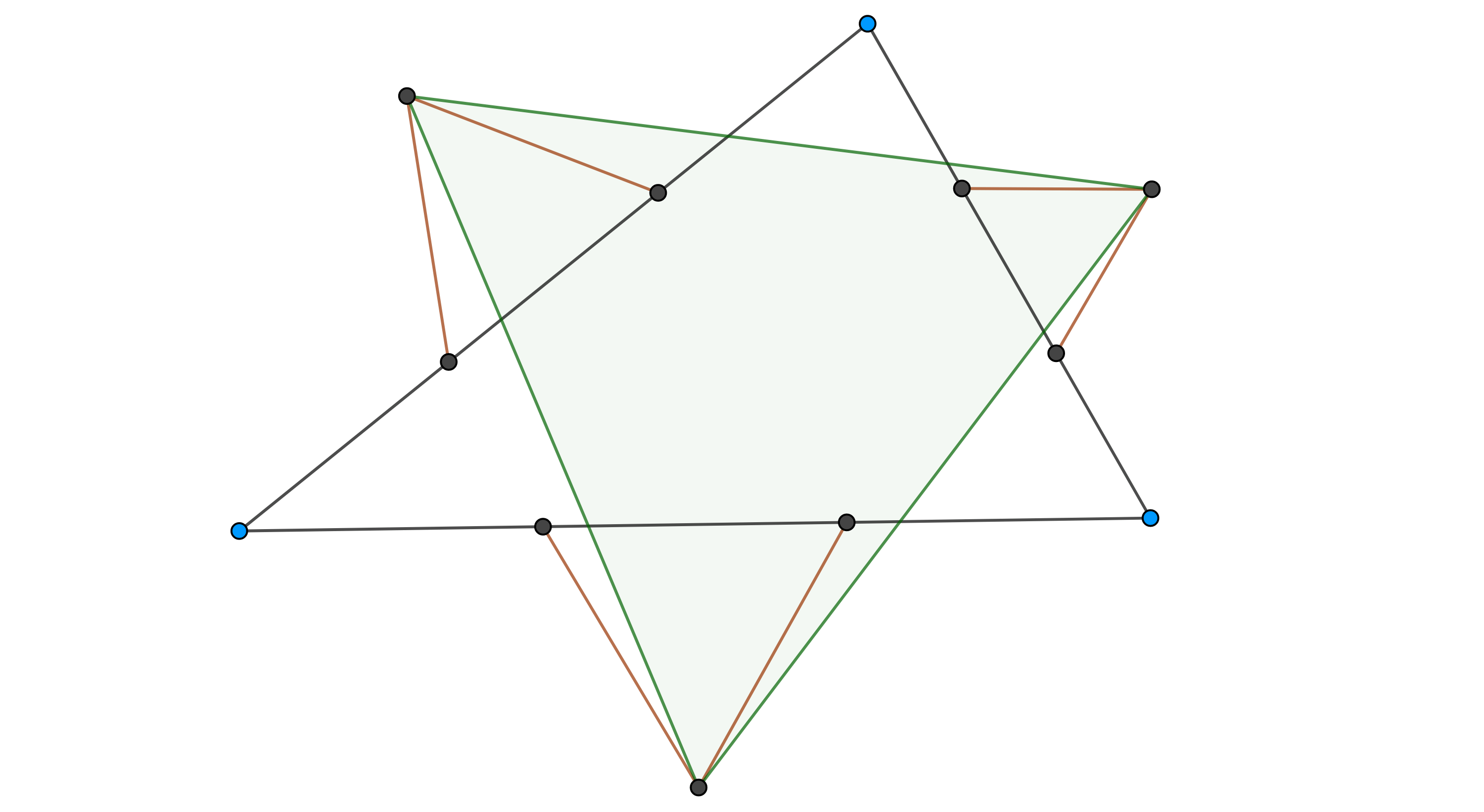
Teorema 3, de Pappus. Si los vértices de un hexágono se encuentran alternadamente sobre dos rectas entonces los lados opuestos se intersecan en tres puntos colineales.
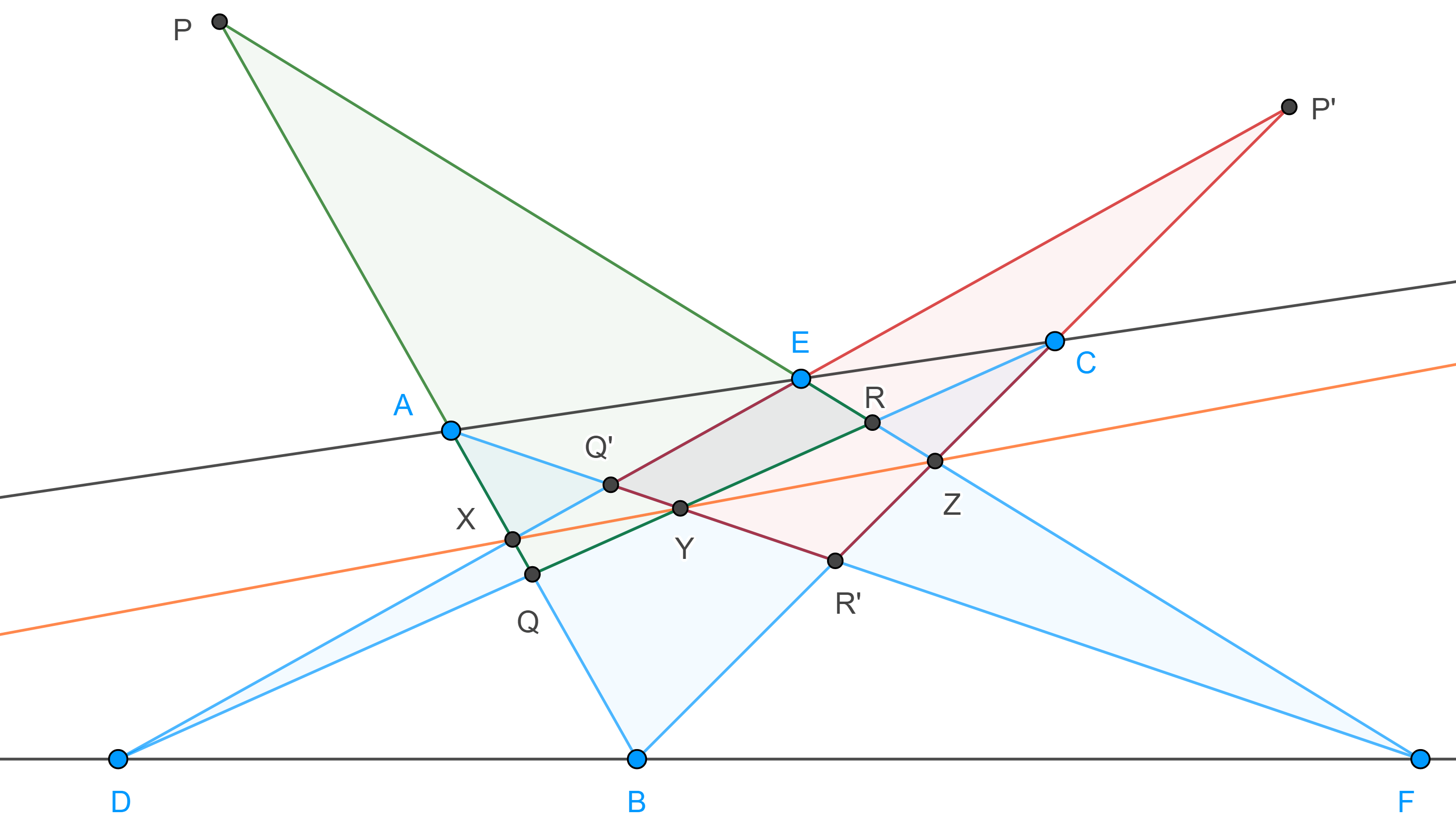
Demostración. Sean $ABCDEF$ un hexágono tal que $AEC$ y $DBF$ son dos rectas distintas,
$P = EF \cap AB$, $Q = AB \cap CD$, $R = CD \cap EF$,
$P’ = BC \cap ED$, $Q’ = DE \cap FA$ y $R’ = FA \cap BC$.
Notemos que las rectas $AEC$ y $DBF$ son dos ejes de perspectiva de $\triangle PQR$ y $\triangle P’Q’R’$, pues
$A = PQ \cap Q’R’$, $C = QR \cap R’P’$, $E = RP \cap P’Q’$,
$B = PQ \cap R’P’$, $D = QR \cap P’Q’$ y $F = RP \cap Q’R’$.
Por el teorema anterior $X = PQ \cap P’Q’$, $Y = QR \cap Q’R’$ y $Z = RP \cap R’P’$, son colineales.
$\blacksquare$
Teorema de Pascal
Teorema 4, de Pascal. En todo hexágono cíclico los pares de lados opuestos se intersecan en tres puntos colineales.
Demostración. Sean $ABCDEF$ un hexágono cíclico,
$X = AB \cap DE$, $Y = BC \cap EF$, $Z = CD \cap FA$ las intersecciones de los lados opuestos,
consideremos $P = DE \cap FA$, $Q = FA \cap BC$ y $R = BC \cap DE$.
Aplicaremos el teorema de Menelao a $\triangle PQR$ y las transversales $AXB$, $CDZ$ y $FEY$.
$\dfrac{PA}{AQ} \dfrac{QB}{BR} \dfrac{RX}{XP} = – 1$,
$\dfrac{PZ}{ZQ} \dfrac{QC}{CR} \dfrac{RD}{DP} = – 1$,
$\dfrac{PF}{FQ} \dfrac{QY}{YR} \dfrac{RE}{EP} = – 1$.
Si multiplicamos las tres ecuaciones y reacomodamos obtenemos
$\dfrac{PZ}{ZQ} \dfrac{QY}{YR} \dfrac{RX}{XP} (\dfrac{PF \times PA}{PE \times PD}) (\dfrac{QB \times QC}{QF \times QA}) (\dfrac{RD \times RE}{RC \times RB}) = -1$.
Por otro lado, las potencias de $P$, $Q$ y $R$ respeto al circuncírculo de $ABCDEF$ son la siguientes
$PF \times PA = PE \times PD$,
$QF \times QA = QB \times QC$,
$RD \times RE = RC \times RB$.
Por lo tanto $\dfrac{PZ}{ZQ} \dfrac{QY}{YR} \dfrac{RX}{XP} = -1$.
Por el teorema de Menelao $X$, $Y$ y $Z$ son colineales.
$\blacksquare$
Casos limite en el teorema de Pascal
Existen casos limite donde podemos hacer uso del teorema de Pascal, es decir, podemos considerar un triángulo, un cuadrilátero o un pentágono como un hexágono donde dos vértices se aproximaron hasta volverse uno solo y como consecuencia el lado comprendido entre ellos se vuelve una tangente al circuncírculo en dicho punto.
A continuación, ilustramos esto con un ejemplo.
Problema 1. Considera $\Gamma$ una circunferencia y $l$ una recta, $K \in l$ fuera de $\Gamma$, $P$, $Q \in \Gamma$, sean $KA$ y $KB$ las tangentes desde $K$ a $\Gamma$, $X = PA \cap l$, $Y = PB \cap l$, $C = QX \cap \Gamma$ y $D = QY \cap \Gamma$. Muestra que las tangentes a $\Gamma$ en $C$ y $D$ se intersecan en $l$.
Demostración. Sea $M$ la intersección de las tangentes a $\Gamma$ en $C$ y $D$, $U = AC \cap BD$ y $V = AD \cap BC$.
Por el teorema de Pascal en el hexágono $APBCQD$, $V$ es colineal con $X$ e $Y$, es decir $V \in l$.
Ahora aplicamos el teorema de Pascal al hexágono $AACBBD$, $U$ es colineal con $V$ y $K$, es decir $U \in l$.
Aplicando nuevamente Pascal a $ACCBDD$ tenemos que $M$ es colineal con $U$ y con $V$.
Por lo tanto, $M \in l$.
$\blacksquare$
Pascal, Desargues y un punto al infinito
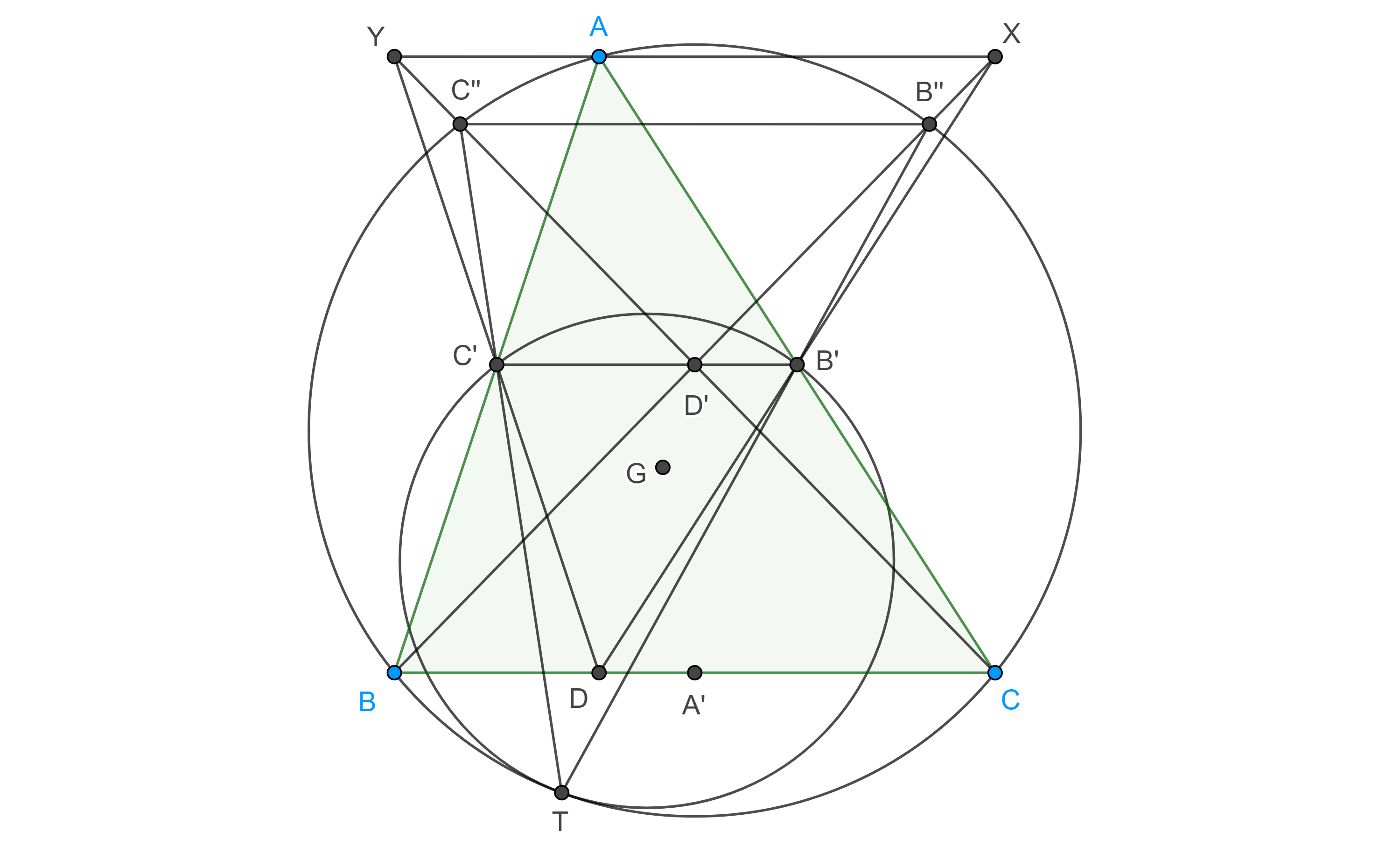
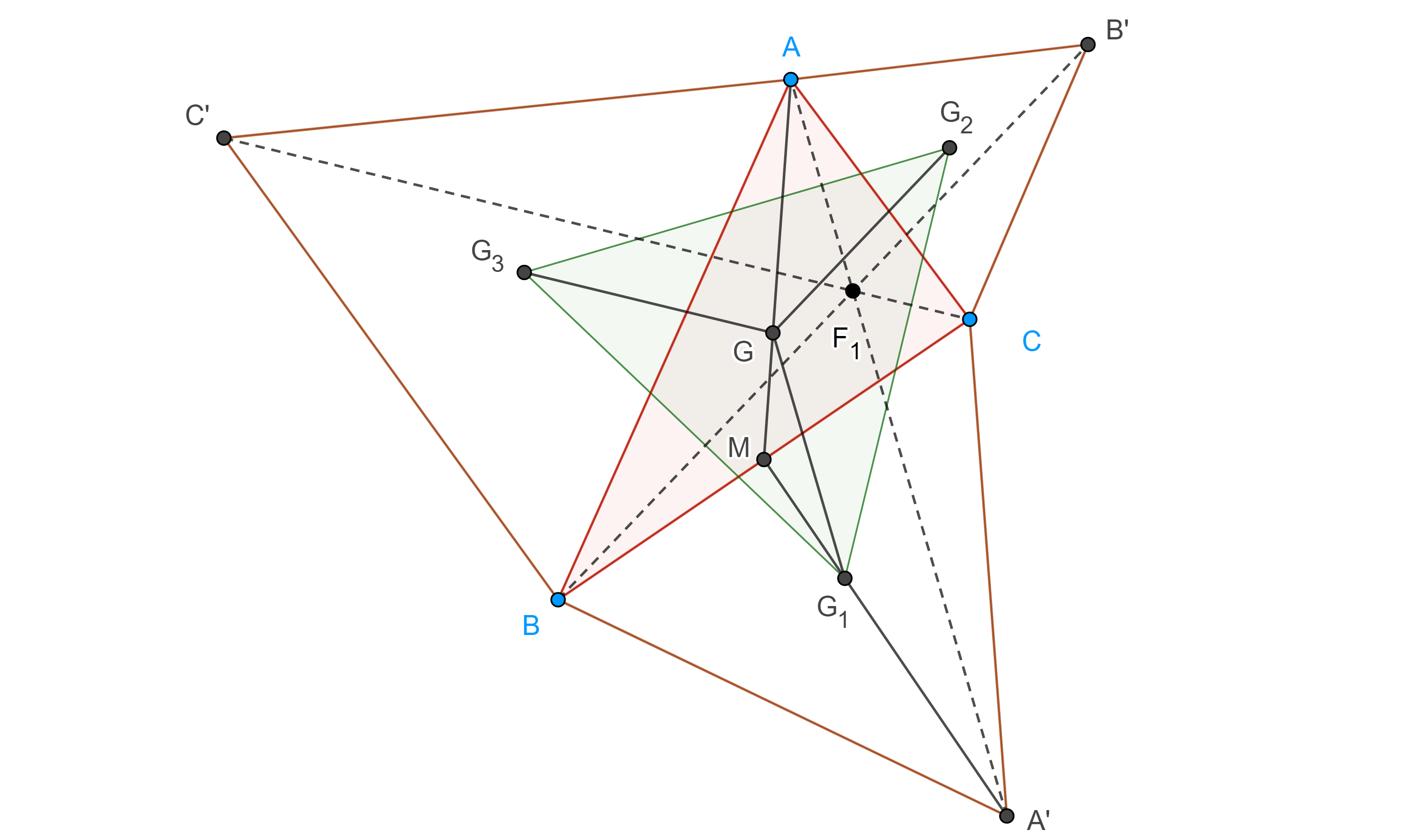
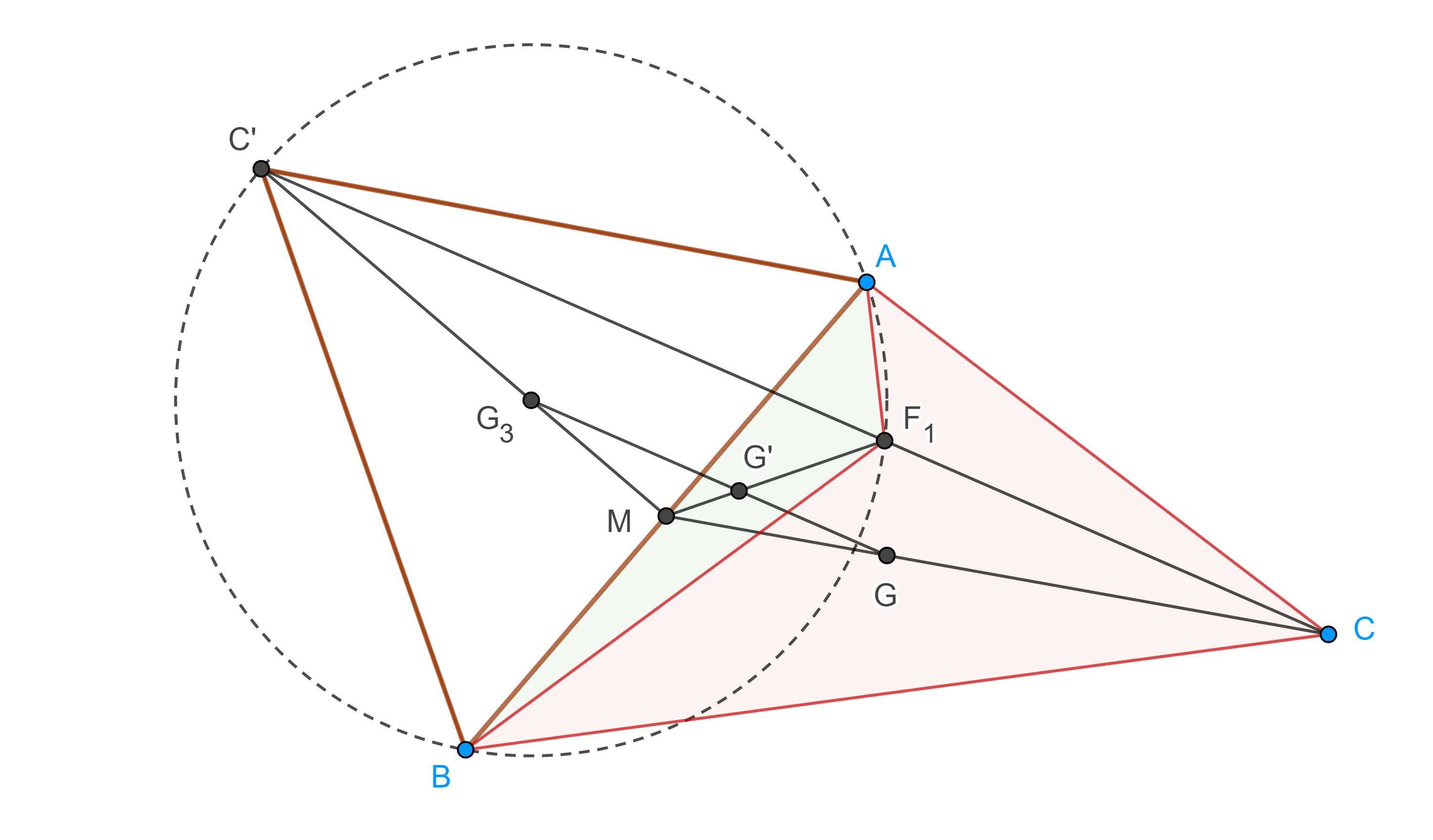
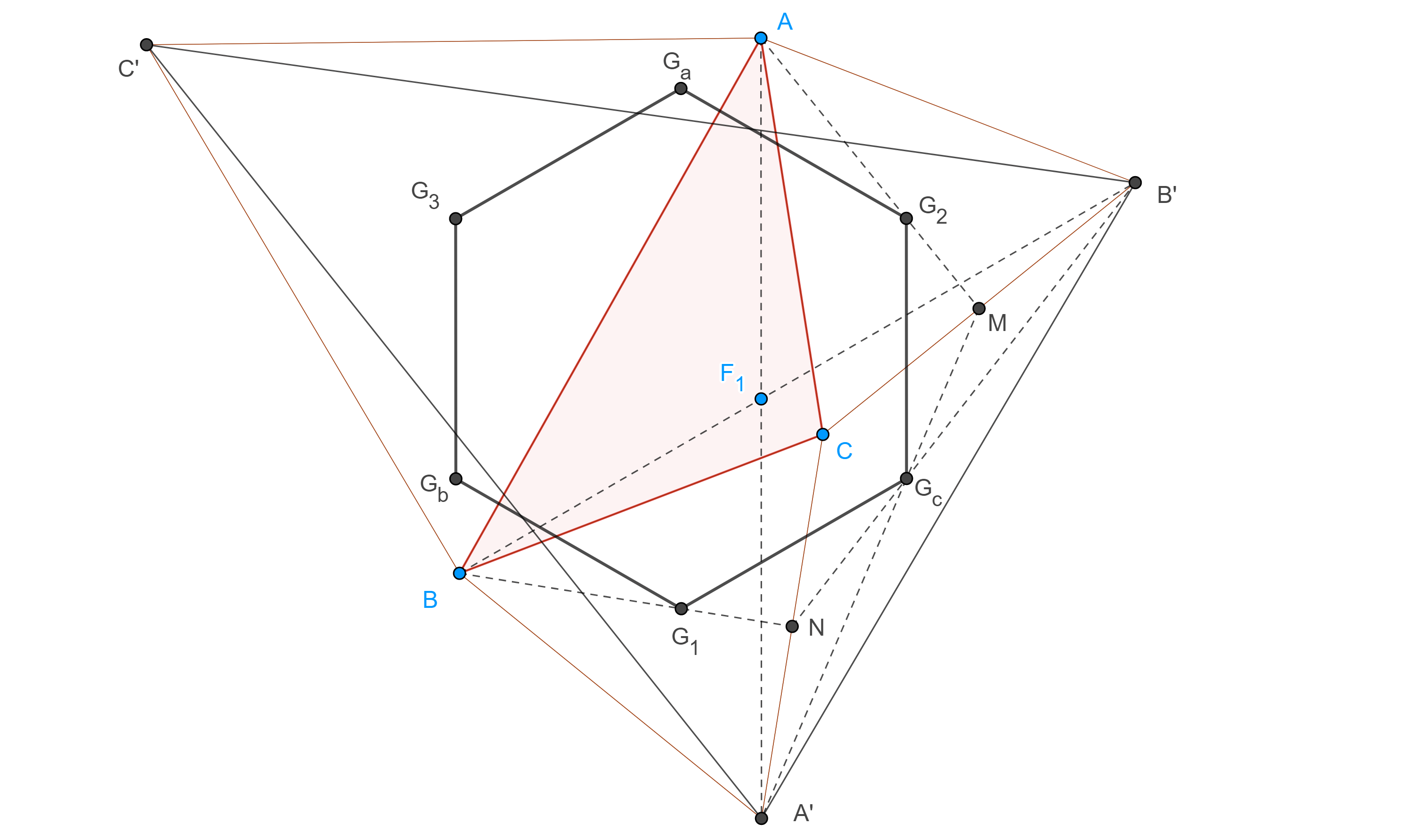
Problema 2. Sean $\triangle ABC$ un triángulo acutángulo, $B’$ y $C’$ los puntos medios de $CA$ y $AB$ respectivamente, sea $\Gamma_1$ una circunferencia que pasa por $B’$ y $C’$ y que es tangente al circuncírculo de $\triangle ABC$, $\Gamma(ABC)$ en $T$. Muestra que $T$, el pie de la altura por $A$, y el centroide de $\triangle ABC$, son colineales.
Demostración. Sean $B’’ = TB’ \cap \Gamma(ABC)$, $C’’ = TC’ \cap \Gamma(ABC)$ y $D’ = BB’’ \cap CC’’$
Por el teorema de Pascal en el hexágono $ABB’’TC’’C$, $B’$, $D’$ y $C’$ son colineales.
Notemos que existe una homotecia con centro en $T$ que lleva a $\Gamma_1$ en $\Gamma(ABC)$, así que, $C’B’ \parallel C’’B’’$.
Como resultado, $\angle C’’CB = \angle CC’’B’’ = \angle CBB’’$, pues $\angle CC’’B’’$ y $\angle CBB’’$ abarcan el mismo arco.
En consecuencia, $\triangle D’BC$ es isósceles, por lo tanto, el pie de la altura por $D’$ en $\triangle D’BC$ es $A’$, el punto medio de $BC$, o conversamente, la proyección de $A’$ el punto medio de $BC$, en $B’C’$ es $D’$.
Recordemos que existe una homotecia con centro en $G$, el centroide de $\triangle ABC$, que lleva a $\triangle A’B’C’$ en $\triangle ABC$, como $D$ es el pie de altura por $A$ en $\triangle ABC$ y $D’$ el pie de la altura por $A’$ en $\triangle A’B’C’$, entonces $D$ y $D’$ son puntos homólogos en esta homotecia, por lo tanto, $D$, $G$ y $D’$ son colineales.
Por otro lado, como $BB’$, $CC’$ y $DD’$ concurren en $G$, $\triangle D’BC$ y $\triangle DB’C’$ están en perspectiva desde $G$.
Por el teorema de Desargues, los puntos $X = D’B \cap DB’$, $Y = D’C \cap DC’$, $P = BC \cap B’C’$, son colineales, pero $P$ es un punto ideal, pues por la homotecia entre $\triangle A’B’C’$ y $\triangle ABC$, $B’C’ \parallel BC$.
En consecuencia, $XY \parallel B’C’$.
Como $DB’ \cap D’B’’ = X$, $DC’ \cap D’C’’ = Y$ y $B’C’ \cap B’’C’’ = P$, entonces $\triangle DB’C’$ y $\triangle D’B’’C’’$ están en perspectiva desde $XY$, por el teorema de Desargues, $DD’$, $B’B’’$ y $C’C’’$ son concurrentes.
Por lo tanto, $T$, $D$ y $G$ son colineales.
$\blacksquare$
Más adelante…
En la siguiente entrada mostraremos el teorema de Ceva, que nos da condiciones necesarias y suficientes para que tres rectas, cada una por un vértice distinto de un triángulo dado, sean concurrentes.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Muestra que si tres triángulos:
$i)$ tienen un eje común de perspectiva, entonces los tres centros de perspectiva son colineales,
$ii)$ tienen un centro común de perspectiva, entonces los tres ejes de perspectiva son concurrentes. - Muestra que todo triángulo esta en perspectiva desde una recta con:
$i)$ su triángulo medial,
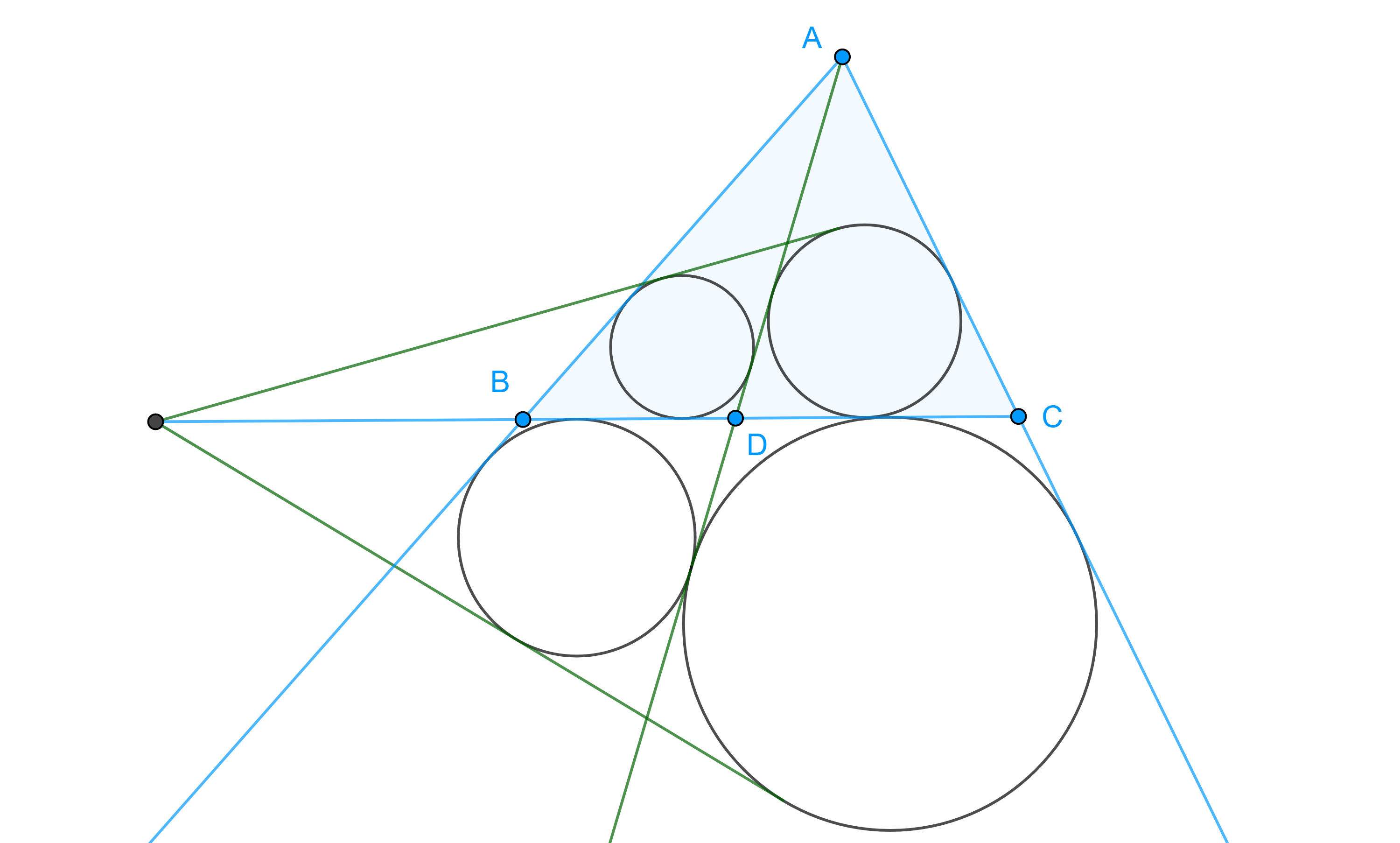
$ii)$ su triángulo órtico. - Sean $\triangle ABC$ y $D \in BC$, $\Gamma_1$, $\Gamma_2$, considera los incírculos de $\triangle ABD$ y $\triangle ADC$ respectivamente, $\Gamma_3,$ $\Gamma_4$ los excírculos tangentes a $BC$ de $\triangle ABD$ y $\triangle ADC$ respectivamente (figura 8). Prueba que las tangentes comunes externas a $\Gamma_1$, $\Gamma_2$ y $\Gamma_3$, $\Gamma_4$, concurren en $BC$.
- Sea $\square BB’C’C$ un rectángulo construido externamente sobre el lado $BC$ de un triángulo $\triangle ABC$, sean sea $A’ \in BC$, el pie de la altura por $A$, $X = AB \cap A’B’$, $Y = CA \cap C’A’$, muestra que $XY \parallel BC$.
- Considera $\Gamma$ el circuncírculo de un triangulo $\triangle ABC$, sean $Q$ el punto medio del arco $\overset{\LARGE{\frown}}{AB}$ que no contiene a $C$, $R$ el punto medio del arco $\overset{\LARGE{\frown}}{CA}$ que no contiene a $B$, $P$ un punto en el arco $\overset{\LARGE{\frown}}{BC}$ que no contiene a $A$, $H = AB \cap PQ$, $J = CA \cap PR$, prueba que $HJ$ pasa por el incentro de $\triangle ABC$.
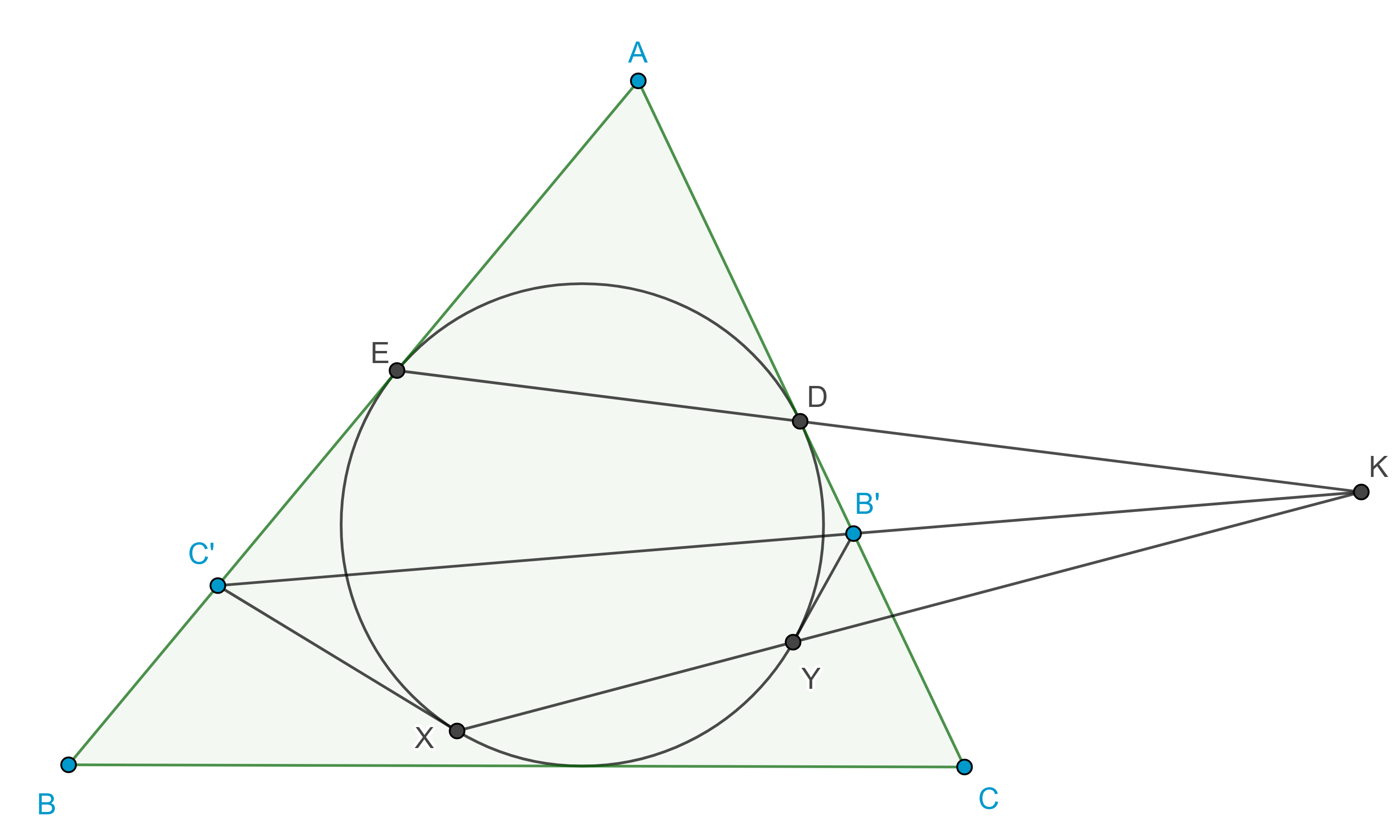
- Sea $\triangle ABC$ y $B’ \in CA$, $C’ \in AB$, sean $D$, $E$ los puntos de tangencia de $\Gamma$ el incírculo de $\triangle ABC$, con $CA$ y $AB$ respectivamente, sean $C’X$ y $B’Y$ segmentos tangentes a $\Gamma$ tal que $X$, $Y \in \Gamma$ (figura 9), demuestra que $B’C’$, $DE$ y $XY$ son concurrentes.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Teorema de Menelao.
- Siguiente entrada del curso: Teorema de Ceva.
- Otros cursos.
Fuentes
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 71-82.
- Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 103-109.
- Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 230-239.
- Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 67-76.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»