Introducción

En esta entrada estudiamos otro tipo de relación, la de semejanza de triángulos, la cual es una de las herramientas más útiles en geometría euclidiana.

Definición. Decimos que dos triángulos $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ son semejantes si sus ángulos respectivos son iguales y sus lados respectivos son proporcionales, es decir,

• $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$, $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$ y
• ${\displaystyle \frac{AB}{A^{\prime }{B}^{\prime }}}={\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}={\displaystyle \frac{AC}{A^{\prime }{C}^{\prime }}}$.

Si dos triángulos son semejantes lo denotamos así $\mathrm{△}ABC\sim \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

Criterio de semejanza ángulo, ángulo, ángulo (AAA o AA)

Teorema 1, criterio de semejanza ángulo, ángulo, ángulo. Si los ángulos correspondientes de dos triángulos son iguales entonces los triángulos son semejantes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ dos triángulos tales que $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$, $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$. Por demostrar que los lados correspondientes son proporcionales.

Sean $D\in AB$ y $E\in AC$ tales que $AD=A^{\prime }{B}^{\prime }$ y $AE=A^{\prime }{C}^{\prime }$, como $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, por el criterio de congruencia LAL, tenemos que los triángulos $\mathrm{△}ADE\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

Por lo tanto, $\mathrm{\angle }EDA=\mathrm{\angle }{C}^{\prime }{B}^{\prime }{A}^{\prime }$, $\mathrm{\angle }AED=\mathrm{\angle }{A}^{\prime }{C}^{\prime }{B}^{\prime }$ y $DE=B^{\prime }{C}^{\prime }$.

Dado que $AB$ es transversal a $DE$ y $BC$ y los ángulos correspondientes son iguales, entonces $DE\parallel BC$.

Por el teorema de Tales, ${\displaystyle \frac{AB}{AD}}={\displaystyle \frac{AC}{AE}}={\displaystyle \frac{BC}{DE}}$,
$\Rightarrow {\displaystyle \frac{AB}{A^{\prime }{B}^{\prime }}}={\displaystyle \frac{AC}{A^{\prime }{C}^{\prime }}}={\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}$.

Así, $\mathrm{△}ABC\sim \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación. Como la suma de los ángulos internos de todo triangulo es igual a $\pi$, entonces si conocemos la magnitud de dos ángulos internos conocemos los tres y por lo tanto podemos referirnos a este criterio como AA.

Criterio de semejanza lado, ángulo, lado (LAL)

Teorema 2, criterio de semejanza lado, ángulo, lado. Si dos triángulos tienen dos lados correspondientes proporcionales y el ángulo entre ellos es igual, entonces los triángulos son semejantes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ dos triángulos tales que ${\displaystyle \frac{AB}{A^{\prime }{B}^{\prime }}}={\displaystyle \frac{AC}{A^{\prime }{C}^{\prime }}}$ y $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$.

Sean $D\in AB$ y $E\in AC$ tales que $AD=A^{\prime }{B}^{\prime }$ y $AE=A^{\prime }{C}^{\prime }$.

Como $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$ por el criterio de congruencia LAL, $\mathrm{△}ADE\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$, así $\mathrm{\angle }EDA=\mathrm{\angle }{C}^{\prime }{B}^{\prime }{A}^{\prime }$ y $\mathrm{\angle }AED=\mathrm{\angle }{A}^{\prime }{C}^{\prime }{B}^{\prime }$.

Por hipótesis sabemos que ${\displaystyle \frac{AB}{A^{\prime }{B}^{\prime }}}={\displaystyle \frac{AC}{A^{\prime }{C}^{\prime }}}$
$\Rightarrow {\displaystyle \frac{AB}{AD}}={\displaystyle \frac{AC}{AE}}$.

Esto implica, por el reciproco del teorema de Tales, que $DE\parallel BC$, se sigue que $\mathrm{\angle }CBA=\mathrm{\angle }EDA$ y $\mathrm{\angle }ACB=\mathrm{\angle }AED$ por ser ángulos correspondientes.

Por transitividad, $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$ y $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$

Por criterio de semejanza AAA, $\mathrm{△}ABC\sim \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Criterio de semejanza lado, lado, lado (LLL)

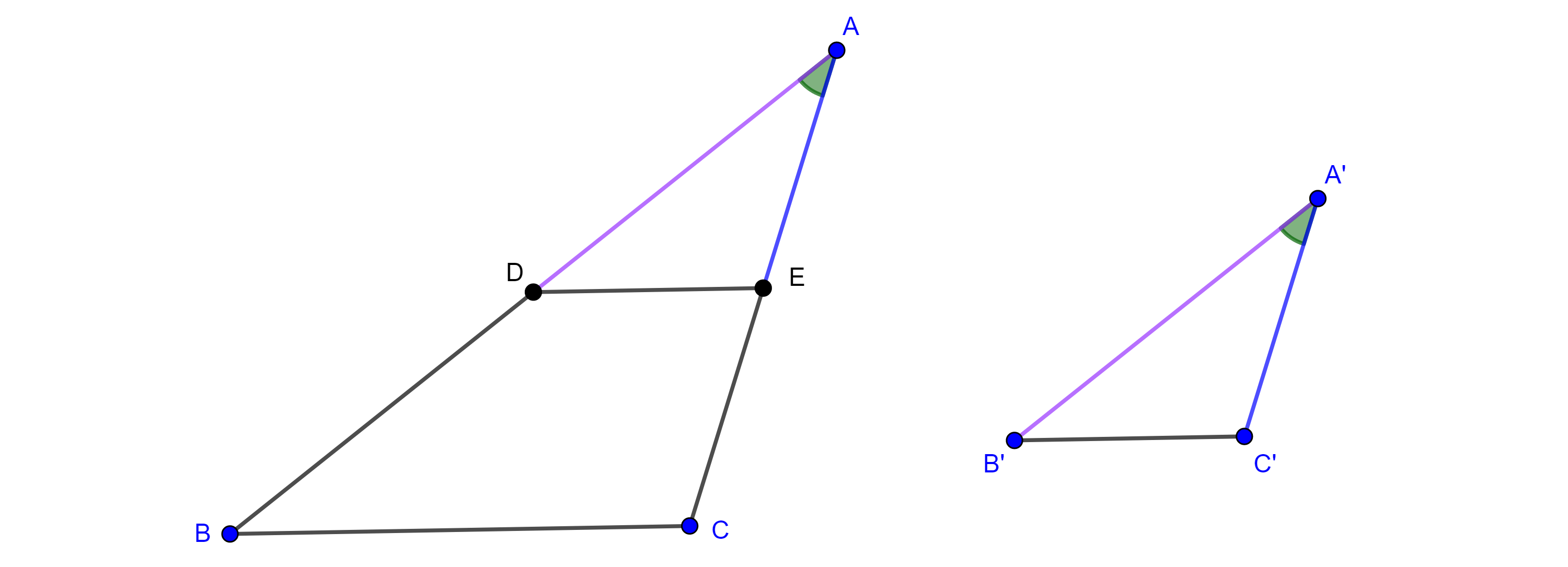
Teorema 3, criterio de semejanza lado, lado, lado. Si los lados correspondientes de dos triángulos son proporcionales entonces los triángulos son semejantes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ dos triángulos tales que ${\displaystyle \frac{AB}{A^{\prime }{B}^{\prime }}}={\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}={\displaystyle \frac{AC}{A^{\prime }{C}^{\prime }}}$, por demostrar que $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime }$, $\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$ y $\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$.

Sean $D\in AB$ y $E\in AC$ tales que $AD=A^{\prime }{B}^{\prime }$ y $AE=A^{\prime }{C}^{\prime }$ (figura 2).

Como $\mathrm{\angle }BAC=\mathrm{\angle }DAE$ y ${\displaystyle \frac{AB}{AD}}={\displaystyle \frac{AC}{AE}}$, por criterio de semejanza LAL, $\mathrm{△}ABC\sim \mathrm{△}ADE$, y en consecuencia ${\displaystyle \frac{AB}{AD}}={\displaystyle \frac{BC}{DE}}$.

$AD=A^{\prime }{B}^{\prime }$, por construcción, y ${\displaystyle \frac{AB}{A^{\prime }{B}^{\prime }}}={\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}$ por hipótesis,
$\Rightarrow {\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}={\displaystyle \frac{AB}{A^{\prime }{B}^{\prime }}}={\displaystyle \frac{AB}{AD}}={\displaystyle \frac{BC}{DE}}$
$\Rightarrow B^{\prime }{C}^{\prime }=DE$.

Por criterio de congruencia LLL, $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }\cong \mathrm{△}ADE$.

Por transitividad, $\mathrm{△}ABC\sim \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Triángulos con lados perpendiculares

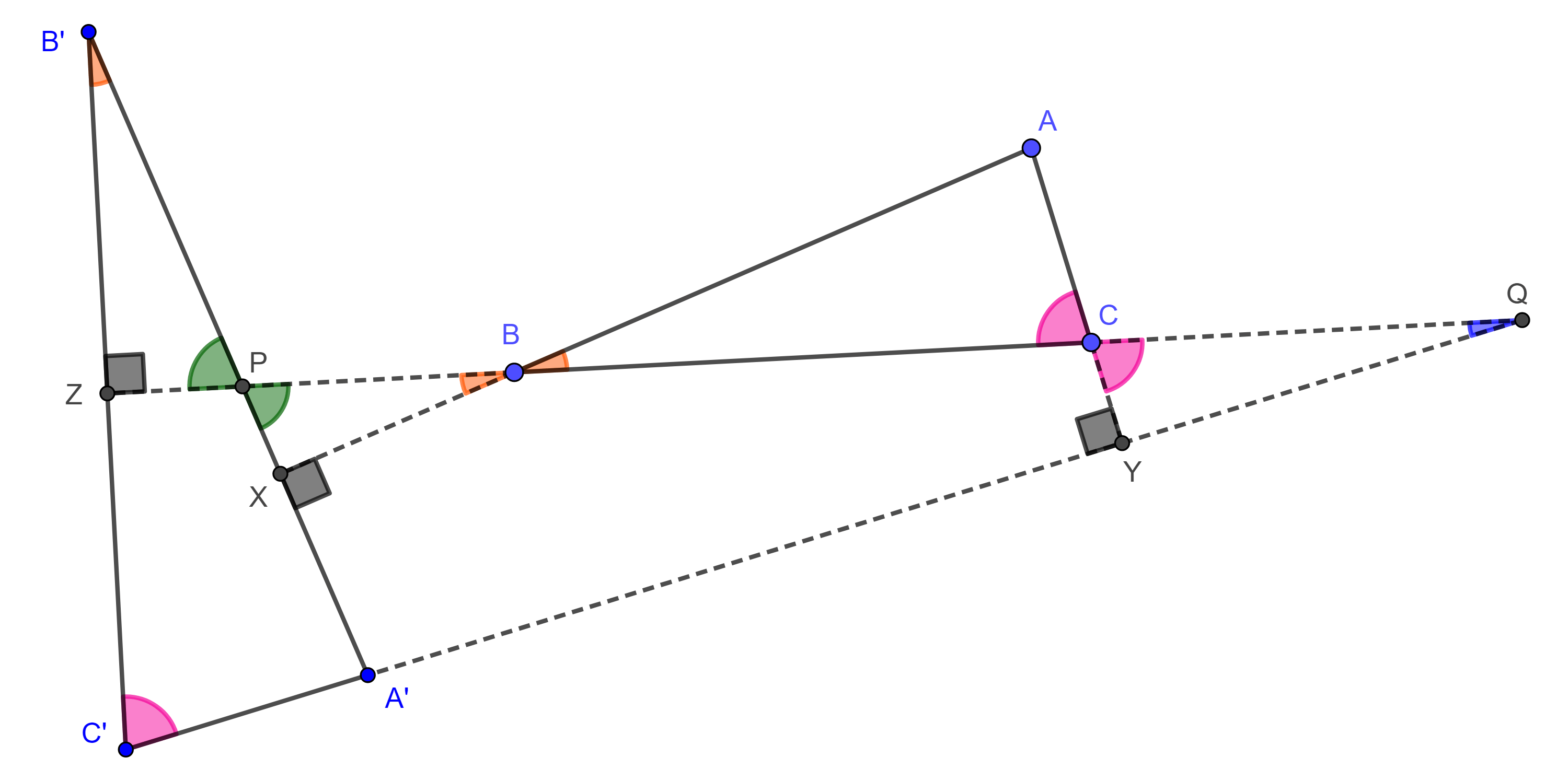
Proposición 1. Dos triángulos cuyos lados correspondientes son perpendiculares son semejantes.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ tales que $AB\perp A^{\prime }{B}^{\prime }$, $BC\perp B^{\prime }{C}^{\prime }$ y $AC\perp A^{\prime }{C}^{\prime }$.

Consideremos $Z$, $P$ y $Q$ las intersecciones de $BC$ con $B^{\prime }{C}^{\prime }$, $A^{\prime }{B}^{\prime }$ y $A^{\prime }{C}^{\prime }$ respectivamente, $X=AB\cap A^{\prime }{B}^{\prime }$ e $Y=AC\cap A^{\prime }{C}^{\prime }$ (figura 3).

$\mathrm{\angle }CBA=\mathrm{\angle }PBX$, por ser opuestos por el vértice,
como $\mathrm{△}BXP$ es rectángulo entonces $\mathrm{\angle }PBX$ y $\mathrm{\angle }XPB$ son complementarios,
$\Rightarrow \mathrm{\angle }CBA$ y $\mathrm{\angle }XPB$ son complementarios,
$\mathrm{\angle }XPB=\mathrm{\angle }{B}^{\prime }PZ$, por ser opuestos por el vértice,
$\Rightarrow \mathrm{\angle }CBA$ y $\mathrm{\angle }{B}^{\prime }PZ$ son complementarios.

Como $\mathrm{△}{B}^{\prime }ZP$ es rectángulo entonces $\mathrm{\angle }{B}^{\prime }PZ$ y $\mathrm{\angle }Z{B}^{\prime }P$ son complementarios,
$\Rightarrow \mathrm{\angle }CBA=\mathrm{\angle }Z{B}^{\prime }P$,
$\Rightarrow \mathrm{\angle }{B}^{\prime }=\mathrm{\angle }B$.

Por otro lado, $\mathrm{\angle }ACB=\mathrm{\angle }YCQ$, por ser opuestos por el vértice,
como $\mathrm{△}CYQ$ es rectángulo entonces $\mathrm{\angle }YCQ$ y $\mathrm{\angle }CQY$ son complementarios,
$\Rightarrow \mathrm{\angle }ACB$ y $\mathrm{\angle }CQY$ son complementarios.

Como $\mathrm{△}{C}^{\prime }ZQ$ es rectángulo entonces $\mathrm{\angle }Q{C}^{\prime }Z$ y $\mathrm{\angle }CQY$ son complementarios,
$\Rightarrow \mathrm{\angle }ACB=\mathrm{\angle }Q{C}^{\prime }Z$,
$\Rightarrow \mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$.

Por criterio de semejanza AA, $\mathrm{△}ABC\sim \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 2. Dos triángulos cuyos lados correspondientes son paralelos son semejantes.

Demostración. Podemos construir un triángulo cuyos lados correspondientes sean perpendiculares a los lados de uno de los triángulos, por transitividad sus lados también serán perpendiculares a los lados del segundo triangulo.

Por la proposición anterior los triángulos originales serán semejantes al triangulo construido y por lo tanto serán semejantes entre sí.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Desigualdad entre bisectrices

Proposición 3. En un triángulo entre cualesquiera dos ángulos internos la bisectriz del mayor es menor a la bisectriz del menor de los ángulos.

Demostración. Sea $\mathrm{△}ABC$ y supongamos que $\mathrm{\angle }B>\mathrm{\angle }C$ y sean $D$ y $E$ las intersecciones de las bisectrices de los ángulos $\mathrm{\angle }B$ y $\mathrm{\angle }C$ respectivamente con los lados opuestos. Debemos mostrar que $BD<CE$.

Sean $F\in AD$ tal que $\mathrm{\angle }DBF=\mathrm{\angle }ACE=\mathrm{\angle }ECB$ y $G$ la intersección de $CE$ con $BF$, por criterio de semejanza AA, $\mathrm{△}FBD\sim \mathrm{△}FCG$, por lo tanto,

$\begin{array}{}\text{(1)}& {\displaystyle \frac{BF}{CF}}={\displaystyle \frac{BD}{CG}}.\end{array}$

Por otro lado, en el triángulo $\mathrm{△}BFC$ tenemos que
$\mathrm{\angle }CBF=\mathrm{\angle }CBD+\mathrm{\angle }DBF$
$={\displaystyle \frac{\mathrm{\angle }B}{2}}+{\displaystyle \frac{\mathrm{\angle }C}{2}}>{\displaystyle \frac{\mathrm{\angle }C}{2}}+{\displaystyle \frac{\mathrm{\angle }C}{2}}=\mathrm{\angle }C$.

Como al ángulo mayor siempre se opone a el lado mayor, tenemos que $FC>BF$ $\iff$ $1>{\displaystyle \frac{BF}{CF}}={\displaystyle \frac{BD}{CG}}$.

Donde la última igualdad se da por la ecuación $(1)$

Por lo tanto, $CE>CG>BD$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Semejanza en el triángulo rectángulo

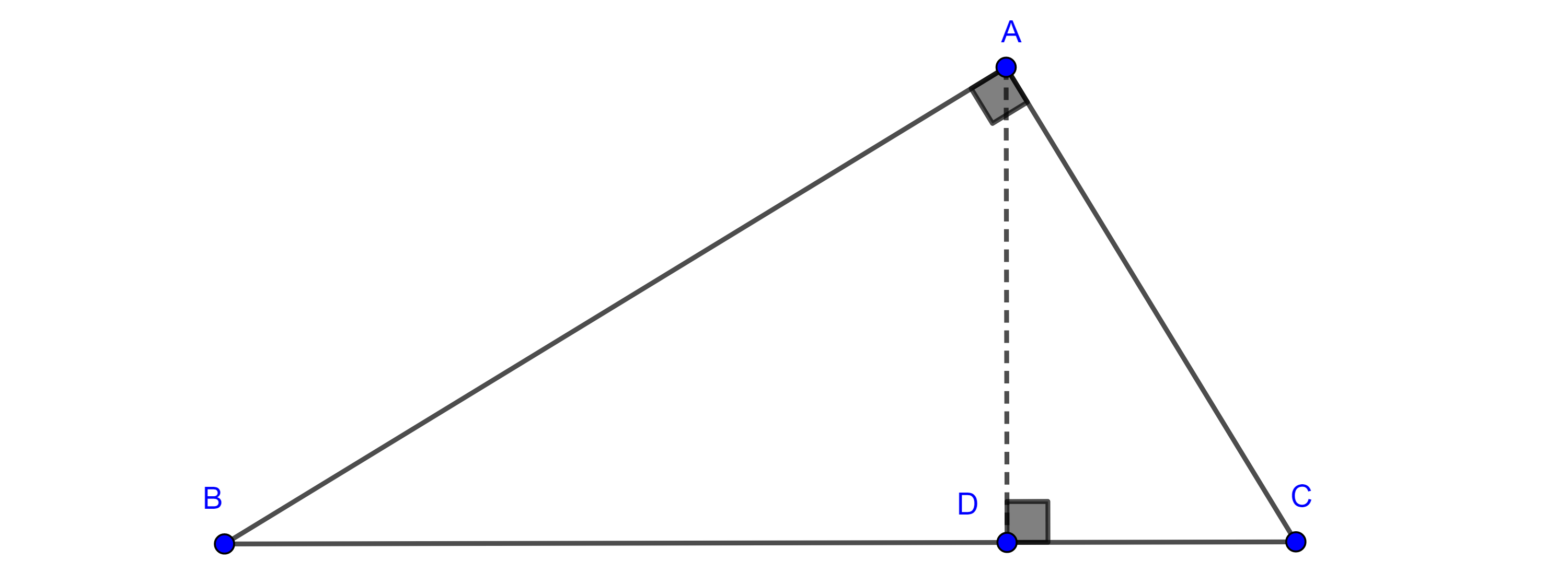
Proposición 4. Sean $\mathrm{△}ABC$ un triángulo rectángulo con $\mathrm{\angle }A={\displaystyle \frac{\pi }{2}}$ y $D$ el pie de la perpendicular a $\overline{BC}$ trazada desde $A$, entonces:
$i)$ $A{D}^2=BD\times DC$,
$ii)$ $A{B}^2=BC\times BD$,
$iii)$ $A{C}^2=BC\times DC$,
$iv)$ $AD\times BC=AB\times AC$.

Demostración. Por criterio de semejanza AA, $\mathrm{△}ABC\sim \mathrm{△}DBA$ y $\mathrm{△}ABC\sim \mathrm{△}DAC$,

$i)$  Por la relación de semejanza tenemos
${\displaystyle \frac{AD}{AC}}={\displaystyle \frac{BD}{AB}}\Rightarrow AD={\displaystyle \frac{BD\times AC}{AB}}$,
${\displaystyle \frac{AD}{AB}}={\displaystyle \frac{DC}{AC}}\Rightarrow AD={\displaystyle \frac{DC\times AB}{AC}}$
$\Rightarrow A{D}^2=BD\times DC$

$ii)$ Como $\mathrm{△}ABC\sim \mathrm{△}DBA$, ${\displaystyle \frac{AB}{BD}}={\displaystyle \frac{BC}{AB}}$
$\Rightarrow A{B}^2=BC\times BD$

$iii)$ Como $\mathrm{△}ABC\sim \mathrm{△}DAC$, ${\displaystyle \frac{AC}{DC}}={\displaystyle \frac{BC}{AC}}$
$\Rightarrow A{C}^2=BC\times DC$

$iv)$ de $ii)$ y $iii)$ tenemos $B{C}^2={\displaystyle \frac{A{B}^2\times A{C}^2}{BD\times DC}}$
y empleando $i)$ obtenemos $A{D}^2\times B{C}^2=(BD\times DC){\displaystyle \frac{A{B}^2\times A{C}^2}{BD\times DC}}$
$\Rightarrow AD\times BC=AB\times AC$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Más adelante…

En la siguiente entrada comenzaremos a distinguir el sentido en el que recorremos un sementó de recta y si la razón en que un punto divide a un segmento es negativa o positiva. Haciendo uso de segmentos dirigidos mostraremos el teorema de Stewart.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Demuestra el teorema de Pitágoras usando semejanza de triángulos.
2. Criterio de semejanza hipotenusa-cateto, muestra que un par de triángulos rectángulos son semejantes si la razón entre sus hipotenusas y la razón entre uno de sus catetos son iguales.
3. Muestra que si en un triángulo dos bisectrices internas tienen la misma longitud, entonces el triángulo es isósceles.
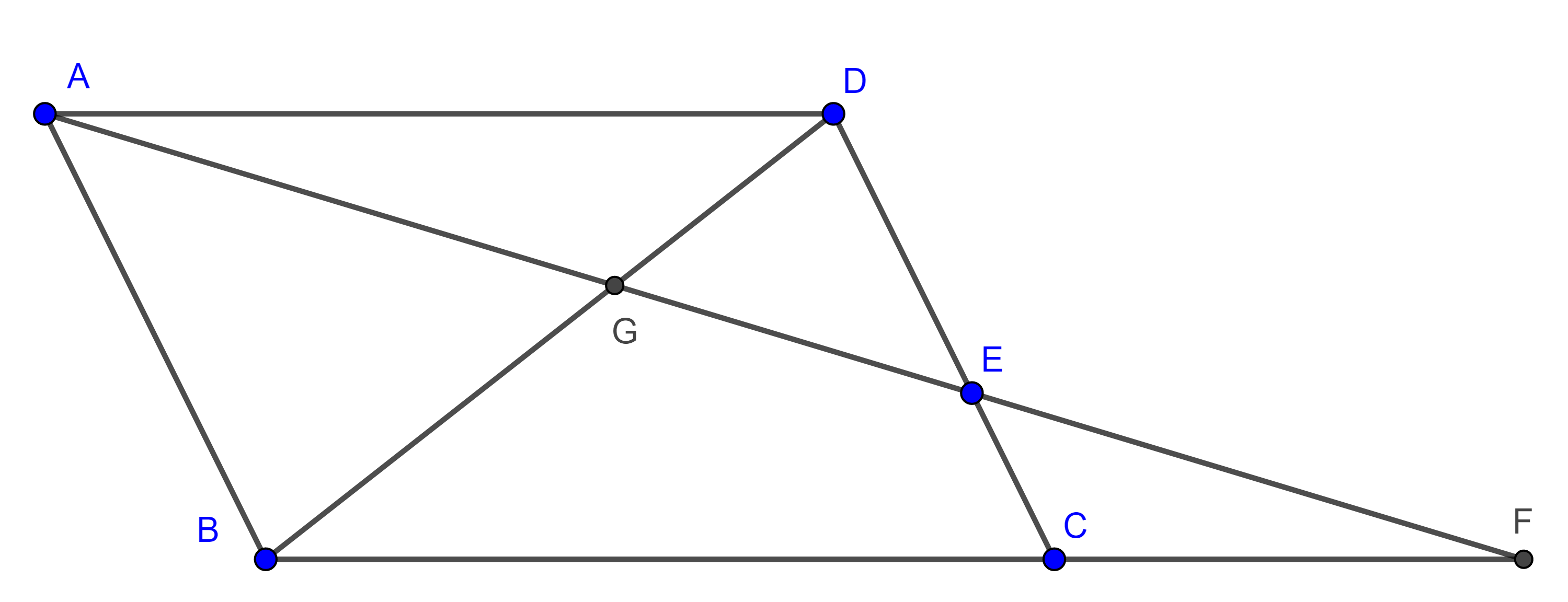
4. Sean $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ un paralelogramo,$E\in CD$, $G$ y $F$ las intersecciones de $AE$ con $BD$ y $BC$ respectivamente (figura 6), encuentra $EF$ en términos de $AG$ y $GE$.

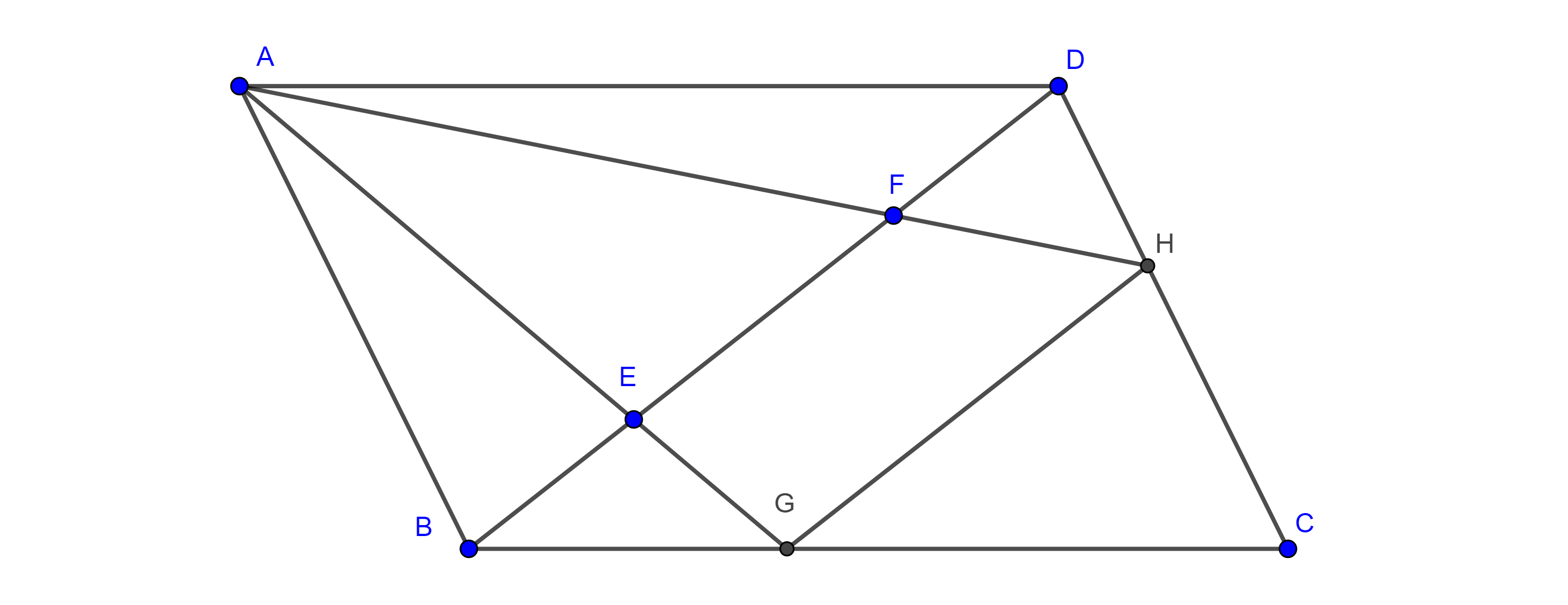
5. Sean $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ un paralelogramo, $E$, $F\in BD$ tales que $BE=DF$, $G=AE\cap BC$ y $H=AF\cap CD$ (figura 7), muestra que $GH\parallel BD$.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Teorema de Tales.
• Siguiente entrada del curso: Segmento dirigido y teorema de Stewart.
• Otros cursos.

Fuentes

• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 18-24.
• Altshiller, N., College Geometry. New York: Dover, 2007, pp 72-73.
• Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 6-11.
• Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»