Introducción
En las entradas anteriores nos enfocamos en desarrollar el concepto de límite y revisamos diversos tipos de funciones, sin embargo, evitamos un tipo particular: las funciones trigonométricas. En esta entrada centraremos nuestra atención en la revisión de estos límites haciendo uso de toda la teoría revisada hasta este punto.
Límite de funciones trigonométricas cuando $x$ tiende a $x_0$
En los primeros ejemplos podrás visualizar la gráfica de la función con la finalidad de tener cierta intuición respecto a los límites, pero, en caso de requerirlo, puedes repasar las funciones trigonométricas.
Ejemplo 1. Prueba que $$\lim_{x \to 0} sen(x) = sen(0).$$
Demostración.
Para probar este límite, procederemos a calcular los límites laterales.
Sea $x \in (0, \pi / 2 )$. Usaremos que $0 < sen(x) < x$ si $x \in (0, \pi / 2 )$.
Además, $$\lim_{x \to 0} = 0 \qquad \text{y} \qquad \lim_{x \to 0} x = 0.$$
Por el teorema del sándwich, podemos concluir que $$\lim_{x \to 0^+} sen(x) = 0 = sen(0). \tag{1}$$
Si $x \in (- \pi / 2, 0)$, entonces $-x \in (0, \pi /2)$. De esta forma, se obtiene que
$$ 0 < sen(-x) < -x.$$
Como $sen(-x) = -sen(x)$, se sigue que $$0 < -sen(x) < -x.$$
Por lo tanto $$ x < sen(x) < 0$$
Nuevamente por el teorema del sándwich, se sigue que $$\lim_{x \to 0^-} sen(x) = 0 = sen(0). \tag{2}$$
De $(1)$ y $(2)$ se concluye que $$\lim_{x \to 0} sen(x) = sen(0).$$
$\square$
Ejemplo 2. Prueba que $$\lim_{x \to 0} cos(x) = cos(0).$$
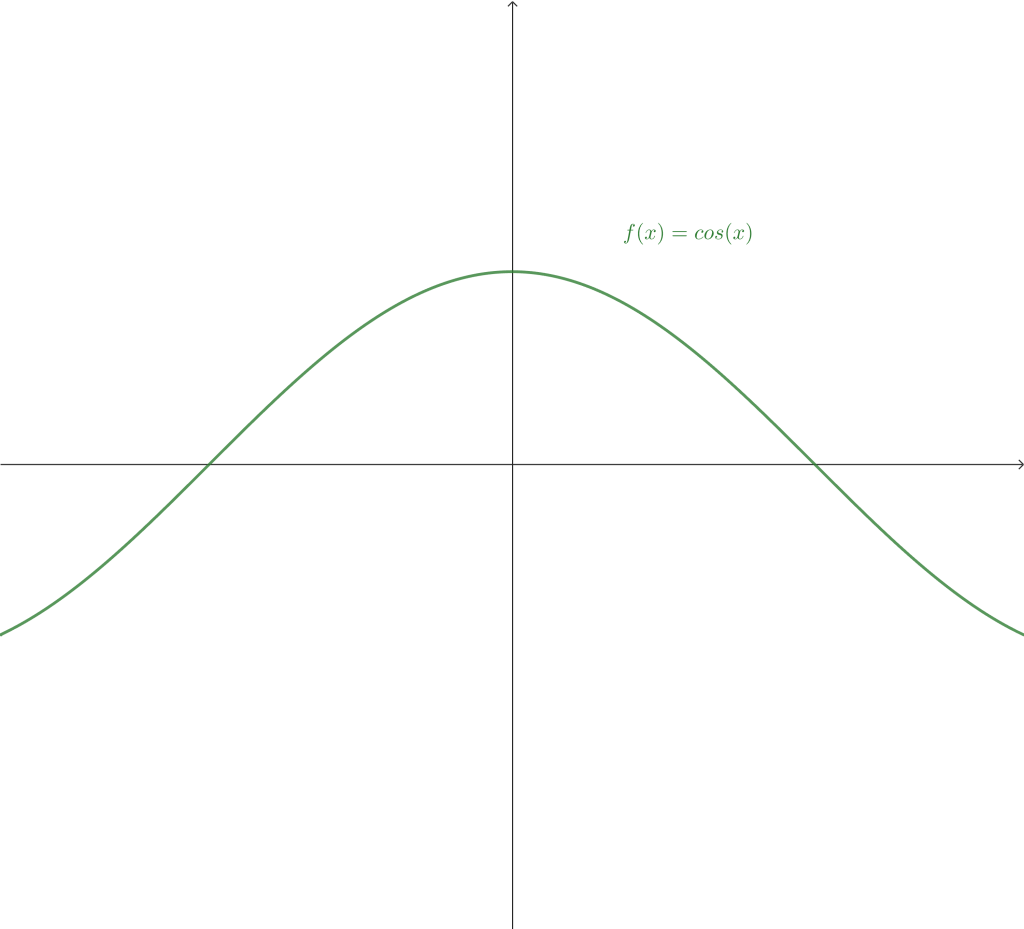
Demostración.
Como $$ cos^2(x)+sen^2(x) = 1,$$ se sigue que $$|cos(x)| = \sqrt{1-sen^2(x)}.$$
Consideremos $x \in (-\pi/2, \pi/2)$, entonces $cos(x) > 0$, y de la expresión anterior se sigue que $$cos(x) = \sqrt{1-sen^2(x)}.$$
De esta manera, se tiene que
\begin{align*}
\lim_{x \to 0} cos(x) & = \lim_{x \to 0} \sqrt{1-sen^2(x)} \\
& = \sqrt{1-0} \\
& = 1 \\
& = cos(0).
\end{align*}
Por lo tanto
$$\lim_{x \to 0} cos(x) = cos(0).$$
$\square$
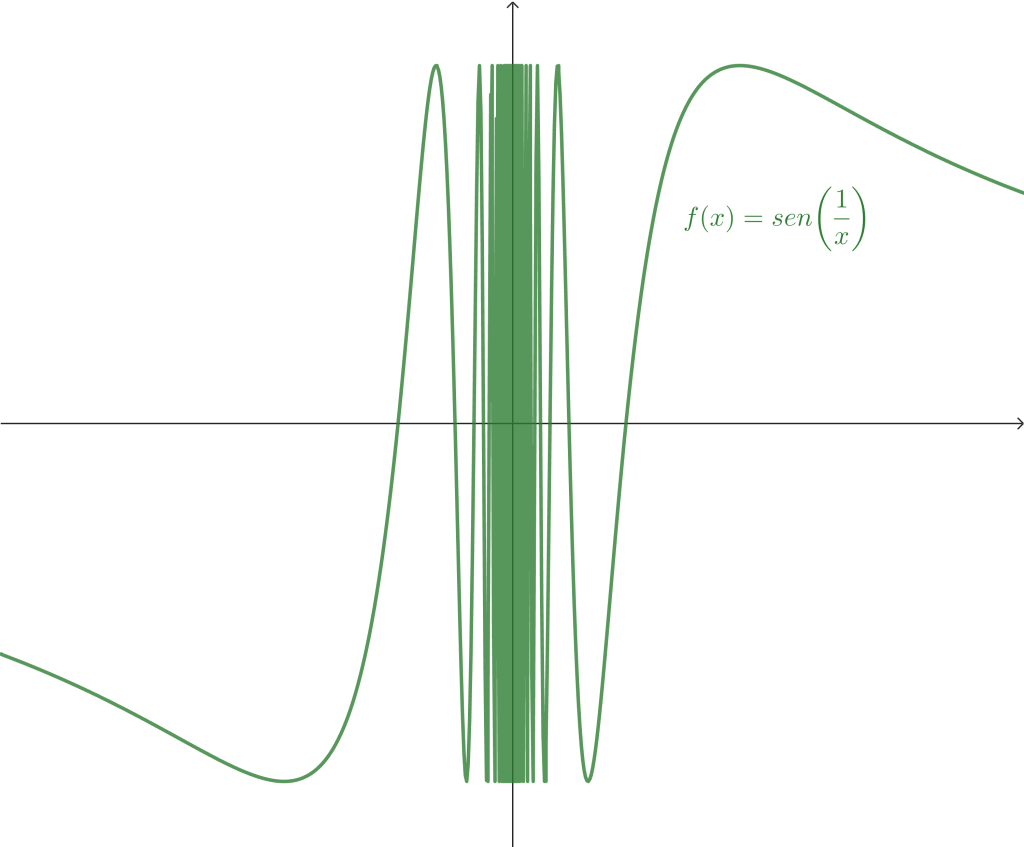
Ejemplo 3. Prueba que el siguiente límite no existe $$\lim_{x \to 0} sen \left( \frac{1}{x} \right).$$
Demostración.
Notemos que por la relación entre el límite de una función y el de una sucesión, basta dar dos sucesiones $\{a_n\}$, $\{b_n\}$ tal que converjan a $x_0 = 0$ y $a_n$, $b_n \neq 0$ para todo $n \in \mathbb{N}$, pero que las sucesiones obtenidas de evaluar la función en los términos de ambas sucesiones, $\{f(a_n)\}$, $\{f(b_n)\}$ converjan a valores distintos.
Definimos $f(x) = sen(\frac{1}{x})$ y consideremos las sucesiones $a_n = (\pi n) ^{-1} \quad$ y $b_n = (\frac{1}{2} \pi + 2 \pi n)^{-1},$ donde $a_n$, $b_n \neq 0$ para todo $n \in \mathbb{N}.$
Veamos que
\begin{align*}
\lim_{n \to \infty} a_n = & \lim_{n \to \infty} (\pi n) ^{-1} \\
= & \lim_{n \to \infty} \frac{1}{\pi n} \\
= & 0.
\end{align*}
$$\therefore \lim_{n \to \infty} a_n = 0.$$
Además,
\begin{align*}
\lim_{n \to \infty} b_n = & \lim_{n \to \infty} \left( \frac{1}{2} \pi + 2 \pi n \right)^{-1}\\ \\
= & \lim_{n \to \infty} \frac{1}{\frac{1}{2} \pi + 2 \pi n} \\ \\
= & \lim_{n \to \infty} \frac{1}{\frac{\pi + 4 \pi n}{2}} \\ \\
= & \lim_{n \to \infty} \frac{2}{\pi + 4 \pi n} \\ \\
= & 0.
\end{align*}
$$\therefore \lim_{n \to \infty} b_n = 0.$$
Es decir, las sucesiones $\{a_n\}$ y $\{b_n\}$ tienden a cero. Y notemos que $f(a_n) = sen(n \pi ) = 0$ y $f(b_n) = sen(\frac{1}{2} \pi + 2 \pi n) = 1$ para todo $n \in \mathbb{N}.$
De esta forma $$\lim_{n \to \infty} f(a_n) \neq \lim_{n \to \infty} f(b_n).$$
Por tanto, podemos concluir que el límite no existe.
$\square$
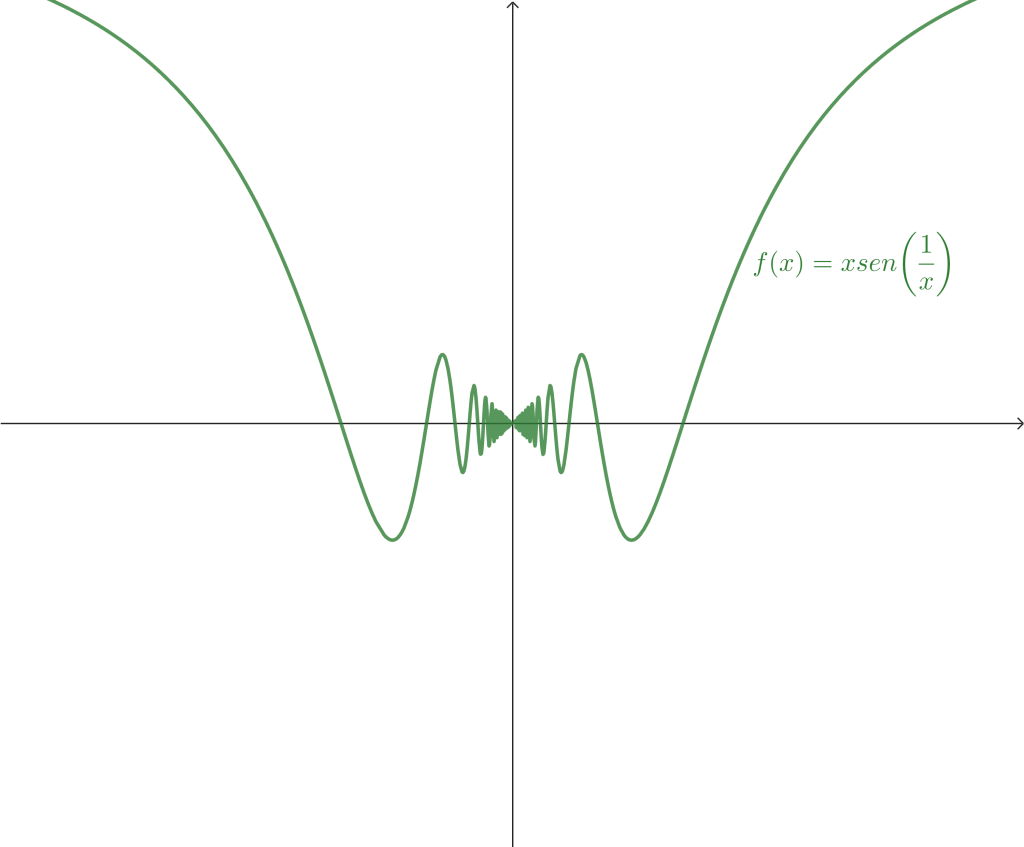
Ejemplo 4. Prueba que $$\lim_{x \to 0} x sen \left( \frac{1}{x} \right) = 0.$$
Demostración.
Haremos la demostración de este límite mediante la definición épsilon-delta.
Sea $\varepsilon > 0$. Consideremos $\delta = \varepsilon.$
Si $0<|x-0| < \delta$, entonces
\begin{gather*}
& |x| < \delta = \varepsilon. \\
\Rightarrow & |x|< \varepsilon.
\end{gather*}
Además, sabemos que $-1 < sen \left( \frac{1}{x} \right) < 1$ para cualquier $x \neq 0.$ Entonces
\begin{align*}
|f(x)-0| = & \left|x sen \left( \frac{1}{x} \right) \right| \\
= & |x|\left|sen \left( \frac{1}{x} \right) \right| \\
\leq & \delta \cdot 1 \\
= & \varepsilon.
\end{align*}
$$\therefore \lim_{x \to 0} x sen \left( \frac{1}{x} \right) = 0.$$
$\square$
El siguiente ejemplo es un límite que nos ayudará en diversas ocasiones, así que vale la pena ponerle particular atención.
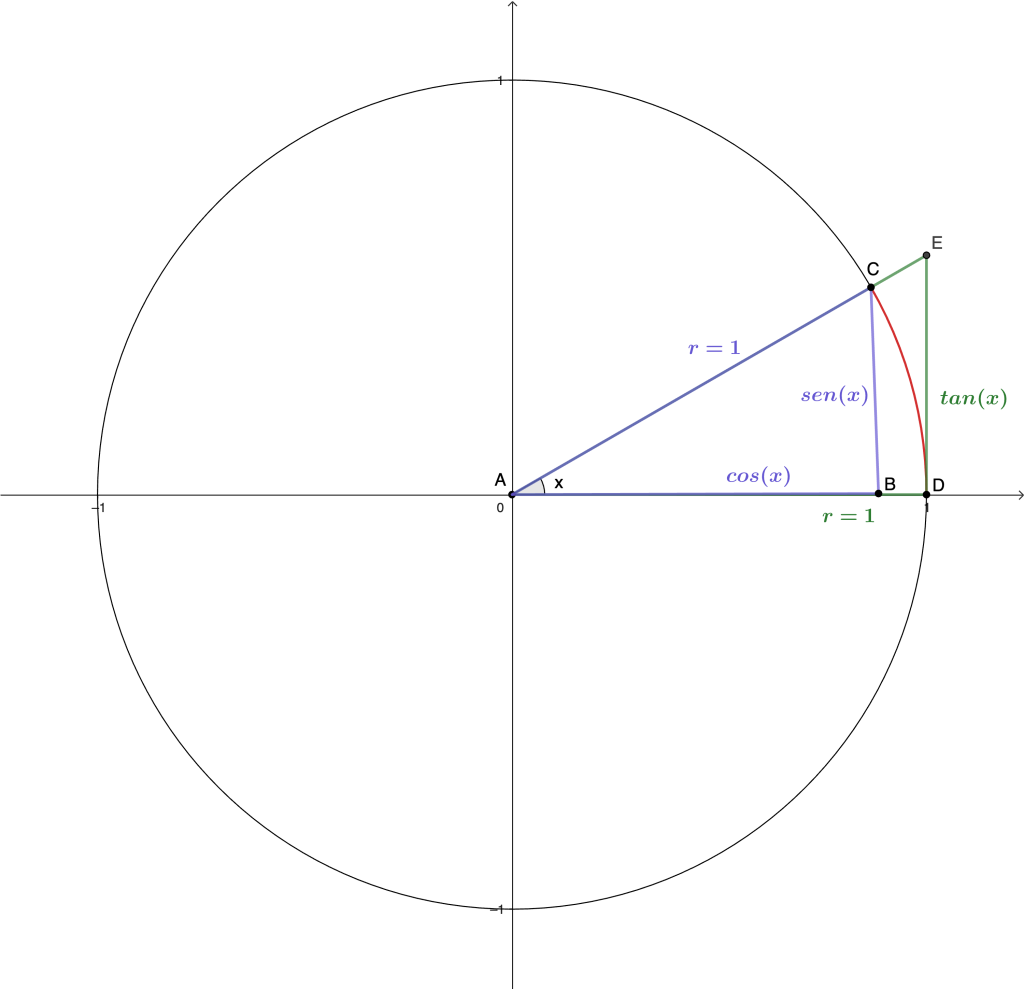
Ejemplo 5. Prueba que $$\lim_{x \to 0 } \frac{sen(x)}{x} = 1.$$
Demostración.
Como nos interesa revisar qué sucede cuando $x \to 0$. Podemos considerar que $x \in (-\frac{\pi}{2}, \frac{\pi}{2})$ con $x\neq 0.$
De esta forma, se tiene que
- Área $\triangle ABC = \frac{sen(x)cos(x)}{2}$.
- Área del sector circular $ADC = \frac{xr^2}{2} = \frac{x}{2}$.
- Área $\triangle ADE = \frac{1 \cdot tan(x)}{2} = \frac{sen(x)}{2cos(x)}$.
Podemos notar que Área $\triangle ABC <$ Área del sector circular $ADC <$Área $\triangle ADE$.
Como $x \in (-\frac{\pi}{2}, \frac{\pi}{2})$ con $x\neq 0$, entonces $sen(x) \neq 0$ y $cos(x) \neq 0$. Así, se sigue que
\begin{gather*}
\frac{sen(x)cos(x)}{2} < \frac{x}{2} < \frac{sen(x)}{2cos(x)}.
\end{gather*}
De donde se obtiene que $$cos(x) < \frac{x}{sen(x)} < \frac{1}{cos(x)}.$$
Y se sigue que $$ cos(x) < \frac{x}{sen(x)} \qquad \text{ y } \qquad \frac{x}{sen(x)} < \frac{1}{cos(x)}.$$
Es decir, $$ \frac{sen(x)}{x} < \frac{1}{cos(x)} \qquad \text{ y } \qquad cos(x) < \frac{sen(x)}{x}. $$
$$ \therefore cos(x) < \frac{sen(x)}{x} < \frac{1}{cos(x)}.$$
Además, $\lim\limits_{x \to 0} cos(x) = 1$ y $\lim\limits_{x \to 0} \frac{1}{cos(x)} = 1$. Por el teorema del del sándwich se concluye que
$$\lim_{x \to 0 } \frac{sen(x)}{x} = 1.$$
$\square$
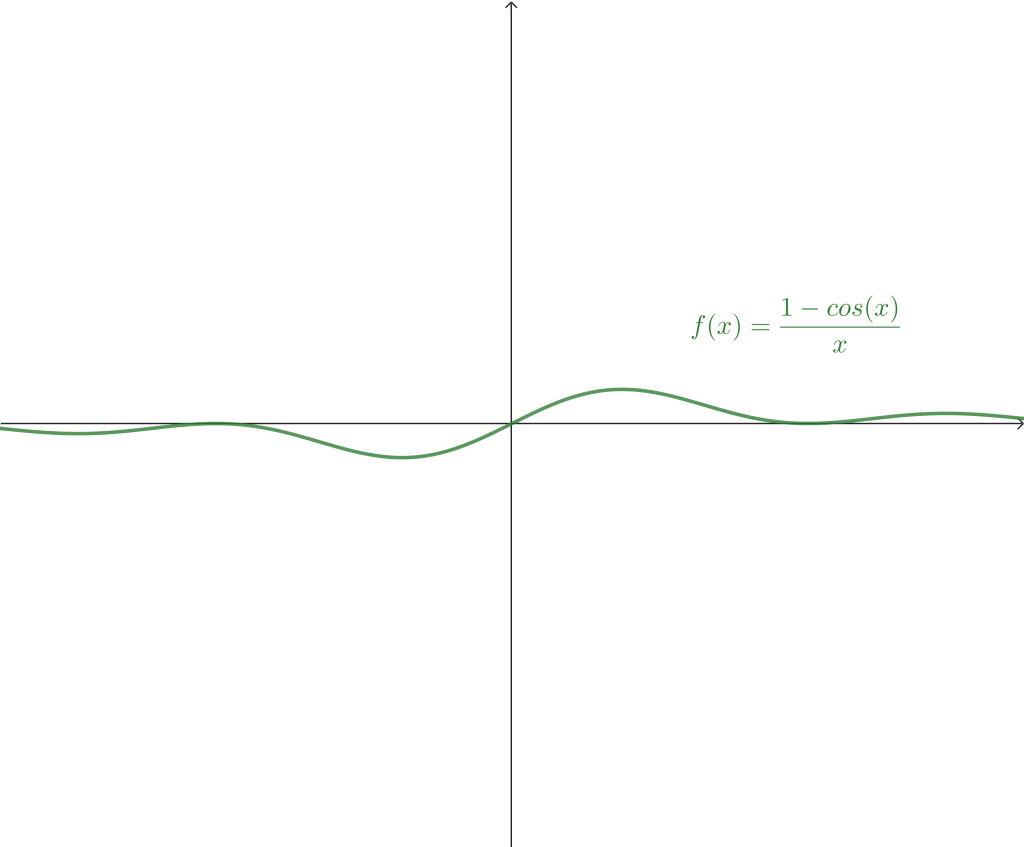
Ejemplo 6. Determina el siguiente límite $$\lim_{x \to 0} \frac{1-cos(x) }{x}.$$
Si $0< |x| < \pi$, entonces
\begin{align*}
\frac{1-cos(x)}{x} = & \frac{1-cos(x)}{x} \cdot \frac{1+cos(x)}{1+cos(x)} \\ \\
= & \frac{1-cos^2(x)}{x (1+cos(x) )} \\ \\
= & \frac{sen^2(x)}{x(1+cos(x))} \\ \\
= & \frac{sen(x)}{x} \frac{sen(x)}{1+cos(x)}.
\end{align*}
Así,
\begin{align*}
\lim_{x \to 0} \frac{1-cos(x) }{x} = & \lim_{x \to 0}\frac{sen(x)}{x} \cdot \frac{sen(x)}{1+cos(x)} \\
= & \lim_{x \to 0} \frac{sen(x)}{x} \cdot \lim_{x \to 0} \frac{sen(x)}{1+cos(x)} \\
= & 1 \cdot \frac{0}{2} \\
= & 0.
\end{align*}
$$\therefore \lim_{x \to 0} \frac{1-cos(x) }{x} = 0.$$
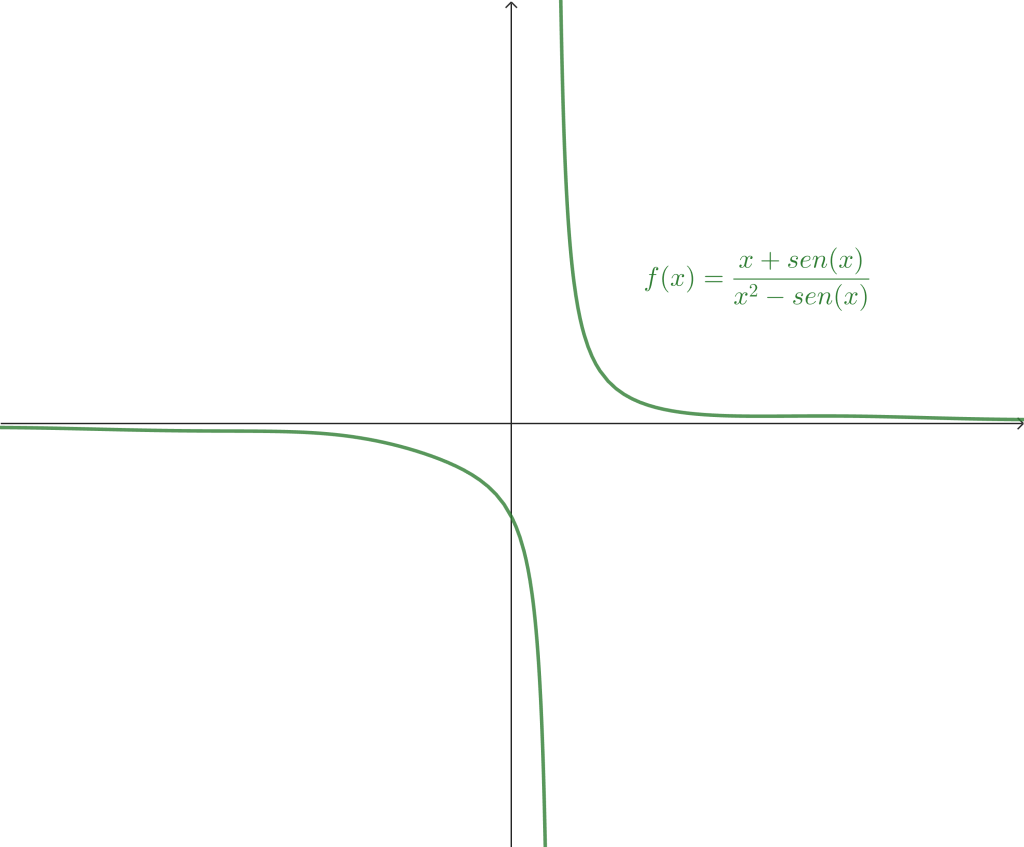
Ejemplo 7. Calcula el siguiente límite $$\lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)}.$$
\begin{align*}
\lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)} = & \lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)} \cdot \frac{\frac{1}{x}}{\frac{1}{x}} \\ \\
= & \lim_{x \to 0} \frac{1+\frac{sen(x)}{x}}{x-\frac{sen(x)}{x}} \\ \\
= & \frac{1+1}{0-1} \\ \\
= & -2.
\end{align*}
$$\therefore \lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)} = -2.$$
Ejemplo 8. Calcula $$\lim_{x \to 0} \frac{sec(x) -1}{x}.$$
\begin{align*}
\lim_{x \to 0} \frac{sec(x) -1}{x} = & \lim_{x \to 0} \frac{\frac{1}{cos(x)} -1}{x} \\ \\
= & \lim_{x \to 0} \frac{\frac{1- cos(x)}{cos(x)}}{x} \\ \\
= & \lim_{x \to 0} \frac{1- cos(x)}{x cos(x)} \\ \\
= & \lim_{x \to 0} \frac{1}{cos(x)} \frac{1- cos(x)}{x} \\ \\
= & 1 \cdot 0 \\ \\
= & 0.
\end{align*}
$$\therefore \lim_{x \to 0} \frac{sec(x) -1}{x} = 0.$$
Límite de funciones trigonométricas cuando $x$ tiende a infinito
Ahora procederemos a revisar algunos ejemplos de funciones trigonométricas cuando $x \to \infty$, o bien, cuando $x \to – \infty.$
Ejemplo 9. Calcula el límite $$\lim_{x \to \infty} \frac{sen(x)}{x}.$$
Sabemos que $-1 \leq sen(x) \leq 1.$ De esta forma, si $x \neq 0$, se tiene que $$ -\frac{1}{x} \leq \frac{sen(x)}{x} \leq \frac{1}{x}.$$
Además, $$ \lim_{x \to \infty} -\frac{1}{x} = 0 = \lim_{x \to \infty} \frac{1}{x}.$$
Por el teorema del sándwich, se concluye que
$$ \lim_{x \to \infty} sen(x) = 0.$$
Ejemplo 10. Calcula el límite $$\lim_{x \to \infty} \frac{x sen(x)}{x^2+5}.$$
\begin{align*}
\lim_{x \to \infty} \frac{x sen(x)}{x^2+5} = & \lim_{x \to \infty} \frac{x sen(x)}{x^2+5} \cdot \frac{\frac{1}{x^2}}{\frac{1}{x^2}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{x sen(x)}{x^2}}{\frac{x^2+5}{x^2}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{sen(x)}{x}}{1+\frac{5}{x^2}} \\ \\
= & \frac{0}{1} \text{, por lo visto en el ejemplo anterior }\\ \\
= & 0.
\end{align*}
$$\therefore \lim_{x \to \infty} \frac{x sen(x)}{x^2+5} = 0.$$
Ejemplo 11. Determina si existe el siguiente límite $$\lim_{x \to \infty} \frac{x^2(1+sen^2(x))}{(x+sen(x))^2}.$$
El límite no existe. Considera las sucesiones generadas por $a_n = \pi n \quad$ y $\quad b_n = \frac{1}{2} \pi + 2 \pi n \quad$ donde $a_n$, $b_n \rightarrow \infty$ cuando $n \rightarrow \infty.$ Notemos que
\begin{align*}
\lim_{n \to \infty} f(a_n) = & \lim_{n \to \infty} \frac{(\pi n)^2(1+sen^2(\pi n))}{(\pi n+sen(\pi n))^2} \\ \\
= & \lim_{n \to \infty} \frac{(\pi n)^2(1+0)}{(\pi n+0)^2} \\ \\
= & \lim_{n \to \infty} \frac{(\pi n)^2}{(\pi n)^2} \\ \\
= & \lim_{n \to \infty} 1 \\ \\
= & 1.
\end{align*}
$$ \therefore \lim_{n \to \infty} f(a_n) = 1.$$
Por otro lado,
\begin{align*}
\lim_{n \to \infty} f(b_n) = & \lim_{n \to \infty} \frac{(\frac{1}{2} \pi + 2 \pi n)^2(1+sen^2(\frac{1}{2} \pi + 2 \pi n))}{(\frac{1}{2} \pi + 2 \pi n+sen(\frac{1}{2} \pi + 2 \pi n))^2} \\ \\
= & \lim_{n \to \infty} \frac{(\frac{1}{2} \pi + 2 \pi n)^2(1+1)}{(\frac{1}{2} \pi + 2 \pi n+1)^2} \\ \\
= & \lim_{n \to \infty} \frac{2(\frac{1}{2} \pi + 2 \pi n)^2}{(\frac{1}{2} \pi + 2 \pi n+1)^2} \\ \\
= & 2.
\end{align*}
$$ \therefore \lim_{n \to \infty} f(b_n) = 2.$$
Como $$\lim_{n \to \infty} f(a_n) \neq \lim_{n \to \infty} f(b_n).$$
Podemos concluir que el límite $\lim_\limits{x \to \infty} \frac{x^2(1+sen^2(x))}{(x+sen(x))^2}$ no existe.
Ejemplo 12. Determina el siguiente límite $$\lim_{x \to -\infty} \frac{3x^2-sen(5x)}{x^2+2}.$$
Recordemos que $-1 < sen(5x) < 1$, de donde se sigue que $-1 < -sen(5x) < 1$, así
\begin{gather*}
& 3x^2-1 < 3x^2-sen(5x) < 3x^2+1.
\end{gather*}
Se sigue que
\begin{gather*}
\frac{3x^2-1}{x^2+2} < \frac{3x^2-sen(5x)}{x^2+2} < \frac{3x^2+1}{x^2+2} \text{, pues } x^2+2 >0.
\end{gather*}
Y notemos que
\begin{align*}
\lim_{x \to -\infty} \frac{3x^2+1}{x^2+2} = & \lim_{x \to -\infty} \frac{\frac{3x^2+1}{x^2}}{\frac{x^2+2}{x^2}} \\ \\
= & \lim_{x \to -\infty} \frac{3+\frac{1}{x^2}}{1+\frac{2}{x^2}} \\ \\
= & \frac{3}{1} \\ \\
=& 3.
\end{align*}
De forma similar, se obtiene que $$\lim_{x \to -\infty} \frac{3x^2-1}{x^2+2}= 3.$$
Por lo que se tiene que $$\lim_{x \to -\infty} \frac{3x^2+1}{x^2+2} = 3 = \lim_{x \to -\infty} \frac{3x^2-1}{x^2+2}.$$ Usando el teorema del sándwich podemos concluir que
$$\lim_{x \to -\infty} \frac{3x^2-sen(5x)}{x^2+2} = 3.$$
Más adelante…
En la siguiente entrada revisaremos el concepto de asíntotas con lo que nos será posible analizar un comportamiento particular que llegan a tener las funciones, el cual es aproximarse a una recta en determinado momento; y, con esto, estaremos finalizando la unidad referente al límite de una función.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
Halla los siguientes límites, justifica en caso de no alguno no exista.
- $$\lim_{x \to 0} \frac{x^2 (3+sen(x))}{(x+sen(x))^2}.$$
- $$\lim_{x \to 1} \frac{sen(x^2-1)}{x-1}.$$
- $$\lim_{x \to \infty} x^2 sen \left(\frac{1}{x} \right).$$
- $$\lim_{x \to \infty} \frac{x + sen^3(x)}{5x+6}.$$
- $$\lim_{x \to 0} \frac{tan^2(x)+2x}{x + x^2}.$$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Límites infinitos
- Siguiente entrada del curso: Asíntotas
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»