Archivo de la etiqueta: ejemplos de límites

Cálculo Diferencial e Integral I: Límites laterales

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En las entradas anteriores hemos trabajado con la definición de límite y revisamos sus propiedades. En esta ocasión, daremos la definición de límite por la derecha y límite por la izquierda, que en conjunto son llamados límites laterales. De igual forma, revisaremos algunos ejemplos y su relación con la definición vista anteriormente.

Límites laterales

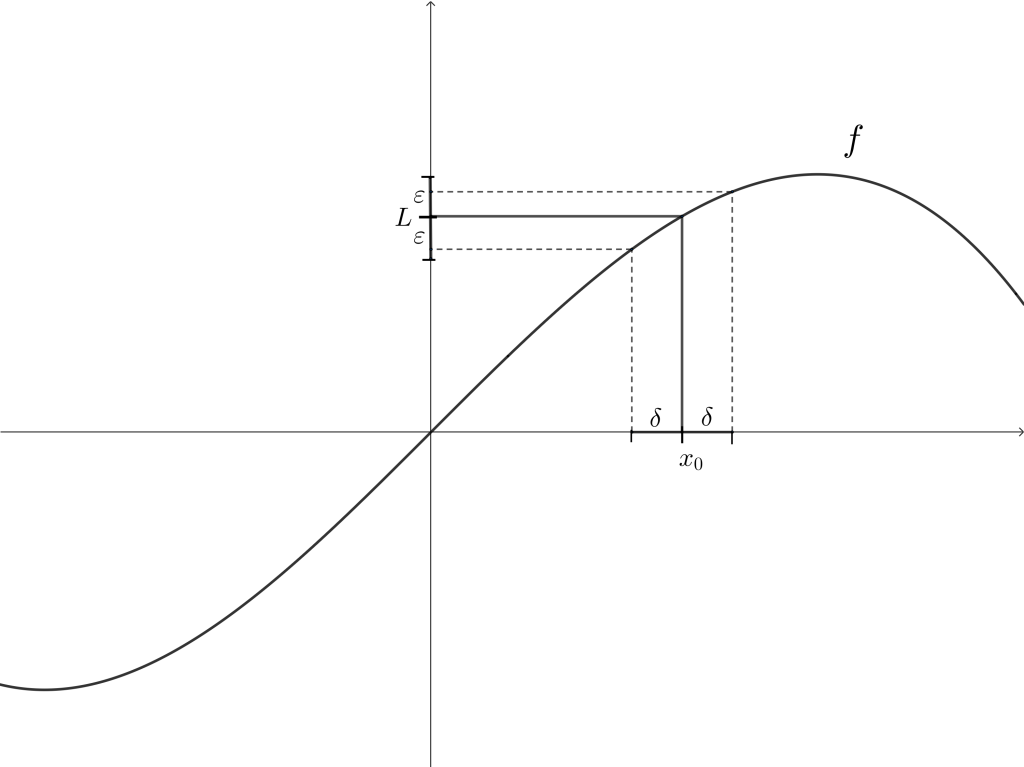
Las definiciones que veremos a continuación se basan en restringir la forma en que nos acercamos a $x_0.$ El límite por la derecha se enfoca en acercarnos por la derecha, es decir, pediremos que $x > x_0,$ lo cual se traducirá en que debe cumplirse que $0<x-x_0 < \delta$. Por otro lado, para el límite por la izquierda debe cumplirse que $x < x_0,$ de esta forma se tendrá que $0<x_0-x< \delta.$ Primero daremos la definición de límite por la derecha.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la derecha de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x-x_0<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la derecha, lo denotamos $$\lim_{x \to x_0+} f(x) = L.$$

Análogamente, tenemos la definición de límite por la izquierda.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la izquierda de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x_0 – x<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la izquierda, lo denotamos $$\lim_{x \to x_0-} f(x) = L.$$

Propiedades de los límites laterales

De forma similar al teorema que vimos para los límites, existe una relación entre el límite lateral de una función y el límite de una sucesión, basta agregar a los supuestos la condición de que la sucesión sea mayor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la derecha y que sea menor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la izquierda.

Teorema. Sea $A \subset \mathbb{R}.$ Definimos la función $f:A \rightarrow \mathbb{R}.$ Entonces, dado un $x_0,$ los siguientes enunciados son equivalentes.

  1. $$\lim_{x \to x_0+} f(x) = L.$$
  2. Para toda sucesión $\{ a_n \}$ en $A$ que converge a $x_0$ y tal que $a_n > x_0$ para todo $n\in \mathbb{N},$ la sucesión $\{f(a_n)\}$ converge a $L.$

El teorema de límite por la izquierda es similar al anterior. Además, la demostración es totalmente análoga a la revisada en una entrada anterior por lo cual quedará como tarea moral. También recordemos que este teorema nos ayuda a determinar las propiedades que tienen los límites laterales debido a la herencia que nos brinda el límite de una sucesión; es gracias a ello que podremos hacer uso de tales propiedades en los siguientes ejemplos.

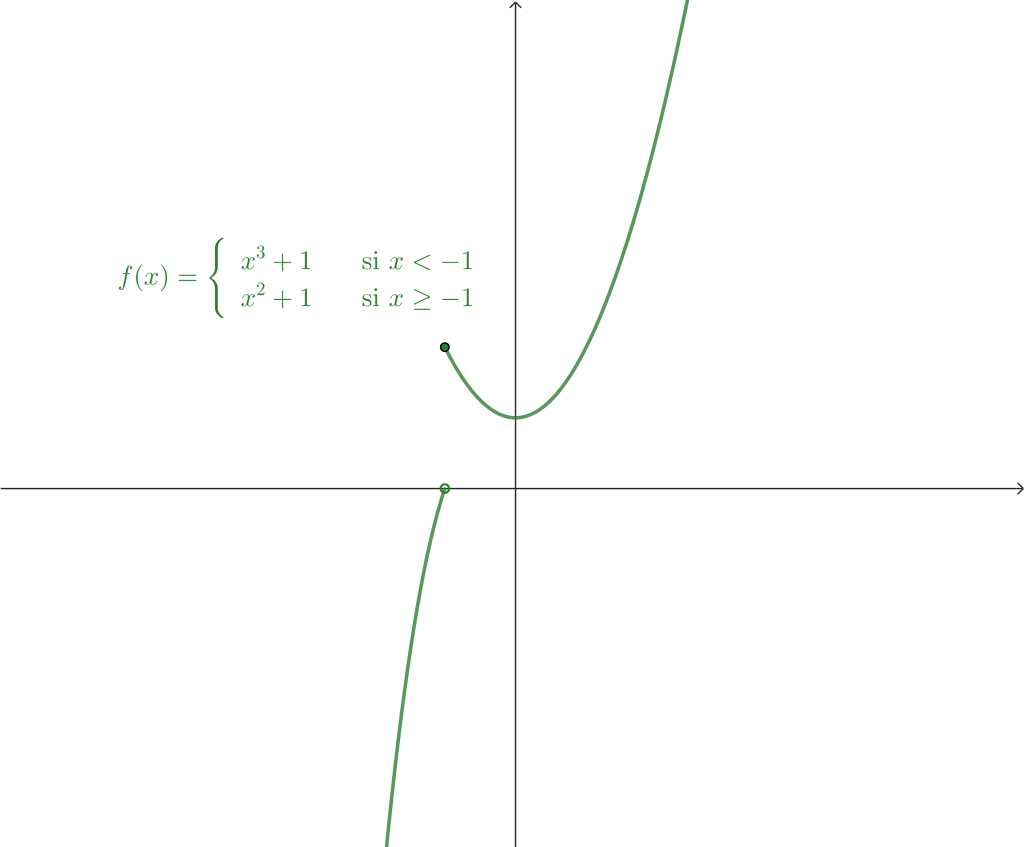
Ejemplo 1. Sea $f: \mathbb{R} \rightarrow \mathbb{R},$ definida de la siguiente forma

$$f(x) =
\begin{cases}
x^3+1 & \quad \text{si } x<-1 \\
x^2+1& \quad \text{si } x \geq -1. \\
\end{cases}
$$

Determina los límites laterales en $x_0 = -1.$

Primero mostraremos la gráfica de la función:

Calculando el límite por la izquierda, tenemos
$$\lim_{x \to -1^-} f(x) = \lim_{x \to -1^-} x^3+1 = 0.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to -1^+} f(x) = \lim_{x \to -1^+} x^2+1= 2.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 0 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 2.$$

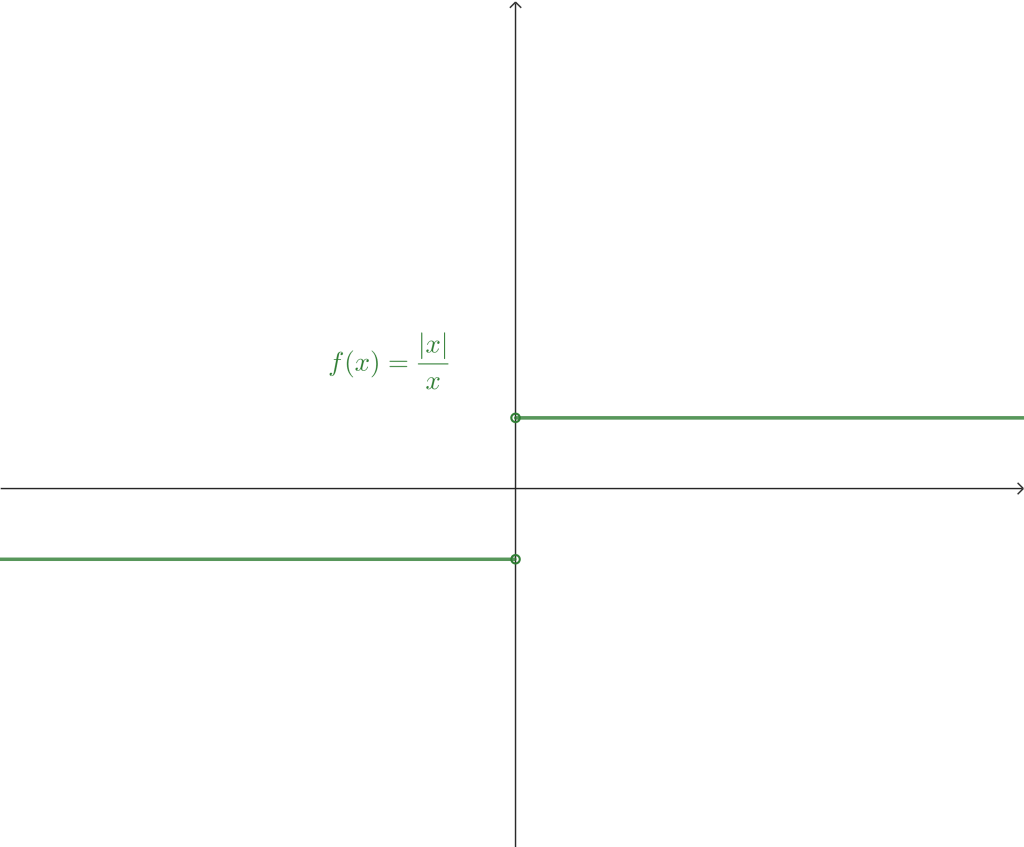
Ejemplo 2. Sea $f: \mathbb{R} \setminus \{0 \} \rightarrow \mathbb{R}.$ Calcula los límites laterales en $x_0 = 0$ de

$$f(x) = \frac{|x|}{x}.$$

La gráfica de la función es la siguiente:

Calculando el límite por la izquierda, tenemos
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} \frac{|x|}{x} \\
= & \lim_{x \to 0^-} \frac{-x}{x} \text{, pues $x$ < 0} \\
= & \lim_{x \to 0^-} -1 \\
= & -1.
\end{align*}
Por otro lado, el límite por la derecha
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} \frac{|x|}{x} \\
= & \lim_{x \to 0^+} \frac{x}{x} \text{, pues $x$ > 0} \\
= & \lim_{x \to 0^+} 1 \\
= & 1.
\end{align*}
Por lo tanto
$$\lim_{x \to 0^-} f(x) = -1 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 1.$$

De los ejemplos revisados, el primero tiene la propiedad de que sus límites laterales son iguales mientras que para el segundo y el tercero tales límites son distintos en $x_0.$

Relación entre el límite de una función y sus límites laterales

Parece inmediato inferir que, considerando un punto $x_0$ dado, si los límites por la izquierda y por la derecha existen y son iguales, entonces el límite de la función sí existe en tal punto. De la misma manera, resulta natural que si el límite existe, entonces los límites laterales también existen y son iguales. Probaremos esta equivalencia, pero para hacerlo, primero demostraremos la siguiente proposición.

Proposición. Sean $x,$ $x_0$ en $\mathbb{R}$ y $\delta >0.$ Entonces $0<|x-x_0|< \delta$ si y solo si $0<x-x_0<\delta \quad$ ó $\quad 0<x_0-x<\delta.$

Demostración.
Supongamos que $0<|x-x_0|< \delta$.

Caso 1: $x-x_0 > 0$.
Entonces $|x-x_0| = x-x_0$, así
\begin{gather*}
0<|x-x_0|< \delta \Leftrightarrow 0< x-x_0 < \delta.
\end{gather*}

Caso 2: $x- x_0 < 0$.
Entonces $|x-x_0| = x_0-x$, así
\begin{gather*}
0<|x-x_0| < \delta \Leftrightarrow 0< x_0-x < \delta.
\end{gather*}

$$\therefore 0<|x-x_0|< \delta \Leftrightarrow 0<x-x_0<\delta \quad \text{ ó } \quad 0<x_0-x<\delta.$$

$\square$

Teorema. El límite de una función $f$ en el punto $x_0$ existe y es igual a $L$ si y solo si los límites laterales existen y son iguales a $L$, es decir

$$\lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

Demostración.

$\Rightarrow]$ Supongamos que $$\lim_{x \to x_0} f(x) = L.$$
Sea $\varepsilon > 0$. Como $f$ converge a $L$ en $x_0$, existe $\delta > 0$ tal que si $0<|x-x_0|< \delta$ se tiene que $|f(x)-L| < \varepsilon.$

Si $0<x-x_0 < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^+} f(x) = L.
\end{gather*}

Si $0<x_0-x < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^-} f(x) = L.
\end{gather*}

$\Leftarrow]$ Supongamos que $$\lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x)$$
Sea $\varepsilon > 0.$

Como $\lim\limits_{x \to x_0^+} f(x) = L$, existe $\delta_1$ tal que si $0<x-x_0<\delta_1$ entonces $|f(x)-L| < \varepsilon.$

Como $\lim\limits_{x \to x_0^-} f(x) = L$, existe $\delta_2$ tal que si $0<x_0-x<\delta_2$ entonces $|f(x)-L| < \varepsilon.$

Consideremos $\delta = min \{ \delta_1, \delta_2\}.$ Por la proposición, si $0<|x-x_0|< \delta$, entonces $0<x-x_0<\delta$ ó $0<x_0-x<\delta.$

Para el primer caso, tenemos que $0<x-x_0<\delta \leq \delta_1$, entonces $|f(x)-L| < \varepsilon.$
Para el segundo caso, se tiene que $0<x_0-x<\delta \leq \delta_2$, entonces $|f(x)-L| < \varepsilon.$

Por lo tanto $$\lim_{x \to x_0} f(x) = L.$$

$$\therefore \lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

$\square$

Observación. Ya que hemos demostrado este teorema, podemos notar que si los límites laterales de una función son distintos en un punto $x_0$, entonces no existe el límite de la función en tal punto.

Finalizaremos esta entrada revisando los siguientes ejemplos.

Ejemplo 3. Determina si existe el límite en $x_0 = 0$ para la siguiente función $$f(x) = x \sqrt{\frac{1}{4x^2}-16}.$$

Veamos primero qué sucede con el límite por la izquierda
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^-} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ \sqrt{4x^2} } \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ 2|x|} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ -2x} \text{, pues $x$ < 0} \\ \\
= & \lim_{x \to 0^-} – \frac{\sqrt{1-64x^2} }{2} \\ \\
= & – \frac{1}{2}.
\end{align*}

De forma similar, tenemos que
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^+} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^+} \frac{ x \sqrt{1-64x^2} }{ 2x} \text{, pues $x$ > 0} \\ \\
= & \lim_{x \to 0^+} \frac{\sqrt{1-64x^2} }{2} \\ \\
= & \frac{1}{2}.
\end{align*}
$$\therefore \lim_{x \to 0^-} f(x) = -\frac{1}{2} \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = \frac{1}{2}.$$

Como los límites laterales son distintos, podemos concluir que el límite de la función $f$ no existe en el punto $x_0 = 0.$

Ejemplo 4. Sea $f: \mathbb{R} \rightarrow \mathbb{R}$, definida de la siguiente forma
$$f(x) =
\begin{cases}
x^2 & \quad \text{si } x<5 \\
2x+15 & \quad \text{si } x \geq 5. \\
\end{cases}
$$
Determina si el límite existe en $x_0 = 5.$

Iniciemos calculando el límite por la izquierda.
$$\lim_{x \to 5^-} f(x) = \lim_{x \to 5^-} x^2 = 25.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to 5^+} f(x) = \lim_{x \to 5^+} 2x+15 = 25.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 25 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 25.$$

Como los límites laterales existen y son iguales, podemos concluir que
$$\lim_{x \to 0} f(x) = 25.$$

Más adelante…

¿Qué sucede cuando en lugar de acercarnos a un punto en particular $x_0$, hacemos que $x$ crezca indefinidamente? Esto y otras ampliaciones del concepto del límite serán revisadas en la siguiente entrada con lo cual estaremos listos para calcular todo tipo de límites y, con ello, podremos conocer el comportamiento que toman las funciones tanto en un punto específico como «en el infinito».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Demuestra que
    $i$) $\lim_\limits{x \to 0^+} f(x) = \lim_\limits{x \to 0^-} f(-x).$
    $ii$) $\lim_\limits{x \to 0} f(|x|) = \lim_\limits{x \to 0^+} f(x).$
  • Usando la definición épsilon-delta de límite por la derecha, prueba que $\lim_{x \to 8^+} \sqrt{x-8} = 0.$
  • Calcula el límite en $x_0 = 5$ de la función
    $$f(x) =
    \begin{cases}
    \frac{x^2-12x+35}{x-5} & \quad \text{si } x < 5 \\
    \frac{x-5}{1- \sqrt{x-4} } & \quad \text{si } x \geq 5.
    \end{cases}
    $$
  • Usando límites laterales, determina si existe $$\lim_{x \to 0} \frac{3x + |x|}{7x-5|x|}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Definición formal de límite de una función

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Anteriormente revisamos una definición intuitiva del límite con la finalidad de facilitar la comprensión de la definición formal. En esta entrada se dará la definición formal, así como algunos ejemplos para que el concepto sea comprendido en su totalidad.

Definición formal de límite

Retomemos la idea intuitiva a la que llegamos al final de la entrada anterior: logramos que $f$ se aproxime arbitrariamente, $\varepsilon$, a $L$ siempre que logremos que $x$ esté lo suficientemente cerca, $\delta$, de $x_0$ sin ser $x_0.$

Observación. Notemos que la última parte la podemos expresar como $0<|x-x_0|< \delta$, pues al pedir que la distancia entre $x$ y $x_0$ sea mayor que $0$ se captura la idea de que $x \neq x_0$.

Es importante resaltar que estamos dando por hecho que se puede evaluar la función $f$ en valores de $x$ cercanos a $x_0$. Es por ello que se presenta la siguiente definición.

Definición. Sea $ A \subset \mathbb{R}$. Un punto $x_0 \in \mathbb{R}$ es un punto de acumulación de $A$ si para todo $\delta > 0$ existe al menos un punto $x \in A$, $x \neq x_0$, tal que $|x-x_0| < \delta$.

Dada la definición anterior, si consideramos una función $f: A \to \mathbb{R}$, para calcular el límite, y asegurar que podemos evaluar $f$ en valores $x$ cercanos a $x_0$, deberemos pedir que $x_0$ sea punto de acumulación del dominio de la función, $A$. Con esto, tenemos todos los elementos para dar la definición de límite.

Definición. Sean $A \subset \mathbb{R}$ y $x_0$ un punto de acumulación de $A$. Para una función $f: A \to \mathbb{R}$, decimos que $L$ es el límite de $f$ en $x_0$ si para todo $\varepsilon > 0$ existe algún $\delta > 0$ tal que, para todo $x \in A$, si $0<|x-x_0|< \delta$, entonces $|f(x)-L|< \varepsilon.$

A continuación tenemos una imagen que nos permitirá visualizar la definición:

En la imagen podemos ver que si definimos un valor arbitrario $\varepsilon >0$, entonces lo que buscamos es un valor positivo $\delta$, tal que si $x$ está a una distancia menor que $\delta$ con respecto a $x_0$, entonces eso implique que $f(x)$ esté a una distancia menor que $\varepsilon$ con respecto a $L.$


A continuación revisaremos un ejemplo sencillo aplicando la definición.

Ejemplo 1. Demuestra que $$\lim_{x \to -1} \frac{x^2-5x-6}{x+1} = -7.$$

Demostración.
Sea $\varepsilon >0$. Notemos que si $x \neq -1$, entonces

\begin{align*}
\left\lvert \frac{x^2-5x-6}{x+1} – (-7) \right\rvert & = \left\lvert \frac{x^2-5x-6}{x+1} +7 \right\rvert \\ \\
& = \left\lvert \frac{x^2-5x-6+7x+7}{x+1} \right\rvert \\ \\
& = \left\lvert \frac{x^2+2x+1}{x+1} \right\rvert \\ \\
& = \left\lvert \frac{(x+1)^2}{x+1} \right\rvert \\ \\
& = \left\lvert x+1 \right\rvert.
\end{align*}
Tomemos entonces $\delta = \varepsilon$. Si $0<|x- (-1) | = |x+1 |< \delta$, entonces
$$\left\lvert \frac{x^2-5x-6}{x+1} – (-7) \right\rvert = \left\lvert x+1 \right\rvert < \delta = \varepsilon.$$
$$\therefore \left\lvert \frac{x^2-5x-6}{x+1} – (-7) \right\rvert < \varepsilon.$$
$$\therefore \lim_{x \to -1} \frac{x^2-5x-6}{x+1} = -7.$$

$\square$

Hagamos algunos comentarios respecto a la demostración. Como primer paso, establecimos un valor arbitrario positivo para $\varepsilon$. Después hicimos algunas manipulaciones algebraicas que nos permitieron simplificar la expresión original en una más simple con la cual logramos encontrar el valor de $\delta$ que sería útil, en este caso, ese valor fue justamente el mismo que $\varepsilon$.

Revisemos un segundo ejemplo.

Ejemplo 2. Sea $f(x) = \frac{3x+1}{2x}$, entonces $$\lim_{x \to 2} f(x) = \frac{7}{4}.$$

Demostración.

Sea $\varepsilon > 0$. Veamos que

\begin{align*}
\left\lvert f(x) – \frac{7}{4}\right\rvert & = \left\lvert \frac{3x+1}{2x} – \frac{7}{4} \right\rvert \\ \\
& = \left\lvert \frac{6x+2-7x}{4x} \right\rvert \\ \\
& = \left\lvert \frac{2-x}{4x} \right\rvert \\ \\
& = \frac{|2-x|}{|4x|} \\ \\
& = \frac{|x-2|}{|4x|} \\ \\
& = \frac{1}{|4x|} \cdot |x-2|.
\end{align*}

De lo anterior, se sigue que
\begin{align*}
\left\lvert f(x) – \frac{7}{4}\right\rvert = \frac{1}{|4x|} \cdot |x-2|. \tag{1}
\end{align*}

Buscamos entonces acotar la expresión $(1)$, para ello podemos ver lo siguiente, si $|x-2| < 1$, entonces

\begin{gather*}
& |2|-|x| \leq |x-2| < 1.
\end{gather*}

De lo anterior, se sigue que

\begin{gather*}
& |2|-|x| < 1. \\
\Leftrightarrow & 2-1 < |x|. \\
\Leftrightarrow & 1 < |x|. \\
\Leftrightarrow & 1 >\frac{1}{|x|}. \\
\Leftrightarrow & \frac{1}{4} >\frac{1}{4|x|} = \frac{1}{|4x|}. \\
\end{gather*}

Por tanto, se tiene que

\begin{align*}
\frac{1}{|4x|} < \frac{1}{4}. \tag{2}
\end{align*}

Entonces si $|x-2| < 1$, por (1) y (2), tenemos lo siguiente
\begin{align*}
\left\lvert f(x) – \frac{7}{4}\right\rvert & = \frac{1}{|4x|} \cdot |x-2| \\ \\
& < \frac{1}{4} \cdot |x-2|.\\
\end{align*}

Previamente acotamos $|x-2|$ por el valor $1$, pero de la última expresión se sigue que deberemos acotarlo también por $4 \varepsilon$ para llegar a nuestro objetivo, tomemos así $\delta = min\{1, 4 \varepsilon\}.$


Si $0<|x- 2| \leq \delta$. Es decir, si $|x- 2| \leq 1$ y $|x- 2| \leq 4\varepsilon$, entonces
$$\left\lvert f(x) – \frac{7}{4}\right\rvert < \frac{1}{4} |x-2| \leq \frac{1}{4} \cdot 4\varepsilon.$$
$$ \therefore \left\lvert f(x) – \frac{7}{4}\right\rvert < \varepsilon.$$

$\square$

Nuevamente haremos énfasis en los pasos generales de la demostración. Iniciamos dando un valor de $\varepsilon$ arbitrario, y la tarea es encontrar el valor $\delta >0$ que acote la distancia entre $x$ y $x_0 = 2$ de tal manera que los valores de la función $f$ se aproximen a $L$ lo suficiente para que su distancia sea menor que $\varepsilon.$

Trabajemos ahora sobre el siguiente ejemplo.

Ejemplo 3. Para todo $x_0 \in \mathbb{R}$ se tiene que $$\lim_{x \to x_0} x^2 = x_0^2.$$

Demostración.

Sea $\varepsilon > 0$ y $x_0 \in \mathbb{R}$. Notemos que

$|x^2 – x_0^2| = |x-x_0||x+x_0|.$

Haciendo uso de una manipulación análoga al del ejemplo anterior, podemos ver que si $|x-x_0| < 1$, entonces

$|x|-|x_0| \leq |x-x_0| < 1 \quad \Rightarrow \quad |x| < 1 + |x_0|.$

Cabe resaltar que en el ejemplo anterior usamos la propiedad $|x_0|-|x| \leq |x-x_0|$, ya que la intención es acotar al recíproco de $x$. En este caso, se emplea $|x|-|x_0| \leq |x-x_0|$, puesto que buscamos acotar directamente a $x$.

Además,
\begin{align*}
|x + x_0| & \leq |x|+ |x_0| \\
& < 1 + |x_0|+|x_0| \text{, pues} \quad |x| < 1 + |x_0| \\
& = 1 + 2|x_0|.
\end{align*}

Así, tenemos que $$ |x + x_0| < 1 + 2|x_0|.$$

En esta ocasión queremos que $|x-x_0| < 1$ y, por la última expresión, también queremos que $|x-x_0| <\frac{\varepsilon}{1+2|x_0|}$, definimos así $\delta = min \{ 1, \frac{\varepsilon}{1+2|x_0|} \}$. Si $0 < |x-x_0| < \delta$, entonces

\begin{align*}
|x^2-x_0^2| & = |x-x_0||x+x_0| \\ \\
& < |x-x_0|(1+2|x_0|) \\ \\
& < \delta (1+2|x_0|) \\ \\
& \leq \frac{\varepsilon}{1+2|x_0|} \cdot (1+2|x_0|)\\ \\
& = \varepsilon.
\end{align*}

Esto implica que
$$|x^2-x_0^2| < \varepsilon.$$
$$\therefore \lim_{x \to x_0} x^2 = x_0^2.$$

$\square$

Unicidad del límite de una función

Después de haber revisado estos ejemplos, la definición de límite de una función (también llamada definición épsilon-delta), estamos listos para revisar la primera propiedad del límite.

Proposición. El límite de una función en $x_0$ es único, es decir, si $f$ tiende a $L$ en $x_0$ y $f$ tiende a $L’$ en $x_0$, entonces $L = L’.$


Demostración.
Sea $\varepsilon > 0$. Como $f$ tiende a $L$ y $L’$ en $x_0$, entonces para $\frac{\varepsilon}{2} > 0$ existen $\delta_1  > 0$ y $\delta_2 > 0$ tales que

\begin{gather*}
\text{Si } 0<|x-x_0|<\delta_1 \quad \Rightarrow \quad |f(x)-L| < \frac{\varepsilon}{2}. \\
\text{Si } 0<|x-x_0|<\delta_2 \quad \Rightarrow \quad |f(x)-L’| < \frac{\varepsilon}{2}. \\
\end{gather*}

Consideremos ahora $\delta = min\{\delta_1, \delta_2 \}$. Entonces si $0<|x-x_0|<\delta$ y, por la desigualdad del triángulo, esto implica que

\begin{align*}
|L-L’| \leq & |L-f(x)|+|L’-f(x)| \\
< & \frac{\varepsilon}{2} + \frac{\varepsilon}{2} \\
= & \varepsilon.
\end{align*}

Se sigue que

$|L-L’| < \varepsilon.$


Como $\varepsilon$ es un valor arbitrario positivo, podemos concluir que $L-L’ = 0$, es decir, $L=L’.$

$\square$

Más adelante…

En la siguiente entrada revisaremos con detalle varias propiedades que tienen los límites para lo cual haremos uso de una bella relación existente entre el límite de una sucesión y el de una función. Una vez revisadas estas propiedades, el cálculo de los límites se hará considerablemente más simple.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Usando la definición épsilon-delta, demuestra lo siguiente:

  • $$\lim_{x \to x_0} c = c.$$
  • $$\lim_{x \to x_0} x = x_0.$$
  • $$\lim_{x \to 5} x+11 = 16.$$
  • $$\lim_{x \to -2c} (2c-3x) = 8c.$$
  • $$\lim_{x \to 0} \frac{x^2}{|x|} = 0.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»