Archivo de la etiqueta: bisectriz

Geometría Moderna I: Puntos notables del triángulo

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada estudiamos la concurrencia de rectas importantes en el triangulo, a saber, las medianas, mediatrices, bisectrices y alturas. Mencionamos también consecuencias inmediatas de los puntos de concurrencia.

Centroide

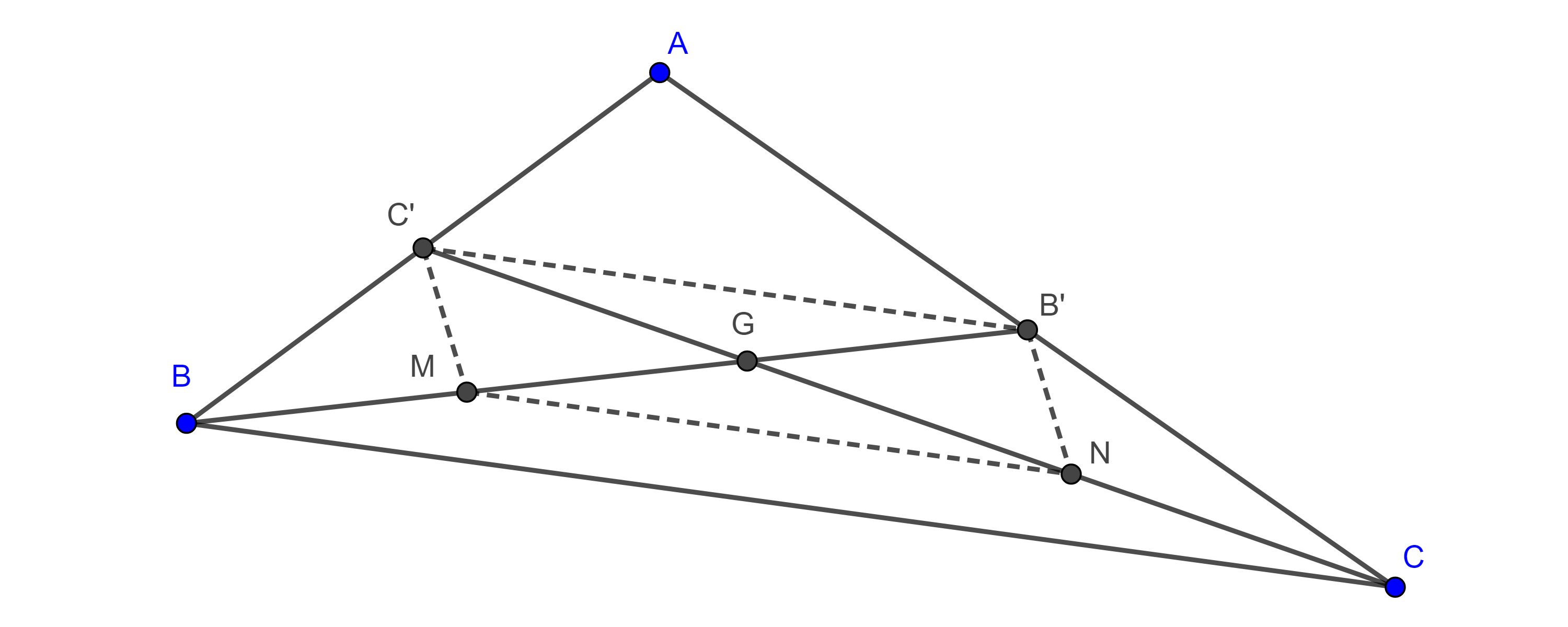
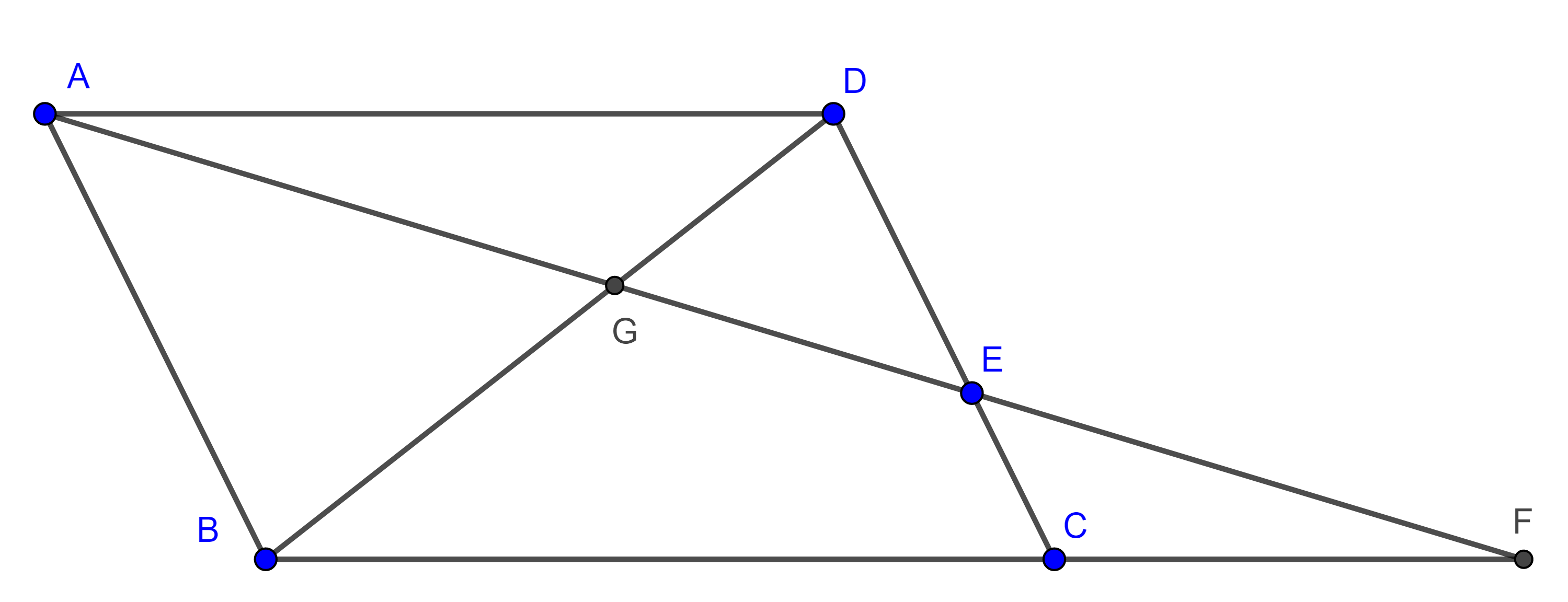
Teorema 1. Las medianas de todo triángulo concurren en un punto que las triseca.

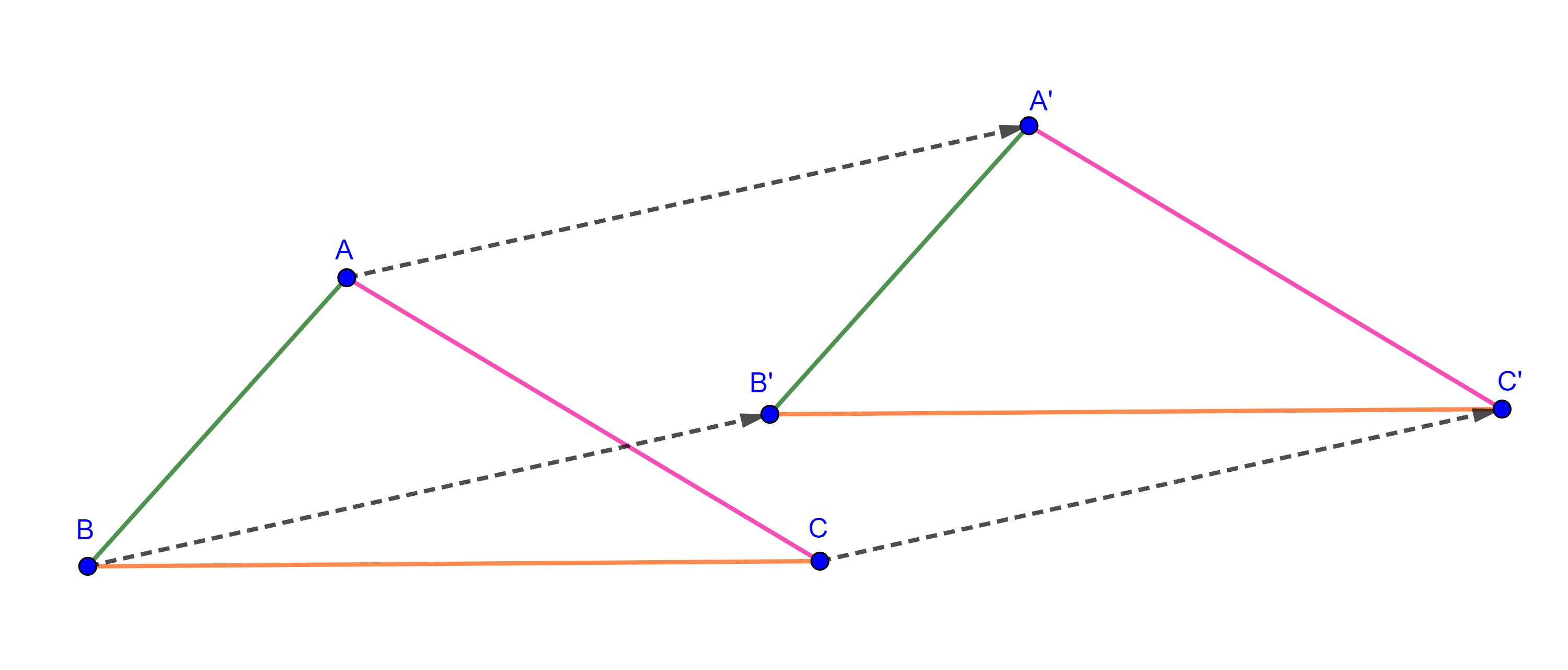
Demostración. Sean $\triangle ABC$, $B’$ y $C’$ los puntos medios de $AC$ y $AB$ respectivamente, por el teorema del segmento medio sabemos que $C’B’ = \dfrac{BC}{2}$ y $C’B’ \parallel BC$.

Figura 1

Sea $G$ la intersección de las medianas $BB’$ y $CC’$, en $\triangle GBC$ consideremos $M$ y $N$ los puntos medios de los lados $GB$ y $GC$ respectivamente, entonces
$MN = \dfrac{BC}{2}$ y $MN \parallel BC$.

Por transitividad $C’B’ = MN$ y $C’B’ \parallel MN$, esto implica que $\square C’MNB’$ es un paralelogramo y por lo tanto sus diagonales se bisecan, es decir,
$C’G = GN$ y $MG = GB’$.

Por construcción, $MG = BM$ y $GN = NC$
$\Rightarrow GB’= \dfrac{BB’}{3}$ y $C’G = \dfrac{CC’}{3}$,
esto es, la medianas $BB’$ y $CC’$ se trisecan

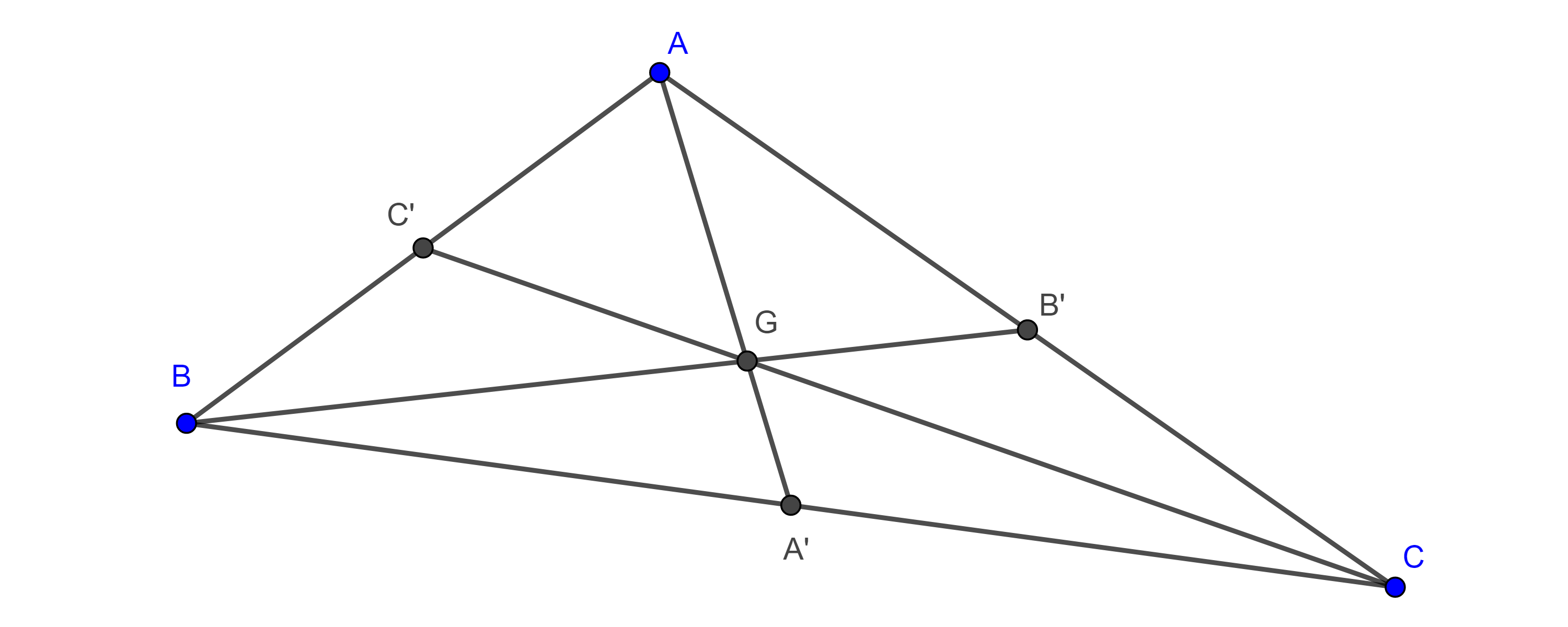
Si repetimos el mismo procedimiento pero ahora con las medianas $AA’$ y $BB’$ encontraremos un punto $G’$ en donde las medianas se trisecaran, $G’B’= \dfrac{BB’}{3}$ y $G’A’ = \dfrac{AA’}{3}$.

Como $GB’= \dfrac{BB’}{3} = G’B’$, concluimos que $G’ = G$.

Por lo tanto, las medianas de un triángulo concurren en un punto que las triseca.

$\blacksquare$

Definición 1. Decimos que el punto en que concurren las medianas de un triángulo es el gravicentro, baricentro o centroide del triángulo y lo denotamos con la letra $G$ mayúscula.

Figura 2

Circuncentro

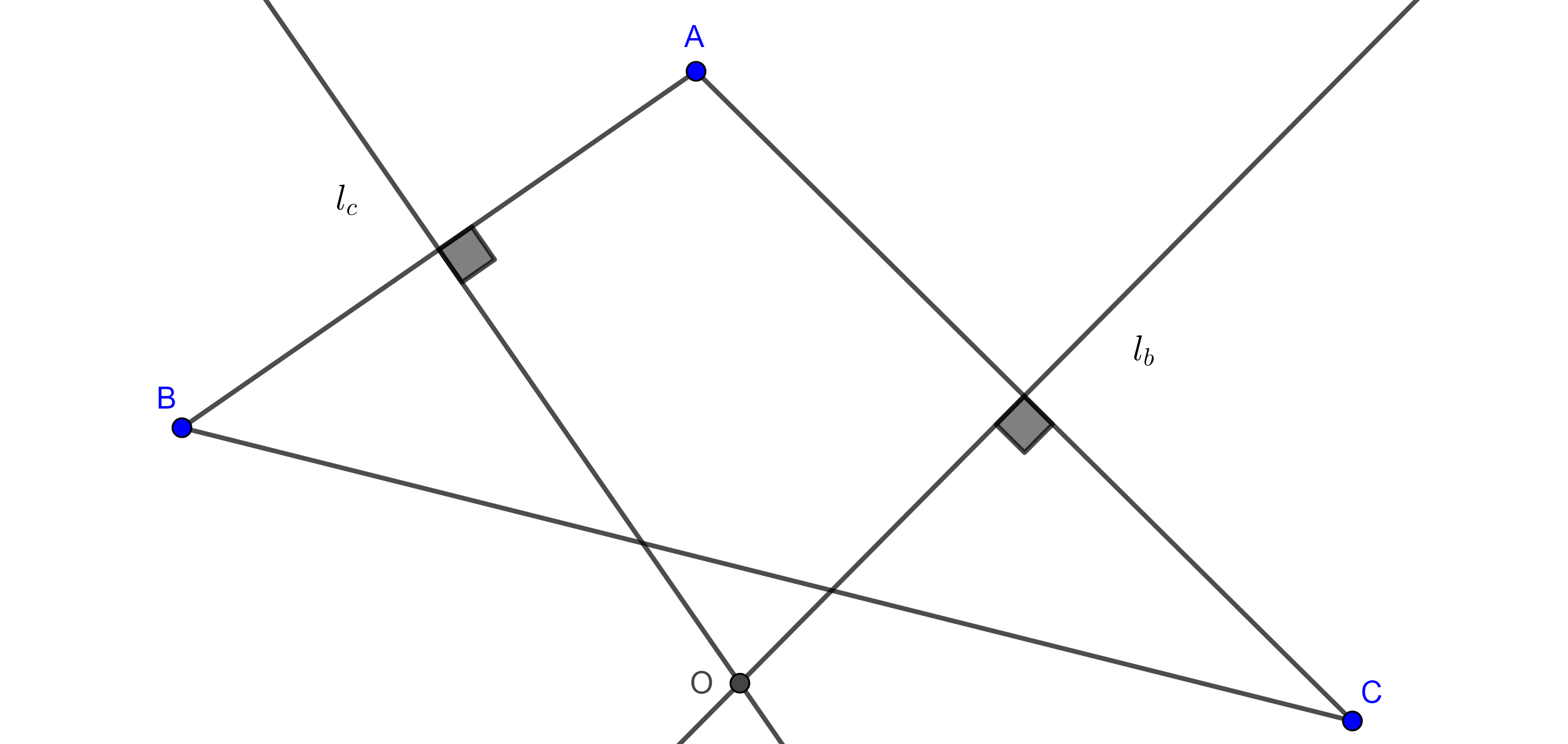
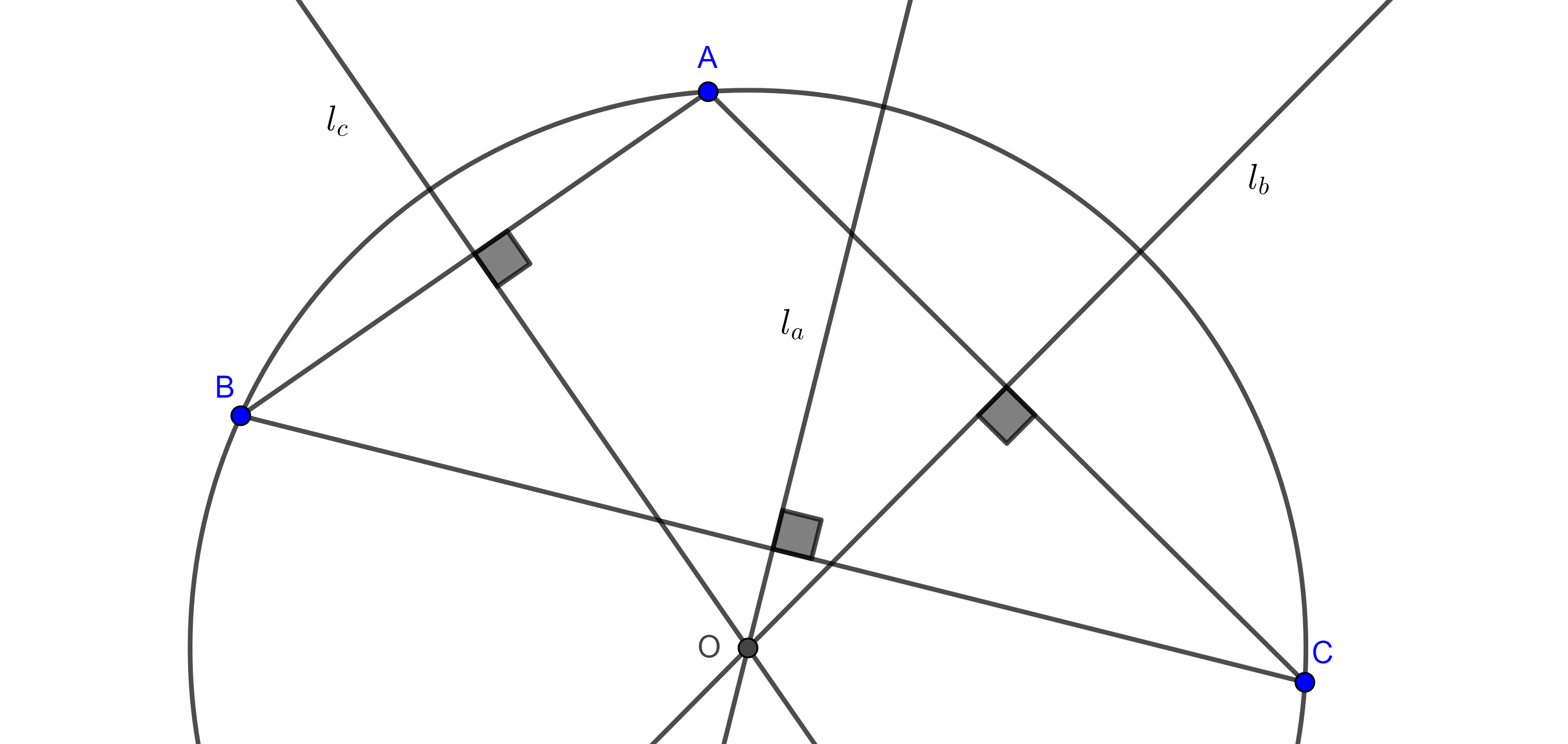
Teorema 2. Las mediatrices de los lados de todo triángulo son concurrentes.

Demostración. Sea $\triangle ABC$, consideremos las mediatrices $l_c$ y $l_b$ de $AB$ y $AC$ respectivamente y $O = l_b \cap l_c$.

Figura 3

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la mediatriz de un segmento si y solo si equidista a los puntos extremos del segmento.

Ya que $O \in l_c$ y $O \in l_b$, entonces $OA = OB$ y $OA = OC$
$\Rightarrow OB = OC$.

Por el resultado mencionado anteriormente $OB = OC$ implica que $O \in l_a$, la mediatriz de $BC$.

Por lo tanto, las mediatrices de un triángulo son concurrentes.

$\blacksquare$

Corolario. Tres puntos distintos y no colineales se encuentran en una única circunferencia.

Demostración. Sea $\triangle ABC$, por el teorema anterior las mediatrices de los segmentos determinados por los vértices del triángulo concurren en un punto $O$ cuya distancia a cada uno de los vértices es la misma $R = OA = OB = OC$.

Por definición de circunferencia, $A$, $B$ y $C$ pertenecen a la circunferencia con centro en $O$ y radio $R$, $A$, $B$, $C \in (O, R) = \Gamma$.

Ahora supongamos que existe $\Gamma’ = (O’, R’)$ tal que $A$, $B$, $C \in \Gamma’$, entonces, por definición, $O’A = O’B = O’C = R’$.

Esto implica que $O’ \in l_a$, $O’ \in l_b$ y $O’ \in l_c$, las mediatices de $BC$, $AC$ y $AB$ respectivamente,
$\Rightarrow O \in l_a \cap l_b \cap l_c$.

Como ya probamos que las mediatrices son concurrentes entonces $O’ = O$ y $R’ = R$, así que $\Gamma$ es única.

$\blacksquare$

Definición 2. Al punto de concurrencia de las mediatrices de los lados de un triángulo le llamamos circuncentro y lo denotamos como $O$.

A la distancia constante de $O$ a los vértices del triángulo le llamamos circunradio denotado con la letra $R$ mayúscula.

A la circunferencia única $(O, R)$ determinada por los vértices del triángulo se le conoce como circuncírculo.

Figura 4

Incentro

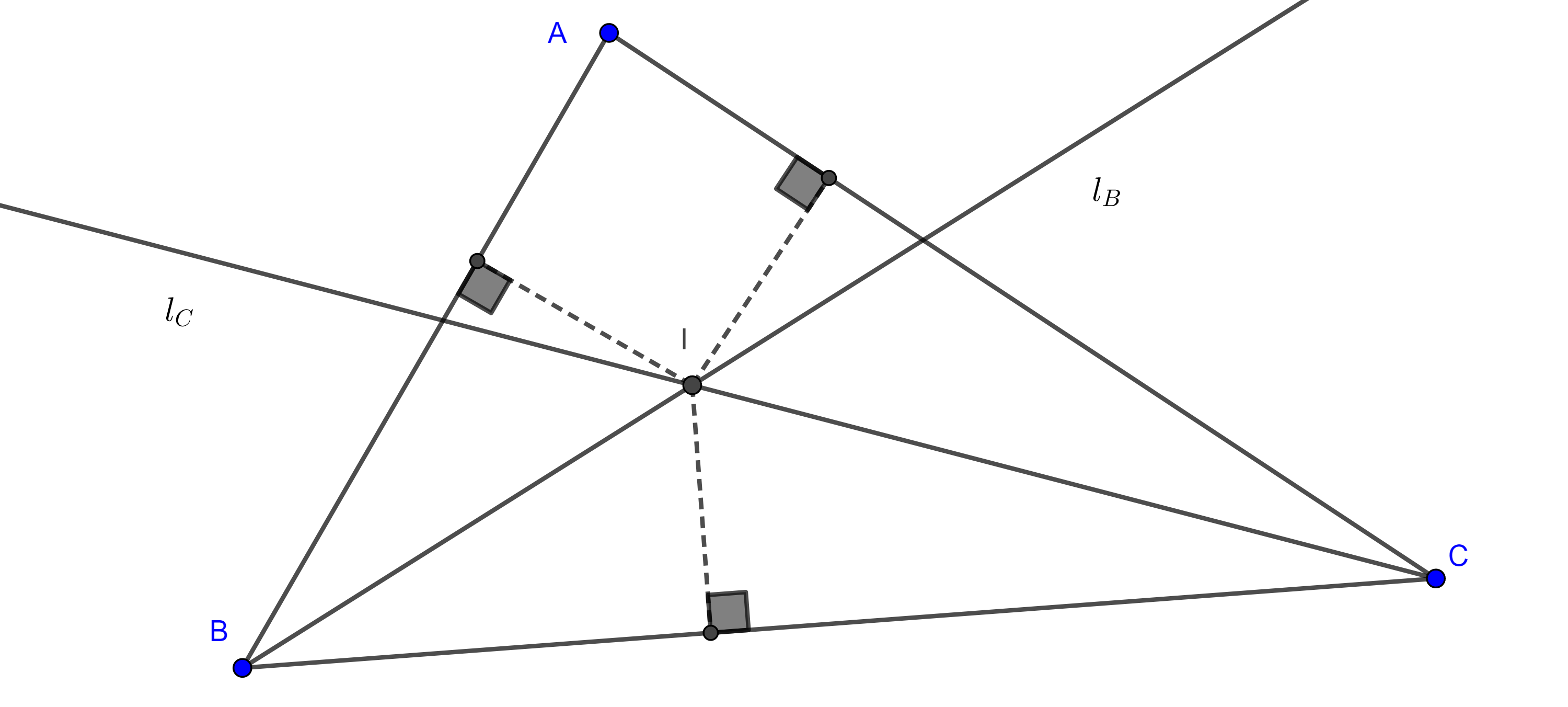
Teorema 3. Las bisectrices interiores de todo triángulo son concurrentes.

Demostración. Sean $l_B$ y $l_C$ las bisectrices de los ángulos interiores en $\angle B$ y $\angle C$ respectivamente e $I = l_{B} \cap l_{C}$.

Figura 5

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la bisectriz de un ángulo si y solo si equidista a los lados que forman el ángulo. Recordemos que la distancia de un punto a una recta es la longitud del punto al pie de la perpendicular a la recta trazada desde el punto.

Denotamos la distancia de un punto $P$ a una recta $l$ como $(P, l)$.

Como $I \in l_{b}$ e $I \in l_{c}$, entonces $(I, AB) = (I, BC)$ y $(I, BC) = (I, AC)$,
$\Rightarrow (I, AB) = (I, AC)$.

Por el resultado citado anteriormente, $(I, AB) = (I, AC)$ implica que $I \in l_A$, la bisectriz interior de $\angle A$.

Por tanto, las bisectrices interiores de un triángulo son concurrentes.

$\blacksquare$

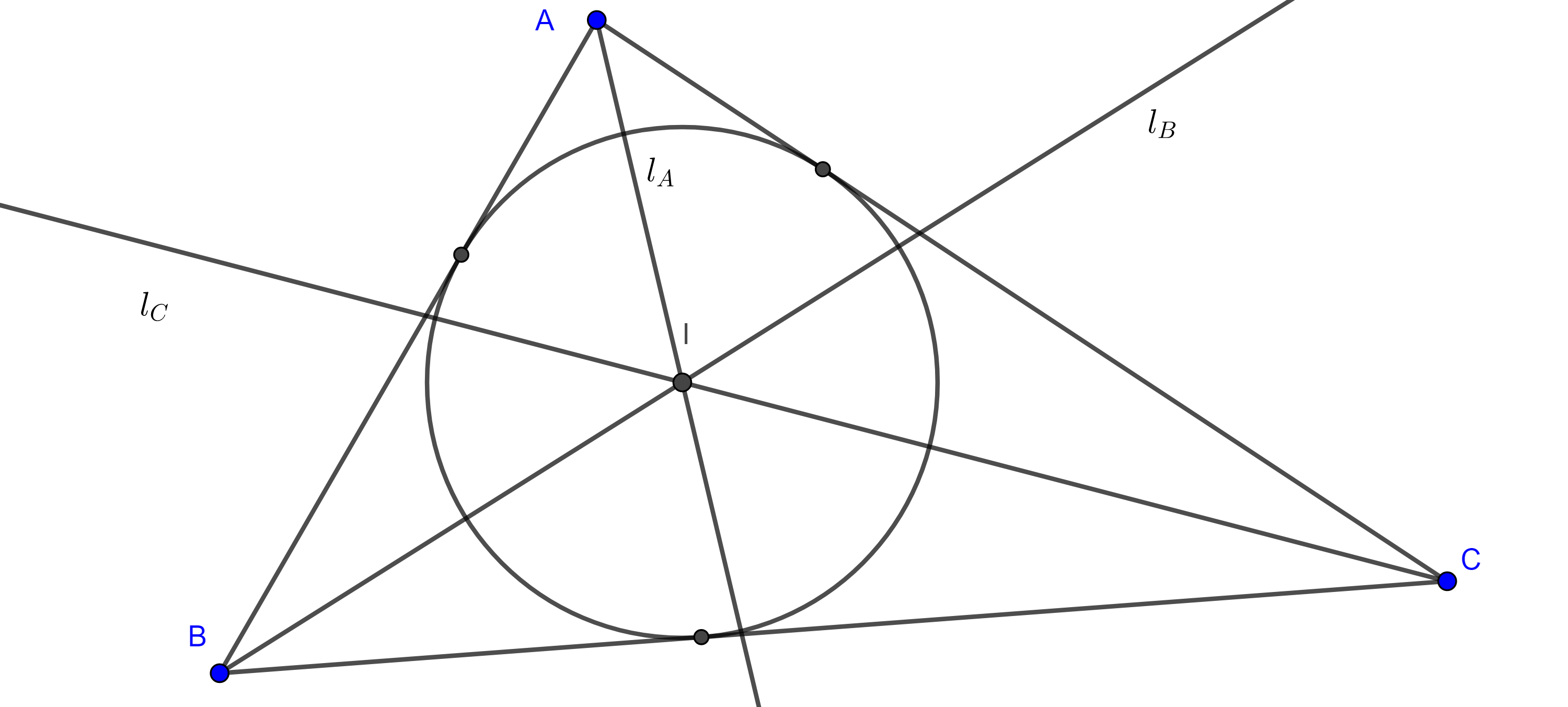
Si consideramos los pies de las perpendiculares a los lados del triángulo trazados desde el punto en que concurren las bisectrices, encontramos tres puntos distintos que equidistan a un punto fijo y por el corolario anterior estos determinan una única circunferencia, esto motiva la siguiente definición.

Definición 3. Al punto de concurrencia de las bisectrices interiores de un triángulo se le conoce como incentro del triángulo y lo denotamos con la letra $I$ mayúscula.

A la distancia de $I$ a los lados del triángulo le llamamos inradio y lo denotamos como $r = (I, AB) = (I, BC) = (I, AC)$.

La circunferencia con centro en $I$ y radio $r$, $(I, r)$, se llama incírculo.

Figura 6

Excentros

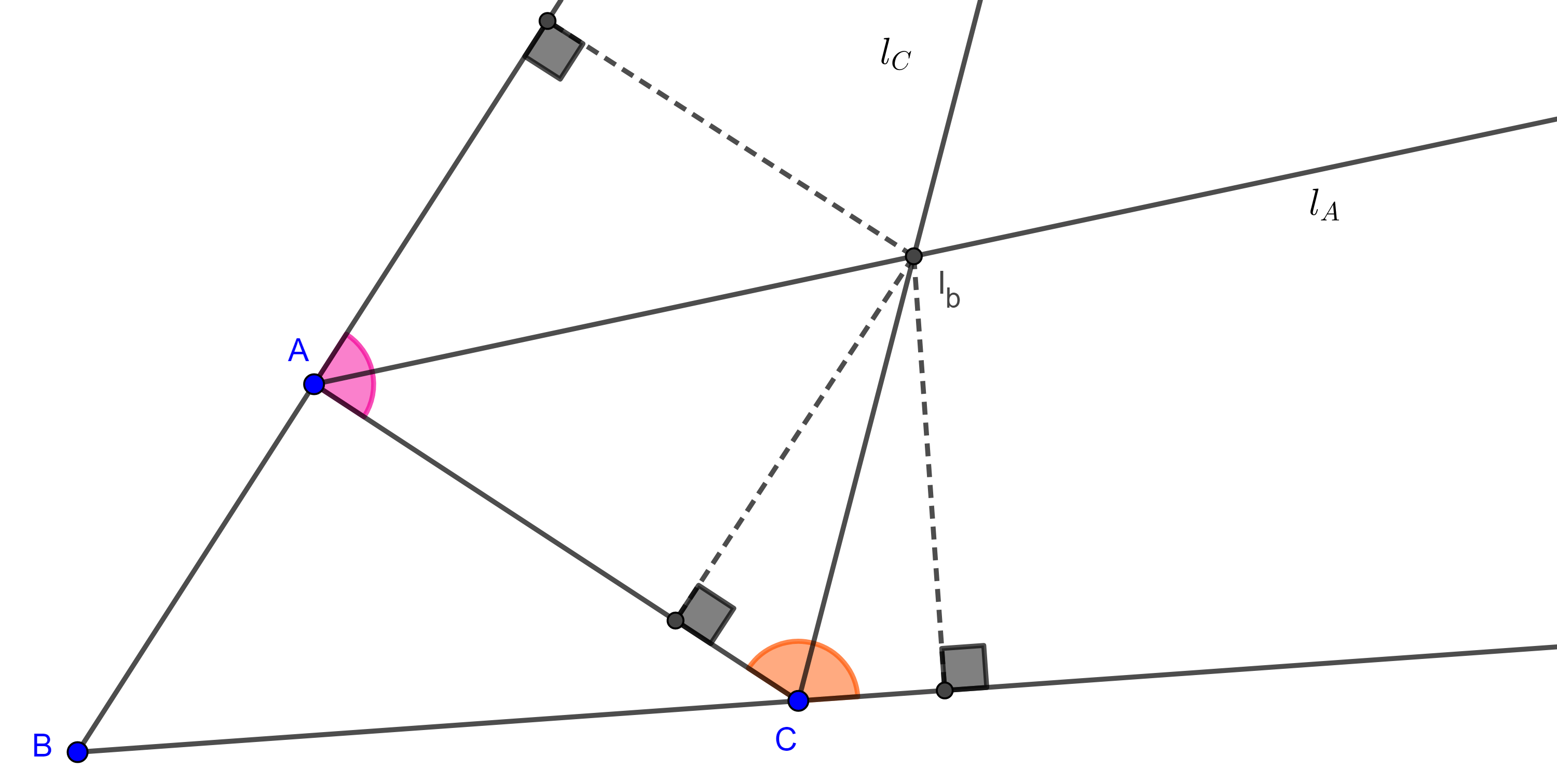
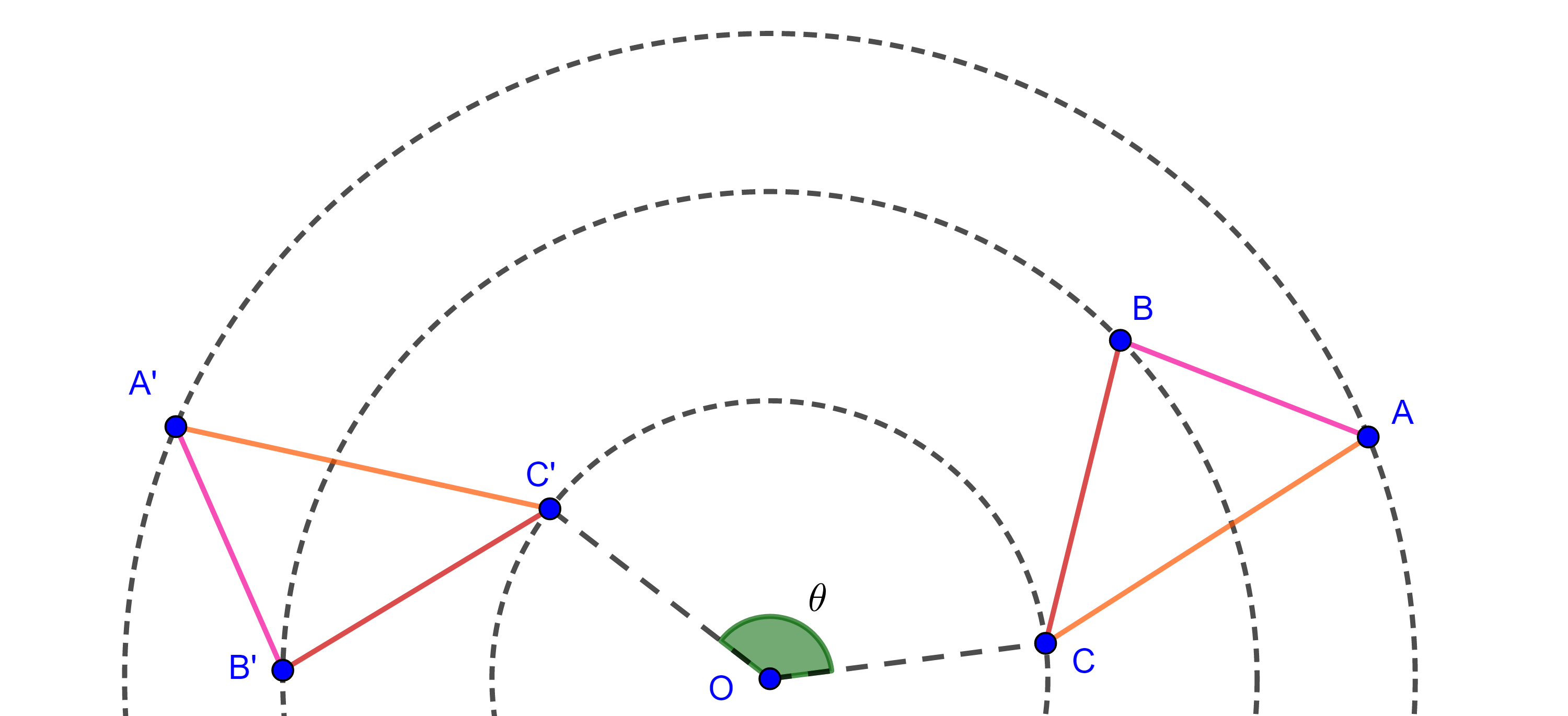
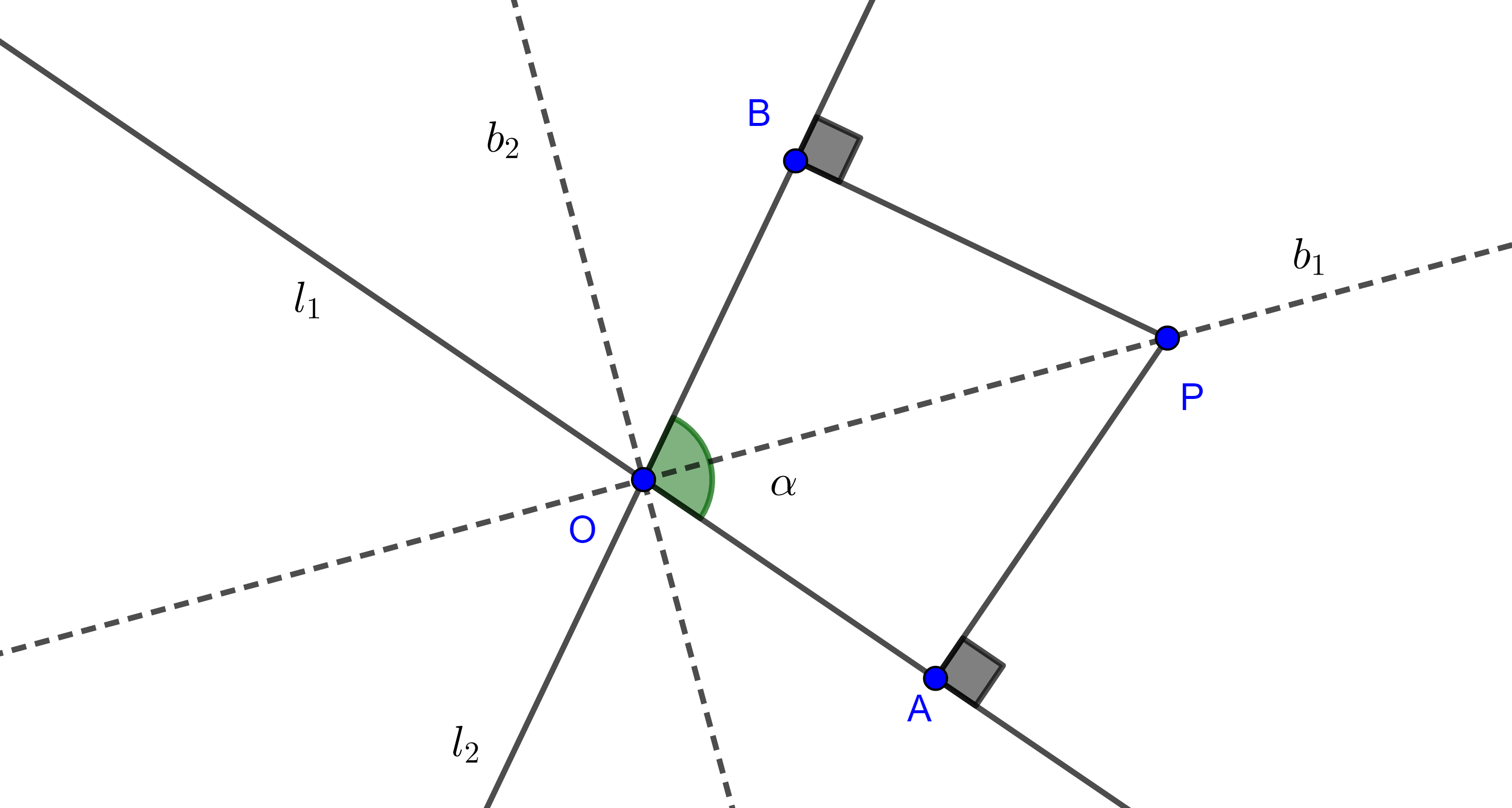
Teorema 4. En todo triángulo las bisectrices exteriores de dos ángulos y la bisectriz interior del tercer ángulo son concurrentes.

Demostración. Sea $\triangle ABC$, $l_A$ y $l_C$ las bisectrices exteriores de $\angle A$ y $\angle C$ respectivamente e $I_b = l_A \cap l_C$.

Figura 7

De manera análoga al caso de las bisectrices internas tenemos que
como $I_b \in l_A$ e $I_b \in l_C$, entonces $(I_b, AB) = (I_b, AC)$ y $(I_b, AC) = (I_b, BC)$,
$\Rightarrow (I_b, AB) = (I_b, BC)$.

Como $I_b$ está en la región acotada por el ángulo $\angle CBA$ entonces $I \in l_B$, la bisectriz interior de $\angle B$.

Por lo tanto, la bisectriz interna de $\angle B$ y las bisectrices externas de $A$ y $C$ son concurrentes.

De manera análoga probamos que las bisectrices externas de $\angle A$ y $\angle B$ concurren con la bisectriz interna de $\angle C$, y las bisectrices externas de $\angle B$ y $\angle C$ concurren con la bisectriz interna de $\angle A$.

$\blacksquare$

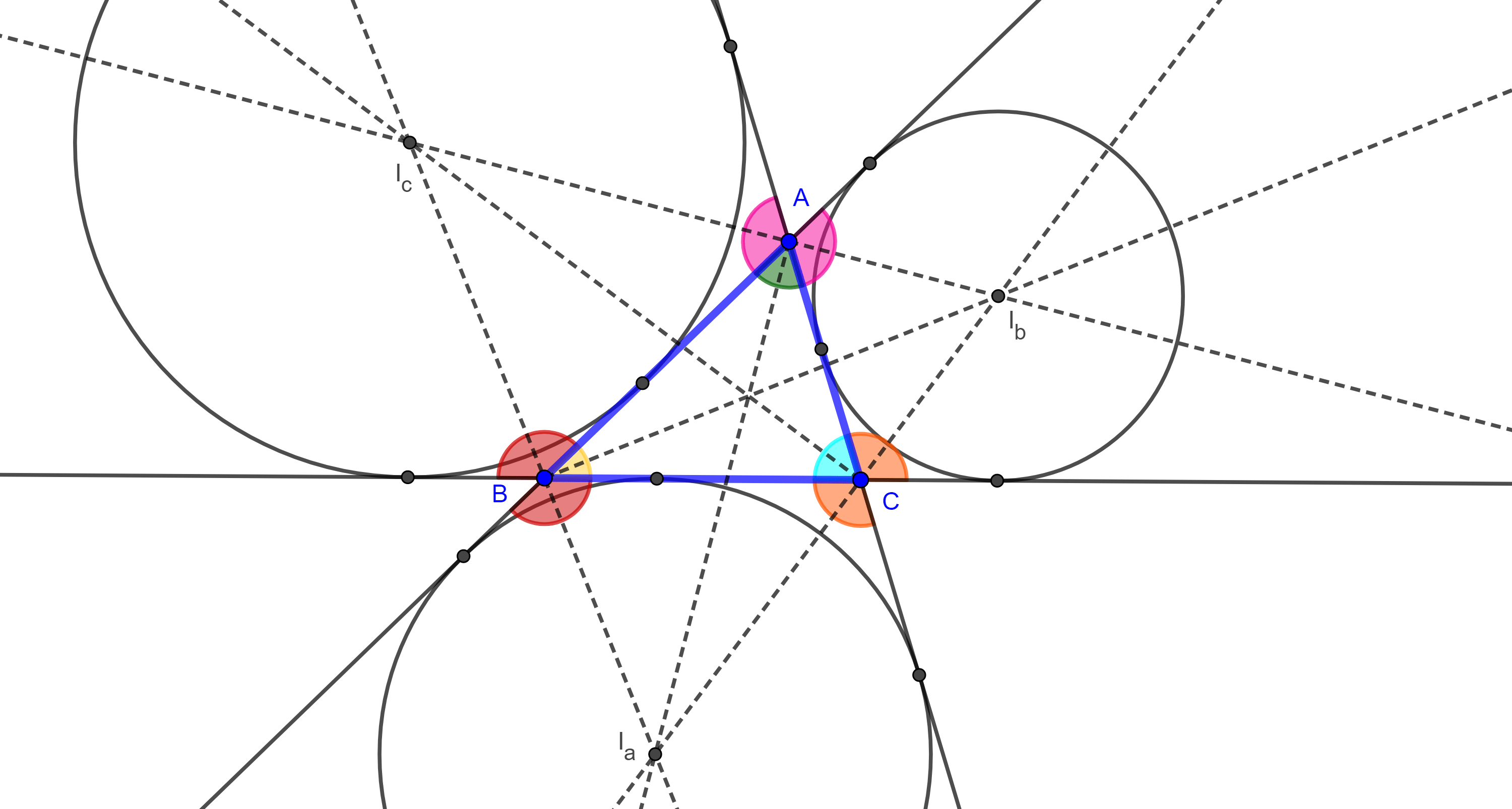
Similarmente a como lo hicimos con el incentro, notamos que, para cada uno de estos tres puntos de concurrencia, existen tres puntos distintos, uno en cada lado del triángulo que equidistan a un punto fijo y por lo tanto determinan una única circunferencia.

Definición 4. A los puntos en que concurren dos bisectrices externas y una bisectriz interna de un triángulo les llamamos excentros del triángulo y los denotamos como $I_a$, $I_b$ e $I_c$ de acuerdo a si se encuentran en la bisectriz interna de $\angle A$, $\angle B$ o $\angle C$ respectivamente y decimos que son opuestos a dichos vértices.

Las distancias de $I_a$, $I_b$ e $I_c$ a los lados del triángulo son los exradios y se les denota como $r_a$, $r_b$ y $r_c$ respectivamente.

A las circunferencias $(I_a, r_a)$, $(I_b, r_b)$ y $(I_c, r_c)$ se les conoce como excírculos del triángulo.

Figura 8

Ortocentro

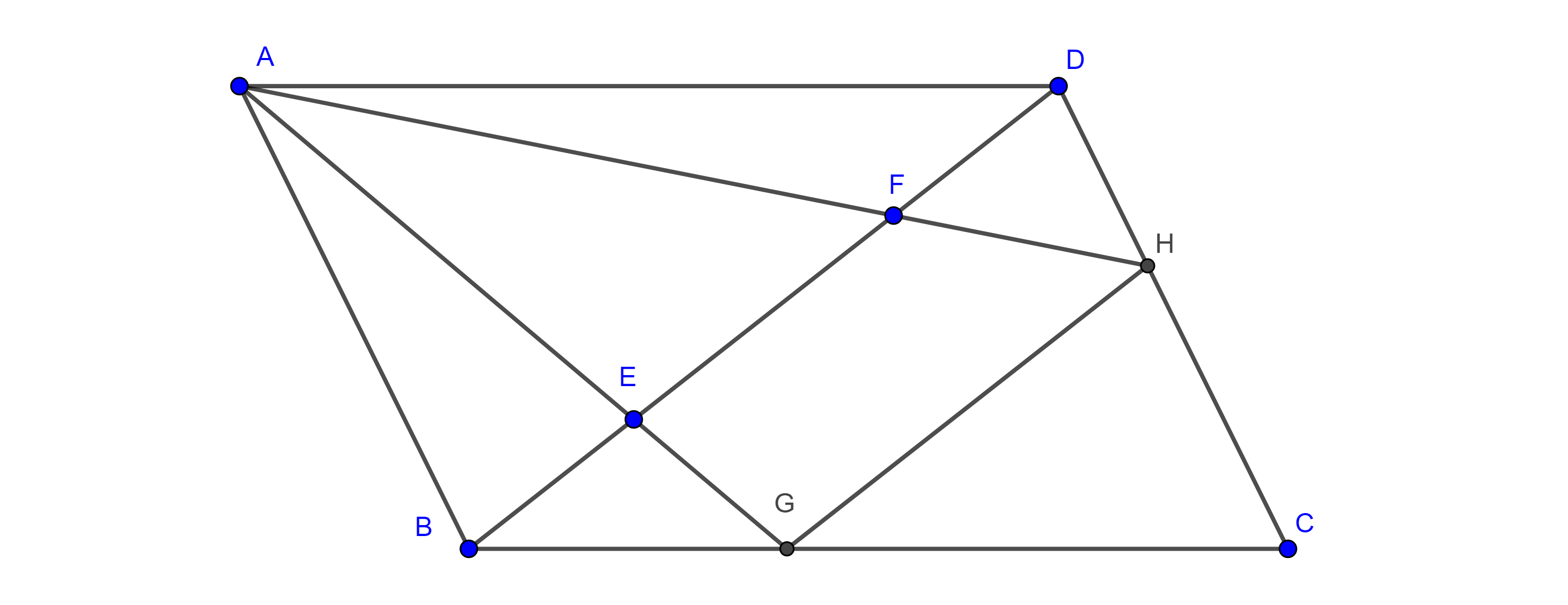
Teorema 5. Las alturas de todo triángulo son concurrentes.

Demostración. Sea $\triangle ABC$, tracemos en cada vértice la paralela al lado opuesto.

Sean $A’$ la intersección de la paralela a $AB$ trazada en $C$ con la paralela a $AC$ trazada en $B$, de manera análoga definimos $B’$ y $C’$.

Figura 9

Por construcción, $\square ABCB’$ es un paralelogramo por lo que $AB’ = BC$, también $\square C’BCA$ es paralelogramo así que $C’A = BC$,
$\Rightarrow AB’ = BC = C’A \Rightarrow A$ es el punto medio de $C’B’$.

De manera similar podemos ver que $B$ es el punto medio de $C’A’$ y $C$ es el punto medio de $A’B’$.

En consecuencia, las alturas del triángulo $\triangle ABC$ son las mediatrices del triángulo $\triangle C’A’B’$ y ya probamos que las mediatrices de los lados de todo triangulo son concurrentes, por lo tanto, las alturas de $\triangle ABC$ son concurrentes.

$\blacksquare$

Definición 5. Al punto en común en que las tres alturas de un triángulo se intersecan le llamamos ortocentro y lo denotamos con la letra $H$ mayúscula.

Figura 10

Más adelante…

En la siguiente entrada demostraremos algunos teoremas que nos permitirán calcular la magnitud de ángulos relativos a una circunferencia.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. ¿Qué puntos notables vistos en esta entrada, caen siempre dentro del triangulo y cuales siempre fuera?
  2. Muestra que una recta paralela a un lado de un triangulo a través del centroide divide el área del triangulo en dos partes tal que la razón de esta áreas es $\dfrac{4}{5}$.
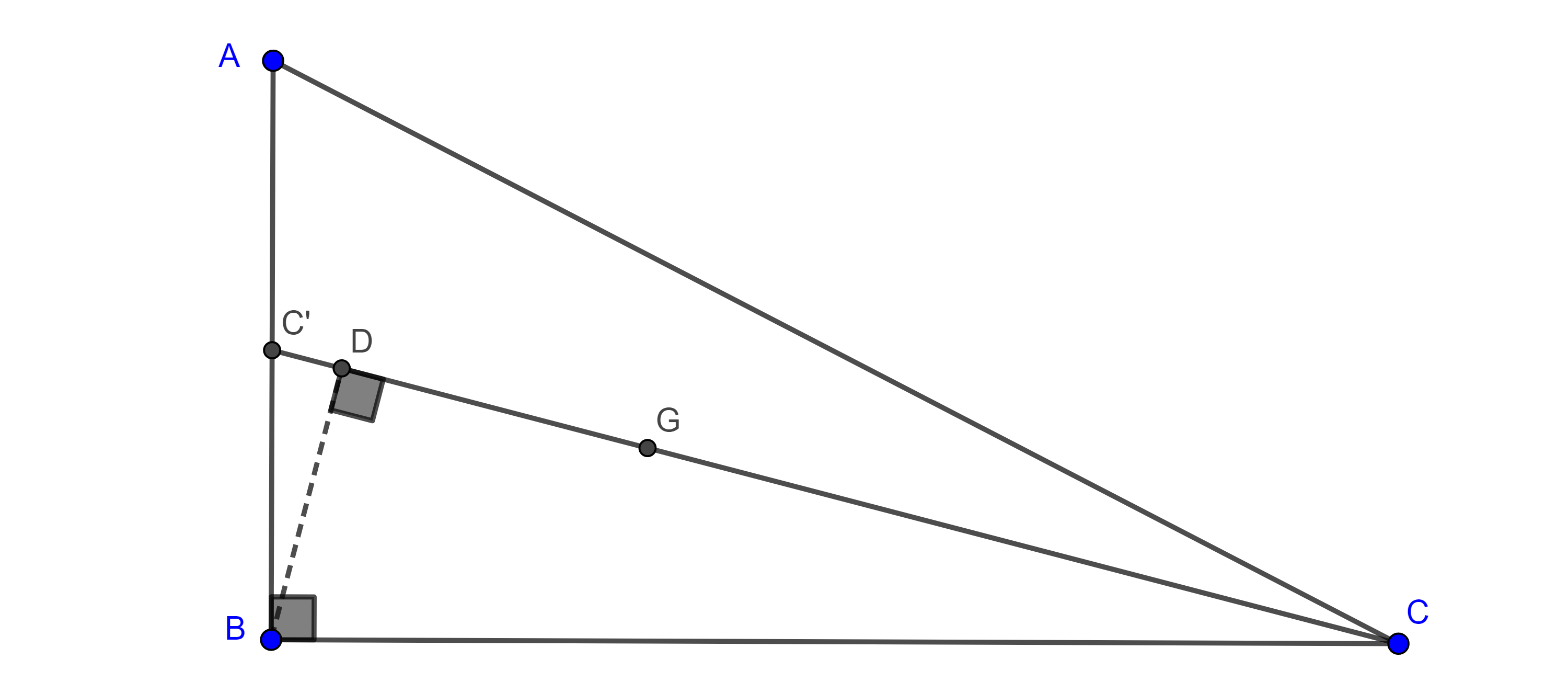
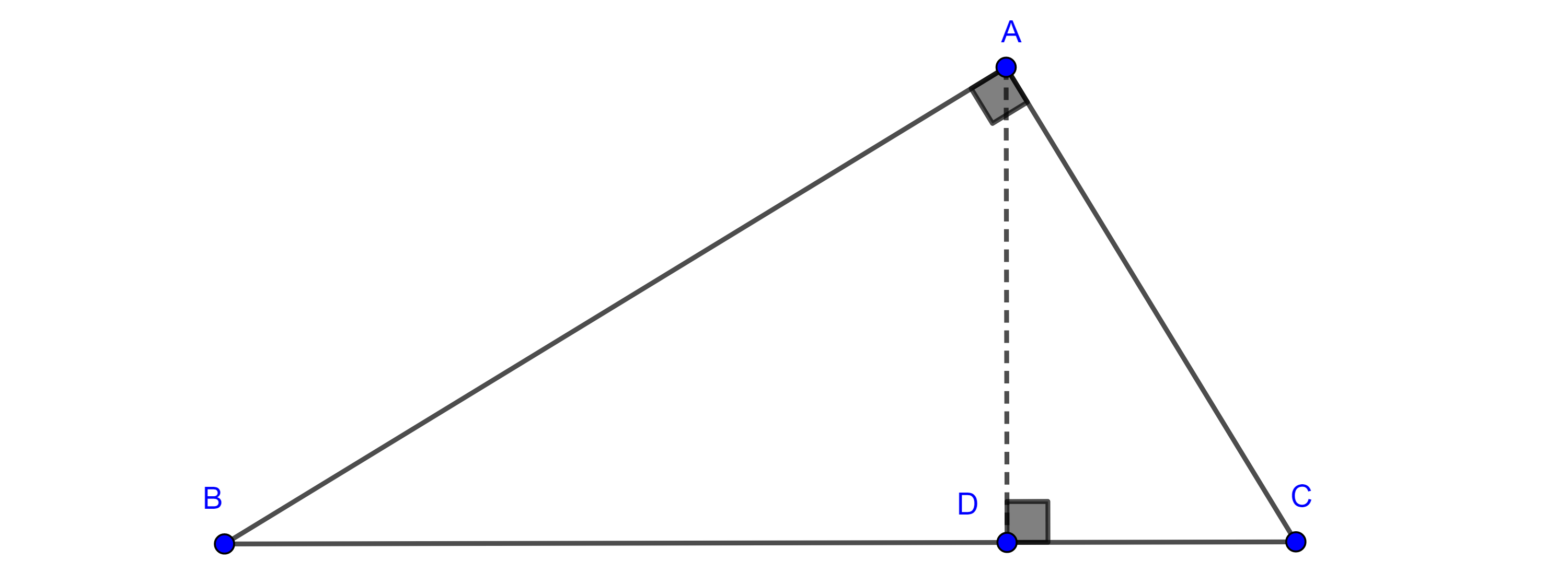
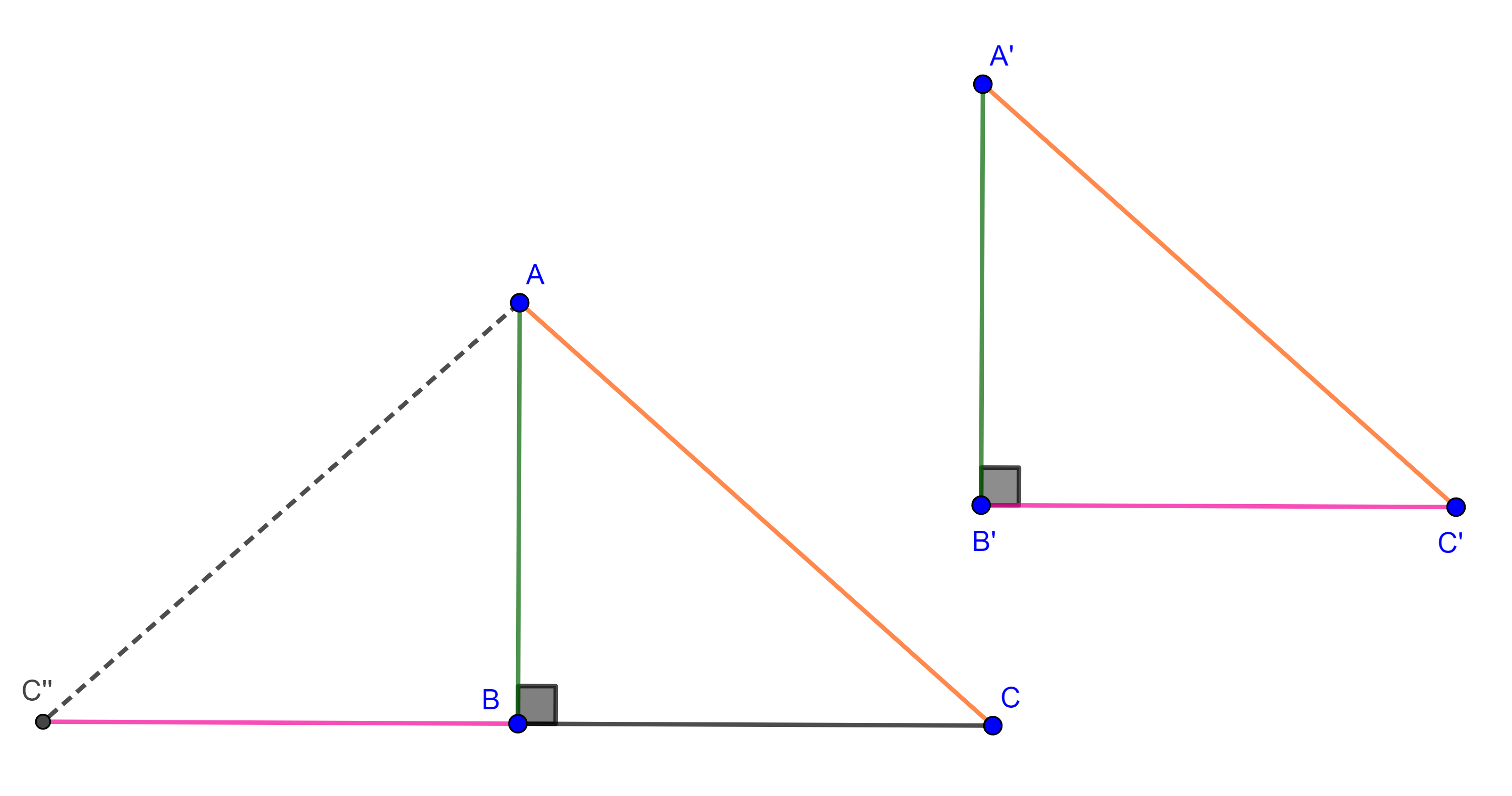
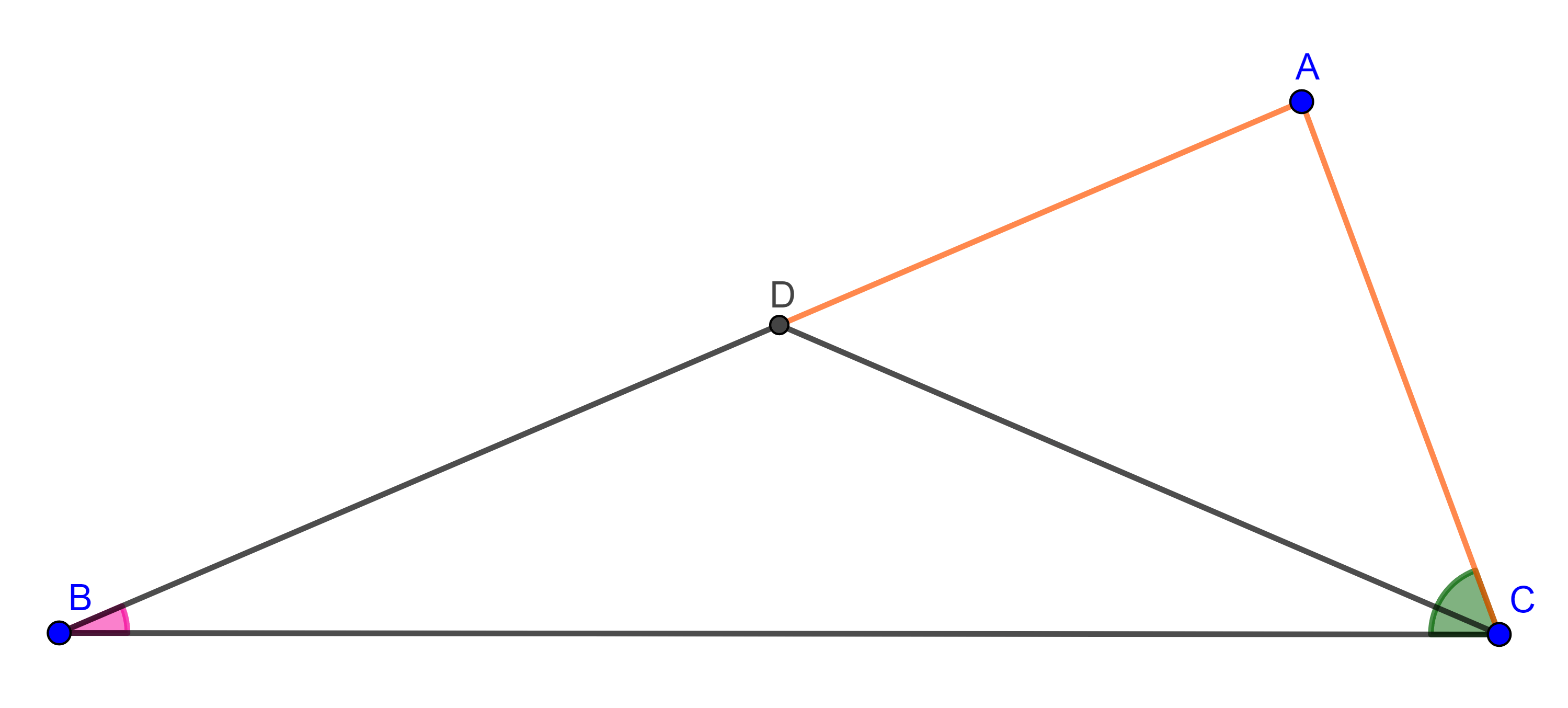
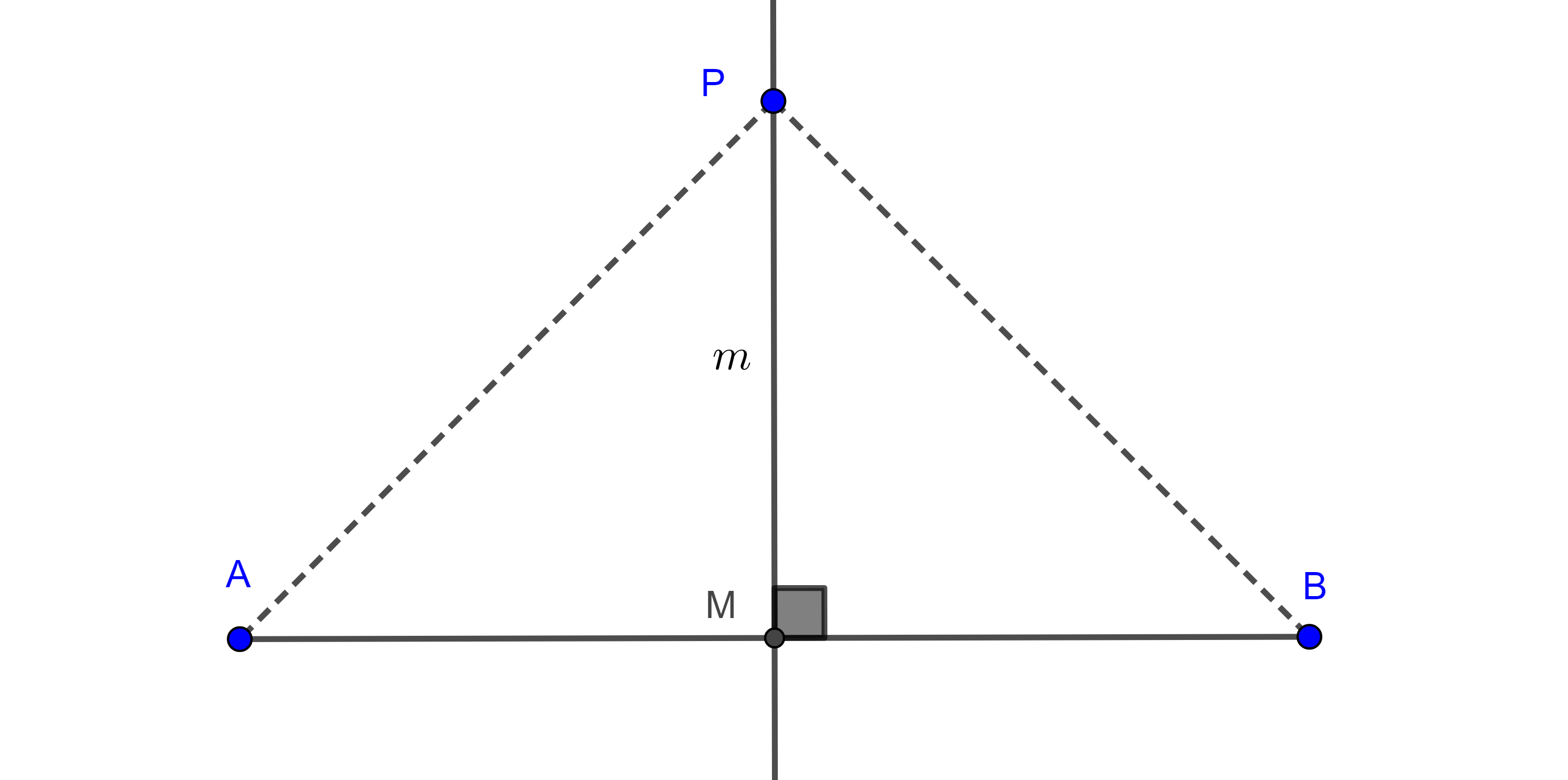
  3. Considera un triangulo rectángulo $\triangle ABC$ con $\angle B = \dfrac{\pi}{2}$, sean $CC’$ la mediana por $C$ y $D$ el pie de la perpendicular a $CC’$ trazada desde $B$ (figura 11), calcula la distancia de $D$ al centroide $G$ del triangulo en términos de los catetos.
Figura 11
  1. Un triángulo rectángulo tiene un ángulo interior de $\dfrac{\pi}{3}$, calcula la distancia del vértice donde se intersecan los catetos al incentro $I$ del triángulo en términos de la hipotenusa.
  2. Sea $\triangle ABC$ un triángulo tal que la mediana $AD$ es perpendicular a la mediana $BE$, encuentra $AB$ si $BC = a$ y $AC = b$.

Entradas relacionadas

Fuentes

  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 29-34.
  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 65-94.
  • Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Semejanza de triángulos

Por Rubén Alexander Ocampo Arellano

3 respuestas

Introducción

En esta entrada estudiamos otro tipo de relación, la de semejanza de triángulos, la cual es una de las herramientas más útiles en geometría euclidiana.

Definición. Decimos que dos triángulos $\triangle ABC$ y $\triangle A’B’C’$ son semejantes si sus ángulos respectivos son iguales y sus lados respectivos son proporcionales, es decir,

  • $\angle A = \angle A’$, $\angle B = \angle B’$, $\angle C = \angle C’$ y
  • $\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} = \dfrac{AC}{A’C’}$.

Si dos triángulos son semejantes lo denotamos así $\triangle ABC \sim \triangle A’B’C’$.

Criterio de semejanza ángulo, ángulo, ángulo (AAA o AA)

Teorema 1, criterio de semejanza ángulo, ángulo, ángulo. Si los ángulos correspondientes de dos triángulos son iguales entonces los triángulos son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ dos triángulos tales que $\angle A = \angle A’$, $\angle B = \angle B’$, $\angle C = \angle C’$. Por demostrar que los lados correspondientes son proporcionales.

Sean $D \in AB$ y $E \in AC$ tales que $AD = A’B’$ y $AE = A’C’$, como $\angle A = \angle A’$, por el criterio de congruencia LAL, tenemos que los triángulos $\triangle ADE \cong \triangle A’B’C’$.

Figura 1

Por lo tanto, $\angle EDA = \angle C’B’A’$, $\angle AED = \angle A’C’B’$ y $DE = B’C’$.

Dado que $AB$ es transversal a $DE$ y $BC$ y los ángulos correspondientes son iguales, entonces $DE \parallel BC$.

Por el teorema de Tales, $\dfrac{AB}{AD} = \dfrac{AC}{AE} = \dfrac{BC}{DE}$,
$\Rightarrow \dfrac{AB}{A’B’} = \dfrac{AC}{A’C’} = \dfrac{BC}{B’C’}$.

Así, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Observación. Como la suma de los ángulos internos de todo triangulo es igual a $\pi$, entonces si conocemos la magnitud de dos ángulos internos conocemos los tres y por lo tanto podemos referirnos a este criterio como AA.

Criterio de semejanza lado, ángulo, lado (LAL)

Teorema 2, criterio de semejanza lado, ángulo, lado. Si dos triángulos tienen dos lados correspondientes proporcionales y el ángulo entre ellos es igual, entonces los triángulos son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ dos triángulos tales que $\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’}$ y $\angle A = \angle A’$.

Sean $D \in AB$ y $E \in AC$ tales que $AD = A’B’$ y $AE = A’C’$.

Figura 2

Como $\angle A = \angle A’$ por el criterio de congruencia LAL, $\triangle ADE \cong \triangle A’B’C’$, así $\angle EDA = \angle C’B’A’$ y $\angle AED = \angle A’C’B’$.

Por hipótesis sabemos que $\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’}$
$\Rightarrow \dfrac{AB}{AD} = \dfrac{AC}{AE}$.

Esto implica, por el reciproco del teorema de Tales, que $DE \parallel BC$, se sigue que $\angle CBA = \angle EDA$ y $\angle ACB = \angle AED$ por ser ángulos correspondientes.

Por transitividad, $\angle A = \angle A’$, $\angle B = \angle B’$ y $\angle C = \angle C’$

Por criterio de semejanza AAA, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Criterio de semejanza lado, lado, lado (LLL)

Teorema 3, criterio de semejanza lado, lado, lado. Si los lados correspondientes de dos triángulos son proporcionales entonces los triángulos son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ dos triángulos tales que $\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} = \dfrac{AC}{A’C’}$, por demostrar que $\angle A = \angle A’$, $\angle B = \angle B’$ y $\angle C = \angle C’$.

Sean $D \in AB$ y $E \in AC$ tales que $AD = A’B’$ y $AE = A’C’$ (figura 2).

Como $\angle BAC = \angle DAE$ y $\dfrac{AB}{AD} = \dfrac{AC}{AE}$, por criterio de semejanza LAL, $\triangle ABC \sim \triangle ADE$, y en consecuencia $\dfrac{AB}{AD} = \dfrac{BC}{DE}$.

$AD = A’B’$, por construcción, y $\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’}$ por hipótesis,
$\Rightarrow \dfrac{BC}{B’C’} = \dfrac{AB}{A’B’} = \dfrac{AB}{AD} = \dfrac{BC}{DE}$
$\Rightarrow B’C’ = DE$.

Por criterio de congruencia LLL, $\triangle A’B’C’ \cong \triangle ADE$.

Por transitividad, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Triángulos con lados perpendiculares

Proposición 1. Dos triángulos cuyos lados correspondientes son perpendiculares son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB \perp A’B’$, $BC \perp B’C’$ y $AC \perp A’C’$.

Consideremos $Z$, $P$ y $Q$ las intersecciones de $BC$ con $B’C’$, $A’B’$ y $A’C’$ respectivamente, $X = AB \cap A’B’$ e $Y = AC \cap A’C’$ (figura 3).

Figura 3

$\angle CBA = \angle PBX$, por ser opuestos por el vértice,
como $\triangle BXP$ es rectángulo entonces $\angle PBX$ y $\angle XPB$ son complementarios,
$\Rightarrow \angle CBA$ y $\angle XPB$ son complementarios,
$\angle XPB = \angle B’PZ$, por ser opuestos por el vértice,
$\Rightarrow \angle CBA$ y $\angle B’PZ$ son complementarios.

Como $\triangle B’ZP$ es rectángulo entonces $\angle B’PZ$ y $\angle ZB’P$ son complementarios,
$\Rightarrow \angle CBA = \angle ZB’P$,
$\Rightarrow \angle B’ = \angle B$.

Por otro lado, $\angle ACB = \angle YCQ$, por ser opuestos por el vértice,
como $\triangle CYQ$ es rectángulo entonces $\angle YCQ$ y $\angle CQY$ son complementarios,
$\Rightarrow \angle ACB$ y $\angle CQY$ son complementarios.

Como $\triangle C’ZQ$ es rectángulo entonces $\angle QC’Z$ y $\angle CQY$ son complementarios,
$\Rightarrow \angle ACB = \angle QC’Z$,
$\Rightarrow \angle C = \angle C’$.

Por criterio de semejanza AA, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Proposición 2. Dos triángulos cuyos lados correspondientes son paralelos son semejantes.

Demostración. Podemos construir un triángulo cuyos lados correspondientes sean perpendiculares a los lados de uno de los triángulos, por transitividad sus lados también serán perpendiculares a los lados del segundo triangulo.

Por la proposición anterior los triángulos originales serán semejantes al triangulo construido y por lo tanto serán semejantes entre sí.

$\blacksquare$

Desigualdad entre bisectrices

Proposición 3. En un triángulo entre cualesquiera dos ángulos internos la bisectriz del mayor es menor a la bisectriz del menor de los ángulos.

Demostración. Sea $\triangle ABC$ y supongamos que $\angle B > \angle C$ y sean $D$ y $E$ las intersecciones de las bisectrices de los ángulos $\angle B$ y $\angle C$ respectivamente con los lados opuestos. Debemos mostrar que $BD < CE$.

Sean $F \in AD$ tal que $\angle DBF = \angle ACE = \angle ECB$ y $G$ la intersección de $CE$ con $BF$, por criterio de semejanza AA, $\triangle FBD \sim \triangle FCG$, por lo tanto,

$\begin{equation} \dfrac{BF}{CF} = \dfrac{BD}{CG}. \end{equation}$

Figura 4

Por otro lado, en el triángulo $\triangle BFC$ tenemos que
$\angle CBF = \angle CBD + \angle DBF $
$= \dfrac{\angle B}{2} + \dfrac{\angle C}{2} > \dfrac{\angle C}{2} + \dfrac{\angle C}{2} = \angle C$.

Como al ángulo mayor siempre se opone a el lado mayor, tenemos que $FC > BF$ $\Leftrightarrow$ $1 > \dfrac{BF}{CF} = \dfrac{BD}{CG}$.

Donde la última igualdad se da por la ecuación $(1)$

Por lo tanto, $CE > CG > BD$.

$\blacksquare$

Semejanza en el triángulo rectángulo

Proposición 4. Sean $\triangle ABC$ un triángulo rectángulo con $\angle A = \dfrac{\pi}{2}$ y $D$ el pie de la perpendicular a $\overline{BC}$ trazada desde $A$, entonces:
$i)$ $AD^2 = BD \times DC$,
$ii)$ $AB^2 = BC \times BD$,
$iii)$ $AC^2 = BC \times DC$,
$iv)$ $AD \times BC = AB \times AC$.

Figura 5

Demostración. Por criterio de semejanza AA, $\triangle ABC \sim \triangle DBA$ y $\triangle ABC \sim \triangle DAC$,

$i)$  Por la relación de semejanza tenemos
$\dfrac{AD}{AC} =\dfrac{BD}{AB} \Rightarrow AD = \dfrac{BD \times AC}{AB}$,
$\dfrac{AD}{AB} =\dfrac{DC}{AC}  \Rightarrow AD = \dfrac{DC \times AB}{AC}$
$\Rightarrow AD^2 = BD \times DC$

$ii)$ Como $\triangle ABC \sim \triangle DBA$, $\dfrac{AB}{BD} =\dfrac{BC}{AB}$
$\Rightarrow AB^2 = BC \times BD$

$iii)$ Como $\triangle ABC \sim \triangle DAC$, $\dfrac{AC}{DC} =\dfrac{BC}{AC}$
$\Rightarrow AC^2 = BC \times DC$

$iv)$ de $ii)$ y $iii)$ tenemos $BC^2 = \dfrac{AB^2 \times AC^2}{BD \times DC}$
y empleando $i)$ obtenemos $AD^2 \times BC^2 = (BD \times DC) \dfrac{AB^2 \times AC^2}{BD \times DC}$
$\Rightarrow AD \times BC = AB \times AC$.

$\blacksquare$

Más adelante…

En la siguiente entrada comenzaremos a distinguir el sentido en el que recorremos un sementó de recta y si la razón en que un punto divide a un segmento es negativa o positiva. Haciendo uso de segmentos dirigidos mostraremos el teorema de Stewart.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra el teorema de Pitágoras usando semejanza de triángulos.
  2. Criterio de semejanza hipotenusa-cateto, muestra que un par de triángulos rectángulos son semejantes si la razón entre sus hipotenusas y la razón entre uno de sus catetos son iguales.
  3. Muestra que si en un triángulo dos bisectrices internas tienen la misma longitud, entonces el triángulo es isósceles.
  4. Sean $\square ABCD$ un paralelogramo,$E \in CD$, $G$ y $F$ las intersecciones de $AE$ con $BD$ y $BC$ respectivamente (figura 6), encuentra $EF$ en términos de $AG$ y $GE$.
Figura 6
  1. Sean $\square ABCD$ un paralelogramo, $E$, $F \in BD$ tales que $BE = DF$, $G = AE \cap BC$ y $H = AF \cap CD$ (figura 7), muestra que $GH \parallel BD$.
Figura 7

Entradas relacionadas

Fuentes

  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 18-24.
  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 72-73.
  • Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 6-11.
  • Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Congruencia de triángulos

Por Rubén Alexander Ocampo Arellano

1 respuesta

Introducción

En esta entrada estudiaremos los criterios de congruencia para triángulos, los cuales estaremos usando a lo largo del curso, nos apoyaremos en las transformaciones rígidas las cuales presentamos a continuación.

Definición 1. Decimos que dos triángulos distintos $\triangle ABC$ y $\triangle A’B’C’$ son congruentes y lo denotamos como $\triangle ABC \cong \triangle A’B’C’$, si los lados y los ángulos correspondientes son iguales, esto es,

  • $\angle A = \angle A’$, $\angle B = \angle B’$, $\angle C = \angle C’$ y
  • $AB = A’B’$, $BC = B’C’$, $AC = A’C’$.

Definición 2. Una transformación rígida es una función del plano en sí mismo, o un subconjunto de él, donde la preimagen y la imagen son congruentes.

Una reflexión en una recta es una transformación rígida que manda a todo punto en la preimagen con su punto simétrico respecto a la recta.

triangulo

Una traslación es una transformación rígida que mueve a todos los puntos en la preimagen una distancia constante en una dirección especifica.

Figura 2

Una rotación es una transformación rígida donde todos los puntos en la preimagen giran alrededor de un punto fijo en un ángulo constante.

Figura 3

Criterio lado, ángulo, lado (LAL)

Teorema 1, de congruencia lado, ángulo, lado. Si en un triángulo dos de sus lados y el ángulo interior que estos forman, son iguales a dos lados y el ángulo interior comprendido entre ellos de un segundo triángulo entonces los triángulos son congruentes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $\angle A = \angle A’$, debemos mostrar que $BC = B’C’$, $\angle B = \angle B’$ y $\angle C = \angle C’$.

Figura 4

La idea es superponer los ángulos $\angle BAC$ y $\angle B’A’C’$ de la siguiente manera, hacemos una composición de transformaciones rígidas para que $A$ y $A’$ coincidan y los segmentos $AB$ y $A’B’$  se superpongan.

Entonces como $AB = A’B’$ los puntos $B$ y $B’$ coincidirán, ahora como $\angle BAC = \angle B’A’C’$ los segmentos $AC$ y $A’C’$ quedaran sobrepuestos, si no es así entonces hacemos una reflexión a través de $AB$ para que esto suceda.

Como $AC$ y $A’C’$  tienen la misma longitud sucederá que $C$ y $C’$ coincidirán, de esta manera los segmentos $BC$ y $B’C’$ coincidirán pero también los pares de ángulos ($\angle CBA$, $\angle C’B’A’$) y ($\angle ACB$, $\angle A’C’B’$) coincidirán.

Por lo tanto, por la noción común numero 4 (cosas que coinciden una con otra son iguales entre sí), tendrán la misma magnitud,
$BC = B’C’$, $\angle CBA = \angle C’B’A’$, $\angle ACB = \angle A’C’B’$.

Como resultado, $\triangle ABC \cong \triangle A’B’C’$.

$\blacksquare$

Notemos que el procedimiento de “superponer” las figuras no se menciona en los axiomas de Euclides ni en las nociones comunes, así que este es un ejemplo de que los postulados de Euclides son incompletos como lo mencionábamos en la entrada anterior.

En el siguiente interactivo se ilustra un caso particular de como con una traslación y una rotación podemos superponer dos triángulos.

Criterio lado, lado, lado (LLL)

Definición 3. La mediatriz de un segmento es la recta perpendicular al segmento y que pasa por su punto medio, es decir, lo biseca.

La bisectriz de un ángulo es la recta que pasa por el vértice del ángulo y lo divide en dos ángulos iguales. Notemos que en un triángulo hay tres bisectrices internas y tres bisectrices externas.

Decimos que un vértice y un lado de un triángulo son opuestos si el lado no contiene al vértice. La altura de un triángulo, es el segmento que une uno de sus vértices con el pie de la perpendicular al lado opuesto.

La mediana de un triángulo es el segmento que une un vértice con el punto medio del lado opuesto.

Proposición. Los ángulos internos de un triángulo isósceles, que no son aquel comprendido entre los lados iguales, son iguales entre sí, además, la bisectriz del ángulo interior formado por los lados iguales, la altura trazada por ese vértice, la mediana y mediatriz del lado opuesto coinciden.

Demostración.  Sea $\triangle ABC$ un triángulo isósceles con $AB = AC$ y tracemos la bisectriz de $\angle A$, sea $M$ el punto en donde la bisectriz corta al lado opuesto.

Figura 5

Los triángulos $\triangle AMB$ y $\triangle AMC$ tienen dos lados iguales, $AB = AC$ por hipótesis y $AM$ es un lado en común, además $\angle BAM = \angle MAC$ por ser $AM$ bisectriz, por criterio LAL los triángulos son congruentes.

Por lo tanto, $BM = CM$, $\angle AMB = \angle CMA$ y $\angle B = \angle C$
esta última igualdad es la primera de las afirmaciones que se quería mostrar.

Por otro lado, como $BM = CM$, entonces $M$ es punto medio de $BC$ por lo que $AM$ es mediana.

Ahora, como $\angle AMB + \angle CMA = \pi$ y $\angle AMB = \angle CMA$, entonces $AM$ es perpendicular a $BC$ y así $AM$ es mediatriz y altura.

$\blacksquare$

Lema. Dado un segmento $AB$ y un punto $P$ no colineal con $A$ y $B$, no existe otro punto $P’$ diferente de $P$ y en el mismo semiplano que $P$ respecto de $AB$, tal que $AP = AP’$ y $BP = BP’$.

Demostración. Por reducción al absurdo, supongamos que existe $P’ \neq P$ talque $AP = AP’$ y $BP = BP’$, entonces consideremos los triángulos isósceles, $\triangle PAP$´ y $\triangle PBP’$.

Por la proposición anterior $\angle APP’ = \angle PP’A$ y $\angle BPP’ = \angle PP’B$.

Figura 6

Pero $\angle APP’ = \angle APB + \angle BPP’ = \angle APB + \angle PP’B$,
$\Rightarrow APP’ > PP’B$.

Por otro lado, $\angle PP’B = \angle PP’A + \angle AP’B$,
$\Rightarrow PP’B > PP’A$.

De las últimas dos desigualdades concluimos que $APP’ > PP’A$, lo cual es una contradicción al axioma de tricotomía pues vimos que $APP’ = PP’A$.

Por lo tanto, no existe $P’$ distinto de $P$ tal que $AP = AP’$ y $BP = BP’$.

$\blacksquare$

Teorema 2, de congruencia lado, lado, lado. Si los lados de un triángulo son iguales a los lados de otro triángulo, entonces los triángulos son congruentes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $BC = B’C’$ y $AC = A’C’$, veamos que los ángulos respectivos tienen la misma magnitud.

Figura 7

Hagamos la composición de transformaciones rígidas necesaria para para hacer coincidir los puntos $B$ y $B’$ de manera que los segmentos $BC$ y $B´C’$ se sobrepongan.

Como $BC = B’C’$ entonces $C$ y $C’$ coincidirán.

Ahora realizamos otra composición de transformaciones rígidas para que $A$ y $A’$ se encuentren en el mismo semiplano respecto de $BC$ y $B’C’$, que ahora son el mismo segmento.

Por el lema anterior, como $AB = A’B’$ y $AC = A’C’$, no es posible que $A \neq A’$, por lo tanto, coinciden, como $\triangle ABC$ y $\triangle A´B´C´$ coinciden, por la noción común número 4, todas sus magnitudes son iguales, por lo que $\angle A = \angle A’$, $\angle B = \angle B’$ y $\angle C = \angle C’$.

$\blacksquare$

Problema. Dado un ángulo construir su bisectriz.

Solución. Sea $\angle ABC$ el ángulo dado, trazamos una circunferencia de radio arbitrario pero positivo que corta a $AB$ en $D$ y a $BC$ en $E$.

Figura 8

Ahora construimos un triángulo equilátero sobre $DE$, como lo hicimos en la primera entrada, cuyo tercer vértice será $F$.

Veamos que $BF$ es la bisectriz de $\angle ABC$. Tenemos que $BD = BE$, pues son radios de una misma circunferencia, $DF = EF$, ya que $\triangle DEF$ es equilátero por construcción, por LLL $\triangle BDF \cong \triangle BEF$, en consecuencia $\angle DBF = \angle FBE$, por lo tanto, $BF$ es bisectriz de $\angle ABC$.

$\blacksquare$

Criterio ángulo, lado, ángulo (ALA)

Teorema 3, de congruencia ángulo, lado, ángulo. Si dos ángulos y el lado comprendido entre ellos de un triángulo son iguales a dos ángulos y el lado comprendido entre ellos de otro triangulo, entonces los triángulos son congruentes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $\angle B = \angle B’$, $\angle C = \angle C’$ y $BC = B’C’$.

Como la suma de los ángulos internos de todo triangulo es $\pi$ entonces
$\angle A + \angle B + \angle C = \pi = \angle A’ + \angle B’ + \angle C’$
$\Rightarrow A = A’$.

Si cualquier otro par de lados correspondientes fuese igual entonces por LAL, los triángulos serian congruentes. Supongamos lo contrario para llegar a una contradicción, es decir, que $AC \neq A’C’$ y $AB \neq A’B’$.

Figura 9

Sin pérdida de generalidad supongamos que $AC > A’C’$.

Construimos sobre $AC$ un punto $A’’$ tal que $A’’B = A’B’$, entonces $\triangle A’’BC \cong \triangle A’B’C’$ por LAL, por lo que $\angle A’’CB = \angle A’C’B’$.

Por hipótesis, $\angle ACB = \angle A’C’B’$ así que $\angle ACB = \angle A’’CB$, pero $\angle ACB > \angle A’’CB$, lo que es una contradicción.

Por lo tanto, $AC = A’C’$ y por LAL, $\triangle ABC \cong \triangle A’B’C’$.

$\blacksquare$

Criterio hipotenusa, cateto

Definición 4. En un triángulo rectángulo a los lados que forman el ángulo recto le llamamos catetos y al lado opuesto al ángulo recto le llamamos hipotenusa.

Teorema 4. De congruencia hipotenusa, cateto. Si la hipotenusa y un cateo de un triángulo rectángulo son iguales a la hipotenusa y un cateto de otro triángulo rectángulo, entonces los triángulos son congruentes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $\angle B = \angle B’ = \dfrac{\pi}{2}$, $AB = A’B’$ y $AC = A’C’$.

Sobre la recta determinada por $B$ y $C$ construimos un punto $C’’$ del lado opuesto a $C$ respecto a $B$, tal que $BC’’ = B’C’$.

Figura 10

Entonces por LAL, $\triangle ABC’’ \cong \triangle A’B’C’$, por lo tanto, $AC’’ = A’C’$, por hipótesis $AC = A’C’$, así que $AC = AC’’$.

Como $\triangle C’’AC$ es isósceles y por construcción $AB$ es la altura trazada desde $A$, por la proposición, $AB$ coincide con la mediatriz de $C’’C$, por lo que $BC’’ = BC$, pero $BC’’ = B’C’$ por construcción, por lo tanto, $BC = B’C’$, finalmente por LLL, $\triangle ABC \cong \triangle A’B’C’$.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos la desigualdad del triangulo y su reciproco, presentaremos el concepto de lugar geométrico y mostraremos un par de ejemplos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que si se hacen dos reflexiones sucesivas con respecto a dos rectas paralelas, el resultado es una traslación.
  2. Muestra que si se hacen dos reflexiones sucesivas con respecto a dos rectas concurrentes, se obtiene una rotación con respecto al punto de intersección entre las rectas.
  3. $i)$ Muestra que si un triangulo tiene dos ángulos iguales, entonces los lados opuestos a estos ángulos también son iguales.
    $ii)$ Muestra que los ángulos internos de un triángulo equilátero son iguales.
  4. Si dos rectas distintas se intersecan forman 4 ángulos, prueba que las bisectrices de ángulos opuestos por el vértice son la misma y que las bisectrices de ángulos adyacentes son perpendiculares.
  5. Dado un segmento, construye su mediatriz.
  6. Demuestra sin usar el quinto postulado (lo que implica que los ángulos interiores de todo triangulo suman dos ángulos rectos), que todo ángulo exterior de un triángulo es mayor que cualquiera de los ángulos interiores no adyacentes a el.
  7. Muestra con un ejemplo que el criterio LLA en general no se cumple, es decir, cuando dos triángulos diferentes tienen dos lados y un ángulo correspondientes iguales, pero el ángulo no es el que forman los lados correspondientes iguales.

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Desigualdad del triángulo y lugar geométrico

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión estudiaremos una propiedad muy importante de los triángulos, la desigualdad del triángulo que básicamente nos dice que la distancia mas corta entre dos puntos es el segmento de recta que los une, también veremos lo que es un lugar geométrico y mostraremos un par de ejemplos importantes.

Desigualdad del triángulo

Proposición 1. En todo triángulo al mayor de los lados se opone el mayor de los ángulos.

Demostración. Sea $\triangle ABC$ tal que $AB > AC$, debemos mostrar que $\angle C > \angle B$.

Figura 1

Como $AB > AC$, podemos construir un punto $D \in AB$ tal que $AD = AC$, ya que $\triangle ADC$ es isósceles, por la proposición de la entrada anterior, se cumple $\angle CDA = \angle ACD$, de aquí se sigue que:

$\begin{equation} \angle C = \angle ACB > \angle ACD = \angle DCA. \end{equation}$

Como $\angle ADC$ es un ángulo exterior de $\triangle DBC$, entonces $\angle ADC$ es mayor que los ángulos internos de $\triangle DBC$, no adyacentes a él, en particular

$\begin{equation} \angle ADC > CBD = \angle B. \end{equation}$

De $(1)$ y $(2)$ se sigue que $\angle C > \angle B$.

$\blacksquare$

Corolario. En todo triángulo el ángulo mayor es opuesto al lado mayor.

Demostración. Sea $\triangle ABC$ tal que $\angle A > \angle B$, por demostrar que $BC > AC$. Supongamos lo contrario.

Figura 2

Caso 1. Si $BC = AC$, entonces $\triangle ABC$ es isósceles por lo que $\angle A = \angle B$, lo que es una contradicción a nuestra hipótesis.

Caso2. Si $BC < AC$, entonces por la proposición anterior $\angle B > \angle A$, esto nuevamente contradice la hipótesis.

Por lo tanto, no queda otra opción más que $\angle A > \angle B$.

$\blacksquare$

Proposición 2. Si dos lados de un triángulo son iguales a dos lados de un segundo triángulo, pero el ángulo comprendido entre el primer par de lados es mayor que el ángulo formado por los lados del segundo triangulo, entonces el lado restante del primer triángulo será mayor al tercer lado del segundo triangulo.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $\angle A > \angle A’$, por demostrar que $BC > B’C’$.

Figura 3

Sobre $A’B’$ y tomando como vértice $A’$ construimos un ángulo igual a $\angle A$, y construimos $D$ tal que $A’D = AC$, entonces por criterio LAL, $\triangle ABC \cong \triangle A’B’D$ por lo que $B’D = BC$.

Notemos que $\triangle C’A’D$ es isósceles, entonces $\angle DC’A = \angle A’DC’$.

Ahora en $\triangle DC’B’$ tenemos $\angle DC’B’ = \angle A’C’B’ + \angle DC’A$,
$\Rightarrow \angle DC’B’ > \angle DC’A = \angle A’DC’$.

Pero $\angle A’DC’ = \angle A’DB’ + \angle B’DC’$,
$\Rightarrow \angle A’DC’ > \angle B’DC’$.

Por transitividad, $\angle DC’B’ > \angle B’DC’$.

Aplicando el corolario obtenemos $B’D > B’C’$, pero $B’D = BC$,
$\Rightarrow BC > B’C’$.

$\blacksquare$

Teorema 1, desigualdad del triángulo. Para todo triangulo se cumple que la suma de cualesquiera dos de sus lados es mayor al lado restante.

Demostración. Sea $\triangle ABC$, sobre la recta que pasa por $B$ y $C$, construimos un punto $D$ tal que $CD = AC$.

Figura 4

Como $\triangle ACD$ es isósceles, $\angle CAD = \angle ADC$, entonces en $\triangle ABD$ tenemos $\angle BAD > \angle CAD = \angle ADC = \angle ADB$, por el corolario anterior $BD > AB$.

Pero $BD = BC + CD = BC + AC$, por lo tanto, $AC + BC > AB$.

Las otras desigualdades, $AB + BC > AC$ y $AB + AC > BC$, se muestran de manera similar.

$\blacksquare$

El reciproco de este teorema también es cierto y lo mostramos a continuación.

Construcción de un triángulo y un ángulo

Teorema 2. Si $a$, $b$ y $c$ son tres números positivos tales que $a + b > c$, $a + c > b$ y $b + c > a$, entonces es posible construir un triángulo de lados $a$, $b$ y $c$.

Demostración. Construyamos un segmento $BC$ de longitud $a$, trazamos una circunferencia con centro en $B$ y radio $c$ $(B, c)$, trazamos otra circunferencia con centro en $C$ y radio $b$ $(C, b)$.

$(B, c)$ y $(C, b)$ se intersecan en dos puntos, sea $A$ uno de estos puntos. $AB = c$ por ser radio de $(B, c)$, $AC = b$ por ser radio de $(C, b)$ y $BC = a$ por construcción.

Figura 5

Notemos que si $(B, c)$ y $(C, b)$ se intersecaran en un solo punto entonces la intersección estaría sobre $BC$ o su extensión, y en tal caso se tendría alguna de las siguientes igualdades
$a = b + c$, $b = a + c$ o $c = a + b$, figura 6.

Figura 6

Y si $(B, c) \cap (C, b) = \varnothing$, entonces alguna de las cantidades seria mayor que la suma de las otras dos, $a > b + c$, $b > a + c$ o $c > a + b$, figura 7, lo que sería una contradicción a nuestras hipótesis.

Figura 7

Por lo tanto, $\triangle ABC$ es el triángulo buscado.

$\blacksquare$

Problema. Sobre una recta dada construir un ángulo igual a un ángulo dado.

Solución. Sea $\angle AOB$ el ángulo dado y $l$ la recta dada.

Con centro en $O$ y radio arbitrario $r > 0$ trazamos una circunferencia $(O, r)$ que corte a $OA$ en $C$ y a $OB$ en $D$.

Figura 8

Tomamos $O’ \in l$ y construimos una circunferencia con centro en $O’$ y radio $r$, $(O’, r)$, tomamos una de las intersecciones de $l$ con $(O’, r)$, digamos $D’$, trazamos otra circunferencia con centro en $D’$ y radio $CD$, $(D’, CD)$, sea $C’$ una de las intersecciones de $(O’, r)$ con $(D´, CD)$, entonces por criterio LLL $\triangle COD \cong \triangle C’O’D’$

Por lo tanto, $\angle AOB = \angle C’O’D’$.

$\blacksquare$

Lugar geométrico

Un lugar geométrico es un conjunto de puntos que cumplen un conjunto de condiciones dadas. Para probar que una figura geométrica es un lugar geométrico por lo general la prueba se divide en dos partes.

  • Probar que todos los puntos que satisfacen las condiciones pertenecen a la figura.
  • Probar que todos los puntos que pertenecen a la figura satisfacen las condiciones.

Teorema 3. El lugar geométrico de los puntos que equidistan a dos puntos dados, es la mediatriz del segmento que une los puntos dados.

Demostración. Sean $AB$ un segmento dado, $M$ el punto medio y $m$ la mediatriz de $AB$ respectivamente.

Figura 9

Primero vemos que los puntos en la mediatriz de $AB$  equidistan de $A$ y $B$.

Sea $P \in m$, por definición de mediatriz, $m \cap AB = M$ y $l \perp AB$.

Entonces por criterio LAL (lado, ángulo, lado), $\triangle PMA \cong \triangle PMB$, en consecuencia, $PA = PB$.

$\blacksquare$

Ahora veamos que todos los puntos que equidistan de $A$ y $B$, son los puntos en la mediatriz $m$ de $AB$.

Sea $P$ un punto que satisface las condiciones dadas, entonces $PA = PB$ y así $\triangle APB$ es isósceles, en la entrada anterior vimos que la mediatriz de un triángulo isósceles, pasa por el vértice que comparten los lados iguales, por lo tanto, $P \in m$.

$\blacksquare$

Definición. Definimos la distancia de un punto $P$ a una recta $l$ como la distancia entre $P$ y el pie de la perpendicular trazada desde $P$ a $l$.

Teorema 4. El lugar geométrico de los puntos que equidistan a dos rectas que se intersecan son las bisectrices de los ángulos formados por las rectas.

Demostración. Sean $l_{1}$ y $l_{2}$, dos rectas que se intersecan en $O$, consideremos $b_{1}$ la bisectriz de uno de los ángulos formados por $l_{1}$ y $l_{2}$, digamos $\alpha$, y sea $b_{2}$ la bisectriz del ángulo suplementario a $\alpha$.

Primero veamos que todos los puntos en la bisectriz de $\alpha$ equidistan a $l_{1}$ y $l_{2}$.

Figura 10

Sea $P \in b_{1}$, y sean $A$ y $B$ las intersecciones de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Como $b_{1}$ es bisectriz, $\angle AOP = \angle POB$, además $\angle PAO = \angle OBP = \dfrac{\pi}{2}$, como la suma de los ángulos internos de todo triángulo es constante entonces $\angle OPA = \angle BPO$.

Entonces en los triángulos $\triangle PAO$ y $\triangle PBO$, $\angle AOP = \angle POB$, $\angle OPA = \angle BPO$ y $OP$ es un lado común.

Por criterio LAL, $\triangle PAO \cong \triangle PBO$, por lo tanto $PA = PB$, así la distancia de $P$ a $l_{1}$ y a $l_{2}$ es la misma.

De manera análoga podemos ver que los puntos en $b_{2}$ son equidistantes a $l_{1}$ y $l_{2}$.

$\blacksquare$

Ahora mostremos que todos los puntos que son equidistantes a $l_{1}$ y $l_{2}$ pertenecen a $b_{1}$ o $b_{2}$.

Sea $P$ un punto que satisface que $PA = PB$, donde $A$ y $B$ son los pies de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Figura 11

Entonces $\triangle PAO$ y $\triangle PBO$ son triángulos rectángulos donde la hipotenusa es la misma, y por hipótesis tienen un cateto igual, $PA = PB$, por criterio hipotenusa – cateto $\triangle PAO \cong \triangle PBO$, en particular $\angle AOP =\angle POB$.

Notemos que las dos rectas dividen al plano en cuatro regiones distintas y en cada región podemos hacer el mismo procedimiento, pero dos rectas que se intersecan solo tienen dos bisectrices distintas.

Por lo tanto si $PA = PB$, entonces $P \in b_{1}$ o $P \in b_{2}$.

$\blacksquare$

Más adelante…

En al siguiente entrada estudiaremos a los paralelogramos y sus propiedades.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $BC > B’C’$, muestra que $\angle A > \angle A’$.
  2. Sea $\square ABCD$ un cuadrado y $O$ un punto en el plano muestra que $OA < OB + OC + OD$.
  3. Sean $\triangle ABC$ y $A’$ un punto en el interior del triángulo, muestra que $AB + AC > A’B + A’C$ y que $\angle BA’C > \angle BAC$.
  4. En un poblado situado junto a un rio, cuyo borde es totalmente recto, hay un incendio en un punto $A$, la estación de bomberos se encuentra en un punto $B$ del mismo lado del río donde se dio el incendio, los bomberos necesitan pasar primero por el río para abastecerse de agua. ¿Qué punto $P$ en el borde del río hace que el trayecto $BP + PA$ sea mínimo?
  5. Muestra que si dos circunferencias se intersecan en un solo punto entonces el punto pertenece al segmento que une los centros o a su extensión.
  6. $i)$ Dados una recta y un punto en ella construye la perpendicular a la recta por el punto dado.
    $ii)$ Dados una recta y un punto fuera de ella construye la paralela a la recta por el punto dado.
    $iii)$ Dados una recta y un punto fuera de ella construye la perpendicular a la recta por el punto dado.
  7. $i)$ Dados una recta y un numero $a > 0$ encuentra el el lugar geométrico de los puntos cuya distancia a la recta es $a$.
    $ii)$ ¿Cuál es el lugar geométrico de los puntos cuya distancia a una circunferencia dada $(O, r)$ es una constante dada $b > 0$?

Entradas relacionadas

Fuentes

  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 9-12, 44-54.
  • Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 16-18.
  • Geometría interactiva
  • Geometry Help

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»