Introducción

En esta entrada estudiaremos el teorema de Tales y algunas aplicaciones. Este teorema nos dice que dos rectas paralelas cortan a otras dos en segmentos proporcionales.

En la entrada anterior definimos el área de un rectángulo y vimos que como consecuencia de esto el área de un triángulo rectángulo era el semiproducto de sus catetos. En esta ocasión necesitaremos hablar del área de un triángulo en general.

Denotaremos al área de un triángulo $\mathrm{△}ABC$ como $(\mathrm{△}ABC)$.

Área del triángulo

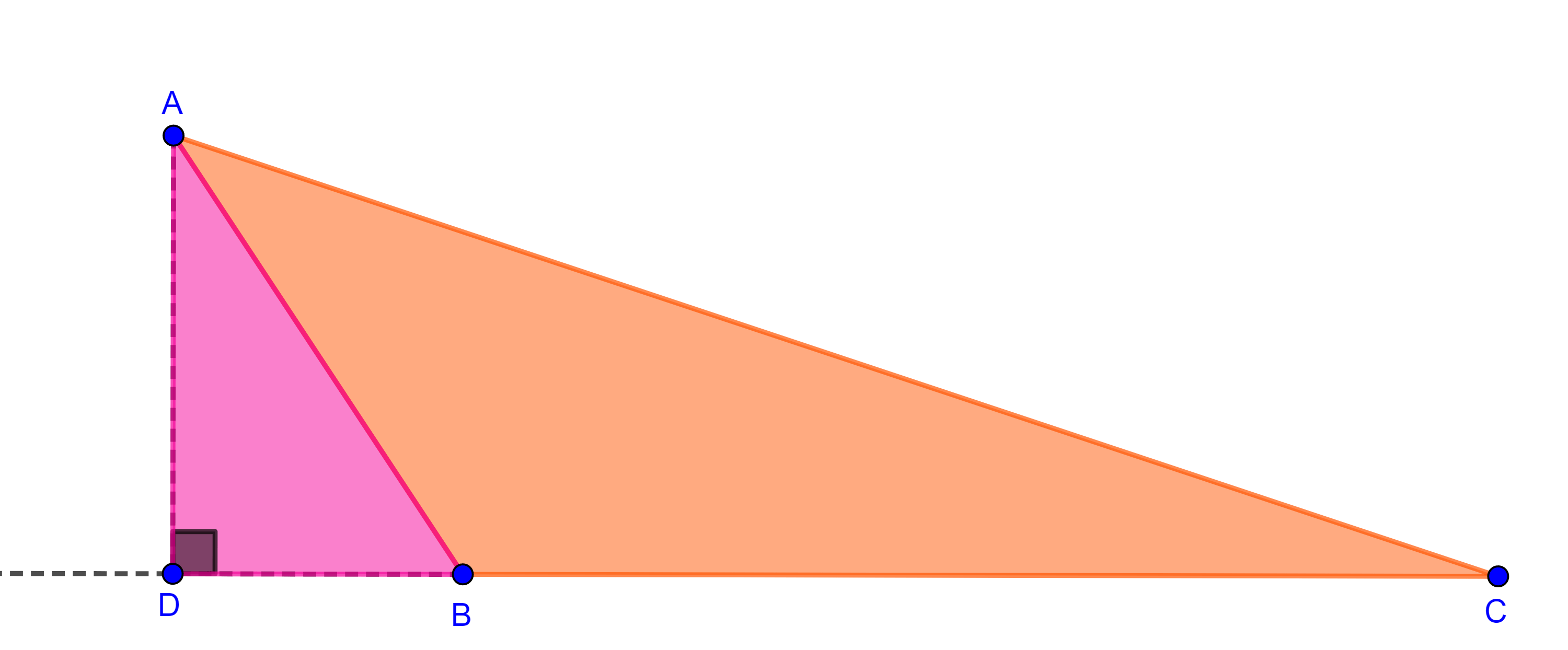
Proposición 1. El área de un triángulo es el producto de la altura trazada por uno de sus vértices por la base o lado contrario a dicho vértice.

Demostración. Sea $\mathrm{△}ABC$ un triángulo, tracemos la altura desde el vértice $A$, existen dos posibilidades, el pie de la altura $D$, se encuentra en el segmento $BC$ o está en la extensión del segmento.

Caso 1, $D\in BC$.

Notemos que se forman dos triángulos rectángulos, $\mathrm{△}ABD$ y $\mathrm{△}ADC$.
$\Rightarrow (\mathrm{△}ABC)=(\mathrm{△}ABD)+(\mathrm{△}ADC)$
$={\displaystyle \frac{BD\times AD}{2}}+{\displaystyle \frac{DC\times AD}{2}}$
$={\displaystyle \frac{(BD+DC)AD}{2}}={\displaystyle \frac{BC\times AD}{2}}$.

Caso 2, $D\notin BC$.

Notemos que se forman dos triángulos rectángulos, $\mathrm{△}ADB$ y $\mathrm{△}ADC$.
$\Rightarrow (\mathrm{△}ABC)=(\mathrm{△}ADC)–(\mathrm{△}ADB)$
$={\displaystyle \frac{DC\times AD}{2}}–{\displaystyle \frac{DB\times AD}{2}}$
$={\displaystyle \frac{(DC–DB)AD}{2}}={\displaystyle \frac{BC\times AD}{2}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

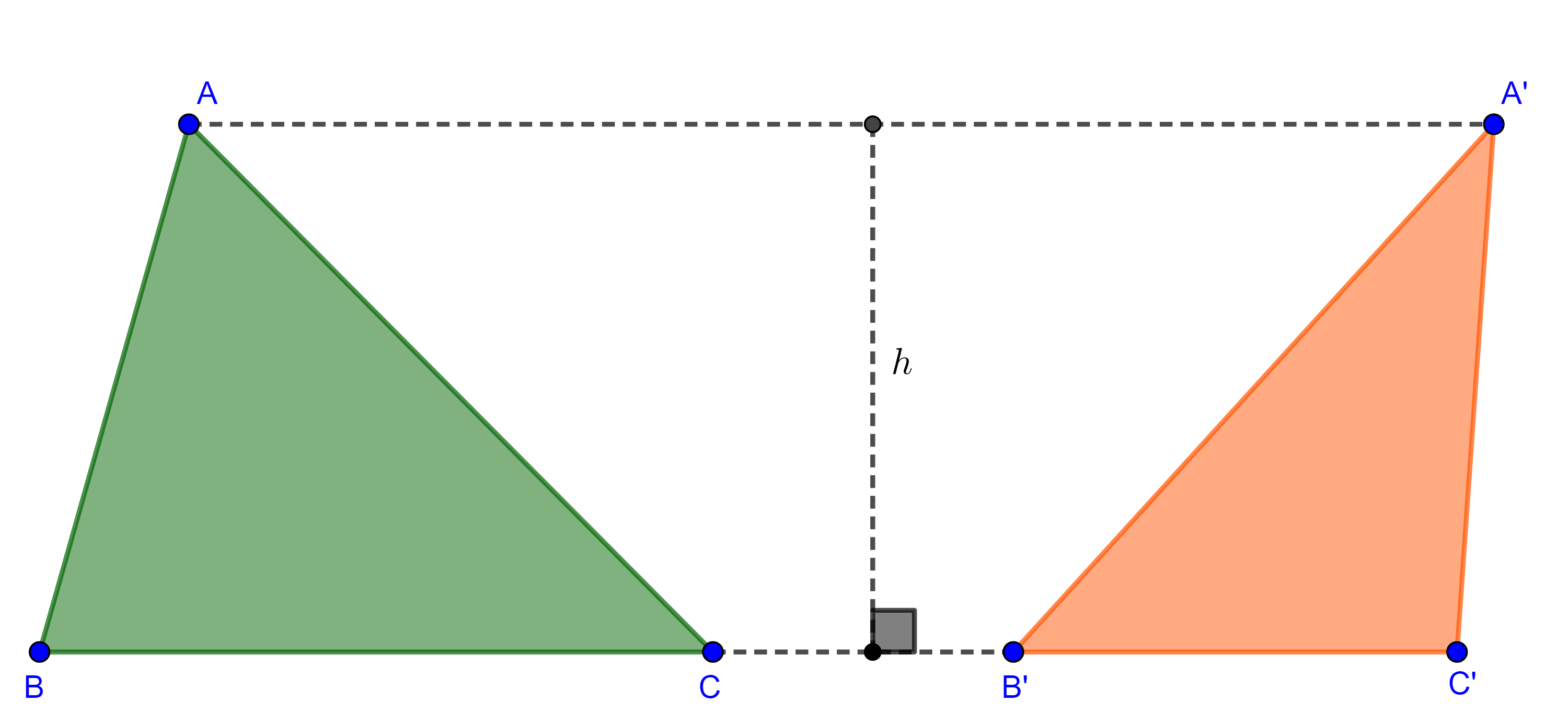
Proposición 2. Si dos triángulos tienen una misma altura entonces las razones entre sus áreas es igual a la razón entre las bases perpendiculares a las alturas.

Demostración. Sean $\mathrm{△}ABC$ y $\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ dos triángulos tales que las alturas trazadas desde $A$ y $A^{\prime }$ son iguales, digamos $h$.

${\displaystyle \frac{(\mathrm{△}ABC)}{(\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime })}}={\displaystyle \frac{{\displaystyle \frac{BC\times h}{2}}}{{\displaystyle \frac{B^{\prime }{C}^{\prime }\times h}{2}}}}$
$={\displaystyle \frac{BC\times h}{B^{\prime }{C}^{\prime }\times h}}={\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema fundamental de la proporcionalidad

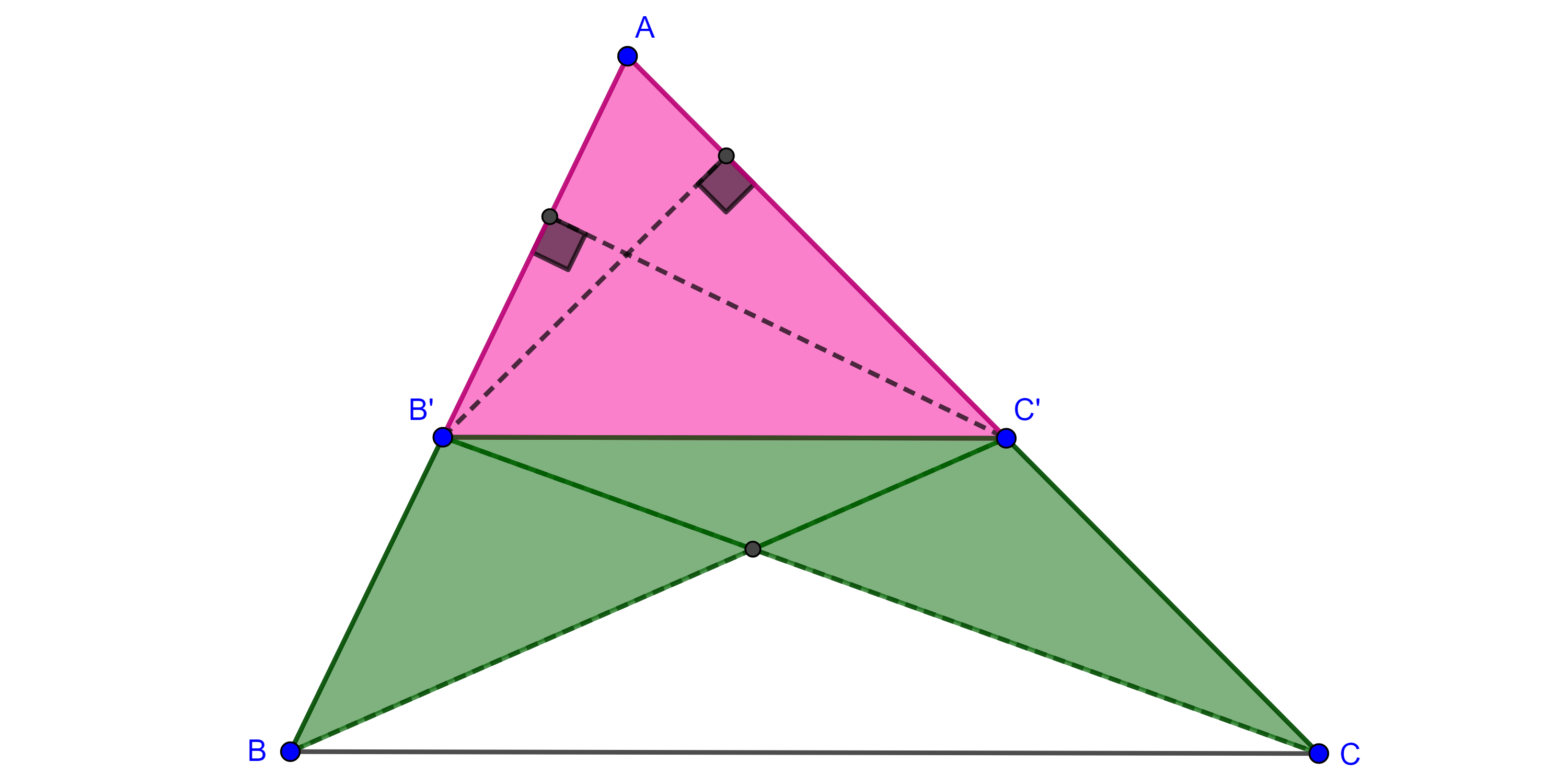
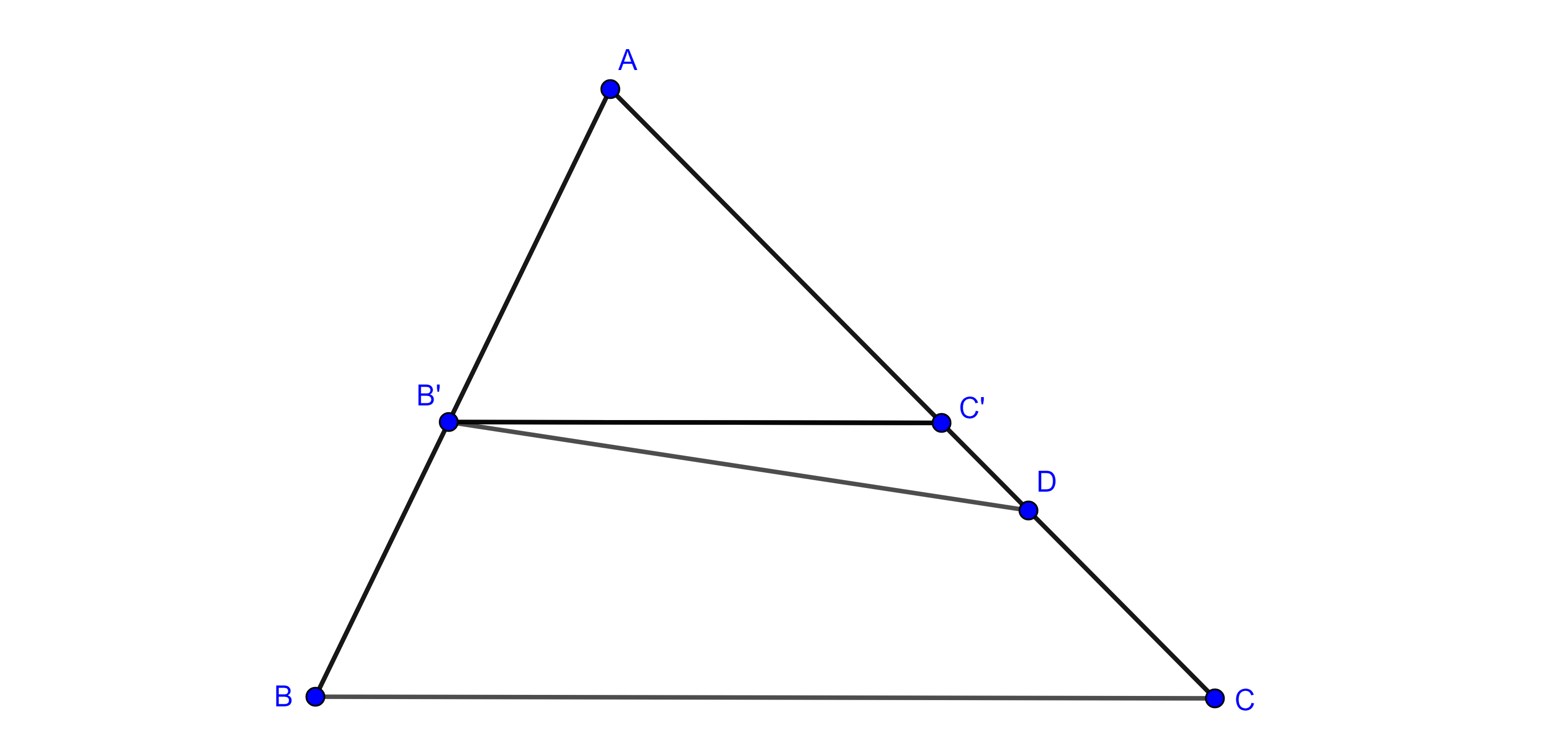
Teorema 1, de Tales. Sean $\mathrm{△}ABC$, $B^{\prime }$ y $C^{\prime }$ en $AB$ y $AC$ respectivamente tales que $B^{\prime }{C}^{\prime }\parallel BC$, entonces
$i)$ ${\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{C^{\prime }C}}$, ${\displaystyle \frac{AB}{A{B}^{\prime }}}={\displaystyle \frac{AC}{A{C}^{\prime }}}$ y ${\displaystyle \frac{A{B}^{\prime }}{B^{\prime }B}}={\displaystyle \frac{A{C}^{\prime }}{C^{\prime }C}}$,
$ii)$ ${\displaystyle \frac{AB}{A{B}^{\prime }}}={\displaystyle \frac{AC}{A{C}^{\prime }}}={\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}$.

Demostración. Como $\mathrm{△}{B}^{\prime }{C}^{\prime }B$ y $\mathrm{△}{B}^{\prime }{C}^{\prime }C$ tienen la misma base $B^{\prime }{C}^{\prime }$ y están contenidos en las mismas paralelas, lo que implica que su altura es la misma, entonces tienen la misma área.

$\begin{array}{}\text{(1)}& (\mathrm{△}{B}^{\prime }{C}^{\prime }B)=(\mathrm{△}{B}^{\prime }{C}^{\prime }C)\end{array}$
$\Rightarrow (\mathrm{△}A{B}^{\prime }{C}^{\prime })+(\mathrm{△}{B}^{\prime }{C}^{\prime }B)=(\mathrm{△}A{B}^{\prime }{C}^{\prime })+(\mathrm{△}{B}^{\prime }{C}^{\prime }C)$
$\begin{array}{}\text{(2)}& \Rightarrow (\mathrm{△}A{C}^{\prime }B)=(\mathrm{△}A{B}^{\prime }C).\end{array}$

De las escuaciones $(1)$ y $(2)$ y la proposición 2 obtenemos
${\displaystyle \frac{(\mathrm{△}A{C}^{\prime }B)}{(B^{\prime }{C}^{\prime }B)}}={\displaystyle \frac{(\mathrm{△}A{B}^{\prime }C)}{(\mathrm{△}{B}^{\prime }{C}^{\prime }C)}}$
$\Rightarrow {\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{C^{\prime }C}}$.

Notemos que ${\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{C^{\prime }C}}$, ${\displaystyle \frac{AB}{A{B}^{\prime }}}={\displaystyle \frac{AC}{A{C}^{\prime }}}$ y ${\displaystyle \frac{A{B}^{\prime }}{B^{\prime }B}}={\displaystyle \frac{A{C}^{\prime }}{C^{\prime }C}}$ son equivalentes.

${\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{C^{\prime }C}}$
$\iff {\displaystyle \frac{A{B}^{\prime }+B^{\prime }B}{B^{\prime }B}}={\displaystyle \frac{A{C}^{\prime }+C^{\prime }C}{C^{\prime }C}}$
$\iff {\displaystyle \frac{A{B}^{\prime }}{B^{\prime }B}}={\displaystyle \frac{A{C}^{\prime }}{C^{\prime }C}}$

${\displaystyle \frac{AB}{A{B}^{\prime }}}={\displaystyle \frac{AC}{A{C}^{\prime }}}$, equivale a
${\displaystyle \frac{A{B}^{\prime }+B^{\prime }B}{A{B}^{\prime }}}={\displaystyle \frac{A{C}^{\prime }+C^{\prime }C}{A{C}^{\prime }}}$
$\iff {\displaystyle \frac{B^{\prime }B}{A{B}^{\prime }}}={\displaystyle \frac{C^{\prime }C}{A{C}^{\prime }}}$
$\iff {\displaystyle \frac{A{B}^{\prime }}{B^{\prime }B}}={\displaystyle \frac{A{C}^{\prime }}{C´C}}$.

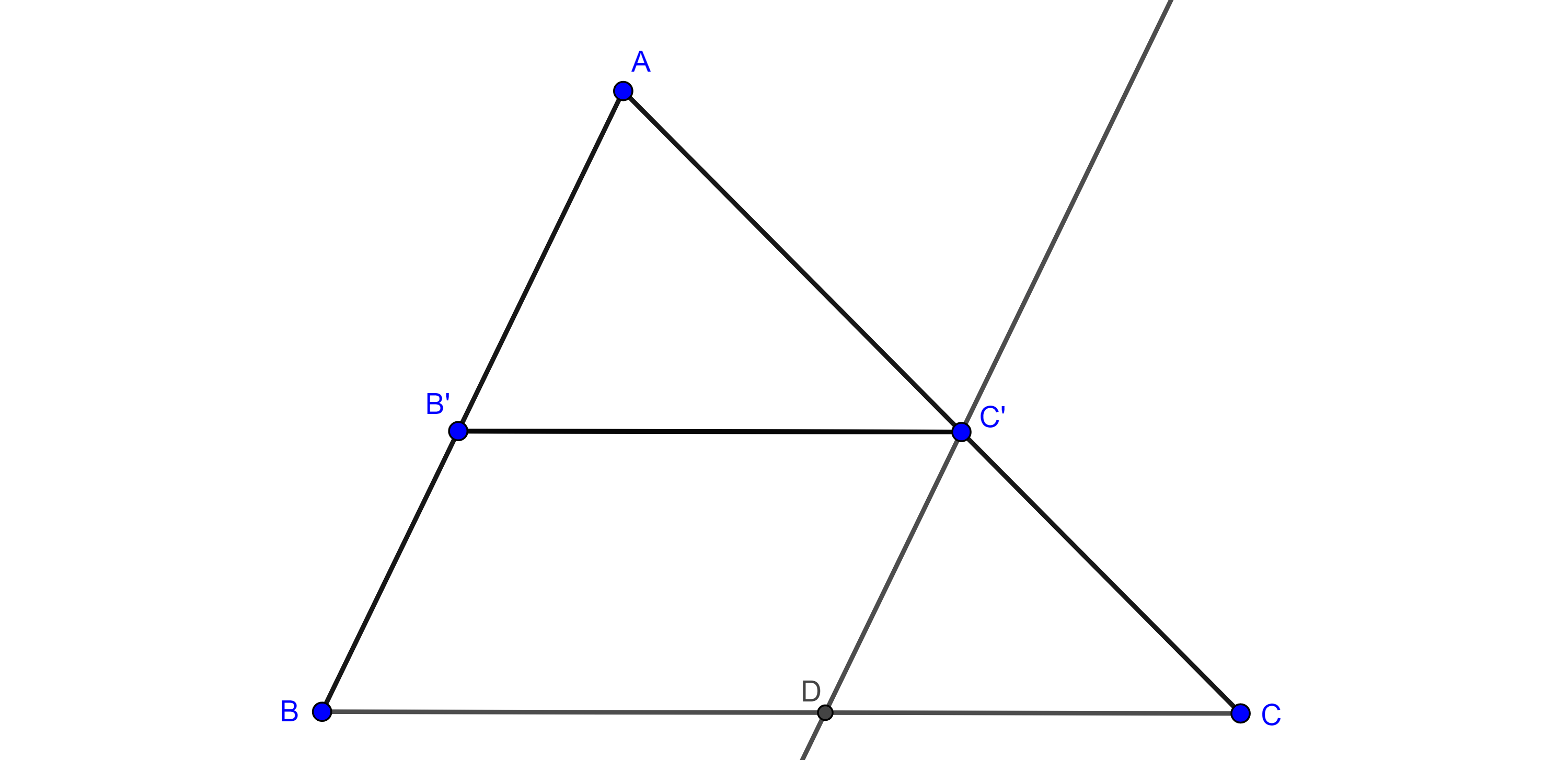
Para la parte $ii)$ trazamos una paralela a $AB$ por $C^{\prime }$ que interseca a $BC$ en $D$, por la parte $i)$, se cumple
${\displaystyle \frac{AC}{A{C}^{\prime }}}={\displaystyle \frac{BC}{BD}}$.

Como $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}{B}^{\prime }BDC$ es paralelogramo $BD=B^{\prime }{C}^{\prime }$
$\Rightarrow {\displaystyle \frac{AC}{A{C}^{\prime }}}={\displaystyle \frac{BC}{B^{\prime }{C}^{\prime }}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Reciproco del teorema de Tales.

Teorema 2, reciproco del teorema de Tales. Sean $\mathrm{△}ABC$, $B^{\prime }$ y $C^{\prime }$ en $AB$ y $AC$ respectivamente tales que, ${\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{C^{\prime }C}}$ o ${\displaystyle \frac{AB}{A{B}^{\prime }}}={\displaystyle \frac{AC}{A{C}^{\prime }}}$ o ${\displaystyle \frac{A{B}^{\prime }}{B^{\prime }B}}={\displaystyle \frac{A{C}^{\prime }}{C^{\prime }C}}$, entonces $B^{\prime }{C}^{\prime }\parallel BC$.

Demostración. Supongamos que $B^{\prime }{C}^{\prime }$ y $BC$ no son paralelas, sea $D\in AC$ tal que $B^{\prime }D\parallel BC$, por el teorema de Tales, ${\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{DC}}$.

Pero por hipótesis ${\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{C^{\prime }C}}$, y por transitividad
${\displaystyle \frac{AC}{DC}}={\displaystyle \frac{AC}{C^{\prime }C}}$
$\Rightarrow DC=C^{\prime }C\Rightarrow D=C^{\prime }\Rightarrow B^{\prime }{C}^{\prime }\parallel BC$.

Por la equivalencia entre las expresiones ${\displaystyle \frac{AB}{B^{\prime }B}}={\displaystyle \frac{AC}{C^{\prime }C}}$, ${\displaystyle \frac{AB}{A{B}^{\prime }}}={\displaystyle \frac{AC}{A{C}^{\prime }}}$ y ${\displaystyle \frac{A{B}^{\prime }}{B^{\prime }B}}={\displaystyle \frac{A{C}^{\prime }}{C^{\prime }C}}$,
queda demostrado el teorema.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema de la bisectriz

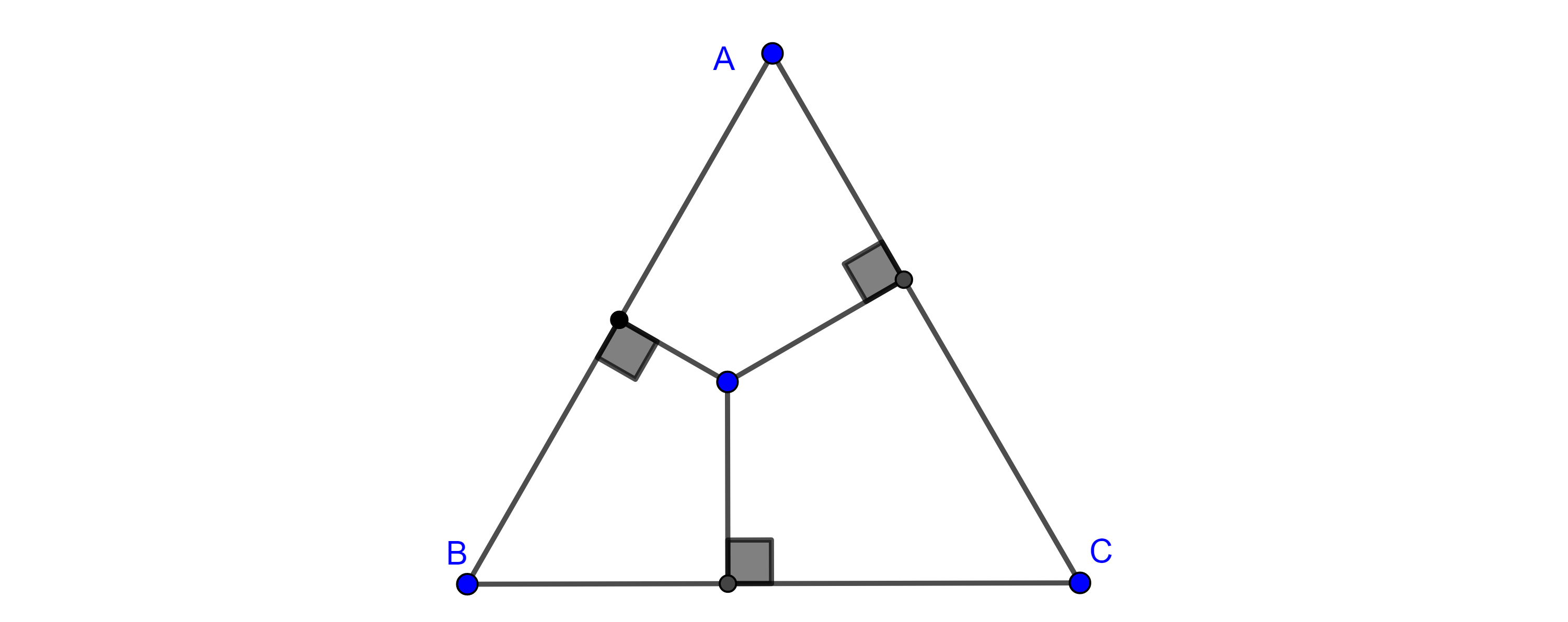
Teorema 3, de la bisectriz. Las bisectrices interna y externa del ángulo de un triángulo dividen al lado opuesto en segmentos proporcionales a los otros dos lados del triángulo.

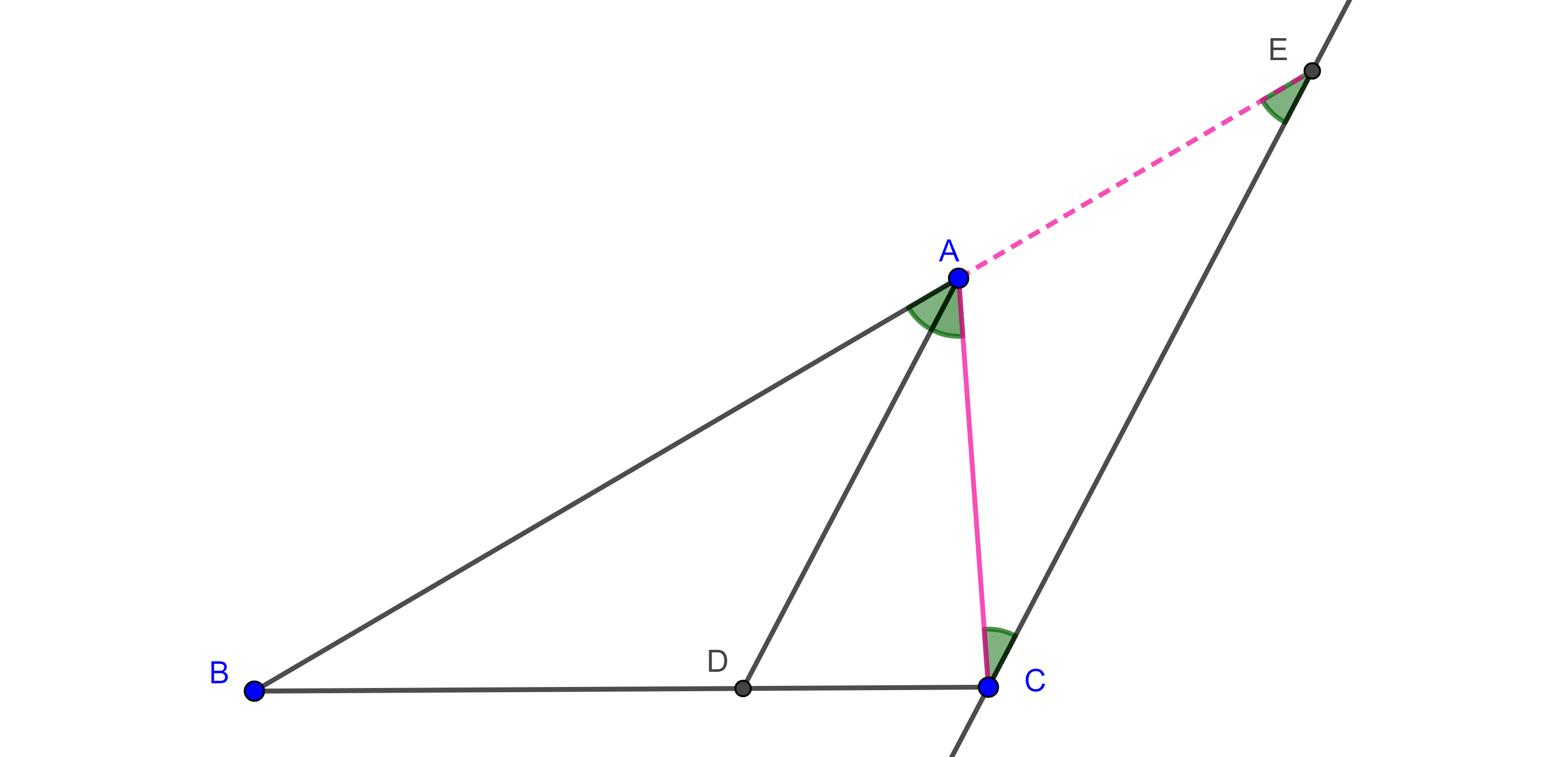
Demostración. Consideremos un triángulo $\mathrm{△}ABC$ y la bisectriz interior de $A$, la cual interseca a $BC$ en $D$.

Trazamos la paralela a $AD$ por $C$, y sea $E$ la intersección de la extensión de $AB$ con la paralela.

Como $AD\parallel CE$ entonces $\mathrm{\angle }BAD=\mathrm{\angle }AEC$ por ser ángulos correspondientes entre paralelas y $\mathrm{\angle }DAC=\mathrm{\angle }ECA$ por ser ángulos alternos internos entre paralelas.

Ya que $AD$ es bisectriz de $A$ entonces $\mathrm{\angle }BAD=\mathrm{\angle }DAC$ y por lo tanto $\mathrm{\angle }AEC=\mathrm{\angle }ECA$
$\Rightarrow \mathrm{△}ACE$ es isósceles, es decir, $AC=AE$.

Aplicando el teorema de Tales a $\mathrm{△}BCE$ tenemos que
${\displaystyle \frac{BD}{DC}}={\displaystyle \frac{AB}{AE}}={\displaystyle \frac{AB}{AC}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Definición. Una ceviana es un segmento que tiene extremos en el vértice de un triángulo y en el lado opuesto a dicho vértice.

Reciproco del teorema de la bisectriz

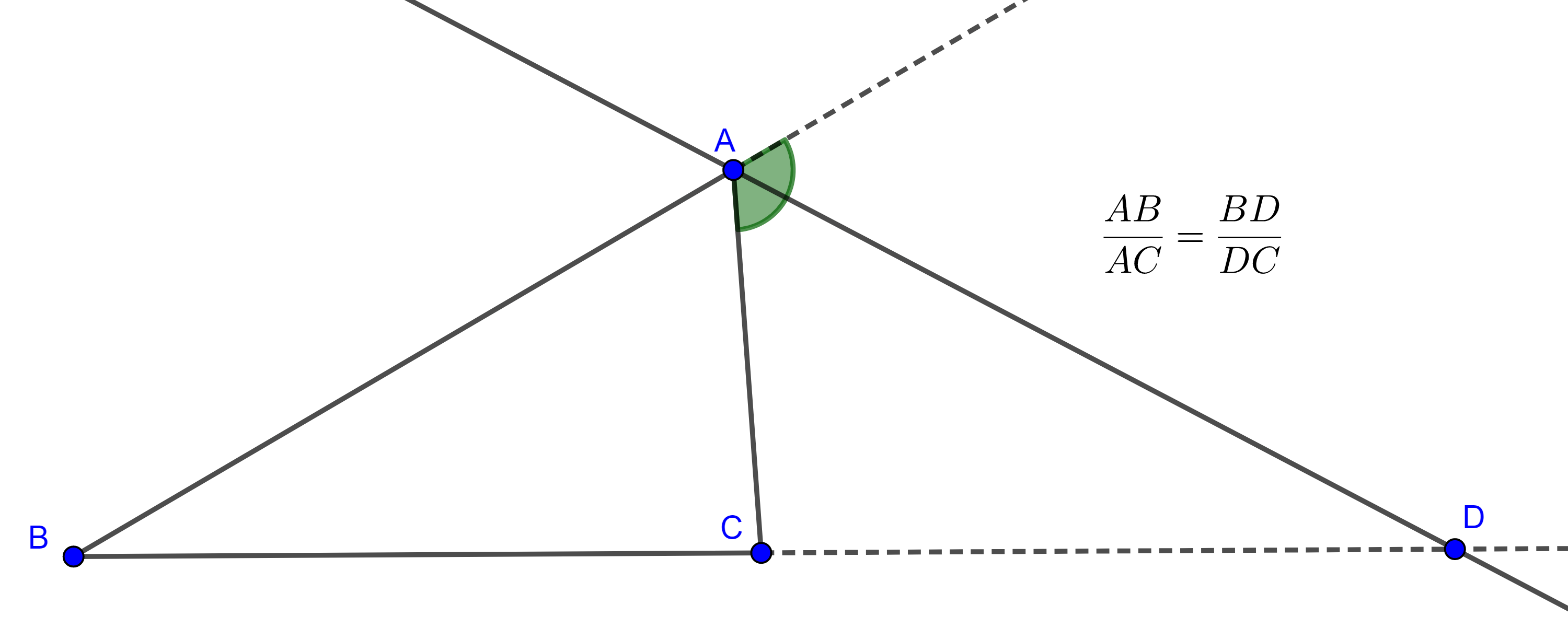
Teorema 4, reciproco del teorema de la bisectriz. Si una ceviana divide internamente al lado de un triángulo en segmentos proporcionales a los otros lados del triángulo entonces es la bisectriz interna del ángulo por donde pasa.

Demostración. Sea $\mathrm{△}ABC$ y $AD$ con $D\in BC$ tal que ${\displaystyle \frac{AB}{AC}}={\displaystyle \frac{BD}{DC}}$.

Extendemos $AB$ del lado de $A$ hasta $E$ talque $AE=AC$ (figura 7), como $\mathrm{△}AEC$ es isósceles entonces
$\begin{array}{}\text{(3)}& \mathrm{\angle }AEC=\mathrm{\angle }ECA.\end{array}$

En el triángulo $\mathrm{△}BCE$ tenemos que ${\displaystyle \frac{AB}{AE}}={\displaystyle \frac{BD}{DC}}$,
por el reciproco del teorema de Tales, $AD\parallel EC$,
$\Rightarrow \mathrm{\angle }BAD=\mathrm{\angle }AEC$, por ser ángulos correspondientes,
$\Rightarrow \mathrm{\angle }DAC=\mathrm{\angle }ECA$, por ser ángulos alternos internos.

Por $(3)$ se sigue que $\mathrm{\angle }BAD=\mathrm{\angle }DAC$, por lo tanto, $AD$ es la bisectriz interna de $A$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

El caso para la bisectriz exterior se deja como ejercicio.

Construcciones

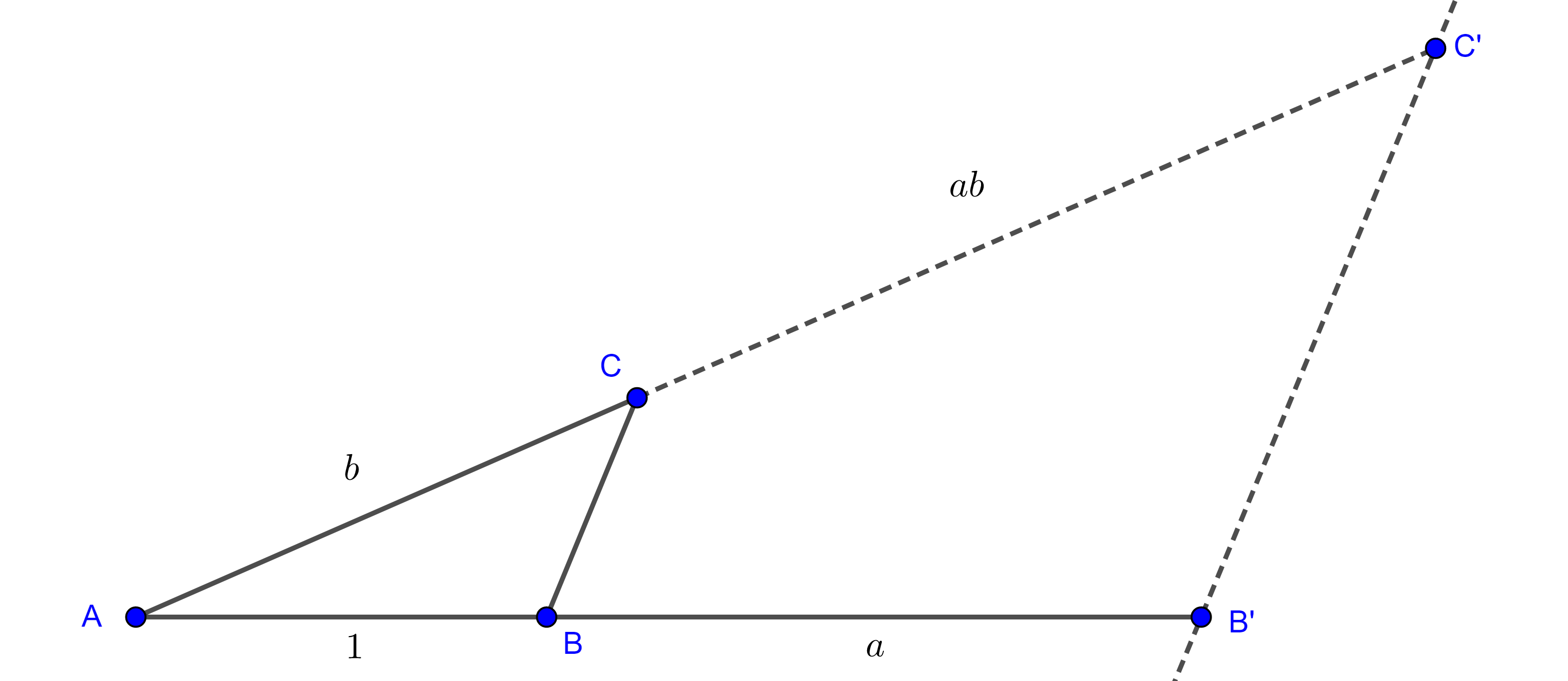
Problema. Dados dos segmentos y un segmento unitario, construye el producto y el cociente de los segmentos dados.

Solución. Sean $a$ y $b$ la magnitud de los segmentos dados.

Sea $AB$ el segmento unitario, extendemos $AB$ hasta $B^{\prime }$ tal que $B{B}^{\prime }=a$.

Levantamos sobre $AB$ en $A$ un segmento $AC=b$, unimos $B$ con $C$ y trazamos por $B^{\prime }$ la paralela a $BC$.

Sea $C^{\prime }$ la intersección de $AC$ con la paralela trazada, por el teorema de Tales aplicado a $\mathrm{△}A{B}^{\prime }{C}^{\prime }$, ${\displaystyle \frac{AB}{B{B}^{\prime }}}={\displaystyle \frac{AC}{C{C}^{\prime }}}$.
$\Rightarrow AB\times C{C}^{\prime }=AC\times B{B}^{\prime }$
$\Rightarrow C{C}^{\prime }=ab$.

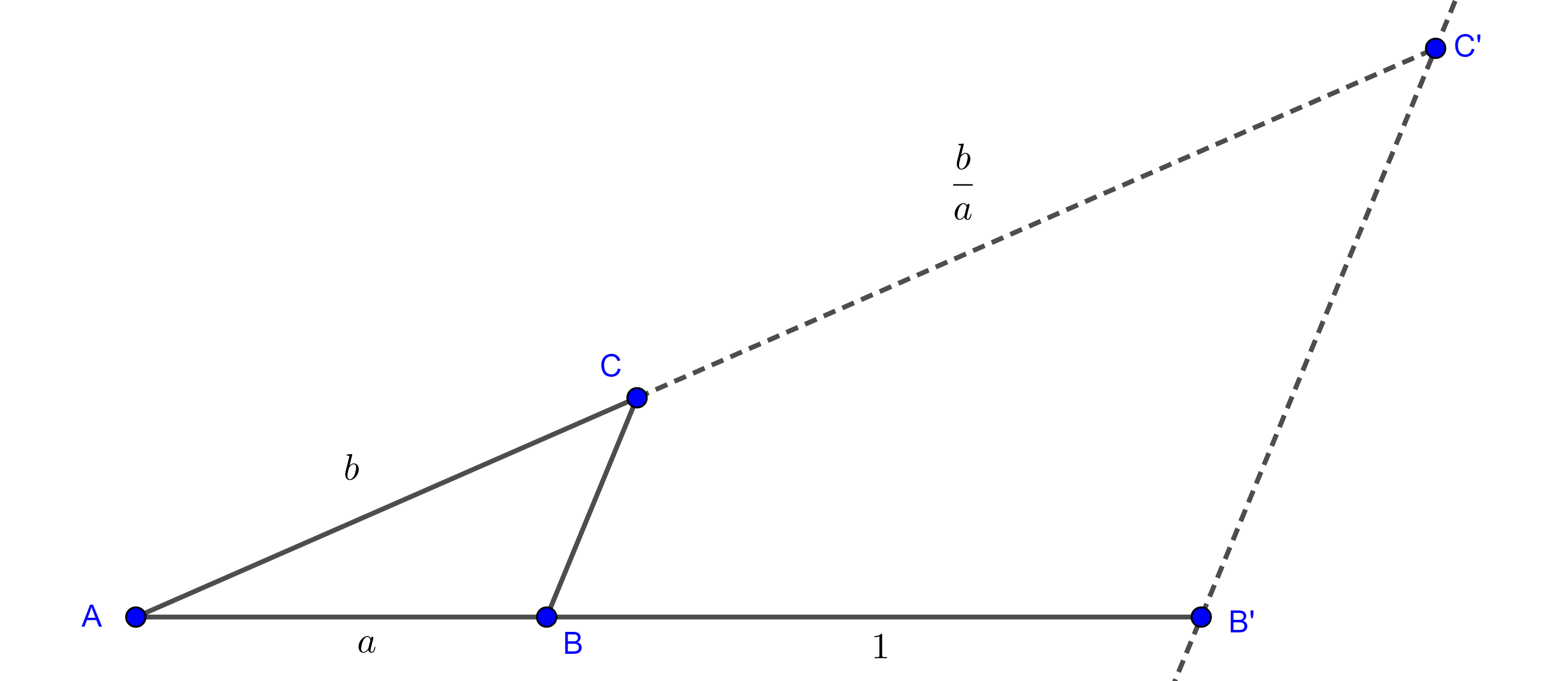
Para el cociente seguimos el mismo procedimiento, pero esta vez con $AB=a$ y $B{B}^{\prime }=1$, por el teorema de Tales obtendremos
$a={\displaystyle \frac{b}{C{C}^{\prime }}}\Rightarrow C{C}^{\prime }={\displaystyle \frac{b}{a}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Más adelante…

En la siguiente entrada y con la ayuda del Teorema de Tales veremos otra herramienta importante en el estudio de la geometría, los criterios de semejanza de triángulos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que la suma de las distancias de un punto interior a los lados de un triangulo equilátero es constante. Este resultado es conocido como teorema de Viviani.

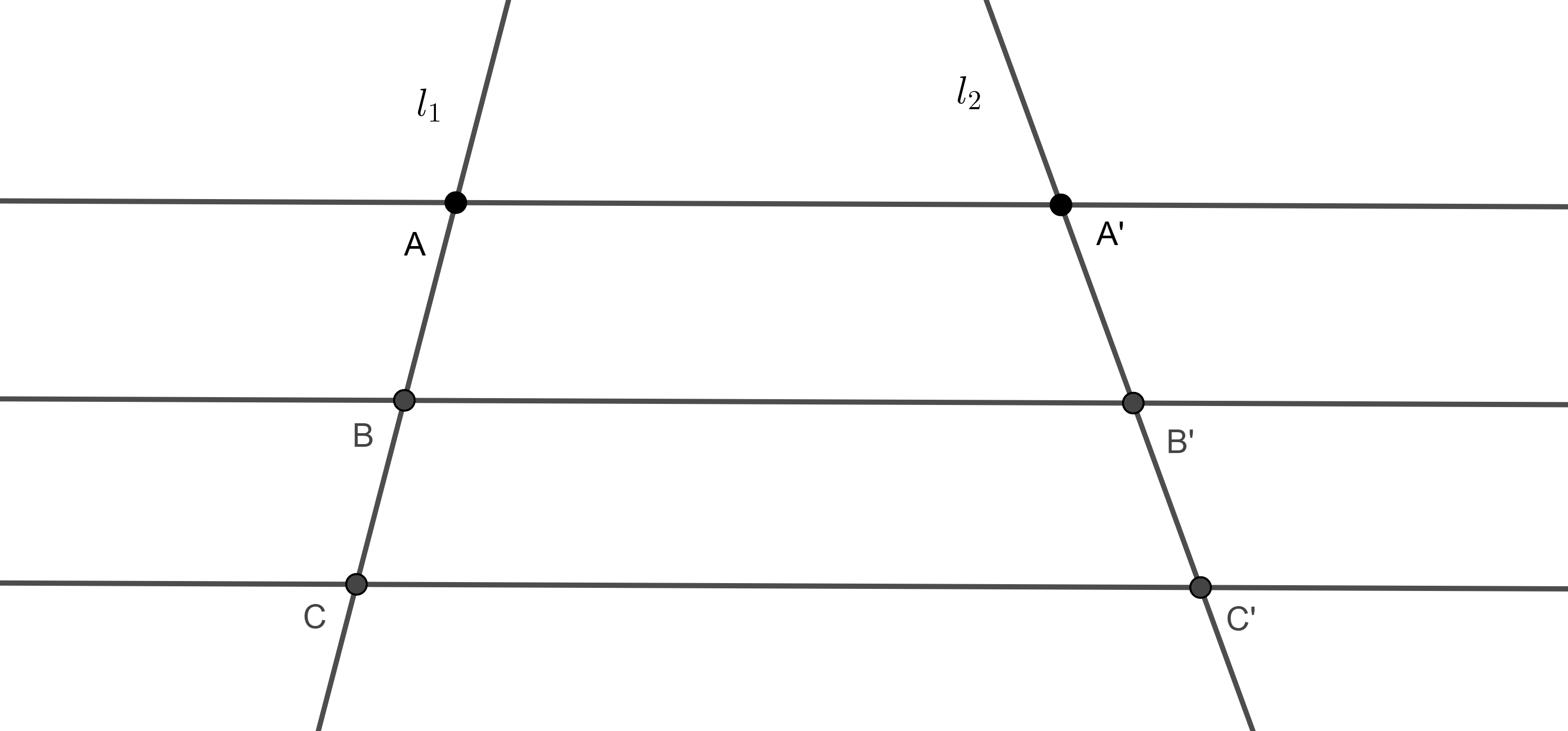
2. $i)$ Muestra que si dos rectas $l_1$ y $l_2$ son transversales a tres paralelas $A{A}^{\prime }$, $B{B}^{\prime }$ y $C{C}^{\prime }$ (figura 11), entonces ${\displaystyle \frac{AB}{BC}}={\displaystyle \frac{A^{\prime }{B}^{\prime }}{B^{\prime }{C}^{\prime }}}$.
   $ii)$ Recíprocamente si ${\displaystyle \frac{AB}{BC}}={\displaystyle \frac{A^{\prime }{B}^{\prime }}{B^{\prime }{C}^{\prime }}}$ y dos de las tres rectas $A{A}^{\prime }$, $B{B}^{\prime }$, $C{C}^{\prime }$son paralelas, entonces las tres rectas son paralelas.

3. Usando el teorema de Tales,
   $i)$ muestra que el segmento que une puntos medios de dos lados de un triangulo es paralelo e igual a la mitad del tercer lado,
   $ii)$ recíprocamente muestra que si una recta pasa por el punto medio de un triangulo y es paralela a un segundo lado entonces pasa por el punto medio del tercer lado.
4. Prueba que un segmento que pasa por el vértice de un triangulo divide externamente al lado opuesto en segmentos proporcionales a los restantes lados del triangulo si y solo si es la bisectriz exterior del ángulo.

5. Divide un segmento dado en una razón dada.
6. Divide un segmento dado en $n$ partes iguales.

Entradas relacionadas

• Ir a Geometría Moderna I
• Entrada anterior del curso: Teorema de Pitágoras.
• Siguiente entrada del curso: Semejanza de triángulos.

Fuentes

• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 13-18, 74-75.
• Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 27-30.
• Geometría interactiva
• Wikipedia
• Math Bits Notebook

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»