Introducción
A lo largo de la segunda unidad abordamos los conceptos de diferenciabilidad y analicidad para una función compleja. En esta cuarta unidad nuestro objetivo será estudiar el concepto de integración para el caso complejo. Como veremos, muchas de las definiciones y propiedades de las integrales de funciones complejas analíticas estarán sustentadas en muchos resultados de nuestros cursos de Cálculo.
En esta entrada algunas definiciones básicas que nos serán de utilidad a o largo de la unidad para definir la integral de una función compleja.
En la segunda unidad del curso definimos de manera formal el concepto de función compleja de variable compleja y mencionamos que es posible trabajar también con funciones reales de variable compleja o funciones complejas de variable real, en esta unidad éstas últimas tomarán un papel importante.
Definición 32.1. (Funciones híbridas.)
Se llama función híbrida a:
- una función real de variable compleja, es decir, $f : S\subset\mathbb{C} \to \mathbb{R}$,
- una función compleja de variable real, es decir, $f : S \subset\mathbb{R} \to \mathbb{C}$.
Observación 32.1.
De forma natural, es claro que para ambos tipos de funciones híbridas hay una noción de continuidad y diferenciabilidad. Sin embargo, solo nos centraremos en definir dichos conceptos para las funciones complejas de variable real, ya que la diferenciabilidad del primer tipo de función híbrida resulta poco interesante, pues una función $f:U \to \mathbb{R}$, con $U\subset\mathbb{C}$ abierto, se puede pensar como una función compleja cuya parte imaginaria es cero y en tal caso, por la proposición 19.3, tendríamos que si $f$ es diferenciable, entonces $f$ debe ser constante.
Por lo tanto, a partir de ahora, al referirnos a una función híbrida asumiremos que estamos considerando a una función compleja de variable real, a menos que se especifique otra cosa.
Observación 32.2.
Dado que $\mathbb{R}\subset\mathbb{C}$, entonces podemos pensar a una función híbrida $f : S \subset\mathbb{R} \to \mathbb{C}$ como una función compleja de variable compleja, cuya parte imaginaria es cero, es decir, $z=t \in \mathbb{R}$. Entonces, por la proposición 12.1, podemos escribir a $f$ como:
\begin{equation*}
f(t) = u(t) + iv(t), \quad \forall t\in S.
\end{equation*}
Definición 32.2. (Continuidad de una función híbrida.)
Sean $(a, b)\subset\mathbb{R}$ un intervalo abierto, $a<b$, y $f : (a, b) \to \mathbb{C}$ una función híbrida. Se dice que $f$ es continua en $t_0 \in (a,b)$ si:
\begin{equation*}
\lim_{t \to t_0} f(t) = f(t_0).
\end{equation*}
Observación 32.3.
De acuerdo con el ejercicio 2 de la entrada 15, tenemos que $f(t) = u(t) + iv(t)$ es una función continua en $(a, b)$ si y solo si las funciones reales $u(t)$ y $v(t)$ son continuas en $(a, b)$.
Definición 32.3. (Continuidad de una función híbrida a trozos.)
Sean $[a, b]\subset\mathbb{R}$ un intervalo cerrado, $a<b$, y $f : [a, b] \to \mathbb{C}$ una función híbrida. Se dice que $f$ es continua a trazos si existe una partición:
\begin{equation*}
P : t_1 < \cdots < t_{n-1},
\end{equation*} del intervalo abierto $(a,b)$ tal que:
- $f(t)$ es continua en todo punto en $(a, b)\setminus\{t_1, t_2, \ldots, t_{n-1}\}$ y existen los límites laterales de $f$ en los extremos del intervalo, es decir:
\begin{equation*}
\lim_{t \to a^+} f(t) \quad \text{y} \quad \lim_{t \to b^-} f(t).
\end{equation*} - Existen y son finitos los límites laterales:
\begin{equation*}
\lim_{t \to t_k^+} f(t) \quad \text{y} \quad \lim_{t \to t_k^-} f(t),
\end{equation*}para todo $k=1, 2,\ldots, n-1$.
Definición 32.4. (Diferenciabilidad de una función híbrida.)
Sean $(a, b)\subset\mathbb{R}$ un intervalo abierto, $a<b$, y $f : (a, b) \to \mathbb{C}$ una función híbrida. Se dice que $f$ es diferenciable en $t_0 \in (a,b)$, si es diferenciable en el sentido real, es decir, si existe el límite:
\begin{equation*}
\dfrac{d}{dt} f(t_0) = f'(t_0) = \lim_{t \to t_0} \frac{f(t) – f(t_0)}{t-t_0} = \lim_{h \to 0} \frac{f(t_0 + h) – f(t_0)}{h},
\end{equation*}en tal caso se dice que $f'(t_0)$ es la derivada de $f$ en $t_0$.
Observación 32.4.
Es posible extender el concepto de diferenciabilidad, de una función híbrida $f$, para un intervalo real cerrado $[a, b]\subset\mathbb{R}$ mediante el concepto de límites laterales, es decir, garantizando la existencia de la derivada en $(a,b)$, de acuerdo con la definición 32.4, y de las derivadas laterales de la función $f$, en los puntos extremos del intervalo $[a,b]$, las cuales están dados por:
\begin{equation*}
f'(a) = \lim_{t \to a^{+}} \frac{f(t) – f(a)}{t-a} \quad \text{y} \quad f'(b) = \lim_{t \to b^{-}} \frac{f(t) – f(b)}{t-b}. \tag{32.1}
\end{equation*}
Observación 32.5.
Sea $f(t) = u(t) + iv(t)$, una función híbrida definida en $(a, b)$. De acuerdo con la proposicición 14.2, es claro que para todo $t\in (a, b)$, se tiene que $f'(t)$ existe si y solo si $u'(t)$ y $v'(t)$ existen, y en tal caso:
\begin{equation*}
f'(t) = u'(t) + i v'(t).
\end{equation*}
Las funciones híbridas satisfacen muchas propiedades sobre derivadas similares a las de las funciones reales, las cuales pueden verificarse fácilmente separando a la función híbrida en su parte real e imaginaria.
Proposición 32.1. (Reglas de derivación para funciones híbridas.)
Sean $(a, b)\subset\mathbb{R}$ un intervalo abierto, $a<b$, y $f , g: (a, b) \to \mathbb{C}$ dos funciones híbridas. Entonces para todo $t\in (a,b)$ y todo $\alpha, \beta \in\mathbb{C}$ se cumple que:
- $\left(\alpha f + \beta g\right)'(t) = \alpha f'(t) + \beta g'(t)$.
- $\left( f \cdot g\right)'(t) = f'(t) g(t) + g'(t) f(t)$.
- $\left( \dfrac{f}{g}\right)'(t) = \dfrac{f'(t) g(t) – g'(t) f(t)}{\left(g(t)\right)^2}$, si $g(t)\neq 0$.
- Regla de la cadena. Si $h:(c,d) \to (a,b)$ es una función diferenciable, entonces:
\begin{equation*}
\left(f \circ h\right)'(t) = f’\left(h(t)\right) h'(t).
\end{equation*}
Demostración. Se deja como ejercicio al lector.
Ejemplo 32.1.
Sea $z\in\mathbb{C}$. Veamos que para $f(t)=e^{zt}$ se cumple que $f'(t)=ze^{zt}$.
Solución. Sea $z=a+ib$, por la proposición 20.2, tenemos que:
\begin{align*}
f'(t) = \frac{d}{dt} e^{zt} & = \frac{d}{dt} e^{at} e^{ibt}\\
& = \frac{d}{dt} e^{at}\left[\operatorname{cos}(bt)+i\operatorname{sen}(bt)\right]\\
& = \frac{d}{dt} e^{at}\operatorname{cos}(bt)+i\frac{d}{dt}e^{at}\operatorname{sen}(bt)\\
& = ae^{at} \operatorname{cos}(bt) – be^{at} \operatorname{sen}(bt) + i\left[ae^{at} \operatorname{sen}(bt) + be^{at} \operatorname{cos}(bt)\right]\\
& =(a+ib)(e^{at}\operatorname{cos}(bt)+ie^{at}\operatorname{sen}(bt)\\
& = z e^{zt}.
\end{align*}
Por lo que $f$ es una función híbrida diferenciable para todo $t\in\mathbb{R}$.
Observación 32.6.
En la regla de la cadena de la proposición anterior hemos considerado composiciones de funciones de la forma:
\begin{equation*}
\mathbb{R} \to \mathbb{R} \to \mathbb{C}.
\end{equation*}
Sin embargo, es posible establecer una regla de la cadena para composiciones de la forma:
\begin{equation*}
\mathbb{R} \to \mathbb{C} \to \mathbb{C}.
\end{equation*}
Para ello recordemos primeramente el siguiente resultado visto en nuestros cursos de Cálculo.
Teorema 32.1. (Regla de la cadena para funciones reales de varias variables.)
Sean $V \subset \mathbb{R}^n$, $U\subset\mathbb{R}^m$ dos conjuntos abiertos, $\gamma : V \to \mathbb{R}^m$ y $f : U \to \mathbb{R}^k$ dos funciones tales que $\gamma\left(V\right) \subset U$. Si $\gamma$ es diferenciable en $t_0 \in V$ y $f$ es diferenciable en $z_0 = \gamma(t_0) \in U$, entonces $f \circ \gamma$ es diferenciable en $t_0$ y se cumple que:
\begin{equation*}
D \left(f \circ \gamma\right)(t_0) = D f \left(z_0\right) \circ D \gamma\left(t_0\right),
\end{equation*}o equivalentemente:
\begin{equation*}
J \left(f \circ \gamma\right)(t_0) = J f \left(z_0\right) J\gamma\left(t_0\right),
\end{equation*}donde $J f(z_0)$ y $J \gamma(t_0)$ son las matrices Jacobianas, de dimensiones $k \times m$ y $m \times n$, respectivamente.
Considerando el resultado anterior tenemos la siguiente:
Proposición 32.2. (Regla de la cadena para la composición de funciones complejas y funciones híbridas.)
Sean $(a, b)\subset\mathbb{R}$ un intervalo real abierto, $a<b$, y $D\subset\mathbb{C}$ un dominio. Si $\gamma:(a, b) \to D$ es una función diferenciable en $t_0 \in (a, b)$ y $f : D \to \mathbb{C}$ es una función analítica en $z_0 = \gamma(t_0) = x_0 + i y_0 \in D$, entonces la función $\varphi=f\circ \gamma$ es diferenciable en $t_0$ y su derivada es:
\begin{equation*}
\varphi'(t_0) = f'(\gamma(t_0)) \gamma'(t_0). \tag{32.2}
\end{equation*}
Debe ser claro que en la igualdad anterior, el término de la derecha corresponde con el producto de los números complejos $f'(\gamma(t_0))$ y $\gamma'(t_0)$.
Demostración. Dadas las hipótesis, sean $f(z) = u(x, y) + iv(x, y)$ y $\gamma(t) = x(t) + i y(t)$.
Notemos que:
\begin{align*}
\varphi(t) = f(\gamma(t)) & = f(x(t) + i y(t))\\
& = u(x(t), y(t)) + iv(x(t), y(t)), \quad \forall t\in(a, b).
\end{align*}
Como $f$ es analítica en $z_0 \in D$, por el teorema 18.3, tenemos que $f$ es dierenciable en el sentido real en $z_0$ y se satisfacen las ecuaciones de C-R en dicho punto. Entonces, de la regla de la cadena para funciones reales de varias variables se sigue que $\varphi = f\circ \gamma$ es diferenciable en $z_0$ y se cumple que:
\begin{equation*}
\varphi'(t_0) = J \left(f \circ \gamma\right)(t_0) = J f \left(z_0\right) J\gamma\left(t_0\right).
\end{equation*}
Dado que se cumplen las ecuaciones de C-R en $z_0 \in D$, entonces, por el ejercicio 3 de la entrada 12, tenemos que:
\begin{align*}
J f \left(z_0\right) & = \begin{pmatrix}
u_x(z_0) & u_y(z_0)\\
v_x(z_0) & v_y(z_0)
\end{pmatrix}\\
& = \begin{pmatrix}
u_x(\gamma(t_0)) & -v_x(\gamma(t_0))\\
v_x(\gamma(t_0)) & u_x(\gamma(t_0))
\end{pmatrix}\\
& = u_x(\gamma(t_0)) + i v_x(\gamma(t_0))\\
& = f'(\gamma(t_0)),
\end{align*}\begin{equation*}
J \gamma\left(t_0\right) = \begin{pmatrix}
x'(t_0)\\
y'(t_0)
\end{pmatrix} = x'(t_0) + i y'(t_0) = \gamma'(t_0),
\end{equation*}por lo que:
\begin{equation*}
\varphi'(t_0) = f'(\gamma(t_0)) \gamma'(t_0).
\end{equation*}
$\blacksquare$
A partir de ahora, nos centraremos en las funciones híbridas que son continuas, ya que como veremos nos serán de gran utilidad al definir el concepto de integral desde la perspectiva compleja. Para hacer clara la notación, utilizaremos letras griegas para hablar de funciones híbridas y reservaremos las letras usuales $f$ y $g$ para hablar de funciones complejas de variable compleja.
Definición 32.5. (Trayectoria y curva en $\mathbb{C}$.)
Sea $[a, b]\subset\mathbb{R}$, con $a<b$, un intervalo real cerrado. A toda función continua $\gamma: [a,b] \to \mathbb{C}$ se le llama una trayectoria en el plano complejo $\mathbb{C}$. A la imagen de $[a, b]$ bajo $\gamma$, es decir, el conjunto:
\begin{equation*}
\Gamma := \gamma\left([a,b]\right) = \left \{\gamma(t) : t\in [a,b] \right\} \subset \mathbb{C},
\end{equation*} se le llama la imagen de la trayectoria o la curva descrita por $\gamma$.
Observación 32.7.
Si consideramos a $z=x+iy \in\mathbb{C}$, tiene sentido adoptar la notación $z(t) = x(t) + iy(t)$ para referirnos a una trayectoria, cuya curva está determinada por cada valor de $t\in [a,b]$, la cual decimos que está parametrizada por las funciones reales continuas $x(t)$ y $y(t)$, definidas en $[a,b]$, a las que llamaremos funciones paramétricas o funciones componentes de $z(t)$. Así, una curva $\gamma$ en $\mathbb{C}$ puede parametrizarse mediante sus funciones componentes como:
\begin{align*}
\gamma(t) &= (x(t), y(t))\\
&= x(t) + iy(t) \in \mathbb{C}, \quad \forall t\in [a,b]. \tag{32.3}
\end{align*}
Observación 32.8.
El uso de la notación $\Gamma$ para referirnos a la curva asociada a la trayectoria $\gamma$ se usará únicamente cuando sea necesario especificar al conjunto de manera explícita. En general, cuando hablemos de $\gamma$ se sobrentenderá que nos referimos a la trayectoria (función híbrida continua) o a su curva asociada (imagen de $\gamma$), por lo que usaremos de forma indistinta la notación y aunque escribamos a $\gamma$ como en (32.3) no debemos confundirnos entre una curva $\Gamma$ y su parametrización $\gamma$. Es común usar alguna letra griega para denotar a alguna curva.
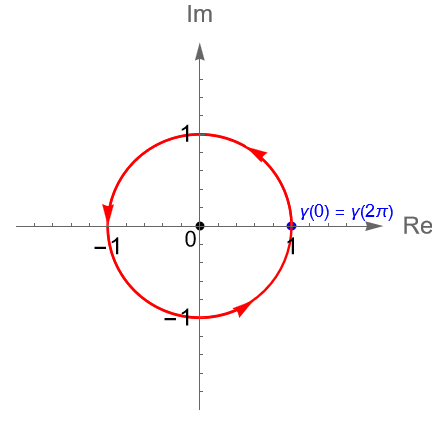
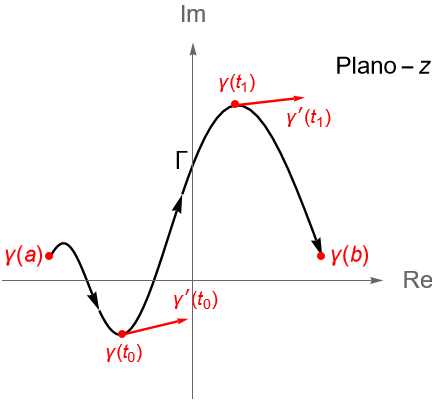
Definición 32.6. (Curva cerrada, orientación, curva simple y curva cerrada simple.)
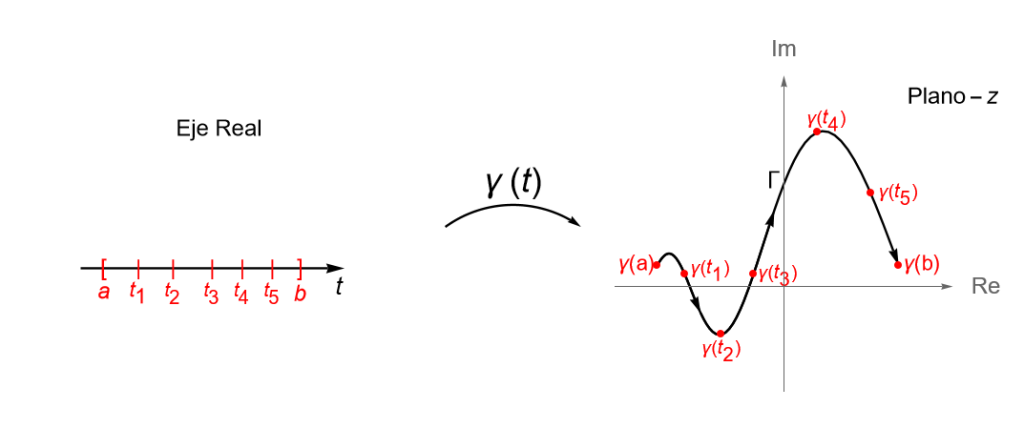
Sea $\gamma: [a,b] \to \mathbb{C}$, con $a<b$, una trayectoria dada por $\gamma(t) = x(t) + iy(t) $, para $t\in [a, b]$. Al punto $\gamma(a) = (x(a), y(a))$ se le llama el {\bf origen} de la curva $\gamma$, mientras que al punto $\gamma(b) = (x(b), y(b))$ se le llama el extremo o final de $\gamma$. Para denotar este sentido en la curva, de manera gráfica se suelen utilizar algunas flechas sobre la gráfica, figura 110, indicando que la curva inicia en $\gamma(a)$ y termina en $\gamma(b)$. Si el origen y el extremo de $\gamma$ son el mismo punto, es decir $\gamma(a) = \gamma(b)$, se dice que la curva es cerrada.
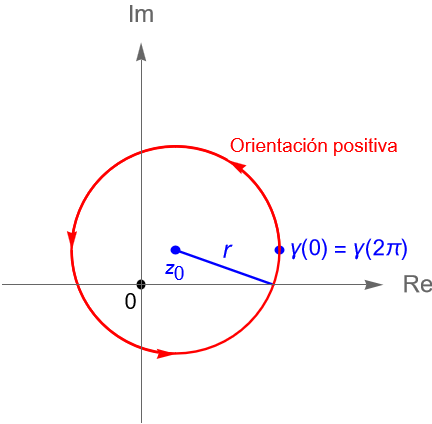
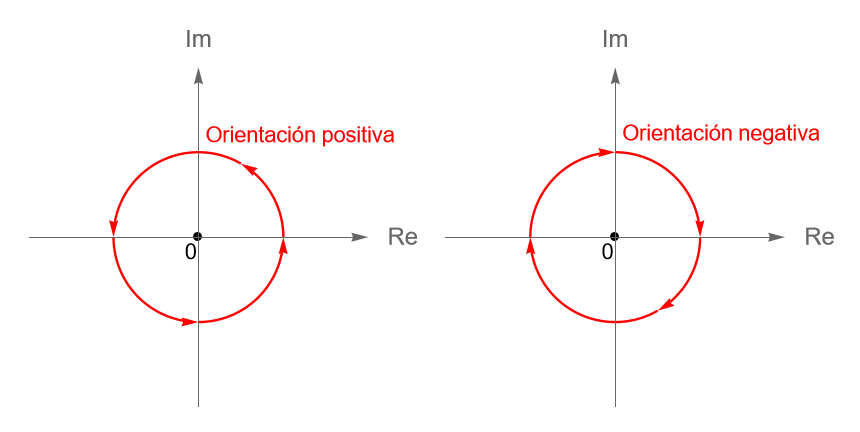
Por otra parte, se dice que el sentido de una curva cerrada o de algún arco de curva tiene orientación o dirección positiva si se recorre en el sentido contrario al de las manecillas del reloj, figura 111, y en caso contrario se dice que tiene orientación o dirección negativa.
Por último, a una curva $\gamma$ que no se corte asimisma, excepto quizás en sus extremos, es decir, $\gamma(t_1) \neq \gamma(t_2)$ si $t_1,t_2\in(a,b)$ y $t_1\neq t_2$, se le llama una curva simple. Si la curva $\gamma$ es cerrada y no se corte asimisma, excepto en sus extremos, se le llama una curva cerrada simple o una curva de Jordan.
Observación 32.9.
Debe ser claro que una curva es simple o cerrada simple, si la función $\gamma$ que la describe es una función inyectiva en $[a,b]$, es decir, su curva asociada no se corta asimisma en más de un punto, correspondiente con sus extremos $\gamma(a) = \gamma(b)$, como podemos ver en el ejemplo 32.3. Aunque no necesariamente una trayectoria debe ser una función inyectiva, por lo que puede suceder que su curva asociada se corte asimisma en más de un punto, incluyendo los extremos, es decir, que la curva se cerrada, pero no simple, como podemos ver en el ejemplo 32.4.
Definición 32.7. (Curva de clase $C^1$ o suave.)
Sea $\gamma : [a, b] \to \mathbb{C}$, con $a<b$, una trayectoria. Se dice que la curva asociada a $\gamma$ es continuamente diferenciable, de clase $C^1$ o suave, lo cual se denota como $\gamma \in C^1\left([a, b]\right)$, si:
- $\gamma$ es diferenciable en $[a, b]$, de acuerdo con la observación 32.4.
- $\gamma’$ es continua en $[a, b]$, es decir, $\gamma’$ es continua en $(a, b)$, y existen los límites laterales de $\gamma’$ en los extremos del intervalo, es decir:
\begin{equation*}
\lim_{t \to a^+} \gamma'(t) \quad \text{y} \quad \lim_{t \to b^-} \gamma'(t).
\end{equation*}
Observación 32.10.
Es importante mencionar que en algunos textos, el término «suave» suele utilizarse para las curvas tales que $\gamma'(t)$ existe y $\gamma'(t) \neq 0$ para todo $t\in[a,b]$, definición 32.8. Sin embargo, para los fines del curso, dicho término se utilizará para hablar de una trayectoria $\gamma(t)$ de clase $C^1([a,b])$.
Definición 32.8. (Curva regular.)
Sea $\gamma: [a,b] \to \mathbb{C}$ una trayectoria, con $a<b$. Se dice que $\gamma$ es una curva regular si:
- $\gamma'(t)$ existe y es continua en $[a,b]$.
- $\gamma'(t) \neq 0$ para todo $t\in(a,b)$.
Observación 32.11.
Para una curva $\gamma$, definida en un intervalo $[a,b]$, tal que $\gamma'(t) \neq 0$ para algún $t\in[a,b]$, debe ser claro que su derivada tiene una interpretación geométrica correspondiente con el vector tangente a la curva $\gamma$ en el punto $\gamma(t)$.
Analicemos los siguientes ejemplos de curvas en el plano complejo $\mathbb{C}$ con las que ya estamos familiarizados.
Ejemplo 32.2. (Segmentos de recta.)
Sean $z_1,z_2\in\mathbb{C}$ con $z_1\neq z_2$. Definimos al segmento de recta con origen $z_1$ y final $z_2$ como la trayectoria:
\begin{equation*}
[z_1, z_2] : [0,1] \to \mathbb{C}, \quad [z_1, z_2](t) := z_1 + (z_2-z_1)t, \quad \forall t\in[0,1].
\end{equation*}
Si $z_1 = a_1 + ib_1$ y $z_2 = a_2 + ib_2$, entonces una parametrización de dicho segmento es $[z_1, z_2](t) = x(t) + iy(t)$, donde:
\begin{equation*}
x(t):=(a_2-a_1)t + a_1, \quad y(t):=(b_2-b_1)t + b_1, \quad t\in[0,1].
\end{equation*}
Notemos que dicha curva es regular ya que $x'(t) = a_2 – a_1 \neq 0$ y $y'(t) = b_2 – b_1 \neq 0$ para todo $ t\in[0,1]$.
Es claro que hemos hecho un abuso en la notación, por lo que es importante no confundir la notación utilizada para la trayectoria $[z,w]$ con la de un intervalo real cerrado.
Observación 32.12.
Es importante enfatizar en el hecho de que una trayectoria puede tener distintas parametrizaciones, pero la misma curva asociada. Por lo que, siempre que sea necesario, se debe especificar la parametrización de la curva con la que se está trabajando.
Ejemplo 32.3.
Consideremos al segmento $[0,1]$. Es claro que la imagen de dicha curva es un segmento de recta en el plano. Sin embargo, notemos que dicha curva puede parametrizarse como:
\begin{align*}
\gamma_1(t) = t, \quad 0\leq t \leq 1,\\
\gamma_2(t) = t^2, \quad 0\leq t \leq 1,\\
\gamma_3(t) = \frac{t}{2}, \quad 0\leq t \leq 2.
\end{align*}
Ejemplo 32.4. (Circunferencias.)
Un ejemplo sencillo de una curva cerrada simple es la circunferencia unitaria $C(0,1)$, con orientación positiva, figura 113, cuya parametrización está dada por:
\begin{equation*}
\gamma(t) = e^{it} = \operatorname{cos}(t) + i \operatorname{sen}(t), \quad 0\leq t \leq 2\pi.
\end{equation*}
Esta curva cerrada es simple y tiene como punto inicial a $\gamma(0) =1$ y punto final a $\gamma(2\pi) =1$.
En general, una circunferencia $C(z_0,r)$, con $r>0$ y $z_0\in\mathbb{C}$ fijo, es un ejemplo de una curva cerrada simple en el plano complejo.
Sean $z_0=a+ib\in\mathbb{C}$ fijo y $r>0$. El conjunto:
\begin{equation*}
C(z_0,r) = \left\{ z = a+r\operatorname{cos}(t) + \left[ b+r\operatorname{sen}(t) \right] \in \mathbb{C} : t\in[0,2\pi]\right\},
\end{equation*}corresponde con la imagen de la trayectoria $ \gamma(t) = z_0 + re^{it}$, con $t\in[0, 2\pi]$, que describe una circunferencia de radio $r>0$ y centro $z_0 = a+ib$, la cual es recorrida en sentido positivo, figura 114, y tiene como parametrización:
\begin{align*}
\gamma(t) & = z_0 + re^{it}\\
& = a +ib + r\left[\operatorname{cos}(t) + i\operatorname{sen}(t)\right]\\
& = a + r\operatorname{cos}(t) + i \left[b +\operatorname{sen}(t)\right], \quad t\in[0, 2\pi],
\end{align*}es decir, $\gamma(t) = x(t) + iy(t)$, donde:
\begin{equation*}
x(t) = a + r\operatorname{cos}(t), \quad y(t) = b +\operatorname{sen}(t), \quad t\in[0, 2\pi].
\end{equation*}
Esta curva cerrada tiene como punto inicial y final a:
\begin{equation*}
z_0 + r = \gamma(0) = \gamma(2\pi).
\end{equation*}
No es difícil verificar que una circunferencia también es una curva regular, por lo que se deja como ejercicio al lector.
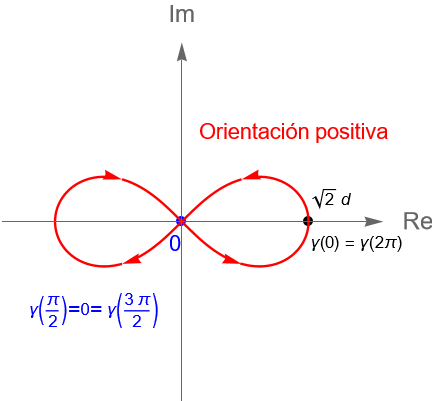
Ejemplo 32.5.
Consideremos a la lemniscata, la cual es una curva en el plano $\mathbb{R}^2$ descrita por la ecuación polar:
\begin{equation*}
r^2 = 2d^2 \operatorname{cos}(2\theta),
\end{equation*}donde $d>0$ es una constante.
Dado que para $\theta \in \left(\dfrac{\pi}{4}, \dfrac{3 \pi}{4}\right) \bigcup \left(-\dfrac{3\pi}{4}, -\dfrac{\pi}{4}\right)$ se tiene que $\operatorname{cos}(2\theta)<0$, entonces para dichos valores de $\theta$ la curva no tiene puntos en el plano.
Una posible parametrización para dicha curva, en el plano complejo $\mathbb{C}$, es $\gamma(t) = x(t)+iy(t)$, donde:
\begin{equation*}
x(t) := \frac{d\sqrt{2}\operatorname{cos}(t)}{1+\operatorname{sen}^2(t)}, \quad y(t) := \frac{d\sqrt{2}\operatorname{sen}(t)\operatorname{cos}(t)}{1+\operatorname{sen}^2(t)}, \quad t\in[0,2\pi].
\end{equation*}
Bajo esta parametrización la curva $\gamma$ tiene una orientación positiva, figura 115. Más aún, como:
\begin{equation*}
\gamma(0) = d\sqrt{2} =\gamma(2\pi),
\end{equation*}entonces dicha curva es cerrada. Sin embargo, la lemniscata no es una curva simple ya que:
\begin{equation*}
\gamma\left(\dfrac{\pi}{2}\right) = 0 = \gamma\left(\dfrac{3\pi}{2}\right),
\end{equation*}con $\dfrac{\pi}{2}, \dfrac{3\pi}{2} \in [0, 2\pi]$ y $\dfrac{\pi}{2} \neq \dfrac{3\pi}{2}$, es decir, $\gamma$ no es inyectiva.
Definición 32.9.
Sea $\gamma : [a,b] \to \mathbb{C}$ una trayectoria y $D \subset \mathbb{C}$ un dominio. Si la curva descrita por $\gamma$ está contenida en $D$, es decir, si la imagen de $\gamma$ es tal que:
\begin{equation*}
\{ \gamma(t) : t\in [a, b]\} \subset D,
\end{equation*}se dice que $\gamma$ es una curva en $D$, lo cual se denota como $\gamma : [a,b] \to D$.
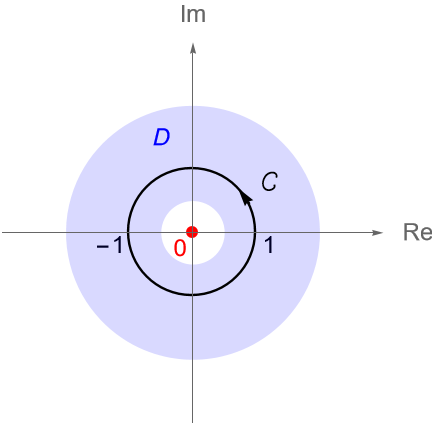
Ejemplo 32.6.
El circulo unitario $\gamma(t) = \operatorname{cos}(t) + i\operatorname{sen}(t)$, con $0 \leq t \leq 2\pi$, figura 116, es una curva en el dominio:
\begin{equation*}
D = \left\{z \in \mathbb{C} : \frac{1}{2} \leq |z| \leq 2 \right\}.
\end{equation*}
Como mencionamos antes, la continuidad de las funciones híbridas resulta fundamental para definir los conceptos básicos para la teoría de la integral compleja.
Definición 32.10 (Curva de clase $C^1$ o suave a trozos.)
Una trayectoria $\gamma: [a,b] \to \mathbb{C}$ es llamada continuamente diferenciable por partes o a trozos, de clase $C^1$ por partes o a trozos o suave por partes o a trozos si existe una partición:
\begin{equation*}
P : a=t_0 < t_1 < \cdots < t_{n-1}<t_n=b,
\end{equation*}del intervalo $[a,b]$ tal que la restricción de $\gamma$ a cada subintervalo $[t_{k-1}, t_k]$, con $1\leq k \leq n$, es de clase $C^1$ o suave, definición 32.7.
En otras palabras, $\gamma$ es continua en $[a,b]$ y para $1\leq k \leq n$:
- $\gamma'(t)$ existe para todo $t\in(t_{k-1}, t_k)$ y en los puntos extremos $t_{k-1}$ y $t_k$ existen los límites laterales (32.1).
- $\gamma'(t)$ es continua en cada intervalo $[t_{k-1}, t_k]$.
Observación 32.13.
Debe ser claro que si $\gamma’$ está definida en $[a,b]$, entonces $\gamma’$ puede tener discontinuidades de salto en algunos $t_k$, ya que aunque existan los límites laterales:
\begin{equation*}
\lim_{t \to t_k^+} \gamma'(t) \quad \text{y} \quad \lim_{t \to t_k^-} \gamma'(t),
\end{equation*}estos pueden no ser iguales.
Definición 32.11. (Contorno o camino en $\mathbb{C}$.)
Se define a un contorno o camino en el plano complejo $\mathbb{C}$, como la unión finita de curvas de clase $C^1$ o de clase $C^1$ a trozos.Es decir, un contorno es una sucesión de curvas suaves $\left\{\gamma_1, \ldots, \gamma_n\right\}$ tal que el punto final de $\gamma_k$ coincide con el punto de origen de $\gamma_{k+1}$, para $1\leq k \leq n-1$.
Es común denotar a un contorno a través de la letra $C$, aunque igual puede utilizarse alguna letra griega.
Ejemplo 32.7.
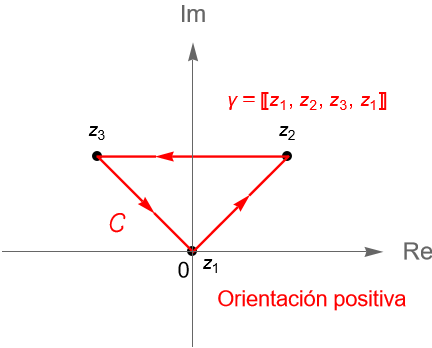
Un ejemplo sencillo de un camino en $\mathbb{C}$ es una poligonal, definición 10.5, la cual podemos pensar como una curva suave a trozos dada por la unión finita de los segmentos de recta $[z_1, z_2], [z_2, z_3], \ldots, [z_{n-1}, z_n]$, cuyo punto de origen es $z_1$ y su punto final es $z_n$. Al igual que cualquier curva, una poligonal puede ser simple, cerrada o cerrada simple.
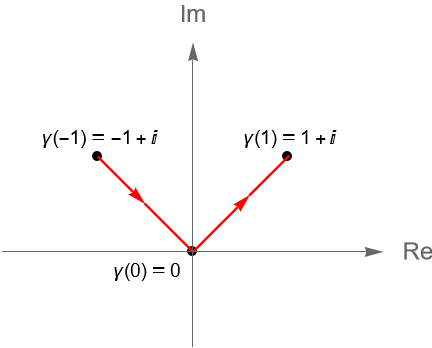
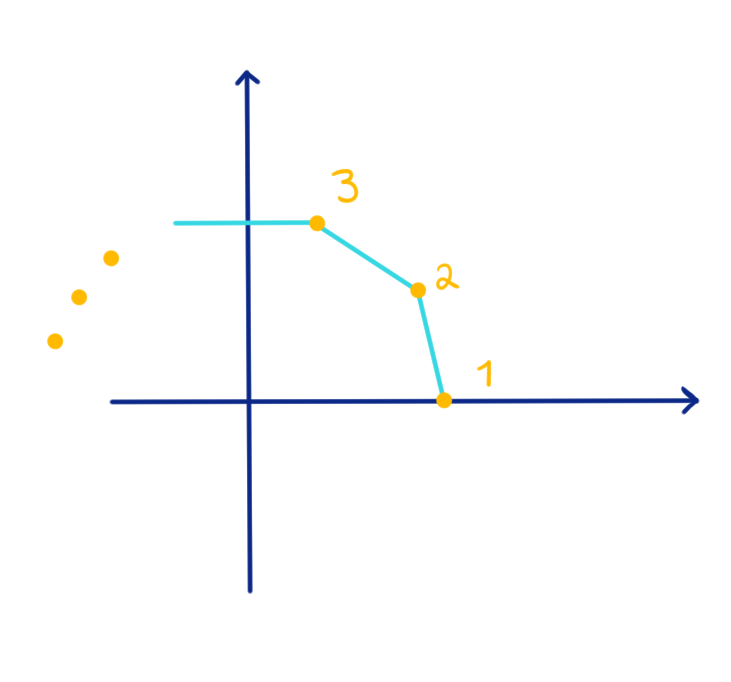
Si consideramos a $z_1=0, z_2 = 1+i$ y $z_3=-1+i$, entonces la poligonal $[z_1, z_2, z_3, z_1]$ resulta ser un camino cerrado simple, figura 117.
Podemos describir al camino $\gamma$, dado por la poligonal $[z_1, z_2, z_3, z_1]$, parametrizando a los segmentos $[z_1, z_2]$, $[z_2, z_3]$ y $[z_3, z_1]$, como las curvas suaves $\gamma_1$, $\gamma_2$ y $\gamma_3$, definidas en el intervalo $[0,1]$, dadas por:
\begin{align*}
\gamma_1(t):=[z_1, z_2](t) & = 0+(1+i-0)t = (1+i)t,\\
\gamma_2(t):=[z_2, z_3](t) & = 1+i+[-1+i-(1+i)]t = 1+i-2t,\\
\gamma_3(t):=[z_3, z_1](t) & = -1+i+[0-(-1+i)]t = (-1+i)(1-t).
\end{align*}
Ejemplo 32.8.
Veamos que la curva dada por $\gamma(t)=t+i|t|$, con $t\in[-1,1]$, no es una curva suave, sin embargo sí es un camino, es decir, una curva suave a trozos.
Solución. Primeramente tenemos que los puntos de origen y final de la curva son, respectivamente:
\begin{equation*}
\gamma(-1)=-1+i|-1|=-1+i \quad \text{y} \quad \gamma(1)=1+i|1|=1+i.
\end{equation*}
Es claro que $\gamma(t)=t+i|t|$ es una trayectoria ya que sus funciones paramétricas $x(t)=t$ y $y(t)=|t|$ son continuas en $[-1,1]$. No es difícil verificar que $\gamma$ es inyectiva y por tanto simple, por lo que se deja como ejercicio al lector.
Podemos visualizar la curva asociada a $\gamma$ en la figura 118.
Gráficamente es claro que en $t=0$ la trayectoria $\gamma$ no es diferenciable. Procedemos a verificarlo de forma analítica. Dado que:
\begin{align*}
\lim_{t\to 0^-} \frac{y(t)-y(0)}{t-0} &= \lim_{t\to 0^-} \frac{|t|}{t} = \lim_{t\to 0^-} \frac{-t}{t} = -1,\\
\lim_{t\to 0^+} \frac{y(t)-y(0)}{t-0} &= \lim_{t\to 0^+} \frac{|t|}{t} = \lim_{t\to 0^+} \frac{t}{t} = 1,
\end{align*}tenemos que $y'(0)$ no existe, entonces, por la observación 32.5, $\gamma'(0)$ no existe, por lo que $\gamma$ no es una curva suave en $[-1,1]$. Sin embargo, notemos que podemos ver a la trayectoria $\gamma$ como:
\begin{equation*}
\gamma(t)= \left\{ \begin{array}{lcc} t-it & \text{si} & -1 \leq t \leq 0 \\ \\ t+it & \text{si} & 0 \leq t \leq 1 \end{array} \right.
\end{equation*}
Veamos entonces que bajo la restricción de $\gamma$ a los intervalos $[-1,0]$ y $[0,1]$ obtenemos curvas suaves.
Para $t\in[-1,0]$ tenemos que $\gamma(t)=t-it$ es una función continua. Más aún, para $t_0\in(-1,0)$ tenemos que:
\begin{equation*}
\gamma'(t_0) = \lim_{t\to t_0} \frac{\gamma(t)-\gamma(t_0)}{t-t_0} = \lim_{t\to t_0} \frac{(t-t_0)(1-i)}{t-t_0} = 1-i.
\end{equation*}
Mientras que:
\begin{align*}
\gamma'(-1) &= \lim_{t \to -1^{+}} \frac{\gamma(t)-\gamma(-1)}{t-(-1)} = \lim_{t \to -1^{+}} \frac{(1-i)(t+1)}{t+1} = 1-i,\\
\gamma'(0) &= \lim_{t \to 0^{-}} \frac{\gamma(t)-\gamma(0)}{t-0} = \lim_{t \to 0^{-}} \frac{t-it}{t} = 1-i,
\end{align*}por lo que es claro que $\gamma'(t)$ existe para todo $t\in[-1,0]$ y es una función continua en dicho intervalo, entonces para $t\in[-1,0]$ tenemos que $\gamma(t)=t-it$ es una curva suave.
De manera análoga, se puede verificar que para $t\in[0,1]$ la trayectoria $\gamma(t)=t+it$ es una curva suave. Por lo tanto, la curva dada por $\gamma(t)=t+i|t|$, con $t\in[-1,1]$, es una curva suave a trazos, es decir, es un camino en $\mathbb{C}$.
Ejemplo 32.9.
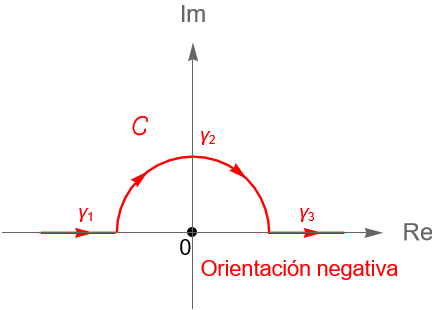
El contorno $C$ dado en la figura 119 está formado por las curvas suaves $\gamma_1(t)=t, \gamma_2(t)=e^{i\frac{\pi}{2}(1-t)}$ y $\gamma_3(t)=t$ determinadas por el segmento de recta $[-2, -1]$, la semicircunferencia unitaria en el semiplano superior y el segmento de recta $[1, 2]$, respectivamente.
Podemos parametrizar al contorno $C$ mediante la trayectoria:
\begin{equation*}
\gamma:[-2,2] \to \mathbb{C},
\end{equation*}dada por:
\begin{equation*}
\gamma(t) = \left\{ \begin{array}{lcc}
t & \text{si} & -2 \leq t \leq -1,\\
\\ e^{i\frac{\pi}{2}(1-t)}, & \text{si} & -1 \leq t \leq 1, \\
\\ t, & \text{si} & 1 \leq t \leq 2. \end{array} \right.
\end{equation*}
Existen dos métodos elementales para modificar o combinar curvas, con el objetivo de obtener nuevas curvas.
Definición 32.12. (Curva opuesta.)
Si $\gamma: [a,b] \to \mathbb{C}$ es una trayectoria, con $a<b$, se define a la curva opuesta de $\gamma$, la cual se denota como $-\gamma$, a la trayectoria:
\begin{equation*}
-\gamma:[a,b]: \to \mathbb{C},
\end{equation*}dada por:
\begin{equation*}
-\gamma(t) := \gamma(b+a-t), \quad \forall t\in[a,b]. \tag{32.4}
\end{equation*}
Debe ser claro que la curva asociada a $\gamma$ y a $-\gamma$ es la misma, pero $\gamma(t)$ y $-\gamma(t)$ recorren dicha curva en sentido contrario, es decir, la orientación de una respecto a la otra es opuesta conforme $t$ toma valores en $[a,b]$. En particular, el punto de origen de una es el punto final de la otra.
Observación 32.14.
Se puede probar que si $\gamma$ es una curva suave a trozos, entonces $-\gamma$ también es una curva suave a trozos, ejercicio 3.
Ejemplo 32.10.
Determinemos la curva opuesta del segmento de recta $[z_1, z_2]$, con $z_1 \neq z_2$.
Solución. De acuerdo con el ejemplo 32.2 sabemos que una parametrización del segmento $[z_1, z_2]$ está dada por la trayectoria:
\begin{equation*}
\gamma:[0,1]: \to \mathbb{C},
\end{equation*}dada por:
\begin{equation*}
\gamma(t) = z_1 + (z_2-z_1)t, \quad \forall t\in[0,1],
\end{equation*}por lo que, considerando (32.4) tenemos que:
\begin{equation*}
-\gamma(t) = \gamma(1-t) = z_1 + (z_2-z_1)(1-t) = z_2 + (z_1-z_2)t, \quad \forall t\in[0,1].
\end{equation*}
Definición 32.13. (Curva suma o yuxtaposición.)
Si $\gamma_1: [a_1,b_1] \to \mathbb{C}$ y $\gamma_2: [a_2,b_2] \to \mathbb{C}$, con $a_i<b_i$ para $i=1, 2$, son dos trayectorias tales que $\gamma_1(b_1) = \gamma_2(a_2)$, se define a la curva suma o a la yuxtaposición de $\gamma_1$ y $\gamma_2$, la cual se denota como $\gamma_1+\gamma_2$, a la trayectoria:
\begin{equation*}
\gamma_1+\gamma_2:[a_1,b_1+b_2-a_2]: \to \mathbb{C},
\end{equation*}dada por:
\begin{equation*}
(\gamma_1+\gamma_2)(t) :=\left\{ \begin{array}{lcc}
\gamma_1(t), & \text{si} & a_1 \leq t \leq b_1,\\ \\ \gamma_2(t-b_1+a_2), & \text{si} & b_1 \leq t \leq b_1 +b_2 – a_2. \end{array} \right.
\end{equation*}
La curva asociada a la trayectoria $\gamma_1+\gamma_2$ corresponde con la curva de $\gamma_1$ seguida de la de $\gamma_2$.
Observación 32.15.
En general, se puede definir por inducción la suma finita $\gamma_1 + \cdots + \gamma_n$, de las trayectorias $\gamma_k: [a_k,b_k] \to \mathbb{C}$, con $1\leq k \leq n$, tales que $\gamma_j(b_j) = \gamma_{j+1}(a_{j+1})$ para $j=1,2,\ldots,n-1$. De hecho se puede probar que la suma de trayectorias de clase $C^1$ a trozos es también una trayectoria suave, ejercicio 3. Más aún, se puede verificar que una trayectoria $\gamma$ de clase $C^1$ a trozos se puede expresar como la suma finita de trayectorias suaves, es decir, $\gamma = \gamma_1 + \cdots + \gamma_n$, ejercicio 6.
Ejemplo 32.11.
De acuerdo con la definición 32.13 y la observación 32.15, no es difícil verificar que el camino $\gamma$ del ejemplo 32.7, que describe a la poligonal $[z_1, z_2, z_3, z_1]$, con $z_1=0, z_2 = 1+i$ y $z_3=-1+i$, figura 117, se puede ver como la suma de las curvas suaves:
\begin{align*}
\gamma_1(t) = (1+i)t, \quad \gamma_2(t) = 1+i-2t, \quad \gamma_3(t) = (-1+i)(1-t), \quad \forall t\in[0,1],
\end{align*}es decir:
\begin{equation*}
\gamma := (\gamma_1+\gamma_2 +\gamma_3) : [0, 3] \to \mathbb{C}
\end{equation*}dada por:
\begin{equation*}
\gamma(t) = (\gamma_1+\gamma_2+\gamma_3)(t) =\left\{ \begin{array}{lcc}
(1+i)t & \text{si} & 0 \leq t \leq 1,\\
\\ 3+i-2t, & \text{si} & 1 \leq t \leq 2, \\
\\ (-1+i)(3-t), & \text{si} & 2 \leq t \leq 3. \end{array} \right.
\end{equation*}
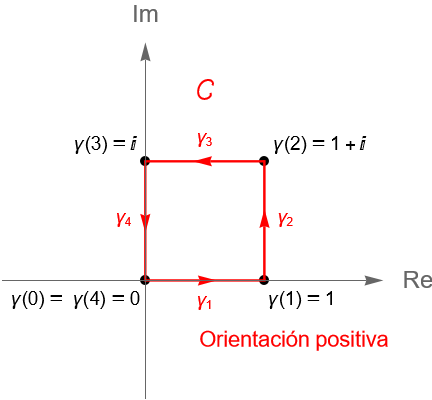
Ejemplo 32.12.
Consideremos a la curva $\gamma:[0,4]\to\mathbb{C}$ dada por:
\begin{equation*}
\gamma(t) = \left\{ \begin{array}{lcc}
t & \text{si} & 0 \leq t \leq 1,\\
\\ 1+i(t-1), & \text{si} & 1 \leq t \leq 2, \\
\\ 3-t+i, & \text{si} & 2 \leq t \leq 3, \\
\\ i(4-t), & \text{si} & 3 \leq t \leq 4. \end{array} \right.
\end{equation*}
Dicha curva es un contorno cerrado simple, ya que es una curva suave a trozos, cerrada simple. Más aún, dicha curva corresponde con la frontera del cuadrado con vértices en $z_1=0, z_2=1, z_3=1+i$ y $z_4=i$, la cual puede verse como la suma de los segmentos de recta $[z_1, z_2]$, $[z_2, z_3]$ y $[z_3, z_1]$, es decir, como la poligonal cerrada $[z_1, z_2, z_3, z_1]$, figura 120.
Definición 32.14. (Reparametrización de una curva en $\mathbb{C}$.)
Sean $\gamma: [a,b] \to \mathbb{C}$ y $\beta: [c,d] \to \mathbb{C}$, con $a<b$ y $c<d$, dos trayectorias suaves. Si existe una biyección $\sigma:[c,d] \to [a,b]$ continua y de clase $C^1$, tal que $\sigma$ es creciente y $\beta=\gamma\circ \sigma$, se dice que $\beta$ es una reparametrización de $\gamma$.
Observación 32.16.
De la definición anterior debe ser claro que aunque la parametrización de $\gamma$ y $\beta$ sea distinta, ambas trayectorias tienen la misma curva asociada y existe una relación entre la parametrización de cada trayectoria descrita por la función $\sigma$. Más aún, se puede verificar que si $\sigma$ es una función de clase $C^1$ o de clase $C^1$ a trozos, se tiene una reparametrización de clase $C^1$ o de clase $C^1$ a trozos, respectivamente.
Ejemplo 32.13.
Veamos que las siguientes trayectorias $\beta$ son una reparametrización de la trayectorias $\gamma$ dadas.
a) Sean $z_1, z_2\in\mathbb{C}$ tales que $z_1 \neq z_2$. Sean $\beta:\left[0, k\right] \to \mathbb{C}$, con $k=|z_2-z_1|>0$, y $\gamma:[0,1] \to \mathbb{C}$ dadas, respectivamente, por:
\begin{equation*}
\beta(t) = z_1 + \frac{(z_2-z_1)t}{k}, \quad \gamma(t) = z_1 + (z_2-z_1)t.
\end{equation*}
Solución. Sea $\sigma:[0,k]\to[0,1]$ dada por $\sigma(t)=\dfrac{t}{k}$, con $k=|z_2-z_1|>0$. Claramente $\sigma$ es una función biyectiva continua, de clase $C^1$ con derivada $\sigma'(t)=\dfrac{1}{k}>0$ para todo $t\in[0,k]$, por lo que $\sigma$ es una función creciente. Más aún, tenemos que:
\begin{equation*}
\gamma(\sigma(t))= \gamma\left(\dfrac{t}{k}\right) = z_1 + \frac{(z_2-z_1)t}{k} = \beta(t), \quad \forall t\in[0,k],
\end{equation*}por lo que $\beta$ es una reparametrización de $\gamma$.
b) Sean $z_0\in\mathbb{C}$ fijo y $r>0$. Sean $\gamma:\left[0, 2\pi\right] \to \mathbb{C}$ y $\beta:[0,1] \to \mathbb{C}$ dadas, respectivamente, por:
\begin{equation*}
\gamma(t) = z_0 + re^{it}, \quad \beta(t) = z_0 + re^{i2\pi t}.
\end{equation*}
Solución. Sea $\sigma:[0,1]\to[0,2\pi]$ dada por $\sigma(t)=2\pi t$. Es claro que $\sigma$ es una función biyectiva continua, de clase $C^1$ con derivada $\sigma'(t)=2\pi>0$ para todo $t\in[0,1]$, por lo que $\sigma$ es una función creciente. Tenemos que:
\begin{equation*}
\gamma(\sigma(t))= \gamma\left(2\pi t\right) = z_0 + re^{i2\pi t} = \beta(t), \quad \forall t\in[0,1],
\end{equation*}por lo que $\beta$ es una reparametrización de $\gamma$.
De nuestros cursos de Cálculo sabemos que la longitud del arco de una curva es una cantidad bastante útil. Recordemos que si $\gamma:[a,b] \to\mathbb{R}^2$ es una curva suave parametrizada por las funciones reales $x, y:[a,b] \to\mathbb{R}$, es decir, $\gamma(t) = (x(t), y(t))$, entonces la longitud del arco de dicha curva se puede obtener como:
\begin{equation*}
\int_{a}^{b} \sqrt{[x'(t)]^2+[y'(t)]^2} \,dt. \tag{32.5}
\end{equation*}
Motivados en lo anterior tenemos la siguiente:
Definición 32.15. (Longitud de una curva en $\mathbb{C}$.)
Sea $\gamma: [a,b] \to \mathbb{C}$, con $a<b$, una trayectoria suave a trozos. Se define la longitud de $\gamma$ como:
\begin{equation*}
\ell(\gamma):= \int_{a}^{b}|\gamma'(t)| \, dt.
\end{equation*}
Definición 32.16. (Curva rectificable en $\mathbb{C}$.)
Sea $\gamma: [a,b] \to \mathbb{C}$, con $a<b$, una trayectoria suave a trozos. Se dice que la curva $\gamma$ es rectificable si tiene longitud finita.
Observación 32.17.
Geométricamente es claro que $\ell(\gamma)$ es igual a longitud del arco de la curva asociada a $\gamma$.
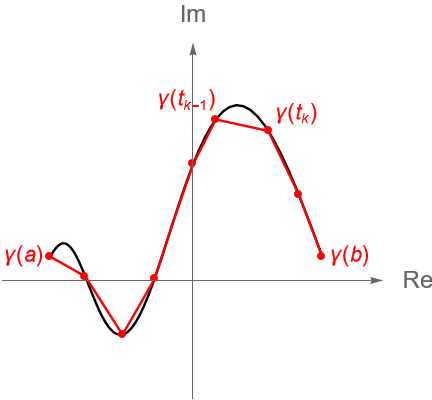
Sabemos que la longitud de la curva $\gamma(t)=x(t)+iy(t)$ se puede aproximar sumando la longitud de segmentos de rectas dados por puntos sobre la curva, es decir, obteniendo la longitud de una poligonal formada por una partición:
\begin{equation*}
P : a=t_0 < t_1 < \cdots < t_{n-1}<t_n=b,
\end{equation*}del intervalo $[a,b]$, figura 121. Dicha longitud se puede obtener mediante:
\begin{equation*}
\sum_{k=1}^n |\gamma(t_k) – \gamma(t_{k-1})| = \sum_{k=1}^n \sqrt{\left[x(t_k)-x(t_{k-1})\right]^2+\left[y(t_k)-y(t_{k-1})\right]^2}.
\end{equation*}
Entonces, la longitud de $\gamma$ es el límite, cuando este existe, de las sumas del lado derecho de la igualdad conforme la partición de $[a,b]$ se refina. Considerando lo anterior, no es difícil mostrar analíticamente que una curva suave a trozos es rectificable, es decir, el límite anterior está dado por (32.5), por lo que los detalles se dejan como ejercicio al lector.
Se puede consultar a detalle la prueba de este hecho en:
- Introducción a funciones analíticas y transformaciones conformes, Gabriel D. Villa Salvador.
- Function of One Complex Variable, John B. Conway.
Ejemplo 32.14.
Determinemos las longitudes de las siguientes trayectorias.
a) Sean $z_1, z_2\in\mathbb{C}$ tales que $z_1 \neq z_2$. Sea $\gamma:\left[0, 1\right] \to \mathbb{C}$, dada por:
\begin{equation*}
\gamma(t) = z_1 + (z_2-z_1)t.
\end{equation*}
Solución. Geométricamente la curva asociada a $\gamma$ es el segmento de recta que une a $z_1$ y $z_2$. Más aún, es claro que $\gamma$ es una curva suave con derivada $\gamma'(t) = z_2-z_1\neq 0$, para todo $t\in[0,1]$, por lo que:
\begin{equation*}
\ell(\gamma) = \int_{0}^{1}|\gamma'(t)| \, dt = \int_{0}^{1}|z_2-z_1| \,dt = |z_2-z_1|.
\end{equation*}
b) Sean $z_0\in\mathbb{C}$ fijo y $r>0$. Sea $\gamma:\left[0, 2\pi\right] \to \mathbb{C}$, dada por:
\begin{equation*}
\gamma(t) = z_0 + re^{it}.
\end{equation*}
Solución. Geométricamente sabemos que la curva asociada a $\gamma$ es la circunferencia con centro en $z_0$ y radio $r$, la cual es una curva suave con derivada:
\begin{equation*}
\gamma'(t) = r ie^{it}\neq 0, \quad \forall t\in[0,1],
\end{equation*}por lo que:
\begin{equation*}
\ell(\gamma) = \int_{0}^{2\pi}|\gamma'(t)| \, dt = \int_{0}^{2\pi}|r ie^{it}| \, dt = \int_{0}^{2\pi} r \, dt = 2\pi r.
\end{equation*}
Tarea moral
- Describe las propiedades de las siguientes curvas.
a) $\gamma(t)=t^2+it^4$, para $t\in[-1,1]$.
b) $\gamma(t)=e^{-it^2}$, para $t\in[0,\sqrt{2\pi}]$.
c) $\gamma(t)=2\operatorname{cos}(t)+i\operatorname{sen}(t)$, para $t\in[0,2\pi]$.
d) $\gamma(t)=exp\left(i\pi\sqrt[3]{t}\right)$, para $t\in[-1,1]$.
e) $\gamma(t)=e^{t}+ie^{-t}$, para $t\in[0,1]$. - Determina las reglas de correspondencia de las trayectorias $-\alpha$, $-\beta$, $-\gamma$, $\alpha-\beta$, $\beta-\gamma$, $\alpha-\beta+\gamma$ y $-\alpha+\beta-\gamma$, para $\alpha(t)=t+it$, $\beta(t)=t+it^2$ y $\gamma(t)=t^2+it$, con $t\in[0,1]$. En cada caso determina la gráfica de la curva correspondiente.
- Sean $\gamma:[a,b]\to\mathbb{C}$ y $\beta:[c,d]\to\mathbb{C}$ dos curvas suaves a trozos tales que $\gamma(b) = \beta(c)$. Prueba que $-\gamma$ y $\gamma+\beta$ son también curvas suaves a trozos.
- Sean $\alpha:[a_1,a_2]\to\mathbb{C}$, $\beta:[b_1,b_2]\to\mathbb{C}$ y $\gamma:[c_1,c_2]\to\mathbb{C}$ tres curvas suaves tales que $\alpha(a_2) = \beta(b_1)$ y $\beta(b_2) = \gamma(c_1)$. Prueba que $\alpha+(\beta+\gamma) = (\alpha+\beta)+\gamma$.
- Sea $\gamma:[a,b]\to\mathbb{C}$ una curva y $a<c<b$. Prueba que $\gamma = \alpha+\beta$, donde $\alpha$ es la restricción de $\gamma$ al intervalo $[a,c]$ y $\beta$ es la restricción de $\gamma$ al intervalo $[c,b]$. ¿Cómo se puede utilizar este hecho para generalizar el resultado para una partición arbitraria $P : a=t_0<t_1<\cdots<t_n=b$ del intervalo $[a,b]$?
- Prueba que una curva suave a trozos $\gamma$ se puede expresar como la suma finita de curvas suaves.
Hint: Utiliza el ejercicio 4. - Sea $f(t)=t^2\operatorname{sen}\left(\frac{1}{t}\right)$ para $t\neq 0$ y $f(0)=0$. Prueba que la curva $\gamma(t)=t+if(t)$, con $t\in[-\pi, \pi]$, no es un contorno.
- Verifica que la trayectoria:
\begin{equation*}
\gamma : [0, 1] \to \mathbb{C}
\end{equation*}dada por:
\begin{equation*}
\gamma(t) = \left\{ \begin{array}{lcc}
3t(1+i) & \text{si} & 0 \leq t \leq \frac{1}{3},\\
\\ 3+i-6t, & \text{si} & \frac{1}{3} \leq t \leq \frac{2}{3}, \\
\\ (-1+i)(3-3t), & \text{si} & \frac{2}{3} \leq t \leq 1. \end{array} \right.
\end{equation*} es otra parametrización del camino $C$ dado en el ejemplo 32.10. - Demuestra la proposición 32.1.
- Determina la derivada de las siguientes funciones híbridas.
a) $f(t)=te^{-it}$.
b) $f(t)=e^{i2t^2}$.
c) $f(t)=(2+i)\operatorname{cos}(3it)$.
d) $f(t)=\operatorname{Log}(it)$.
e) $f(t)=\dfrac{2+i+t}{-i-2t}$.
f) $f(t)=\left(\dfrac{t+i}{t-i}\right)^2$.
Más adelante…
En esta primera entrada, de la cuarta unidad, hemos abordado algunos conceptos básicos pero elementales para la teoría de la integración compleja, entre ellos definimos lo que es una función híbrida, trayectoria, curva y contorno en el plano complejo $\mathbb{C}$. Vimos algunas de las propiedades de las funciones híbridas y probamos un resultado con el que ya estamos familiarizados por nuestros cursos de Cálculo, correspondiente con la regla de la cadena para la composición de funciones complejas y funciones híbridas.
En la siguiente entrada definiremos de manera formal a la integral para el caso complejo. Como veremos muchas de las definiciones que daremos estarán sustentadas en los resultados de Cálculo para las integrales de funciones reales e integrales de línea para funciones de varias variables.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Funciones complejas elementales como series de potencias.
- Siguiente entrada del curso: Integrales de funciones híbridas.