Una de las cosas más impresionantes sobre las matemáticas es que la gente que
la practica no están normalmente interesadas en su aplicación, porque
las matemáticas en si mismas son una forma de hermoso arte.
– Danica McKellar
Introducción
¡Hemos llegado a la última entrada del curso!
Concluiremos esta unidad con la introducción a un importante teorema de la teoría cualitativa de las ecuaciones diferenciales. El teorema de Poincaré – Bendixson.
La demostración a este teorema suele ser compleja y requiere de definiciones y resultados previos, algunos de ellos sobre topología elemental. En este curso sólo enunciaremos este teorema en una versión simplificada de manera que podamos aplicarlo a los sistemas no lineales de dos ecuaciones diferénciales, por esta razón es que este teorema también se conoce como teorema de Poincaré – Bendixson en el plano.
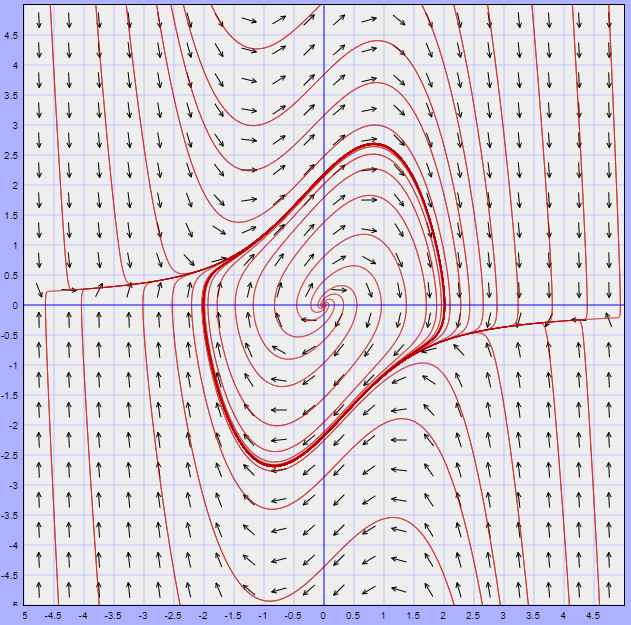
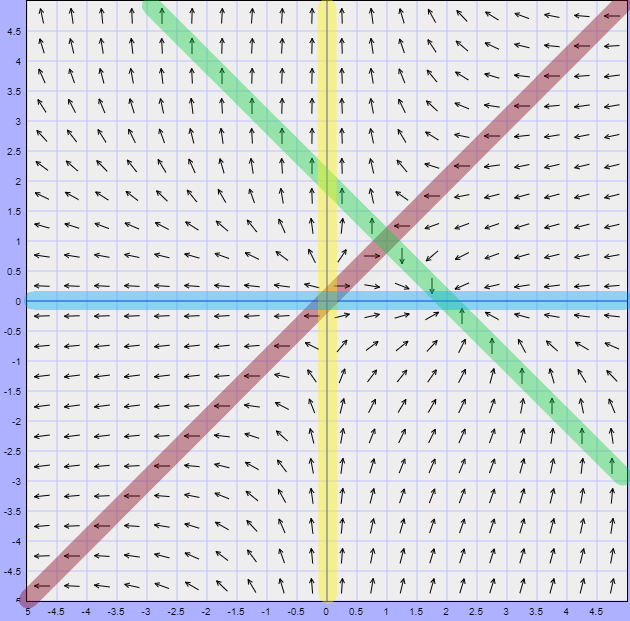
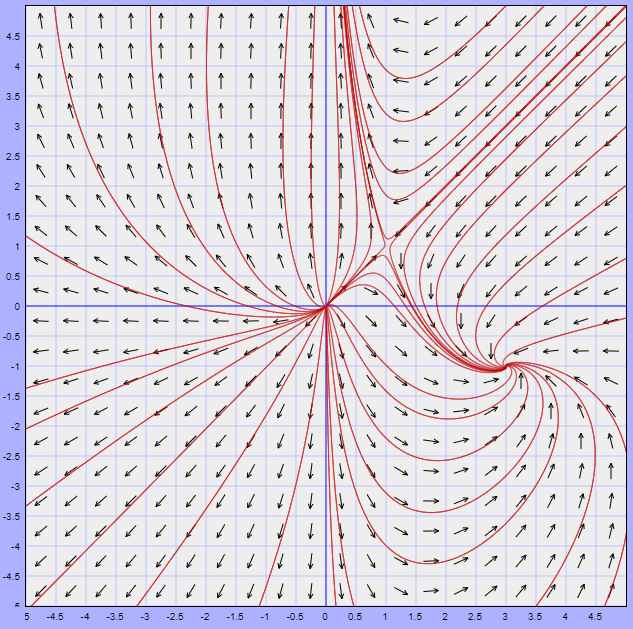
En la entrada sobre linearización visualizamos el plano fase del sistema
\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -x + \mu(1 -x^{2})y \label{1} \tag{1}
\end{align*}
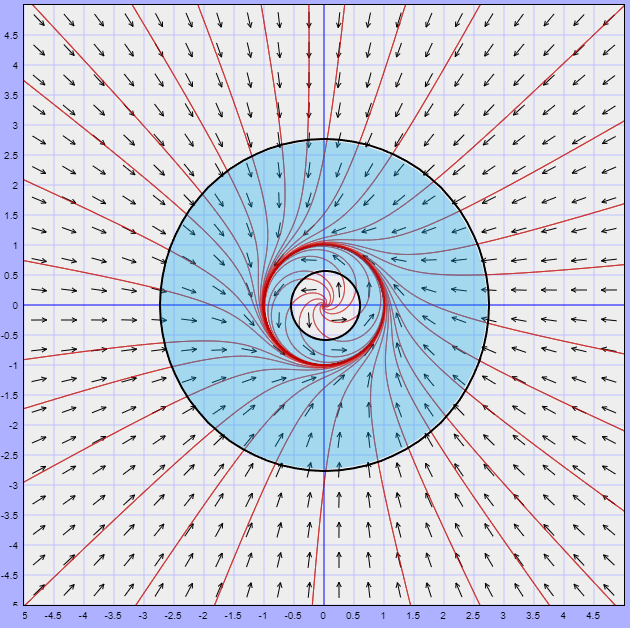
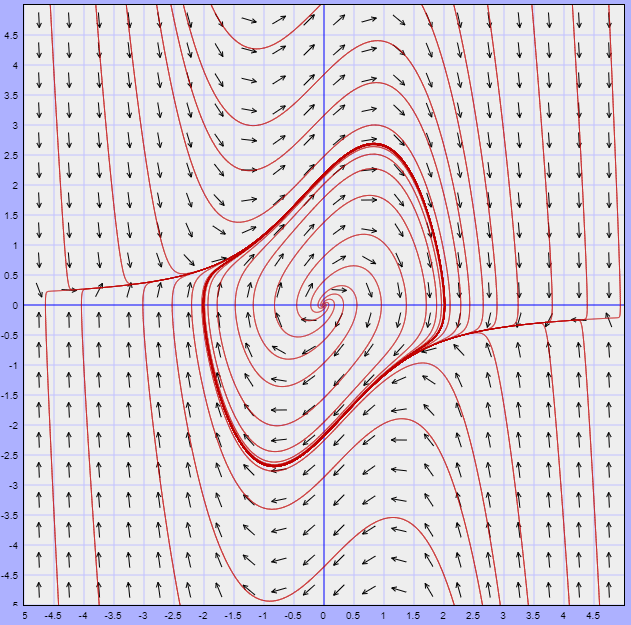
Para el caso en el que $\mu = 1$. Dicho plano fase fue el siguiente.
El sistema (\ref{1}) en realidad se deduce de la ecuación diferencial de segundo orden
$$\dfrac{d^{2}y}{dt^2} + \mu(y^{2} -1) \dfrac{dy}{dt}+ y = 0 \label{2} \tag{2}$$
la cual lleva por nombre ecuación de Van der Pol y representa el movimiento de un oscilador con amortiguamiento no lineal.
Lo que podemos observar del plano fase es que existe una trayectoria límite (resaltada en rojo) que de alguna manera divide al plano fase en secciones. Si nos concentramos en la trayectoria periódica formada, entonces podemos hablar de la zona interior y la zona exterior a dicha trayectoria y lo que observamos es que por fuera de ella todas las trayectorias tienden a la trayectoria periódica, mientras que dentro de ella todas se alejan del origen para aproximarse, de igual manera, a la trayectoria límite.
Esto es lo que se conoce como un ciclo límite y lo presentan algunos sistemas no lineales. El teorema de Poincaré – Bendixson nos dará las condiciones necesarias para asegurar que un sistema no lineal presenta ciclos límites.
Antes de continuar haremos un breve paréntesis para recordar un par de resultados importantes de las coordenadas polares que nos servirán para hacer más sencillos los cálculos de los ejemplos que realicemos más adelante.
Coordenadas polares
Las coordenadas cartesianas se relacionan con las polares a través de las siguientes relaciones.
\begin{align*}
x &= r \cos(\theta) \\
y &= r \sin(\theta) \label{3} \tag{3}
\end{align*}
Es claro que
\begin{align*}
r^{2} &= x^{2} + y^{2} \\
\theta &= \arctan \left( \dfrac{y}{x} \right) \label{4} \tag{4}
\end{align*}
Derivemos explícitamente cada una de estas ecuaciones. Por un lado, derivando la ecuación de $r$, se tiene
$$2r \dfrac{dr}{dt} = 2x \dfrac{dx}{dt} + 2y \dfrac{dy}{dt}$$
o bien,
$$r \dfrac{dr}{dt} = x \dfrac{dx}{dt} + y \dfrac{dy}{dt}$$
Utilizando la notación prima, el primer resultado que nos interesa es el siguiente.
$$r r^{\prime} = x x^{\prime} + y y^{\prime} \label{5} \tag{5}$$
Por otro lado, para la ecuación de $\theta$ se tiene
$$\dfrac{d \theta}{dt} = \dfrac{1}{1 + \left( \dfrac{y^{2}}{x^{2}} \right)} \left( \dfrac{x \dfrac{dy}{dt} -y \dfrac{dx}{dt}}{x^{2}} \right) = \dfrac{x \dfrac{dy}{dt} -y \dfrac{dx}{dt}}{x^{2} + y^{2}}$$
Nuevamente usando la notación prima, el segundo resultado que nos interesa es el siguiente.
$$r^{2} \theta^{\prime} = x x^{\prime} -y y^{\prime} \label{6} \tag{6}$$
Las ecuaciones (\ref{5}) y (\ref{6}) nos serán de utilidad a continuación.
Un ciclo límite
Antes de revisar algunos conceptos y de presentar el teorema de Poincaré – Bendixson, consideremos el siguiente sistema no lineal.
\begin{align*}
x^{\prime} &= -y + x(1 -x^{2} -y^{2}) \\
y^{\prime} &= x + y(1 -x^{2} -y^{2}) \label{7} \tag{7}
\end{align*}
Es sencillo hacer notar que el único punto de equilibrio del sistema es el origen $Y_{0} = (0, 0)$.
Utilizando las relaciones (\ref{5}) y (\ref{6}) podemos transformar el sistema en coordenadas polares. Comencemos por obtener la ecuación diferencial para $r$, para ello sustituyamos $x^{\prime}$ y $y^{\prime}$ del sistema (\ref{7}) en la ecuación (\ref{5}).
$$rr^{\prime} = x [-y + x(1 -x^{2} -y^{2})] + y[x + y(1 -x^{2} -y^{2})]$$
Desarrollando, obtenemos
$$r r^{\prime} = r^{2}(1 -r^{2}) \label{8} \tag{8}$$
Para el caso de $\theta$ sustituimos (\ref{7}) en (\ref{6}).
$$r^{2} \theta^{\prime} = x[-y + x(1 -x^{2} -y^{2})] -y[x + y(1 -x^{2} -y^{2})]$$
Desarrollando, obtenemos
$$r^{2} \theta^{\prime} = r^{2} \label{9} \tag{9}$$
Por lo tanto, el sistema no lineal (\ref{7}) en coordenadas polares es el siguiente.
\begin{align*}
r^{\prime} &= r(1 -r^{2}) \\
\theta^{\prime} &= 1 \label{10} \tag{10}
\end{align*}
Este sistema esta desacoplado, de manera que podemos resolver cada ecuación por separado para obtener las funciones $r(t)$ y $\theta(t)$ explícitamente.
Comencemos con la ecuación de $r^{\prime}$. Dicha ecuación es separable.
\begin{align*}
\dfrac{dr}{dt} &= r(1 -r^{2}) \\
dr &= r(1 -r^{2}) dt \\
\int{\dfrac{dr}{r(1 -r^{2})}} &= \int{dt} \\
\end{align*}
Por un lado, tomando fracciones parciales, se tiene
\begin{align*}
\int{\dfrac{dr}{r(1 -r^{2})}} &= \int{ \left( \dfrac{1}{r} -\dfrac{1}{2(r + 1)} -\dfrac{1}{2(r -1)} \right) dr} \\
&= \int{\dfrac{dr}{r}} -\int{\dfrac{dr}{2(r + 1)}} -\int{\dfrac{dr}{2(r -1)}} \\
&= \ln|r|-\dfrac{1}{2} \ln|r + 1| -\dfrac{1}{2} \ln|r -1| + c_{1}\\
\end{align*}
y por otro lado,
$$\int{dt} = t + c_{2}$$
De ambos resultados se tiene que
$$\ln|r|-\dfrac{1}{2} \ln|r + 1| -\dfrac{1}{2} \ln|r -1| = t + c_{3}$$
Multipliquemos ambos lados de la igualdad por $-2$.
$$-2 \ln|r| + \ln|r + 1| + \ln|r -1| = -2t -2c_{3}$$
Ahora tomemos exponencial en ambos lados,
\begin{align*}
r^{-2}(r + 1)(r -1) &= e^{-2t -2c_{3}} \\
1 -r^{-2} &= e^{-2t} e^{-2c_{3}} \\
r^{-2} &= 1 -ce^{-2t}
\end{align*}
Por lo tanto,
$$r^{2} = \dfrac{1}{1 + ce^{-2t}} \label{11} \tag{11}$$
Como $r \geq 0$, entonces
$$r(t) = \dfrac{1}{\sqrt{1+ ce^{ -2t}}} \label{12} \tag{12}$$
Para el caso de la ecuación de $\theta^{\prime}$ es inmediato que
$$\theta(t) = t + t_{0} \label{13} \tag{13}$$
Por lo tanto, la solución general de (\ref{10}) es
\begin{align*}
r(t) &= \dfrac{1}{\sqrt{1+ ce^{ -2t}}} \\
\theta(t) &= t + t_{0} \label{14} \tag{14}
\end{align*}
De manera que la correspondiente solución del sistema no lineal (\ref{7}) es
\begin{align*}
x(t) &= \dfrac{\cos (t + t_{0})}{\sqrt{1 + ce^{ -2t}}} \\
y(t) &= \dfrac{\sin (t + t_{0})}{\sqrt{1+ ce^{ -2t}}} \label{15} \tag{15}
\end{align*}
Analizando el resultado (\ref{14}) se tienen 3 casos:
Si $c = 0$ se obtiene la solución
\begin{align*}
r(t) &= 1 \\
\theta(t) &= t + t_{0} \label{16} \tag{16}
\end{align*}
Que no es más que la circunferencia de radio $1$, $(x^{2} + y^{2} = 1)$ en sentido anti-horario.
Si $c < 0$ es claro que $r > 1$, $\theta = t + t_{0}$ y además,
$$ \lim_{t \to -\infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = \infty \hspace{1cm} y \hspace{1cm} \lim_{t \to \infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = 1 \label{17} \tag{17}$$
Finalmente, si $c > 0$ se observa que $r < 1$, $\theta = t + t_{0}$ y además,
$$\lim_{t \to -\infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = 0 \hspace{1cm} y \hspace{1cm} \lim_{t \to \infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = 1 \label{18} \tag{18}$$
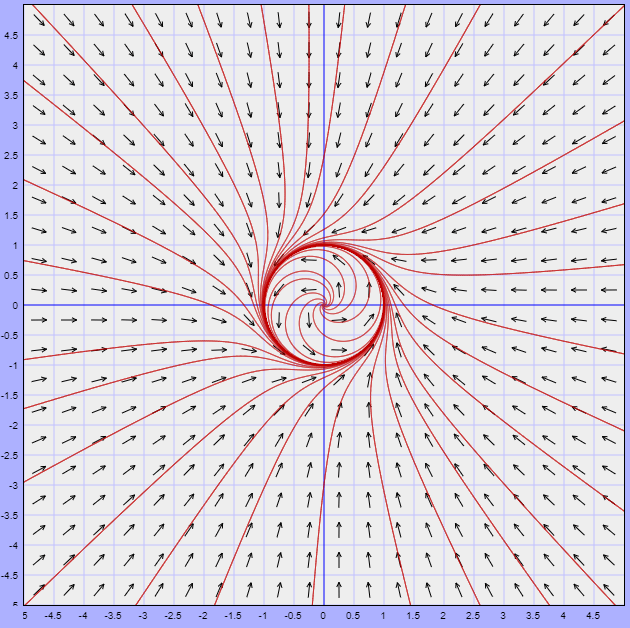
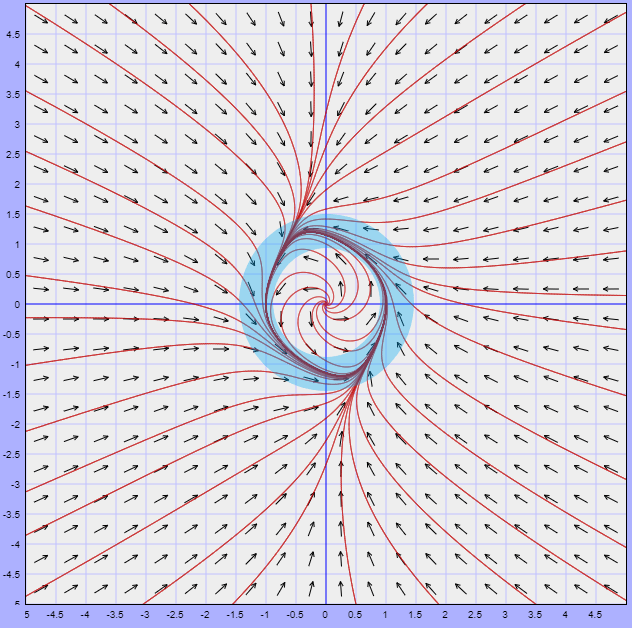
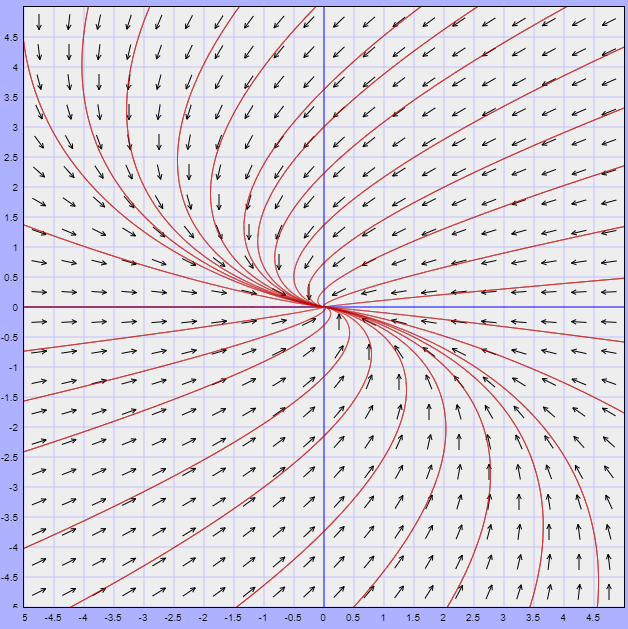
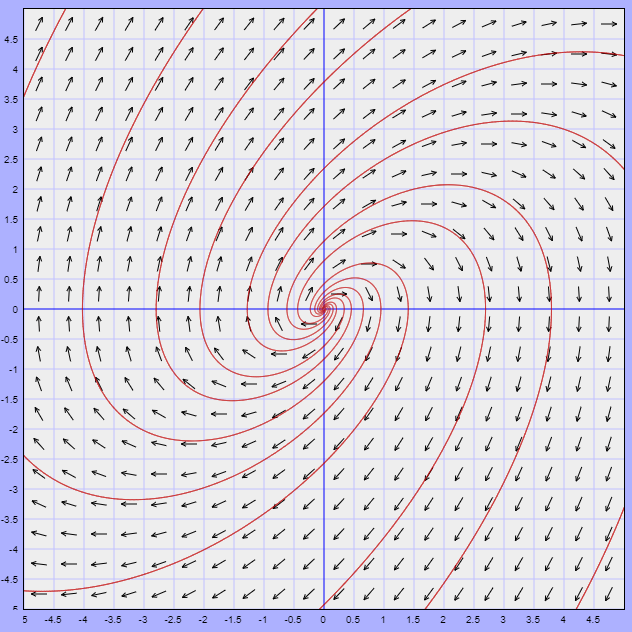
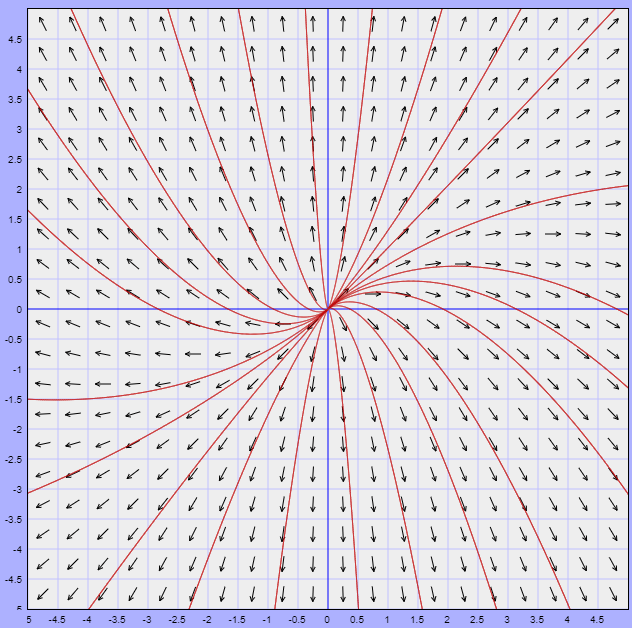
Lo que obtenemos es una curva cerrada o ciclo límite correspondiente a una trayectoria periódica para $r = 1$ y todas las demás trayectorias se acercan en espiral desde el exterior y el interior cuando $t \rightarrow \infty$, tal como se muestra en la siguiente figura.
Nota: Este plano fase está definido con las trayectorias dadas por (\ref{15}), es decir, corresponde al plano $XY$.
Lo que hemos hecho es probar que el sistema no lineal (\ref{7}) tiene una trayectoria periódica, pero lo hemos hecho resolviendo el sistema explícitamente. Sin embargo, no siempre será sencillo resolver las ecuaciones involucradas, desearíamos de alguna manera saber si un sistema no lineal tiene o no trayectorias periódicas, pero sin conocer las soluciones explícitas. ¡Esto es posible con ayuda del teorema de Poincaré – Bendixson!.
Teorema de Poincaré – Bendixson en el plano.
Consideremos un sistema no lineal
\begin{align*}
x^{\prime} &= F_{1}(x, y) \\
y^{\prime} &= F_{2}(x, y) \label{19} \tag{19}
\end{align*}
La definición formal de ciclo límite es la siguiente.
En el ejemplo visto es claro que se trata de un ciclo límite estable.
En este caso, para que sean claras las siguientes definiciones, detonaremos a una solución del sistema (\ref{19}) como $Y(t; x, y)$ indicando que tanto $x$ como $y$ dependen de la variable $t$.
$$\lim_{n \to \infty} Y(t_{n}; x, y) = Y_{0} \label{20} \tag{20}$$
$$\lim_{n \to \infty} Y(t_{n}; x, y) = Y_{0} \label{21} \tag{21}$$
Ejemplo: Un sistema lineal cuyo punto de equilibrio es nodo atractor
tiene como punto $\omega -$límite al punto $Y_{0} = (0, 0)$, ya que cualquier trayectoria $Y(t_{n}; x, y)$ tiende a dicho punto para $t_{n} \rightarrow \infty$. Mas aún, el conjunto $\omega -$límite es $\omega(Y) = \{ (0, 0) \}$.
$\square$
Los conjuntos $\alpha -$límite y $\omega -$límite se pueden describir como el lugar geométrico donde nace y muere la trayectoria de la solución de un sistema dinámico dado.
En el primer ejemplo visto anteriormente obtuvimos una trayectoria periódica definida por la circunferencia $x^{2} + y^{2} = 1$, o bien $r = 1$. De acuerdo al plano fase, dicha circunferencia es un conjunto $\omega -$límite tanto para las trayectorias $Y(t; x, y)$ fuera de la circunferencia unitaria $(r > 0)$ como para las trayectorias $Y(t; x, y)$, dentro de la circunferencia unitaria $(r < 1)$.
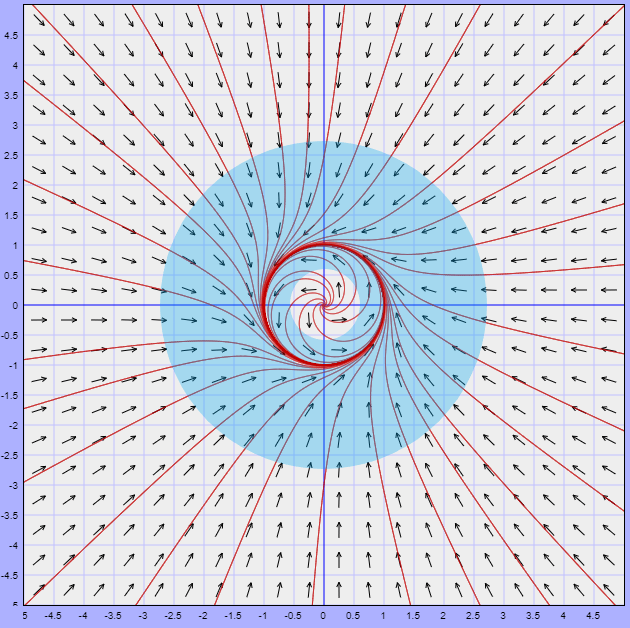
Observando nuevamente el plano fase del sistema del ejemplo desarrollado, es posible encontrar un región por fuera de la circunferencia unitaria en la que las trayectorias se comiencen a trazar a partir de $t = 0$. Lo mismo se puede hacer en una región dentro de la circunferencia unitaria, de manera que dicha circunferencia quede completamente contenida en la unión de ambas regiones. Esto lo sabemos de los resultados (\ref{17}) y (\ref{18}).
Dicha unión de conjuntos corresponde al conjunto $U \subset \mathbb{R}^{2}$, en este caso, positivamente invariante ya que para todo punto $(x, y) \in U$ las trayectorias $Y(t; x, y) \in U$ para todo $t \geq 0$.
Ahora conocemos los conceptos básicos que nos permitirán comprender el teorema de Poincaré – Bendixson. Cabe mencionar que existen varias formas de enunciar este teorema dependiendo incluso de la profundidad teórica que se este tratando, sin embargo el resultado siempre será el mismo. Lo que haremos en este curso será enunciar el teorema de Poincaré-Bendixson de una forma un poco intuitiva, posteriormente lo enunciaremos nuevamente de forma formal y como corolarios de este teorema enunciaremos dos resultados importantes que incluso se pueden encontrar como enunciados del mismo teorema de Poincaré – Bendixson.
Comenzamos por enunciar el teorema de Poincaré – Bendixson de forma intuitiva.
\begin{align*}
x^{\prime} &= F_{1}(x, y) \\
y^{\prime} &= F_{2}(x, y)
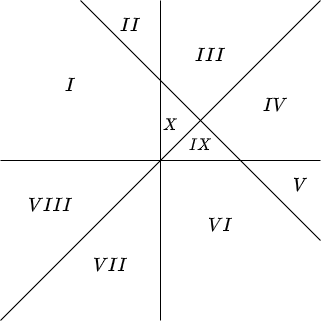
\end{align*} con $\varphi_{2}$ en el interior de $\varphi_{1}$. Entonces si en cada punto de la curva $\varphi_{1}$ el vector está dirigido hacia el interior de $\varphi_{1}$ y en cada punto de la curva $\varphi_{2}$ el vector está dirigido hacia el exterior de $\varphi_{2}$, entonces se puede afirmar que al menos existe un ciclo límite comprendido entre $\varphi_{1}$ y $\varphi_{2}$.
Si recurrimos una vez más a nuestro ejemplo, podemos tomar la curva $\varphi_{1}$ como la frontera exterior del conjunto $U$, mientras que la curva $\varphi_{2}$ como la frontera interior del mismo conjunto.
Lo que observamos es que el campo vectorial sobre los puntos de la curva $\varphi_{1}$ está dirigido hacia el interior de dicha curva, mientras que el campo vectorial sobre los puntos de la curva $\varphi_{2}$ está dirigido hacia el exterior. Es decir, en ambos casos el campo vectorial incide a la región positivamente invariante $U$ y sabemos que efectivamente hay una un ciclo límite comprendido entre ambas trayectorias.
Enunciemos ahora el teorema de Poincaré – Bendixson de manera más formal.
\begin{align*}
x^{\prime} &= F_{1}(x, y) \\
y^{\prime} &= F_{2}(x, y)
\end{align*} que permanece en una región acotada del plano que no contiene puntos de equilibrio del sistema. Entonces su trayectoria debe describir una espiral que se aproxima a una curva cerrada simple, la cual a su vez es la trayectoria de una solución periódica del sistema no lineal.
En esta entrada no demostraremos el teorema de Poincaré – Bendixson, sin embargo, en la sección de videos se ha hecho un enorme esfuerzo por desarrollar con detalle la teoría previa para su demostración, así como la demostración del teorema. Se recomienda visitar la entrada.
Antes de realizar algunos ejemplos enunciemos dos resultados importantes que se deducen del teorema de Poincaré – Bendixson.
Concluiremos esta entrada realizando algunos ejemplos en los que apliquemos el teorema de Poincaré – Bendixson, así como ambos corolarios para determinar que los sistemas no lineales estudiados presentan soluciones periódicas.
Ejemplo: Demostrar que el siguiente sistema no lineal tiene una trayectoria periódica.
\begin{align*}
x^{\prime} &= x -y -\left( x^{2} + \dfrac{3}{2}y^{2} \right)x \\
y^{\prime} &= x + y -\left( x^{2} + \dfrac{1}{2}y^{2} \right)y
\end{align*}
Solución: Por su puesto que intentar resolver el sistema para conocer explícitamente a la trayectoria periódica puede ser muy complicado, incluso si conociéramos métodos de resolución. Para poder aplicar el teorema de Poincaré – Bendixson lo que haremos será encontrar una región $U \subset \mathbb{R}^{2}$ que sea positivamente (o negativamente) invariante y que no contenga puntos de equilibrio del sistema.
Como ejercicio moral muestra que el único punto de equilibrio del sistema es el origen $Y_{0} = (0, 0)$. Esto nos indica que la región $U$ no debe contener al origen.
Nuevamente usemos coordenadas polares con la intención de hallar el intervalo en el que $r$ puede estar comprendido y cuyos valores extremos definan la región $U$ que buscamos.
Sustituyamos $x^{\prime}$ y $y^{\prime}$ del sistema no lineal en la ecuación (\ref{5}).
\begin{align*}
r r^{\prime} &= x \left[ x -y -\left( x^{2} + \dfrac{3}{2}y^{2} \right) x \right] + y \left[ x + y -\left( x^{2} + \dfrac{1}{2}y^{2} \right) y \right] \\
&= x^{2} + y^{2} -x^{4} -\dfrac{1}{2}y^{4} -\dfrac{5}{2}x^{2}y^{2} \\
&= (x^{2} + y^{2}) -(x^{4} +2x^{2}y^{2} + y^{4}) + \dfrac{1}{2}y^{4} -\dfrac{1}{2}x^{2}y^{2} \\
&= r^{2} -r^{4} + \dfrac{1}{2}y^{2}(y^{2} -x^{2})
\end{align*}
En el siguiente procedimiento haremos uso de las identidades trigonométricas
\begin{align*}
\cos(2 \theta) &= \cos^{2}(\theta) -\sin^{2}(\theta) \\
\cos(2 \theta) &= 1 -2\sin^{2}(\theta) \label{22} \tag{22}
\end{align*}
Si usamos las transformaciones (\ref{3}) y las identidades anteriores, tenemos lo siguiente.
\begin{align*}
y^{2}(y^{2} -x^{2}) &= r^{2} \sin^{2}(\theta) [r^{2} \sin^{2}(\theta) -r^{2} \cos^{2}(\theta)] \\
&= -r^{4} \sin^{2}(\theta) [\cos^{2}(\theta) -\sin^{2}(\theta)] \\
&= -r^{4} \sin^{2}(\theta) \cos(2 \theta) \\
&= -r^{4} \left[ \dfrac{1 -\cos(2 \theta)}{2} \right] \cos(2 \theta) \\
&= r^{4} \left[ \dfrac{\cos^{2}(2 \theta) -\cos(2 \theta)}{2} \right]
\end{align*}
Sustituyamos este resultado en nuestro desarrollo de $rr^{\prime}$.
$$rr^{\prime} = r^{2} -r^{4} + \dfrac{1}{2} r^{4} \left[ \dfrac{\cos^{2}(2 \theta) -\cos(2 \theta)}{2} \right]$$
De donde
$$r^{\prime} = r -r^{3} \left( 1+ \dfrac{\cos(2 \theta)}{4} -\dfrac{\cos^{2}(2 \theta)}{4} \right)$$
Para encontrar la región $U$ que contenga a la trayectoria periódica se debe hacer $r^{\prime} = 0$, debido a que tal región debe ser tangente a la trayectoria periódica en algún punto en el cual $r^{\prime} = 0$, entonces
$$r^{\prime} = r -r^{3} \left( 1+ \dfrac{\cos(2 \theta)}{4} -\dfrac{\cos^{2}(2 \theta)}{4} \right) = 0$$
Factorizando convenientemente se tiene,
$$\cos(2 \theta) -\cos^{2}(2 \theta) = 4 \left( \dfrac{1}{r^{2}} -1 \right)$$
Se puede hacer uso de un graficador para mostrar que
$$-2 \leq \cos(2 \theta) -\cos^{2}(2 \theta) < \dfrac{1}{4} \label{23} \tag{23}$$
Entonces se cumple la siguiente desigualdad
$$-2 \leq 4 \left ( \dfrac{1}{r^{2}} -1 \right ) < \dfrac{1}{4}$$
Desarrollando se tiene lo siguiente.
$$-\dfrac{1}{2} \leq \dfrac{1}{r^{2}} -1 < \dfrac{1}{16}$$
$$\dfrac{1}{2} \leq \dfrac{1}{r^{2}} < \dfrac{17}{16}$$
$$\dfrac{16}{17} \leq r^{2} < 2$$
Finalmente, el radio $r > 0$ tiene como desigualdades a
$$\dfrac{4}{\sqrt{17}} \leq r < \sqrt{2}$$
Observemos que si $r = \dfrac{4}{\sqrt{17}}$, entonces $r^{\prime} > 0$. En este caso, cualquier trayectoria por un punto en el conjunto
$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \left( \dfrac{4}{\sqrt{17}} \right)^{2} \right\}$$
sale del disco abierto
$$x^{2} + y^{2} < \left ( \dfrac{4}{\sqrt{17}} \right )^{2}$$
Por otro lado, si $r = \sqrt{2}$, entonces $r^{\prime} < 0$. En este caso, cualquier trayectoria por el punto
$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} > \sqrt{2} \right\}$$
entra al disco cerrado
$$x^{2} + y^{2} \leq \sqrt{2}$$
Por lo tanto, el conjunto
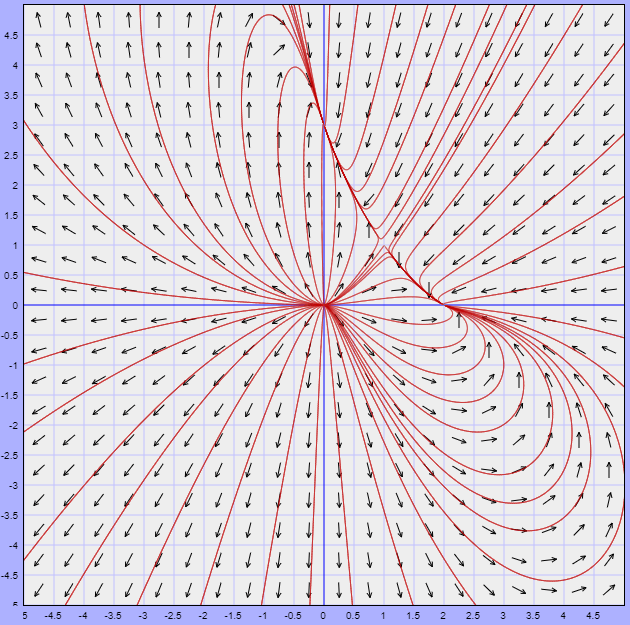
$$U = \left\{ (x, y) \in \mathbb{R}^{2} : \left( \dfrac{4}{\sqrt{17}} \right)^{2} \leq x^{2} + y^{2} \leq (\sqrt{2})^{2} \right\}$$
es un conjunto positivamente invariante. Esto quiere decir que para cualquier punto que se tome en el conjunto $U$, la trayectoria por este punto permanecerá en tal conjunto.
Como el punto de equilibrio $(0, 0)$ no pertenece a $U$, entonces por el teorema de Poincaré – Bendixson se concluye que existe una trayectoria periódica contenida en $U$.
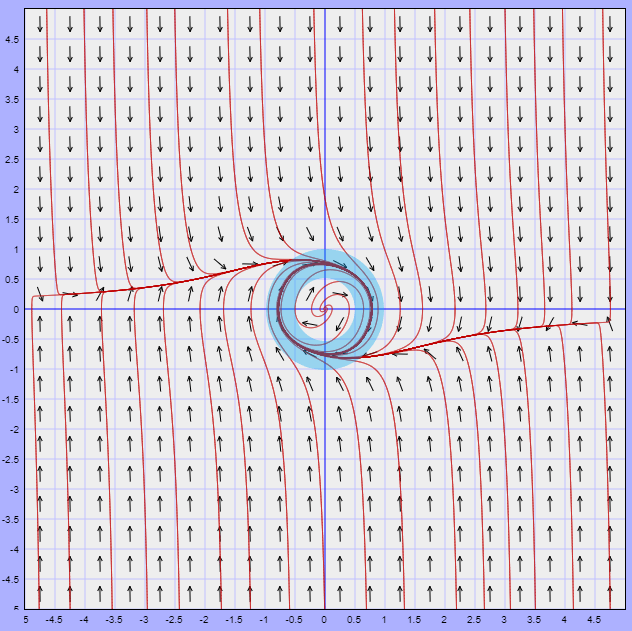
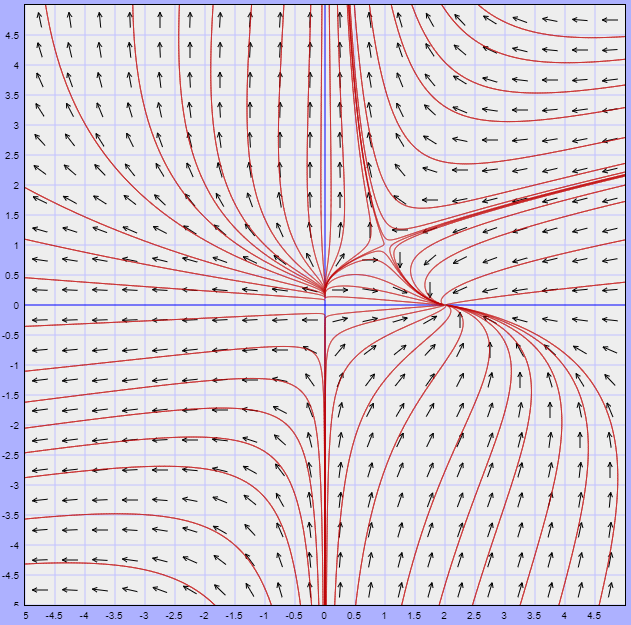
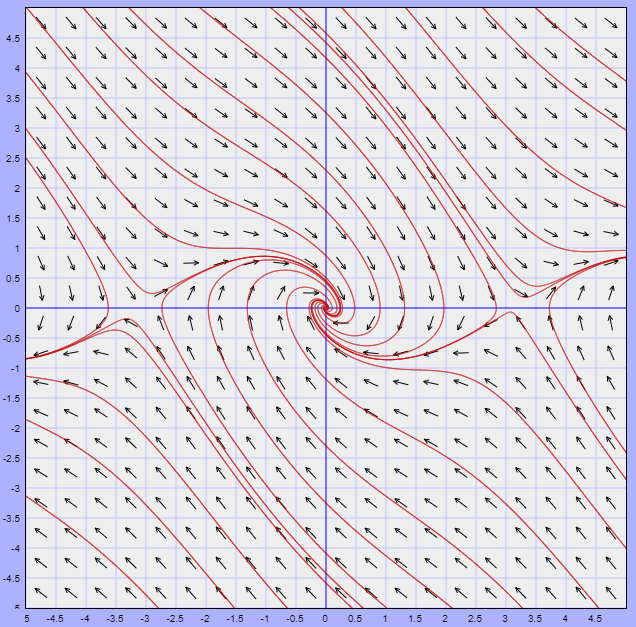
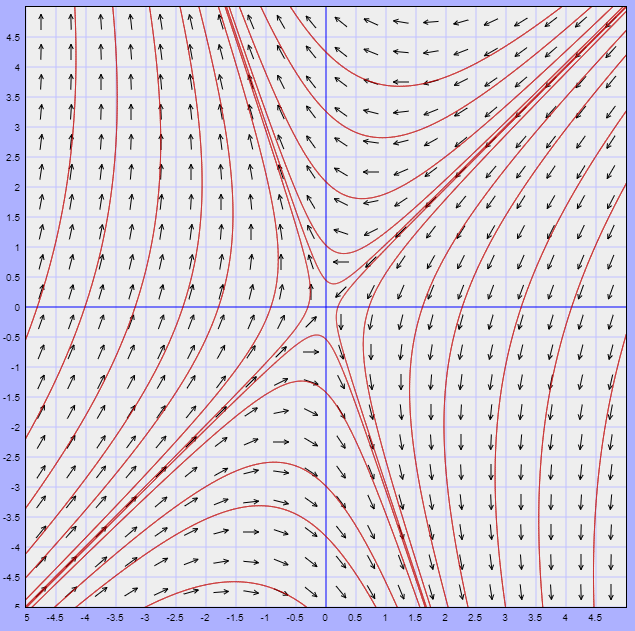
El plano fase del sistema no lineal, indicando la región $U$, se muestra a continuación.
En la figura observamos que efectivamente la región $U$ contiene un conjunto límite correspondiente a una trayectoria periódica del sistema no lineal.
$\square$
Realicemos un ejemplo más.
Ejemplo: Mostrar que el siguiente sistema no lineal tiene por lo menos una trayectoria periódica.
\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -x + y(1 -x^{2} -2y^{2})
\end{align*}
Solución: El punto $Y_{0} = (0, 0)$ es el único punto de equilibrio del sistema. Debemos construir una región $U$ en la cual se pueda aplicar el Teorema de Poincaré – Bendixson.
Apliquemos la ecuación (\ref{5}).
\begin{align*}
rr^{\prime} &= x x^{\prime} + y y^{\prime} \\
&= x[y] + y[-x + y(1 -x^{2} -2y^{2})] \\
&= xy -xy + y^{2} -x^{2}y^{2} -2y^{4} \\
&= y^{2}(1 -x^{2} -2y^{2}) \\
&= r^{2} \sin^{2}(\theta) [1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta)]
\end{align*}
De donde,
$$r^{\prime} = r \sin^{2}(\theta) [1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta)]$$
Hacemos $r^{\prime} = 0$.
$$r \sin^{2}(\theta) [1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta)] = 0$$
Como queremos hallar el intervalo que comprende a $r$ nos quedamos con la ecuación
$$1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta) = 0$$
Desarrollando, se tiene
\begin{align*}
1 &= r^{2} \cos^{2}(\theta) + 2r^{2} \sin^{2}(\theta) \\
&= r^{2} [1 -\sin^{2}(\theta) + 2\sin^{2}(\theta) ]\\
&= r^{2} [1 + \sin^{2}(\theta)]
\end{align*}
De donde,
$$r^{2} = \dfrac{1}{1 + \sin^{2}(\theta)}$$
Sabemos que
$$0 \leq \sin^{2}(\theta) \leq 1$$
Entonces,
$$1 \leq 1 + \sin^{2}(\theta) \leq 2$$
$$\dfrac{1}{2} \leq \dfrac{1}{1 + \sin^{2}(\theta)} \leq 1$$
es decir,
$$\dfrac{1}{2} \leq r^{2} \leq 1$$
O bien,
$$\dfrac{1}{2} \leq x^{2} + y^{2} \leq 1$$
Esta desigualdad nos define la región $U$. Notemos que $r^{\prime} > 0$ para $x^{2} + y^{2} < \dfrac{1}{2}$. En este caso, cualquier trayectoria por el punto
$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \dfrac{1}{2} \right\}$$
sale del disco abierto
$$x^{2} + y^{2} < \dfrac{1}{2}$$
Por otro lado, $r^{\prime} \leq 0$ para $x^{2} + y^{2} > 1$. En este caso cualquier trayectoria por el punto
$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} > 1 \right\}$$
entra al disco cerrado
$$x^{2} + y^{2} \leq 1$$
Por lo tanto, el conjunto
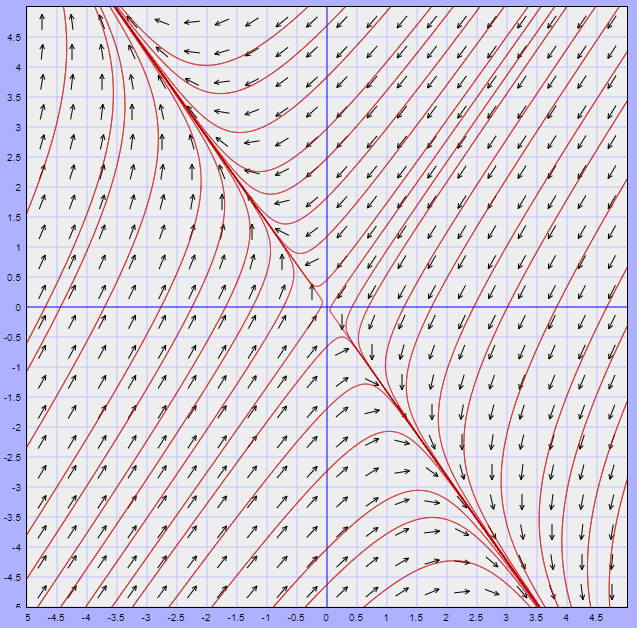
$$U = \left\{ (x, y) \in \mathbb{R}^{2} : \dfrac{1}{2}< x^{2} + y^{2} < 1 \right\}$$
es positivamente invariante. Es decir, para cualquier punto que se tome en el conjunto $U$, la trayectoria por dicho punto permanecerá allí para $t \geq 0$. Como el origen no esta contenido en la región $U$, entonces es posible aplicar el Teorema de Poincaré – Bendixson mostrando así que existe al menos una órbita periódica en dicha región.
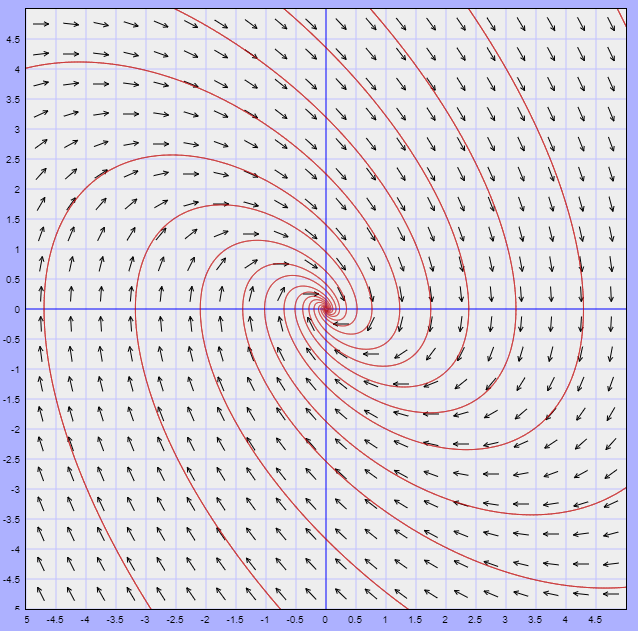
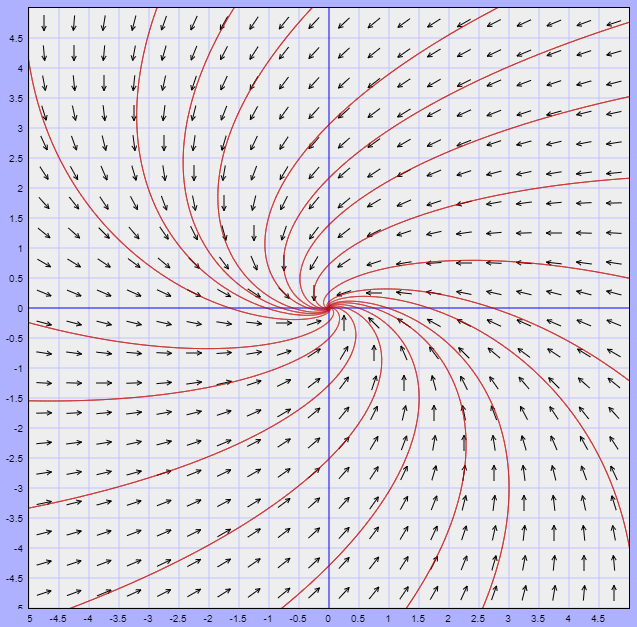
El plano fase del sistema, indicando la región $U$, es el siguiente.
Efectivamente existe una trayectoria periódica contenida en la región $U$.
$\square$
Concluyamos con un último ejemplo.
Ejemplo: Mostrar que el siguiente sistema no lineal tiene por lo menos una trayectoria periódica.
\begin{align*}
x^{\prime} &= -y + x(r^{4} -3r^{2} + 1) \\
y^{\prime} &= x + y(r^{4} -3r^{2} + 1)
\end{align*}
con $r^{2} = x^{2} + y^{2}$.
Solución: El único punto de equilibrio del sistema es el origen $Y_{0} = (0, 0)$. Determinemos la región $U$ en la que podamos aplicar el teorema de Poincaré – Bendixson.
Sustituyamos las ecuaciones $x^{\prime}$ y $y^{\prime}$ del sistema en la ecuación (\ref{5}).
\begin{align*}
rr^{\prime} &= xx^{\prime} + yy^{\prime} \\
&= x[-y + x(r^{4} -3r^{2} + 1)] + y[ x + y(r^{4} -3r^{2} + 1)] \\
&= -xy + x^{2}(r^{4} -3r^{2} + 1) + xy + y^{2}(r^{4} -3r^{2} + 1) \\
&= (x^{2} + y^{2}) (r^{4} -3r^{2} + 1) \\
&= r^{2}(r^{4} -3r^{2} + 1)
\end{align*}
De donde,
$$r^{\prime} = r(r^{4} -3r^{2} + 1)$$
Si hacemos $r^{\prime} = 0$, obtenemos la ecuación de interés.
$$r^{4} -3r^{2} + 1 = 0$$
Hacemos $s = r^{2}$, de manera que la ecuación anterior se pueda escribir como
$$s^{2} -3s + 1 = 0$$
Las raíces de esta ecuación son
$$s_{1} = r^{2}_{1} = \dfrac{3 + \sqrt{5}}{2} \hspace{1cm} y \hspace{1cm} s_{2} = r^{2}_{2} = \dfrac{3 -\sqrt{5}}{2}$$
Si $r^{2} = \dfrac{3 + \sqrt{5}}{2}$ se verifica que $r^{\prime} > 0$ de forma que cualquier trayectoria por el punto
$$(x_{0}, y_{0}) \in \left \{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \dfrac{3 + \sqrt{5}}{2} \right \}$$
sale del disco cerrado
$$x^{2} + y^{2} \leq \dfrac{3 + \sqrt{5}}{2}$$
Si $r^{2} = \dfrac{3 -\sqrt{5}}{2}$ se verifica nuevamente que $r^{\prime} > 0$ de forma que cualquier trayectoria por el punto
$$(x_{0}, y_{0}) \in \left \{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \dfrac{3 -\sqrt{5}}{2} \right \}$$
sale del disco abierto
$$x^{2} + y^{2} < \dfrac{3 -\sqrt{5}}{2}$$
De ambos resultados notamos que el conjunto
$$U = \left \{ (x, y) \in \mathbb{R}^{2} : \dfrac{3 -\sqrt{5}}{2} \leq x^{2} + y^{2} \leq \dfrac{3 + \sqrt{5}}{2} \right \}$$
no es un conjunto ni positivamente ni negativamente invariante, pues en ambos casos las trayectorias salen de ambos discos.
Si tomamos $r = 1$ observamos que $r^{\prime} < 0$, es decir las trayectorias por un punto
$$(x_{0}, y_{0}) \in \left \{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} > 1 \right \}$$
entran al disco cerrado
$$x^{2} + y^{2} \leq 1$$
Este importante resultado nos indica que la región $U$ se puede dividir en dos regiones en las que una de ellas será positivamente invariante y la otra negativamente invariante, dichas regiones son.
$$U_{1} = \left \{ (x, y) \in \mathbb{R}^{2} : \dfrac{3 -\sqrt{5}}{2} \leq x^{2} + y^{2} \leq 1 \right \}$$
$$U_{2} = \left \{ (x, y) \in \mathbb{R}^{2} : 1 < x^{2} + y^{2} \leq \dfrac{3 + \sqrt{5}}{2} \right \}$$
Es claro que $U_{1}$ es un conjunto negativamente invariante y $U_{2}$ un conjunto positivamente invariante.
Como ninguna de ambas regiones contiene al punto de equilibrio, entonces podemos aplicar el teorema de Poincaré – Bendixson sobre cada una de las regiones deduciendo que en cada una de ellas existe una trayectoria periódica que corresponden a soluciones periódicas del sistema no lineal.
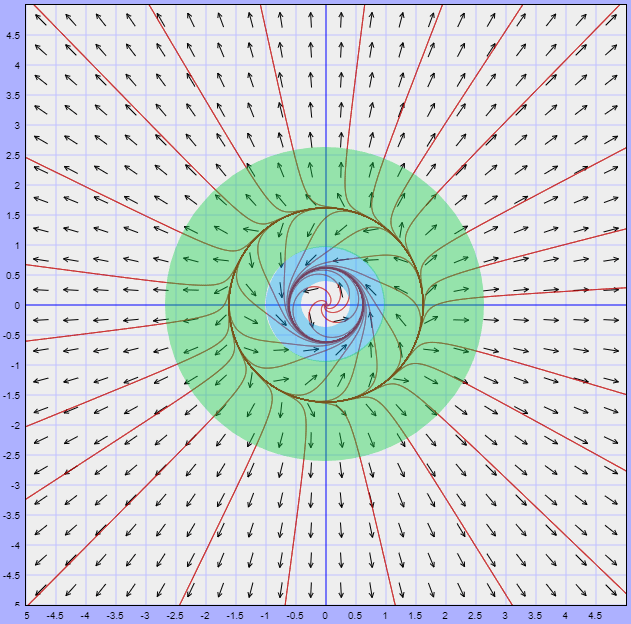
El plano fase del sistema, indicando ambas regiones, es el siguiente.
En este ejemplo mostramos que el sistema no lineal tiene dos trayectorias periódicas como solución.
$\square$
Felicidades, ¡Hemos concluido el curso!
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Mostrar que los siguientes sistemas no lineales tienen por lo menos un trayectoria periódica. Verifica tu resultado visualizando el plano fase del sistema.
- $x^{\prime} = -y -\dfrac{x(x^{2} + y^{2} -2)}{\sqrt{x^{2} + y^{2}}}$
$y^{\prime} = x -\dfrac{y(x^{2} + y^{2} -2)}{\sqrt{x^{2} + y^{2}}}$
- $x^{\prime} = y + x(x^{2} + y^{2} -1)(x^{2} + y^{2} -2)$
$y^{\prime} = -x + y(x^{2} + y^{2} -1)(x^{2} + y^{2} -2)$
- $x^{\prime} = xy + x \cos (x^{2} + y^{2})$
$y^{\prime} = -x^{2} + y \cos (x^{2} + y^{2})$
Más adelante…
Hemos concluido con el curso de Ecuaciones Diferenciales I.
Esperamos que este curso haya sido de tu agrado, lo hayas disfrutado y hayas aprendido mucho.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Las nulclinas en el estudio cualitativo de los sistemas no lineales
- Video relacionado al tema: Teorema de Poincaré–Bendixson en el plano
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»