(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
Anteriormente en nuestro curso, definimos una caracterización única para las permutaciones, aprendimos que la factorización completa es única salvo por el orden de los factores. Ahora, podemos analizar a los ciclos que aparecen en dicha factorización completa.
La unicidad de la factorización completa nos asegura que la cantidad de ciclos que la conforman y la longitud de éstos no van a cambiar sin importar la factorización que escojamos. Estudiar estas propiedades de la factorización completa motiva la definición de estructura cíclica y de permutación conjugada, dos definiciones centrales de esta entrada.
Además de la factorización completa, existen otras maneras de descomponer a las permutaciones. Intuitivamente, podemos pensar a las permutaciones como reacomodos, entonces es posible llegar a cualquier acomodo intercambiando elementos de dos en dos, es decir podemos reacomodar los números de $1$ a $n$ como queramos mediante intercambios dos a dos.
Se verá que toda permutación se descompone siempre como un producto de una cantidad par de intercambios, o siempre con una cantidad impar de intercambios. Para ello seguiremos el enfoque presentado en el libro de Herstein, al igual que en el libro Grupos I de Avella, Mendoza, Sáenz y Souto, y en el libro de Dummit mencionados en la bibliografía, en los que se introduce un polinomio en varias indeterminadas llamado el polinomio de Vandermonde.
Misma Estructura Cíclica
Recordemos que toda permutación se puede factorizar en una factorización completa y que toda factorización completa es única salvo por el orden de sus factores. Entonces la cantidad de ciclos y su longitud no va a cambiar, independientemente de la factorizacoón completa que escojamos. Esto motiva la siguiente definición.
Definición. Sean $\alpha, \beta \in S_n$. Decimos que $\alpha$ y $\beta$ tienen la misma estructura cíclica si su factorización completa tiene el mismo número de $r-$ciclos para toda $r \in \z^+$.
Ejemplo.
En $S_9$, tomemos $\alpha$ y $\beta$ como sigue
\begin{align*}
\alpha &= (2 \; 4 \; 7 \; 9)(1 \; 3)(5 \; 6)(8)\\
\beta &= (2 \; 4)(1 \; 5 \; 8 \; 9)(3 \; 7)(6).
\end{align*}
Claramente, $\alpha$ y $\beta$ tienen la misma estructura cíclica, ya que ambas están formadas por un $4-$ciclo, dos transposiciones y un $1$-ciclo.
Permutación Conjugada
Definición. Sean $\alpha, \beta \in S_n$. Decimos que $\beta$ es conjugada de $\alpha$ si existe $\gamma \in S_n$ tal que $\beta = \gamma \alpha \gamma^{-1}$.
Ejemplo.
Tomemos $\gamma = (1 \; 2 \; 3)$. Entonces $\gamma = (1\;2\;4)$ y $\alpha = (3 \; 5 \; 6 \; 8)$. Luego, podemos calcular a $\beta$ como sigue,
\begin{align*}
\gamma\alpha\gamma^{-1} &= (1 \; 2 \; 3)(3 \; 5 \; 6 \; 8)(1 \; 3 \; 2) \\
& = (1 \; 5 \; 6 \; 8) = \beta.
\end{align*}
Así, $\beta = (1 \; 5 \; 6 \; 8)$ es conjugada de $(1 \; 5 \; 6 \; 8) = \alpha$.
Podemos observar que si consideramos la relación en $S_n$ dada por $\alpha \sim \beta$ si y sólo si $\alpha$ es conjugada de $\beta$, es una relación de equivalencia. Aquí no lo demostraremos, pero queda como tarea moral. Aunque no es evidente en primera instancia, el hecho de que dos permutaciones sean conjugadas puede analizarse a partir de la estructura cíclica que tienen. En la tarea moral hay ejercicios relacionados con ello.
¿A qué nos referimos con reacomodos?
Vimos que toda permutación se puede descomponer en ciclos disjuntos y, bajo condiciones específicas, esta descomposición es única salvo por orden de factores. Sin embargo, hay otras maneras de descomponer a una permutación, las podemos pensar a las permutaciones como reacomodos. Es claro que podemos llegar a cualquier reacomodo intercambiando los elementos de 2 en 2.
A continuación, ilustramos esto con un ejemplo.
Tomemos $\sigma = (1 \; 2 \; 3 \; 4 \; 5)$, en esta permutación los números $1,2,3,4$ y $5$ cambian ya que el $1$ va a dar a $2$, el $2$ al $3$, etc., así que si reacomodamos los números $1,2,3,4,5$ de acuerdo a lo que nos indica $\sigma,$ en vez la lista $1\;2\;3\;4\;5$ tendremos ahora la lista $2\;3\;4,5\;1.$ Entonces nos preguntamos, ¿cómo podemos llegar de la lista $1\;2\;3\;4\;5$ a la lista $2\;3\;4\;5\;1$ sólo mediante intercambios dos a dos?
Primero, observemos que lo único que tenemos que hacer es pasar el 1 hasta el final. Luego, tomemos en cuenta que nuestra propuesta es intercambiar los elementos de dos en dos. Así, el proceso es el siguiente:
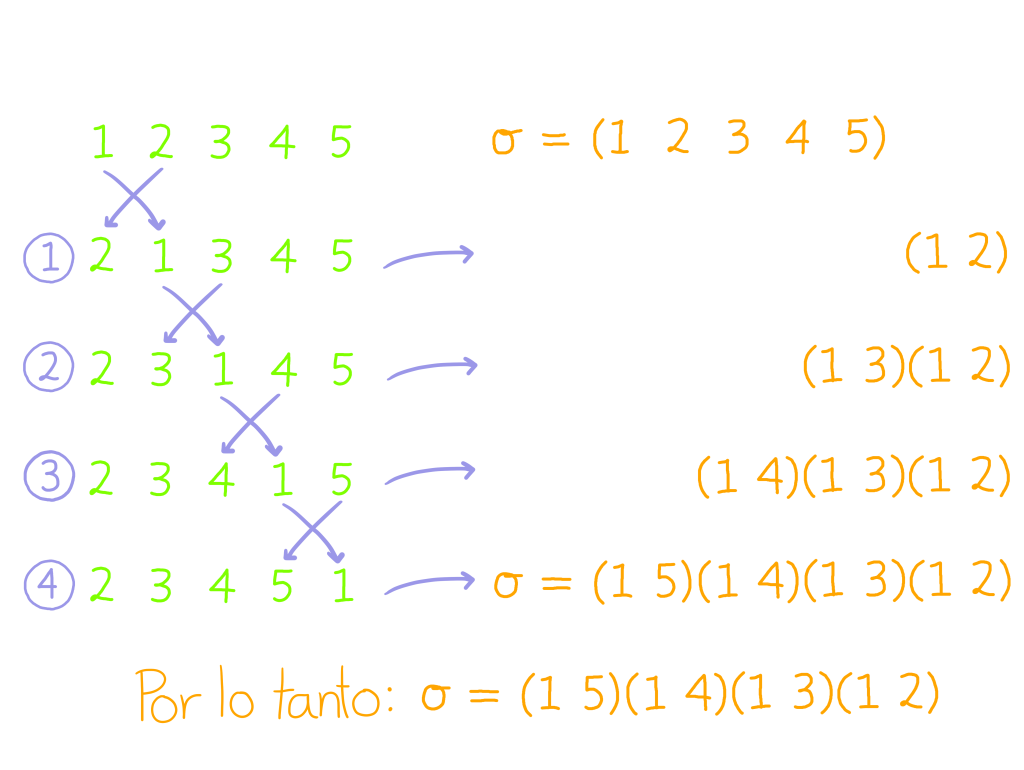
- Intercambiamos 1 y 2, así nuestra lista quedaría $2 \; 1 \; 3 \; 4 \; 5.$ Observemos que el 2 ya queda en la posición deseada.
- Sobre el resultado anterior, intercambiamos 1 y 3. Hasta el momento tenemos el reacomodo $2 \; 3 \; 1 \; 4 \; 5$.
- Ahora, nos toca intercambiar 1 y 4. Así obtenemos $2 \; 3 \; 4 \; 1 \;5.$
- Por último, nos queda acomodar el último número, así que intercambiamos 1 y 5.
Al final, llegamos al reacomodo buscado. Esto nos indica que para permutar los números $1,2,3,4$ y $5$ de acuerdo a $\sigma$ basta con intercambiar el uno con el dos, luego el uno con el tres, después el uno con el cuatro y finalmente el uno con el cinco. En otras palabras, la permutación sigma se obtiene de aplicar sucesivamente las transposiciones $(1 \; 2)$, $(1 \; 3)$, $(1 \; 4)$ y $(1 \; 5)$. Debido a que escribimos la composición de permutaciones de derecha a izquierda, nuestra sigma quedaría de la siguiente manera:
$$\sigma = (1 \; 2 \; 3 \; 4 \; 5) = (1 \; 5) (1 \; 4) (1 \; 3) (1 \; 2).$$
Este ejemplo nos ilustra cómo podemos descomponer un ciclo como producto de transposiciones. Probaremos esto en el caso general, y dado que toda permutación es un producto de ciclos y cada ciclo se puede descomponer en producto de transposiciones, entonces podremos concluir que toda permutación es un producto de transposiciones.
Teorema. La siguiente igualdad de conjuntos se cumple,
$$S_n = \left< \{\tau \in S_n | \tau \text{ es una transposición} \} \right>.$$
Demostración.
Como toda permutación es un producto de ciclos, basta ver que todo ciclo es un producto de transposiciones. Así,
\begin{align*}
(i_1 \; \cdots \; i_r) = (i_1 \; i_r) \cdots (i_1\; i_3)(i_1 \; i_2).
\end{align*}
Por lo tanto $S_n = \left< \{ \tau \in S_n | \tau \text{ es una transposición} \}\right>$.
$\square$
El polinomio de Vandermonde
Hemos probado que toda permutación se puede expresar como un producto de transposiciones, esto es importante porque las transposiciones son permutaciones muy sencillas, sin embargo estas descomposiciones no son únicas, pueden cambiar los factores que aparecen, su orden e incluso en el número de factores que presentan. A pesar de ello siempre tienen un número par o siempre un número impar de transposiciones. Con el fin probar este resultado introduciremos un polinomio con distintas indeterminadas que permutaremos usando permutaciones, para lo cual consideraremos polinomios en varias indeterminadas, que serán permutadas por los elementos del grupo simétrico.
Definición. Sea $P(x_1, \dots, x_n)$ un polinomio en las indeterminadas $x_1, \dots, x_n$ con coeficientes enteros y $\alpha \in S_n$. El polinomio $\alpha P$ se define como
\begin{align*}
\alpha P(x_1,\dots,x_n) = P(x_{\alpha(1)},\dots,x_{\alpha(n)}).
\end{align*}
Ejemplo.
Consideremos el polinomio $P(x_1,x_2,x_3,x_4,x_5) =-3x_1x_2+x_3x_5^2+x_1x_2x_3x_4x_5$ y $\alpha =(1\, 2\, 3)(4\, 5)$. Entonces
\begin{align*}
\alpha P(x_1,x_2,x_3,x_4) = &(1\, 2\, 3)(4\, 5) P(x_1,x_2,x_3,x_4) \\
=&-3x_{\alpha(1)}x_{\alpha(2)}+x_{\alpha(3)}x_{\alpha(5)}^2+x_{\alpha(1)}x_{\alpha(2)}x_{\alpha(3)}x_{\alpha(4)}x_{\alpha(5)}\\=&-3x_2x_3+x_1x_4^2+x_2x_3x_1x_5x_4.\end{align*}
Definición. El polinomio de Vandermonde en las indeterminadas $x_1, \dots, x_n$ con coeficientes enteros es
\begin{align*}
V(x_1,\dots,x_n) = \prod_{1 \leq i < j \leq n}(x_i – x_j).
\end{align*}
Dado $\alpha \in S_n$, el $\alpha-$polinomio de Vandermonde es $\alpha P$, es decir:
\begin{align*}
\alpha \; V(x_1, \dots, x_n) = \prod_{1 \leq i < j \leq n}(x_{\alpha(i)} – x_{\alpha(j)}).
\end{align*}
Ejemplo.
Consideremos,
\begin{align*}
V(x_1,x_2,x_3,x_4) = & (x_1 – x_2)(x_1 – x_3)(x_1 – x_4) \\
& (x_2 – x_3) (x_2 – x_4)(x_3-x_4).
\end{align*}
Calculemos ahora $(2 \; 4) \, V(x_1,x_2,x_3,x_4)$. Observemos que los únicos factores de $V$ que cambian son aquellos donde aparece el subíndice $2$ o el $4$, y éstos se intercambian, por ejemplo el factor $ (x_1 – x_2)$ cambiará al factor $ (x_1 – x_4)$. Así
\begin{align*}
(2 \; 4) \, V(x_1,x_2,x_3,x_4) = &(x_1 – x_4)(x_1 – x_3)(x_1-x_2)\\
&(x_4-x_3)(x_4 – x_2)(x_3-x_2) \\
= & \,- V(x_1,x_2,x_3,x_4).
\end{align*}
Observación 1. Dado que cada factor del polinomio de Vandermonde se queda igual o cambia de signo, sólo pueden suceder dos cosas, $\alpha V = V$ ó $\alpha V = – V$ para todo $\alpha \in S_n$, de acuerdo a si hay un número impar de cambios de signo o si hay un número par de cambio de signo.
Observación 2. Sea $\alpha\in S_n$. Tenemos que $ \alpha (- V) =-\alpha V$.
Observación 3. Sean $\alpha, \beta \in S_n$. Tenemos que $ \alpha (\beta V) =(\alpha\beta)V$.
Demostración.
Sea $\alpha \in S_n$. Tenemos que:
\begin{align*}\alpha (\beta V(x_1, \dots, x_n))=&\alpha V(x_{\beta(1)}, \dots, x_{\beta(n)})= V(x_{\alpha(\beta(1))}, \dots, x_{\alpha(\beta(n))})\\=&V(x_{(\alpha\beta)(1)}, \dots, x_{(\alpha\beta)(n)})=(\alpha\beta)V(x_1, \dots, x_n).\end{align*}
$\square$
Vandermonde y las Transposiciones
Veamos cuál es el efecto que tienen dos permutaciones sobre un polinomio. Primero analizaremos qué efecto tienen las transposiciones en el polinomio de Vandermonde. Seguiremos para ello la idea del libro de Dummit que se menciona en la bibliografía, veremos primero qué efecto tiene la transposición $(1\; 2)$, y con ello entenderemos qué efecto tienen el resto de las transposiciones.
Lema. Sea $\tau \in S_n$ una transposición. Entonces $\tau V = -V$.
Demostración.
Caso 1: $\tau=(1\; 2)$.
Al aplicar $\tau$ a $V$ los factores $x_i-x_j$ con $i,j\notin \{1,2\}$ se preservan, mientras que el factor $x_1-x_2$ cambia a $x_2-x_1$ provocando un cambio de signo. Por otro lado los factores $x_1-x_j$ con $j\in\{3,\dots ,n\}$ y los factores $x_2-x_j$ con $j\in\{3,\dots ,n\}$ no producen cambios de signo. Concluimos entonces que sólo un factor produce un cambio de signo y así $(1\; 2) V=-V.$
Caso 2: $\tau\neq(1\; 2)$. Es decir, $\tau =(1\; l)$ con $l\in\{3,\dots ,n\}$, o $\tau =(2\; l)$ con $j\in\{3,\dots ,n\}$, o bien $\tau =(k\; l)$ con $k,j\notin\{1,2\}.$
Notemos que \begin{align*}(2\; l)(1\; 2)(2\; l)&=(1\, l)\text{ , para } l\in\{3,\dots ,n\},\\ (1\; l)(1\; 2)(1\; l)&=(2\, l)\text{ , para } l\in\{3,\dots ,n\},\\(1\; k)(2\; l)(1\; 2)(1\;k)(2\; l)&=(k\, l)\text{ , para } k,j\notin\{1,2\}.\end{align*} Así, siempre existe $\alpha \in S_n$ tal que $\alpha (1\; 2) \alpha =\tau$.
Si $\alpha V=V$, tenemos que $$\tau V=(\alpha(1\; 2)\alpha)V=(\alpha ((1\; 2)(\alpha V)))=(\alpha ((1\; 2) V))=\alpha (-V)=-\alpha V=-V.$$
Si $\alpha V=-V$, tenemos que $$\tau V=(\alpha(1\; 2)\alpha)V=(\alpha ((1\; 2)(\alpha V)))=(\alpha ((1\; 2) (-V))=\alpha V=-V.$$
$\square$
Teoremas importantes
Teorema. Sean $r\in\mathbb{Z}^+$ y $\alpha = \tau_1 \cdots \tau_r \in S_n$, $\tau_1, \dots, \tau_r$ transposiciones. Entonces
$$\alpha V = (-1)^r \,V.$$
Demostración. Por inducción sobre $r$.
Base de inducción: Supongamos que $r = 1$.
Entonces, desarrollando $\alpha V$ y usando el lema previo obtenemos
\begin{align*}
\alpha V &= \tau_1 V\\
&= -V = (-1)^1 V & \text{ Por el Lema anterior.}
\end{align*}
Así, se cumple la proposición para al caso base.
Ahora, sea $r > 1$.
Hipótesis de Inducción: Supongamos que el resultado se cumple para el producto de $r-1$ transposiciones.
P.D. $\alpha V = (-1)^r V$.
Desarrollando $\alpha V$ y usando el lema previo, obtenemos:
\begin{align*}
\alpha V &= (\tau_1 \, \tau_2 \cdots \tau_r) V\\
&= ((\tau_1 \, \tau_2 \cdots \tau_{r-1})\tau_r) V & \text{Agrupamos}\\
&= (\tau_1 \cdots \tau_{r-1})(\tau_r V) &\text{Observación 3}\\
&= (\tau_1 \cdots \tau_{r-1})(- V) &\text{Lema anterior}\\
&= -(\tau_1 \cdots \tau_{r-1}) V &\text{Observación 2.}
\end{align*}
Ahora, como $\tau_2 \cdots \tau_r$ tiene $r-1$ transposiciones, podemos aplicar la hipótesis de inducción y continuar con las igualdades.
\begin{align*}
-(\tau_2 \cdots \tau_r) V = -(-1)^{r-1} V = (-1)^r \,V.
\end{align*}
Así, demostramos lo deseado.
$\square$
Teorema. Sean $r,t\in\mathbb{Z}^+$, $\alpha = \tau_1 \cdots \tau_r = \rho_1 \cdots \rho_t \in S_n$, con $\tau_1, \cdots, \tau_r$, $\rho_1, \cdots, \rho_t$ transposiciones. Entonces $r$ y $t$ tienen la misma paridad.
Demostración.
Por el teorema anterior, obtenemos:
\begin{align*}
\alpha V = (\rho_1 \cdots \rho_t) V = (-1)^t \,V.
\end{align*}
Por otro lado, por el teorema anterior también obtenemos:
\begin{align*}
\alpha V = (\tau_1 \cdots \tau_r) V = (-1)^r \,V.
\end{align*}
Entonces $(-1)^t V = (-1)^r V$. Por lo tanto $t$ y $r$ tienen la misma paridad.
$\square$
Tarea moral
- Prueba que la relación en $S_n$ dada por $\alpha \sim \beta$ si y sólo si $\beta$ es conjugada de $\alpha$, es una relación de equivalencia.
- Encuentra $\sigma\alpha\sigma^{-1}$ en cada inciso:
- $\alpha = ( 2 \; 3 \; 5), \; \sigma = (1\; 3 \; 5 \; 6)$.
- $\alpha = (5 \; 4 \; 3 \; 1), \; \sigma = (2 \; 4 \; 5 \; 7 \; 8)$.
- $\alpha = (1 \; 7 \; 5 \; 4 \; 2 \; 3), \; \sigma = (1 \; 2 \; 4 \; 6 \; 7)$.
- Sean $\alpha,\sigma \in S_n$ con $\sigma = (i_1\; i_2 \; \cdots \; i_r) \in S_n$ un $r-$ciclo.
- Considera $\alpha = (1 \; 9 \; 4)(10 \; 2 \; 8 \; 5 \; 3)(3 \; 5 \; 6 \; 8)(7 \; 2) \in S_{10}$.
- Escribe a $\alpha$ como un producto de transposiciones de al menos tres formas distintas y compara la cantidad de transposiciones que se usan en cada caso.
- Con lo anterior, determina quién es $\alpha V$.
- ¿Qué forma cíclica tiene $\alpha\sigma\alpha^{-1}$?
- ¿Cómo podemos describir a la permutación $\alpha\sigma\alpha^{-1}$ a partir de cómo son $\alpha$ y $\sigma$ sin necesidad de hacer paso a paso la composición? ¿puedes encontrar una fórmula que lo describa?
Más adelante…
Todavía nos quedan propiedades del polinomio de Vandermonde que estudiar. En la siguiente entrada profundizaremos en ellas. Por ejemplo, ¿existe una manera de determinar el signo que tendrá el $\alpha-$polinomio de Vandermonde? ¿Cómo se relaciona con la descomposición de la permutación $\alpha$? ¿Hay manera de relacionar las permutaciones que dan lugar a polinomios con el mismo signo? Éstas y otras preguntas las responderemos a continuación.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Factorización Completa.
- Siguiente entrada del curso: Paridad de una permutación.
- Resto de cursos: Cursos.