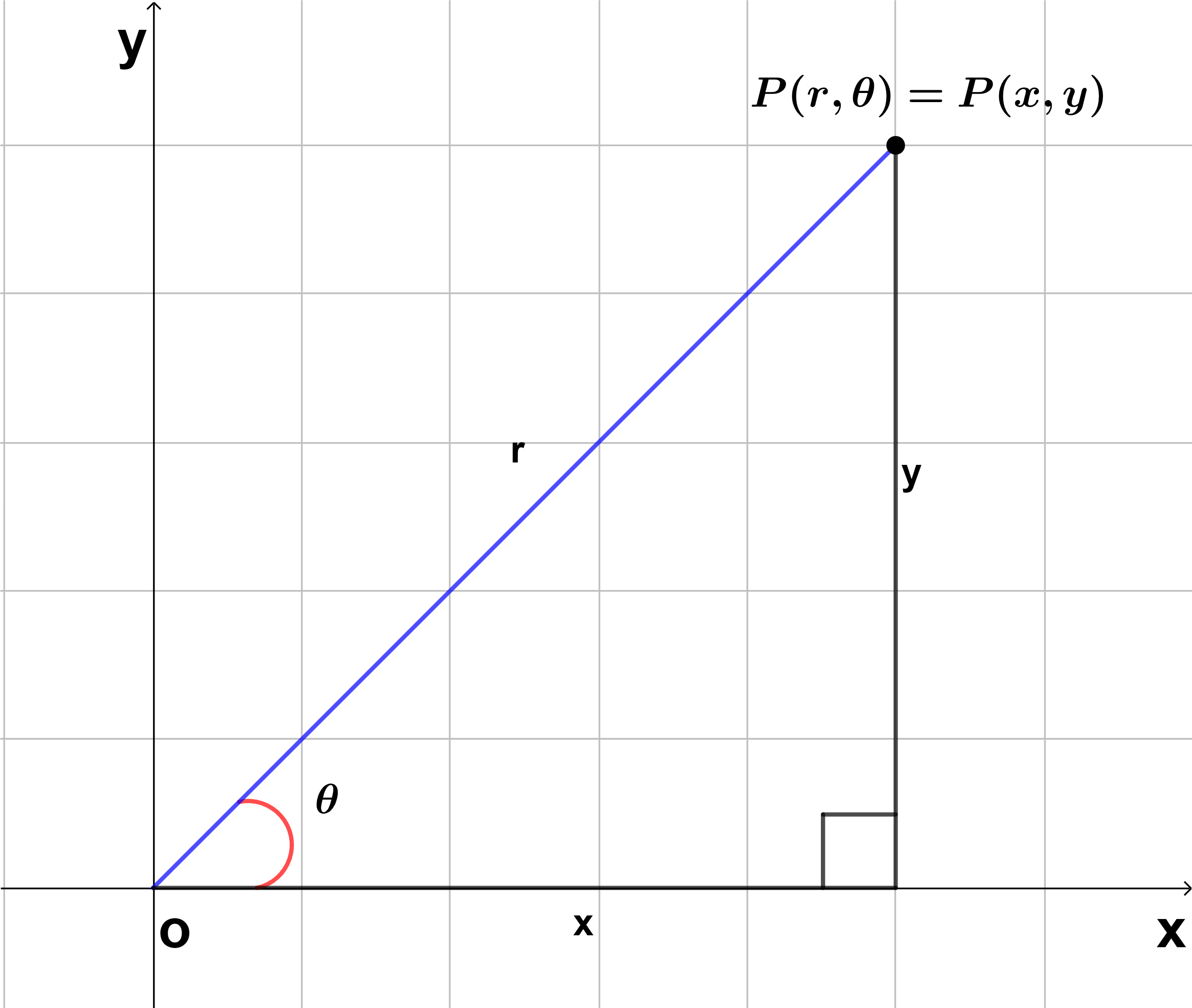Introducción

En las secciones anteriores vimos una introducción a las curvas paramétricas, así como calcular las tangentes a estas curvas. En esta sección veremos una introducción a las coordenadas polares, ya que es importante en las matemáticas y futuras materias en su estudio.

Coordenadas polares

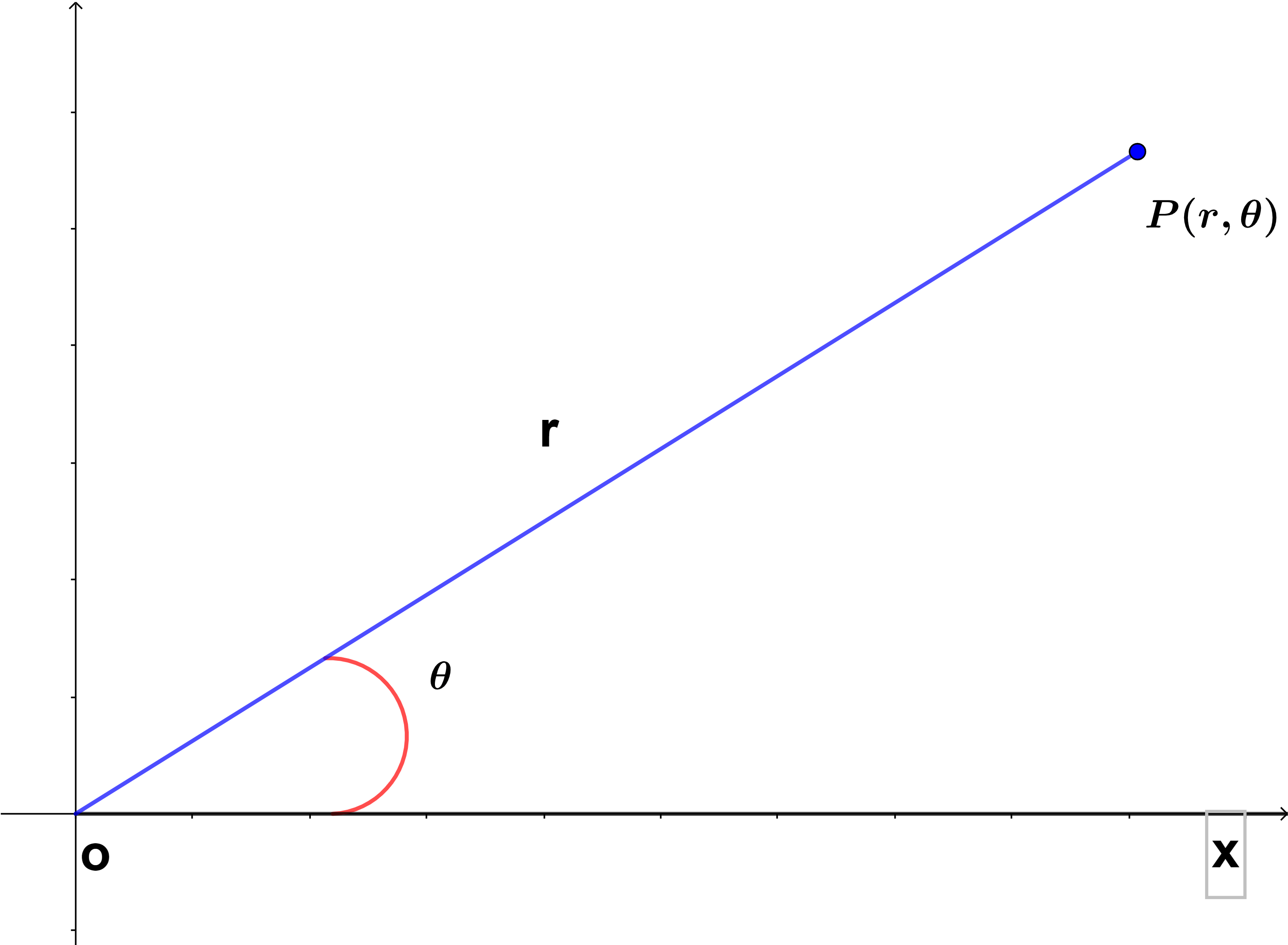
Las coordenadas polares son un sistema coordenado bidimensional en el que un punto en este plano es determinado por una distancia y un ángulo. El origen $O$ es llamado polo, y una semirrecta desde $O$ se llama eje polar como en la figura $(1)$, este eje generalmente se traza horizontalmente a la derecha correspondiente a la parte positiva del eje $x$ en las coordenadas cartesianas.

Sea $P$ un punto cualquiera en el sistema coordenado, entonces su distancia de $O$ a $P$ es $r$ denominándose distancia radial o radio vector y $\theta$ es el ángulo entre el eje polar y la recta $OP$ denominada como ángulo polar o coordenada angular, este ángulo generalmente se mide en radianes, por lo que el punto $P$ representa el par ordenado $P(r, \theta)$ y $r$, $\theta$ se llaman coordenadas polares del punto $P$.

$\theta$ es positivo cuando se mide en sentido contrario a las manecillas del reloj y negativo cuando se mide en sentido a las manecillas del reloj, mientras que $r$ siempre es mayor o igual a cero $(r \geq 0)$, en el caso del origen, el valor de $r$ es cero, pero el valor de $\theta$ se indefine, por lo que se define el valor en el origen como $(0, 0^{\circ})$.

Veamos unos ejemplos sencillos.

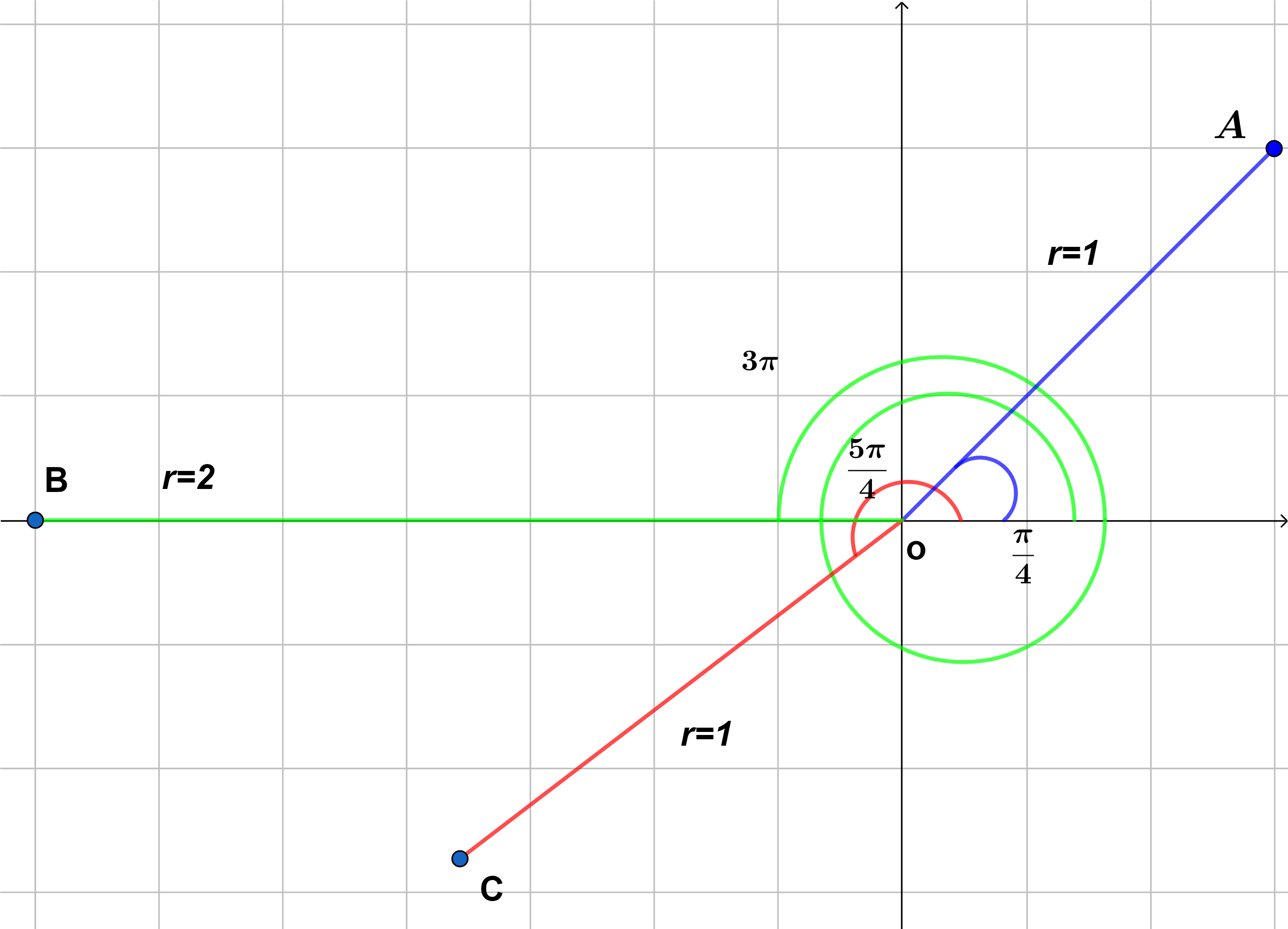
• Graficar los siguientes puntos cuya coordenadas son: $A=(1, \frac{\pi}{4})$, $B=(2, 3\pi)$ y $C=(1, \frac{5\pi}{4})$

Para graficar los puntos en coordenadas polares es sencillo, nos fijamos en la coordenada angular de cada punto y partimos del eje polar, dibujando los ángulos de cada punto con su respectivo radio vector como se muestra en la figura $(2)$. Vemos en el caso del punto $B$ en donde la coordenada angular es $3\pi$ por lo que se tiene que dar una vuelta completa $(2\pi)$ más $pi$.

Conversión de coordenadas

Para pasar de las coordenadas cartesianas a las coordenadas polares, veamos la siguiente figura:

Vemos que el punto $O$ es el origen de las coordenadas cartesianas que coincide con el origen de las coordenadas polares, sea un punto cualquier $P$ con coordenadas cartesianas $P(x, y)$ y coordenadas polares $P(r, \theta)$ en el plano, formando un triángulo rectángulo y sabemos que:

$$\cos(\theta )=\frac{x}{r} \hspace{1.5cm}\sin(\theta )=\frac{y}{r}$$

Por tanto:

$$ x=r\cos(\theta )\hspace{1.5cm} y=r\sin(\theta) \tag{1}$$

A estas dos ecuaciones $(1)$ nos permite cambiar de coordenadas polares a coordenadas cartesianas. Para coordenadas cartesianas a coordenadas polares tenemos la siguiente relación:

$$r^{2}=x^{2}+r^{2} \hspace{1.5cm}\tan(\theta )=\frac{y}{x}$$

Se dejará como tarea moral deducir las relaciones anteriores.

Observación: Vea que en el caso de $r$ se tiene dos soluciones, pero sabemos que se toma el valor positivo. En el caso de calcular la coordenada angular, al despejar la variable $\theta$ tendremos la función tangente inversa, el cual el dominio es $(\frac{-\pi}{2}, \frac{\pi}{2} )$, para obtener un único valor de $\theta$ en el intervalo $[0, 2\pi)$ nos basamos en la siguiente fórmula:

$$\theta =  \left\{ \begin{array}{c}\arctan\left( \frac { y }{ x } \right) \quad ~ ~ ~~~~si~ x<0,~ y\leq 0 \\ \frac { \pi }{ 2 } ~ ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~ ~ ~ ~ ~ si~ x=0,~ y>0 \\ arctan\left(\frac{y}{x}\right) +\pi~ si~ x<0 \\ \frac { 3\pi }{ 2 } ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~ ~ ~ ~ ~ si~ x=0,~ y<0 \\ \arctan\left( \frac { y }{ x } \right) +2\pi ~ ~ si~ x=0,~ y<0 \end{array}\right.$$

Veamos un ejemplo:

• Convierta el punto $(2, \frac{\pi}{3})$ de coordenadas polares a coordenadas cartesianas.

Por la relación (1) tenemos que:

$x=r\cos(\theta )=2\cos(\frac{\pi}{3})=2\frac{1}{2}=1$

$y=r\sin(\theta)=2\sin(\frac{\pi}{3})=2\frac{\sqrt{3}}{2}=\sqrt{3}$

Por tanto el punto en coordenadas cartesianas es: $(1, \sqrt{3})$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Convierta los siguientes puntos en coordenadas cartesianas a coordenadas polares: $(-2, 2)$, $(-3, -3)$, $(4, -2)$.
2. Deduzca la relación para pasar de coordenadas cartesianas a coordenadas polares.
3. ¿Qué curva representa la ecuación polar $r=2$?
4. Determinar la ecuación polar para la circunferencia $x^{2}+(y-3)^{2}=9$
5. Bosqueje la curva $r=1+\sin(\theta)$

Más adelante…

En esta sección vimos una introducción a las coordenadas polares y como pasar de estas coordenadas a las coordenadas cartesianas y viceversa, en la siguiente sección veremos algunas figuras en estas coordenadas y calcularemos el área de una curva polar.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II.
• Entrada anterior del curso: Cálculo Diferencial e Integral II: Tangentes a curvas paramétricas – El blog de Leo (nekomath.com)
• Siguiente entrada del curso: Cálculo Diferencial e Integral II: Área en coordenadas polares – El blog de Leo (nekomath.com)