Introducción

En la sección anterior vimos una introducción a las coordenadas polares, ahora veremos como calcular el área de una región acotada por una curva polar.

Área en coordenadas polares

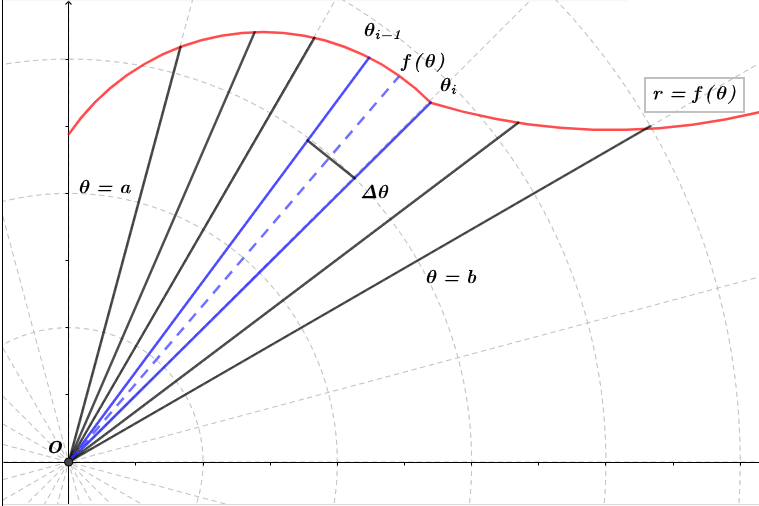
Sea la curva polar $r=f(\theta)$ y los rayos $\theta=a$ y $\theta=b$ como se muestra en la figura $(1)$, con $f$ una función positiva y $0 < b-a \leq 2\pi$. Dividimos el intervalo $[a, b]$ en $n$ subintervalos $[\theta_{i-1}, \theta_{i}]$ con amplitud $\Delta \theta$, sea $\theta^{*}_{n}$ un punto medio en el intervalo $[\theta_{i-1}, \theta_{i}]$, entonces el área $\Delta A_{i}$ se aproxima al área de un circulo con un ángulo $\Delta \theta$ y radio $f(\theta^{*}_{n})$, recordando que el área del sector de un circulo es proporcional a su ángulo central:

$$A=\frac{\theta}{2\pi}\pi r^{2}=\frac{1}{2}r^{2}\theta$$

Entonces tenemos que:

$$\Delta A_{i}\approx \frac{1}{2}[f(\theta^{*}_{n})]^{2}\Delta \theta $$

Si sumamos todos los $n$ subintervalos, se tiene que:

$$\sum_{i=1}^{n}\Delta A_{i}\approx \sum_{i=1}^{n} \frac{1}{2}[f(\theta^{*}_{n})]^{2}\Delta \theta $$

Si hacemos tender $n \to \infty$, entonces:

$$\lim_{n \to \infty} \sum_{i=1}^{n} \frac{1}{2}[f(\theta^{*}_{n})]^{2}\Delta \theta=\int_{a}^{b} \frac{1}{2}[f(\theta^{*}_{n})]^{2} d \theta$$

Por tanto, el área para calcular la región acotada por la curva $r=f(\theta)$ y los rayos $\theta=a$ y $\theta=b$ esta dado como:

$$A=\int_{a}^{b} \frac{1}{2}[f(\theta^{*}_{n})]^{2} d \theta \tag{1}$$

A menudo, la ecuación $(1)$ se expresa como:

$$A=\int_{a}^{b} \frac{1}{2}r^{2} d \theta $$

Ejemplos

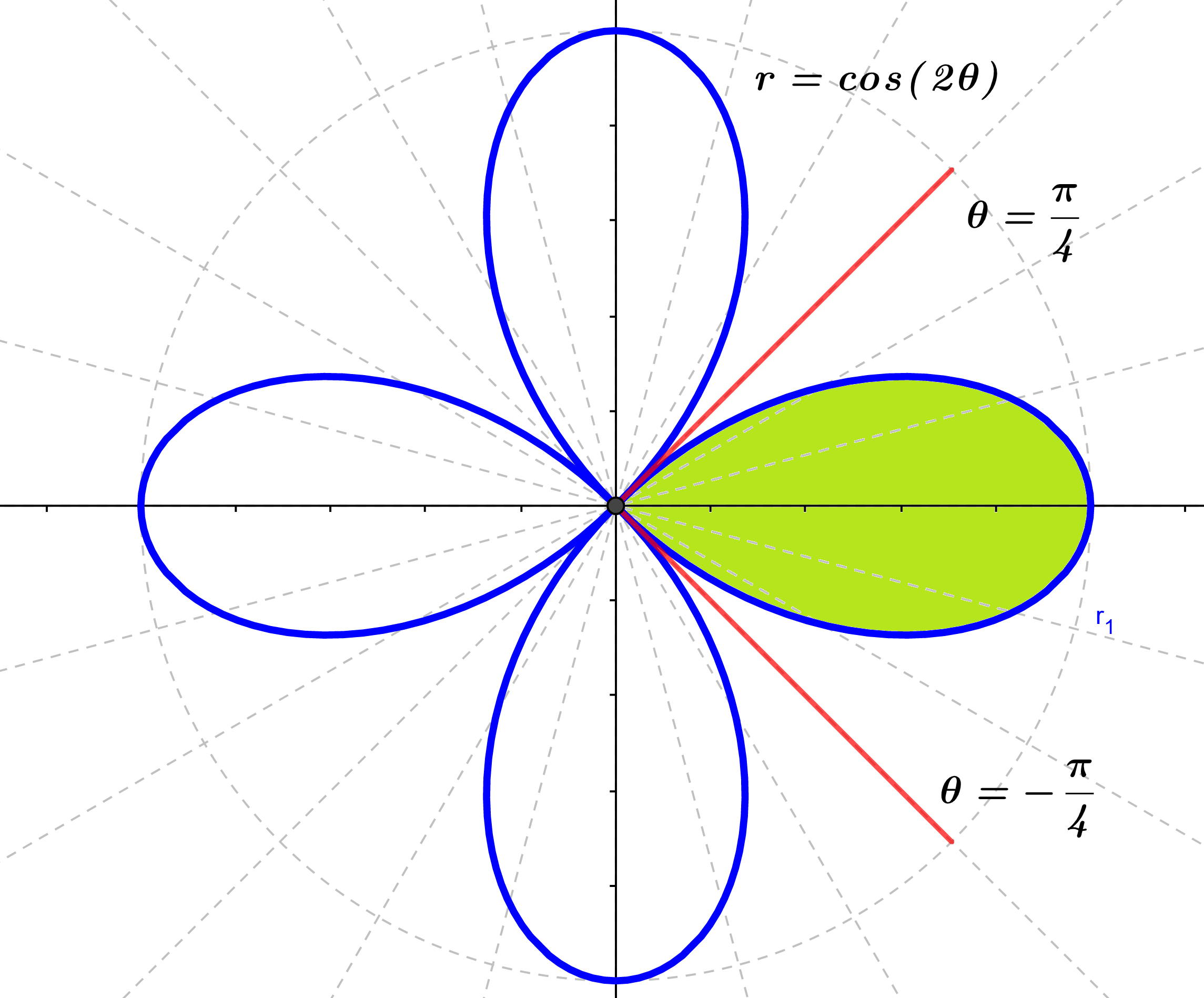
• Determine el área encerrada por un bucle de la rosa de cuatro hojas cuya curva esta dada como: $r=\cos(2\theta)$.

Como queremos solo un bucle, de la figura $(2)$, vemos que los rayos $\theta=\frac{\pi}{4}$ y $\theta=-\frac{\pi}{4}$ encierran el bucle derecho de la rosa, por lo que el área la calculamos como:

$$A=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\frac{1}{2}r^{2}d\theta=\frac{1}{2}\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}(\cos(2\theta))^{2}d\theta=\int_{0}^{\frac{\pi}{4}}(\cos(2\theta))^{2}d\theta$$

Utilizamos una relación para el coseno:

$$\cos^{2}(2x)=\frac{1}{2}(1+\frac{1}{4}\cos(4x))$$

Por ende:

$$A=\int_{0}^{\frac{\pi}{4}}(\cos(2\theta))^{2}d\theta=\int_{0}^{\frac{\pi}{4}}\frac{1}{2}(1+\cos(4\theta))d\theta=\frac{1}{2}\left [ \theta+\frac{1}{4}\sin(4\theta) \right ]\bigg|_{0}^{\frac{\pi}{4}}=\frac{\pi}{8}$$

Por tanto el área de un bucle de la rosa es: $A=\frac{\pi}{8}$

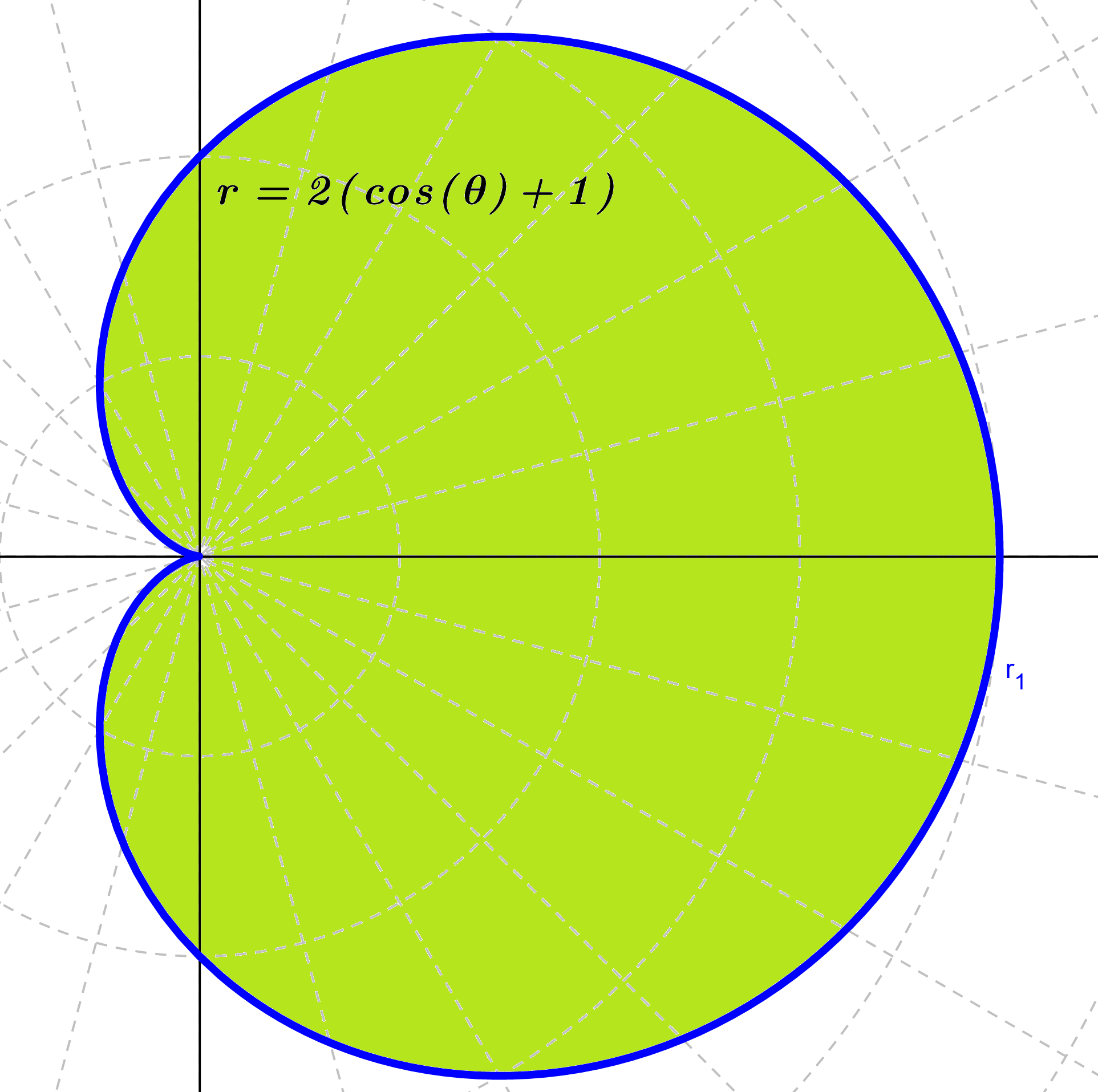
• Determinar el área de la región en el plano, acotada por la cardioide $r=2(1+\cos(\theta))$.

Como queremos toda el área del cardioide entonces integramos de $0$ a $2\pi$, por lo que:

$$A=\int_{0}^{2\pi} \frac{1}{2}r^{2}d\theta=\int_{0}^{2\pi} \frac{1}{2}4(1+\cos(\theta))^{2}d\theta=\int_{0}^{2\pi}2(1+2\cos(\theta)+\cos^{2}(\theta))d\theta$$

Utilizamos la relación:

$$\cos^{2}(x)=\frac{1+\cos(2x)}{2}$$

Por tanto:

$$\int_{0}^{2\pi} (2+4\cos(\theta)+1+\cos(2\theta)d\theta=\int_{0}^{2\pi} (3+4\cos(\theta)+\cos(2\theta)d\theta=\left [ 3\theta+4\sin(\theta)+\frac{\sin(2\theta)}{2} \right ]\bigg|_{0}^{2\pi}=6\pi$$

$\space$

El área entre dos curvas acotadas por las curvas $r_{1}=f(\theta)$ y $r_{2}=f(\theta)$, $(\theta)=a$ y $(\theta)=b$, con $f(\theta) \geq g(\theta) \geq 0$ y $0 < b-a \leq 2\pi$ se puede calcular mediante la siguiente formula:

$$\int_{a}^{b}\frac{1}{2}[f(\theta )-g(\theta )]^{2}d\theta$$

La idea de la deducción de esta formula es la misma idea al aproximar el área de una curva en coordenadas polares de esta sección, en este caso es sobre dos curvas.

En este tipo de coordenadas es un poco complicado dibujar este tipo de graficas por lo que hay algunas herramientas útiles en internet como Geogebra y Wolfram para visualizar estas curvas, incluso, si sabe programar, lo puede intentar con el lenguaje de programación de su agrado.

Tarea moral

Los siguientes ejercicios no son para evaluación pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionado con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Deduzca la formula para calcular el área entre dos curvas en coordenadas polares.
2. Encuentre el área de la región acotada por: $r=\sqrt{\theta}$.
3. Encuentre el área de la región acotada por: $r=\theta^{2}$ y el sector$0\leq \theta \leq \frac{\pi}{4}$.
4. Encuentre el área de la región acotada por: $r=e^{\frac{\theta}{2}}$ y el sector$0\leq \theta \leq 2\pi$.
5. Encuentre el área de la región acotada por: $r=\sqrt{sin(\theta)}$ y el sector$0\leq \theta \leq \pi$.
6. Encuentre el área de la región acotada por el circulo $r=1$ y fuera del cardioide $r=1-\cos(\theta)$.

Más adelante…

En esta sección vimos como calcular el área de una curva en coordenadas polares y entre dos curvas, obsérvese que la idea de calcular estas áreas es la misma que en coordenadas cartesianas, al igual, la idea de calcular la longitud de arco en coordenadas polares será la misma que en coordenadas cartesianas, el calculo de la longitud de arco con curvas polares lo veremos en la siguiente sección.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II.
• Entrada anterior del curso: Cálculo Diferencial e Integral II: Coordenadas Polares – El blog de Leo (nekomath.com)
• Siguiente entrada del curso: Cálculo Diferencial e Integral II: Longitud de arco en coordenadas polares – El blog de Leo (nekomath.com)