Introducción
Ahora veremos cuales son las características que debe cumplir una función para ser par o impar. Veremos geométricamente qué ocurre con estas funciones. De igual manera, veremos qué ocurre al realizar operaciones entre ellas.
Definición de función par
Definición: Decimos que $f: A \rightarrow B$ una función es par si y sólo si para todo $x \in A$ ocurre que:
$$f(x)=f(-x)\quad\text{.}$$
Ejemplo
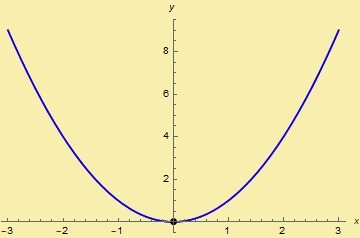
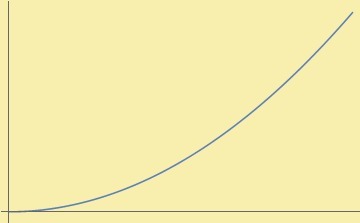
La función $f(x)=x^{2}$ cumple ser par ya que:
$$f(-x)=(-x)^{2}=x^{2}=f(x)$$
para todo $x \in \r$.
De su gráfica observamos que $f$ se refleja respecto al eje $y$:
Definición de función impar
Definición: Decimos que $f: A \rightarrow B$ una función es impar si y sólo si para todo $x \in A$ ocurre que:
$$f(-x)= – f(x)\quad\text{.}$$
Ejemplo
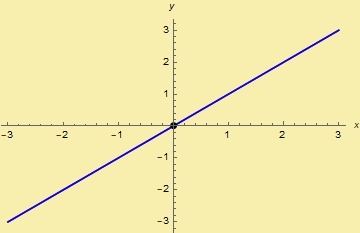
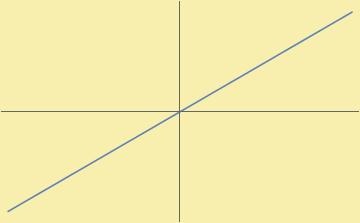
La función $g(x)=x$ cumple ser impar ya que:
$$g(-x)=(-x) = – (x) = -g(x)$$
para todo $x \in \r$.
De su gráfica observamos que $f$ se refleja respecto al origen:
Un teorema importante
Teorema: Cualquier función $f: \r \rightarrow \r$ puede expresarse como la suma de una función par e impar, es decir,
$$f(x)= P(x)+ I(x)$$
para toda $x \in \r$, donde $P(x)$ e $I(x)$ son únicas.
Demostración: Consideremos las funciones $P(x)$ par e $I(x)$ impar como sigue:
\begin{align*}
P(x)&=\frac{f(x)+f(-x)}{2} & I(x)&=\frac{f(x)-f(-x)}{2}
\end{align*}
Vemos que al realizar la suma obtenemos:
\begin{align*}
P(x)+I(x) &= \frac{f(x)+f(-x)}{2} + \frac{f(x)-f(-x)}{2}\\
&= \frac{f(x)+f(-x)+f(x)-f(-x)}{2}\\
&= \frac{2f(x)}{2}\\
&= f(x)
\end{align*}
Ahora nos falta ver qué $P(x)$ e $I(x)$ son únicas. Como ya sabemos que $f(x)= P(x)+ I(x)$ tenemos lo siguiente:
\begin{align}
f(x)&=P(x)+I(x)\\
f(-x)&=P(x)-I(x)\\
\end{align}
Así sumando $(1)$ y $(2)$ obtenemos:
\begin{align*}
f(x)+f(-x) &= 2 P(x)\\
P(x) &= \frac{f(x)+f(-x)}{2}
\end{align*}
Ahora restando $(1)$ y $(2)$ obtenemos:
\begin{align*}
f(x)-f(-x) &= 2 I(x)\\
I(x) &= \frac{f(x)-f(-x)}{2}
\end{align*}
Dado que tenemos la igualdad $f(x)= P(x)+ I(x)$ concluimos que $P(x)$ e $I(x)$ son únicas.
$\square$
Ejercicio
Consideremos las funciones $f,g: \r \rightarrow \r$. ¿Cómo es $f+g$, $fg$ y $f \circ g$ si:
- $f$ y $g$ son pares
- $f$ y $g$ son impares
- $f$ es par y $g$ es impar
- $f$ es impar y $g$ es par
es par, impar o no necesariamente alguna de las anteriores?
En la suma de funciones
1. Si $f$ y $g$ son pares $\Rightarrow f+g$ es par.
Demostración:
Vemos que al desarrollar:
\begin{align*}
(f+g)(-x)&= f(-x)+g(-x)\tag{ definición de $f+g$}\\
&= f(x)+g(x)\tag{ por $f$ y $g$ pares}\\
&= (f+g)(x)\tag{ definición de $f+g$}\\
\end{align*}
3. Si $f$ es par y $g$ es impar $\Rightarrow f+g$ no necesariamente es par o impar.
Consideremos $f(x)= x^{2}$ y $g(x)=x$. Luego si $x=1$ entonces:
\begin{align*}
(f+g)(-1)&= f(-1)+g(-1) & (f+g)(1)&= f(1)+g(1)\\
&= 1-1 & &= 1+1\\
&= 0 & &=2
\end{align*}
$\therefore (f+g)(-1) \neq (f+g)(1)$
$\therefore f+g$ no es par.
Además veamos que $-(f+g)(1)=-2$ por lo que:
$$-(f+g)(1) \neq (f+g)(-1)$$
$\therefore f+g$ tampoco es impar.
En el producto de funciones
1. Si $f$ y $g$ son pares $\Rightarrow fg$ es par.
Demostración:
Si tomamos $fg(-x)$ observamos lo siguiente:
\begin{align*}
(fg)(-x)&= f(-x)g(-x) \tag{definción de $fg$}\\
&= f(x)g(x) \tag{por$f$ y $g$ pares}\\
&= (fg)(x)
\end{align*}
$\therefore fg$ es par.
2. Si $f$ y $g$ son impares $\Rightarrow fg$ es par.
Demostración:
Comenzando con $fg(-x)$ y desarrollando tenemos:
\begin{align*}
(fg)(-x)&= f(-x)g(-x) \tag{definción de $fg$}\\
&= (-f(x))(-g(x)) \tag{por$f$ y $g$ impares}\\
&=f(x)g(x)\\
&= (fg)(x)
\end{align*}
$\therefore fg$ es par.
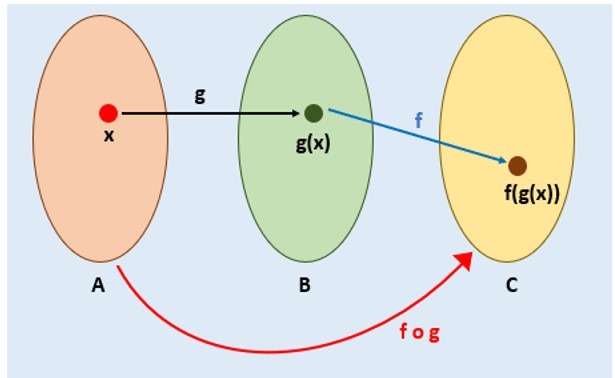
En la composición de funciones
3. Si $f$ es par y $g$ es impar $\Rightarrow f \circ g$ es par.
Demostración:
Realizando la composición $(f \circ g)(-x)$:
\begin{align*}
(f \circ g)(-x)&=f(g(-x)) \tag{definción de $f \circ g$}\\
&= f(-g(x)) \tag{ por $g$ impar}\\
&= f(g(x)) \tag{por $f$ par}\\
&=(f \circ g)(x)
\end{align*}
$\therefore f \circ g$ es par.
4.Si $f$ es impar y $g$ es par $\Rightarrow f \circ g$ es par.
Demostración:
Procediendo análogamente al punto anterior:
\begin{align*}
(f \circ g)(-x)&=f(g(-x)) \tag{definción de $f \circ g$}\\
&= f(g(x)) \tag{ por $g$ par}\\
&=(f \circ g)(x)
\end{align*}
$\therefore f \circ g$ es par.
Los puntos faltantes se dejarán como ejercicios de Tarea moral, para resolverlos se debe proceder como en los incisos anteriores según sea el caso.
Más adelante
En la siguiente entrada, continuaremos con las funciones crecientes y decrecientes. Veremos qué características debe cumplir una función para poder determinar si crece o decrece en un intervalo. También exploraremos qué significa ser una función acotada y algunas pruebas relacionadas con este concepto.
Tarea moral
- Prueba que las funciones $P(x)$ e $I(x)$ cumplen con ser par e impar respectivamente:
\begin{align*}
P(x)&=\frac{f(x)+f(-x)}{2} & I(x)&=\frac{f(x)-f(-x)}{2}
\end{align*} - Demuestra que la función constante cero es la única que cumple ser par e impar.
- Exprese a las siguientes funciones como suma de una función par y una impar:
- $f(x)= x^{2}-4x+2$
- \begin{multline*}h(x)=\frac{1}{1+x^{2}}\end{multline*}
- Termina los puntos faltantes del ejercicio anterior:
- Para $f+g$ cuando $f$ y $g$ son impares
- Para $f+g$ cuando $f$ es impar y $g$ es par.
- Para $fg$ cuando $f$ es par y $g$ es impar
- Para $fg$ cuando $f$ es impar y $g$ es par
- Para $f \circ g$ cuando $f$ y $g$ son pares
- Para $f \circ g$ cuando $f$ y $g$ son impares
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Funciones inyectivas, sobreyectivas y biyectivas. Función inversa.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Funciones crecientes y decrecientes. Funciones acotadas.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»