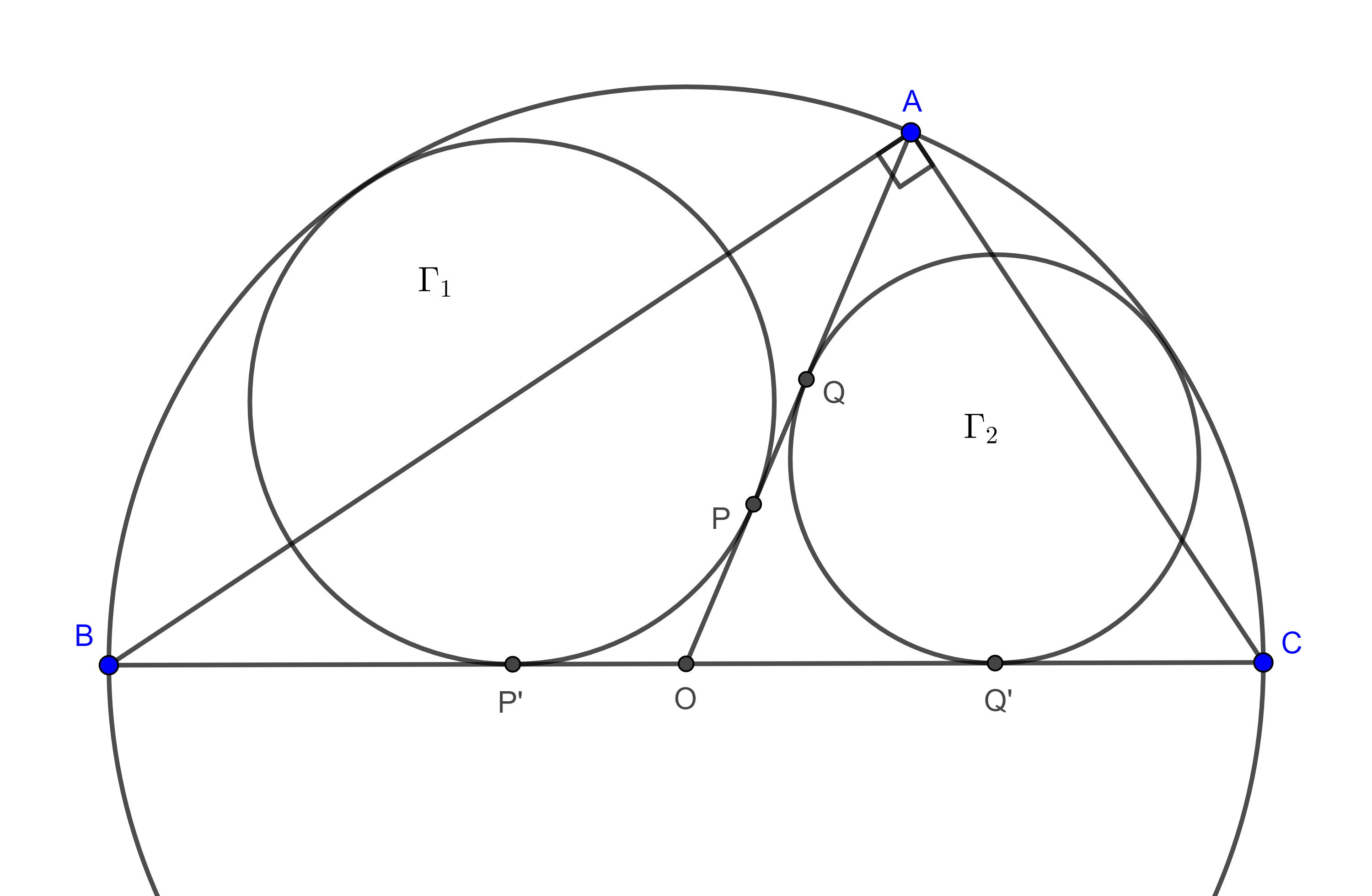Archivo de la etiqueta: teorema de Ptolomeo

Geometría Moderna I: Teorema de Casey

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión demostraremos el teorema generalizado de Ptolomeo conocido como teorema de Casey, el cual nos dice que los vértices del cuadrilátero cíclico, al que hace mención el teorema de Ptolomeo, pueden ser considerados como circunferencias de radio distinto de cero, y los lados o diagonales del cuadrilátero cíclico se pueden pensar como segmentos tangentes entre dos circunferencias.

Tangente común a dos circunferencias

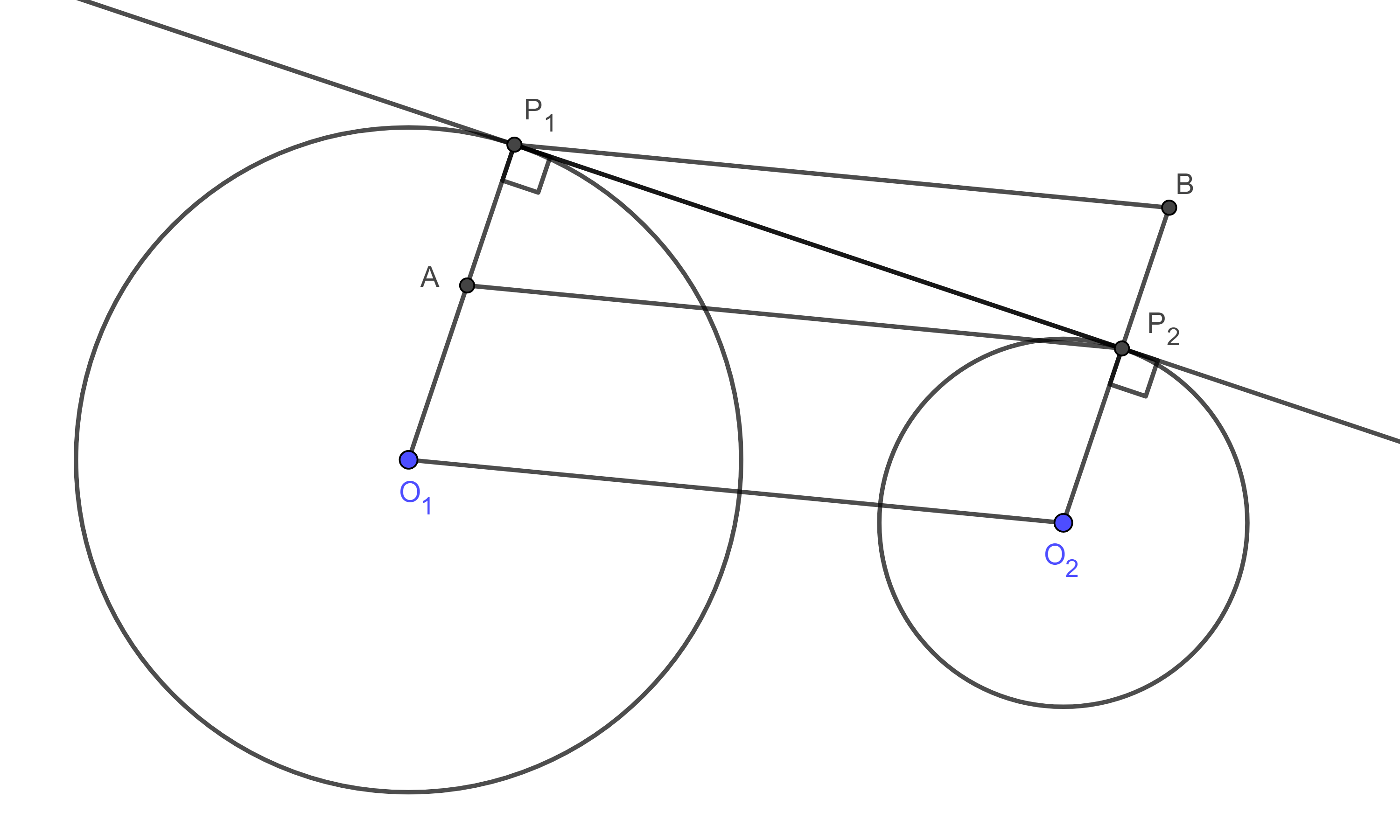
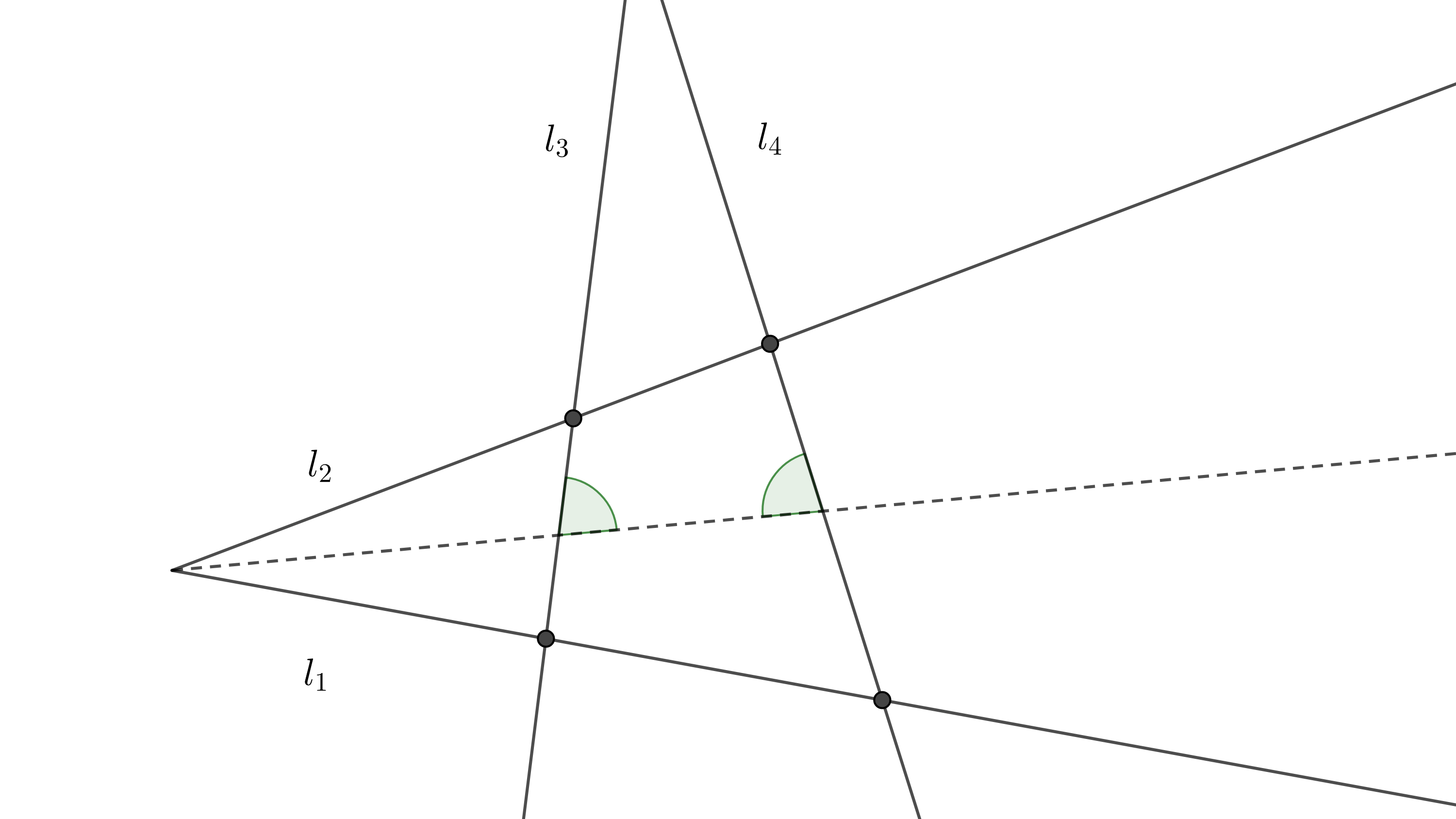
Proposición 1. Sean $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, dos circunferencias tal que ninguna contiene a la otra y $P_{1}$, $P_{2}$ los puntos en que una recta es tangente a ambas circunferencias, entonces:

$i)$ Si $P_{1}P_{2}$ es exterior, es decir, no cruza el segmento $O_{1}O_{2}$ (figura 1),
$P_{1}P_{2}^2 = O_{1}O_{2}^2 – (R_{1} – R_{2})^2$,
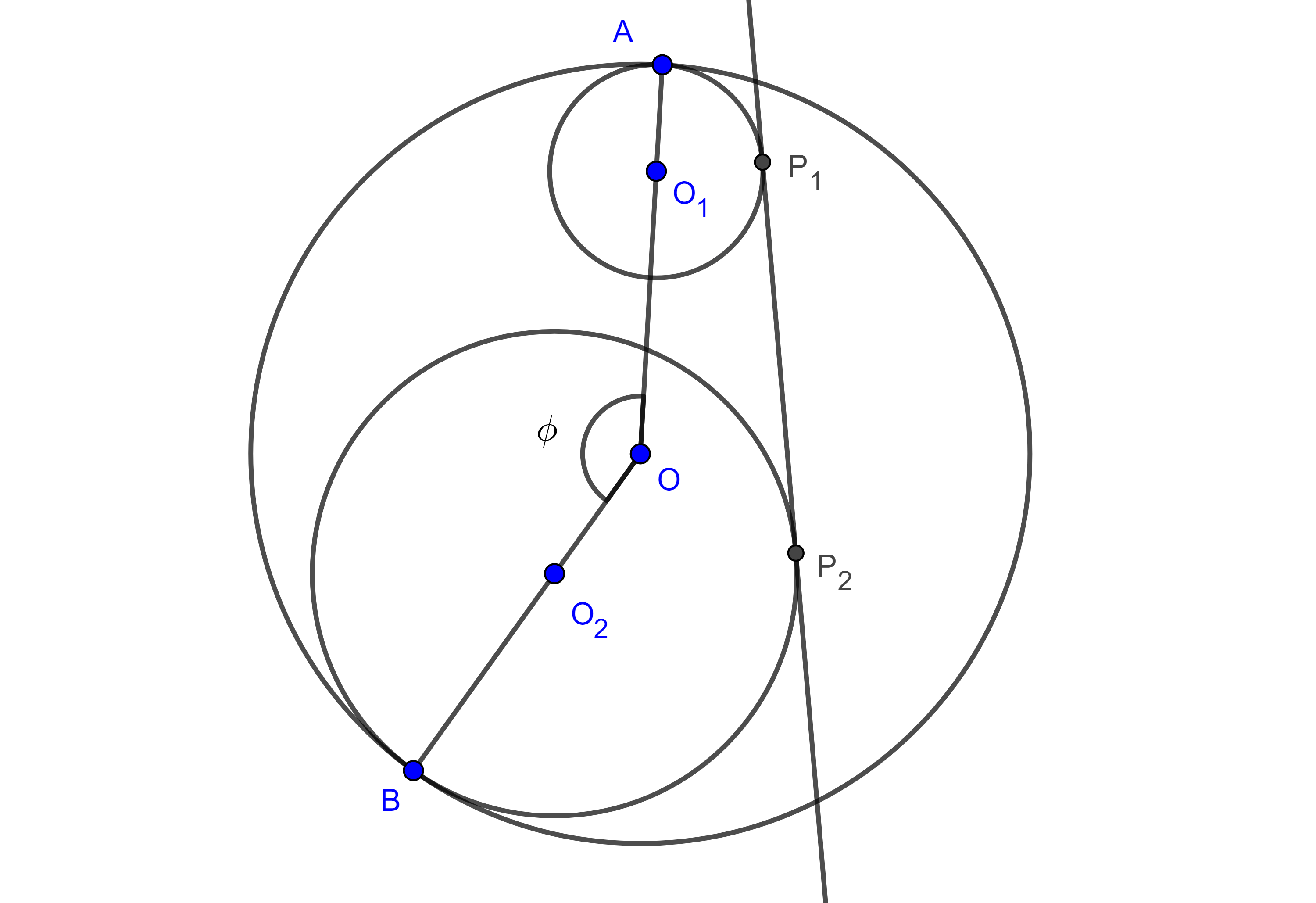
$ii)$ Si $P_{1}P_{2}$ es interior, es decir, interseca al segmento $O_{1}O_{2}$ (figura 2),
$P_{1}P_{2}^2 = O_{1}O_{2}^2 – (R_{1} + R_{2})^2$.

Demostración. Sin pérdida de generalidad supongamos $R_{1} \geq R_{2}$.

$i)$ Sean $A$ la intersección de $O_{1}P_{1}$ con la paralela a $O_{1}O_{2}$ desde $P_{2}$, $B$ la intersección de $O_{2}P_{2}$ con la paralela a $O_{1}O_{2}$ desde $P_{1}$.

Figura 1

Como $O_{1}P_{1} \perp P_{1}P_{2}$ y $O_{2}P_{2} \perp P_{1}P_{2}$ entonces $O_{1}P_{1} \parallel O_{2}P_{2}$.

Por lo tanto, $\square P_{1}O_{1}O_{2}B$, $\square P_{1}AP_{2}B$ y $\square AO_{1}O_{2}P_{2}$ son paralelogramos.

En consecuencia,
$P_{1}B = O_{1}O_{2}$ y $P_{2}B = AP_{1} = R_{1} -AO_{1} = R_{1} – R_{2}$.

Como $\angle BP_{2}P_{1} = \dfrac{\pi}{2}$ podemos aplicar el teorema de Pitágoras a $\triangle BP_{2}P_{1}$.

$P_{1}P_{2}^2 = P_{1}B^2 – P_{2}B^2 = O_{1}O_{2}^2 – (R_{1} – R_{2})^2$.

$\blacksquare$

$ii)$ Sea $C$ la intersección de $O_{2}P_{2}$ con la paralela a $P_{1}P_{2}$ desde $O_{1}$.

Como $O_{1}C \parallel P_{1}P_{2}$ y $P_{1}P_{2} \perp O_{2}P_{2}$ entonces $\angle O_{1}CO_{2} = \dfrac{\pi}{2}$, además $\square CO_{1}P_{1}P_{2}$ es un rectángulo.

Por lo tanto,
$CO_{1} = P_{1}P_{2}$ y $CP_{2} = O_{1}P_{1} = R_{1}$.

Figura 2

Como resultado de aplicar el teorema de Pitágoras a $\triangle O_{1}CO_{2}$ obtenemos,

$P_{1}P_{2}^2 = CO_{1}^2 = O_{1}O_{2}^2 – CO_{2}^2$
$= O_{1}O_{2}^2 – (CP_{2} + P_{2}O_{2})^2 = O_{1}O_{2}^2 – (R_{1} + R_{2})^2$.

$\blacksquare$

Teorema de Casey

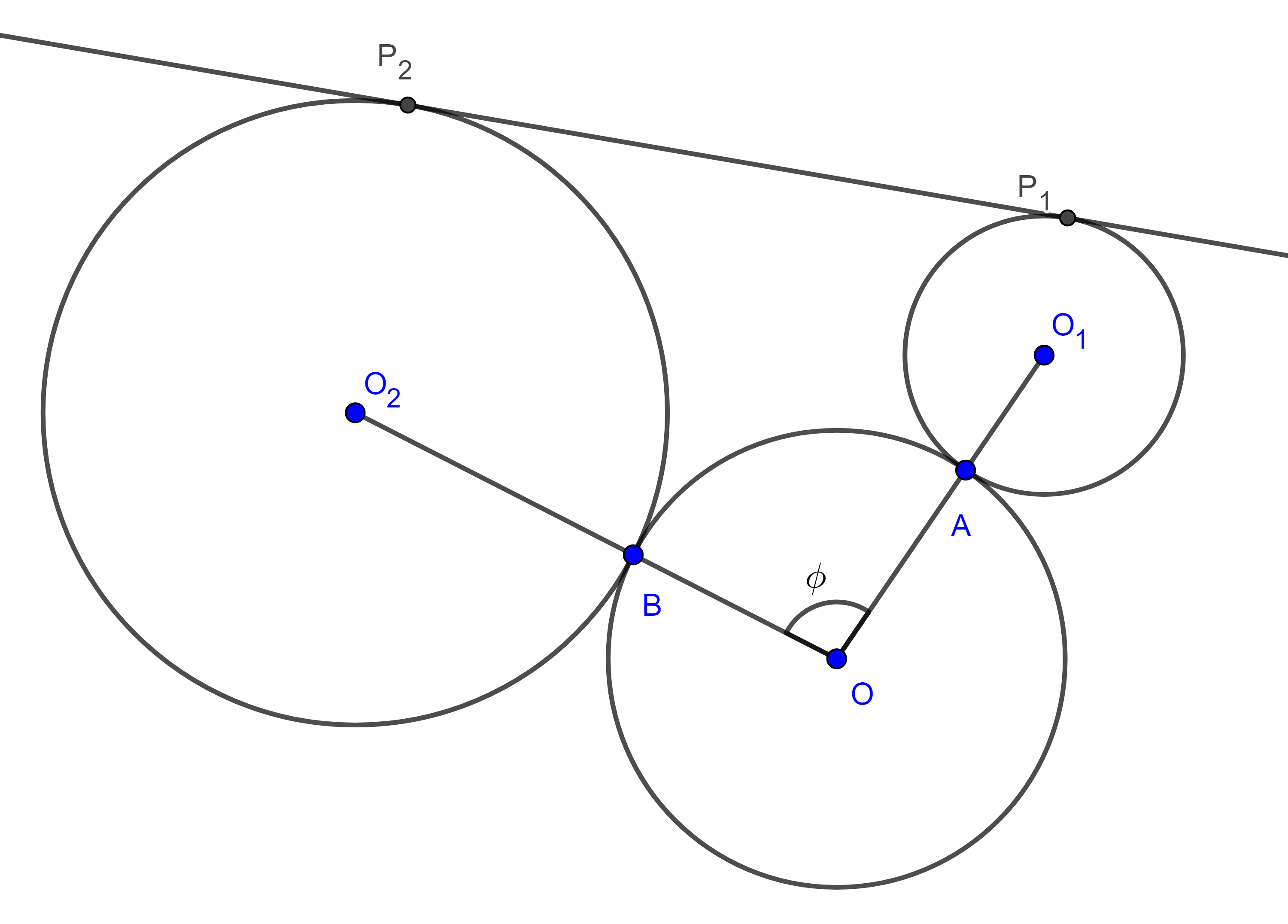
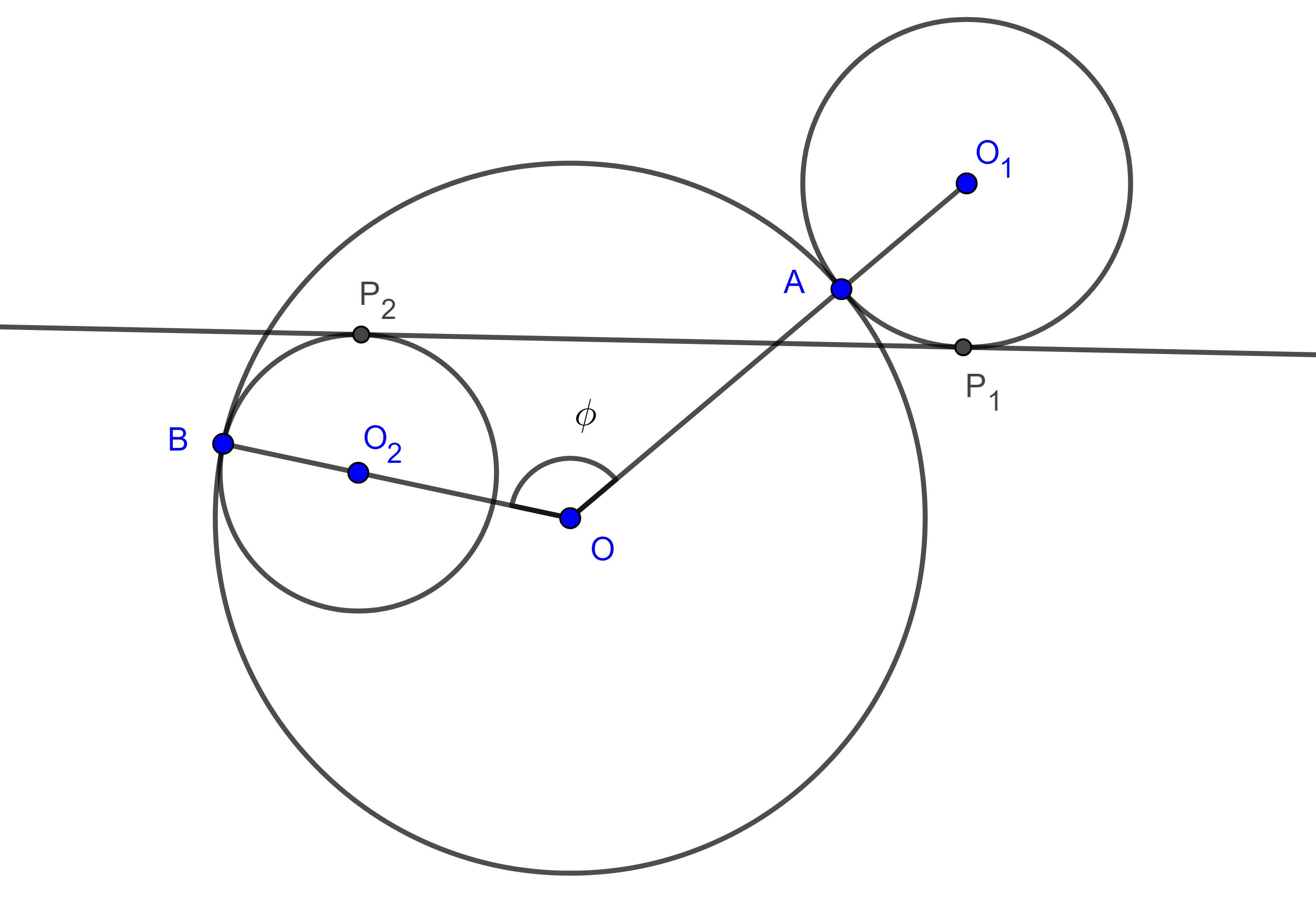
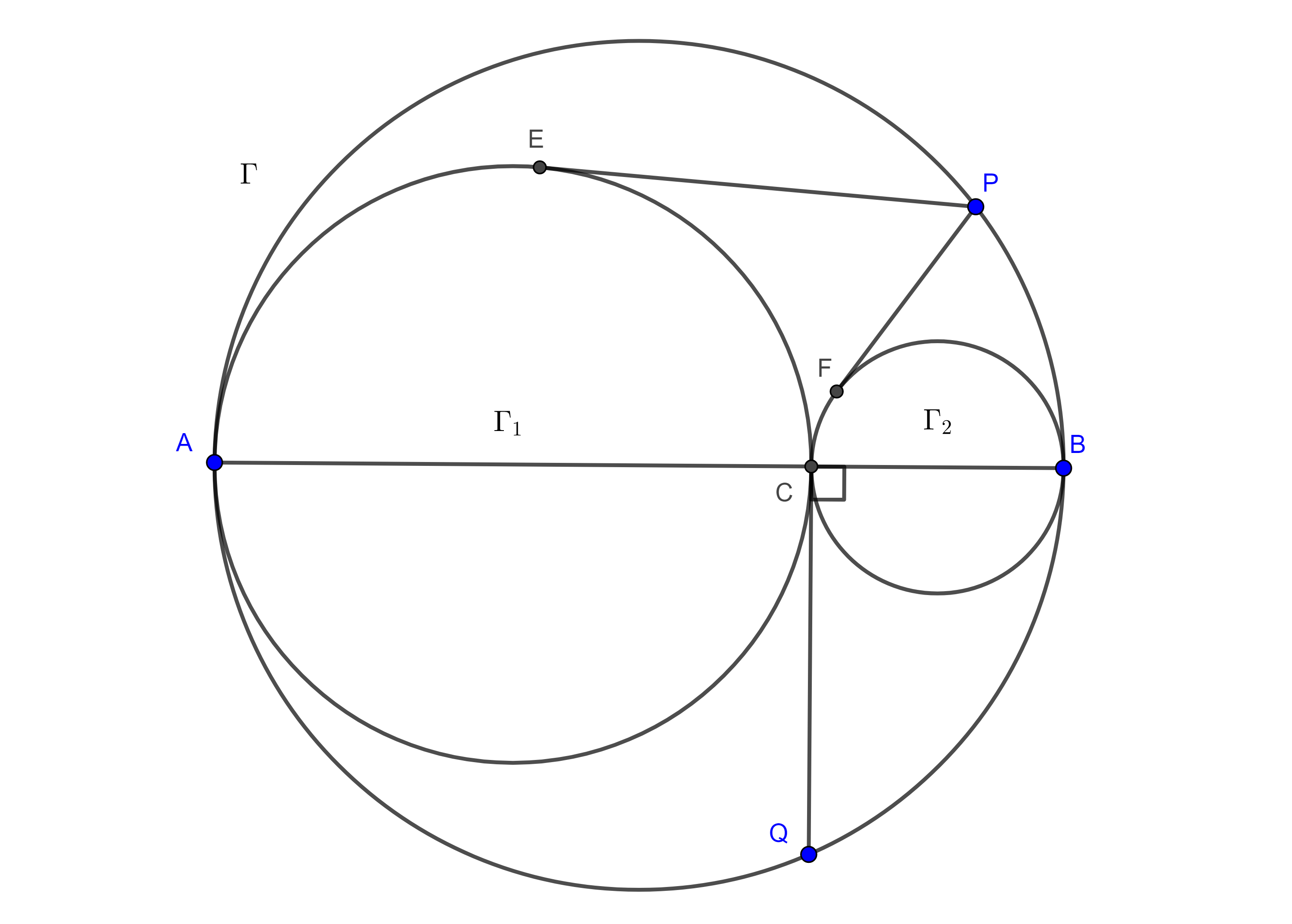
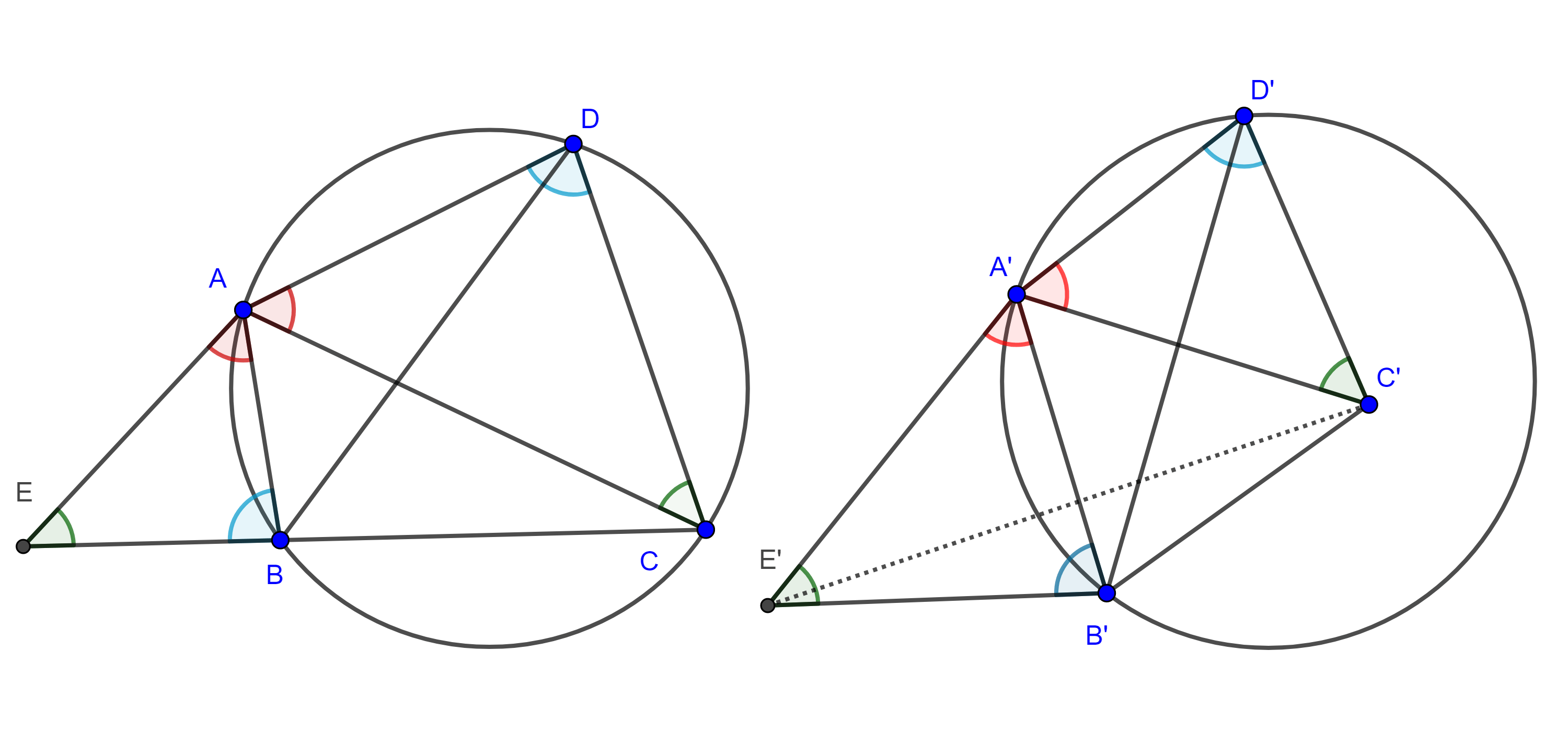
Proposición 2. Sean $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, dos circunferencias tangentes a una tercera circunferencia $(O, R)$, en dos puntos distintos $A$ y $B$ respectivamente, considera $P_{1}$, $P_{2}$ los puntos en que una recta es tangente a $(O_{1}, R_{1})$ y a $(O_{2}, R_{2})$, entonces:

$i)$ Si $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, son interiores a $(O, R)$ y $P_{1}P_{2}$ es exterior (figura 3),
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R – R_{1})(R – R_{2})}$,
$ii)$ Si $(O_{1}, R_{1})$, $(O_{2}, R_{2})$, son exteriores a $(O, R)$ y $P_{1}P_{2}$ es exterior (figura 4),
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R + R_{1})(R + R_{2})}$,
$iii)$ Si $(O_{1}, R_{1})$ es exterior, $(O_{2}, R_{2})$ es interior a $(O, R)$ y $P_{1}P_{2}$ es interior (figura 5),
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R + R_{1})(R –  R_{2})}$.

Figura 3

Demostración. Sea $\phi = \angle AOB$.
$i)$ Aplicamos la ley de cosenos a $\triangle O_{1}OO_{2}$ y a $\triangle AOB$,

$O_{1}O_{2}^2 = O_{1}O^2 + O_{2}O^2 – 2O_{1}O \times O_{2}O \cos \phi$
$\begin{equation} = (R – R_{1})^2 + (R – R_{2})^2 – 2(R – R_{1})(R – R_{2})\cos \phi. \end{equation}$

$AB^2 = AO^2 + BO^2 – 2AO \times BO \cos \phi = 2R^2 – 2R^2\cos \phi$
$\Leftrightarrow$
$\begin{equation} \cos \phi = 1 – \dfrac{AB^2}{2R^2}. \end{equation}$

Por la proposición anterior parte $i)$ y de las ecuaciones $(1)$ y $(2)$ tenemos

$P_{1}P_{2}^2 = O_{1}O_{2}^2 – (R_{1} – R_{2})^2$
$= (R – R_{1})^2 + (R – R_{2})^2 – 2(R – R_{1})(R – R_{2})(1 – \dfrac{AB^2}{2R^2}) – (R_{1} – R_{2})^2$
$= R^2 – 2RR_{1} + R_{1}^2 + R^2 – 2RR_{2} + R_{2}^2 – 2(R^2 – RR_{2} – RR_{1} + R_{1}R_{2})$
$+ 2(R – R_{1})(R – R_{2})\dfrac{AB^2}{2R^2} – (R_{1} – R_{2})^2$
$= (R – R_{1})(R – R_{2})(\dfrac{AB^2}{R^2})$.

Por lo tanto,
$P_{1}P_{2} = \dfrac{AB}{R} \sqrt{(R – R_{1})(R – R_{2})}$.

$ii)$ y $iii)$ se muestran con un razonamiento similar.

$\blacksquare$

Figura 4
Figura 5

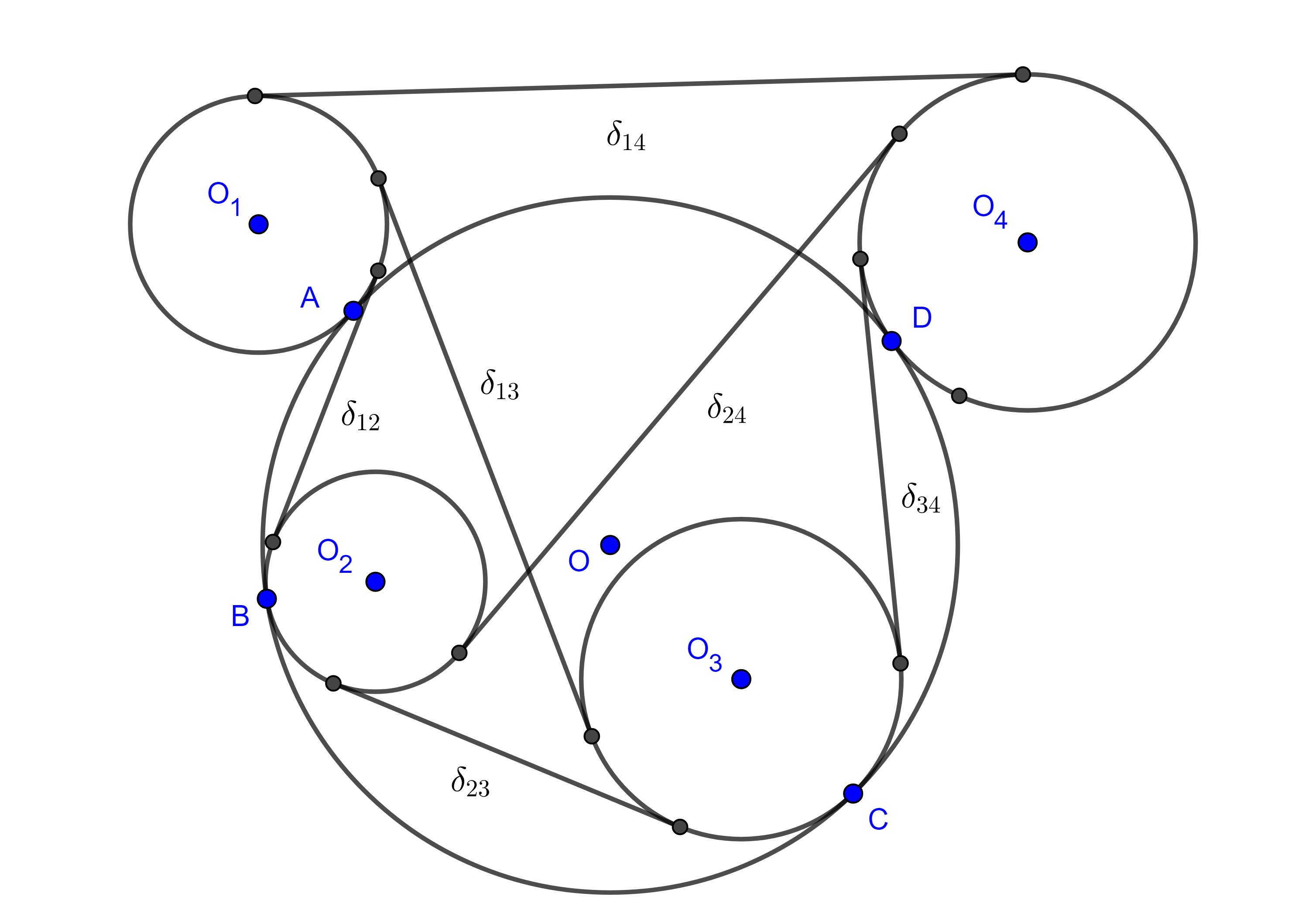
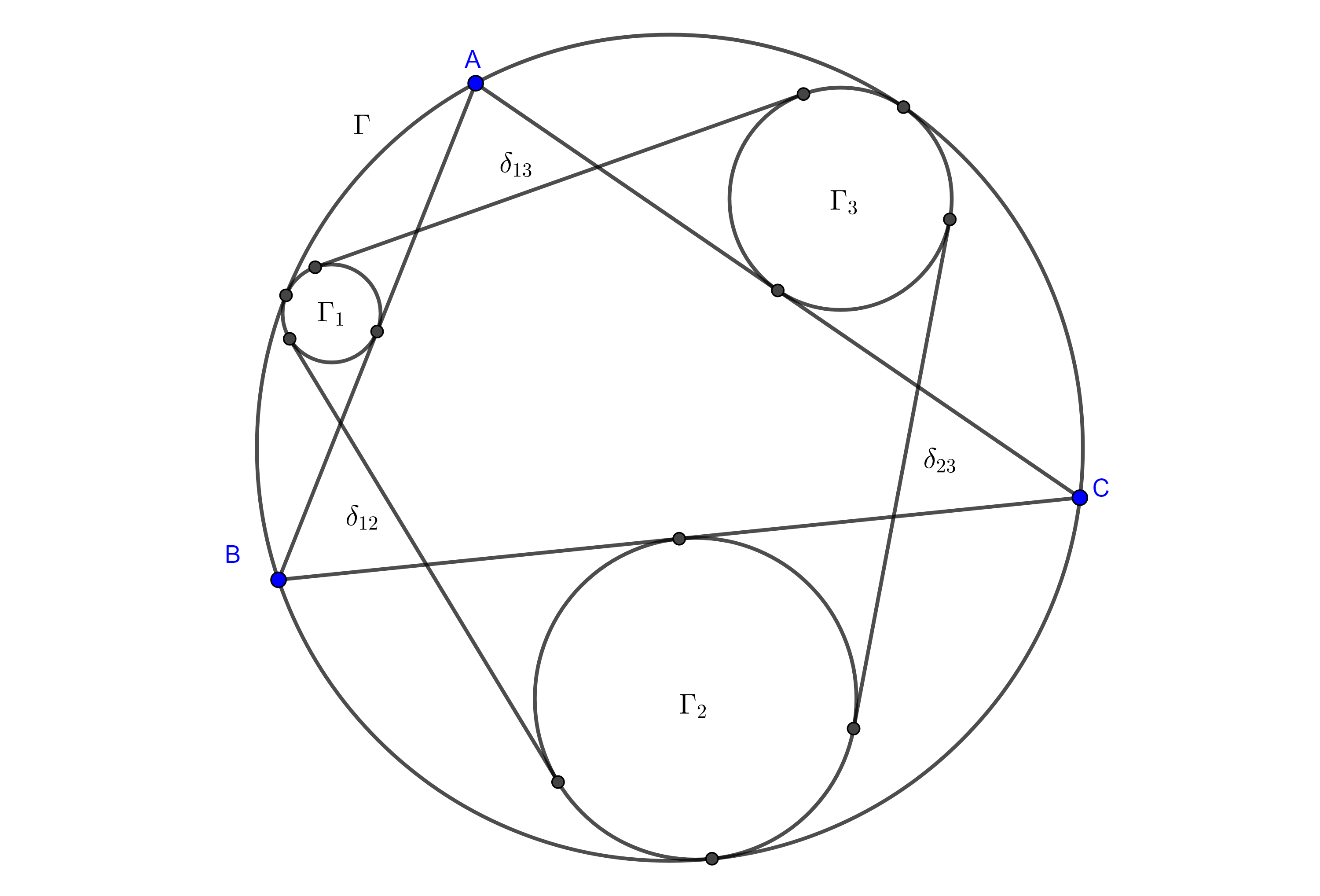
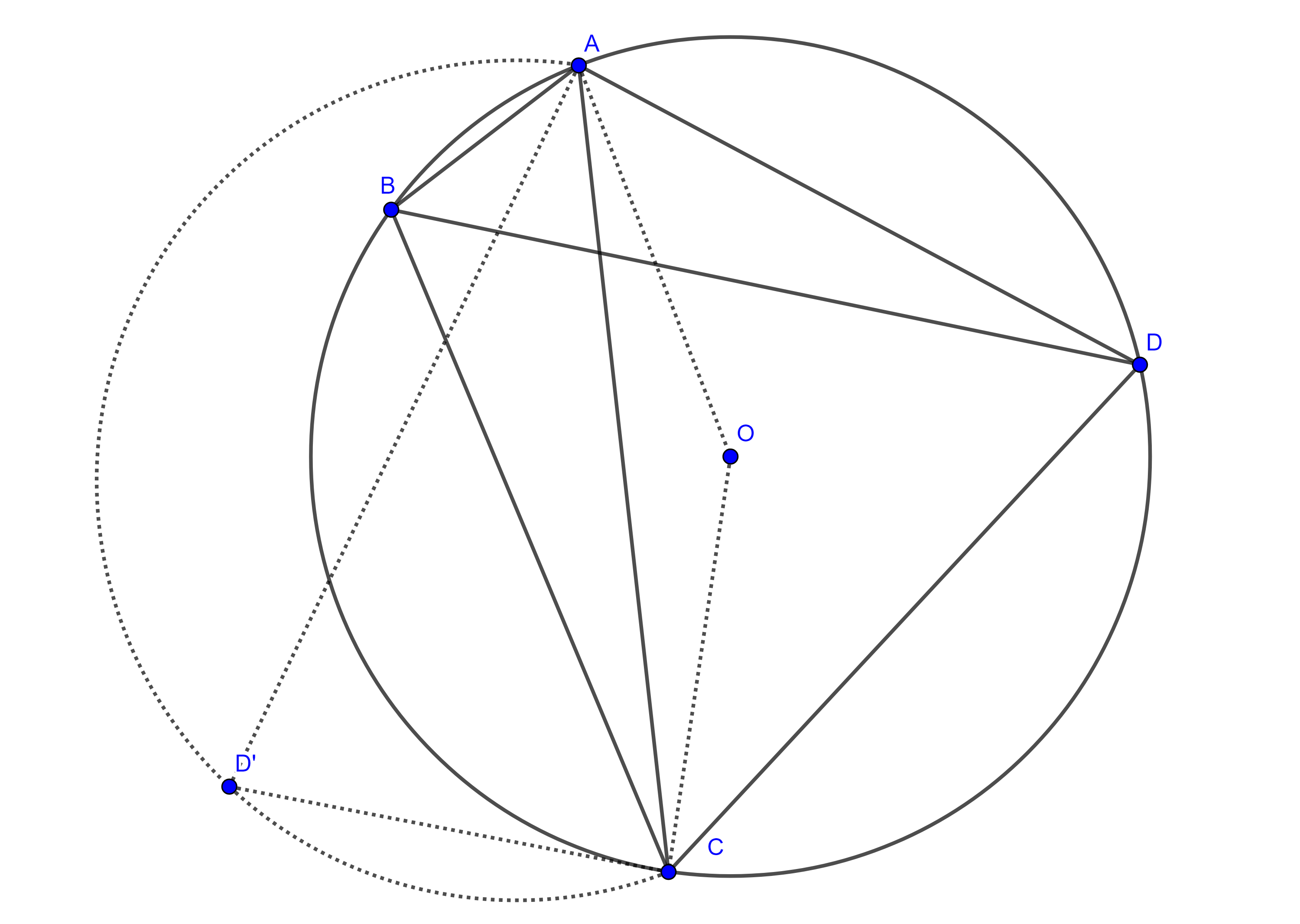
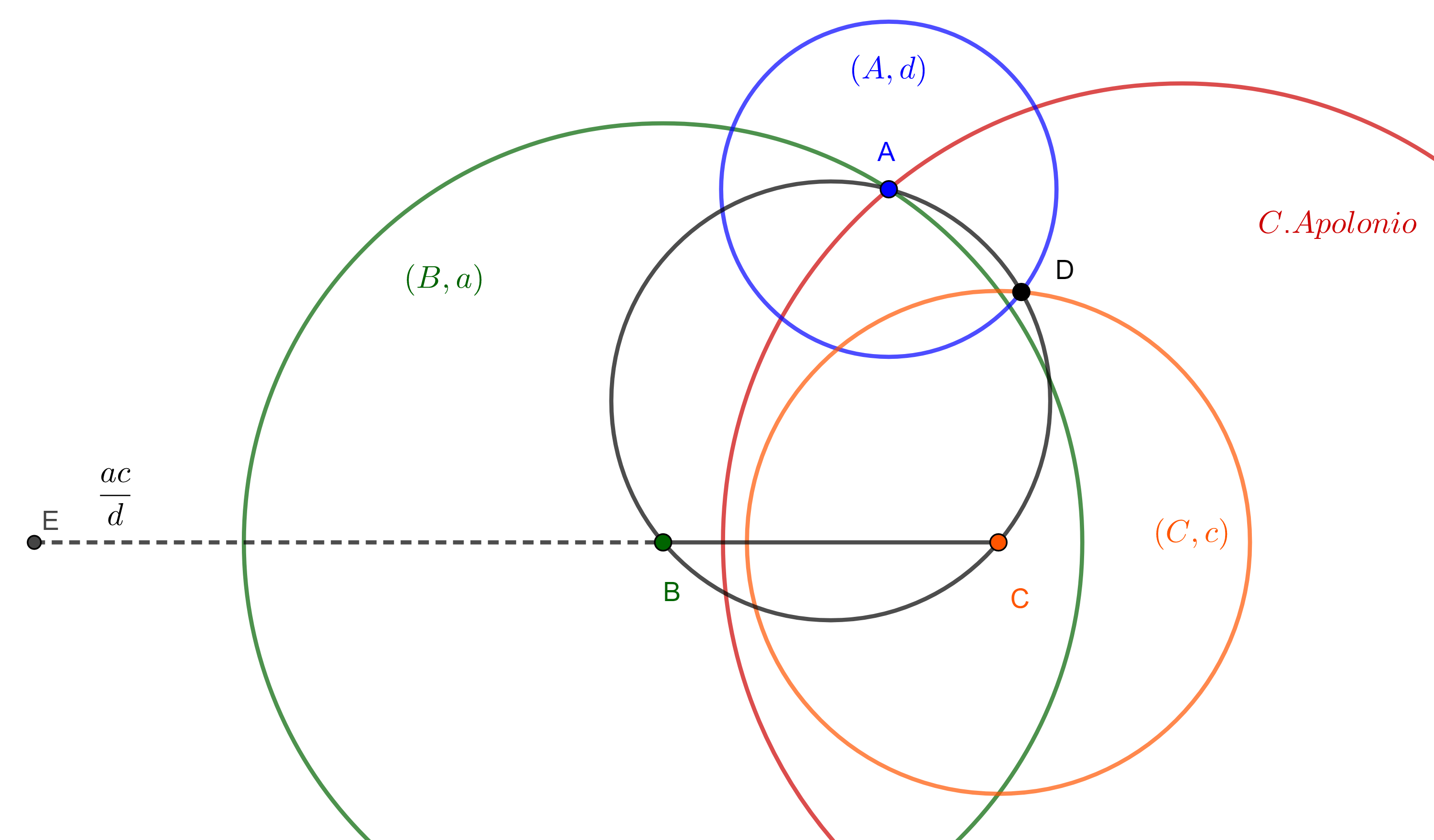
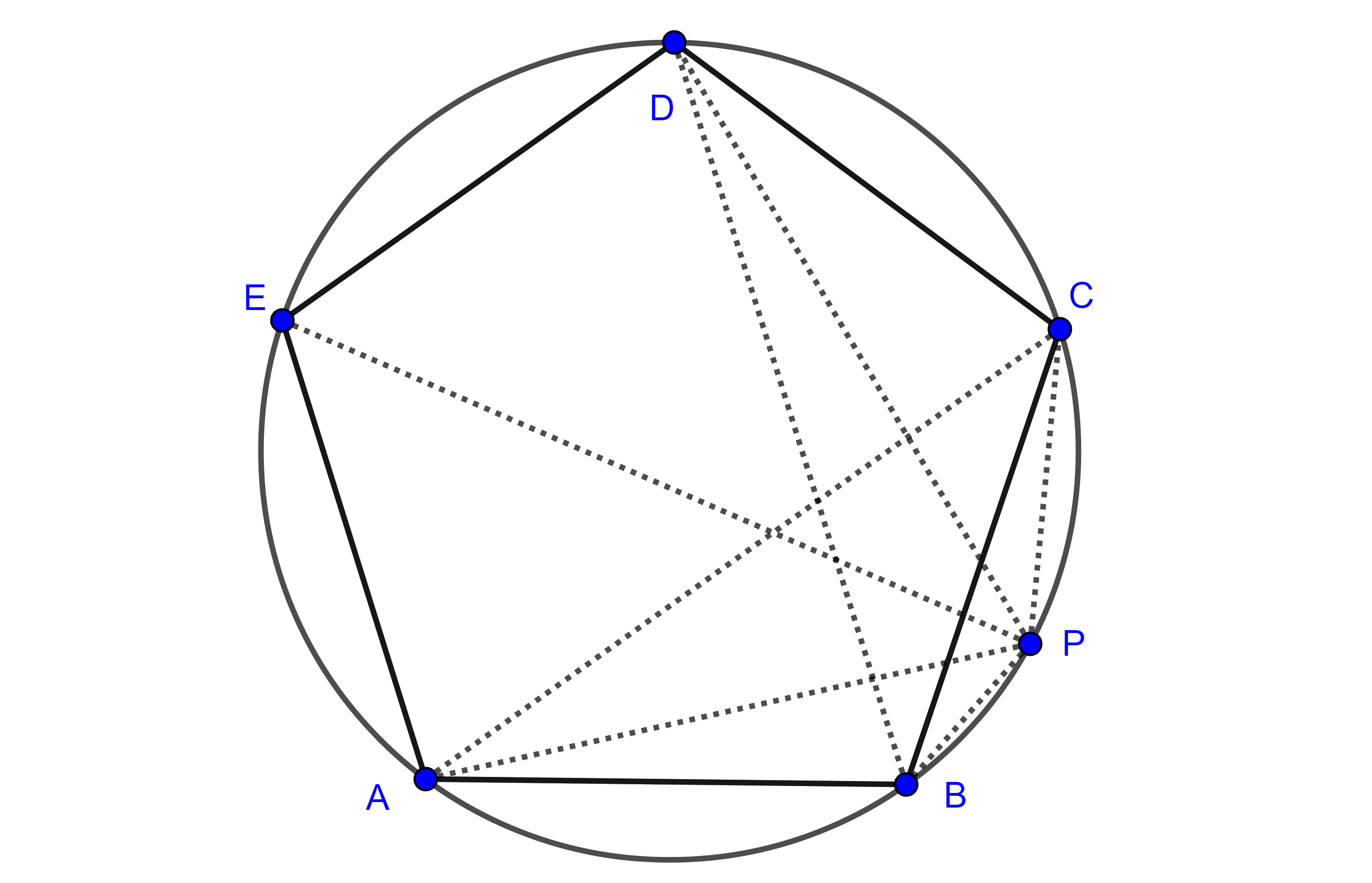
Teorema de Casey. Sean $(O_{i}, R_{i})$, $i = 1, 2, 3, 4$ circunferencias tangentes a una quinta circunferencia $(O, R)$, respectivamente en los puntos $A$, $B$, $C$ y $D$, en ese orden (figura 6), y denotemos como $\delta_{ij}$ a la medida de la tangente común a $(O_{i}, R_{i})$ y $(O_{j}, R_{j})$ la cual tomaremos como exterior si ambas circunferencias son interiores a $(O, R)$ o si ambas son exteriores a $(O, R)$, pero si una es interior y la otra es exterior a $(O, R)$ entonces tomaremos el segmento de la tangente interior a ambas circunferencias.

Bajo estas condiciones se verifica la siguiente igualdad
$\delta_{12} \delta_{34}  + \delta_{14}\delta_{23}  = \delta_{13}\delta_{24}$.

Demostración. Mostraremos el caso en que dos circunferencias son interiores y dos son exteriores a $(O, R)$, todos los demás casos son análogos.

Figura 6

Tenemos que sustituir el valor de cada segmento de tangente de acuerdo a la proposición 2 y recordar que por el teorema de Ptolomeo, $AB \times CD + AD \times BC = AC \times BD$.

$\delta_{12} \delta_{34}  + \delta_{14}\delta_{23}$ 
$= \dfrac{AB}{R} \sqrt{(R + R_{1})(R –  R_{2})} \dfrac{CD}{R} \sqrt{(R + R_{4})(R –  R_{3})}$
$+ \dfrac{BC}{R} \sqrt{(R – R_{2})(R – R_{3})} \dfrac{AD}{R} \sqrt{(R + R_{1})(R + R_{4})}$
$= \dfrac{ AB \times CD + AD \times BC }{R} \sqrt{(R + R_{1})(R –  R_{2})(R + R_{4})(R –  R_{3})}$
$=\dfrac{ AC \times BD }{R} \sqrt{(R + R_{1})(R –  R_{2})(R + R_{4})(R –  R_{3})}$
$= \dfrac{AC}{R} \sqrt{(R + R_{1})(R –  R_{3})} \dfrac{BD}{R} \sqrt{(R + R_{4})(R –  R_{2})}$
$= \delta_{13}\delta_{24}$.

$\blacksquare$

Notemos que cuando las 4 circunferencias tangentes a $(O, R)$ tienen radio igual a $0$, el resultado es el teorema de Ptolomeo.

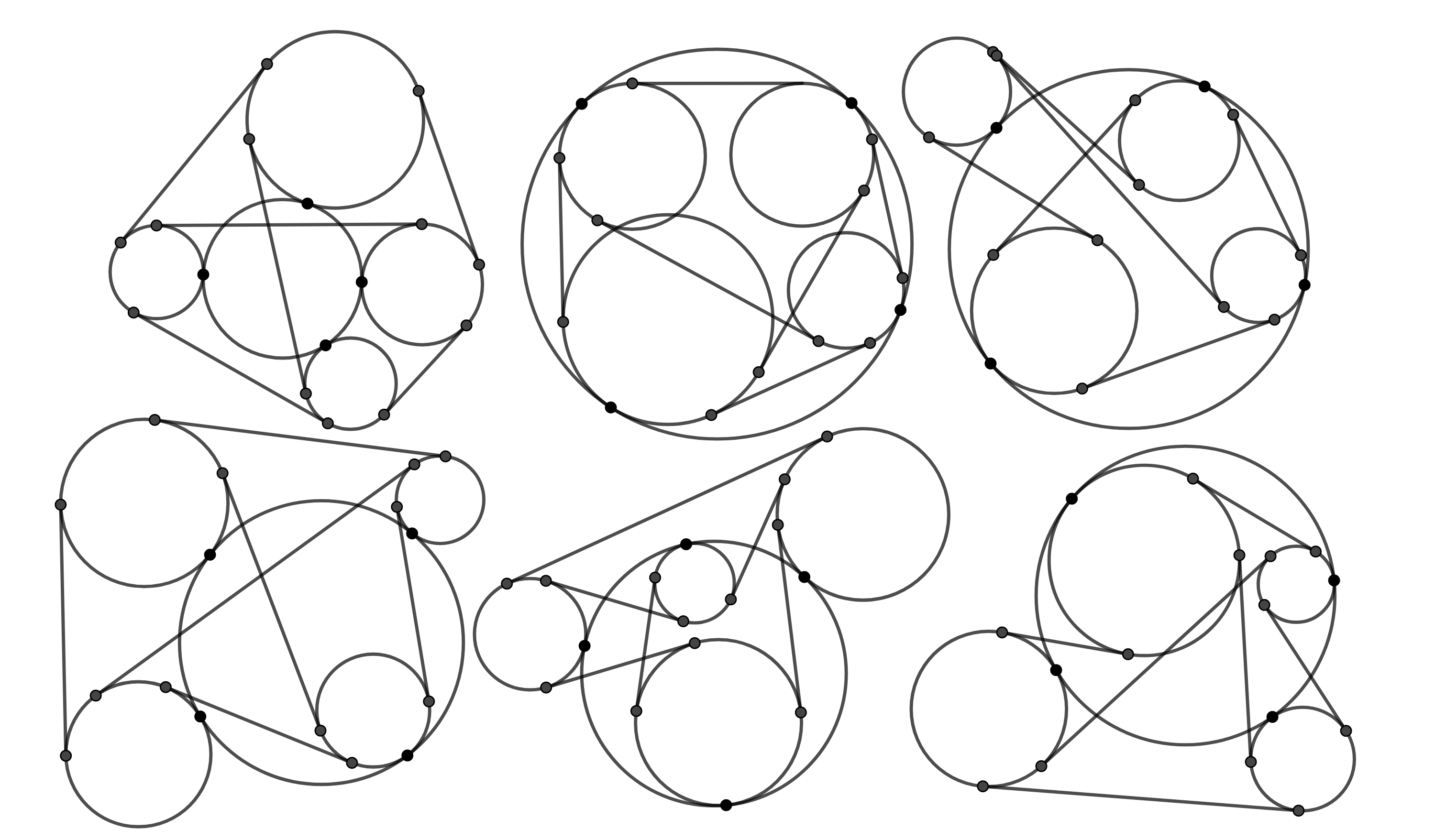
En la siguiente figura se ilustran todos los posibles casos del teorema de Casey.

Figura 7

Problemas

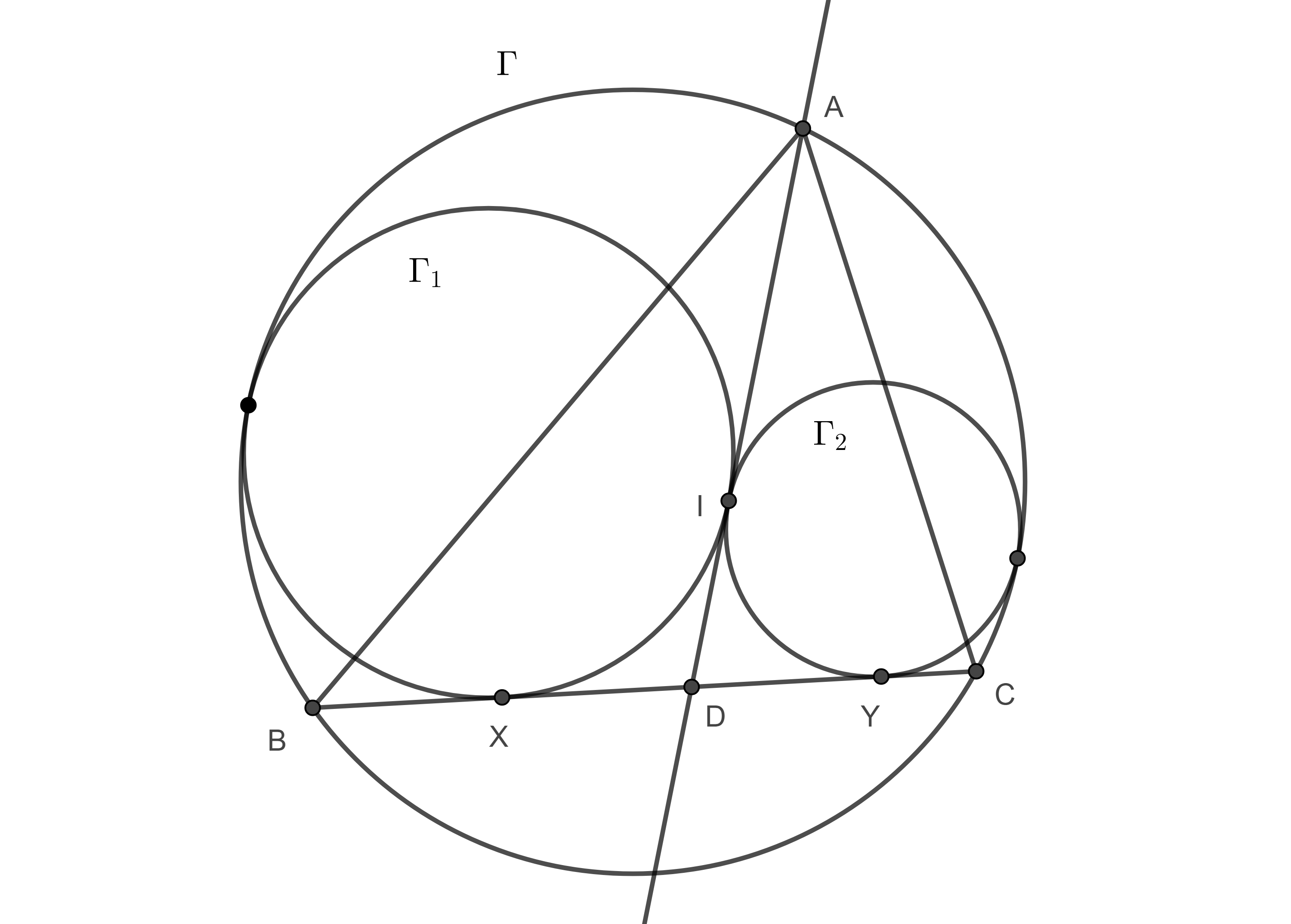
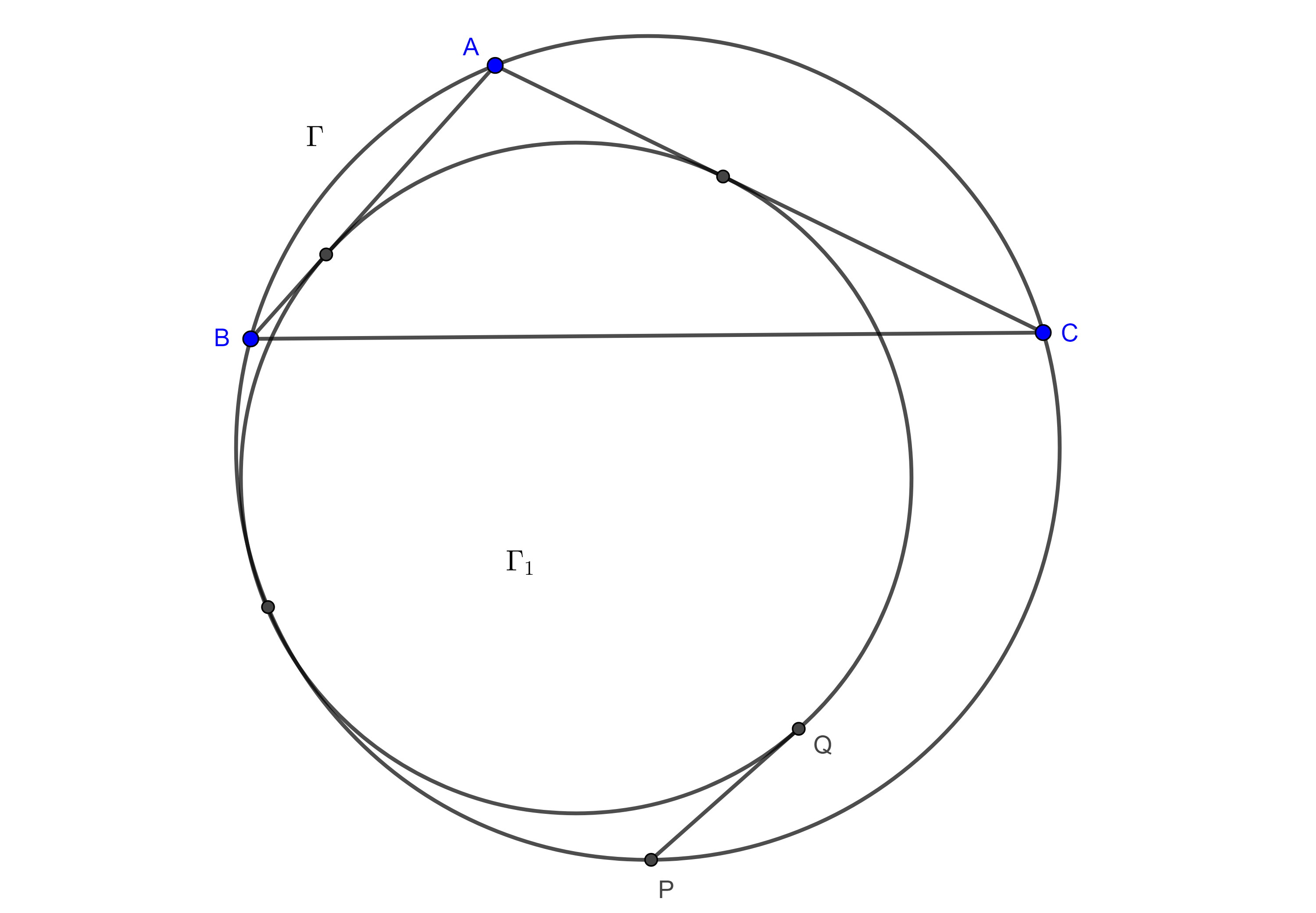
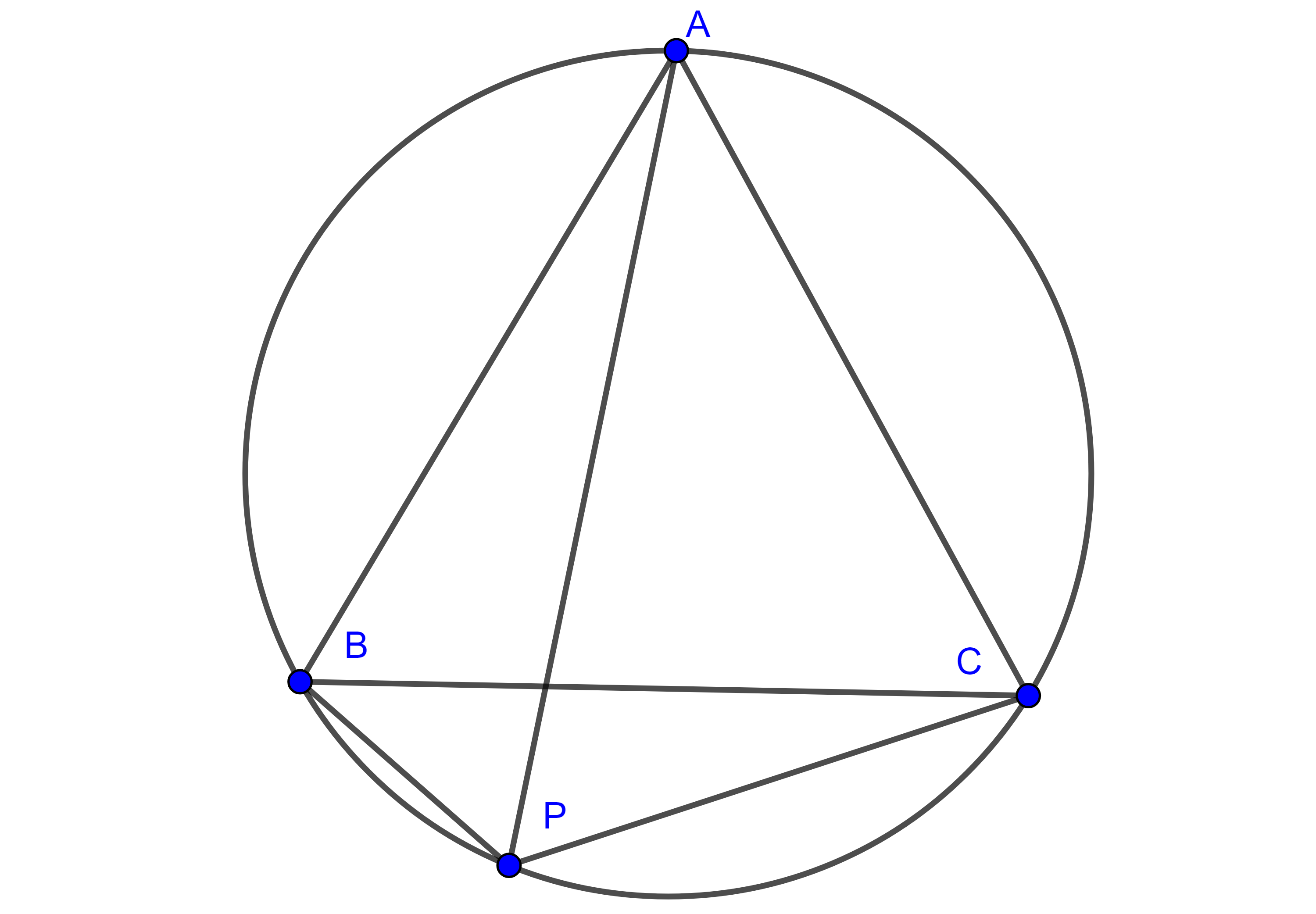
Problema 1. Sean $\Gamma_{1}$, $\Gamma_{2}$, dos circunferencias tangentes entre si (exteriormente) en $I$ y al mismo tiempo son tangentes a una tercera circunferencia $\Gamma$ (interiormente), consideremos la recta tangente a $\Gamma_{1}$, $\Gamma_{2}$ por $I$ y su intersección, $A$, con $\Gamma$ y otra tangente exterior común a $\Gamma _{1}$, $\Gamma _{2}$, en $X$, $Y$ respectivamente la cual interseca a $\Gamma$ en $B$ y $C$ (figura 8). Entonces $I$ es el incentro de $\triangle ABC$.

Figura 8

Demostración. Sea $D = BC \cap AI$, entonces $DX = DI = DY$.

Consideremos los puntos $A$, $B$  y $C$ como circunferencias de radio $0$.

Como resultado de aplicar el teorema de Casey a $(A, 0)$, $\Gamma_{1}$, $(B, 0)$, y $(C, 0)$ tangentes a $\Gamma$, obtenemos,

$\begin{equation} AI \times BC + BX \times AC = AB \times XC = AB \times (2DI + CY). \end{equation}$

Hacemos lo mismo con los círculos $(A, 0)$, $(B, 0)$, $(C, 0)$ y $\Gamma_{2}$ tangentes a $\Gamma$.

$\begin{equation} AB \times CY + AI \times BC = AC \times BY = AC \times (BX + 2DI). \end{equation}$

Restamos $(4)$ a $(3)$
$BX \times AC – AB \times CY = 2 AB \times DI + AB \times CY – 2 AC \times DI – AC \times BX$
$\Leftrightarrow AC \times DI + AC \times BX = AB \times DI + AB \times CY$
$\Leftrightarrow AC \times BD = AC(DI + BX) = AB(DI + CY) = AB \times CD$.

En consecuencia,
$\begin{equation} \dfrac{BD}{CD} = \dfrac{AB}{AC}. \end{equation}$

Por el reciproco del teorema de la bisectriz, la última igualdad nos dice que $AD$ es bisectriz de $\angle A$.

Ahora sumamos $(4)$ y $(3)$
$2AI \times BC + BX \times AC + AB \times CY$
$= 2AB \times DI + AB \times CY + 2AC \times DI + AC \times BX$
$\Leftrightarrow AI \times BC = AB \times DI + AC \times DI$.

En consecuencia,
$\dfrac{AI}{DI} = \dfrac{AB + AC}{BC}$.

Por otra parte, de $(5)$ tenemos
$\dfrac{BD}{CD} = \dfrac{AB}{AC}$
$\Leftrightarrow \dfrac{BC}{CD}  = \dfrac{BD + CD}{CD} = \dfrac{AB + AC}{AC}$
$\Leftrightarrow \dfrac{AC}{CD} = \dfrac{AB + AC}{BC}$.

Por lo tanto, $\dfrac{AI}{DI} = \dfrac{AC}{CD}$, se sigue que $CI$ es bisectriz de $\angle C$.

Como resultado, $I$ es el incentro de $\triangle ABC$.

$\blacksquare$

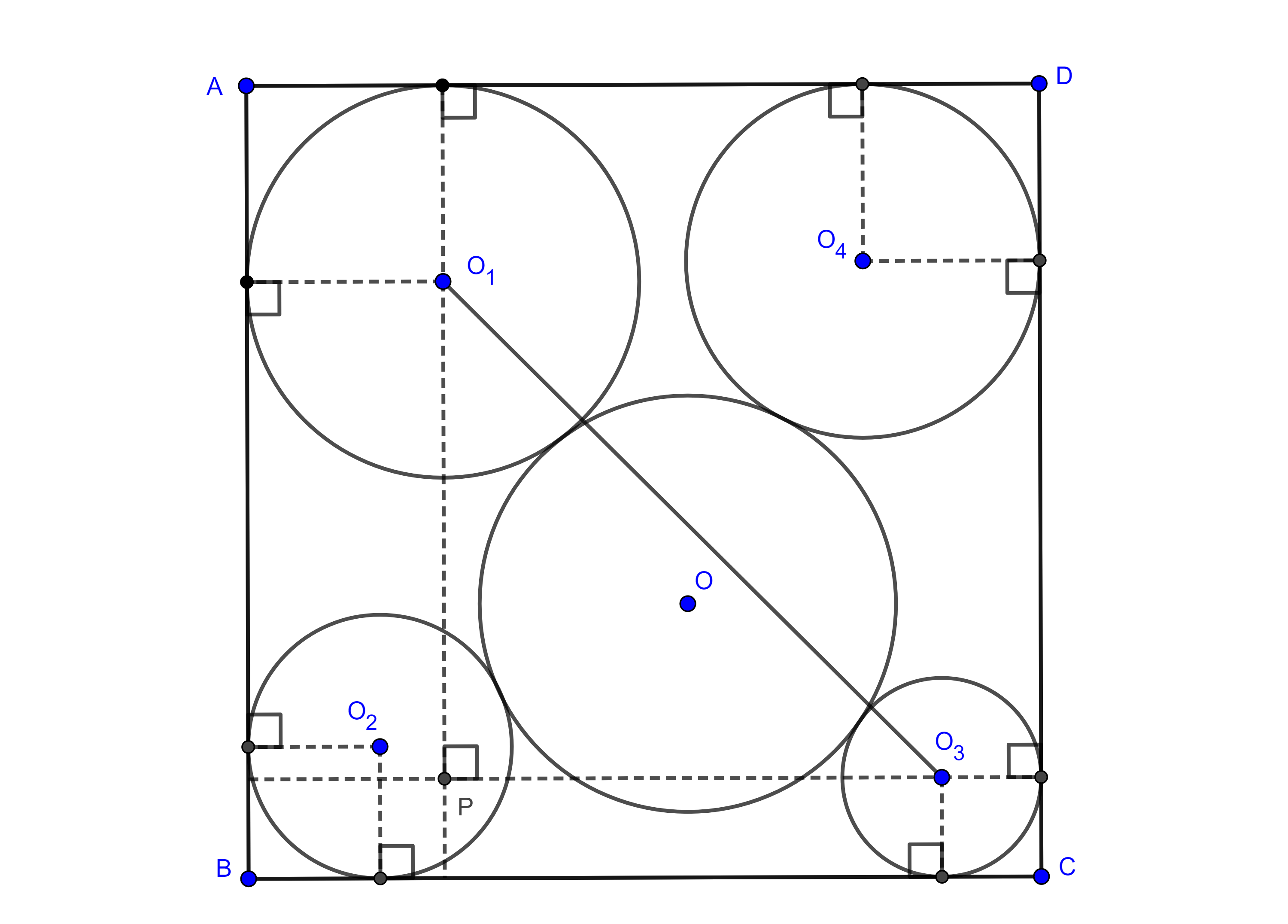
Problema 2. Sea $\square ABCD$ un cuadrado y $(O, R)$ un círculo en el interior de $\square ABCD$, y consideremos $(O_{i}, R_{i})$, $i = 1,2,3,4$ cuatro circunferencias cada una tangente a dos lados del cuadrado y a $(O, R)$ al mismo tiempo, encuentra una representación del lado del cuadrado en términos de los $R_{i}$, con $i = 1,2,3,4$.

Figura 9

Solución. Por construcción, cada lado del cuadrado es tangente a dos circunferencias así que si $\delta_{ij}$ denota la longitud del segmento tangente común a dos circunferencias entonces,

$\delta_{12} = AB – R_{1} – R_{2}$,
$\delta_{23} = AB – R_{2} – R_{3}$,
$\delta_{34} = AB – R_{3} – R_{4}$,
$\delta_{14} = AB – R_{1} – R_{4}$.

Para calcular $\delta_{13}$ consideremos $P$ la intersección de la perpendicular a $BC$ por $O_{1}$, con la perpendicular a $AB$ por $O_{3}$ entonces $\triangle O_{1}PO_{3}$ es rectángulo y por el teorema de Pitágoras

$O_{1}O_{3}^2 = 2(AB – R_{1} – R_{3})^2$.

Por la proposición 1 parte $i)$ tenemos que
$\delta_{13}^2 = O_{1}O_{3}^2 – (R_{1} – R_{3})^2 = 2(AB – R_{1} – R_{3})^2 – (R_{1} – R_{3})^2$.

Por lo tanto,
$\delta_{13} = \sqrt{2(AB – R_{1} – R_{3})^2– (R_{1} – R_{3})^2}$.

Igualmente vemos que $\delta_{24} = \sqrt{2(AB – R_{2} – R_{4})^2 – (R_{2} – R_{4})^2}$.

Aplicamos el teorema de Casey a $(O_{i}, R_{i})$ $i = 1, 2, 3, 4$ tangentes a $(O, R)$
$\delta_{12}\delta_{34} + \delta_{14}\delta_{32} = \delta_{13}\delta_{24}$
$= (AB – R_{1} – R_{2})( AB – R_{3} – R_{4}) + (AB – R_{2} – R_{3})( AB – R_{1} – R_{4})$
$= \sqrt{2(AB – R_{1} – R_{3})^2 – (R_{1} – R_{3})^2}\sqrt{2(AB – R_{2} – R_{4})^2 – (R_{2} – R_{4})^2}$.

Despejando $AB$ se puede llegar a la expresión
$AB = \dfrac{2(R_{1}R_{3} – R_{2}R_{4}) + \sqrt{2(R_{1} – R_{2}) (R_{1} – R_{4}) (R_{3} – R_{2}) (R_{3} – R_{4}) }}{R_{1} – R_{2} + R_{3} – R_{4}}$.

No se desarrollará este último procedimiento por ser largo, para llegar al resultado solo hay que desarrollar los productos y después reagrupar para despejar $AB$.

$\blacksquare$

Problema 3. Sean $\triangle ABC$ un triángulo rectángulo con $\angle BAC =\dfrac{\pi}{2}$, $(O, R)$ su circuncírculo, considera dos circunferencias $\Gamma_{1}$ tangente a $OA$ en $P$, a $OB$ y a $(O, R)$ (internamente) y $\Gamma_{2}$ tangente a $OA$ en $Q$, a $OC$ y a $(O, R)$ (internamente). Muestra que $\dfrac{AB}{AC} = \dfrac{AP}{AQ}$.

Figura 10

Demostración. Sean $P’$ y $Q’$ los puntos de tangencia de $\Gamma_{1}$ y $\Gamma_{2}$ con $OB$ y $OC$ respectivamente, entonces $OP = OP’$ por ser segmentos tangentes a $\Gamma_{1}$ trazados desde $O$.

Igualmente vemos que $OQ = OQ’$.

Como $\triangle ABC$ es rectángulo y $BC$ es la hipotenusa, entonces $O$ es el punto medio de $BC$.

Por lo tanto, $R = OB = OA = OC$.

Como resultado obtenemos, $AP = BP’$ y $AQ = CQ’$.

Ahora aplicamos el teorema de Casey a los círculos $(A, 0)$, $\Gamma_{1}$, $(B, 0)$ y $\Gamma_{2}$ tangentes a $(O, R)$.

$AP \times BQ’ + AQ \times BP’ = AB \times P’Q’$
$\Leftrightarrow AP(BQ’ + AQ) = AB \times P’Q’$

Por lo tanto,
$\begin{equation} AP \times BC = AB \times P’Q’. \end{equation}$

Hacemos lo mismo para $A$, $\Gamma_{1}$, $C$ y $\Gamma_{2}$ tangentes a $(O, R)$.

$AP \times CQ’ + AQ \times CP’ = AC \times P’Q’$
$\Leftrightarrow AQ(AP + CP’) = AC \times P’Q’$.

Por lo tanto,
$\begin{equation} AQ \times BC = AC \times P’Q’. \end{equation}$

Haciendo el cociente de $(6)$ sobre $(7)$ obtenemos el resultado buscado, $\dfrac{AP}{AQ} = \dfrac{AB}{AC}$.

$\blacksquare$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Completa la prueba de la proposición 2 parte $ii)$ y $iii)$.
  2. Sean $l_{1}$ y $l_{2}$ dos rectas paralelas y tangentes a una circunferencia $(O, R)$, considera otras dos circunferencias, $(O_{1}, R_{1})$ tangente a $l_{1}$ y a $(O, R)$, y $(O_{2}, R_{2})$ tangente a $l_{2}$, y a las primeras dos circunferencias $(O, R)$, $(O_{1}, R_{1})$. Muestra que $R = 2 \sqrt{R_{1}R_{2}}$.
  3. Sean $AB$ el diámetro de una circunferencia $\Gamma$, $P$, $Q \in \Gamma$ en arcos distintos respecto de $AB$, trazamos $C$ el pie de la perpendicular a $AB$ trazada desde $Q$ y considera $\Gamma_{1}$, $\Gamma_{2}$ dos circunferencias de diámetro $AC$ y $CB$ respectivamente. Sean $PE$ y $PF$ segmentos tangentes a $\Gamma_{1}$ y $\Gamma_{2}$ respectivamente. Prueba que $PE + PF = PQ$.
Figura 11
  1. Sean $\triangle ABC$ y $\Gamma$ su circuncírculo con $AB = c$, $BC = a$ y $AC = b$, considera $\Gamma_{1}$, $\Gamma_{2}$ y $\Gamma_{3}$ círculos tangentes a $AB$, $BC$ y $AC$ respectivamente en sus puntos medios y al mismo tiempo tangentes al arco $\overset{\LARGE{\frown}}{AB}$, $\overset{\LARGE{\frown}}{BC}$ y $\overset{\LARGE{\frown}}{CA}$ respectivamente, denota $\delta_{ij}$ al segmento de tangente exterior y común a $\Gamma_{i}$, $\Gamma_{j}$. Muestra que $\delta_{ij} = \dfrac{a + b + c}{4}$, $i, j = 1, 2, 3$, $i \neq j$.
Figura 12
  1. Considera $\triangle ABC$ y su circuncírculo $\Gamma$, sea $\Gamma_{1}$ una circunferencia tangente a $AB$ en $P$, a $AC$ en $Q$ y a $\Gamma$ internamente, muestra que el punto medio de $PQ$ es el incentro de $\triangle ABC$.
  2. Sean $\triangle ABC$ y $\Gamma$ su circuncírculo con $AC > AB$. Una circunferencia $\Gamma_{1}$ es tangente a $AB$, $AC$ y al circuncírculo internamente, $P$ es el punto medio del arco $\overset{\LARGE{\frown}}{BC}$ y $\overline{PQ}$ es un segmento tangente a $\Gamma_{1}$. Muestra que $\dfrac{PQ}{PA} = \dfrac{AC – AB}{AC + AB}$.
Figura 13

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Teorema de Ptolomeo

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

El teorema de Ptolomeo nos da una caracterización del cuando un cuadrilátero convexo es cíclico en términos de los productos entre sus lados y sus diagonales. Necesitaremos antes una caracterización diferente de cuadrilátero cíclico.

Cuadriláteros cíclicos

Definición. Si los vértices de un polígono están en una misma circunferencia decimos que está inscrito en ella o que es cíclico.

Teorema 1. Un cuadrilátero convexo es cíclico si y solo si los ángulos opuestos son suplementarios.

Demostración. Sea $\square ABCD$ un cuadrilátero cíclico inscrito en $(O, r)$, la circunferencia con centro en $O$.

Los ángulos opuestos $\angle ADC$ y $\angle CBA$ son subtendidos por los arcos $AC$ y $CA$ respectivamente y por el teorema de la medida del ángulo inscrito tenemos que
$\angle ADC + \angle CBA = \dfrac{\angle AOC}{2} + \dfrac{\angle COA}{2} = \dfrac{2\pi}{2} = \pi$.

Figura 1

De manera análoga se ve que $\angle BAD$ y $\angle DCB$ son suplementarios.

Por lo tanto, los ángulos opuestos de un cuadrilátero cíclico son suplementarios.

$\blacksquare$

Ahora supongamos que los ángulos opuestos $\angle ADC$ y $\angle CBA$ de $\square ABCD$ son suplementarios.

Consideremos el circuncírculo de $\triangle ABC$, entonces todos los puntos en el arco $\overset{\LARGE{\frown}}{CA}$ que no contiene a $B$ subtienden un ángulo $\angle ADC$ suplementario a $\angle CBA$, pero este lugar geométrico es único.

Por lo tanto $D \in \overset{\LARGE{\frown}}{CA}$ y en consecuencia $\square ABCD$ es cíclico.

$\blacksquare$

Teorema de Ptolomeo

Teorema 2, desigualdad de Ptolomeo. En todo cuadrilátero convexo la suma de los productos entre lados opuestos es mayor o igual al producto de las diagonales, y la igualdad se da si y solo si es el cuadrilátero es cíclico.

Demostración. Sea $\square ABCD$ un cuadrilátero convexo, construyamos sobre el segmento $AB$ (figura 2), un triángulo $\triangle ABE$ semejante a $\triangle ADC$ tal que $\angle ABE = \angle ADC$ y $\angle BAE = \angle CAD$ entonces

$\begin{equation} \dfrac{EA}{CA} = \dfrac{BA}{DA} \Leftrightarrow \dfrac{EA}{BA} = \dfrac{CA}{DA}. \end{equation}$

Figura 2

Dado que $\angle CAE = \angle BAD$ y por $(1)$, por criterio lado, ángulo, lado, los triángulos $\triangle EAC$ y $\triangle BAD$ son semejantes, entonces de la primera y segunda relaciones de semejanza tenemos que
$\dfrac{EB}{CD} = \dfrac{AB}{AD}$ y $\dfrac{EC}{BD} = \dfrac{AC}{AD}$
$\Leftrightarrow$ $EB = \dfrac{AB \times CD}{AD}$ y $EC = \dfrac{AC \times BD}{AD}$.

Ahora notemos que tenemos dos casos:

Caso 1. (izquierda figura 2)
$B \in EC$ $\Leftrightarrow$ $\angle CBA + \angle ADC = \angle CBA + \angle ABE = \pi$ $\Leftrightarrow$ $\square ABCD$ es cíclico,
y en tal caso $EC = EB + BC$ $\Leftrightarrow$ $\dfrac{AC \times BD}{AD} = \dfrac{AB \times CD}{AD} + BC$
$\Leftrightarrow$ $AC \times BD = AB \times CD + AD \times BC$.

Caso 2. (derecha figura 2)
$E$, $B$ y $C$ son tres puntos no colineales $\Leftrightarrow$ $\angle CBA + \angle ADC = \angle CBA + \angle ABE \ne \pi$ $\Leftrightarrow$ $\square ABCD$ no es cíclico, entonces aplicando la desigualdad del triángulo a $\triangle EBC$ tenemos que
$EC < EB + BC$ $\Leftrightarrow$ $AC \times BD < AB \times CD + AD \times BC$.

De lo anterior se sigue que $AB \times CD + AD \times BC \geq AC \times BD$, con la igualdad si y solo si $\square ABCD$ es cíclico.

$\blacksquare$

Construcción del cuadrilátero cíclico

Problema 1. Construir un cuadrilátero convexo y cíclico dados sus cuatro lados $a$, $b$, $c$ y $d$.

Solución. Notemos primero que es necesario que la suma de cualesquiera tres de los lados dados sea mayor que el lado restante.

Si un lado es mayor que la suma de los otros tres no es posible construir ningún cuadrilátero y si es igual entonces solo es posible construir un cuadrilátero degenerado donde todos los vértices están alineados.

Supongamos que $AB = a$, $BC = b$, $CD = c$ y $DA = d$, la prueba del teorema de Ptolomeo nos sugiere una manera de resolver este problema.

Trazamos el segmento $BC$ y lo extendemos del lado de $B$ hasta un punto $E$ tal que $EB = \dfrac{ac}{d}$, el cual es posible construir pues podemos construir el producto de dos magnitudes y el inverso de una magnitud dadas.

Aquí usaremos que $B \in EC$ $\Leftrightarrow$ $\square ABCD$ es cíclico y que los triángulos $\triangle ABE$ y $\triangle ADC$ son semejantes, como en la prueba anterior.

La razón de semejanza está dada por $\dfrac{AE}{AC} = \dfrac{BE}{CD} = \dfrac{ac}{dc} = \dfrac{a}{d}$.

Esto último nos dice que la razón entre las distancias de $A$ a los puntos $E$ y $C$ es una razón fija por lo tanto $A$ esta en la circunferencia de Apolonio determinada por $E$, $C$ y la razón $\dfrac{a}{d}$.

Por otro lado, el vértice $A$ se encuentra en la circunferencia con centro en $B$ y radio $a$, por lo tanto, $A$ esta determinado por la intersección de $(B, a)$ y la circunferencia de Apolonio mencionada.

Ahora que conocemos la diagonal $AC$ podemos completar el triángulo $\triangle ACD$ trazando circunferencias $(A, d)$ y $(C, c)$, una de las intersecciones será el cuarto vértice del cuadrilátero buscado.

Figura 3

Por construcción $\triangle ABE$ y $\triangle ADC$ son semejantes por lo que $\angle CBA$ y $\angle ADC$ son suplementarios.

Por lo tanto $\square ABCD$ es cíclico.

$\blacksquare$

Distancia de los vértices de un polígono cíclico a un punto del circuncírculo

Problema 2. Sean $\triangle ABC$ isósceles con $AB = AC$ y $P$ un punto en el arco $\overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\triangle ABC$, muestra que $\dfrac{PA}{PB + PC} = \dfrac{AC}{BC}$.

Figura 4

Solución. Aplicando el teorema de Ptolomeo a $\square ABPC$ tenemos que
$PA \times BC = AB \times PC + AC \times PB $
$= AC \times PC + AC \times PB = AC(PC + PB)$.

Por lo tanto, $\dfrac{PA}{PB + PC} = \dfrac{AC}{BC}$.

$\blacksquare$

Problema 3. Sean $ABCDE$ un pentágono regular inscrito en una circunferencia y $P$ un punto en el arco $\overset{\LARGE{\frown}}{BC}$, muestra que $PA + PD = PB + PC + PE$.

Solución. Como el pentágono es regular, entonces sus diagonales tienen la misma longitud.

Figura 5

Aplicando el teorema de Ptolomeo a $\square ABPC$  y $\square BPCD$ obtenemos
$BC \times PA = AB \times PC + AC \times PB = BC \times PC + AC \times PB$
$BC \times PD = PB \times CD + PC \times BD = PB \times BC + PC \times AC$.

Sumando estas dos últimas igualdades tenemos
$\begin{equation} BC(PA + PD) = BC(PB + PC) + AC(PB + PC). \end{equation}$

Por otra parte dado que $\triangle BEC$ es isósceles podemos aplicar el resultado del problema anterior y obtenemos $\dfrac{PE}{PB + PC} = \dfrac{EC}{BC}$

$\Leftrightarrow$ $\begin{equation} \dfrac{PE \times BC}{PB + PC} = EC = AC. \end{equation}$

Sustituyendo $(3)$ en $(2)$ resulta
$BC(PA + PD) = BC(PB + PC) + \dfrac{PE \times BC}{PB + PC} (PB + PC)$.

Por lo tanto, $PA + PD = PB  + PC + PE$.

$\blacksquare$

Hexágono cíclico

Problema 4. Sea $ABCDEF$ un hexágono convexo inscrito en una circunferencia. Consideremos las diagonales que dividen al hexágono en dos cuadriláteros cíclicos, $AD = d$, $CF = e$ y $BE = f$ y los lados del hexágono que no comparten vértices con dichas diagonales $BC = a$, $EF = a’$, $DE = b$, $AB = b’$, $AF = c$, $CD = c’$ respectivamente, entonces $def = aa’d + bb’e + cc’f + abc +a’b’c’$.

Figura 6

Demostración. Aplicando el teorema de Ptolomeo a $\square ABCD$ y $\square BCDE$ obtenemos
$ad + b’c’ = AC \times BD$ y $ab + c’f = BD \times CE$.

Multiplicamos por $a’$ y $c$ respectivamente y después sumamos el resultado y obtenemos:
$aa’d + a’b’c’ + abc + cc’f $
$= a’(AC \times BD) + c(BD \times CE) = BD(a’AC + cCE)$.

Aplicando Ptolomeo a $\square ACEF$ obtenemos $a’AC + cCE = eAE$.

Por lo tanto $aa’d + a’b’c’ + abc + cc’f = BD(eAE) = e (BD \times AE)$.

Ahora consideramos $\square ABDE$ y por el teorema de Ptolomeo obtenemos
$BD \times AE = df -bb’$.

En consecuencia tenemos $aa’d + a’b’c’ + abc + cc’f = e(df – bb’)$.

Por lo tanto, $def = aa’d + bb’e + cc’f + abc +a’b’c’$.

$\blacksquare$

Más adelante…

En la próxima entrada estudiaremos trigonometría y mostraremos algunas identidades trigonométricas aplicando el teorema de Ptolomeo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que un cuadrilátero convexo es cíclico si y solo si:
    $i)$ un ángulo interno formado con una diagonal y un lado es igual al ángulo interno formado con la otra diagonal y el lado opuesto,
    $ii)$ las mediatrices de los lados del cuadrilátero son concurrentes.
  2. Sean $l_{1}$, $l_{2}$ y $l_{3}$, $l_{4}$ dos pares de rectas tales que la bisectriz del primer par es transversal al segundo par y forma ángulos internos iguales entonces decimos que $l_{3}$ y $l_{4}$ son antiparalelas respecto a $l_{1}$ y $l_{2}$. Muestra que un cuadrilátero convexo es cíclico si y solo si un par de lados opuestos es antiparalelo respecto al otro par de lados opuestos.
Figura 7
  1. Como podrás haber notado nuestra construcción del cuadrilátero cíclico no es única pues partimos de una suposición arbitraria, que $AB = a$, $BC = b$, $CD = c$ y $DA = d$ para $a$, $b$, $c$ y $d$ dados. Muestra que es posible construir tres cuadriláteros cíclicos diferentes con los mismos lados y que de estos se obtienen tres diagonales diferentes.
  2. Expresa la razón de las diagonales de un cuadrilátero cíclico en términos de sus lados.
  3. Considera $\triangle ABC$ equilátero y $P$ un punto en el arco $\overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\triangle ABC$, prueba que $PA = PB + PC$.
  4. Sean $\square ABCD$ un cuadrado y $P \in \overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\square ABCD$, muestra que $\dfrac{PA +PC}{PD + PB} = \dfrac{PD}{PA}$.
  5. Si $ABCDEF$ es un hexágono regular y $P \in \overset{\LARGE{\frown}}{BC}$ del circuncírculo de $ABCDEF$, muestra que $PE + PF = PA + PB + PC + PD$.
  6. Sean $\triangle ABC$ equilátero, $P \in \overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\triangle ABC$ y $D$ la intersección de $BC$ con $AP$, demuestra que $\dfrac{1}{PD} = \dfrac{1}{PB} + \dfrac{1}{PC}$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 127-131.
  • Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 15-19, 31-34.
  • Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 33-35.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 62-66.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»