Archivo de la etiqueta: Números reales

Cálculo Diferencial e Integral I: Valor absoluto y desigualdades

Por Karen González Cárdenas

Introducción

En esta entrada nos dedicaremos a resolver desigualdades que involucran el valor absoluto. Para ello retomaremos la definición del valor absoluto de un número real y utilizaremos algunos resultados que probaremos a continuación.

Un par de resultados importantes

Lema: Para todo $a \in R$ . $a \leq | a |$ y $- a \leq | a |$ .

Demostración: Procederemos a revisar los siguientes dos casos.
CASO 1: Si $a \geq 0$ .
Por un lado tenemos por la definición de valor absoluto $| a | = a$ .
$∴ | a | \geq a .$
Y por otro que $a \geq 0 \geq - a$ , así por transitividad se concluye que:
$| a | \geq - a .$

CASO 2: Si $a \leq 0$ .
Así se sigue por definición que $| a | = - a$ entonces tenemos que $| a | \geq - a$ .
Y análogamente al caso anterior: $- a \geq 0 \geq a \Rightarrow | a | \geq a$ .

Teorema: Consideremos $a, x \in R$ con $a \geq 0$ .

$\begin{aligned} | x | \leq a & \Leftrightarrow - a \leq x y x \leq a \\ \Leftrightarrow x \in [- a, a] . \end{aligned}$
$\begin{aligned} | x | \geq a & \Leftrightarrow - a \geq x o x \geq a \\ \Leftrightarrow x \in (- \infty, - a] \cup [a, \infty) . \end{aligned}$

NOTA.- « $\Leftrightarrow$ » se lee como «si y sólo si». Y recordemos que $\Rightarrow$ significa «entonces».
Demostración:
1. $\Rightarrow$ : Por hipótesis tenemos que $| x | \leq a$ , aplicando el lema anterior:
$x \leq | x | y - x \leq | x |$
Por transitividad: $x \leq a y - x \leq a$
$∴ x \leq a y x \leq - a$

Lo anterior nos indica lo siguiente: $x \in (- \infty, a]$ y $x \in [- a, \infty)$ . Así al tomar la intersección de estos intervalos, obtenemos:
$(- \infty, a] \cap [- a, \infty) = [- a, a]$

$\Leftarrow$ : Ahora consideremos $x \in [- a, a]$ , así tenemos que:
$x \in [- a, a] = (- \infty, a] \cap [- a, \infty)$
Aplicando la respectiva definición de intervalo e intersección:
$x \leq a y x \leq - a$
Y por el lema:
$x \leq | x | y - x \leq | x |$

$∴ | x | \leq a$

2. El punto 2 se quedará de ejercicio para la Tarea moral.

Ahora continuaremos con ejercicios de desigualdades, en ellos deberemos encontrar todos los valores que las satisfagan.

Ejercicio 1

$| x - 3 | = 8$
Recordemos que debido a la definición de valor absoluto, siempre deberemos considerar casos.
Para resolver este ejercicio deberemos considerar los siguientes:
CASO 1: $x - 3 \geq 0$
Por lo que $| x - 3 | = x - 3$ y sustituyendo tenemos:
$\begin{aligned} x - 3 = 8 & \Leftrightarrow x = 8 + 3 \\ \Leftrightarrow x = 11. \end{aligned}$
CASO 2: $x - 3 < 0$
Así $| x - 3 | = - x + 3$ , por lo que se sigue:
$\begin{aligned} - x + 3 = 8 & \Leftrightarrow - x = 8 - 3 \\ \Leftrightarrow - x = 5 \\ \Leftrightarrow x = - 5. \end{aligned}$

De los casos anteriores obtenemos que los valores de $x$ que satisfacen la igualdad son
$x = 11$ o $x = - 5$

Ejercicio 2

$| 3 x - 3 | \leq 2 x + 1$
Para este ejercicio aplicando el teorema tendríamos:
$- 2 x - 1 \leq 3 x - 3$ y $3 x - 3 \leq 2 x + 1$ .
Comenzaremos desarrollando la primera desigualdad:
$\begin{aligned} - 2 x - 1 \leq 3 x - 3 & \Leftrightarrow - 2 x - 3 x \leq - 3 + 1 \\ \Leftrightarrow - 5 x \leq - 2 \\ \Leftrightarrow 5 x \geq 2 \\ \Leftrightarrow x \geq \frac{2}{5} . \end{aligned}$
$∴ x \in [\frac{2}{5}, \infty)$
Y de la segunda obtenemos:
$\begin{aligned} 3 x - 3 \leq 2 x + 1 & \Leftrightarrow 3 x - 2 x \leq 1 + 3 \\ \Leftrightarrow x \leq 4. \end{aligned}$
$∴ x \in (- \infty, 4]$

Por lo que al tomar la intersección de ambos intervalos nos queda que los valores que satisfacen la desigualdad son:
$x \in (- \infty, 4] \cap [\frac{2}{5}, \infty) = [\frac{2}{5}, 4]$

$∴ x \in [\frac{2}{5}, 4]$

Ejercicio 3

$| 2 x + 1 | - | 3 x + 2 | < 1$
Debido a que tenemos dos valores absolutos, para resolver este ejercicio necesitaremos considerar los siguientes casos:

$2 x + 1 \geq 0$ y $3 x + 2 \geq 0$
$2 x + 1 \leq 0$ y $3 x + 2 \leq 0$
$2 x + 1 \geq 0$ y $3 x + 2 \leq 0$
$2 x + 1 \leq 0$ y $3 x + 2 \geq 0$

Nuestra solución final será la unión de todas las soluciones obtenidas en los casos anteriores.

CASO 1: $2 x + 1 \geq 0$ y $3 x + 2 \geq 0$

Desarrollando las desigualdades:
$\begin{aligned} 2 x + 1 \geq 0 & y 3 x + 2 \geq 0 \\ \Leftrightarrow 2 x \geq - 1 & y 3 x \geq - 2 \\ \Leftrightarrow x \geq - \frac{1}{2} & y x \geq - \frac{2}{3} \end{aligned}$

$\Leftrightarrow x \geq - \frac{1}{2}$

Aplicando el valor absoluto obtenemos:
$\begin{aligned} | 2 x + 1 | - | 3 x + 2 | < 1 & \Leftrightarrow 2 x + 1 - (3 x + 2) < 1 \\ \Leftrightarrow 2 x + 1 - 3 x - 2 - 1 < 0 \\ \Leftrightarrow - x - 2 < 0 \\ \Leftrightarrow x + 2 > 0 \\ \Leftrightarrow x > - 2 \end{aligned}$
Por lo que al tomar la siguiente intersección tenemos que la solución de este caso es:
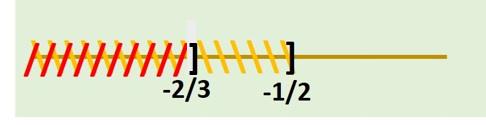
$[- \frac{1}{2}, \infty) \cap (- 2, \infty) = [- \frac{1}{2}, \infty)$

CASO 2: $2 x + 1 \leq 0$ y $3 x + 2 \leq 0$
Tendríamos que:
$\begin{aligned} 2 x + 1 \leq 0 & y 3 x + 2 \leq 0 \\ \Leftrightarrow 2 x \leq - 1 & y 3 x \leq - 2 \\ \Leftrightarrow x \leq - \frac{1}{2} & y x \leq - \frac{2}{3} \end{aligned}$

$\Leftrightarrow x \leq - \frac{2}{3}$
Al sustituir tenemos:
$\begin{aligned} | 2 x + 1 | - | 3 x + 2 | < 1 & \Rightarrow - (2 x + 1) - (- (3 x + 2)) < 1 \\ \Rightarrow - 2 x - 1 + 3 x + 2 - 1 < 0 \\ \Rightarrow x < 0 \end{aligned}$

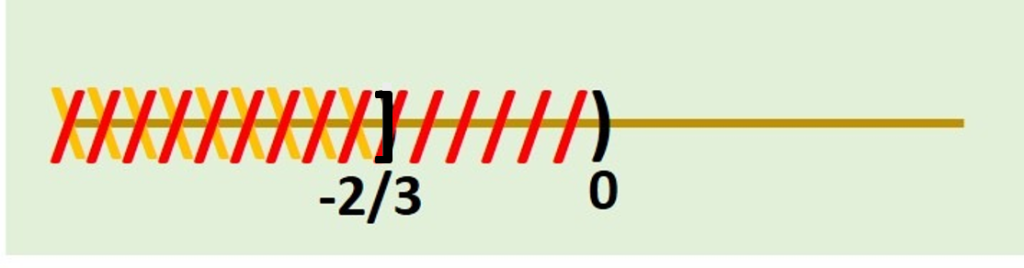
Así tenemos la solución:
$(- \infty, 0) \cap (- \infty, - \frac{2}{3}] = (- \infty, - \frac{2}{3}]$

CASO 3: $2 x + 1 \geq 0$ y $3 x + 2 \leq 0$
Ahora se sigue que:
$\begin{aligned} 2 x + 1 \geq 0 & y 3 x + 2 \leq 0 \\ \Leftrightarrow 2 x \geq - 1 & y 3 x \leq - 2 \\ \Leftrightarrow x \geq - \frac{1}{2} & y x \leq - \frac{2}{3} \end{aligned}$
Así observamos:
$(- \infty, - \frac{2}{3}] \cap [- \frac{1}{2}, \infty) = \emptyset$

CASO 4: $2 x + 1 \leq 0$ y $3 x + 2 \geq 0$
Desarrollando:
$\begin{aligned} 2 x + 1 \leq 0 & y 3 x + 2 \geq 0 \\ \Leftrightarrow 2 x \leq - 1 & y 3 x \geq - 2 \\ \Leftrightarrow x \leq - \frac{1}{2} & y x \geq - \frac{2}{3} \end{aligned}$

$\Leftrightarrow - \frac{2}{3} \leq x \leq - \frac{1}{2}$
Aplicando la definición del valor absoluto:
$\begin{aligned} | 2 x + 1 | - | 3 x + 2 | < 1 & \Rightarrow - (2 x + 1) - (3 x + 2) < 1 \\ \Leftrightarrow - 2 x - 1 - 3 x - 2 - 1 < 0 \\ \Leftrightarrow - 5 x - 4 < 0 \\ \Leftrightarrow 5 x + 4 > 0 \\ \Leftrightarrow 5 x > - 4 \\ \Leftrightarrow x > - \frac{4}{5} \end{aligned}$
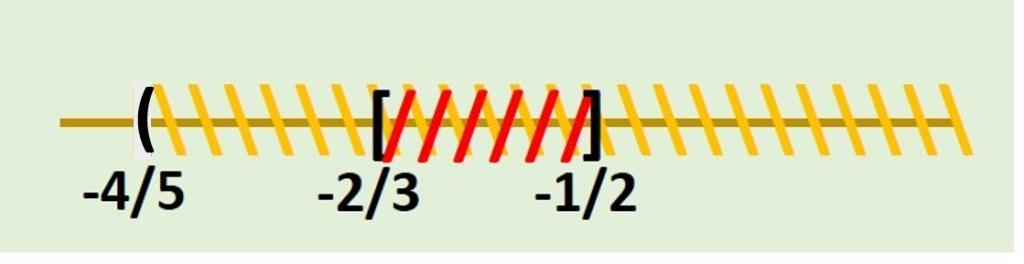
Concluimos que la solución a este caso es:
$[- \frac{2}{3}, - \frac{1}{2}] \cap (- \frac{4}{5}, \infty) = [- \frac{2}{3}, - \frac{1}{2}]$

Finalizamos considerando como solución total a la unión de los intervalos obtenidos en los cuatro casos:
$(- \infty, - \frac{2}{3}] \cup [- \frac{2}{3}, - \frac{1}{2}] \cup [- \frac{1}{2}, \infty) = (- \infty, \infty)$

Observemos que para la resolución de este tipo de desigualdades, siempre deberemos considerar los casos correspondientes a los signos del argumento de la función valor absoluto, es decir, cuando el argumento es positivo y cuando es negativo. En la sección de Tarea moral encontrarás ejercicios que te ayudarán a reforzar lo visto en esta entrada.

Más adelante

Ahora que ya hemos visto el procedimiento para encontrar los valores que satisfacen una desigualdad con valor absoluto, en la siguiente entrada lo utilizaremos para continuar resolviendo ejercicios que lo involucren adicionando el concepto de raíz cuadrada de un número real. Veremos que el valor absoluto está relacionado con la definición formal de raíz cuadrada y algunos resultados útiles.

Tarea moral

Demuestra el punto 2 del teorema, recordemos que $a \geq 0$ :
$\begin{aligned} | x | \geq a & \Leftrightarrow - a \geq x o x \geq a \\ \Leftrightarrow x \in (- \infty, - a] \cup [a, \infty) \end{aligned}$

Encuentra los valores que satisfacen las siguientes desigualdades:

$| x - 3 | < 8$
$| 3 x - 3 | > 2 x + 1$
$| x - 1 | | x + 2 | = 3$
$| x - 1 | + | x - 2 | > 1$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Valor absoluto. Desigualdad del triángulo.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Raíz cuadrada y desigualdades.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Valor absoluto. Desigualdad del triángulo

Por Karen González Cárdenas

Deja un comentario

Introducción

En esta entrada veremos una función muy particular: el valor absoluto. Ésta nos permitirá «medir la distancia» entre un par de números reales. Finalizaremos con la demostración de la Desigualdad del triángulo y algunas de sus consecuencias. Esta desigualdad es usada en las demostraciones de Límite y Continuidad que veremos más adelante.

Definición formal

Definición (Valor absoluto): Para todo $x \in R$ definimos la función valor absoluto como sigue:
$| x | = {\begin{cases} x & si x \geq 0 \\ - x & si x < 0 \end{cases}$

Recordando las propiedades de orden, la definición quedaría de la siguiente manera:
$| x | = {\begin{cases} x & si x = 0 o x \in P \\ - x & si - x \in P \end{cases}$
Esta última nos será de utilidad para la demostración de la desigualdad del triángulo que veremos más adelante.

Observación: De la definición anterior notamos que para toda $x \in R$ , su valor absoluto $| x |$ es mayor o igual a cero.

Midiendo distancias

Si observamos la definición del valor absoluto, notamos que asocia a cualquier número real con su distancia respecto al cero. Veámoslo en los ejemplos siguientes:

$| - 3 | = 3$

$| 14 | = 14$

En consecuencia, si consideramos la distancia entre cualquier par de números reales tendríamos la siguiente definición.

Definición: Para cualesquiera $a, b \in R$ tenemos que están a distancia $| a - b |$ .
Observemos que la distancia siempre será positiva o cero.

Desigualdad del triángulo

Teorema (Desigualdad del triángulo): Para todo $a, b \in R$ se cumple la siguiente desigualdad:
$| a + b | \leq | a | + | b | .$

Demostración: Dada la definición del valor absoluto, debemos considerar casos sobre los signos de $a$ y $b$ .
CASO 1: $a \geq 0$ y $b \geq 0$ .
Recordemos que $P$ es cerrado bajo la suma, por lo que tenemos lo siguiente:
$\begin{aligned} | a + b | & = a + b \\ = | a | + | b | . \end{aligned}$
La última igualdad se sigue de $a = | a |$ y $b = | b |$ .

Para los siguientes casos haremos uso de los siguientes resultados que serán demostrados posteriormente:

Resultados: Para cualesquiera $a, b, c \in R$ se cumplen:

$- a - b = - (a + b)$ .
Si $b < 0 \Rightarrow b < - b$ .
Si $a < b \Rightarrow a + c < b + c$ .

CASO 2: $a < 0$ y $b < 0$ .
Notemos que $- a \in P$ y $- b \in P$ por lo que $- a - b \in P$ . Así se sigue que:
$\begin{aligned} (por ser a + b negativo) & | a + b | & = - (a + b) \\ (por el resultado 1) & = - a - b \\ = (- a) + (- b) \\ = | a | + | b |, \end{aligned}$
porque $| a | = - a$ y $| b | = - b$ .

CASO 3: $a \geq 0$ y $b < 0$ .
Para esta demostración debemos considerar dos subcasos.
SUBCASO 1: $a + b \geq 0$ .
Dado lo anterior aplicando la definición de valor absoluto ocurre que:
$\begin{aligned} | a + b | & = a + b \\ (por los resultados 2 y3) & < a - b . \end{aligned}$
Como tenemos que $a - b = | a | + | b |$ , concluimos:
$| a + b | < | a | + | b | .$
SUBCASO 2: $a + b < 0$ .
Procederemos análogamente al subcaso anterior:
$\begin{aligned} | a + b | & = - (a + b) \\ = - a - b \\ (por resultados 2 y3) & < a - b . \end{aligned}$
Ya que $a - b = | a | + | b |$ , tenemos:
$| a + b | < | a | + | b | .$

CASO 4: $a < 0$ y $b \geq 0$ .
Al igual que en el caso 3, para verificar la desigualdad se deberán considerar dos subcasos. La demostración de este caso se deja como parte de la Tarea moral.

Para poder dar por terminada la prueba, debemos demostrar los siguientes resultados auxiliares que utilizamos:

Resultados: Para cualesquiera $a, b, c \in R$ se cumplen:

$- a - b = - (a + b)$ .
Si $b < 0 \Rightarrow b < - b$ .
Si $a < b \Rightarrow a + c < b + c$ .

Demostración:
1. Debemos verificar que $- a - b = (- a) + (- b)$ es inverso aditivo de $a + b$ .
$\begin{aligned} (a + b) + ((- a) + (- b)) & = (b + a) + ((- a) + (- b)) \\ = ((b + a) + (- a)) + (- b) \\ = (b + (a + (- a)) + (- b) \\ = (b + 0) + (- b) \\ = b + (- b) \\ = 0. \end{aligned}$
Concluimos que $(- a) + (- b) = - (a + b)$ .

2. Ya que $b < 0$ sabemos que $- b \in P$ . Queremos probar que $- b - b > 0$ .
Observemos que: $- b - b = (- b) + (- b) \in P$ .
Por lo que concluimos que $b < - b$ .

3. Bastaría ver que $(b + c) - (a + c) \in P$ . Debido a que $b - a \in P$ . Observamos lo siguiente.
$\begin{aligned} b - a & = (b - a) + 0 \\ = (b - a) + (c - c) \\ = (b + c) - (a + c) . \end{aligned}$
$∴ (b + c) - (a + c) \in P .$
$∴ b + c > a + c .$

Observemos que las demostraciones de estos resultados no utilizan la desigualdad del triángulo, más bien hacen uso de las propiedades vistas en las entradas anteriores.

Consecuencias de la desigualdad del triángulo

Proposición (Consecuencias de la desigualdad del triángulo): Sean $a, b \in R$ . Se cumplen las siguientes desigualdades:

$| a - b | \leq | a | + | b |$
$| a | - | b | \leq | a - b |$
$| b | - | a | \leq | a - b |$

En esta ocasión sólo probaremos el punto 2.

Demostración:
2. Como $| a | = | a + 0 |$ , al desarrollar esta igualdad obtenemos:
$\begin{aligned} | a | & = | a + 0 | \\ = | a + (b + (- b)) | \\ = | (a - b) + b | \\ (por la desigualdad del triángulo) & \leq | a - b | + | b | \end{aligned}$
$∴ | a | \leq | a - b | + | b |$
$∴ | a | - | b | \leq | a - b |$

Más adelante

En la próxima entrada comenzaremos a resolver desigualdades donde el valor absoluto se encuentra involucrado.

Tarea moral

Propiedades del valor absoluto.
Prueba los siguientes resultados:
- $| a | = | - a | .$
- $| a b | = | a | | b |$ .
- $| \frac{1}{a} | = \frac{1}{| a |}$ con $a \neq 0$ .
- $\frac{| a |}{| b |} = | \frac{a}{b} |$ con $b \neq 0$ .
Desigualdad del triángulo.
- Realiza la prueba del CASO 4 .
- Demuestra que para cualesquiera $a, b \in R$ :
  - $| a - b | \leq | a | + | b |$ .
  - $| b | - | a | \leq | a - b |$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I:Intervalos y desigualdades en los números reales.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Valor absoluto y desigualdades
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Intervalos y desigualdades en los números reales

Por Karen González Cárdenas

1 respuesta

Introducción

Ahora veremos los intervalos de los números reales, su definición y su representación en la recta real. Para ello nos apoyaremos de varios ejemplos y ejercicios. Recordemos que al representar gráficamente a los números reales lo hacemos por medio de una recta, donde un punto será la representación de un número y la recta todo el conjunto $R$ .

De igual manera, abordaremos en esta entrada la resolución de desigualdades en los reales, donde los intervalos están íntimamente relacionados.

Intervalos en los reales

Definición: Sean $a, b \in R$ . Definimos, haciendo uso de la siguiente notación, los siguientes intervalos en $R$ de la siguiente manera:

Intervalo cerrado:
$[a, b] := {x : a \leq x \leq b} .$

Intervalo abierto
$(a, b) := {x : a < x < b} .$
Abierto por la izquierda/ Cerrado por la derecha
$(a, b] := {x : a < x \leq b} .$
Abierto por la derecha/Cerrado por la izquierda
$[a, b) := {x : a \leq x < b} .$

Casos especiales

Sea $a \in R$ . Para los intervalos que involucran al infinito tenemos las siguientes definiciones:

$(- \infty, a) := {x : x < a} .$
$(- \infty, a] := {x : x \leq a} .$
$(a, \infty) := {x : a < x} .$
$[a, \infty) := {x : a \leq x} .$
$(- \infty, \infty) := R .$

Cabe mencionar que los símbolos $- \infty$ y $\infty$ son solamente notación, ya que no existe ningún número « $\infty$ » tal que cumpla $\infty \geq x$ para todo $x \in R$ .

Representación gráfica

A continuación veremos la representación de cada uno de los intervalos anteriores en la recta real. Esto nos ayudará más adelante con la resolución de desigualdades. En cada una de las imágenes la sección de la recta real sombreada con amarillo «\\» representará los valores considerados por el intervalo.

$[a, b]$

$(a, b)$

*No consideramos los valores de $a$ y $b$ .*

$(a, b]$

$[a, b)$

$(- \infty, a)$

Todos los valores estrictamente menores que $a$ .

$(- \infty, a]$

Todos los valores menores o iguales que $a$ .

$(a, \infty)$

*Todos los valores estrictamente mayores que $a$ .*

$[a, \infty)$

*Todos los valores mayores o iguales que $a$ .*

$(- \infty, \infty)$

Ahora que ya hemos definido a los intervalos en los reales $R$ , veremos algunos ejercicios de representación gráfica de intervalos.

Algunos ejemplos de intervalos

A continuación daremos la representación gráfica de los siguientes intervalos.

$(1, 14]$
Aplicando la definición correspondiente obtenemos la siguiente representación:

$(- 15, - 2) \cup [6, 10)$
Graficamos primero ambos intervalos en la recta real, por lo que tenemos lo siguiente:

Ya que estamos considerando la unión de los intervalos, por su definición tenemos que el conjunto resultante sería el azul:

$(- 3, 0) \cap (- 2, 4]$
Vemos que al graficar ambos intervalos obtenemos:

Como queremos la intersección de dichos intervalos, el intervalo resultante sería en el que encontremos elementos en común, así sería:

Se invita a demostrar esta igualdad haciendo uso de la definición de igualdad de conjuntos.

$[- 6, 1) \cup (- 1, 7]$
Comenzamos graficando ambos intervalos en la recta real:

Así considerando la definición de unión obtenemos el siguiente intervalo:

Se invita a demostrar esta igualdad haciendo uso de la definición de igualdad de conjuntos.

$[- 10, 0) \cap [0, 5)$
Graficando los intervalos anteriores tenemos:

Debido a que queremos la intersección de ambos intervalos, observamos que por su definición no poseen ningún elemento en común, así su intersección sería vacía: $[- 10, 0) \cap [0, 5) = \emptyset$

$(- \infty, - 2) \cup (- 3, 0) \cup [- 1, \infty)$
Si graficamos los tres intervalos anteriores vemos que tendríamos lo siguiente:

Así al aplicar la definición de unión nos percatamos que se trata de toda la recta $R$ :

Una vez que hemos visto estos ejemplos procederemos a los ejercicios que involucran desigualdades. Cabe mencionar que todos los resultados probados anteriormente relacionados al Orden en $R$ los estaremos utilizando sin repetir dichas demostraciones.

Desigualdades en los reales

Encuentra todos los números reales $x$ que cumplan con las siguientes desigualdades:

$4 - x < 3 - 2 x .$

Comenzamos con restar $4$ en ambos lados de la desigualdad:
$\begin{aligned} \Rightarrow 4 - x - 4 < 3 - 2 x - 4 \\ \Rightarrow - x + (4 - 4) < - 2 x + (3 - 4) \\ \Rightarrow - x < - 2 x - 1 \\ \Rightarrow - x + 2 x < (- 2 x + 2 x) - 1 \\ \Rightarrow x < - 1 . \end{aligned}$

Así observamos que todas las $x$ que cumplen la desigualdad son aquellas que $x < - 1$ , es decir, las que pertenecen al intervalo:
$(- \infty, - 1) .$

$(x - 1) (x - 3) > 0 .$

Como estamos buscando que el producto sea positivo, debemos considerar los siguientes dos casos:
CASO 1: $(x - 1) > 0$ y $(x - 3) > 0 .$
Por lo anterior queremos encontrar a todos los reales que satisfacen que $x > 1$ y $x > 3$ .
Al graficar dichos intervalos observamos lo siguiente:

Ya que estamos considerando la intersección, el intervalo buscado sería:
$(3, \infty) .$

CASO 2: $(x - 1) < 0$ y $(x - 3) < 0$ .

Ahora queremos a todos los números que cumplan con que $x < 1$ y $x < 3$ , así tenemos:

Por lo que el intervalo buscado es:
$(- \infty, 1) .$

Considerando la unión de los intervalos obtenidos en los CASOS 1 y 2 tenemos que el conjunto solución es:
$(- \infty, 1) \cup (3, \infty) .$

$\frac{1}{x} + \frac{1}{1 - x} > 0 .$

Comenzaremos realizando la suma de fracciones:
$\begin{aligned} \frac{1}{x} + \frac{1}{1 - x} > 0 & \Rightarrow \frac{1 - x + x}{x (1 - x)} > 0 \\ \Rightarrow \frac{1}{x (1 - x)} > 0 \end{aligned}$
Como ya tenemos que el numerador es mayor que cero: $1 > 0$ , la igualdad se satisface si y sólo si $x (x - 1) > 0$ . Por lo que debemos considerar los siguientes casos:

CASO 1: $x > 0$ y $1 - x > 0$ .
Por lo que tendríamos las siguientes condiciones: $x > 0$ y $1 > x$ .

De lo anterior vemos que los valores que cumplen ambas condiciones son aquellos que pertenecen al intervalo:
$(0, 1) .$

CASO 2: $x < 0$ y $1 - x < 0$ .
De lo anterior tenemos que: $x < 0$ y $1 < x$ .

Observamos que no existen valores que cumplan ambas condiciones.
De los casos vistos tenemos que los valores que cumple la desigualdad son todos aquellos que pertenecen al intervalo: $(0, 1) .$

Más adelante

En la próxima entrada veremos la función valor absoluto. Daremos su definición formal y su interpretación geométrica. De igual manera veremos un resultado muy importante que lo involucra: la desigualdad del triángulo.

Tarea moral

Da la representación geométrica de los siguientes intervalos:

$(- 15, - 2) \cap [6, 10),$
$(- 3, 0) \cup (- 2, 4],$
$[- 6, 1) \cap (- 1, 7],$
$(- \infty, - 2) \cup [0, \infty) .$

Encuentra todos los números reales $x$ que cumplan con las siguientes desigualdades:

$5 - x^{2} < - 2,$
$x^{2} - 2 x + 2 > 0 .$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Propiedades de orden de los números reales.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Valor Absoluto. Desigualdad del Triángulo.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Propiedades de orden de los números reales

Por Karen González Cárdenas

2 respuestas

Introducción

Comenzaremos a revisar un conjunto de propiedades muy particular que nos permitirán ordenar a los números reales. De acuerdo a este orden podremos decir para un par de números reales, quién es mayor o menor que otro. Así a la lista de propiedades vista previamente le agregaremos las siguientes.

Noción de orden en $R$

O1.-Existe un subconjunto $P \subseteq R$ tal que para todo $a \in R$ ocurre una y sólo una de las siguientes afirmaciones:

$a = 0$ ,
$a \in P$ ,
$- a \in P .$

O2.-Si $a, b \in P$ entonces $a + b \in P$ .

O3.-Si $a, b \in P$ entonces $a \cdot b \in P$ .

Los elementos de $P$ son llamados números reales positivos.

Definición: Decimos que:

$a > b$ si $a - b \in P$ .
$a < b$ si $b > a$ .
$a \geq b$ si $a - b \in P$ o $a = b$ .
$a \leq b$ si $b - a \in P$ o $a = b$ .

Tricotomía

Proposición (Tricotomía): Para cualesquiera $a, b \in R$ , tenemos que cumple una y sólo una de las siguientes afirmaciones:

$a = b$
$a > b$
$b > a$

Demostración:

Sean $a, b \in R$ . Como por la cerradura de la suma S1 tenemos que: $a + (- b) = a - b \in R$

Por O1 se cumple una y sólo una de las siguientes afirmaciones:

$a - b = 0$ ,
$a - b \in P$ ,
$- (a - b) \in P$ .

Aplicando las definiciones anteriores nos quedaría:

$a - b = 0 \Rightarrow a = b$ ,
$a - b \in P \Rightarrow a > b$ ,
$- (a - b) \in P \Rightarrow b - a \in P \Rightarrow b > a .$

Leyes de los signos

Definición: Diremos que $a$ es positivo si $a \in P$ y que es negativo si $- a \in P$ .

Proposición (Leyes de los signos): Sean $a, b \in R$ . Se cumplen las siguientes afirmaciones:

Si $a, b > 0$ entonces $a \cdot b > 0$ .
Si $a, b < 0$ entonces $a \cdot b > 0$ .
Si $a > 0$ , $b < 0$ entonces $a \cdot b < 0$ .
Si $a < 0$ , $b > 0$ entonces $a \cdot b < 0$ .

Demostración:

Consideremos $a > 0$ y $b > 0$ . Así tenemos que $a \in P$ y $b \in P$ entonces por O3 $a \cdot b \in P$ .
$∴ a \cdot b > 0$
Ahora tomemos $a < 0$ y $b < 0$ . Por lo que $- a \in P$ y $- b \in P$ entonces por O3 $(- a) \cdot (- b) \in P$ .
$∴ a \cdot b > 0$

Algunos resultados importantes

Proposición: Sean $a, b, c, d \in R$ . Tenemos que se cumplen los siguientes resultados:

Si $a > b$ entonces $a + c > b + c$ .
Si $a < b$ y $c < 0$ entonces $a c > b c$ .
Si $a < b$ y $c > 0$ entonces $a c < b c$ .
Si $a < b$ y $c < d$ entonces $a + c < b + d$ .
Si $a < b$ y $c > d$ entonces $a - c < b - d$ .
Si $a < b$ entonces $- b < - a$ .

Demostración:
Demostraremos los puntos 1,3,4 y 5, mientras que dejaremos como ejercicios al lector los puntos 2 y 6.

Como $a > b$ esto significa que $a - b \in P$ .
Así se sigue que:
$\begin{aligned} a - b & = a + 0 - b \\ = a + (c - c) - b \\ = (a + c) - (c + b) . \end{aligned}$
De lo anterior concluimos que $(a + c) - (c + b) \in P$ , es decir, $a + c > c + b$ .
Tarea moral.
Por hipótesis tenemos que $a < b$ y $c > 0$ por lo que ocurre: $b - a \in P$ y $c \in P$ .
Por O3 afirmamos que $c (b - a) \in P$ . Observemos que: $c (b - a) = c b - c a = b c - a c$ .
$∴ b c - a c \in P .$
$∴ b c > a c .$
Ya que $a < b$ y $c < d$ se sigue que $b - a \in P$ y $d - c \in P$ . Así por O2 tenemos:
$(b - a) + (d - c) \in P .$
Notemos que:
$\begin{aligned} (b - a) + (d - c) & = b - a + d - c \\ = b + d - a - c \\ = (b + d) - (a + c) . \end{aligned}$
$∴ (b + d) - (a + c) \in P .$
$∴ b + d > a + c .$
Tenemos que $a < b$ y $c > d$ $\Rightarrow b - a \in P$ y $c - d \in P$ .
Por O2 se sigue que $(b - a) + (c - d) \in P$ . Y como tenemos lo siguiente:
$\begin{aligned} (b - a) + (c - d) & = b - a + c - d \\ = (b - d) + (- a + c) \\ = (b - d) - (a - c) . \end{aligned}$
Así concluimos que: $(b - d) - (a - c) \in P$ .
$∴ b - d > a - c .$
Tarea moral.

Transitividad

Proposición (Transitividad): Para $a, b \in R$ se cumplen las siguientes propiedades:

Si $a > b$ y $b > c \Rightarrow a > c$ .
Si $a < b$ y $b < c \Rightarrow a < c$ .

Demostración:

Cómo $a > b$ y $b > c$ sabemos que $a - b \in P$ y $b - c \in P$ .
Entonces tenemos por O2 $(a - b) + (b - c) \in P$ . Y como:
$(a - b) + (b - c) = a + (- b + b) - c = a - c .$
Así $a - c \in P$ y por lo tanto $a > c$ .
Ya que $b > a$ y $c > b$ . Aplicando el punto anterior se sigue que:
$c > a \Rightarrow a < c .$

El cuadrado de un número real

Proposición: Para todo $a \in R$ se cumple lo siguiente:

$a^{2} \geq 0 .$

Demostración: Tomemos $a \in R$ . Por la propiedad O1 debemos considerar los siguientes tres casos.

Caso $a = 0$ :
Como $a = 0$ , al multiplicar por $a$ en ambos lados de la igualdad tenemos:
$\begin{aligned} \Rightarrow a \cdot a = 0 \cdot a \\ \Rightarrow a \cdot a = 0 \cdot 0 \\ \Rightarrow a^{2} = 0 . \end{aligned}$
Concluimos así $a^{2} \geq 0$ .
Caso $a > 0$
Así $a \in P$ y por O3 tenemos que $a \cdot a \in P$ . Por lo que $a^{2} \in P$ , es decir, $a^{2} > 0$ . Se concluye $a^{2} \geq 0$ .
Caso $a < 0$
Ahora tenemos que $- a \in P$ y por O3 que $- a \cdot - a \in P$ . Así $a^{2} = (- a) (- a) \in P$ , por lo que $a^{2} \geq 0$ .

De los casos anteriores probamos que $a^{2} \geq 0$ para todo $a \in R$

Más adelante

Ya que hemos definido las propiedades de orden y varios de sus resultados más importantes. En la siguiente entrada comenzaremos por definir a los intervalos en los reales y a resolver desigualdades apoyándonos en todo lo visto en esta entrada.

Tarea moral

Demuestra los puntos 3 y 4 de las Leyes de los signos.

Si $a > 0$ , $b < 0$ entonces $a \cdot b < 0$ .
- Sugerencia: Prueba $a \cdot (- b)$ es inverso aditivo de $a b$ , es decir, $a b + a \cdot (- b) = 0$
Si $a < 0$ , $b > 0$ entonces $a \cdot b < 0$ .
- Sugerencia: Aplica o prueba el resultado $(- a) (b) = - (a b)$ .

Prueba los puntos 2 y 6 de la sección Algunos resultados importantes:

Si $a < b$ y $c < 0$ entonces $a c > b c$ .
Si $a < b$ entonces $- b < - a$ .

Muestre que para $a, b \in R$ se cumplen las siguientes propiedades:

Si $a > 1$ entonces $a^{2} > a$ .
Si $0 < a < 1$ entonces $a^{2} < a$ .
Consideremos $0 < a < b$ , demostrar que se cumple la siguiente desigualdad:
$a < \sqrt{a b} < \frac{a + b}{2} < b$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Propiedades algebraicas de los números reales (Parte 2)
Entrada siguiente del curso: Cálculo Diferencial e Integral I:Intervalos y desigualdades en los números reales.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Propiedades algebraicas de los números reales (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción

Continuaremos revisando resultados derivados de las Propiedades básicas de los números reales vistas en la entrada anterior.

Resultados relacionados a la multiplicación

Proposición. Demostraremos lo siguiente:

Sean $a, b \in R$ . Si $a b = 0 \Rightarrow a = 0$ ó $b = 0$ .
Sea $a \in R, a \neq 0$ . Si $a x = a$ , entonces $x = 1$ .
Sean $a, b, c \in R$ con $a \neq 0$ . Si $a b = a c \Rightarrow b = c$ .

Demostración:

Procederemos a demostrar por contradicción. Así suponemos que $a b = 0$ , $a \neq 0$ y $b \neq 0$ . Entonces por la propiedad M5 existen $a^{- 1}, b^{- 1} \in R$ tales que $a \cdot a^{- 1} = 1$ y $b \cdot b^{- 1} = 1$ .
Y como $a b = 0$ se sigue:
$\begin{aligned} (por multiplicar b^{- 1}) & \Rightarrow (a b) \cdot b^{- 1} = 0 \cdot b^{- 1} \\ (por M3) & \Rightarrow a (b \cdot b^{- 1}) = 0 \cdot b^{- 1} \\ (por M5) & \Rightarrow a (1) = 0 \cdot b^{- 1} \\ (por M4) & \Rightarrow a = 0 \cdot b^{- 1} \\ (por M2) & \Rightarrow a = b^{- 1} \cdot 0 \\ (por resultado a \cdot 0 = 0) & \Rightarrow a = 0 \Rightarrow\Leftarrow \end{aligned}$
Lo anterior es una contradicción, pues supusimos que $a \neq 0$ .
$∴ a = 0 o b = 0$ .

Observación: Utilizaremos el símbolo $\Rightarrow\Leftarrow$ para referirnos a una contradicción en las pruebas.

Otra alternativa de demostración para este punto 1 es la siguiente:
Vamos a suponer que $a b = 0$ y $a \neq 0$ . Por M5 sabemos que existe $a^{- 1} \in R$ inverso multiplicativo de $a$ , así tenemos que:
$\begin{aligned} (por multiplicar a^{- 1}) & \Rightarrow a^{- 1} \cdot (a b) = a^{- 1} \cdot 0 \\ (por M3) & \Rightarrow (a^{- 1} \cdot a) b = a^{- 1} \cdot 0 \\ (por M5) & \Rightarrow 1 \cdot b = a^{- 1} \cdot 0 \\ (por M4) & \Rightarrow b = a^{- 1} \cdot 0 \\ (por resultado a \cdot 0 = 0) & \Rightarrow b = 0 \end{aligned}$
Análogamente, si consideramos $b \neq 0$ obtendríamos que $a = 0$ .
$∴ a = 0$ ó $b = 0$
Como por hipótesis tenemos que $a x = a$ .
$\begin{aligned} (por sumar - a) & \Rightarrow a x + (- a) = a + (- a) \\ (por S5) & \Rightarrow a x + (- a) = 0 \\ (por - a = (- 1) (a)) & \Rightarrow a x + (- 1) (a) = 0 \\ (por M2) & \Rightarrow a x + (a) (- 1) = 0 \\ (por D) & \Rightarrow a (x + (- 1)) = 0 \end{aligned}$

Por el punto anterior 1 tenemos que $a = 0$ ó $x + (- 1) = 0$ . Pero como por hipótesis tenemos que $a \neq 0$ entonces $x + (- 1) = 0$ .

Como ya vimos que el inverso aditivo es único $\Rightarrow x$ es el inverso aditivo de $- 1$ , que por el resultado $- (- a) = a$ usando $a = 1$ , sabemos que es 1.
$∴ x = 1$
Como por hipótesis tenemos que $a \neq 0$ entonces existe $a^{- 1} \in R$ por M5.
Así multiplicando por $a^{- 1}$ en ambos lados de la igualdad $a b = a c$ tenemos:
$\begin{aligned} \Rightarrow a^{- 1} (a b) = a^{- 1} (a c) \\ (por M3) & \Rightarrow (a^{- 1} a) b = (a^{- 1} a) c \\ (por M5) & \Rightarrow 1 \cdot b = 1 \cdot c \\ (por M4) & \Rightarrow b = c \end{aligned}$
$∴ b = c$

Como vimos en las pruebas anteriores, conforme vayamos probando más propiedades los resultados que obtendremos se volverán más interesantes. A continuación demostraremos algunos con los que seguramente ya estás familiarizado.

Algunos productos notables

Notación: Definimos $x - y := x + (- y)$ .

Proposición: Para $x, y \in R$ se cumple lo siguiente:

Diferencia de cuadrados: $x^{2} - y^{2} = (x - y) (x + y)$ .
Si $x^{2} = y^{2}$ entonces $x = y$ o $x = - y$ .
Diferencia de cubos: $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$ .
Suma de cubos: $x^{3} + y^{3} = (x - y) (x^{2} - x y + y^{2})$ .

Demostración:

Partiremos de $(x - y) (x + y)$ , así obtenemos lo siguiente:
$\begin{aligned} (por D) & (x - y) (x + y) & = (x - y) x + (x - y) y \\ (por M2) & = x (x - y) + y (x - y) \\ = x (x + (- y)) + y (x + (- y)) \\ (por D) & = x \cdot x + x \cdot (- y) + y \cdot x + y \cdot (- y) \\ (por - x y = x (- y)) & = x^{2} - x y + y x - y^{2} \\ (por M2) & = x^{2} - x y + x y - y^{2} \\ (por S5) & = x^{2} + 0 - y^{2} \\ (por S4) & = x^{2} - y^{2} \\ ∴ (x - y) (x + y) & = x^{2} - y^{2} \end{aligned}$
Sabemos que $x^{2} = y^{2}$ . Veamos que si sumamos $- y^{2}$ en ambos lados obtenemos:
$x^{2} - y^{2} = y^{2} - y^{2} \Rightarrow x^{2} - y^{2} = 0$
Aplicando el punto anterior se sigue que:
$(x - y) (x + y) = 0$
Recordando la proposición vista al principio de la entrada decimos que: $x - y = 0$ , o bien, $x + y = 0$ .
Por un lado tenemos que al sumar $y$ en $x - y = 0$ :
$\begin{aligned} (x - y) + y & = 0 + y \\ (por S3 y S4) & x + ((- y) + y) & = y \\ (por S5) & x & = y \end{aligned}$
$∴ x = y$

Y por otro tenemos que al sumar $- y$ en $x + y = 0$ :
$\begin{aligned} (x + y) - y & = 0 - y \\ (por S3 y S4) & x + (y + (- y)) & = - y \\ (por S5) & x & = - y \end{aligned}$
$∴ x = - y$
De lo anterior concluimos que $x = y$ , ó $x = - y$ .

Los incisos 3 y 4 se dejarán como ejercicios en la Tarea moral.

Propiedades relacionadas a los inversos multiplicativos

Notación: Denotaremos al inverso multiplicativo de $a \in R$ como $a^{- 1} = \frac{1}{a}$ . Consecuentemente, definimos $\frac{a}{b} := a \cdot b^{- 1}$ .

Proposición: Para $a, b, c, d \in R$ se cumple lo siguiente:

Para $a, b \neq 0$ , $(a b)^{- 1} = a^{- 1} b^{- 1} .$
Para $b, c \neq 0$ , $\frac{a}{b} = \frac{a c}{b c} .$
Para $b, d \neq 0$ , $\frac{a}{b} + \frac{c}{d} = \frac{a d + b c}{b d} .$
Para $b, d \neq 0$ , $\frac{a}{b} \cdot \frac{c}{d} = \frac{a c}{b d} .$
Para $b, c, d \neq 0$ , $\frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a d}{b c} .$
Para $b, d \neq 0$ , $\frac{a}{b} = \frac{c}{d} \Rightarrow a d = b c .$

Demostración:

Observemos que por la propiedad de cerradura M1, $a b \in R$ y $a b \neq 0$ . Así por M5 se sigue que: $\begin{matrix} (1) & (a b) (a b)^{- 1} = 1 . \end{matrix}$
De este modo, lo que queremos probar es: $(a b) (a^{- 1} b^{- 1}) = 1 .$
Comenzando por el lado izquierdo de la igualdad tenemos:
$\begin{aligned} (por M3) & (a b) (a^{- 1} b^{- 1}) & = a (b (a^{- 1} b^{- 1})) \\ (por M2) & = a (b (b^{- 1} a^{- 1})) \\ (por M3) & = a ((b b^{- 1}) a^{- 1}) \\ (por M5) & = a ((1) a^{- 1}) \\ (por M4) & = a a^{- 1} \\ (por M5) & = 1 . \end{aligned}$
Concluimos que $(a b) (a^{- 1} b^{- 1}) = 1$ . Al igualar con $(1)$ nos queda: $(a b) (a b)^{- 1} = (a b) (a^{- 1} b^{- 1}) .$ Y aplicando el punto 3 de la primera sección de esta entrada tenemos: $(a b)^{- 1} = a^{- 1} b^{- 1} .$
Recordemos que por la definición $\frac{a}{b} = a b^{- 1}$ . Por lo que tendríamos:
$\begin{aligned} \frac{a c}{b c} & = (a c) (b c)^{- 1} \\ (por el punto anterior) & = (a c) (b^{- 1} c^{- 1}) \\ (por M3) & = ((a c) b^{- 1}) c^{- 1} \\ (por M3) & = (a (c b^{- 1})) c^{- 1} \\ (por M2) & = (a (b^{- 1} c)) c^{- 1} \\ (por M3) & = (a b^{- 1}) c) c^{- 1} \\ (por M3) & = (a b^{- 1}) (c c^{- 1}) \\ (por M5) & = (a b^{- 1}) (1) \\ (por M4) & = a b^{- 1} . \end{aligned}$
$∴ \frac{a}{b} = \frac{a c}{b c} .$
La propiedad 3 queda como ejercicio para nuestro lector.
Procedamos a demostrar la propiedad 4, comenzaremos por $\frac{a c}{b d} = \frac{a c}{b d} .$
Así por definición tenemos lo siguiente:
$\begin{aligned} \frac{a c}{b d} & = (a c) (b d)^{- 1} \\ (por el primer punto) & = (a c) (b^{- 1} d^{- 1}) \\ (por M3) & = ((a c) b^{- 1}) d^{- 1} \\ (por M3) & = (a (c b^{- 1})) d^{- 1} \\ (por M2) & = (a (b^{- 1} c)) d^{- 1} \\ (por M3) & = ((a b^{- 1}) c) d^{- 1} \\ (por M3) & = (a b^{- 1}) (c d^{- 1}) \\ = \frac{a}{b} \cdot \frac{c}{d} . \end{aligned}$
$∴ \frac{a}{b} \cdot \frac{c}{d} = \frac{a c}{b d} .$
La propiedad 5 queda como ejercicio para nuestro lector.
Sean $b, d \neq 0$ . Supongamos que: $\frac{a}{b} = \frac{c}{d} .$
$P . d .$ $a d = b c$ .
Ya que $\frac{a}{b} = \frac{c}{d},$ por definición tenemos $a b^{- 1} = c d^{- 1}$ .
Multiplicando por $b$ se sigue que:
$\begin{aligned} \Rightarrow (a b^{- 1}) b = (c d^{- 1}) b \\ (por M3) & \Rightarrow a (b^{- 1} b) = c (d^{- 1} b) \\ (por M5 y M2) & \Rightarrow a (1) = c (b d^{- 1}) \\ (por M4 y M3) & \Rightarrow a = (c b) d^{- 1} . \end{aligned}$

Ahora multiplicaremos la igualdad anterior por $d$ :
$\begin{aligned} \Rightarrow a d = ((c b) d^{- 1}) d \\ (por M3) & \Rightarrow a d = (c b) (d^{- 1} d) \\ (por M5) & \Rightarrow a d = (c b) (1) \\ (por M4) & \Rightarrow a d = c b \\ (por M2) & \Rightarrow a d = b c . \end{aligned}$

Más adelante

Durante las últimas dos entradas vimos las propiedades relacionadas con la suma y la multiplicación de los números reales. Sin embargo, no son las únicas propiedades que este conjunto de números cumple. En la siguiente entrada comenzaremos a ver las propiedades de orden de los números reales y algunas de sus consecuencias.

Tarea moral

Prueba los puntos 3 y 4 de la sección «Algunos productos notables».

Diferencia de cubos: $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$
Suma de cubos: $x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2})$
Sugerencia: Utiliza el punto anterior «Diferencia de cubos» y prueba que $y^{3} = - (- y)^{3}$ .

Prueba los puntos 3 y 5 de la sección anterior:

Para $b, d \neq 0$ , $\frac{a}{b} + \frac{c}{d} = \frac{a d + b c}{b d} .$
Para $b, c, d \neq 0$ , $\frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a d}{b c} .$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Propiedades algebraicas de los números reales (Parte 1)
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Propiedades de orden de los números reales
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Introducción

Un par de resultados importantes

Ejercicio 1

Ejercicio 2

Ejercicio 3

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Definición formal

Midiendo distancias

Desigualdad del triángulo

Consecuencias de la desigualdad del triángulo

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Intervalos en los reales

Casos especiales

Representación gráfica

Algunos ejemplos de intervalos

Desigualdades en los reales

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Noción de orden en R

Tricotomía

Leyes de los signos

Algunos resultados importantes

Transitividad

El cuadrado de un número real

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Resultados relacionados a la multiplicación

Algunos productos notables

Propiedades relacionadas a los inversos multiplicativos

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Noción de orden en $R$