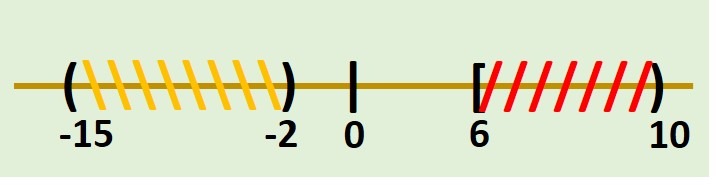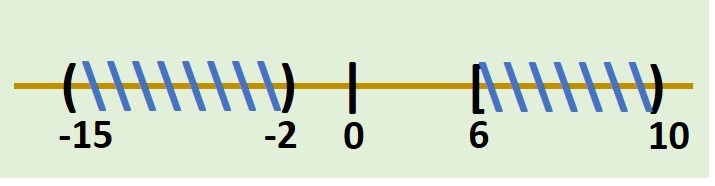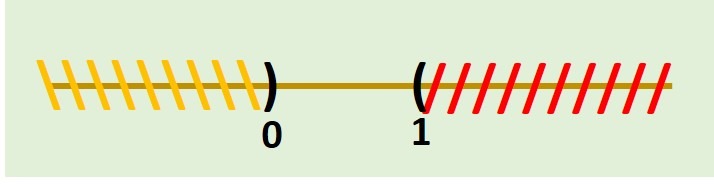Introducción
Ahora veremos los intervalos de los números reales, su definición y su representación en la recta real. Para ello nos apoyaremos de varios ejemplos y ejercicios. Recordemos que al representar gráficamente a los números reales lo hacemos por medio de una recta, donde un punto será la representación de un número y la recta todo el conjunto $\r$.
De igual manera, abordaremos en esta entrada la resolución de desigualdades en los reales, donde los intervalos están íntimamente relacionados.
Intervalos en los reales
Definición: Sean $a,b \in \r$. Definimos, haciendo uso de la siguiente notación, los siguientes intervalos en $\RR$ de la siguiente manera:
- Intervalo cerrado:
\[
[a,b]:=\left\{x : a \leq x \leq b\right\} \quad\text{.}
\]
- Intervalo abierto
\[
(a,b):=\left\{x : a < x < b\right\}\quad\text{.}
\] - Abierto por la izquierda/ Cerrado por la derecha
\[
(a,b]:=\left\{x : a < x \leq b\right\}\quad\text{.}
\] - Abierto por la derecha/Cerrado por la izquierda
\[
[a,b):=\left\{x : a \leq x < b\right\}\quad\text{.}
\]
Casos especiales
Sea $a\in \r$. Para los intervalos que involucran al infinito tenemos las siguientes definiciones:
- \[
(-\infty ,a):=\left\{x : x < a \right\}\quad\text{.}
\] - \[
(-\infty ,a]:=\left\{x : x \leq a \right\}\quad\text{.}
\] - \[
(a, \infty) :=\left\{x : a < x\right\}\quad\text{.}
\] - \[
[a, \infty) :=\left\{x : a \leq x\right\}\quad\text{.}
\] - \[
(- \infty, \infty) :=\r\quad\text{.}
\]
Cabe mencionar que los símbolos $- \infty$ y $\infty$ son solamente notación, ya que no existe ningún número «$\infty$» tal que cumpla $\infty \geq x$ para todo $x\in \r$.
Representación gráfica
A continuación veremos la representación de cada uno de los intervalos anteriores en la recta real. Esto nos ayudará más adelante con la resolución de desigualdades. En cada una de las imágenes la sección de la recta real sombreada con amarillo «\\\» representará los valores considerados por el intervalo.
\[ [a,b] \]
\[ (a,b) \]
\[ (a,b] \]
\[ [a,b) \]
\[ (-\infty ,a) \]
\[ (-\infty ,a] \]
\[ (a, \infty) \]
\[ [a, \infty) \]
\[ (- \infty, \infty) \]
Ahora que ya hemos definido a los intervalos en los reales $\r$, veremos algunos ejercicios de representación gráfica de intervalos.
Algunos ejemplos de intervalos
A continuación daremos la representación gráfica de los siguientes intervalos.
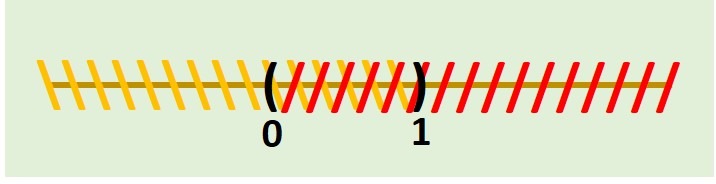
- \[ (1,14 ] \]
Aplicando la definición correspondiente obtenemos la siguiente representación:
- \[ (-15,-2) \cup [6,10) \]
Graficamos primero ambos intervalos en la recta real, por lo que tenemos lo siguiente:
Ya que estamos considerando la unión de los intervalos, por su definición tenemos que el conjunto resultante sería el azul:
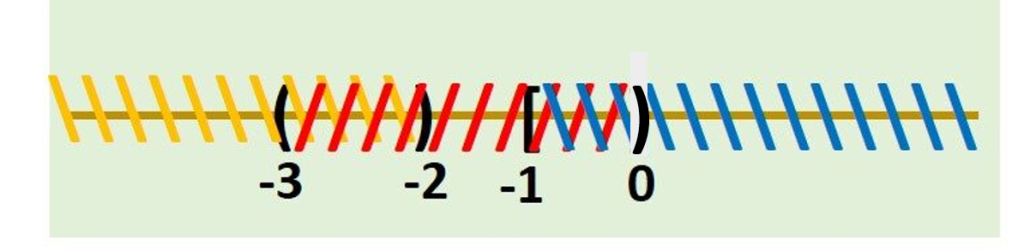
- \[ (-3, 0) \cap (-2, 4] \]
Vemos que al graficar ambos intervalos obtenemos:
Como queremos la intersección de dichos intervalos, el intervalo resultante sería en el que encontremos elementos en común, así sería:
Se invita a demostrar esta igualdad haciendo uso de la definición de igualdad de conjuntos.
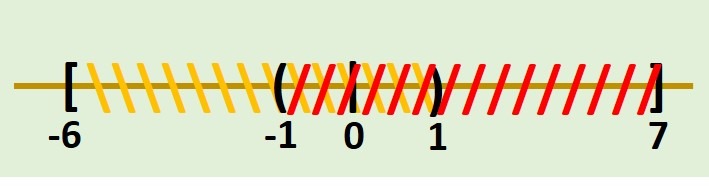
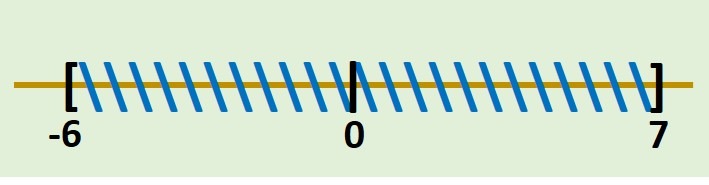
- \[ [-6,1) \cup (-1,7] \]
Comenzamos graficando ambos intervalos en la recta real:
Así considerando la definición de unión obtenemos el siguiente intervalo:
Se invita a demostrar esta igualdad haciendo uso de la definición de igualdad de conjuntos.
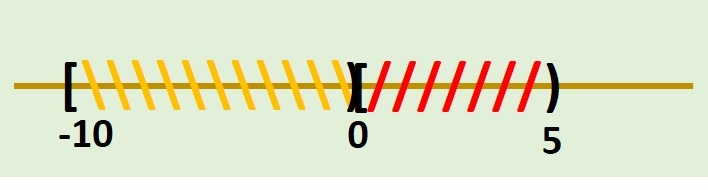
- \[ [-10, 0) \cap [0, 5) \]
Graficando los intervalos anteriores tenemos:
Debido a que queremos la intersección de ambos intervalos, observamos que por su definición no poseen ningún elemento en común, así su intersección sería vacía: $[-10, 0) \cap [0, 5) = \emptyset$
- \[ (-\infty,-2) \cup(-3,0) \cup [-1, \infty) \]
Si graficamos los tres intervalos anteriores vemos que tendríamos lo siguiente:
Así al aplicar la definición de unión nos percatamos que se trata de toda la recta $\r$:
Una vez que hemos visto estos ejemplos procederemos a los ejercicios que involucran desigualdades. Cabe mencionar que todos los resultados probados anteriormente relacionados al Orden en $\r$ los estaremos utilizando sin repetir dichas demostraciones.
Desigualdades en los reales
Encuentra todos los números reales $x$ que cumplan con las siguientes desigualdades:
- $$4- x < 3 -2x \quad\text{.}$$
Comenzamos con restar $4$ en ambos lados de la desigualdad:
\begin{align*}
&\Rightarrow 4- x-4 < 3 -2x-4\\
&\Rightarrow -x+ (4 -4) < -2x+(3-4)\\
&\Rightarrow -x<-2x-1\\
&\Rightarrow-x+ 2x < (-2x +2x)-1\\
&\Rightarrow x<-1\quad\text{.}
\end{align*}
Así observamos que todas las $x$ que cumplen la desigualdad son aquellas que $x<-1$, es decir, las que pertenecen al intervalo:
$$(-\infty,-1)\quad\text{.}$$
- $$(x-1)(x-3)>0\quad\text{.}$$
Como estamos buscando que el producto sea positivo, debemos considerar los siguientes dos casos:
CASO 1: $(x-1)>0$ y $(x-3)>0\text{.}$
Por lo anterior queremos encontrar a todos los reales que satisfacen que $x>1$ y $x>3$.
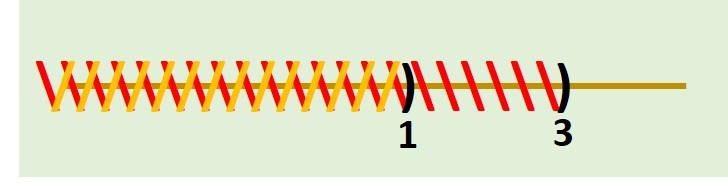
Al graficar dichos intervalos observamos lo siguiente:
Ya que estamos considerando la intersección, el intervalo buscado sería:
$$(3, \infty)\quad\text{.}$$
CASO 2: $(x-1)<0$ y $(x-3)<0$.
Ahora queremos a todos los números que cumplan con que $x<1$ y $x<3$, así tenemos:
Por lo que el intervalo buscado es:
$$(-\infty,1)\quad\text{.}$$
Considerando la unión de los intervalos obtenidos en los CASOS 1 y 2 tenemos que el conjunto solución es:
$$(-\infty,1) \cup (3, \infty)\quad\text{.}$$
- $$\frac{1}{x} + \frac{1}{1-x} > 0\quad\text{.}$$
Comenzaremos realizando la suma de fracciones:
\begin{align*}
\frac{1}{x} + \frac{1}{1-x} > 0 &\Rightarrow \frac{1-x+x}{x(1-x)}>0\\
&\Rightarrow \frac{1}{x (1-x)}>0\\
\end{align*}
Como ya tenemos que el numerador es mayor que cero: $1>0$, la igualdad se satisface si y sólo si $x (x-1) > 0$. Por lo que debemos considerar los siguientes casos:
CASO 1: $x>0$ y $1-x >0$.
Por lo que tendríamos las siguientes condiciones: $x>0$ y $1>x$.
De lo anterior vemos que los valores que cumplen ambas condiciones son aquellos que pertenecen al intervalo:
$$(0,1)\quad\text{.}$$
CASO 2: $x<0$ y $1-x < 0$.
De lo anterior tenemos que: $x < 0$ y $1<x$.
Observamos que no existen valores que cumplan ambas condiciones.
De los casos vistos tenemos que los valores que cumple la desigualdad son todos aquellos que pertenecen al intervalo: $$(0,1)\quad\text{.}$$
Más adelante
En la próxima entrada veremos la función valor absoluto. Daremos su definición formal y su interpretación geométrica. De igual manera veremos un resultado muy importante que lo involucra: la desigualdad del triángulo.
Tarea moral
Da la representación geométrica de los siguientes intervalos:
- \[ (-15,-2) \cap [6,10)\text{,} \]
- \[ (-3, 0) \cup (-2, 4] \text{,}\]
- \[ [-6,1) \cap (-1,7] \text{,}\]
- \[ (-\infty,-2) \cup [0, \infty) \text{.}\]
Encuentra todos los números reales $x$ que cumplan con las siguientes desigualdades:
- $$5-x^{2} < -2\text{,}$$
- $$x^{2} -2x +2 > 0\text{.}$$
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Propiedades de orden de los números reales.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Valor Absoluto. Desigualdad del Triángulo.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»