Introducción
En esta entrada veremos un conjunto de circunferencias que surgen de una construcción particular a partir del punto simediano o punto de Lemoine, las circunferencias de Lemoine, y su generalización, las circunferencias de Tucker.
Primera circunferencia de Lemoine
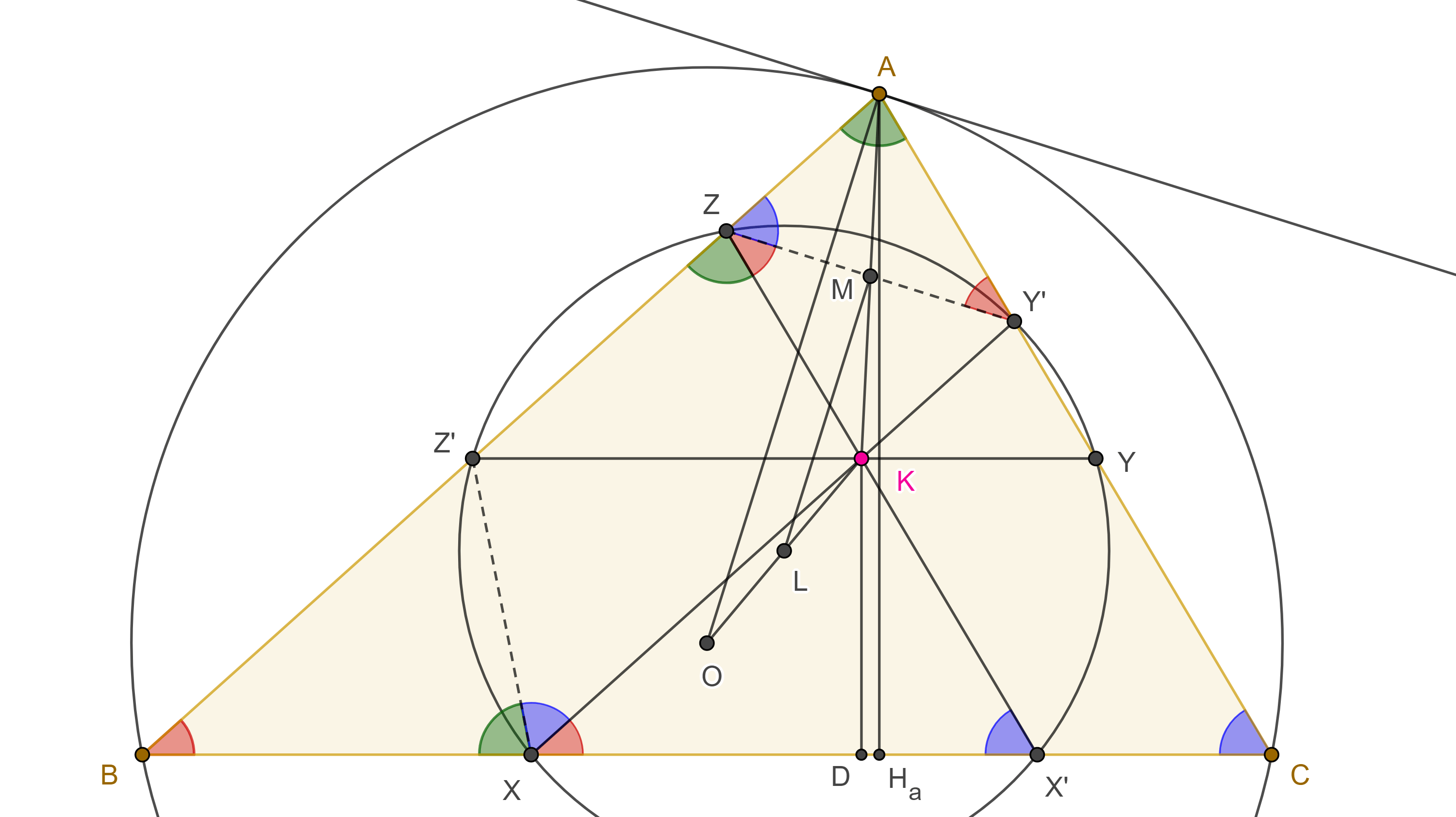
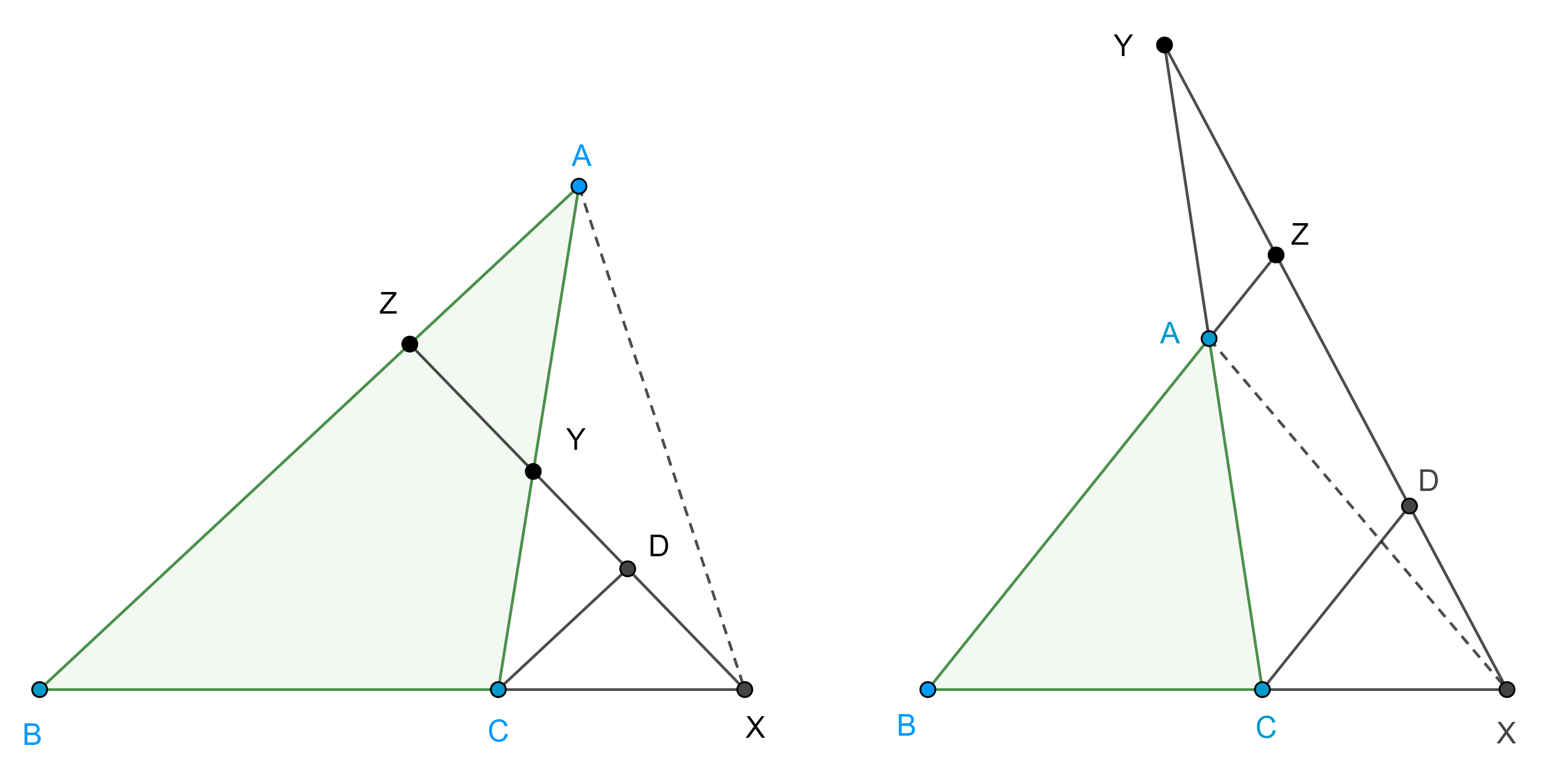
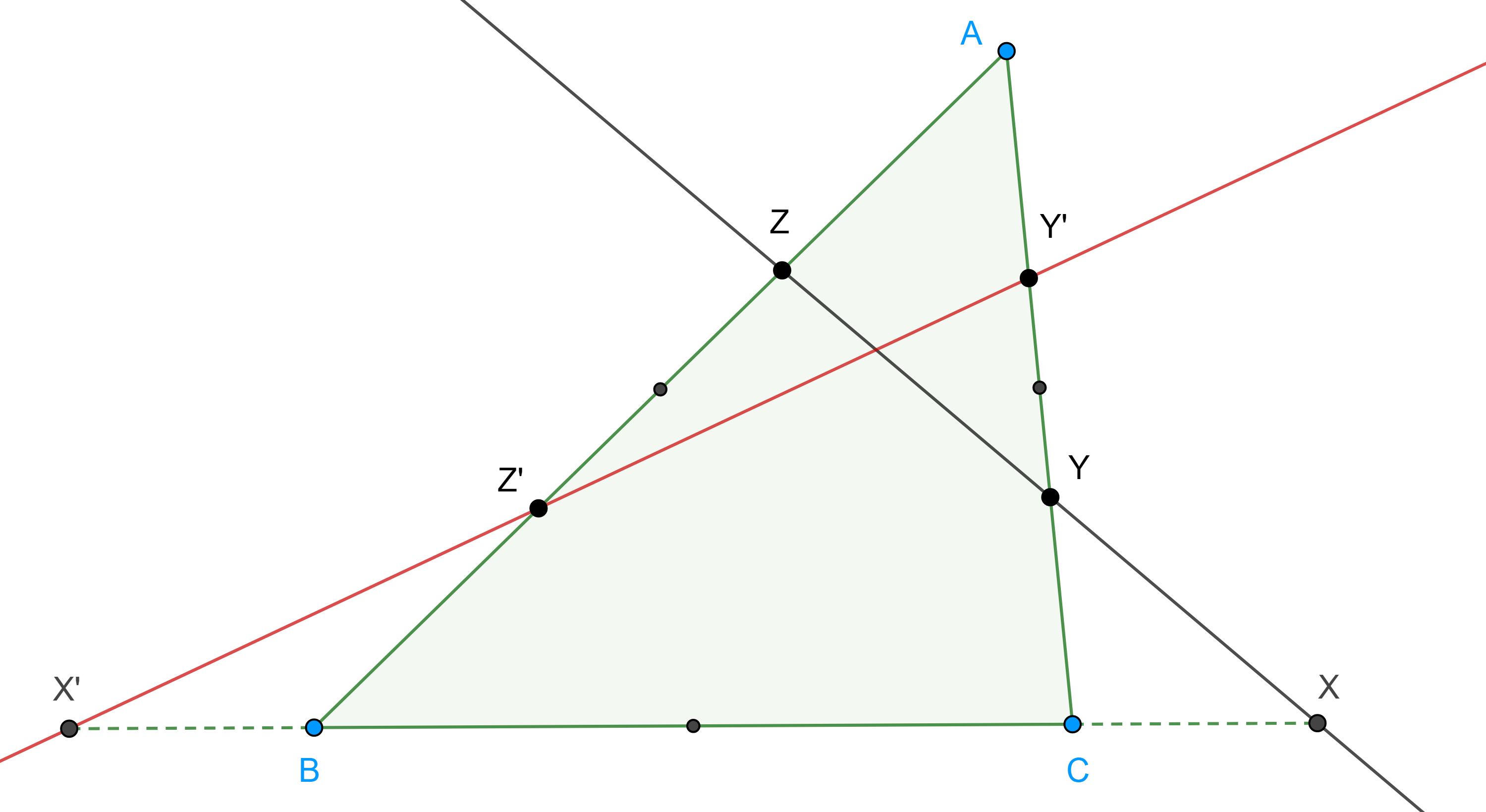
Teorema 1. Si por el punto simediano de un triángulo dado trazamos paralelas a los lados del triángulo, entonces estas tres paralelas intersecan a los lados del triángulo en seis puntos cíclicos, a dicha circunferencia se le conoce como primera circunferencia de Lemoine.
Demostración. En $\triangle ABC$, sean $K$ el punto de Lemoine, $Z’KY \parallel BC$, $X’KZ \parallel CA$, $Y’KX \parallel AB$, $X$, $X’ \in BC$, $Y$, $Y’ \in CA$, $Z$, $Z’ \in AB$.
Dado que $KY’ \parallel AZ$ y $KZ \parallel AY’$, $\square AZKY’$ es paralelogramo, por lo tanto, $AK$ biseca a $ZY’$, de esto se sigue que $ZY’$ es antiparalela a $BC$ respecto a $AB$ y $CA$.
Como $Z’Y \parallel BC$, entonces $Z’Y$ y $ZY’$ son antiparalelas respecto a $AB$ y $CA$, es decir, $\square ZZ’YY’$ es cíclico.
Igualmente podemos ver qué $XZ’$, $CA$ son antiparalelas respecto a $AB$, $BC$ y que $\square Z’XX’Z’$ es cíclico.
Como $Z’Y \parallel BC$ y $\square ZZ’YY’$ es cíclico entonces $\angle Z’ZY’ = \angle A + \angle B$.
Como $XZ’$ y $CA$ son antiparalelas entonces $\angle Z’XB = \angle A$, ya que $AB \parallel XY’$ tenemos que $\angle CXY’ = \angle B$, por lo anterior tenemos que $\angle Y’XZ’ = \angle C$.
Entonces, como los ángulos $\angle Y’XZ’$, $\angle Z’ZY’$ son suplementarios, $\square Z’XY’Z$ es cíclico, por lo tanto, $X$, $Y$, $Y’$, $Z$, $Z’$, están en la misma circunferencia.
Finalmente, como $X’$ esta en el circuncírculo de $\triangle XZZ’$ entonces el hexágono $XY’ZX’YZ’$ es cíclico.
$\blacksquare$
Proposición 1. El centro de la primera circunferencia de Lemoine es el punto medio entre el circuncentro y el punto de Lemoine.
Demostración. En la figura 1, del teorema anterior, sean $O$ el circuncentro de $\triangle ABC$ y $M= AK \cap ZY’$, considera $L$ el punto medio de $KO$, con $K$ el punto de Lemoine.
Como $\square AZKY’$ es paralelogramo, entonces $M$ es punto medio de $AK$ y $ZY’$.
En $\triangle AOK$, $LM$ es un segmento medio, por lo tanto, $ML \parallel AO$.
Ya que $ZY’$, $BC$ son antiparalelas respecto a $AB$, $CA$, entonces $ZY’$ es paralela a la tangente al circuncírculo de $\triangle ABC$ por $A$, por lo tanto, $AO \perp ZY’$.
En consecuencia, $ML \perp ZY’$, como $M$ es el punto medio de $ZY’$ entonces $L$ esta en la mediatriz de $ZY’$.
Igualmente vemos que $L$ esta en la mediatriz de $XZ’$, $YX’$, por lo tanto, $L$ es el centro de la primera circunferencia de Lemoine.
$\blacksquare$
Proposición 2. Las cuerdas de la primera circunferencia de Lemoine, contenidas en los lados del triángulo, son proporcionales a los cubos de dichos lados.
Demostración. Sean $D$ y $H_a$ las proyecciones de $K$ y $A$ en $BC$ respectivamente (figura 1), como $Y’X \parallel AB$ y $X’Z \parallel CA$ entonces $\triangle ABC$ y $\triangle KXX’$ son semejantes.
Por lo tanto,
$\dfrac{XX’}{BC} = \dfrac{KD}{AH_a} $
$= \dfrac{BC \times 2(\triangle ABC)}{AB^2 + BC^2 + CA^2} \times \dfrac{BC}{2(\triangle ABC)}$.
Donde la segunda igualdad se sigue del corolario 2 de la entrada anterior y de considerar el área de $\triangle ABC$.
$\Rightarrow XX’ = \dfrac{BC^3}{AB^ + BC^2 + CA^2}$.
De manera similar se ve que
$YY’ = \dfrac{CA^3}{AB^ + BC^2 + CA^2}$,
$ZZ’ = \dfrac{AB^3}{AB^ + BC^2 + CA^2}$.
$\blacksquare$
Segunda circunferencia de Lemoine
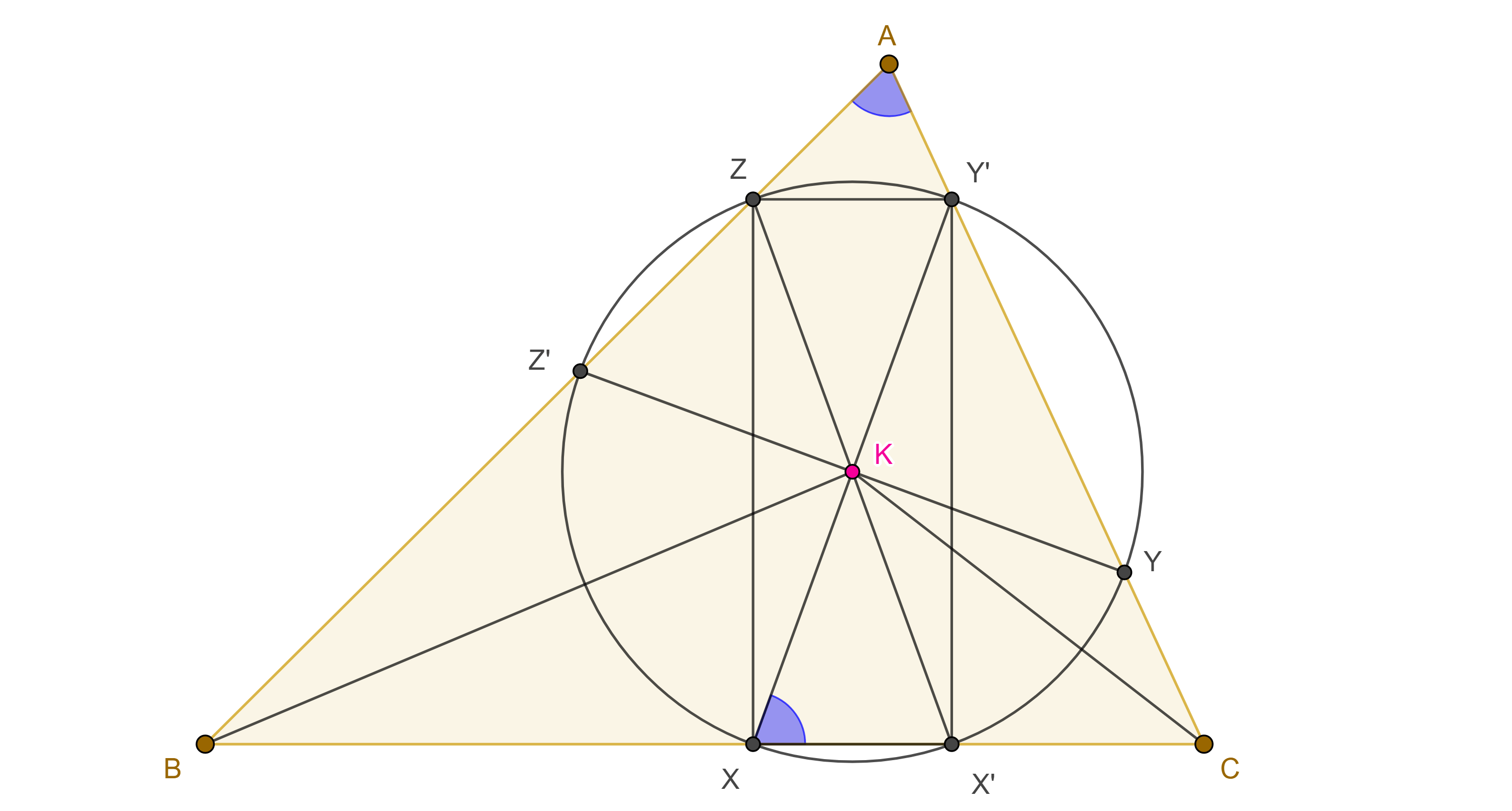
Teorema 2. Si por el punto simediano $K$ de un triángulo trazamos antiparalelas a los lados del triángulo, entonces estas tres antiparalelas intersecan a los lados del triángulo en seis puntos cíclicos con centro en $K$, a dicha circunferencia se le conoce como segunda circunferencia de Lemoine.
Demostración. En $\triangle ABC$ sean $K$ el punto de Lemoine, $Z’KY$ antiparalela a $BC$ respecto a $AB$ y $CA$, $X’KZ$ antiparalela a $CA$ respecto a $AB$ y $BC$, $Y’KX$ antiparalela a $AB$ respecto a $BC$ y $CA$, $X$, $X’ \in BC$, $Y$, $Y’ \in CA$, $Z$, $Z’ \in AB$.
Como $X’Z$ y $CA$ son antiparalelas, entonces $BK$ biseca a $X’Z$, de manera análoga vemos que $CK$ biseca a $Y’X$.
Dado que las antiparalelas $X’Z$ e $Y’X$ se intersecan en la $A$-simediana, entonces son iguales en magnitud.
Como resultado, concluimos que $\square XX’Y’Z$ es un rectángulo, por lo tanto, $X$, $X’$, $Y’$, $Z$, están en una circunferencia con centro en $K$.
Igualmente podemos ver que $AK$ biseca a $YZ’$ y que $XY’ = YZ’ = ZX’$.
Por lo tanto, el hexágono $XY’ZX’YZ’$ es cíclico.
Proposición 4. Las cuerdas de la segunda circunferencia de Lemoine, contenidas en los lados del triángulo son proporcionales a los cosenos de los ángulos opuestos a dichos lados, razón por la cual también es conocida como circunferencia de los cosenos.
Demostración. Dado que $Y’X$ y $AB$ son antiparalelas respecto a $BC$ y $CA$ (figura 2), entonces $\angle X’XY’ = \angle A$.
Como $\triangle Y’X’X$ es un triangulo rectángulo, entonces $\cos \angle A = \cos \angle X’XY’ = \dfrac{XX’}{Y’X}$.
Como $Y’X = X’Z = Z’Y = q$, entonces $XX’ = q \cos \angle A$.
Igualmente podemos ver que $YY’ = q \cos \angle B$ y $ZZ’ = q \cos \angle C$.
$\blacksquare$
Circunferencia de Tucker
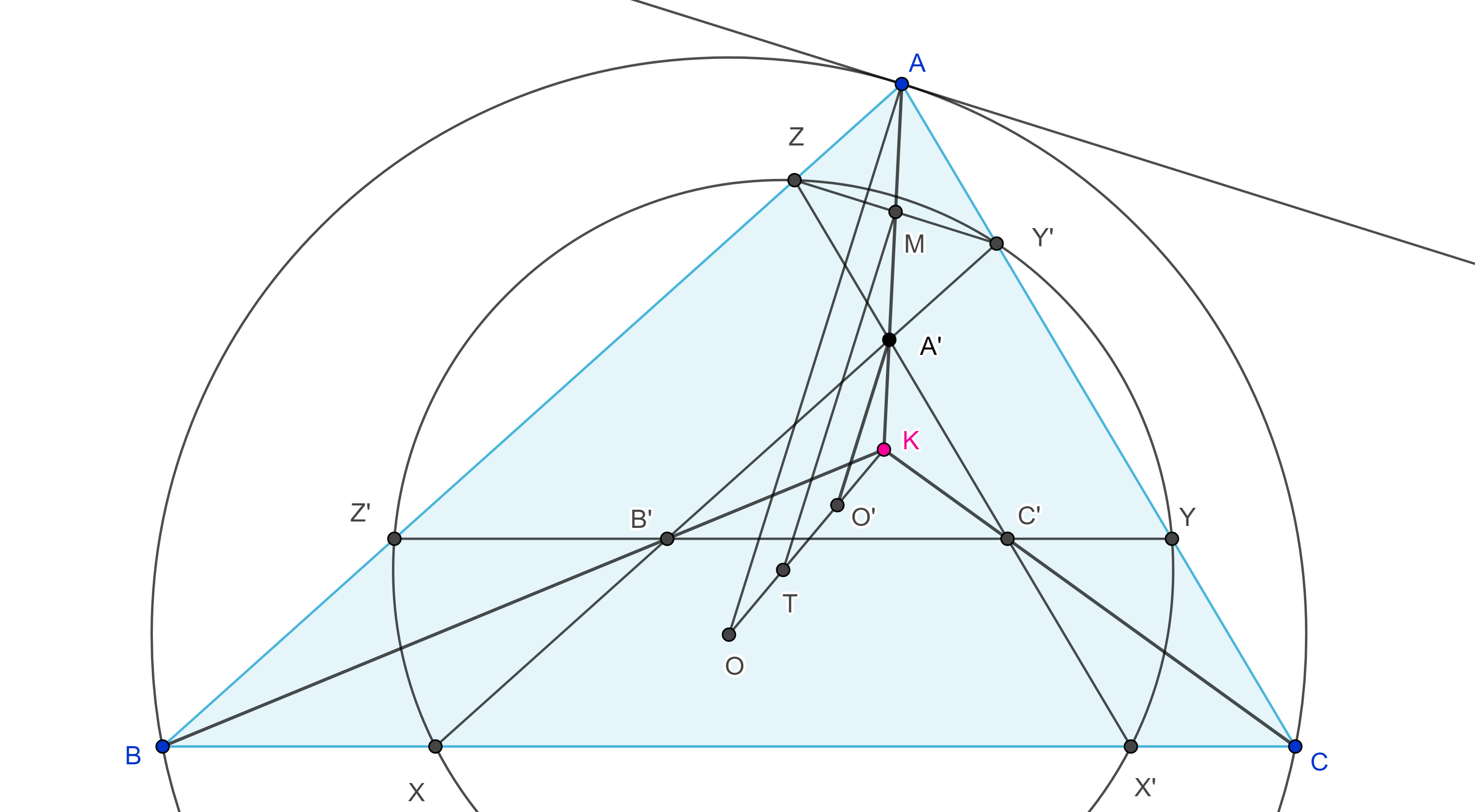
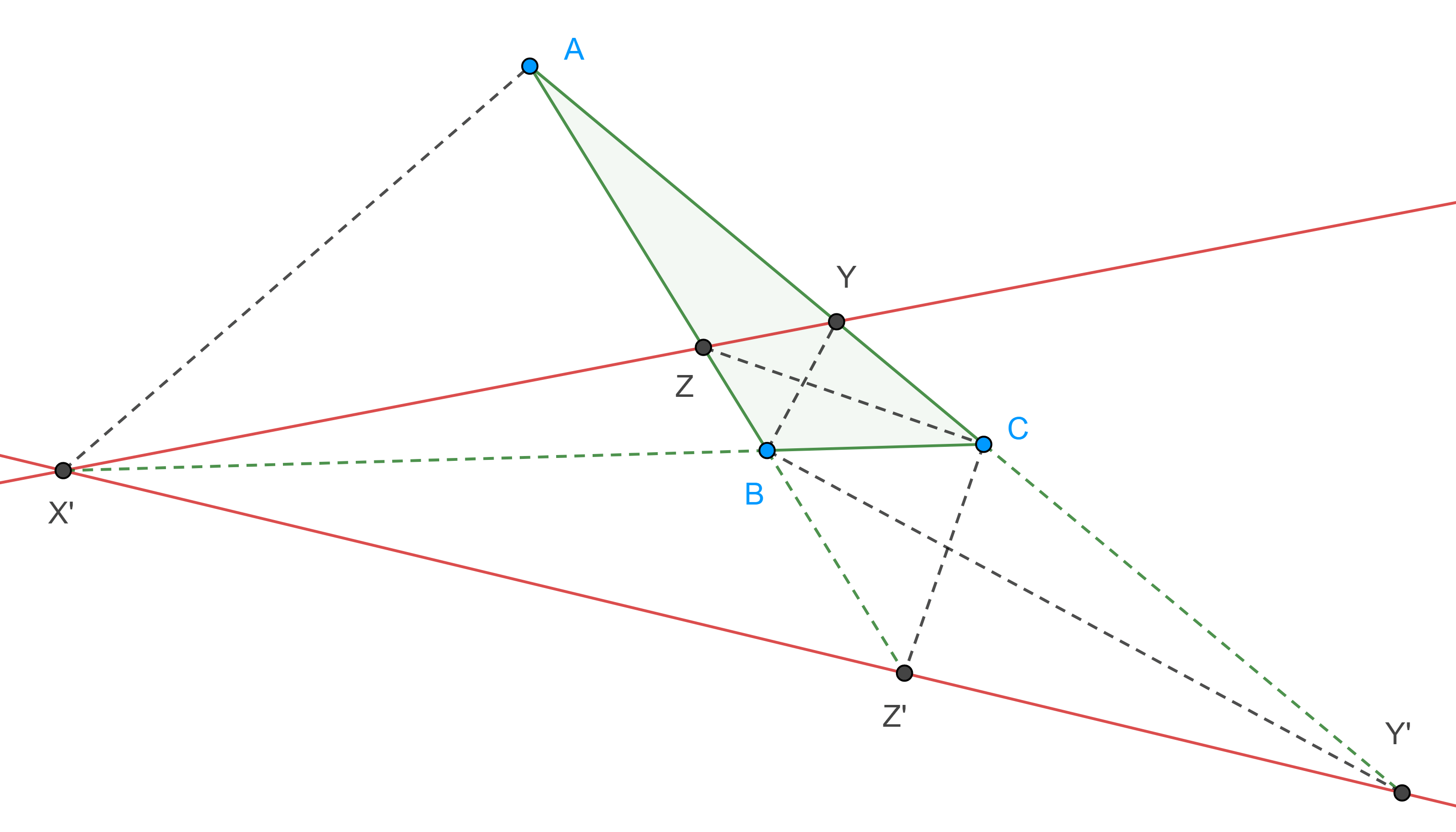
Teorema 3. Si aplicamos una homotecia a un triángulo con centro en su punto de Lemoine entonces los lados del triángulo imagen cortaran a los lados del triángulo original en seis puntos cíclicos, a esta circunferencia se le conoce como circunferencia de Tucker.
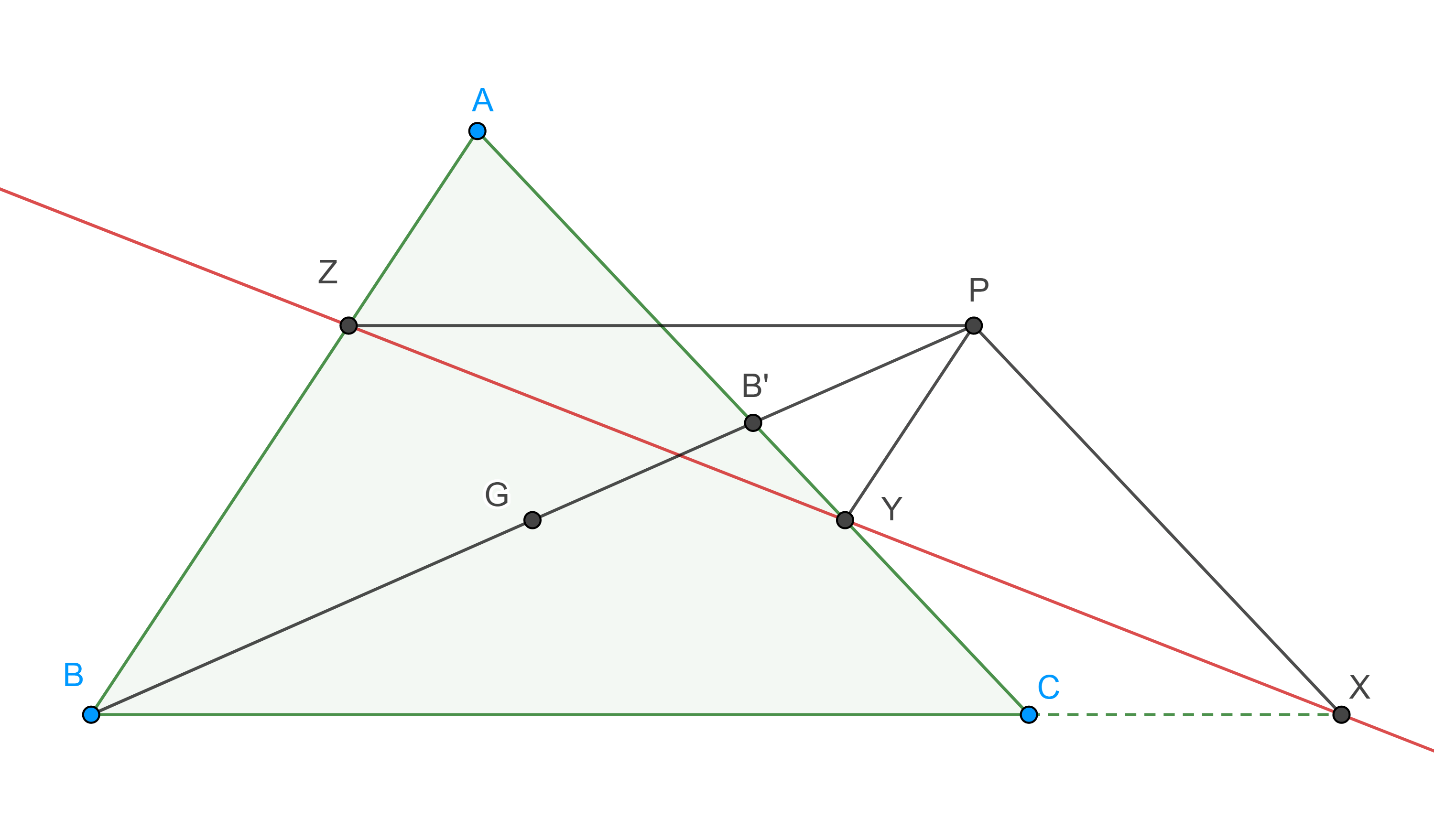
Demostración. Sea $K$ el punto de Lemoine de $\triangle ABC$ y $\triangle A’B’C’$ su imagen bajo una homotecia con centro en $K$, entonces los lados correspondientes son paralelos.
Sean $X$, $X’$ las intersecciones de $A’B’$ y $C’A’$ con $BC$, $Y$, $Y’$ las intersecciones de $B’C’$ y $A’B’$ con $CA$, $Z$, $Z’$ las intersecciones de $C’A’$ y $B’C’$ con $AB$.
Como $AZA’Y’$ es un paralelogramo entonces $AK$ biseca $Y’Z$, por lo tanto $Y’Z$ es antiparalela a $BC$ respecto a $AB$, $CA$.
De manera análoga, los pares de rectas $XZ’$, $CA$; $YX’$, $AB$ son antiparalelas.
A partir de aquí la demostración es igual a la del teorema 1.
$\blacksquare$
Proposición 5. El centro de la circunferencia de Tucker se encuentra en la recta que une al punto de Lemoine con el circuncentro del triángulo.
Demostración. Sean $O$ el circuncentro de $\triangle ABC$ y $M$ el punto medio de $Y’Z$ (figura 3), como $\triangle ABC$ y $\triangle A’B’C’$ son homotéticos la paralela por $A’$ a $AO$ interseca a $KO$ en $O’$ el circuncentro de $\triangle A’B’C’$.
Por $M$ trazamos una paralela a $AO$ que interseca a $KO$ en $T$.
Como $A’O’ \parallel MT$ entonces $\dfrac{KA’}{A’M} =\dfrac{KO’}{O’T}$.
Como $AO \parallel MT$ entonces $\dfrac{KM}{MA} =\dfrac{KT}{TO}$.
Pero
$\dfrac{KM}{KT} = \dfrac{KA’ + A’M}{KO’ + O’T}$
$= (\dfrac{A’M \times KO’}{O’T} + A’M)(\dfrac{1}{ KO’ + O’T}) $
$= A’M(\dfrac{KO’ + O’T}{O’T})(\dfrac{1}{ KO’ + O’T}) = \dfrac{A’M}{O’T}$.
Por lo tanto, como $M$ también es el punto medio de $AA’$ por ser $\square AZA’Y’$ paralelogramo, tenemos
$1 = \dfrac{A’M}{MA} = \dfrac{O’T}{TO}$.
Es decir, $T$ es el punto medio de $OO’$.
Por otra parte $AO \perp Y’Z$, pues $Y’Z$ es paralela a la tangente al circuncírculo de $\triangle ABC$ en $A$, entonces $TM \perp Y’Z$.
Por lo tanto, $T$ esta en la mediatriz de $Y’Z$.
Igualmente vemos que $T$ esta en la mediatriz de $Z’X$, $X’Y$, en consecuencia, $T$ es el centro de la circunferencia de Tucker y está en la recta $KO$.
$\blacksquare$
Circunferencia de Taylor
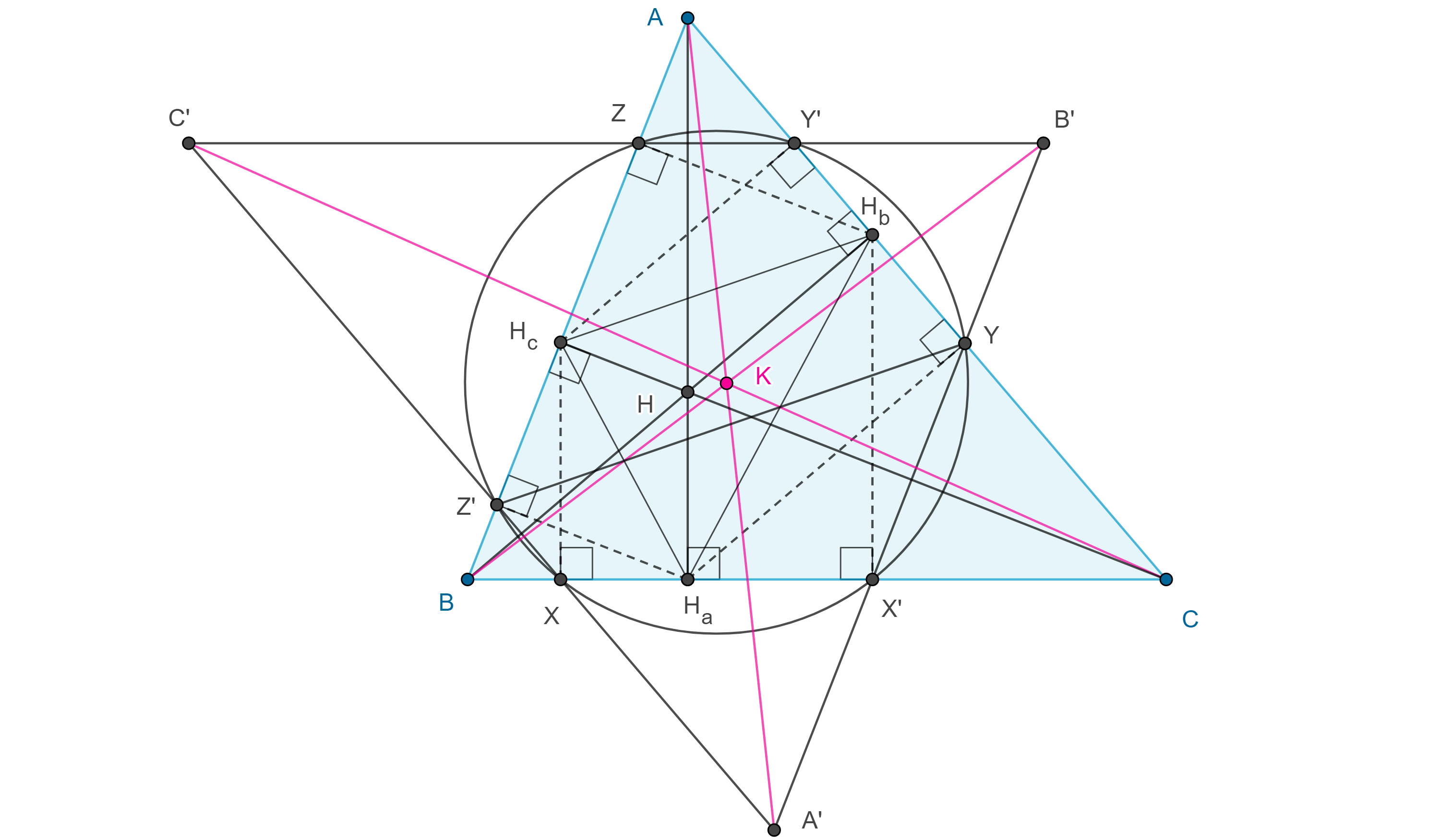
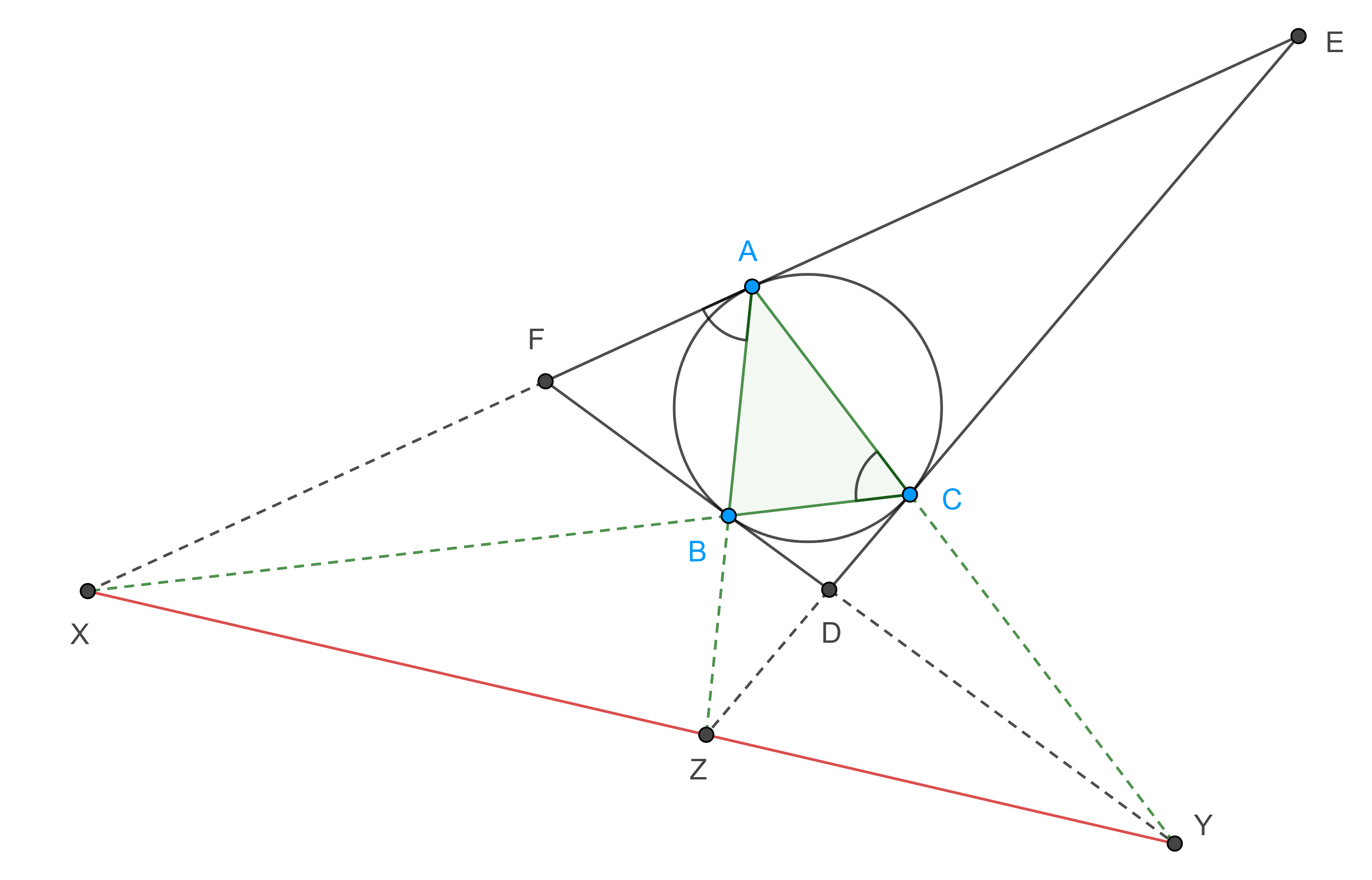
Teorema 4. Dado un triángulo, las proyecciones de los vértices de su triángulo órtico en los lados del triángulo original están en una circunferencia de Tucker, a esta circunferencia se le conoce como circunferencia de Taylor.
Demostración. Sea $\triangle ABC$ y $\triangle H_aH_bH_c$ su triangulo órtico, sean $X$, $X’$ las proyecciones de $H_c$ y $H_b$ en $BC$, $Y$, $Y’$ las proyecciones de $H_a$ y $H_c$ en $CA$, $Z$, $Z’$ las proyecciones de $H_b$ y $H_a$ en $AB$.
$\square H_cBCH_b$ es cíclico pues $\angle BH_cC = \angle BH_bC = \dfrac{\pi}{2}$, así que $\angle H_bH_cZ = \angle C$.
$\angle ZH_cH_bY’$ también es cíclico pues $\angle H_cZH_b = \angle H_cY’H_b = \dfrac{\pi}{2}$, así que $\angle AY’Z = \angle H_bH_cZ = \angle C$.
Por lo tanto, $ZY’ \parallel BC$.
Igualmente vemos que $XZ’ \parallel CA$ y $YX’ \parallel AB$.
En consecuencia, el triángulo $\triangle A’B’C’$ que se forma al extender $ZY’$, $XZ’$, $YX’$, es inversamente homotético con $\triangle ABC$.
Sea $H$ el ortocentro de $\triangle ABC$, como $HH_c \parallel H_aZ’$ y $HH_b \parallel H_aY$, entonces
$\dfrac{HH_c}{H_aZ’} = \dfrac{AH}{AH_A} = \dfrac{HH_b}{H_aY}$.
Por criterio de semejanza LAL, $\triangle HH_cH_b \sim \triangle H_aZ’Y$, por lo tanto, $Z’Y \parallel H_cH_b$.
De esto último y tomando en cuenta que $\square H_cBCH_b$ es cíclico, se sigue que $\square Z’BCY$ es cíclico, es decir $Z’Y$ y $BC$ son antiparalelas respecto de $AB$, $CA$.
Por otra parte, $\square AZ’A’Y$ es paralelogramo, así que $AA’$ biseca a $Z’Y$.
Esto implica que $AA’$ es la $A$-simediana de $\triangle ABC$.
De manera análoga vemos que $BB’$ y $CC’$ son simedianas, por lo tanto, $AA’$, $BB’$, $CC’$ concurren en el punto simediano $K$ de $\triangle ABC$.
Por el teorema anterior, se sigue que $X$, $X’$, $Y$, $Y’$, $Z$, $Z’$, están en una circunferencia de Tucker.
$\blacksquare$
Más adelante…
En la siguiente entrada estudiaremos propiedades mas generales de rectas que como la mediana y la simediana, son reflexión respecto de la bisectriz de un ángulo.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- En la figura 1, muestra que:
$i)$ $X’Y = Y’Z = Z’X$,
$ii)$ el incírculo del triángulo que se forma al extender $X’Y$, $Y’Z$ y $Z’X$, es concéntrico con la primer circunferencia de Lemoine de $\triangle ABC$. - Muestra que si tres diámetros de una circunferencia tienen sus extremos en los lados de un triángulo, entonces dicha circunferencia es la segunda circunferencia de Lemoine del triángulo y su centro es el punto de Lemoine.
- Muestra que el circuncírculo de un triángulo, la primera y la segunda circunferencias de Lemoine, son circunferencias de Tucker y encuentra la razón de homotecia con centro en el punto de Lemoine, que da origen a cada una.
- Demuestra que el centro de la circunferencia de Taylor de un triángulo es el punto de Spieker de su triángulo órtico. En la figura 4, el incentro del triángulo medial de $\triangle H_aH_bH_c$.
- En la figura 4 demuestra que:
$i)$ el punto de Lemoine de $\triangle ABC$ coincide con el punto de Gergonne del triángulo medial de su triángulo órtico, $\triangle H_aH_bH_c$,
$ii)$ el punto de Nagel del triángulo órtico $\triangle H_aH_bH_c$ es colineal con el ortocentro y el circuncentro de $\triangle A’B’C’$,
$iii)$ las bisectrices internas del triángulo medial de $\triangle H_aH_bH_c$, son perpendiculares a los lados de $\triangle ABC$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Punto simediano.
- Siguiente entrada del curso: Rectas isogonales.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 257-260, 284-287.
- Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 87-98.
- Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 271-277.
- Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 76-79.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»