Archivo de la etiqueta: rectas antiparalelas

Geometría Moderna I: Circunferencias de Lemoine

Por Rubén Alexander Ocampo Arellano

Introducción

En esta entrada veremos un conjunto de circunferencias que surgen de una construcción particular a partir del punto simediano o punto de Lemoine, las circunferencias de Lemoine, y su generalización, las circunferencias de Tucker.

Primera circunferencia de Lemoine

Teorema 1. Si por el punto simediano de un triángulo dado trazamos paralelas a los lados del triángulo, entonces estas tres paralelas intersecan a los lados del triángulo en seis puntos cíclicos, a dicha circunferencia se le conoce como primera circunferencia de Lemoine.

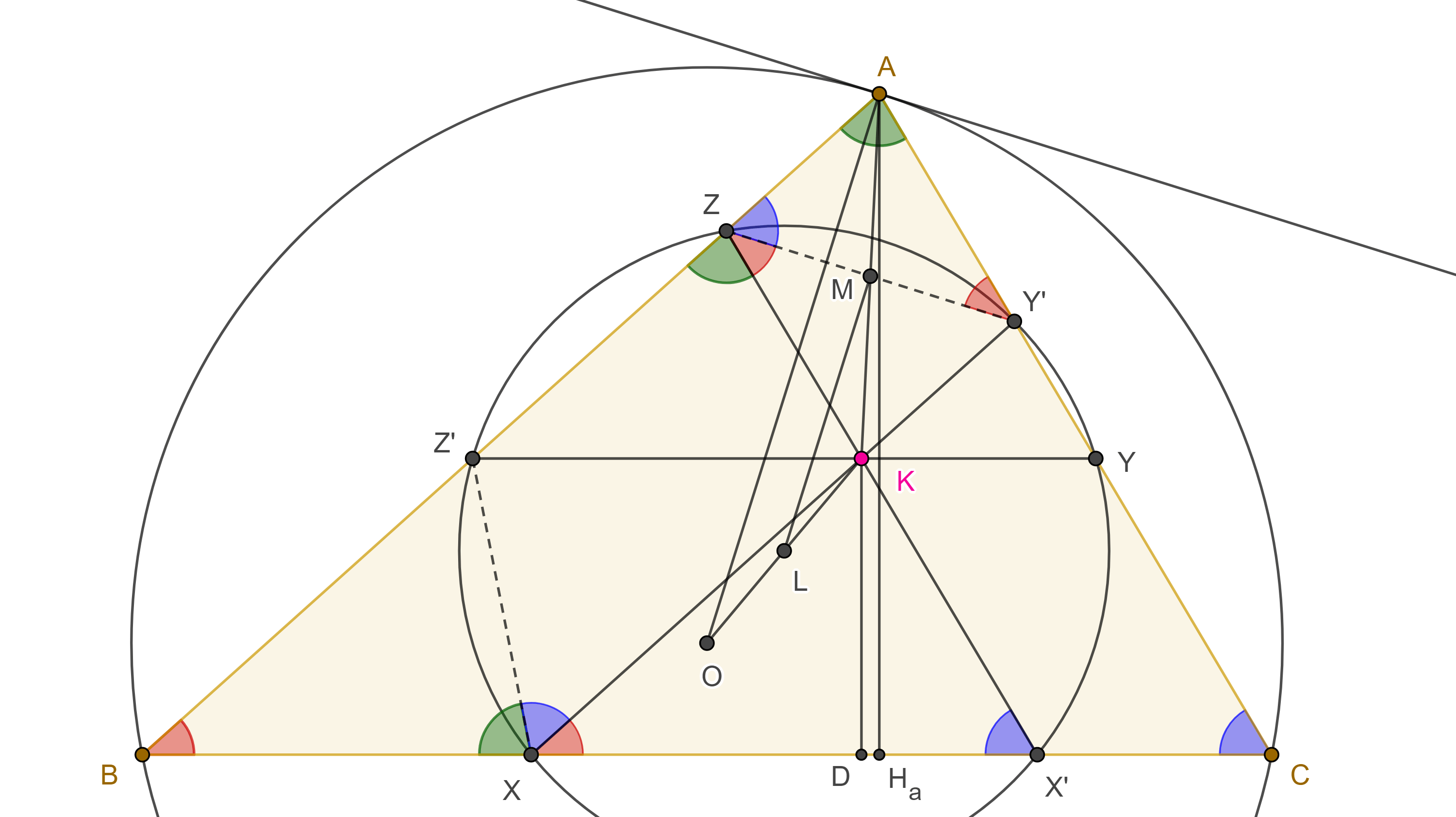
Demostración. En $△ A B C$ , sean $K$ el punto de Lemoine, $Z^{'} K Y ∥ B C$ , $X^{'} K Z ∥ C A$ , $Y^{'} K X ∥ A B$ , $X$ , $X^{'} \in B C$ , $Y$ , $Y^{'} \in C A$ , $Z$ , $Z^{'} \in A B$ .

Dado que $K Y^{'} ∥ A Z$ y $K Z ∥ A Y^{'}$ , $A Z K Y^{'}$ es paralelogramo, por lo tanto, $A K$ biseca a $Z Y^{'}$ , de esto se sigue que $Z Y^{'}$ es antiparalela a $B C$ respecto a $A B$ y $C A$ .

Como $Z^{'} Y ∥ B C$ , entonces $Z^{'} Y$ y $Z Y^{'}$ son antiparalelas respecto a $A B$ y $C A$ , es decir, $Z Z^{'} Y Y^{'}$ es cíclico.

Igualmente podemos ver qué $X Z^{'}$ , $C A$ son antiparalelas respecto a $A B$ , $B C$ y que $Z^{'} X X^{'} Z^{'}$ es cíclico.

Como $Z^{'} Y ∥ B C$ y $Z Z^{'} Y Y^{'}$ es cíclico entonces $∠ Z^{'} Z Y^{'} = ∠ A + ∠ B$ .

Como $X Z^{'}$ y $C A$ son antiparalelas entonces $∠ Z^{'} X B = ∠ A$ , ya que $A B ∥ X Y^{'}$ tenemos que $∠ C X Y^{'} = ∠ B$ , por lo anterior tenemos que $∠ Y^{'} X Z^{'} = ∠ C$ .

Entonces, como los ángulos $∠ Y^{'} X Z^{'}$ , $∠ Z^{'} Z Y^{'}$ son suplementarios, $Z^{'} X Y^{'} Z$ es cíclico, por lo tanto, $X$ , $Y$ , $Y^{'}$ , $Z$ , $Z^{'}$ , están en la misma circunferencia.

Finalmente, como $X^{'}$ esta en el circuncírculo de $△ X Z Z^{'}$ entonces el hexágono $X Y^{'} Z X^{'} Y Z^{'}$ es cíclico.

Proposición 1. El centro de la primera circunferencia de Lemoine es el punto medio entre el circuncentro y el punto de Lemoine.

Demostración. En la figura 1, del teorema anterior, sean $O$ el circuncentro de $△ A B C$ y $M = A K \cap Z Y^{'}$ , considera $L$ el punto medio de $K O$ , con $K$ el punto de Lemoine.

Como $A Z K Y^{'}$ es paralelogramo, entonces $M$ es punto medio de $A K$ y $Z Y^{'}$ .

En $△ A O K$ , $L M$ es un segmento medio, por lo tanto, $M L ∥ A O$ .

Ya que $Z Y^{'}$ , $B C$ son antiparalelas respecto a $A B$ , $C A$ , entonces $Z Y^{'}$ es paralela a la tangente al circuncírculo de $△ A B C$ por $A$ , por lo tanto, $A O ⊥ Z Y^{'}$ .

En consecuencia, $M L ⊥ Z Y^{'}$ , como $M$ es el punto medio de $Z Y^{'}$ entonces $L$ esta en la mediatriz de $Z Y^{'}$ .

Igualmente vemos que $L$ esta en la mediatriz de $X Z^{'}$ , $Y X^{'}$ , por lo tanto, $L$ es el centro de la primera circunferencia de Lemoine.

Proposición 2. Las cuerdas de la primera circunferencia de Lemoine, contenidas en los lados del triángulo, son proporcionales a los cubos de dichos lados.

Demostración. Sean $D$ y $H_{a}$ las proyecciones de $K$ y $A$ en $B C$ respectivamente (figura 1), como $Y^{'} X ∥ A B$ y $X^{'} Z ∥ C A$ entonces $△ A B C$ y $△ K X X^{'}$ son semejantes.

Por lo tanto,
$\frac{X X^{'}}{B C} = \frac{K D}{A H_{a}}$
$= \frac{B C \times 2 (△ A B C)}{A B^{2} + B C^{2} + C A^{2}} \times \frac{B C}{2 (△ A B C)}$ .

Donde la segunda igualdad se sigue del corolario 2 de la entrada anterior y de considerar el área de $△ A B C$ .

$\Rightarrow X X^{'} = \frac{B C^{3}}{A B^{+} B C^{2} + C A^{2}}$ .

De manera similar se ve que
$Y Y^{'} = \frac{C A^{3}}{A B^{+} B C^{2} + C A^{2}}$ ,
$Z Z^{'} = \frac{A B^{3}}{A B^{+} B C^{2} + C A^{2}}$ .

Segunda circunferencia de Lemoine

Teorema 2. Si por el punto simediano $K$ de un triángulo trazamos antiparalelas a los lados del triángulo, entonces estas tres antiparalelas intersecan a los lados del triángulo en seis puntos cíclicos con centro en $K$ , a dicha circunferencia se le conoce como segunda circunferencia de Lemoine.

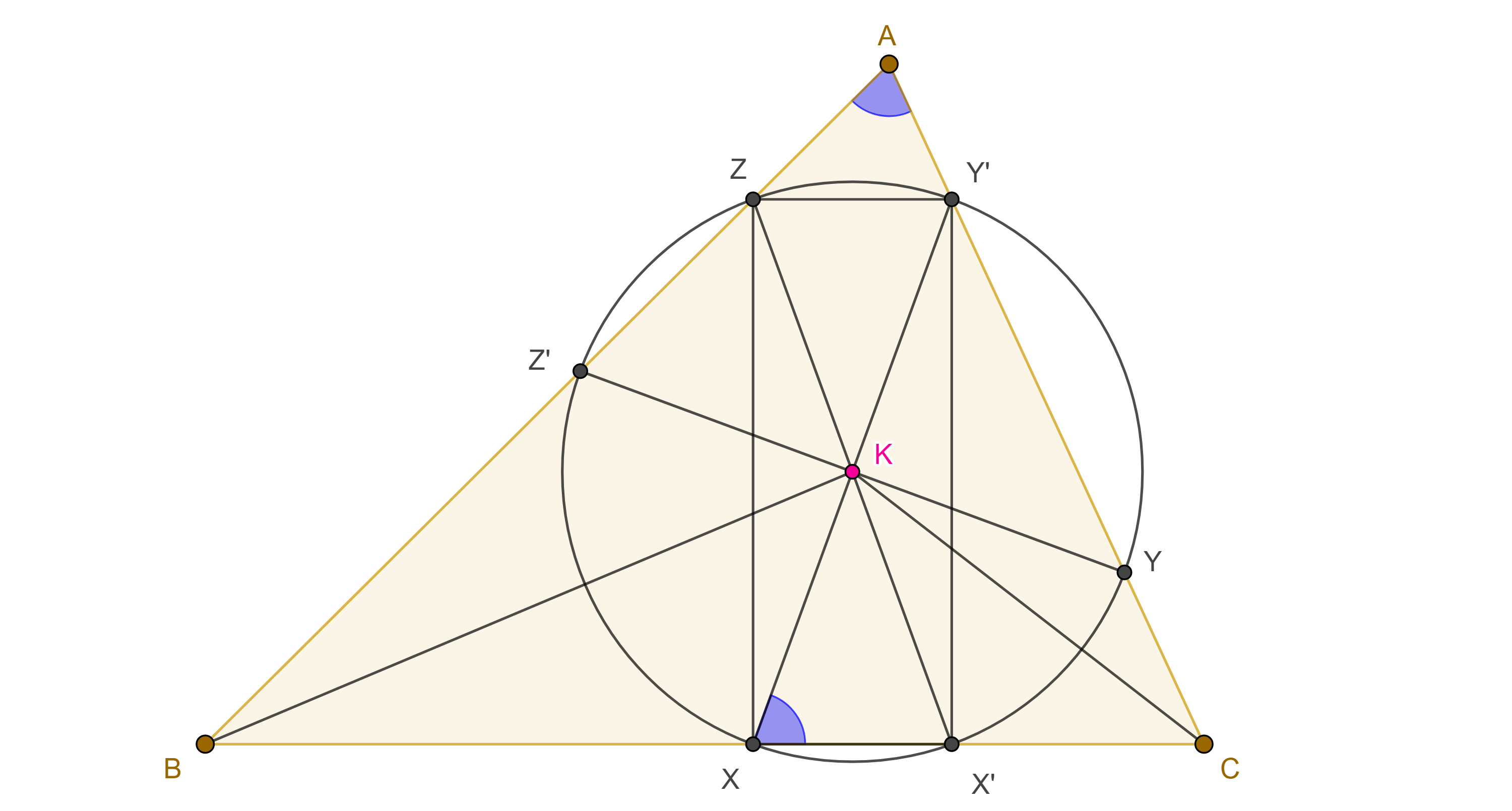
Demostración. En $△ A B C$ sean $K$ el punto de Lemoine, $Z^{'} K Y$ antiparalela a $B C$ respecto a $A B$ y $C A$ , $X^{'} K Z$ antiparalela a $C A$ respecto a $A B$ y $B C$ , $Y^{'} K X$ antiparalela a $A B$ respecto a $B C$ y $C A$ , $X$ , $X^{'} \in B C$ , $Y$ , $Y^{'} \in C A$ , $Z$ , $Z^{'} \in A B$ .

Como $X^{'} Z$ y $C A$ son antiparalelas, entonces $B K$ biseca a $X^{'} Z$ , de manera análoga vemos que $C K$ biseca a $Y^{'} X$ .

Dado que las antiparalelas $X^{'} Z$ e $Y^{'} X$ se intersecan en la $A$ -simediana, entonces son iguales en magnitud.

Como resultado, concluimos que $X X^{'} Y^{'} Z$ es un rectángulo, por lo tanto, $X$ , $X^{'}$ , $Y^{'}$ , $Z$ , están en una circunferencia con centro en $K$ .

Igualmente podemos ver que $A K$ biseca a $Y Z^{'}$ y que $X Y^{'} = Y Z^{'} = Z X^{'}$ .

Por lo tanto, el hexágono $X Y^{'} Z X^{'} Y Z^{'}$ es cíclico.

Proposición 4. Las cuerdas de la segunda circunferencia de Lemoine, contenidas en los lados del triángulo son proporcionales a los cosenos de los ángulos opuestos a dichos lados, razón por la cual también es conocida como circunferencia de los cosenos.

Demostración. Dado que $Y^{'} X$ y $A B$ son antiparalelas respecto a $B C$ y $C A$ (figura 2), entonces $∠ X^{'} X Y^{'} = ∠ A$ .

Como $△ Y^{'} X^{'} X$ es un triangulo rectángulo, entonces $\cos ∠ A = \cos ∠ X^{'} X Y^{'} = \frac{X X^{'}}{Y^{'} X}$ .

Como $Y^{'} X = X^{'} Z = Z^{'} Y = q$ , entonces $X X^{'} = q \cos ∠ A$ .

Igualmente podemos ver que $Y Y^{'} = q \cos ∠ B$ y $Z Z^{'} = q \cos ∠ C$ .

Circunferencia de Tucker

Teorema 3. Si aplicamos una homotecia a un triángulo con centro en su punto de Lemoine entonces los lados del triángulo imagen cortaran a los lados del triángulo original en seis puntos cíclicos, a esta circunferencia se le conoce como circunferencia de Tucker.

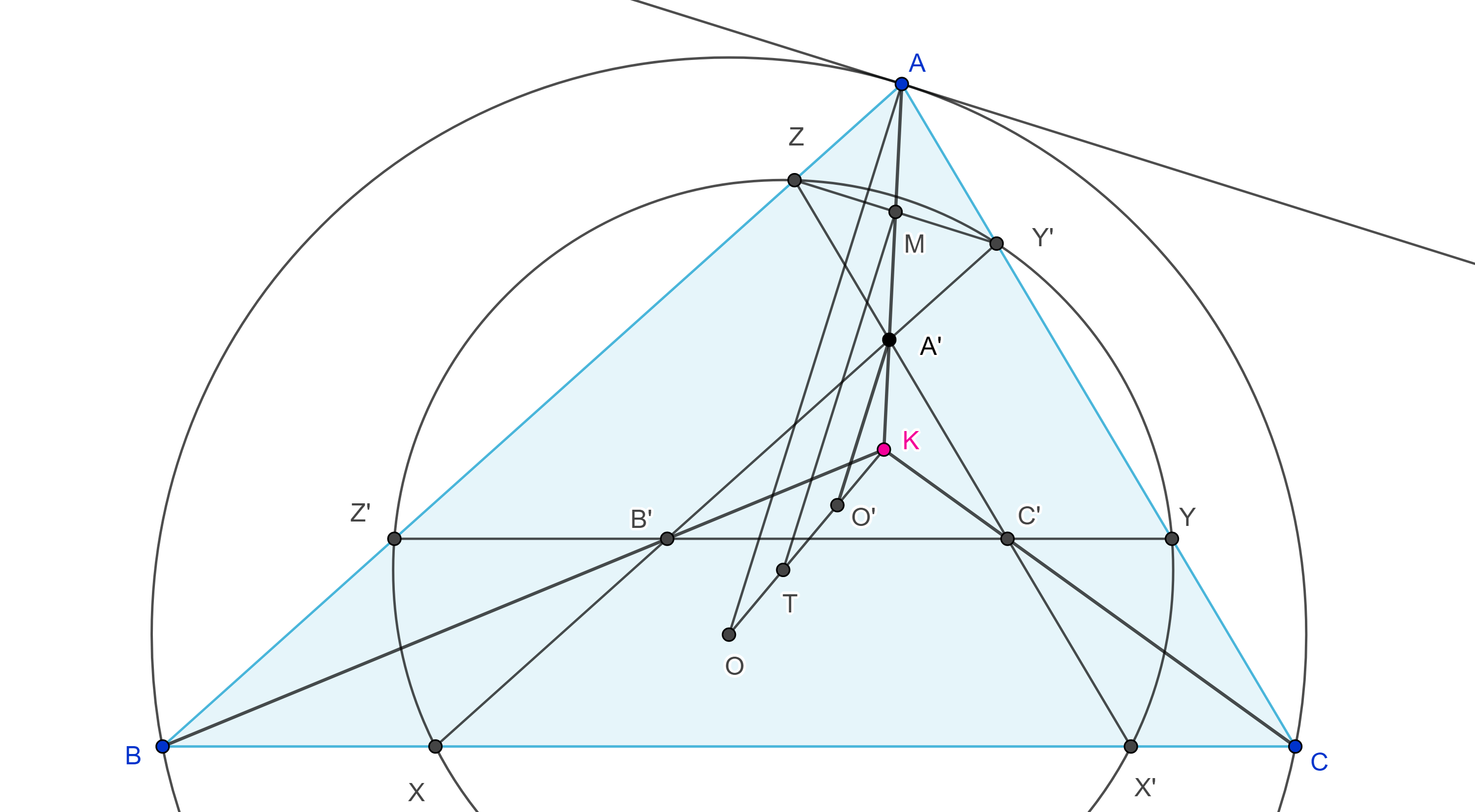
Demostración. Sea $K$ el punto de Lemoine de $△ A B C$ y $△ A^{'} B^{'} C^{'}$ su imagen bajo una homotecia con centro en $K$ , entonces los lados correspondientes son paralelos.

Sean $X$ , $X^{'}$ las intersecciones de $A^{'} B^{'}$ y $C^{'} A^{'}$ con $B C$ , $Y$ , $Y^{'}$ las intersecciones de $B^{'} C^{'}$ y $A^{'} B^{'}$ con $C A$ , $Z$ , $Z^{'}$ las intersecciones de $C^{'} A^{'}$ y $B^{'} C^{'}$ con $A B$ .

Como $A Z A^{'} Y^{'}$ es un paralelogramo entonces $A K$ biseca $Y^{'} Z$ , por lo tanto $Y^{'} Z$ es antiparalela a $B C$ respecto a $A B$ , $C A$ .

De manera análoga, los pares de rectas $X Z^{'}$ , $C A$ ; $Y X^{'}$ , $A B$ son antiparalelas.

A partir de aquí la demostración es igual a la del teorema 1.

Proposición 5. El centro de la circunferencia de Tucker se encuentra en la recta que une al punto de Lemoine con el circuncentro del triángulo.

Demostración. Sean $O$ el circuncentro de $△ A B C$ y $M$ el punto medio de $Y^{'} Z$ (figura 3), como $△ A B C$ y $△ A^{'} B^{'} C^{'}$ son homotéticos la paralela por $A^{'}$ a $A O$ interseca a $K O$ en $O^{'}$ el circuncentro de $△ A^{'} B^{'} C^{'}$ .

Por $M$ trazamos una paralela a $A O$ que interseca a $K O$ en $T$ .

Como $A^{'} O^{'} ∥ M T$ entonces $\frac{K A^{'}}{A^{'} M} = \frac{K O^{'}}{O^{'} T}$ .

Como $A O ∥ M T$ entonces $\frac{K M}{M A} = \frac{K T}{T O}$ .

Pero
$\frac{K M}{K T} = \frac{K A^{'} + A^{'} M}{K O^{'} + O^{'} T}$
$= (\frac{A^{'} M \times K O^{'}}{O^{'} T} + A^{'} M) (\frac{1}{K O^{'} + O^{'} T})$
$= A^{'} M (\frac{K O^{'} + O^{'} T}{O^{'} T}) (\frac{1}{K O^{'} + O^{'} T}) = \frac{A^{'} M}{O^{'} T}$ .

Por lo tanto, como $M$ también es el punto medio de $A A^{'}$ por ser $A Z A^{'} Y^{'}$ paralelogramo, tenemos
$1 = \frac{A^{'} M}{M A} = \frac{O^{'} T}{T O}$ .

Es decir, $T$ es el punto medio de $O O^{'}$ .

Por otra parte $A O ⊥ Y^{'} Z$ , pues $Y^{'} Z$ es paralela a la tangente al circuncírculo de $△ A B C$ en $A$ , entonces $T M ⊥ Y^{'} Z$ .

Por lo tanto, $T$ esta en la mediatriz de $Y^{'} Z$ .

Igualmente vemos que $T$ esta en la mediatriz de $Z^{'} X$ , $X^{'} Y$ , en consecuencia, $T$ es el centro de la circunferencia de Tucker y está en la recta $K O$ .

Circunferencia de Taylor

Teorema 4. Dado un triángulo, las proyecciones de los vértices de su triángulo órtico en los lados del triángulo original están en una circunferencia de Tucker, a esta circunferencia se le conoce como circunferencia de Taylor.

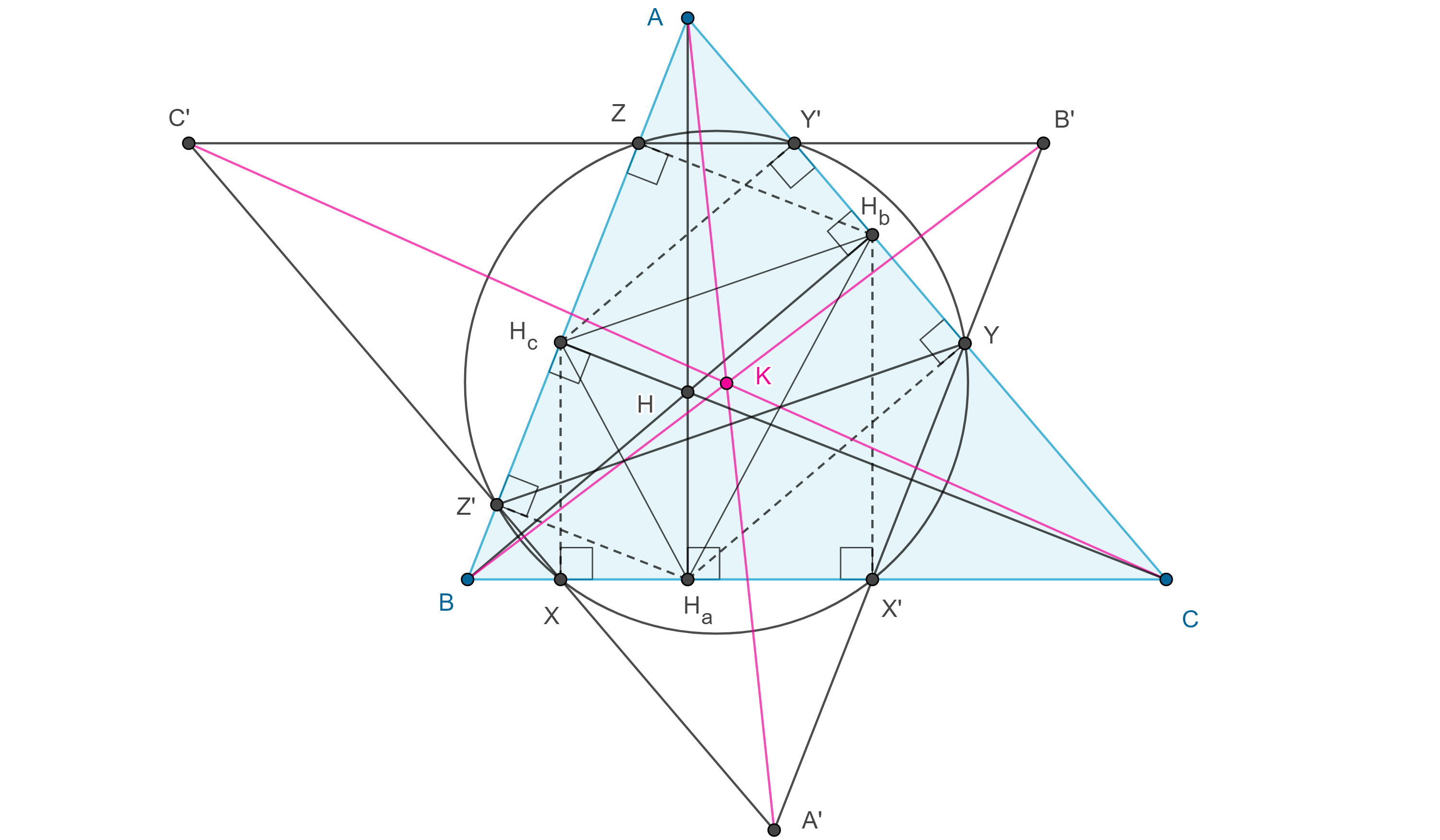
Demostración. Sea $△ A B C$ y $△ H_{a} H_{b} H_{c}$ su triangulo órtico, sean $X$ , $X^{'}$ las proyecciones de $H_{c}$ y $H_{b}$ en $B C$ , $Y$ , $Y^{'}$ las proyecciones de $H_{a}$ y $H_{c}$ en $C A$ , $Z$ , $Z^{'}$ las proyecciones de $H_{b}$ y $H_{a}$ en $A B$ .

$H_{c} B C H_{b}$ es cíclico pues $∠ B H_{c} C = ∠ B H_{b} C = \frac{π}{2}$ , así que $∠ H_{b} H_{c} Z = ∠ C$ .

$∠ Z H_{c} H_{b} Y^{'}$ también es cíclico pues $∠ H_{c} Z H_{b} = ∠ H_{c} Y^{'} H_{b} = \frac{π}{2}$ , así que $∠ A Y^{'} Z = ∠ H_{b} H_{c} Z = ∠ C$ .

Por lo tanto, $Z Y^{'} ∥ B C$ .

Igualmente vemos que $X Z^{'} ∥ C A$ y $Y X^{'} ∥ A B$ .

En consecuencia, el triángulo $△ A^{'} B^{'} C^{'}$ que se forma al extender $Z Y^{'}$ , $X Z^{'}$ , $Y X^{'}$ , es inversamente homotético con $△ A B C$ .

Sea $H$ el ortocentro de $△ A B C$ , como $H H_{c} ∥ H_{a} Z^{'}$ y $H H_{b} ∥ H_{a} Y$ , entonces
$\frac{H H_{c}}{H_{a} Z^{'}} = \frac{A H}{A H_{A}} = \frac{H H_{b}}{H_{a} Y}$ .

Por criterio de semejanza LAL, $△ H H_{c} H_{b} \sim △ H_{a} Z^{'} Y$ , por lo tanto, $Z^{'} Y ∥ H_{c} H_{b}$ .

De esto último y tomando en cuenta que $H_{c} B C H_{b}$ es cíclico, se sigue que $Z^{'} B C Y$ es cíclico, es decir $Z^{'} Y$ y $B C$ son antiparalelas respecto de $A B$ , $C A$ .

Por otra parte, $A Z^{'} A^{'} Y$ es paralelogramo, así que $A A^{'}$ biseca a $Z^{'} Y$ .

Esto implica que $A A^{'}$ es la $A$ -simediana de $△ A B C$ .

De manera análoga vemos que $B B^{'}$ y $C C^{'}$ son simedianas, por lo tanto, $A A^{'}$ , $B B^{'}$ , $C C^{'}$ concurren en el punto simediano $K$ de $△ A B C$ .

Por el teorema anterior, se sigue que $X$ , $X^{'}$ , $Y$ , $Y^{'}$ , $Z$ , $Z^{'}$ , están en una circunferencia de Tucker.

Más adelante…

En la siguiente entrada estudiaremos propiedades mas generales de rectas que como la mediana y la simediana, son reflexión respecto de la bisectriz de un ángulo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

En la figura 1, muestra que:
$i)$ $X^{'} Y = Y^{'} Z = Z^{'} X$ ,
$i i)$ el incírculo del triángulo que se forma al extender $X^{'} Y$ , $Y^{'} Z$ y $Z^{'} X$ , es concéntrico con la primer circunferencia de Lemoine de $△ A B C$ .
Muestra que si tres diámetros de una circunferencia tienen sus extremos en los lados de un triángulo, entonces dicha circunferencia es la segunda circunferencia de Lemoine del triángulo y su centro es el punto de Lemoine.
Muestra que el circuncírculo de un triángulo, la primera y la segunda circunferencias de Lemoine, son circunferencias de Tucker y encuentra la razón de homotecia con centro en el punto de Lemoine, que da origen a cada una.
Demuestra que el centro de la circunferencia de Taylor de un triángulo es el punto de Spieker de su triángulo órtico. En la figura 4, el incentro del triángulo medial de $△ H_{a} H_{b} H_{c}$ .
En la figura 4 demuestra que:
$i)$ el punto de Lemoine de $△ A B C$ coincide con el punto de Gergonne del triángulo medial de su triángulo órtico, $△ H_{a} H_{b} H_{c}$ ,
$i i)$ el punto de Nagel del triángulo órtico $△ H_{a} H_{b} H_{c}$ es colineal con el ortocentro y el circuncentro de $△ A^{'} B^{'} C^{'}$ ,
$i i i)$ las bisectrices internas del triángulo medial de $△ H_{a} H_{b} H_{c}$ , son perpendiculares a los lados de $△ A B C$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Punto simediano.
Siguiente entrada del curso: Rectas isogonales.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 257-260, 284-287.
Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 87-98.
Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 271-277.
Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 76-79.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Simediana

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

La simediana es un tipo especial de ceviana relacionada con la mediana de un triángulo, veremos algunas caracterizaciones y propiedades.

Simediana, primera caracterización

Definición 1. Una simediana de un triángulo es la reflexión de una mediana respecto de la bisectriz interna que pasa por el mismo vértice. Un triángulo tiene tres simedianas.

Notación. Denotaremos a la intersección de una simediana con el lado opuesto como $S$ .

Teorema 1. Una ceviana de un triángulo divide internamente al lado opuesto en la razón de los cuadrados de los lados adyacentes si y solo si es simediana.

Demostración. Sean $A A^{'}$ la mediana y $A S$ la simediana en un triángulo $△ A B C$ .

Sea $H$ el pie de la altura por $A$ , calculamos las áreas de los triángulos $△ B A S$ , $△ B A A^{'}$ , $△ S A C$ y $△ A^{'} A C$ .

$\begin{matrix} (1) & (△ B A S) = \frac{B S \times A H}{2} = \frac{B A \times A S \sin ∠ B A S}{2}, \end{matrix}$
$\begin{matrix} (2) & (△ B A A^{'}) = \frac{B A^{'} \times A H}{2} = \frac{B A \times A A^{'} \sin ∠ B A A^{'}}{2}, \end{matrix}$
$\begin{matrix} (3) & (△ S A C) = \frac{S C \times A H}{2} = \frac{S A \times A C \sin ∠ S A C}{2}, \end{matrix}$
$\begin{matrix} (4) & (△ A^{'} A C) = \frac{A^{'} C \times A H}{2} = \frac{A A^{'} \times A C \sin ∠ A^{'} A C}{2} . \end{matrix}$

Sea $L$ la intersección de la bisectriz de $A$ con $B C$ , entonces
$\begin{matrix} (5) & ∠ B A S = ∠ B A L - ∠ S A L = ∠ L A C - ∠ L A A^{'} = ∠ A^{'} A C, \end{matrix}$
$∠ B A A^{'} = ∠ B A L + ∠ L A A^{'} = ∠ L A C + ∠ S A L = ∠ S A C .$

Haciendo el cociente de $(1)$ con $(4)$ y de $(2)$ con $(3)$ obtenemos
$\frac{B S}{A^{'} C} = \frac{B A \times A S}{A A^{'} \times A C}$ ,
$\frac{B A^{'}}{S C} = \frac{B A \times A A^{'}}{S A \times A C}$ .

Multiplicando estas dos ecuaciones obtenemos el resultado esperado
$\frac{B S}{S C} = \frac{B A^{2}}{A C^{2}}$ .

El reciproco también es cierto, pues el punto $S$ que divide a $B C$ en la razón $\frac{B A^{2}}{A C^{2}}$ , es único.

Exsimediana

Definición 2. Las tangentes al circuncírculo de un triángulo por sus vértices se conocen como simedianas externas o exsimedianas.

Corolario. La simediana y la exsimediana que pasan por el mismo vértice de un triángulo son conjugadas armónicas respecto de los lados del triángulo que forman dicho vértice.

Demostración. En la entrada teorema de Menelao mostramos que la exsimediana de un triángulo divide externamente al lado opuesto en la razón de los cuadrados de los lados que pasan por el mismo vértice.

El resultado se sigue del hecho de que el conjugado armónico es único y el teorema 1.

Teorema 2. Una simediana y las exsimedianas que pasan por vértices distintos son concurrentes, al punto de concurrencia se le conoce como punto exsimediano.

Demostración. En $△ A B C$ , $A P$ y $C P$ son tangentes al circuncírculo $Γ$ de $△ A B C$ en $A$ y en $C$ respectivamente y se cortan en $P$ (figura 2).

Sea $D = B P \cap Γ$ , $D \neq B$ , por la proposición 5 de la entrada anterior, $A B C D$ es un cuadrilátero armónico.

Entonces, por el teorema 2 de la entrada anterior, el Haz $B (B C D A)$ es armónico, es decir, la tangente a $Γ$ en $B$ , y $B D$ son conjugadas armónicas respecto de $B A$ y $B C$ .

Como el conjugado armónico es único, $B P$ es simediana de $△ A B C$ , por el corolario anterior.

Antiparalelas (1)

Teorema 3. La $B$ -simediana de un triángulo $△ A B C$ es el lugar geométrico de los puntos que bisecan a las antiparalelas de $A C$ respecto a $A B$ y $B C$ .

Demostración. Sean $D \in A B$ y $E \in B C$ tales que $A C$ y $D E$ son antiparalelas respecto a $A B$ y $B C$ , entonces $A D E C$ es cíclico.

Por lo tanto, $∠ A C E$ y $∠ E D A$ son suplementarios, en consecuencia, $∠ A C B = ∠ A C E = ∠ B D E$ .

Sea $T B$ tangente al circuncírculo de $△ A B C$ en $B$ , entonces $∠ A B T = ∠ A C B$ pues abarcan el mismo arco, por lo tanto, la $B$ -exsimediana y $D E$ son paralelas.

Sea $B S$ una ceviana de $△ A B C$ , entonces por la proposición 2 de la entrada anterior $B S$ biseca a $D E$ si y solo si el haz $B (T C S A)$ es armónico.

En consecuencia, como el conjugado armónico de $B T$ respecto de $B C$ y $B A$ es la $B$ -simediana, $B S$ biseca a $D E$ si y solo si $B S$ es simediana de $△ A B C$ .

Antiparalelas (2)

Proposición. 1 Si dos antiparalelas a dos de los lados de un triángulo tienen la misma longitud, entonces estas se intersecan en la simediana relativa al tercer lado, el reciproco también es cierto.

Demostración. Sean $△ A B C$ , $E$ , $G \in B C$ , $F \in A B$ y $H \in C A$ , tales que $E F$ , $A C$ son antiparalelas respecto a $A B$ y $B C$ ; $A B$ , $G H$ son antiparalelas respecto a $B C$ y $C A$ , y $E F = G H$ .

Como $A F E C$ y $A B G H$ son cíclicos, entonces, $∠ F E B = ∠ B A C = ∠ C G H$ , por lo tanto $P G = P E$ .

Sea $P = E F \cap G H$ , dado que $F E = G H$ entonces $F P = H P$ .

Si $S = A P \cap B C$ , considera $I \in A B$ , $J \in C A$ , tales que $I S ∥ F E$ y $J S ∥ G H$ , entonces $△ A S I \sim △ A P F$ y $△ A S J \sim △ A P H$ .

Por lo tanto, $\frac{S I}{P F} = \frac{A S}{A P} = \frac{S J}{P H}$ , como $P F = P H$ entonces $S I = S J$ .

Por otro lado $△ S B I \sim △ A B C \sim △ S J C$ , esto es
$\frac{S B}{S I} = \frac{A B}{A C}$ y $\frac{S J}{S C} = \frac{A B}{A C}$ .

Como resultado de multiplicar estas dos ecuaciones obtenemos
$\frac{B S}{S C} = \frac{A B^{2}}{A C^{2}}$ .

Por el teorema 1, esto implica que $A S$ es la $A$ -simediana de $△ A B C$ .

Notemos que el reciproco también es cierto, esto es, si dos antiparalelas a dos de los lados de un triángulo se intersecan en la simediana relativa al tercer lado, entonces estas tienen la misma longitud.

Esto lo podemos ver tomando la prueba anterior en sentido contrario.

Otra caracterización importante

Teorema 4. Una simediana es el lugar geométrico de los puntos (dentro de los ángulos internos del triángulo o sus ángulos opuestos por el vértice) tales que la razón de sus distancias a los lados adyacentes a la simediana, es igual a la razón entre esos lados.

Demostración. Sean $△ A B C$ , $A^{'}$ el punto medio de $B C$ y $P \in A A^{'}$ , considera las proyecciones $P_{c}$ , $P_{b}$ de $P$ en $A B$ y $A C$ respectivamente y $A_{c}^{'}$ , $A_{b}^{'}$ , las correspondientes de $A^{'}$ .

Como $△ A P P_{c} \sim △ A A^{'} A_{c}^{'}$ y $△ A P P_{b} \sim △ A A^{'} A_{b}^{'}$ entonces
$\frac{P P_{c}}{A^{'} A_{c}^{'}} = \frac{A P}{A A^{'}} = \frac{P P_{b}}{A^{'} A_{b}^{'}}$ .

Tomando en cuenta que los triángulos $△ A B A^{'}$ y $△ A A^{'} C$ tienen la misma altura desde $A$ , tenemos lo siguiente:
$\frac{A C}{A B} = \frac{P P_{c}}{P P_{b}} = \frac{A^{'} A_{c}^{'}}{A^{'} A_{b}^{'}}$
$\Leftrightarrow A C \times A^{'} A_{b}^{'} = A B \times A^{'} A_{c}^{'}$
$\Leftrightarrow (△ A A^{'} C) = (△ A A^{'} B)$
$\Leftrightarrow A^{'} C = B A^{'}$ .

Por lo tanto, la mediana de un triángulo es el lugar geométrico de los puntos tales que la razón de sus distancias a los lados adyacentes a la mediana es el inverso de la razón entre dichos lados.

Denotamos la distancia de un punto $P$ a una recta $l$ como $d (P, l)$ .

Para $P \in A A^{'}$ considera $P^{'} \in A S$ su reflexión respecto de la bisectriz de $∠ B A C$ , entonces

$\frac{d (P^{'}, A B)}{d (P^{'}, A C)} = \frac{d (P, A C)}{d (P^{'}, A B)} = \frac{A B}{A C}$ .

Proposición 2. La recta que une las proyecciones de un punto en la simediana (mediana) de un triángulo, sobre los lados adyacentes, es perpendicular a la mediana (simediana) que pasa por el mismo vértice.

Demostración. En un triángulo $△ A B C$ sean $A A^{'}$ la mediana y $A S$ la simediana, considera $P \in A S$ y $D$ , $E$ , las proyecciones de $P$ en $C A$ y $A B$ respectivamente.

Como $∠ P E A + ∠ A D P = π$ entonces $A E P D$ es cíclico, así que $∠ E A P = ∠ E D P$ , por la ecuación $(5)$ , $∠ E A P = ∠ A^{'} A D$ .

Sean $F = P D \cap A A^{'}$ y $G = D E \cap A A^{'}$ , en los triángulos $△ A D F$ y $△ D G F$ , $∠ F A D = ∠ G D F$ y $∠ D F G$ es un ángulo común, por lo tanto son semejantes.

Como $P D ⊥ A C$ entonces $D E ⊥ A A^{'}$ .

El caso para la mediana es análogo.

Más adelante…

Así como las medianas de un triángulo son concurrentes, las simedianas también son concurrentes, pero dicho punto tiene propiedades importantes por si mismo, y de eso hablaremos en la próxima entrada.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Muestra que las segundas intersecciones de una mediana y su correspondiente simediana con el circuncírculo del triángulo, determinan una recta paralela al lado del triángulo relativo a la mediana considerada.
Sea $△ A B C$ un triángulo acutángulo, $D$ y $A^{'}$ las proyecciones de $A$ y $O$ , el circuncírculo de $△ A B C$ , en $B C$ respectivamente, sean $E = B O \cap A D$ , $F = C O \cap A D$ y considera $P$ el segundo punto en común entre los circuncírculos de $△ A B E$ y $△ A F C$ , demuestra que $A P$ es la $A$ -simediana de $△ A B C$ .
Sea $P$ un punto dentro de un triángulo isósceles $△ A B C$ con $A B = A C$ , tal que $∠ P B C = ∠ A C P$ , si $A^{'}$ es el punto medio de $B C$ , muestra que $∠ B P A^{'}$ y $∠ C P A$ son suplementarios.
Sean $△ A B C$ , $D \in A B$ y $E \in C A$ tal que $D E ∥ B C$ , considera $P = B E \cap C D$ , los circuncírculos de $△ B D P$ y $△ C E P$ se intersecan en $P$ y $Q$ , muestra que $∠ B A Q = ∠ P A C$ .
La $A$ -simediana $A S$ y la $A$ -meidnana $A A^{'}$ de un triángulo $△ A B C$ intersecan otra vez a su circuncírculo en $S^{'}$ y $L$ respectivamente, prueba que la rectas de Simson de $S^{'}$ y $L$ son perpendiculares a $A A^{'}$ y a $A S$ respectivamente.
Muestra que las exsimedianas de un triángulo tienen la misma propiedad que se señala en el teorema 4 respecto a las simedianas, pero esta vez para los puntos dentro de los ángulos externos del triángulo.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Haz armónico.
Siguiente entrada del curso: Punto simediano.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 247-252.
Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 86-92.
Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 129-145.
Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 66-70.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: rectas antiparalelas

Geometría Moderna I: Circunferencias de Lemoine

Introducción

Primera circunferencia de Lemoine

Segunda circunferencia de Lemoine

Circunferencia de Tucker

Circunferencia de Taylor

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Geometría Moderna I: Simediana

Introducción

Simediana, primera caracterización

Exsimediana

Antiparalelas (1)

Antiparalelas (2)

Otra caracterización importante

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos