Introducción
Si trazamos perpendiculares a los lados de un triángulo desde un punto en el plano lo más probable es que los puntos de intersección sean los vértices de un triángulo, en esta entrada veremos bajo que condición estos puntos son colineales, a dicha recta se le conoce como recta de Simson.
Recta de Simson
Teorema 1, de Simson. Los pies de las perpendiculares desde un punto en el plano a los lados de un triángulo son colineales si y solo si el punto está en el circuncírculo del triángulo.
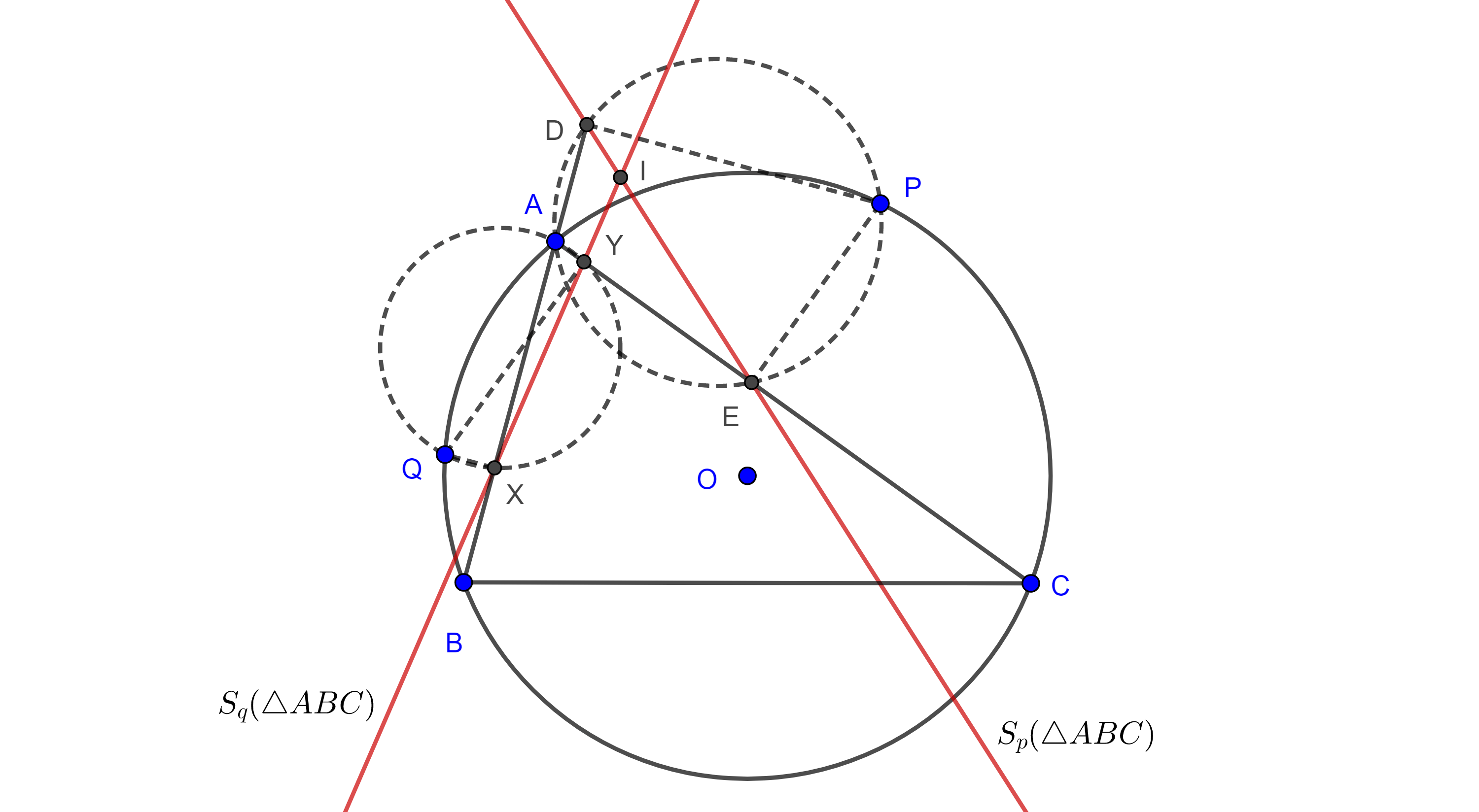
Demostración. Sea $\triangle ABC$ y $P$ un punto dentro del ángulo $\angle CBA$, consideremos $D$, $E$ y $F$ las proyecciones de $P$ en $AB$, $BC$ y $AC$ respectivamente, sean $\Gamma_1$ y $\Gamma_2$ las circunferencias cuyos diámetros son $PA$ y $PC$ respectivamente.
Como $AP$ subtiende ángulos rectos en $D$ y $F$ entonces $D$, $F \in \Gamma_1$, de manera análoga vemos que $F$, $E \in \Gamma_2$.
Supongamos que $P$ está en el arco $\overset{\LARGE{\frown}}{CA}$ del circuncírculo de $\triangle ABC$ que no contiene a $B$, entonces,
$\angle PFD = \angle PAD$ pues abarcan el mismo arco en $\Gamma_1$ además $\angle PAD = \pi – \angle BAP$ pues $B$, $A$ y $D$ son colineales.
Ya que $\square PFEC$ es cíclico, $\angle EFP = \pi – \angle PCE = \pi – \angle PCB$.
Como $\square ABCP$ es cíclico entonces $\angle BAP + \angle PCB = \pi$, por lo tanto
$\angle EFP + \angle PFD = \pi – \angle PCB + \pi – \angle BAP$
$= 2\pi – (\angle PCB + \angle BAP) = \pi$
Por lo tanto, $D$, $E$ y $F$ son colineales.
$\blacksquare$
Ahora supongamos que $D$, $E$ y $F$ son colineales.
$\angle BAP = \pi – \angle PAD = \pi – \angle PFD$
$\angle PCB = \angle PCE = \pi – \angle EFP$
$\Rightarrow \angle BAP + \angle PCB =\pi$
Por lo tanto, $\square ABCP$ es cíclico.
$\blacksquare$
Definición. La recta $DEF$ del teorema anterior se conoce como recta de Simson de $P$ respecto a $\triangle ABC$, la denotaremos como $S_p(\triangle ABC)$ y diremos que $P$ es el polo de $S_p(\triangle ABC)$ respecto $\triangle ABC$.
Corolario. Si las perpendiculares desde un punto $P$ en el circuncírculo de $\triangle ABC$ a los lados $AB$, $BC$ y $AC$ intersecan otra vez al circuncírculo en $D’$, $E’$ y $F’$ respectivamente, entonces $AE’$, $BF’$ y $C E’$ son paralelas a $S_p(\triangle ABC)$.
Demostración. En la figura 1, $\angle PEF = \angle PCF$, pues abarcan el mismo arco en $\Gamma_2$, $\angle PCF = \angle PCA = \angle PE’A$ pues abarcan el mismo arco en el circuncírculo de $\triangle ABC$.
$\Rightarrow \angle PEF = \angle PE’A$.
Como los ángulos correspondientes son iguales entonces $AE’ \parallel FE$.
$\blacksquare$
La recta de Simson y el ortocentro
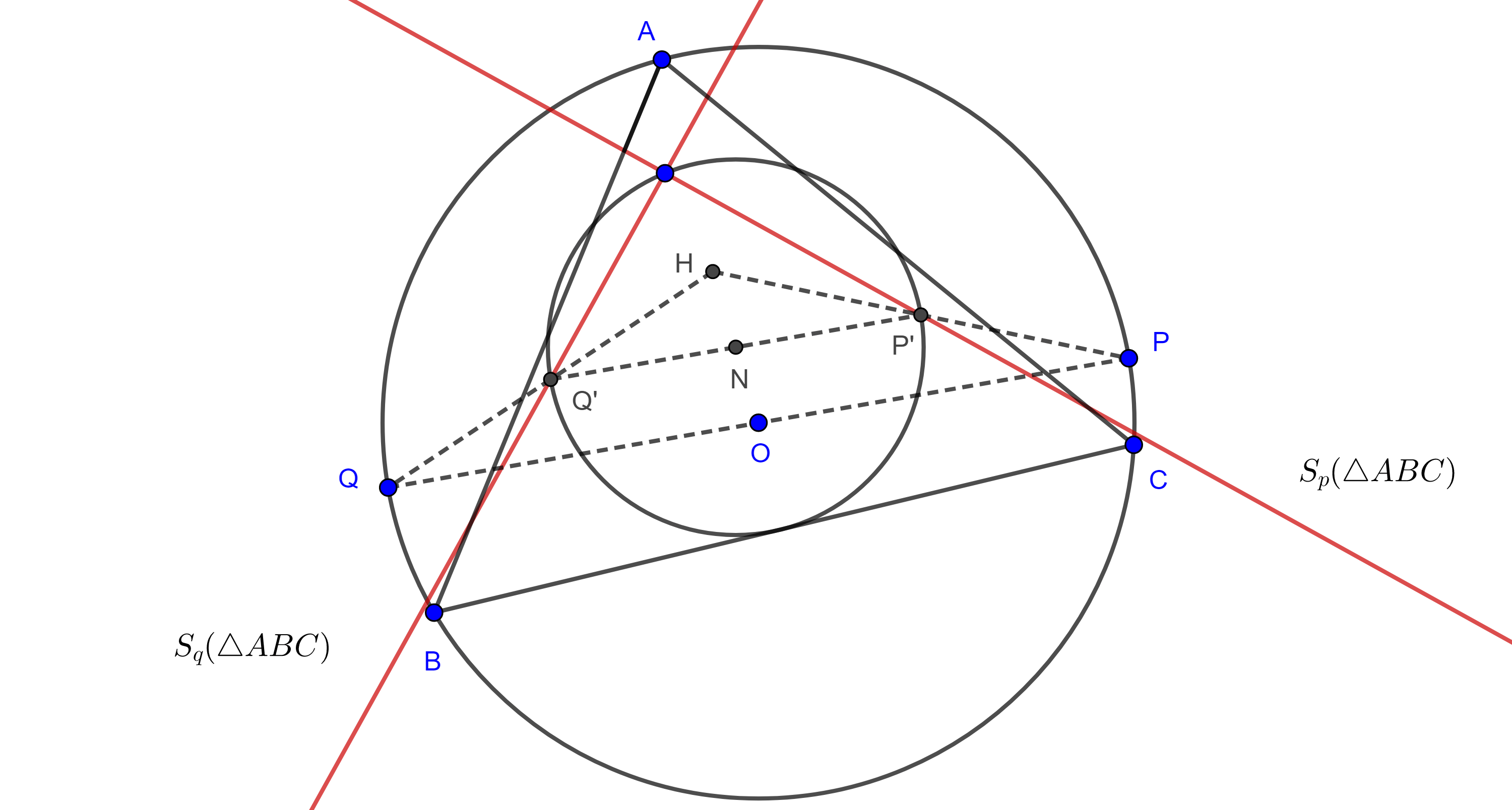
Teorema 2. La recta de Simson de un punto biseca el segmento que une al polo con el ortocentro del triángulo.
Demostración. Sea $H$ el ortocentro de $\triangle ABC$, $A’$ la segunda intersección de $AH$ con el circuncírculo de $\triangle ABC$, $\Gamma(O)$ y $P \in \Gamma(O)$.
Consideremos $D$ el pie de la altura por $A$, $G = PA’ \cap BC$, $E$ y $F$ las proyecciones de $P$ en $BC$ y $AC$ respectivamente.
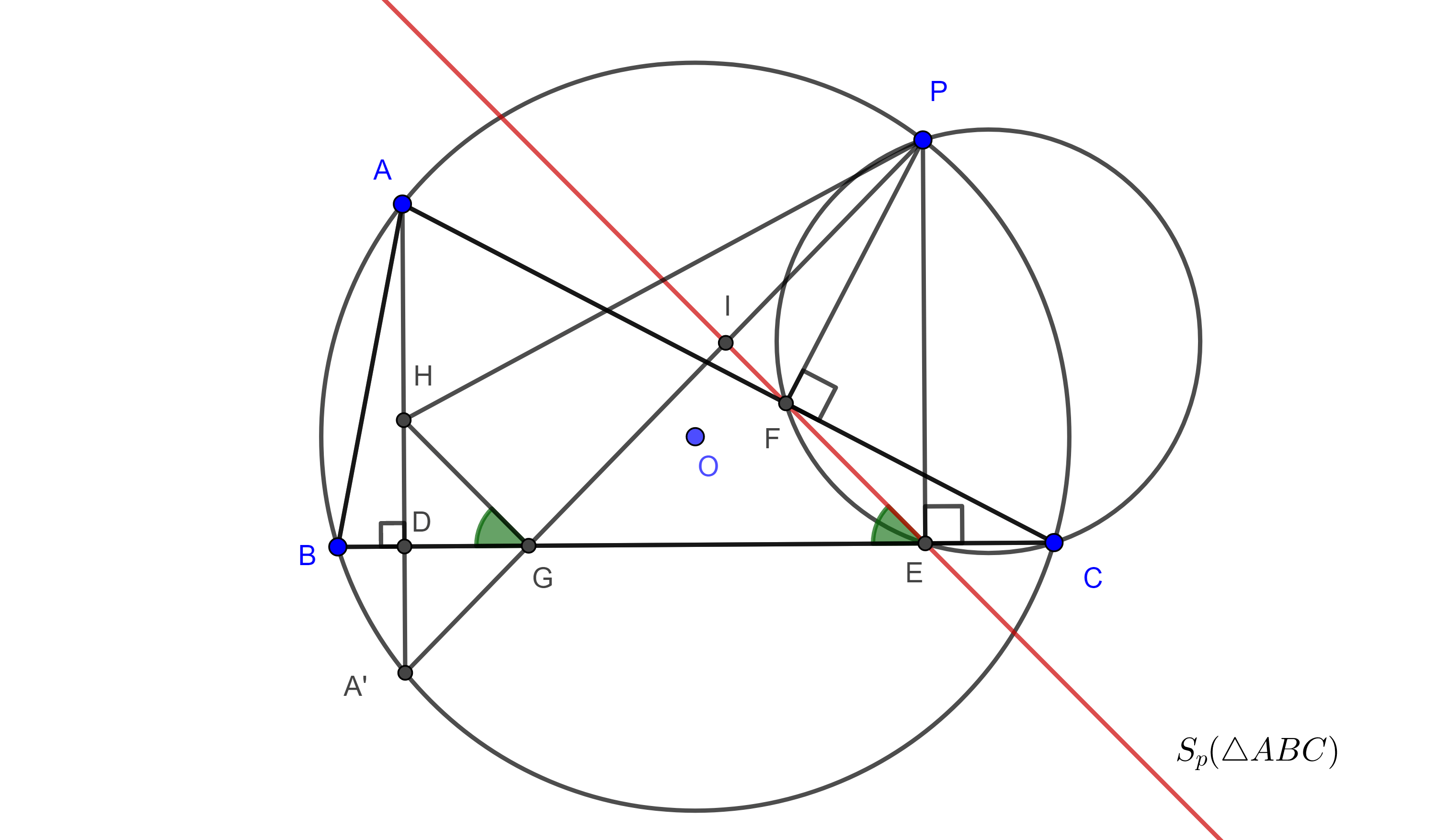
Ya que $D$ es el punto medio de $HA’$, entonces $BC$ es mediatriz de $HA’$ y así $\triangle HGA’$ es isósceles.
Considerando los triángulos rectángulos $\triangle A’GD$, $\triangle PGE$ y que $\square ABCP$, $\square PFEC$ son cíclicos tenemos lo siguiente:
$\angle HGD = \angle DGA’ = \dfrac{\pi}{2} – \angle GA’D $
$= \dfrac{\pi}{2} – \angle PA’A = \dfrac{\pi}{2} – \angle PCA$
$= \dfrac{\pi}{2} – \angle PCF = \dfrac{\pi}{2} – \angle PEF = \angle FED$.
Como los ángulos correspondientes son iguales entonces, $HG \parallel FE$.
Por otro lado, sea $I = PA’ \cap EF$, entonces
$\angle IEG = \angle HGD = \angle DGA’ = \angle EGI$
$\Rightarrow IG = IE$.
Como $\triangle PEG$ es rectángulo, entonces $\angle GPE$, $\angle EGP$ y $\angle PEI$ y $\angle IEG$ son pares de ángulos complementarios y como $\angle EGI = \angle IEG$, entonces $\angle IPE = \angle PEI$ $\Rightarrow IE =IP$.
En consecuencia, $I$ es el punto medio de $PG$.
Entonces en $\triangle PGH$, $FE$ pasa por el punto medio de $PG$ y es paralelo a $HG$.
Por el recíproco del teorema del segmento medio del triángulo, $FE$ biseca a $PH$.
$\blacksquare$
Ángulo entre rectas de Simson
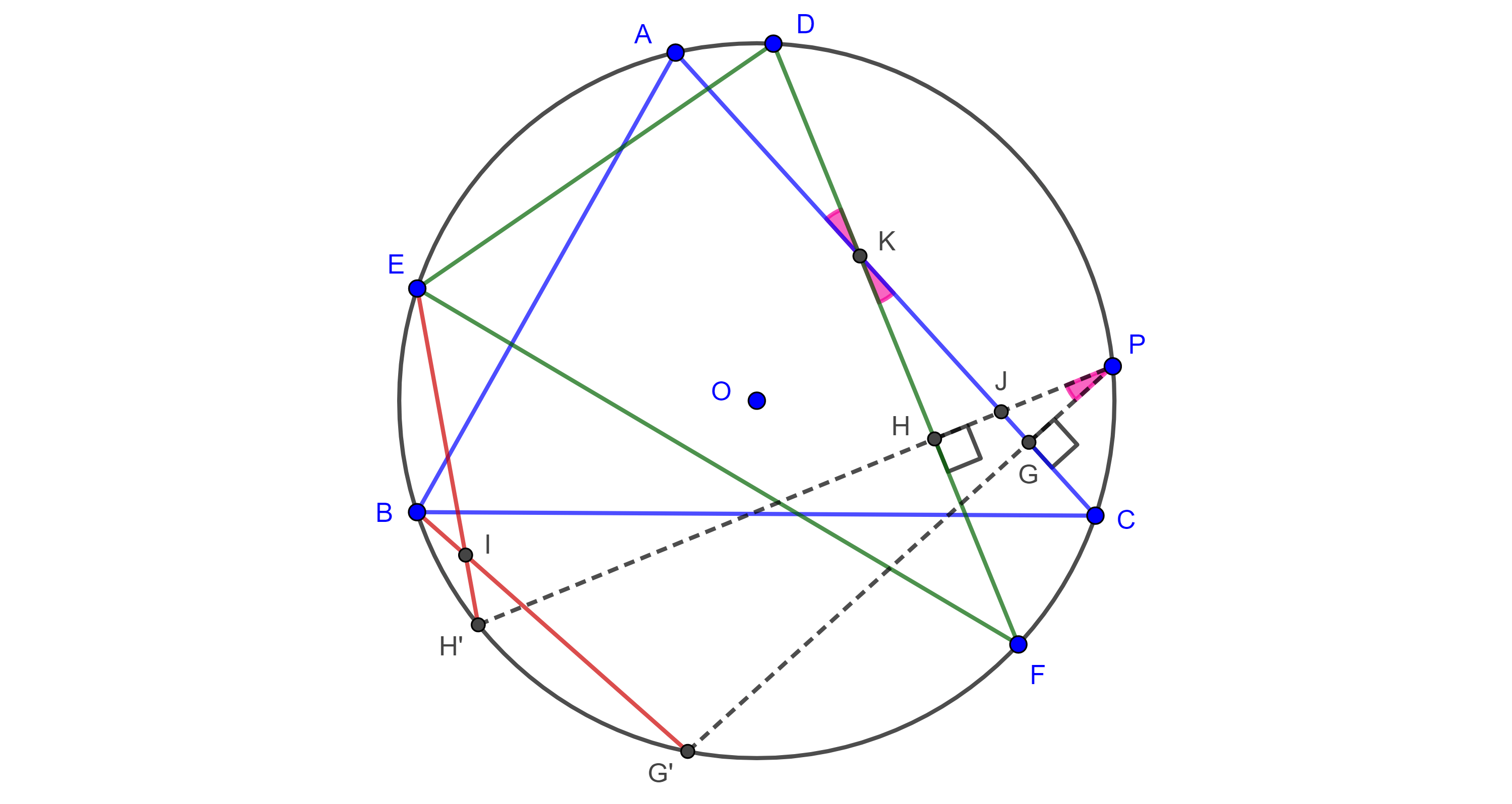
Teorema 3. El ángulo entre dos rectas de Simpson de dos puntos distintos respecto al mismo triangulo, es igual a la mitad del ángulo central formado por estos dos puntos en el circuncírculo del triángulo.
Demostración. Sean $P$ en el arco $\overset{\LARGE{\frown}}{CA}$ y $Q$ en el arco $\overset{\LARGE{\frown}}{AB}$ de $\Gamma(O)$, el circuncírculo de $\triangle ABC$, consideremos $D$, $E$ y $X$, $Y$ las correspondientes proyecciones de $P$ y $Q$ en $AB$ y $AC$ respectivamente.
Sea $I = DE \cap XY$, considerando los triángulos $\triangle DIX$, $\triangle APE$, $\triangle QAY$ y que $\square AEPD$, $\square AQXY$ son cíclicos tenemos lo siguiente:
$\angle DIY = \pi – \angle XDI – \angle IXD$
$= \pi – \angle ADE – \angle YXA = \pi – \angle APE – \angle YQA$
$= \pi – (\dfrac{\pi}{2} – \angle EAP) – (\dfrac{\pi}{2} – \angle QAY)$
$ = \angle QAC + \angle CAP = \angle QAP = \dfrac{\angle QOP}{2}$.
La última igualdad se da por el teorema del ángulo inscrito. Si P y Q están en el mismo arco la demostración es análoga.
$\blacksquare$
Teorema 4. Las rectas de Simson de dos puntos diametralmente opuestos en el circuncírculo de un triángulo, se intersecan en la circunferencia de los nueve puntos del triángulo.
Demostración. Sea $\triangle ABC$ y $PQ$ diámetro del circuncírculo $\Gamma(O)$ de $\triangle ABC$.
El ángulo central $\angle POQ$ es igual a $\pi$ y por el teorema 3, sus rectas de Simson son perpendiculares.
Recordemos que existe una homotecia con centro en el ortocentro $H$ de $\triangle ABC$, donde la imagen del circuncírculo de $\triangle ABC$ es la circunferencia de los nueve puntos $\Gamma(N)$ de $\triangle ABC$,
Por lo tanto esta homotecia lleva al diámetro $PQ$ del circuncírculo $\Gamma(O)$ en el diámetro $P’Q’$ de $\Gamma(N)$.
Por el teorema 2, $P’$ y $Q’$ son los puntos medios de los segmentos $HP$ y $HQ$ respectivamente, entonces las rectas de Simson de $P$ y $Q$, $S_p(\triangle ABC)$ y $S_q(\triangle ABC)$, pasan por $P’$ y $Q’$ respectivamente.
Como $S_p(\triangle ABC) \perp S_q(\triangle ABC)$ y $P’Q’$ es diámetro de $\Gamma(N)$, entonces $S_p(\triangle ABC) \cap S_q(\triangle ABC) \in \Gamma(N)$.
$\blacksquare$
Rectas de Simson de un punto respecto de dos triángulos
Teorema 5. Las rectas de Simson de un punto respecto de dos triángulos inscritos en la misma circunferencia forman un ángulo constante, independiente de la posición del punto en la circunferencia.
Demostración. Sean $\triangle ABC$ y $\triangle DEF$ inscritos en $\Gamma(O)$ y $P \in \Gamma(O)$.
Consideremos $G$ y $H$, las proyecciones de $P$ en $AC$ y $DF$ respectivamente, y sean $G’ = PG \cap \Gamma(O)$, $H’ = PH \cap \Gamma(O)$.
Por el corolario, $BG’$ y $EH’$, son paralelas $S_p(\triangle ABC)$ y $S_p(\triangle DEF)$ respectivamente, por lo que el ángulo entre $BG’$ y $EH’$ es el ángulo entre las rectas de Simson.
Sean $I = BG’ \cap EH’$, $J$ y $K$ las intersecciones de $AC$ con $PH$ y $DF$ respectivamente.
Entonces $\angle JPG$, $\angle GJP$ y $\angle HKJ$, $\angle KJH$ son pares de ángulos complementarios en $\triangle PGJ$ y $\triangle KHJ$ respectivamente, pero $\angle GJP = \angle KJH$ por ser opuestos por el vértice.
Por lo tanto,
$\angle H’PG’ = \angle JPG = \angle HKJ$
$= \angle FKC = \dfrac{\angle FOC + \angle DOA}{2}$.
Finalmente,
$\angle EIB = \dfrac{\angle EOB + \angle H’OG’}{2}$
$= \dfrac{\angle EOB}{2} + \angle H’PG’$
$= \dfrac{\angle EOB + \angle FOC + \angle DOA}{2}$.
Estos ángulos son independientes de $P$.
$\blacksquare$
Cuadrángulo ortocéntrico
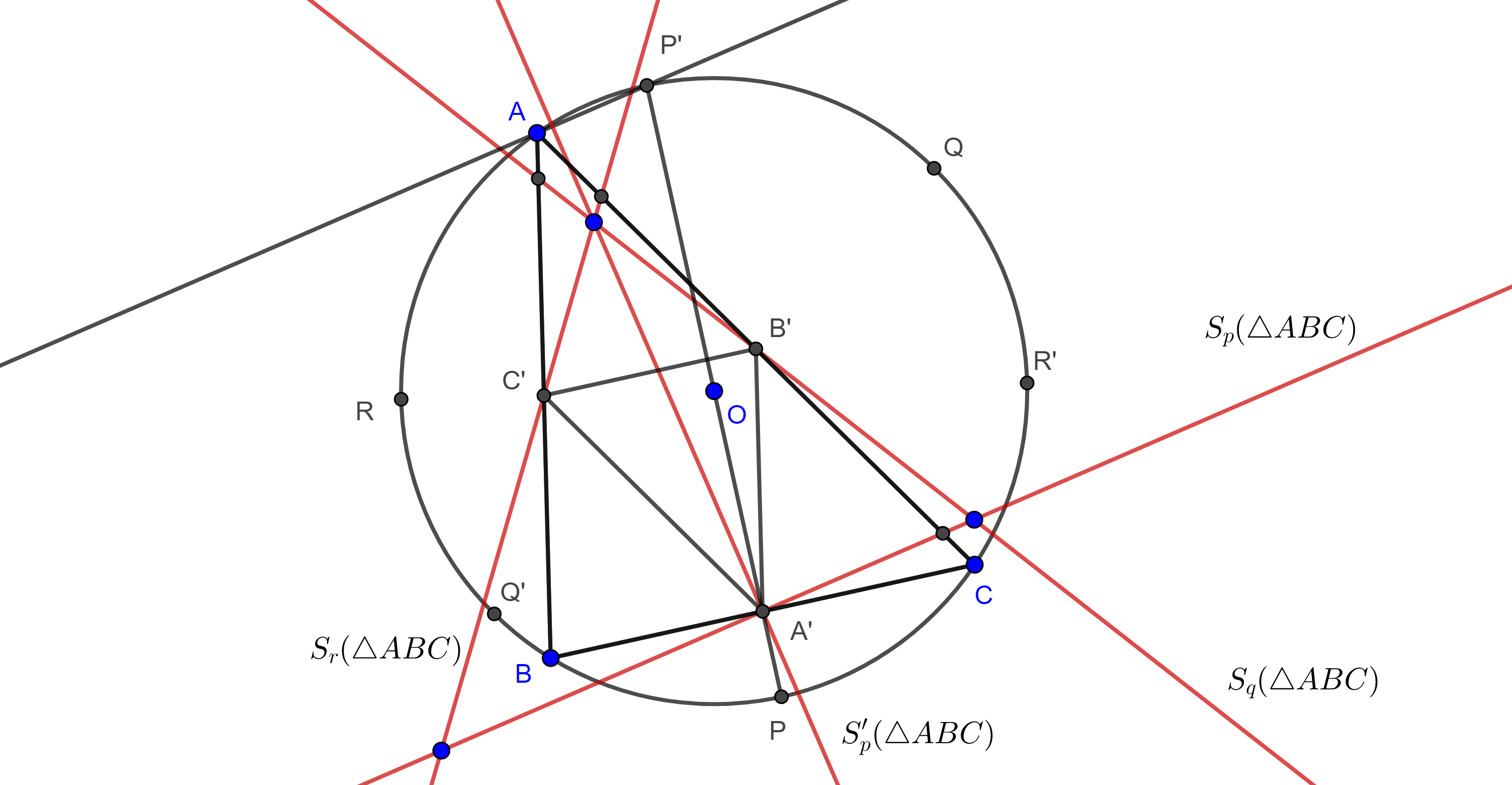
Proposición. Sean $\triangle ABC$, $P$, $Q$ y $R$ los puntos medios de los arcos $\overset{\LARGE{\frown}}{BC}$, $\overset{\LARGE{\frown}}{CA}$ y $\overset{\LARGE{\frown}}{AB}$ de $\Gamma(O)$, el circuncírculo de $\triangle ABC$, considera $P’$, $Q’$ y $R’$, los puntos diametralmente opuestos de $P$, $Q$ y $R$ respectivamente, entonces las intersecciones de las rectas de Simson de $P$, $P’$, $Q$, $Q’$, $R$ y $R’$ respecto de $\triangle ABC$ forman un cuadrángulo ortocéntrico cuyo triángulo órtico es el triángulo medial de $\triangle ABC$.
Demostración. Sean $A’$, $B’$ y $C’$ los puntos medios de $BC$, $AC$ y $AB$ respectivamente.
Como $P$ es el punto medio de $\overset{\LARGE{\frown}}{BC}$ entonces $OP$ y $AP$ son las bisectrices de $\angle BOC$ y $\angle BAC$ respectivamente, entonces $PA \perp BC$, por lo que la recta de $S_p(\triangle ABC)$ pasa por $A’$.
Como $PP’$ es diámetro entonces $\angle PAP’$ es ángulo recto, por lo que $AP’$ es la bisectriz externa de $\angle A$.
Bajo la homotecia con centro en el centroide de $\triangle ABC$ y razón $\dfrac{-1}{2}$, el triángulo medial $\triangle A’B’C’$ es imagen de $\triangle ABC$, por lo que la imagen de $AP’$ bajo esta transformación es la bisectriz externa de $\angle B’A’C’$ que al mismo tiempo es paralela a $AP’$.
Por el corolario, $AP’$ es paralela a $S_p(\triangle ABC)$, la cual contiene a $A’$.
Como la paralela a $AP’$ que pasa por $A’$ es única, entonces $S_p(\triangle ABC)$ coincide con la bisectriz exterior de $\angle B’A’C’$.
De manera análoga podemos ver que $S_q(\triangle ABC)$ y $S_r(\triangle ABC)$ son las bisectrices externas de $\angle B’$ y $\angle C’$ respectivamente.
Por otro lado, como $P’A \perp BC$ entonces la recta de Simson de $P’$ pasa por $A’$, por el teorema 3, $S_p(\triangle ABC) \perp S_p'(\triangle ABC)$.
Por lo tanto $S_p’(ABC)$ es la bisectriz interna de $\angle A’$.
De manera análoga, podemos ver que $S_q’(ABC)$ y $S_r’(ABC)$ son las bisectrices internas de $\angle B’$ y $\angle C’$ respectivamente
En consecuencia, las intersecciones de las rectas de Simson de $P$, $P’$, $Q$, $Q’$, $R$ y $R’$ son el incentro y los excentros de $\triangle A’B’C’$.
Por lo tanto, estas intersecciones forman un cuadrángulo ortocéntrico, cuyo triángulo órtico es $\triangle A’B’C’$, el triángulo medial de $\triangle ABC$.
$\blacksquare$
Más adelante…
En la próxima entrada hablaremos sobre el teorema de Napoleón, que nos dice que si construimos triángulos equiláteros sobre los lados de un triangulo cualquiera los centroides de estos forman un triángulo equilátero, también veremos que relación hay entre este teorema y los puntos de Fermat.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- $i)$ ¿Qué puntos pertenecen a su propia recta de Simson?
$ii)$ Muestra que el punto diametralmente opuesto a uno de los vértices de un triángulo en su circuncírculo, tiene como recta de Simson el lado opuesto al vértice considerado. - Encuentra el punto en el circuncírculo de un triángulo cuya recta de Simson respecto al triángulo tiene una dirección dada.
- $i)$Si las perpendiculares desde un punto $P$ en el circuncírculo $\Gamma$ de $\triangle ABC$ intersecan otra vez a $\Gamma$ en $E’$, $F’$ y $D’$, donde muestra que $\triangle ABC$ y $\triangle E’F’D’$ son simétricos respecto a un eje, (figura 1).
$ii)$ En un círculo dado inscribir un triángulo tal que la recta de Simson de un punto dado en este círculo corresponda a una recta dada. Un vértice puede ser elegido arbitrariamente. - Si la recta de Simson de un punto $P$ pasa por el punto diametralmente opuesto a $P$, muestra que la recta de Simson de $P$ también pasa por el centroide del triangulo considerado.
- Considera $\triangle ABC$ y su circuncírculo $\Gamma$, $P$ y $P’ \in \Gamma$, muestra que las paralelas a $S_p(\triangle ABC)$ y $S_p'(\triangle ABC)$ que pasan por $P’$ y $P$ respectivamente se intersecan $\Gamma$.
- Si dos triángulos están inscritos en la misma circunferencia y son simétricos respecto al centro de la circunferencia, demuestra que las rectas de Simson de cualquier punto en la circunferencia respecto a los dos triángulos son perpendiculares.
- Muestra que los puntos simétricos con respecto a los lados de un triángulo, de un punto en su circuncírculo, son colineales con el ortocentro del triángulo.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Cuadrángulo ortocéntrico.
- Siguiente entrada del curso: Puntos de Fermat y triángulos de Napoleón.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 140-150.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 111-116.
- Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 43-45.
- Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 19-22.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»