Archivo de la etiqueta: inversa

Álgebra Lineal I: Técnicas básicas de cálculo de determinantes

Por Leonardo Ignacio Martínez Sandoval

6 respuestas

Introducción

Ya definimos a los determinantes para vectores, para transformaciones y para matrices. Además, mostramos algunas propiedades básicas de determinantes y las usamos para resolver varios problemas. Como hemos discutido, los determinantes guardan información importante sobre una transformación lineal o sobre una matriz. También ayudan a implementar la técnica de diagonalización la cual introdujimos hace algunas entradas y en la cual profundizaremos después. Es por esta razón que es importante tener varias técnicas para el cálculo de determinantes.

Fuera de este curso, los determinantes sirven en muchas otras áreas de las matemáticas. Cuando se hace cálculo de varias variables ayudan a enunciar el teorema del cambio de variable. En combinatoria ayudan a calcular el número de árboles generadores de una gráfica. Más adelante en tu formación matemática es probable que te encuentres con otros ejemplos.

Calculo de determinantes de $2\times 2$

Como ya discutimos anteriormente, una matriz en $M_2(F)$, digamos $A=\begin{pmatrix}a&b\\ c&d\end{pmatrix}$ tiene determinante $ad-bc$.

Problema. Calcula el determinante de la matriz $$\begin{pmatrix} 0 & 1\\ 1 & 1\end{pmatrix}^8.$$

Solución. Por la fórmula para el determinante de las matrices de $2\times 2$, se tiene que $\begin{vmatrix} 0 & 1\\ 1 & 1\end{vmatrix} = 0\cdot 1 – 1\cdot 1 = -1.$

Como el determinante es multiplicativo, $\det(A^2)=\det(A)\det(A)=(\det(A))^2$, e inductivamente se puede mostrar que para todo entero positivo $n$ se tiene que $\det(A^n)=(\det(A))^n$. De esta forma, el determinante que buscamos es $(-1)^8=1$.

$\triangle$

Observa que hubiera tomado más trabajo elevar la matriz a la octava potencia. Aunque esto usualmente no es recomendable, en este problema hay algo interesante que sucede con esta matriz. Llamémosla $A=\begin{pmatrix} 0 & 1\\ 1 & 1\end{pmatrix}$. Haciendo las cuentas para las primeras potencias, se tiene que
\begin{align*}
A&=\begin{pmatrix} 0 & 1\\ 1 & 1\end{pmatrix}\\
A^2&=\begin{pmatrix} 1 & 1\\ 1 & 2\end{pmatrix}\\
A^3&=\begin{pmatrix} 1 & 2\\ 2 & 3\end{pmatrix}\\
A^4&=\begin{pmatrix} 2 & 3\\ 3 & 5\end{pmatrix}\\
A^5&=\begin{pmatrix} 3 & 5\\ 5 & 8\end{pmatrix}
\end{align*}

Aquí aparece la sucesión de Fibonacci, dada por $F_0=0$, $F_1=1$ y $F_{n+2}=F_{n+1}+F_n$ para $n\geq 0$, cuyos primeros términos son $$0,1,1,2,3,5,8,13,21,\ldots.$$ De hecho se puede probar por inducción que $$A^n=\begin{pmatrix} F_{n-1} & F_n\\ F_n & F_{n+1}\end{pmatrix}.$$

Así, por un lado el determinante de la matriz $A^n$ es $F_{n-1}F_{n+1}-F_n^2$, usando la fórmula de determinante de $2\times 2$. Por otro lado, es $(-1)^n$, por el argumento del problema. Con esto hemos demostrado que para cualquier entero $n$ tenemos la siguiente identidad para los números de Fibonacci: $$F_{n-1}F_{n+1}-F_n^2 = (-1)^n.$$

Cálculo de determinantes de $3\times 3$

Para calcular el determinante de una matriz en $M_3(F)$ por definición, digamos de $A=\begin{pmatrix}a&b&c\\ d&e&f\\ g&h&i\end{pmatrix}$, tenemos que hacer una suma de $3!=6$ términos. Si se hacen las cuentas de manera explícita, el valor que se obtiene es $$aei+bfg+cdh-ceg-afh-bdi.$$

Esto se puede recordar mediante el siguiente diagrama, en el cual se ponen la primera y la segunda columna de nuevo, a la derecha. Las diagonales hacia abajo son términos positivos y las diagonales hacia arriba son términos negativos.

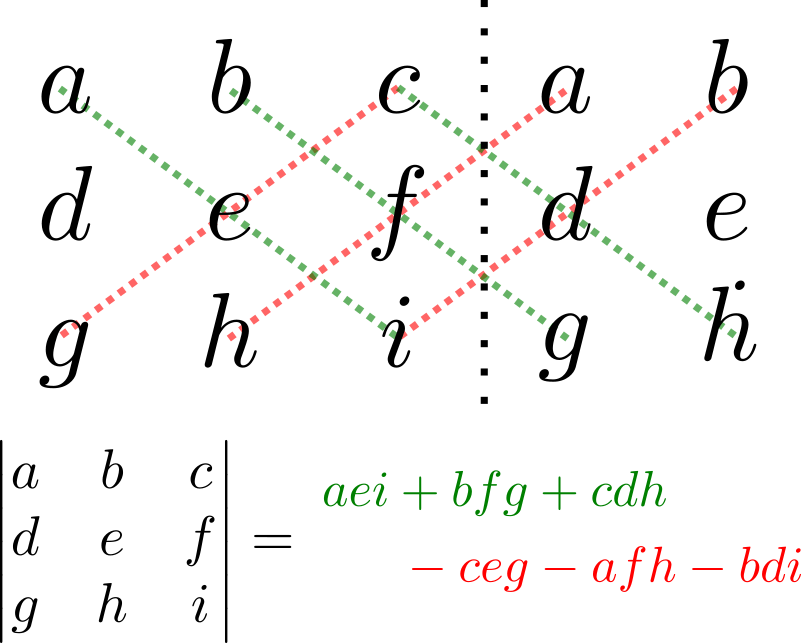
Cálculo de determinantes de matrices de 3x3
Cálculo de determinantes de $3\times 3$

Veamos un ejemplo de un problema en el que se puede aprovechar esta técnica.

Problema. Determina para qué reales $a,b,c$ se tiene que los vectores $(a,b,0)$, $(a,0,b)$ y $(0,a,b)$ son una base de $\mathbb{R}^3$.

Solución. Para que estos vectores sean una base de $\mathbb{R}^3$, basta con que sean linealmente independientes, pues son $3$. Como hemos visto en entradas anteriores, para que sean linealmente independientes, es necesario y suficiente que el determinante de la matriz $\begin{pmatrix}a&b&0\\ a&0&b\\ 0&a&b\end{pmatrix}$ sea distinto de cero.

Usando la técnica de arriba, hacemos siguiente diagrama:

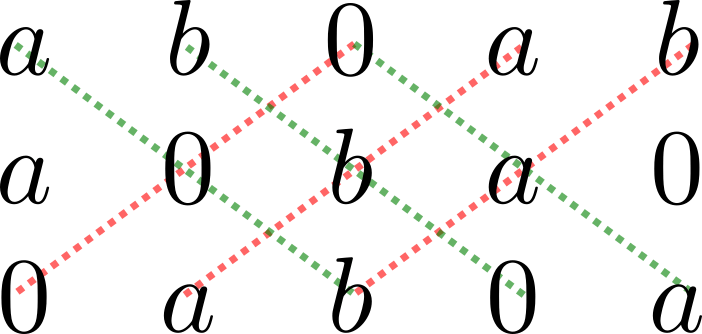
De aquí, vemos que el determinante es $$0+0+0-0-a^2b-ab^2=-ab(a+b).$$ Esta expresión es igual a cero si $a=0$, si $b=0$ o si $a+b=0$. En cualquier otro caso, el determinante no es cero, y por lo tanto los vectores forman una base.

$\triangle$

Ten mucho cuidado. Esta técnica no funciona para matrices de $4\times 4$ o más. Hay una forma sencilla de convencerse de ello. Por ejemplo, el determinante de una matriz de $4\times 4$ debe tener $4!=24$ sumandos. Si intentamos copiar la técnica de arriba, tendremos solamente $8$ sumandos ($4$ en una diagonal y $4$ en otra). Para cuando tenemos matrices de $4\times 4$ o más, tenemos que recurrir a otras técnicas.

Reducción gaussiana para determinantes

Cuando vimos el tema de sistemas de ecuaciones hablamos del algoritmo de reducción gaussiana, y vimos que este siempre lleva una matriz en $M_{m,n}(F)$ a su forma escalonada reducida mediante operaciones elementales. Cuando aplicamos el algoritmo a matrices en $M_n(F)$, siempre llegamos a una matriz triangular, en donde sabemos fácilmente calcular el determinante: es simplemente el producto de las entradas en la diagonal. Nota cómo lo anterior también se cumple para las matrices diagonales, pues son un caso particular de matrices triangulares.

Por esta razón, es fundamental para el cálculo de determinantes saber qué le hacen las operaciones elementales al determinante de una matriz.

Teorema. Las operaciones elementales tienen el siguiente efecto en el determinante de una matriz $A$:

  1. Si todos los elementos de un renglón o columna de $A$ se multiplican por $\lambda$, entonces el determinante se multiplica por $\lambda$.
  2. Cuando se intercambian dos renglones o columnas de $A$, el determinante se multiplica por $-1$.
  3. Si a un renglón de $A$ se le suma un múltiplo escalar de otro renglón, entonces el determinante no cambia. Sucede algo análogo para columnas.

Demostración. El punto $1$ ya lo demostramos en la entrada anterior, en donde vimos que el determinante es homogéneo.

Para los puntos $2$ y $3$, usemos que si $e_1,\ldots e_n$ es la base canónica de $F^n$, el determinante de una matriz con renglones $R_1,\ldots,R_n$ es $$\det_{(e_1,\ldots,e_n)}(R_1,\ldots,R_n).$$

Intercambiar los renglones $i$ y $j$ es hacer $\det_{(e_1,\ldots,e_n)}(R_{\sigma(1)},\ldots,R_{\sigma(n)})$ para la transposición $\sigma$ que intercambia $i$ y $j$. Como el determinante es antisimétrico y $\sigma$ tiene signo $-1$, obtenemos la conclusión.

Hagamos ahora el tercer punto. Tomemos $i\neq j$ y un escalar $\lambda$. Si al $i$-ésimo renglón de $A$ le sumamos $\lambda$ veces el $j$-ésimo renglón de $A$, esto es lo mismo que multiplicar a $A$ por la izquierda por la matriz $B$ que tiene unos en la diagonal y $\lambda$ en la entrada $(i,j)$. La matriz $B$ es triangular, de modo que su determinante es el producto de las entradas, que es $1$. De esta forma, $$\det(BA)=\det(B)\det(A)=\det(A).$$

$\square$

Así, una estrategia para calcular el determinante de una matriz es hacer reducción gaussiana hasta llegar a una matriz diagonal (incluso es suficiente que sea triangular superior) de determinante $\Delta$. Si en el camino se hicieron $r$ intercambios de renglones y se multiplicaron los renglones por escalares $\lambda_1,\ldots,\lambda_s$, entonces el determinante de $A$ será $$\frac{(-1)^r \Delta}{\lambda_1\cdot\ldots\cdot \lambda_s}.$$

Otras propiedades para calcular determinantes

Aquí recolectamos otras propiedades de determinantes que pueden ayudar a calcularlos. Ya mostramos todas ellas, salvo la número $2$. Esta la mostramos después de la lista.

  1. Si se descompone una columna de una matriz como suma de dos columnas, entonces el determinantes es la suma de los determinantes en los que ponemos cada columna en vez de la original.
  2. Si $A$ es una matriz en $M_n(\mathbb{C})$, entonces el determinante de la matriz conjugada $\overline{A}$ es el conjugado del determinante de $A$.
  3. El determinante es multiplicativo.
  4. Si $A$ es una matriz en $M_n(F)$, el determinante de $\lambda A$ es $\lambda^n$ veces el determinante de $A$.
  5. El determinante de una matriz triangular es el producto de sus entradas en la diagonal.
  6. El determinante de una matriz invertible es el inverso multiplicativo del determinante de la matriz.
  7. Una matriz tiene el mismo determinante que su transpuesta.

Proposición. Si $A$ es una matriz en $M_n(\mathbb{C})$, entonces el determinante de la matriz conjugada $\overline{A}$ es el conjugado del determinante de $A$.

Demostración. La conjugación compleja abre sumas y productos. Aplicando esto repetidas veces obtenemos la siguiente cadena de igualdades:

\begin{align*}
\overline{\det(A)}&=\overline{\sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}}\\
&=\sum_{\sigma \in S_n} \overline{\text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}}\\
&=\sum_{\sigma \in S_n} \text{sign}(\sigma)\overline{a_{1\sigma(1)}}\cdot\ldots\cdot \overline{a_{n\sigma(n)}}\\
&=\det(\overline{A}).
\end{align*}

$\square$

Hay una última técnica que es fundamental para el cálculo de determinantes: la expansión de Laplace. En algunos textos incluso se usa para definir el determinante. Probablemente la conoces: es la que consiste en hacer el determinante «con respecto a una fila o columna» y proceder de manera recursiva. Hablaremos de ella más adelante y veremos por qué funciona.

Dos problemas de cálculo de determinantes

Problema 1. Considera la matriz $$A=\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ -1 & -3 & 0 & 1\end{pmatrix}.$$ Calcula los siguientes determinantes:

  • $\det A$
  • $\det(^t A)$
  • $\det(A^{-1})$
  • $\det(^t A A)$
  • $\det(-2A)$

Solución. Hagamos primero el determinante de la matriz $A$. Para ello, haremos operaciones elementales como sigue
\begin{align*}
&\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ -1 & -3 & 0 & 1\end{pmatrix}\\
\to&\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ 0 & -\frac{14}{5} & \frac{2}{5} & 1\end{pmatrix}\\
\to &\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ 0 & 0 & -\frac{12}{5} & \frac{33}{5}\end{pmatrix}\\
\to& \begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ 0 & 0 & 0 & \frac{189}{25}\end{pmatrix}.
\end{align*}

En el primer paso sumamos $1/5$ veces el primer renglón al último. Luego, sumamos $14/5$ veces el segundo renglón al último. Finalmente, sumamos $12/25$ veces el tercer renglón al último. De esta forma, nunca cambiamos el determinante de la matriz. Así, del determinante de $A$ es el mismo que el de la matriz final, que por ser triangular superior es el producto de las entradas en su diagonal. De este modo, $$\det(A) = 5\cdot 1 \cdot 5 \cdot \frac{189}{5} = 189.$$

El determinante de una matriz es igual al de su transpuesta, así que $\det(^t A)=\det(A)$. El determinante $\det(A^{-1})$ es el inverso multiplicativo de $\det(A)$, así que es $\frac{1}{189}$.

Como el determinante es multiplicativo, $$\det({^tA}A)=\det({^tA})\det(A)=189\cdot 189=35721.$$

Finalmente, usando que el determinante es homogéneo y que estamos en $M_4(\mathbb{R})$, tenemos que
\begin{align*}
\det(-2A)&=(-2)^4\det(A)\\
&=16\cdot 189\\
&=3024.
\end{align*}

$\triangle$

Problema 2. Sean $a,b,c$ números complejos. Calculando el determinante de la matriz $$A=\begin{pmatrix}a&b&c\\ c&a&b\\ b&c&a\end{pmatrix}$$ en $M_3(\mathbb{C})$ de dos formas distintas, muestra que $$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca).$$

Solución. Usando la técnica para determinantes de $3\cdot 3$ tenemos que por un lado,
\begin{align*}
\det(A) &= a^3 + b^3 + c^3 – abc – bca – cab\\
&=a^3+b^3+c^3-3abc.
\end{align*}

Por otro lado, el determinante no cambia si al primer renglón le sumamos los otros dos, así que el determinante de $A$ también es $$\begin{vmatrix}a+b+c&a+b+c&a+b+c\\ c&a&b\\ b&c&a\end{vmatrix}.$$ Como el determinante es homogéneo, podemos factorizar $a+b+c$ de la primera entrada para obtener que $$\det(A)=(a+b+c)\begin{vmatrix}1&1&1\\ c&a&b\\ b&c&a\end{vmatrix}.$$

Aplicando de nuevo la fórmula de determinantes de $3\times 3$, tenemos que $$\begin{vmatrix}1&1&1\\ c&a&b\\ b&c&a\end{vmatrix} = a^2+b^2+c^2-ab-bc-ca.$$

Concluimos entonces que $$\det(A)=(a+b+c)(a^2+b^2+c^2-ab-bc-ca).$$ Igualando ambas expresiones para $\det(A)$ obtenemos la identidad deseada.

$\triangle$

Más adelante…

En esta entrada vimos varias formas para calcular el determinante de una matriz. Cuando nos enfrentemos con un problema que requiere el cálculo de un determinante, tenemos que elegir la que más nos convenga (o la que requiera menos pasos). La mejor forma de desarrollar un poco de «intuición» al momento de elegir el mejor método para calcular determinantes es haciendo ejercicios.

A continuación pondremos en práctica lo que aprendimos en esta entrada haciendo varios ejercicios de cálculo de determinantes.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Sea $\alpha$ un número real. Encuentra el determinante de la matriz $$\begin{pmatrix}\sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha \end{pmatrix}.$$
  • Determina para qué valores de $a$ la matriz $$\begin{pmatrix} a & 0 & a & 0 & a \\0 & a & 0 & a & 0 \\ 0 & 0 & a & 0 & 0 \\ 0 & a & 0 & a & 0 \\ a & 0 & a & 0 & a \end{pmatrix}$$ es invertible.
  • Encuentra el determinante de la matriz $$\begin{pmatrix} 2 & 1 & 0 & 0 & 0 \\0 & 2 & 1 & 0 & 0 \\ 0 & 0 & 2 & 1 & 0 \\ 0 & 0 & 0 & 2 & 1 \\ 1 & 0 & 0 & 0 & 2 \end{pmatrix}.$$
  • Sea $x$ un número complejo. Muestra que el determinante de la matriz $$\begin{pmatrix}3x^2-6x+5&2x^2-4x+2&x^2-2x\\ 2x^2-4x+2&2x^2+2x+1&x^2-x\\ x^2-2x&x^2-x&x^2\end{pmatrix}$$ es $x^6$. Sugerencia. Hay una solución simple, factorizando a la matriz como el producto de dos matrices triangulares, una superior y una inferior, una transpuesta de la otra.
  • Muestra que si $A=\begin{pmatrix}0& 1 \\ 1 & 1\end{pmatrix}$, entonces $$A^n=\begin{pmatrix} F_{n-1} & F_n\\ F_n & F_{n+1}\end{pmatrix},$$ donde $\{F_n\}$ es la sucesión de Fibonacci. Muestra que para los números de Fibonacci se satisface que $$F_{2n}=F_n(F_{n+1}+F_{n-1}).$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Mariposa de 7 equivalencias de matrices invertibles

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

Una de las nociones más importantes en álgebra lineal es la de «matriz invertible». Llamemos $I_n$ a la matriz identidad de $n\times n$, es decir, a la que tiene $1$ en cada entrada de la diagonal principal, y $0$ en las demás.

Una matriz $A$ de $n\times n$ es invertible si existe una matriz $B$ de $n\times n$ tal que $AB=I_n=BA$.

Una consecuencia rápida es que dicha matriz $B$ es única, así que le podemos dar la notación $A^{-1}$. De la definición (y asociatividad) se puede ver rápido que si $A_1$ y $A_2$ son invertibles, entonces su producto $A_1A_2$ también, con inversa $A_2^{-1}A_1^{-1}$, en otras palabras, «producto de invertibles es invertible».

Un detalle curioso de la definición es que pide no sólo que $AB=I_n$, sino que para la misma matriz $B$ también se tenga que $BA=I_n$. Por un lado, a priori esto tiene sentido pues el producto de matrices no es conmutativo, es decir, ocurre a veces que $AB\neq BA$. Sin embargo, como veremos más adelante en esta entrada, en la definición de matriz invertible basta con tener una de estas igualdades.

De hecho, la idea de esta entrada es presentar y demostrar varias equivalencias a la afirmación «$A$ es una matriz invertible». La presentación sigue un poco el orden de ideas del capítulo 3.4 del libro Essential Linear Algebra with Applications: A Problem-Solving Approach de Titu Andreescu. La idea es explicar el siguiente diagrama, en donde agrupamos a las equivalencias en grupitos que corresponden a partes de una mariposa:

Algunas definiciones

Antes de enunciar el resultado principal, conviene recordar algunas definiciones y un par de resultados importantes.

Una operación elemental es aplicar a una matriz de las siguientes operaciones:

  • Intercambio de dos filas.
  • Multiplicar todas las entradas de alguna de sus filas por un elemento $c$ no cero.
  • Sumar a una fila un múltiplo de otra fila.

Una matriz elemental es una matriz obtenida de aplicar a $I_n$ exactamente una operación elemental.

Una fila de una matriz es una fila cero si todas sus entradas son iguales a cero. A la primer entrada no cero (de izquierda a derecha) de una fila que no sea fila cero se le llama pivote. Una matriz es escalonada reducida si cumple las siguientes tres propiedades:

  1. Todas las filas cero están hasta abajo.
  2. En todas las filas no cero los pivotes son iguales a $1$.
  3. Si una fila no cero $F_1$ está arriba de otra fila no cero $F_2$, entonces el pivote de $F_1$ está estrictamente a la izquierda del pivote de $F_2$.
  4. Si una entrada tiene al pivote de una fila, entonces todas las demás entradas de la columna son iguales a $0$.

Un resultado (no trivial) es que cualquier matriz se puede llevar a una (y sólo una) matriz escalonada reducida $A_{\text{red}}$ usando únicamente operaciones elementales, a la cual le llamamos su forma escalonada reducida. Estas son todas las definiciones que necesitamos. Estamos listos para pasar al enunciado del teorema principal.

Teorema de la mariposa de equivalencias

Teorema: Sea $A$ una matriz de $n\times n$ con entradas en un campo $F$. Entonces, todas las siguientes afirmaciones son equivalentes:

  1. $A$ es una matriz invertible.
  2. La forma escalonada reducida $A_{\text{red}}$ de $A$ es $I_n$.
  3. $A$ es producto de matrices elementales.
  4. Para todo $b\in F^n$, el sistema de ecuaciones $Ax=b$ tiene una única solución $x\in F^n$.
  5. Para todo $b\in F^n$, el sistema de ecuaciones $Ax=b$ tiene una solución $x\in F^n$.
  6. Existe una matriz $B$ de $n\times n$ tal que $AB=I_n$.
  7. Existe una matriz $B$ de $n\times n$ tal que $BA=I_n$.

Por supuesto, estas no son todas las formas de caracterizar una matriz invertible. Hay otras formas de hacerlo en términos de determinantes, por ejemplo. En el camino recordaremos varias de las definiciones que están en este teorema.

Le llamo el teorema de la mariposa de equivalencias porque podemos agrupar a estos números en tres «grupos» principales de equivalencias «parecidas», que además nos van a recordar cómo va la prueba.

Primero veremos la equivalencia entre 1, 2 y 3 (un ala). Luego, entre 1,4,5 (otra ala). Después, entre 1 y 6 (antena derecha). Finalmente, entre 1 y 7 (antena izquierda).

Un par de lemas auxiliar

Antes de demostrar el teorema de equivalencias, enunciamos y argumentamos dos resultados útiles

Es fácil convencerse de que aplicar una operación elemental a una matriz $A$ es lo mismo que multiplicar a $A$ por la izquierda por la matriz elemental correspondiente a la operación. Como toda matriz $A$ se puede llevar a su forma escalonada reducida mediante operaciones elementales, concluimos lo siguiente.

Lema 1: Para toda matriz $A$ existe una matriz $E$ que es producto de matrices elementales tal que $EA$ es la forma escalonada reducida de $A$, es decir $EA=A_{\text{red}}$.

También es fácil convencerse de que cada matriz elemental es invertible, pues las operaciones elementales se pueden revertir, y la inversa de la matriz elemental $M$ es precisamente la matriz elemental correspondiente a la operación inversa. Además, producto de matrices invertibles es invertible. De este modo, concluimos lo siguiente:

Lema 2: Si $E$ es una matriz que es producto de matrices elementales, entonces $E$ es invertible y también es producto de matrices elementales.

La demostración del teorema de la mariposa

Usaremos el diagrama de la mariposa para demostrar todas las equivalencias. Lo que haremos es probar una implicación por cada una de las siguientes flechas:


Empezamos con el ala izquierda de la mariposa.

(1) implica (2): Tomemos una matriz invertible $A$. Por el Lema 1, existe una matriz producto de elementales tal que $EA=A_{\text{red}}$. Como $E$ y $A$ son invertibles, entonces $A_{\text{red}}$ también es invertible.

Si $A_{\text{red}}$ tuviera una fila cero, digamos la $j$, no sería invertible. Esto sucede ya que para cualquier matriz $B$ de $n\times n$ tendríamos que la fila $j$ de $AB$ también sería cero, y entonces $AB$ nunca sería $I_n$. Como sabemos que $A_{\text{red}}$ es invertible, entonces todas sus filas no son cero y por lo tanto todas tienen pivote. Así, tenemos $n$ pivotes y por lo tanto tiene que haber exactamente un pivote por columna. Como $A_{\text{red}}$ es escalonada reducida, estos pivotes tienen que estar exactamente uno en cada entrada de la diagonal principal. Como además cada pivote es la única entrada no cero de su columna, concluimos que $A_{\text{red}}$ es la identidad.

(2) implica (3): Tomemos una matriz $A$ cuya forma escalonada reducida es la identidad. Por el Lema 1, existe una matriz producto de elementales tal que $EA=A_{\text{red}}=I_n$. Por el Lema 2, $E$ es invertible y $E^{-1}$ es producto de matrices elementales. Multiplicando por $E^{-1}$ a la izquierda a la identidad $EA=I_n$ obtenemos $A=E^{-1}$, es decir, $A$ es producto de matrices elementales.

(3) implica (1): Finalmente, si $A$ es producto de matrices elementales, por el Lema 2 tenemos que $A$ es invertible.

Con esto terminamos la primer ala de la mariposa. Notemos que cierran un ciclo, así que a partir de ahora podemos usar libremente la equivalencia entre 1, 2 y 3. Hagamos la segunda ala.

(1) implica (4): Supongamos que $A$ es invertible y tomemos cualquier $b$ en $F^n$. Notemos que $A^{-1}b$ es solución de $Ax=b$ pues satisface $A(A^{-1}b)=I_n b=b$. Además, si $x$ y $y$ son soluciones de $Ax=b$, tendríamos que $Ax=Ay$ y mutiplicando por $A^{-1}$ a la izquierda tendríamos que $x=y$. De este modo, $Ax=b$ tiene una única solución para todo $b$ en $F^n$.

(4) implica (5): Esta demostración es inmediata. Si $Ax=b$ tiene una única solución, en particular tiene una solución.

(5) implica (1): Supongemos que $Ax=b$ tiene una solución $x$ en $F^n$ para todo $b$ en $F^n$. Afirmamos que esto implica que $A_{\text{red}}x=b$ tiene solución para para todo $b$ en $F^n$. Tomemos una $b$ en $F^n$. Por el Lema 1, hay una matriz invertible $E$ tal que $A_{\red}=EA$. Por hipótesis, existe una solución $x$ para $Ax=E^{-1}b$. Tomemos esa $x$. Notemos que $A_{\text{red}}x=(EA)x=E(Ax)=E(E^{-1}b)=b$. Es decir, justo esa $x$ es solución para $A_{\text{red}}x=b$.

En particular, $A_{\text{red}}x=e_j$ tiene solución para cuando $e_j$ es el vector cuya $j$-ésima entrada es $1$ y las demás cero. Así, es imposible que la $j$-ésima fila de $A_{\text{red}}$ sea cero, ya que en caso contrario $Ax$ siempre tendría $j$-ésima entrada cero y $Ax=e_j$ no tendría solución. Como ya vimos antes, si $A_{\text{red}}$ no tiene filas cero, entonces es la identidad. Por la equivalencia entre (1) y (2) concluimos que $A$ es invertible.

Esto termina las equivalencias en la segunda ala, así que ahora podemos usar libremente las implicaciones entre 1, 2, 3, 4 y 5. Ya nada más nos faltan las antenas.

Por supuesto, las implicaciones (1) implica (6) y (1) implica (7) son triviales, pues la matriz de (1) en particular funciona para (6) y (7). Lo que falta ver son los regresos de estas implicaciones.

(6) implica (1): Supongamos que existe una matriz $B$ tal que $AB=I_n$. Tomemos $b$ en $F^n$. Notemos que $Bb$ es solución de $Ax=b$ pues $A(Bb)=(AB)b=I_nb=b$. De este modo, $Ax=b$ tiene solución para todo $b$ en $F^n$ y por la equivalencia entre (1) y (5) tenemos que $A$ es invertible. Si tomamos a su inversa $A^{-1}$ y la multiplicamos a la izquierda en la hipótesis, obtenemos $B=A^{-1}$, de modo que también $BA=I_n$.

(7) implica (1): Supongamos que existe una matriz $B$ tal que $BA=I_n$. Por la equivalencia entre (1) y (6), tenemos que $B$ es invertible, de inversa $B^{-1}$. De este modo, $A=(B^{-1}B)A=B^{-1}(BA)=B^{-1}I_n=B^{-1}$. De este modo, $A$ es la inversa de una matriz invertible y por tanto es invertible, y por lo tanto $AB=B^{-1}B=I_n$.

¡Listo! Con esto tenemos la equivalencia entre todas las afirmaciones.

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

Una prueba del teorema de la función inversa

Por Leonardo Ignacio Martínez Sandoval

6 respuestas

Introducción

Uno de los teoremas clave de los cursos de cálculo de varias variables es el teorema de la función inversa (TFI). En la Facultad de Ciencias de la UNAM se estudia en la materia Cálculo III. En esta entrada me gustaría presentar de la manera más auto-contenida posible este resultado.

Platicaré un poco de las definiciones de los términos que aparecen en el enunciado, así como de la intuición de por qué el teorema es cierto. Después presentaré los ingredientes principales para una prueba. Finalmente, presentaré la prueba intentando motivarla y dividiéndola en secciones pequeñas.

El enunciado con el que trabajaremos es el siguiente:

Teorema de la función inversa. Sea $F:\mathbb{R}^n\to \mathbb{R}^n$ una función de clase $\mathcal{C}^1$ con matriz Jacobiana $DF$. Supongamos que $F(a)=b$ y que $DF(a)$ es invertible. Entonces existen vecindades abiertas $U$ y $V$ de $a$ y $b$ respectivamente para las cuales:

a) $F:U\to V$ es una biyección,
b) su inversa $F^{-1}:V\to U$ es de clase $\mathcal{C}^1$ y
c) $DF^{-1}(b)=DF(a)^{-1}$.

Lo que nos espera es aproximadamente lo que está en el siguiente diagrama, donde las flechas indican a grandes rasgos qué resultado se usa para probar qué otro.

Definiciones e intuición

La función con la que comenzamos es una función de $\mathbb{R}^n$ a $\mathbb{R}^n$, así que la podemos descomponer en sus funciones coordenadas de la siguiente manera: $$F(x)=(F_1(x), F_2(x),\ldots, F_n(x)).$$

Que la función sea de clase $\mathcal{C}^1$ quiere decir que las derivadas parciales con respecto a cada una de las variables existen, que estas son continuas y que localmente $F$ «se comporta» como la transformación lineal correspondiente a la matriz Jacobiana siguiente:

$$DF(x)=\begin{pmatrix}
\frac{\partial F_1}{\partial x_1}(x) & \cdots & \frac{\partial F_1}{\partial x_n}(x)\\
\vdots & \ddots & \vdots \\
\frac{\partial F_n}{\partial x_1}(x) & \cdots & \frac{\partial F_n}{\partial x_n}(x)
\end{pmatrix}.$$

Entonces, a grandes rasgos lo que nos dice el teorema de la función inversa es lo siguiente. Si $F$ se comporta como una transformación lineal $T$ invertible «cerquita» del punto $a$, entonces en realidad es invertible «cerquita» del punto $a$ y más aún, la inversa se comporta como la transformación lineal $T^{-1}$ «cerquita» del punto $b=f(a)$.

Suena bastante razonable, pero hay algunos aspectos que son sorprendentes. Uno es que se garantiza la invertibilidad en todo un abierto $U$. Si no se requiriera que fuera abierto, sería chafa porque podríamos tomar $U=\{a\}$ y $V=\{b\}$ y la restricción sería trivialmente invertible. Lo otro es que el teorema también garantiza que la inversa es diferenciable, lo cual de entrada no es evidente.

Para la prueba necesitamos hablar de dos normas. Cuando tengamos un vector $x=(x_1,\ldots,x_n)$ en $\mathbb{R}^n$, $\norm{x}$ denotará la norma euclideana $$\norm{x}=\sqrt{\sum_{i=1}^nx_i^2}.$$

Necesitaremos también la norma de Frobenius. Como recordatorio, para una matriz $A=(a_{ij})$ de $n\times n$, su norma de Frobenius está dada por $$\norm{A}=\sqrt{\sum_{i=1}^n\sum_{j=1}^n a_{ij}^2},$$

o equivalentemente, si $A_i$ es el $i$-ésimo renglón de $A$, tenemos que

$$\norm{A}=\sqrt{\sum_{i=1}^n\norm{A_{i}}^2},$$

pues ambas expresiones suman todas las entradas de la matriz al cuadrado.

Ingredientes para la prueba

Pasemos ahora a algunos resultados auxiliares que es más cómodo probar desde antes. Algunos de ellos son más generales que lo que enuncio (e incluso con la misma prueba), pero con el fin de que la demostración sea auto-contenida, he decidido enunciar sólo lo que necesitamos.

Teorema del punto fijo de Banach (para $\mathbb{R}^n$). Sea $X$ un compacto de $\mathbb{R}^n$ y $\varphi:X\to X$ una función continua. Supongamos que $\varphi$ es una contracción, es decir, que existe un real $0<\lambda<1$ para el cual $\norm{\varphi(x)-\varphi(y)}\leq\lambda \norm{x-y}$ para todos $x,y \in X$.

Entonces $\varphi$ tiene un único punto fijo, es decir existe uno y sólo un punto $x_0\in X$ para el cual $\varphi(x_0)=x_0$.

Para probar el teorema del punto fijo de Banach basta tomar cualquier punto inicial $x_1$ y considerar la sucesión $\{x_m\}$ construida recursivamente con la regla $x_m=\varphi(x_{m-1})$ para $m\geq 2$. Usando que $\varphi$ es contracción y la fórmula para series geométricas se puede mostrar inductivamente que para $m>m’$ se tiene

$$\norm{x_m-x_m’}\leq\lambda ^{m’-1} \norm{x_2-x_1} \left(\frac{1}{1-\lambda}\right).$$

Como $\lambda<1$, el lado derecho se hace arbitrariamente pequeño conforme $m’$ se hace grande, así que ésta es una sucesión de Cauchy. Por la compacidad de $X$ y completud de $\mathbb{R}^n$, tenemos que la sucesión converge a un punto $x_0$. Por continuidad, este punto satisface:

$$x_0=\lim_{m\to \infty} x_{m+1} = \lim_{m\to \infty} \varphi(x_m)=\varphi\left(\lim_{m\to \infty} x_m\right) = \varphi(x_0).$$

La unicidad no necesita la compacidad de $X$, sino únicamente que $\varphi$ sea contracción. En efecto, si hay otro punto fijo $x$ entonces

$$\norm{x-x_0}=\norm{\varphi(x)-\varphi(x_0)}\leq \lambda \norm{x-x_0},$$

de donde $\norm{x-x_0}=0$, pues si no se tendría una contradicción. Así, $x=x_0$.

Desigualdades para la norma de Frobenius. Para $x\in \mathbb{R}^n$ y $A,B$ matrices reales de $n\times n$ tenemos que
a) $\norm{Ax}\leq \norm{A} \norm{x}$ y
b) $\norm{AB}\leq \norm{A} \norm{B}$.

La desigualdad (a) se prueba usando la desigualdad de Cauchy-Schwarz. En efecto, si $A_1,\ldots, A_n$ son los renglones de la matriz $A$, tenemos que $$Ax=(A_1\cdot x, A_2\cdot x, \ldots, A_n\cdot x),$$

entrada a entrada tenemos por Cauchy-Schwarz que

$$(A_i\cdot x)^2\leq \norm{A_i}^2\norm{x}^2,$$

de modo que sumando para $i=1,\ldots, n$ tenemos que

$$\norm{Ax}^2\leq \left(\sum_{i=1}^n \norm{A_i}^2\right)\norm{x}^2=\norm{A}^2\norm{x}^2,$$

lo cual prueba la desigualdad (a). La desigualdad (b) se prueba de manera similar, tomando fila por fila a la matriz $A$ y columna por columna a la matriz $B$.

Desigualdad del valor medio. Sea $U\subset \mathbb{R}^n$ un abierto convexo y $F:U\to \mathbb{R}^n$ una función de clase $\mathcal{C}^1$. Sean $x,y$ puntos en $U$ para los cuales la cual la norma de Frobenius del Jacobiano $\norm{DF}$ está acotada sobre el segmento $xy$ por una constante $C$. Entonces:

$$\norm{F(x)-F(y)}\leq C \norm{x-y}.$$

La desigualdad del valor medio requiere de algunos pasos intermedios. Definamos $h=y-x$. La clave es probar las siguientes tres afirmaciones:

\begin{align*}
F(x)-F(y)&=\int_0^1 DF(x+th) h \,dt\\
\norm{\int_0^1 DF(x+th) h \, dt } &\leq \int_0^1 \norm{DF(x+th)}\norm{h}\, dt\\
\int_0^1 \norm{DF(x+th)}\norm{h}\, dt &\leq C \norm{h}.
\end{align*}

La primera es una «generalización» del teorema del valor medio de una variable. Se prueba coordenada a coordenada usando el Teorema Fundamental del Cálculo, la regla de la cadena y un intercambio de integral con suma (usando la continuidad de las derivadas parciales).

La segunda se prueba usando desigualdad del triángulo para integrales y la desigualdad (a) que probamos arriba para la norma de Frobenius.

La tercera se sigue de manera inmediata de la cota hipótesis para la matriz Jacobiana, pues $x+th=x+t(y-x)$ recorre el segmento $xy$ conforme $t$ recorre el intervalo $[0,1]$.

Combinando las tres afirmaciones concluimos

$$\norm{F(x)-F(y)}\leq C\norm{h}=C\norm{y-x},$$

que es justo lo que queríamos probar.

Con esto terminamos los pre-requisitos para probar el TFI. Aquí ya se ve algo interesante sucediendo. En el TFI queremos mostrar que cierta restricción es biyectiva, osea que cierto sistema de ecuaciones tiene una y sólo una solución. Esto se asemeja al teorema del punto fijo de Banach, donde, bajo ciertas condiciones de contracción, hay uno y sólo un punto fijo. El teorema de la desigualdad media puede ayudar a mostrar que una función contrae. Todo esto no es casualidad. A continuación veremos cómo combinar estos ingredientes.

Demostración del TFI

Estamos listos para dar la demostración del teorema de la función inversa. Por comodidad, aquí lo enunciamos de nuevo:

Teorema de la función inversa. Sea $F:\mathbb{R}^n\to \mathbb{R}^n$ una función de clase $\mathcal{C}^1$ con matriz Jacobiana $DF$. Supongamos que $F(a)=b$ y que $DF(a)$ es invertible. Entonces existen vecindades abiertas $U$ y $V$ de $a$ y $b$ respectivamente para las cuales:

a) $F:U\to V$ es una biyección,
b) su inversa $F^{-1}:V\to U$ es de clase $\mathcal{C}^1$ y
c) $DF^{-1}(b)=DF(a)^{-1}$.

Para el teorema necesitamos definir quién es el abierto $U$. Lo tomaremos como $U:=B(a,\epsilon)$, una bola abierta y centrada en $a$ de radio $\epsilon$. La idea es tomar $\epsilon$ tan pequeño como para que para $x\in U$ tengamos que $DF(x)$ sea invertible y

$$\norm{DF(a)-DF(x)}\leq \frac{1}{2\norm{DF(a)^{-1}}}.$$

Ambas cosas las podemos hacer pues la asignación $x \mapsto DF(x)$ es continua ya que $F$ es de clase $\mathcal{C}^1$. En el transcurso de la prueba discutiremos la motivación de esta elección. A $V$ lo tomaremos como $F(U)$.

Lo primero que haremos es reformular parte (a) en términos de puntos fijos. Queremos que la restricción $F:U\to V$ que estamos buscando sea biyectiva. En otras palabras, para $y\in V$ queremos que la ecuación $y=F(x)$ tenga una y sólo una solución $x$ en $U$. Como por hipótesis la matriz $DF(a)$ es invertible, esto sucede si y sólo si

$$x+DF(a)^{-1}(y-F(x))=x,$$

es decir, si y sólo si $x$ es un punto fijo de la función $\varphi_y(x)=x+DF(a)^{-1}(y-F(x))$. Parece un poco artificial haber introducido a $DF(a)^{-1}$, pero como veremos a continuación tiene sentido pues nos ayudará para que $\varphi_y$ sea contracción.

Teniendo en mente que queremos usar la desigualdad del valor medio, calculamos y acotamos la norma de la derivada de $\varphi_y$ como sigue

\begin{align*}
\norm{D\varphi_y (x)} &= \norm{I – DF(a)^{-1} DF(x)} \\
&= \norm{DF(a)^{-1}(DF(a) – DF(x))}\\
&\leq \norm{DF(a)^{-1}}\norm{DF(a)-DF(x)}
\end{align*}

Aquí es donde usamos (y se motiva parte de) nuestra elección de $U$: nos permite acotar $\norm{DF(a)-DF(x)}$ superiormente con $\frac{1}{2\norm{DF(a)^{-1}}} $ y por lo tanto podemos concluir la desigualdad anterior como

\begin{align}\norm{D\varphi_y (x)} \leq \frac{1}{2}.\end{align}

Por la desigualdad del valor medio, concluimos la siguiente observación clave.

Observacion. Para $y$ en $V$ tenemos que $\varphi_y$ es contracción en $U$ con factor $\lambda=\frac{1}{2}$. En otras palabras, para $x,w$ en $U$, tenemos $$\norm{\varphi_y(x)-\varphi_y(w)}\leq \frac{\norm{x-x’}}{2}.$$

La prueba a partir de ahora se divide en los siguientes pasos:

  1. Mostrar que $F:U\to V$ es biyectiva.
  2. Mostrar que $V$ es abierto
  3. Mostrar que $F^{-1}:V\to U$ es diferenciable y y $DF^{-1}(b)=DF(a)^{-1}$
  4. Mostrar que las derivadas parciales son continuas

$F:U\to V$ es biyectiva.

La suprayectividad la tenemos gratis, pues por definición $V=F(U)$.

Para la inyectividad, tomamos $y\in V$ y supongamos que existen $x$ y $w$ en $U$ tales que $F(x)=y=F(w)$. Esto quiere decir que $x$ y $w$ son puntos fijos de la contracción $\varphi_y$. Como vimos en la prueba del teorema del punto fijo de Banach, esto implica que $x=w$. Así, $x=w$, de modo que $F:U\to V$ es inyectiva y por lo tanto es biyectiva.

Nota: Aquí no estamos usamos el teorema del punto fijo de Banach pues $U$ no es compacto. Sólo estamos usando que las contracciones son inyectivas.

$V$ es abierto

Tomemos $y’$ en $V$, es decir, para la cual existe $x’$ en $U$ con $F(x’)=y’$. Queremos ver que si «$y$ está muy cerquita de $y’$» , entonces hay una solución para $F(x)=y$ con $x$ en $U$.

Como $U$ es abierto, existe $r$ tal que la bola $B(x’,2r)$ abierta de centro $x’$ y radio $2r$ se queda contenida en $U$. Tomemos $y$ en la bola $B\left(y’,\frac{r}{2\norm{DF(a)^{-1}}}\right)$. Vamos a ver que $F(x)=y$ tiene solución en $U$. Consideremos la función $\varphi_y$, pero restringida a la bola cerrada $X:=\overline{B}(x’,r)\subset U$. Mostraremos que la imagen de $\varphi_y$ se queda contenida en $\overline{B}(x’,r)$. En efecto:

\begin{align*}
\norm{\varphi_y(x)-x’}&=\norm{\varphi_y(x)-\varphi_y(x’)+DF(a)^{-1}(y-y’)}\\
&\leq \norm{\varphi_y(x)-\varphi_y(x’)}+\norm{DF(a)^{-1}}\norm{y-y’}\\
&\leq \frac{\norm{x-x’}}{2}+\frac{r}{2}\leq r.
\end{align*}

De este modo, $\varphi_y$ es una contracción del compacto $X$ a sí mismo. Por lo tanto, tiene un punto fijo en $X$, de modo que $F(x)=y$ para $x\in X\subset U$. Esto muestra que $V=F(U)$ es abierto.

$F^{-1}:V\to U$ es diferenciable y $DF^{-1}(b)=DF(a)^{-1}$

Vamos a demostrar que $F^{-1}:V\to U$ es diferenciable a partir de la definición de diferenciabilidad. Más aún, veremos que si $y=F(x)$ para $x$ en $U$, entonces $DF^{-1}(y)=DF(x)^{-1}$. Aquí es donde se termina de motivar nuestra elección en $U$, pues nos garantiza que a la derecha en efecto tenemos una matriz invertible.

Tomemos entonces $y=F(x)$. Nos interesa el límite cuando $\norm{h}\to 0$ de la siguiente expresión

$$\frac{\norm{F^{-1}(y+h)-F^{-1}(y)-DF(x)^{-1}h}}{\norm{h}},$$

Como $U$ es abierto, si $\norm{h}$ es pequeña entonces $y+h$ está en $U$. De este modo, existe $k$ tal que $x+k \in U$ y $F(x+k)=y+h$. Así, la expresión anterior la podemos reescribir como

\begin{align}\frac{\norm{DF(x)^{-1}(F(x+k)-F(x)-DF(x)k)}}{\norm{k}}\frac{\norm{k}}{\norm{h}}\end{align}

Antes de continuar, probemos una desigualdad auxiliar. Notemos que

\begin{align*}
\norm{k}-\norm{DF^{-1}(a)h} &\leq \norm{k-DF^{-1}(a)h}\\
&=\norm{\varphi_y(x+k)-\varphi_y(x)}\\
&\leq\frac{\norm{k}}{2},
\end{align*}

así,

\begin{align}\norm{k}\leq 2\norm{DF^{-1}(a)h} \leq 2\norm{DF^{-1}(a)}\norm{h}.\end{align}

Substituyendo el valor de $\norm{k}$ en (2), concluimos que la expresión es menor o igual a

\begin{align}2\norm{DF(x)^{-1}}\frac{\norm{F(x+k)-F(x)-DF(x)k}}{\norm{k}}\norm{DF^{-1}(a)}\end{align}

Estamos listos para terminar. La desigualdad (3) también garantiza que $\norm{k}\to 0$ cuando $\norm{h}\to 0$. Así, como $F$ es diferenciable, tenemos que la expresión (4) tiende a $0$. Esto muestra que $F^{-1}$ es diferenciable en $y$ con $DF^{-1}(y)=DF(x)^{-1}$, tal como queríamos.

Las derivadas parciales son continuas

Esta parte es sencilla a partir de la parte anterior. Tenemos que:

$$DF^{-1}(b)=DF(F^{-1}(b))^{-1}$$

Por la regla de Cramer la inversa de una matriz depende continuamente de las entradas de la matriz original. Además, la asignación $b \mapsto F^{-1}(b)$ es continua. Así, las entradas de $DF^{-1}(b)$ (las derivadas parciales de $F^{-1}$) dependen continuamente de las derivadas parciales de $F$, que dependen continuamente de $b$ por hipótesis.

Con esto termina la prueba.

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario: