En mi opinión, todas las cosas en la naturaleza ocurren matemáticamente.
– Descartes
Introducción
Continuaremos con nuestro estudio cualitativo de los sistemas lineales homogéneos compuestos por dos ecuaciones diferenciales de primer orden con coeficientes constantes.
\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx + dy \label{1} \tag{1}
\end{align*}
Este sistema lo podemos escribir como
$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{2} \tag{2}$$
en donde
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix}, \hspace{1cm} \mathbf{Y} = \begin{pmatrix}
x \\ y
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix}$$
En esta entrada analizaremos el caso en el que los vectores propios de $\mathbf{A}$ son repetidos.
El caso $\lambda_{1} = \lambda_{2} = 0$ lo revisaremos en la siguiente entrada cuando veamos que ocurre si uno o ambos de los valores propios son nulos.
Los casos que estudiaremos son
- $\lambda_{1} = \lambda_{2} < 0$
- $\lambda_{1} = \lambda_{2} > 0$
Sin embargo se presentan dos situaciones distintas en este caso.
Recordemos que cuando estudiamos este caso en la unidad anterior se presentaba el problema de que podían faltarnos soluciones linealmente independientes que nos permitieran determinar la solución general del sistema. Por ejemplo, si el sistema está compuesto por $n$ ecuaciones diferenciales de primer orden, entonces debemos encontrar $n$ soluciones linealmente independientes para poder formar la solución general, sin embargo, si algunos valores propios resultan ser repetidos, entonces sólo obtendremos $k$ soluciones linealmente independientes, una por cada valor propio distinto, y nos faltarán encontrar $n -k$ soluciones para formar la solución general. Los conceptos de exponencial de una matriz y de vector propio generalizado resultaron útiles para resolver este problema.
En este caso estamos estudiando un sistema con dos ecuaciones diferenciales lo que vuelve al problema anterior relativamente más sencillo, pues habrá ocasiones en los que es posible determinar dos vectores propios de $\mathbf{A}$ linealmente independientes asociados al mismo valor propio $\lambda$, pero en otras ocasiones sólo habrá un vector propio asociado al único valor propio $\lambda$, así que tendremos que encontrar un vector propio generalizado. Por supuesto, cada caso tendrá efectos muy distintos en el plano fase del sistema.
Estudiemos cada situación y hagamos un análisis cualitativo para cada caso.
Sistemas con vectores propios arbitrarios
Consideremos la matriz
$$\mathbf{A} = \begin{pmatrix}
\lambda & 0 \\ 0 & \lambda
\end{pmatrix} \label{3} \tag{3}$$
con $\lambda$ una constante.
Notemos lo siguiente.
$$\mathbf{AK} = \begin{pmatrix}
\lambda & 0 \\ 0 & \lambda
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
\lambda k_{1} \\ \lambda k_{2}
\end{pmatrix} = \lambda \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \lambda \mathbf{K}$$
Hemos obtenido que
$$\mathbf{AK} = \lambda \mathbf{K} \label{4} \tag{4}$$
Es decir, $\lambda$ es el valor propio de $\mathbf{A}$.
Intentemos determinar los vectores propios de $\mathbf{A}$.
$$(\mathbf{A} -\lambda \mathbf{I}) \mathbf{K} = \begin{pmatrix}
\lambda -\lambda & 0 \\ 0 & \lambda -\lambda
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 & 0 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Vemos que cualquier vector
$$\mathbf{K} = \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} \label{5} \tag{5}$$
es vector propio de $\mathbf{A}$.
Supongamos que la matriz (\ref{3}) es la matriz de coeficientes de un sistema lineal
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
\lambda & 0 \\ 0 & \lambda
\end{pmatrix} \mathbf{Y} \label{6} \tag{6}$$
Considerando los resultados anteriores podemos establecer que su solución general es de la forma
$$\mathbf{Y}(t) = c_{1}e^{\lambda t} \mathbf{K}_{1} + c_{2}e^{\lambda t} \mathbf{K}_{2} \label{7} \tag{7}$$
En donde $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ son vectores propios de $\mathbf{A}$ linealmente independientes. Como vimos, estos vectores pueden ser arbitrarios, así que podemos elegir los vectores canónicos
$$\mathbf{K}_{1} = \begin{pmatrix}
1 \\ 0
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{K}_{2} = \begin{pmatrix}
0 \\ 1
\end{pmatrix}$$
De esta forma, la solución general del sistema (\ref{6}) es
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \begin{pmatrix}
1 \\ 0
\end{pmatrix} + c_{2} e^{\lambda t} \begin{pmatrix}
0 \\ 1
\end{pmatrix} \label{8} \tag{8}$$
Si dejamos de usar la notación matricial y escribimos las funciones $x(t)$ y $y(t)$, tenemos
\begin{align*}
x(t) &= c_{1} e^{\lambda t} \\
y(t) &= c_{2} e^{\lambda t} \label{9} \tag{9}
\end{align*}
Observemos que
$$\dfrac{y}{x} = \dfrac{c_{2}}{c_{1}}$$
es decir,
$$y(x) = Cx \label{10} \tag{10}$$
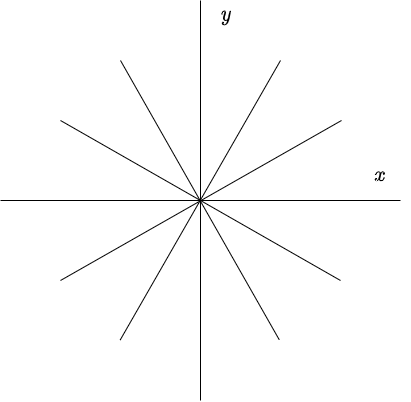
Con $C$ una constante. Esta función en el plano $XY$ o plano fase corresponde a infinitas rectas, una por cada posible valor de la constante $C$.
Este caso corresponde a una situación de las dos que pueden ocurrir. Aún nos falta determinar el sentido de las trayectorias en el plano fase, éste será determinado por el signo de los valores propios.
A continuación haremos un análisis más detallado sobre los casos que se pueden presentar.
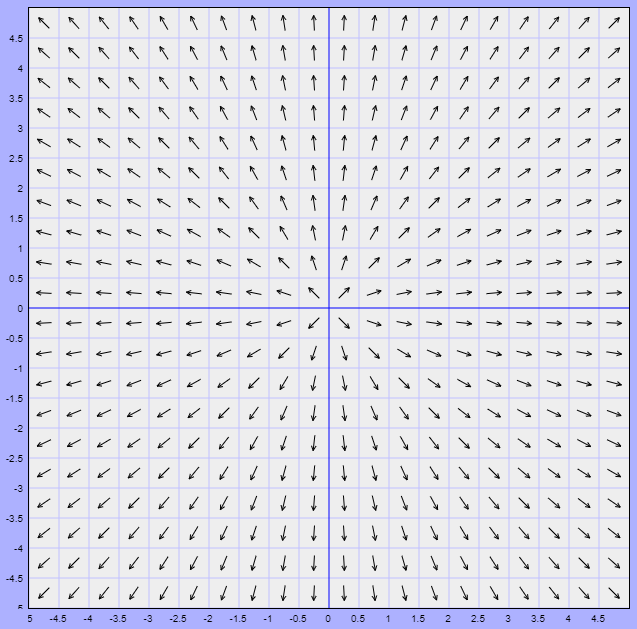
Sistemas lineales con valores propios negativos repetidos
Caso 1a: $\lambda_{1} = \lambda_{2} = \lambda < 0$ y dos vectores linealmente independientes.
Este caso corresponde al visto anteriormente.
Supongamos que la matriz $\mathbf{A}$ del sistema (\ref{1}) tiene dos vectores propios linealmente independientes $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ con valor propio $\lambda < 0$. En este caso la solución general del sistema (\ref{1}) se puede expresar como
$$\mathbf{Y}(t) = c_{1}e^{\lambda t}\mathbf{K}_{1} + c_{2}e^{\lambda t} \mathbf{K}_{2} = e^{\lambda t} (c_{1} \mathbf{K}_{1} + c_{2} \mathbf{K}_{2}) \label{11} \tag{11}$$
Observemos que el vector $e^{\lambda t} (c_{1} \mathbf{K}_{1} + c_{2} \mathbf{K}_{2})$ es paralelo al vector $(c_{1} \mathbf{K}_{1} + c_{2} \mathbf{K}_{2})$ para toda $t$. Por lo tanto, la trayectoria de cualquier solución $\mathbf{Y}(t)$ de (\ref{1}) es una semirrecta en el plano fase.
Como $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ son linealmente independientes, el conjunto de vectores $\left \{ c_{1} \mathbf{K}_{1} + c_{2} \mathbf{K}_{2} \right \}$, para todas las elecciones de $c_{1}$ y $c_{2}$, cubren cualquier dirección en el plano $XY$.
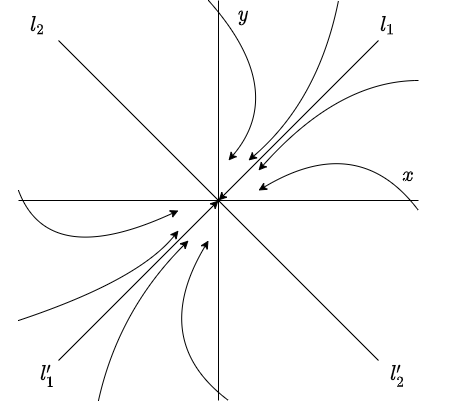
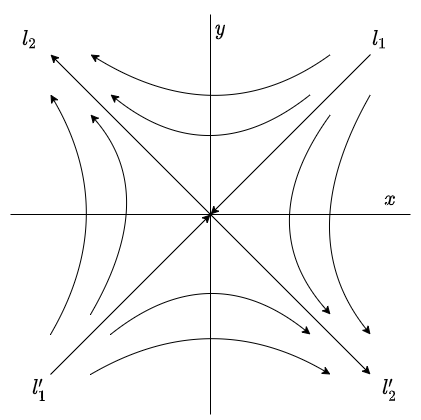
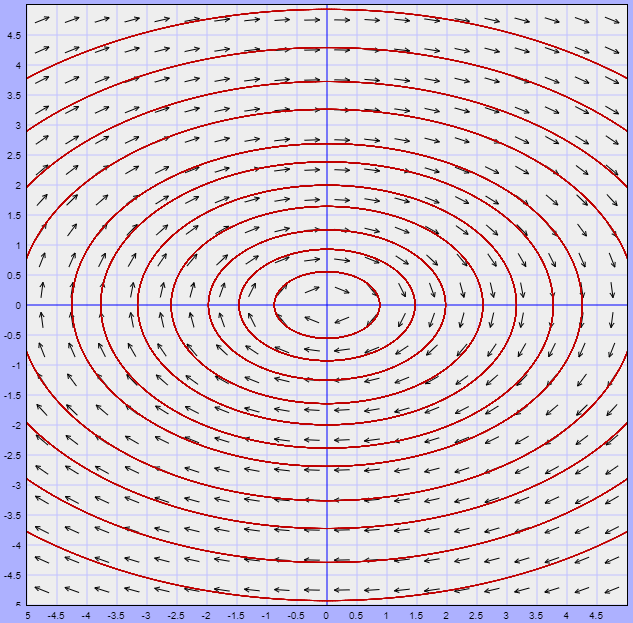
El plano fase con estas características es el siguiente.
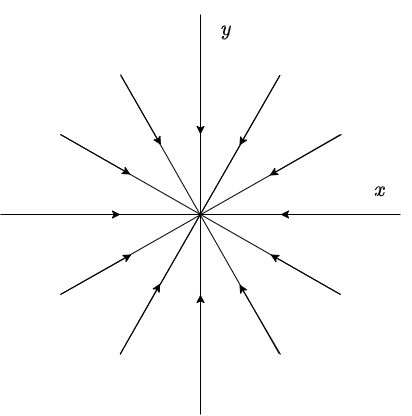
El sentido de las trayectorias es hacia el origen debido a que si $t \rightarrow \infty$, entonces $e^{\lambda t} \rightarrow 0$ ya que $\lambda < 0$.
Se dice que el punto de equilibrio $Y_{0} = (0, 0)$ es un atractor y es asintóticamente estable.
Caso 1b: $\lambda_{1} = \lambda_{2} = \lambda < 0$ y sólo un vector linealmente independiente.
Este caso resulta ser más interesante. Supongamos que $\mathbf{A}$ tiene solamente un vector propio $\mathbf{K}$ linealmente independiente, con valor propio $\lambda$. La solución de (\ref{1}) en este caso es
$$\mathbf{Y}_{1}(t) = e^{\lambda t} \mathbf{K} \label{12} \tag{12}$$
Para encontrar una segunda solución de (\ref{1}) que sea linealmente independiente de $\mathbf{Y}_{1}$ buscamos un vector $\hat{\mathbf{K}}$, tal que se cumpla simultáneamente
$$(\mathbf{A} -\lambda \mathbf{I})^{2} \hat{\mathbf{K}} = \mathbf{0} \hspace{1cm} y \hspace{1cm} (\mathbf{A} -\lambda \mathbf{I}) \hat{\mathbf{K}} \neq \mathbf{0} \label{13} \tag{13}$$
Es decir, $\hat{\mathbf{K}}$ es un vector propio generalizado y sabemos que una segunda solución de (\ref{1}) es de la forma
$$\mathbf{Y}_{2}(t) = e^{\lambda t} \left[ \hat{\mathbf{K}} + t(\mathbf{A} -\lambda \mathbf{I}) \hat{\mathbf{K}} \right] \label{14} \tag{14}$$
De modo que la solución general del sistema (\ref{1}), en este caso, es
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \mathbf{K} + c_{2} e^{\lambda t} \left[ \hat{\mathbf{K}} + t(\mathbf{A} -\lambda \mathbf{I}) \hat{\mathbf{K}} \right] \label{15} \tag{15}$$
para alguna elección de constantes $c_{1}$ y $c_{2}$.
Esta ecuación puede simplificarse observando que $(\mathbf{A} -\lambda \mathbf{I}) \hat{\mathbf{K}}$ debe ser un múltiplo $k$ de $\mathbf{K}$. Esto se sigue inmediatamente de la ecuación
$$(\mathbf{A} -\lambda \mathbf{I}) \left[ (\mathbf{A} -\lambda \mathbf{I}) \hat{\mathbf{K}} \right ] = \mathbf{0} \label{16} \tag{16}$$
y el hecho de que $\mathbf{A}$ sólo tiene un vector propio $\mathbf{K}$ linealmente independiente.
Entonces, la solución (\ref{15}) puede escribirse como
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \mathbf{K} + c_{2} e^{\lambda t}(\hat{\mathbf{K}} + tk \mathbf{K}) = e^{\lambda t}(c_{1} \mathbf{K} + c_{2} \hat{\mathbf{K}} + c_{2} tk \mathbf{K}) \label{17} \tag{17}$$
Observemos que toda solución de (\ref{1}) de la forma (\ref{17}) tiende a $(0, 0)$ cuando $t$ tiende a infinito. Además, notemos que $c_{1} \mathbf{K} + c_{2} \hat{\mathbf{K}}$ es muy pequeño comparado con $c_{2} tk \mathbf{K}$ si $c_{2}$ es diferente de cero y $t$ es muy grande. Por lo tanto, la tangente a la trayectoria de $\mathbf{Y}(t)$ tiende a $\pm \mathbf{K}$, dependiendo del signo de $c_{2}$, cuando $t$ tiende a infinito.
El plano fase con estas características es el siguiente.
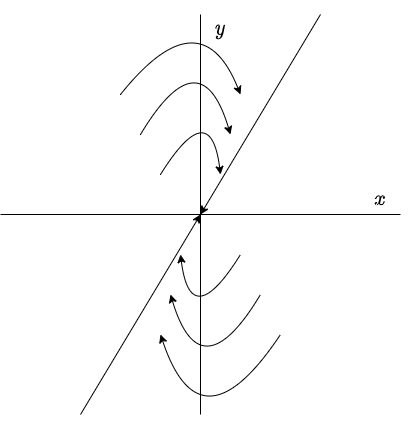
Nuevamente decimos que el punto de equilibrio $Y_{0} = (0, 0)$ es un atractor y es asintóticamente estable ya que todas las trayectorias tienden a él.
Ambas situaciones también se presentan cuando $\lambda > 0$.
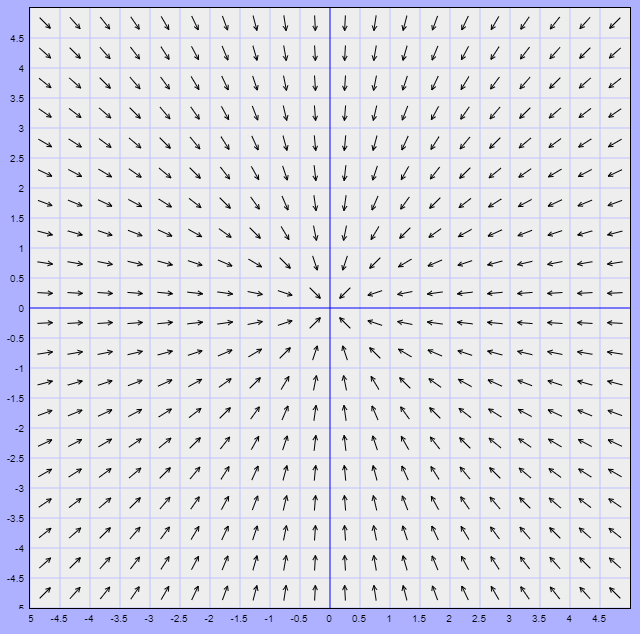
Sistemas lineales con valores propios positivos repetidos
Caso 2a: $\lambda_{1} = \lambda_{2} = \lambda > 0$ y dos vectores linealmente independientes.
Sean $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ los dos vectores linealmente independientes de la matriz de coeficientes $\mathbf{A}$ asociados al único valor propio $\lambda$. Nuevamente la solución general de (\ref{1}) será
$$\mathbf{Y}(t) = c_{1}e^{\lambda t}\mathbf{K}_{1} + c_{2}e^{\lambda t} \mathbf{K}_{2} = e^{\lambda t} (c_{1} \mathbf{K}_{1} + c_{2} \mathbf{K}_{2})$$
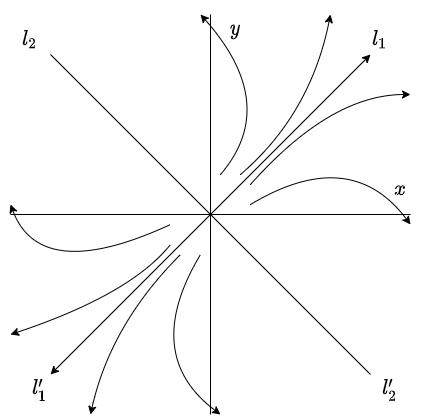
El análisis es exactamente el mismo que en el caso 1a, sin embargo, como $\lambda > 0$, entonces $e^{\lambda t} \rightarrow \infty$ conforme $t \rightarrow \infty$. Por lo tanto, el plano fase para este caso es exactamente el mismo que el del caso 1a con la excepción de que el sentido de las flechas es el opuesto.
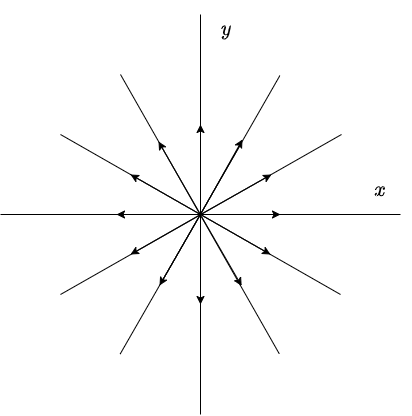
En este caso se dice que el punto de equilibrio $Y_{0} = (0, 0)$ es un repulsor, por lo tanto inestable.
Concluyamos con el último caso.
Caso 2b: $\lambda_{1} = \lambda_{2} = \lambda > 0$ y sólo un vector linealmente independiente.
Sea $\mathbf{K}$ el único vector propio de $\mathbf{A}$ asociado al valor propio $\lambda$. Y sea $\hat{\mathbf{K}}$ un vector propio generalizado de $\mathbf{A}$. La solución general del sistema lineal (\ref{1}) es
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \mathbf{K} + c_{2} e^{\lambda t} \left[ \hat{\mathbf{K}} + t(\mathbf{A} -\lambda \mathbf{I}) \hat{\mathbf{K}} \right]$$
Vimos anteriormente que esta solución puede escribirse como
$$\mathbf{Y}(t) = e^{\lambda t}(c_{1} \mathbf{K} + c_{2} \hat{\mathbf{K}} + c_{3} t \mathbf{K})$$
En este caso las trayectorias son exactamente las mismas que en el caso 2a por el mismo análisis, sin embargo la dirección de las flechas es el opuesto debido a que $\lambda > 0$.
El plano fase es el siguiente.
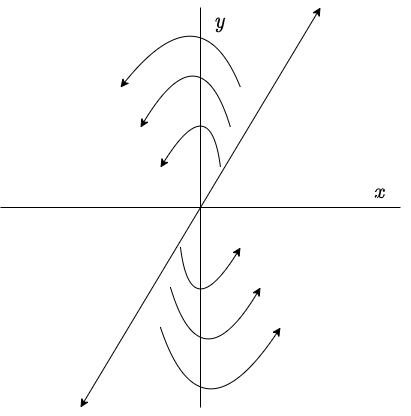
El punto de equilibrio $Y_{0} = (0, 0)$ es un repulsor e inestable.
Concluyamos esta entrada realizando un ejemplo por cada caso.
Comencemos con un ejemplo del caso 1a y 2a.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-5 & 0 \\ 0 & -5
\end{pmatrix} \mathbf{Y}$$
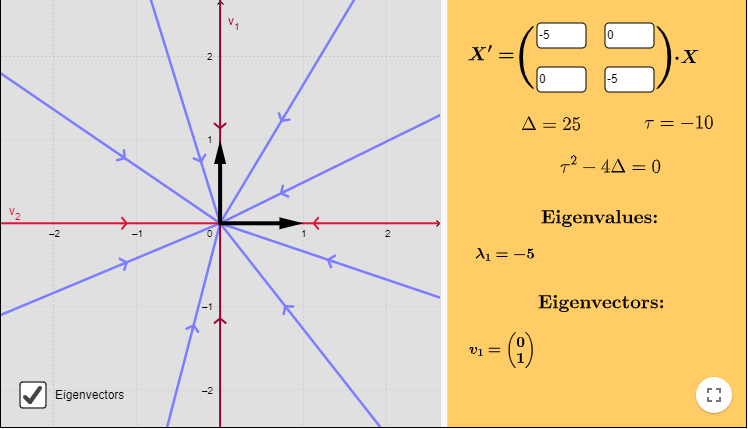
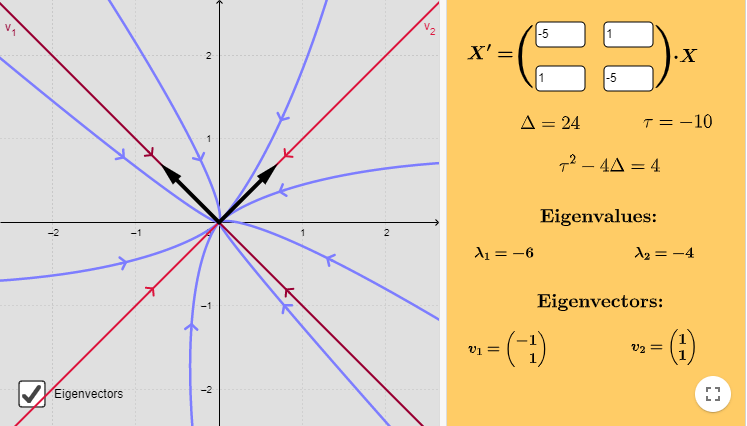
Solución: Nuestro ejemplo corresponde a un sistema lineal de la forma (\ref{6}), de manera que el único valor propio es $\lambda = -5$. Sólo para verificarlo veamos que
$$\begin{vmatrix}
-5 -\lambda & 0 \\ 0 & -5 -\lambda
\end{vmatrix} = (-5 -\lambda)^{2} = 0$$
La única raíz es $\lambda = -5$, es decir, hay un valor propio con multiplicidad $2$.
Cualquier par de vectores linealmente independientes son vectores propios de la matriz de coeficientes. Elegimos los vectores canónicos.
$$\mathbf{K}_{1} = \begin{pmatrix}
1 \\ 0
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{K}_{2} = \begin{pmatrix}
0 \\ 1
\end{pmatrix}$$
Por lo tanto, la solución general es
$$\mathbf{Y}(t) = c_{1}e^{-5t} \begin{pmatrix}
1 \\ 0
\end{pmatrix} + c_{2}e^{-5t} \begin{pmatrix}
0 \\ 1
\end{pmatrix}$$
Las solución la podemos escribir como
\begin{align*}
x(t) &= c_{1}e^{-5t} \\
y(t) &= c_{2}e^{-5t}
\end{align*}
Notemos que si $t \rightarrow \infty$, entonces $(x, y) \rightarrow (0, 0)$, lo que nos indica que las semirrectas correspondientes a las soluciones del sistema tienden al punto de equilibrio $Y_{0} = (0, 0)$, esto convierte a dicho punto en un atractor.
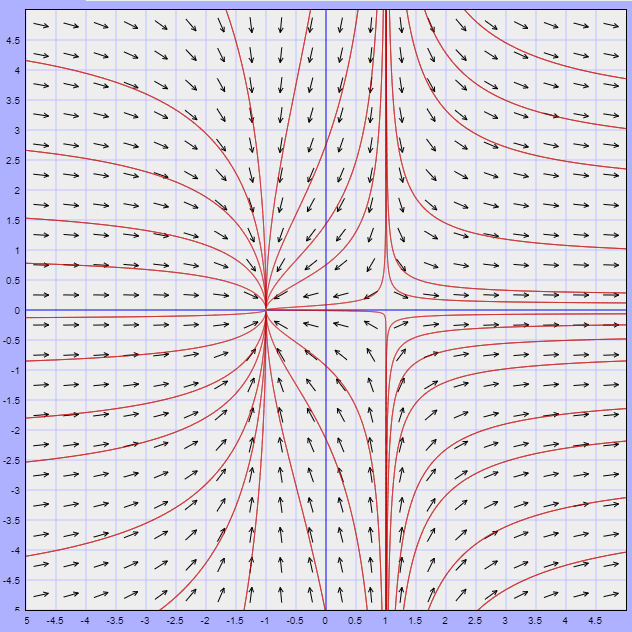
El plano fase, indicando algunas trayectorias y los vectores propios, se muestra a continuación.
La función vectorial que define al campo vectorial es
$$F(x, y) = (-5x, -5y)$$
En la siguiente figura se muestra el campo vectorial y algunas trayectorias correspondientes a soluciones particulares del sistema.
$\square$
Si modificamos el sistema del ejemplo anterior por
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
5 & 0 \\ 0 & 5
\end{pmatrix}\mathbf{Y}$$
Entonces, la solución general será
$$\mathbf{Y}(t) = c_{1}e^{5t} \begin{pmatrix}
1 \\ 0
\end{pmatrix} + c_{2}e^{5t} \begin{pmatrix}
0 \\ 1
\end{pmatrix}$$
O bien,
\begin{align*}
x(t) &= c_{1}e^{5t} \\
y(t) &= c_{2}e^{5t}
\end{align*}
En este caso $x(t)$ y $y(t)$ tienden a infinito conforme $t$ también lo hace. Las trayectorias corresponden a semirrectas que parten del origen hacia infinito, por tanto, $Y_{0} = (0, 0)$ es un repulsor.
El plano fase es el siguiente.
$\square$
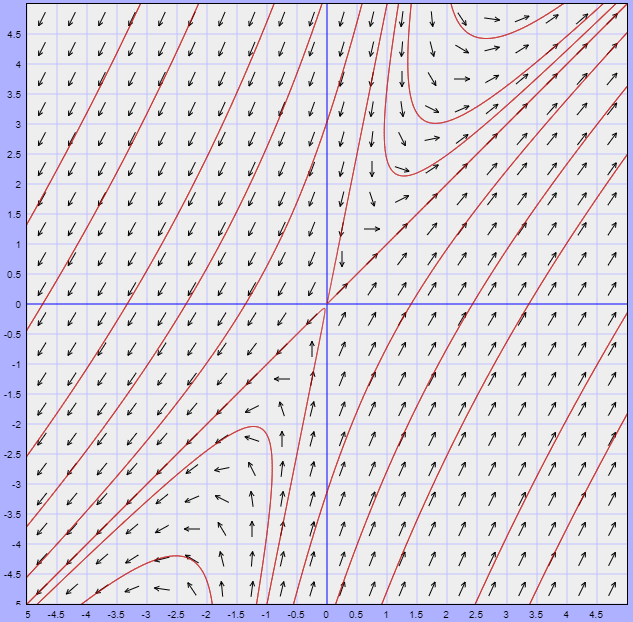
Ahora veamos un ejemplo para el caso 1b y uno para el caso 2b, es decir, en la situación en la que sólo tenemos un único vector propio.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
1 & -1 \\ 1 & 3
\end{pmatrix} \mathbf{Y}$$
Solución: Determinemos los valores propios.
$$\begin{vmatrix}
1 -\lambda & -1 \\ 1 & 3 -\lambda
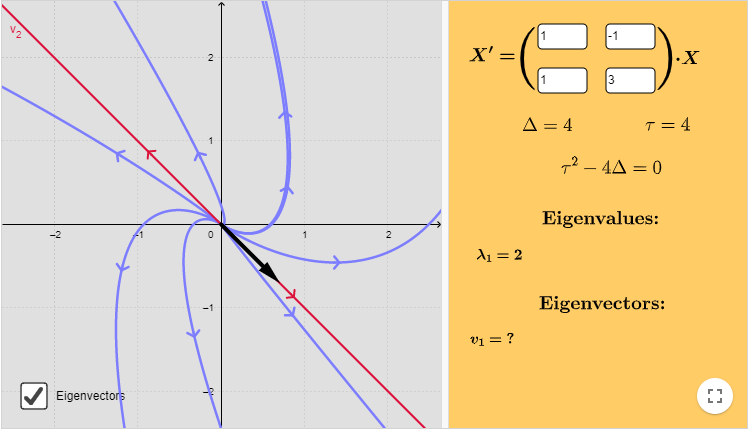
\end{vmatrix} = \lambda^{2} -4 \lambda + 4 = (\lambda -2)^{2} = 0$$
El valor propio con multiplicidad $2$ es $\lambda = 2$. Determinemos un vector propio resolviendo la siguiente ecuación.
$$(\mathbf{A} -2 \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
-1 & -1 \\ 1 & 1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Del sistema obtenemos que $k_{1} = -k_{2}$. Sea $k_{1} = 1$, entonces $k_{2} = -1$. Por lo tanto, el vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
1 \\ -1
\end{pmatrix}$$
Determinemos ahora un vector propio generalizado resolviendo la siguiente ecuación.
$$(\mathbf{A} -2 \mathbf{I})^{2} \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
-1 & -1 \\ 1 & 1
\end{pmatrix} \begin{pmatrix}
-1 & -1 \\ 1 & 1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 & 0 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Esta ecuación se cumple para cualquier vector que no sea vector propio, es decir, que cumpla que
$$(\mathbf{A} -2 \mathbf{I}) \mathbf{K} \neq \mathbf{0}$$
Como el único vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
1 \\ -1
\end{pmatrix}$$
Elegimos el vector ortogonal
$$\mathbf{K}_{2} = \begin{pmatrix}
1 \\ 1
\end{pmatrix}$$
Notemos que se cumple
$$\begin{pmatrix}
1 \\ 1
\end{pmatrix} = c \begin{pmatrix}
1 \\ -1
\end{pmatrix}$$
sólo si $c = 0$, así que ambos vectores $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ son linealmente independientes.
La solución general del sistema tiene la siguiente forma.
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \mathbf{K}_{1} + c_{2} e^{\lambda t} \left[ \mathbf{K}_{2} + t(\mathbf{A} -\lambda \mathbf{I}) \mathbf{K}_{2} \right]$$
Sustituyendo, se tiene
\begin{align*}
\mathbf{Y}(t) &= c_{1}e^{2t} \begin{pmatrix}
1 \\ -1
\end{pmatrix} + c_{2}e^{2t} \left[ \begin{pmatrix}
1 \\ 1
\end{pmatrix} + t \begin{pmatrix}
-1 & -1 \\ 1
& 1
\end{pmatrix} \begin{pmatrix}
1 \\ 1
\end{pmatrix} \right] \\
&= c_{1}e^{2t} \begin{pmatrix}
1 \\ -1
\end{pmatrix} + c_{2}e^{2t} \left[ \begin{pmatrix}
1 \\ 1
\end{pmatrix} + t \begin{pmatrix}
-2 \\ 2
\end{pmatrix} \right] \\
&= c_{1}e^{2t} \begin{pmatrix}
1 \\ -1
\end{pmatrix} + c_{2}e^{2t} \left[ \begin{pmatrix}
1 \\ 1
\end{pmatrix} + 2t \begin{pmatrix}
-1 \\ 1
\end{pmatrix} \right]
\end{align*}
La solución general del sistema es
$$\mathbf{Y}(t) = c_{1}e^{2t} \begin{pmatrix}
1 \\ -1
\end{pmatrix} + c_{2}e^{2t} \left[ \begin{pmatrix}
1 \\ 1
\end{pmatrix} -2t \begin{pmatrix}
1 \\ -1
\end{pmatrix} \right]$$
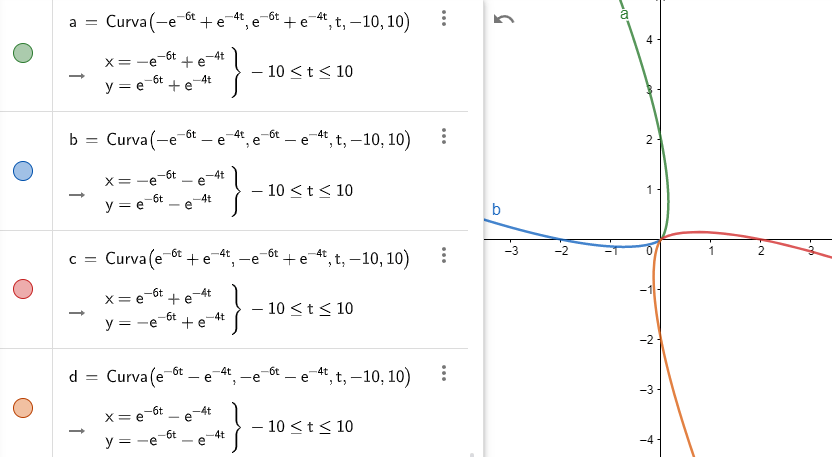
Observemos que, tal como lo mostramos en la teoría (\ref{17}), esta solución es de la forma
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \mathbf{K}_{1} + c_{2} e^{\lambda t}(\mathbf{K}_{2} + tk \mathbf{K}_{1})$$
Las funciones $x(t)$ y $y(t)$ son
\begin{align*}
x(t) &= c_{1}e^{2t} + c_{2}e^{2t}(1 -2t) \\
y(t) &= -c_{1}e^{2t} + c_{2}e^{2t}(1+ 2t)
\end{align*}
Muestra explícitamente que
$$\lim_{t \to -\infty} x(t) = \lim_{t \to -\infty} y(t) = 0$$
Mientras que
$$\lim_{t \to \infty} x(t) = \lim_{t \to \infty} y(t) = \infty$$
Esto nos indica que las trayectorias parten del origen y se extienden por todo el plano infinitamente.
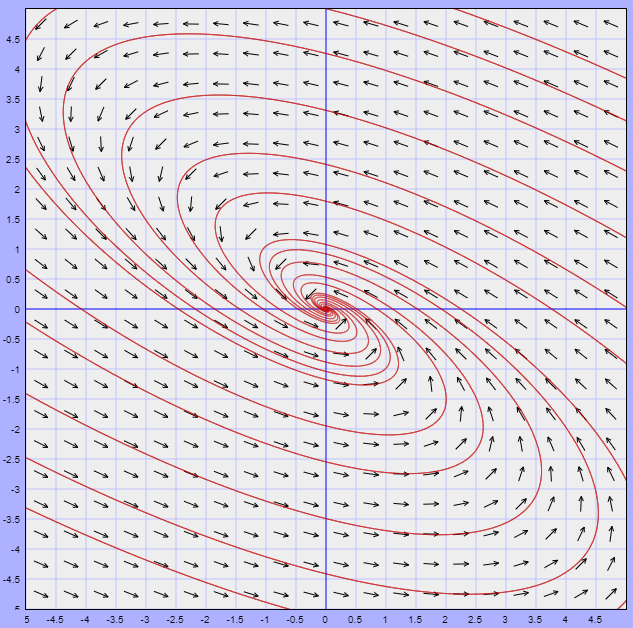
A continuación se muestra el correspondiente plano fase del sistema indicando algunas trayectorias y al único vector propio de la matriz $\mathbf{A}$.
El punto de equilibrio $Y_{0} = (0, 0)$ es un repulsor.
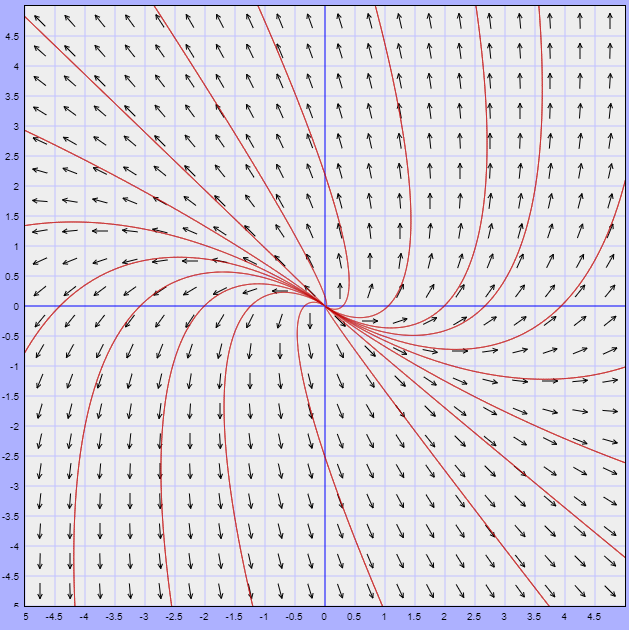
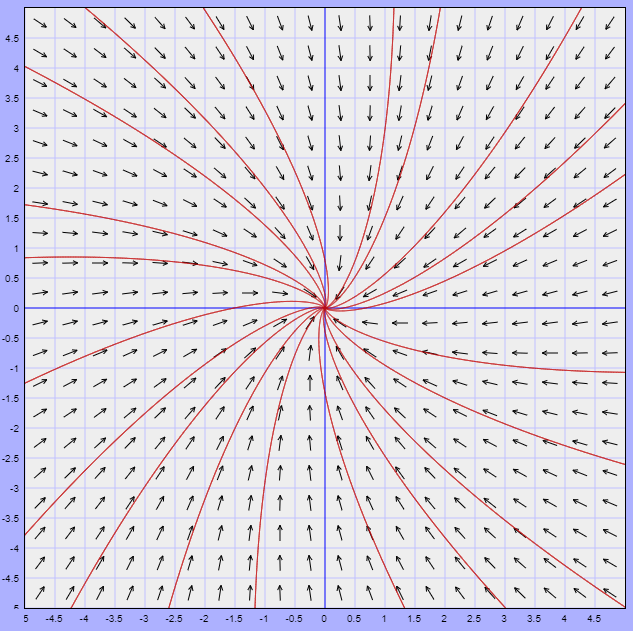
El campo vectorial asociado lo obtenemos de la función vectorial
$$F(x, y) = (x -y,x +3y)$$
El campo vectorial y algunas trayectoria del sistema se visualizan en la siguiente figura.
$\square$
Realicemos un último ejemplo.
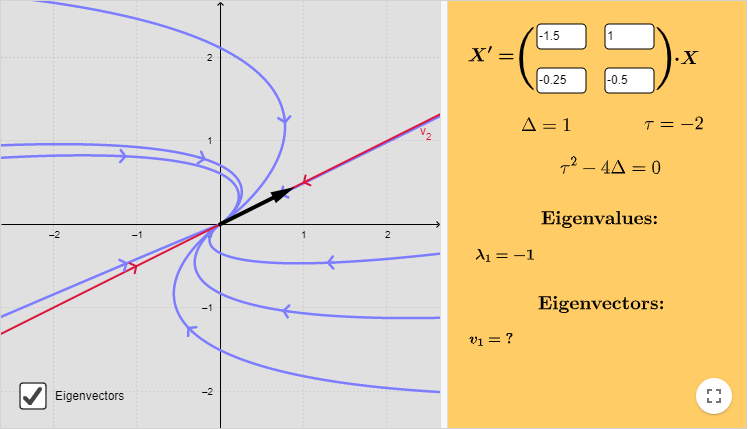
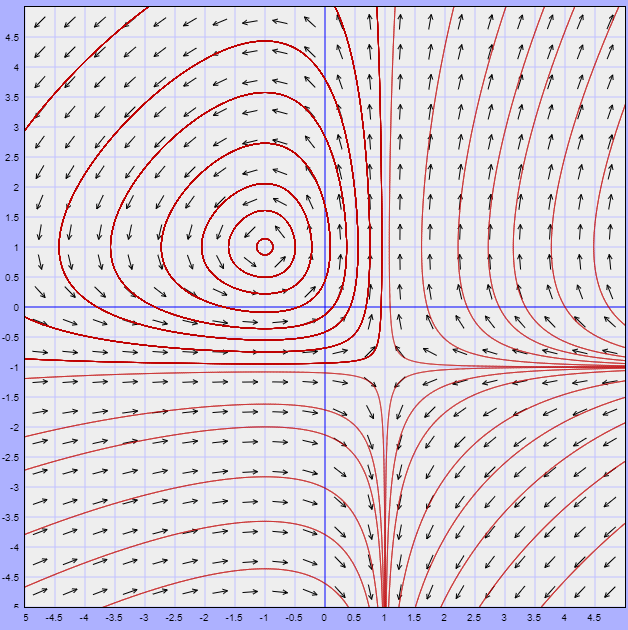
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-3/2 & 1 \\ -1/4 & -1/2
\end{pmatrix} \mathbf{Y}$$
Solución: Determinemos los valores propios.
$$\begin{vmatrix}
-3/2 -\lambda & 1 \\ -1/4 & -1/2 -\lambda
\end{vmatrix} = \lambda^{2} + 2 \lambda + 1 = (\lambda + 1)^{2} = 0$$
El valor propio es $\lambda = -1$ con multiplicidad $2$. Determinemos un vector propio resolviendo la siguiente ecuación.
$$(\mathbf{A} + \mathbf{I}) \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
-1/2 & 1 \\ -1/4 & 1/2
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Del sistema obtenemos que $k_{2} = \dfrac{1}{2}k_{1}$. Sea $k_{1} = 2$, entonces $k_{2} = 1$. Por lo tanto, el vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
2 \\ 1
\end{pmatrix}$$
Determinemos un vector propio generalizado resolviendo la siguiente ecuación.
$$(\mathbf{A} -\mathbf{I})^{2} \mathbf{K} = \mathbf{0}$$
o bien,
$$\begin{pmatrix}
-1/2 & 1 \\ -1/4 & 1/2
\end{pmatrix} \begin{pmatrix}
-1/2 & 1 \\ -1/4 & 1/2
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 & 0 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Nuevamente podemos elegir cualquier vector arbitrario que no sea vector propio, es decir, que cumpla que
$$(\mathbf{A} + \mathbf{I}) \mathbf{K} \neq \mathbf{0}$$
Elegimos el vector
$$\mathbf{K}_{2} = \begin{pmatrix}
0 \\ 2
\end{pmatrix}$$
La ecuación
$$\begin{pmatrix}
0 \\ 2
\end{pmatrix} = c \begin{pmatrix}
2 \\ 1
\end{pmatrix} $$
se cumple sólo si $c = 0$, por lo tanto $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ son linealmente independientes.
Sabemos que la solución general es de la forma
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \mathbf{K}_{1} + c_{2} e^{\lambda t} \left[ \mathbf{K}_{2} + t(\mathbf{A} -\lambda \mathbf{I}) \mathbf{K}_{2} \right]$$
Sustituyendo, se tiene
\begin{align*}
\mathbf{Y}(t) &= c_{1}e^{-t} \begin{pmatrix}
2 \\ 1
\end{pmatrix} + c_{2}e^{-t} \left[ \begin{pmatrix}
0 \\ 2
\end{pmatrix} + t \begin{pmatrix}
-1/2 & 1 \\ -1/4 & 1/2
\end{pmatrix} \begin{pmatrix}
0 \\ 2
\end{pmatrix} \right] \\
&= c_{1}e^{ -t} \begin{pmatrix}
2 \\ 1
\end{pmatrix} + c_{2}e^{ -t} \left [ \begin{pmatrix}
0 \\ 2
\end{pmatrix} + t \begin{pmatrix}
2 \\ 1
\end{pmatrix} \right]
\end{align*}
Esta solución la podemos escribir como
\begin{align*}
x(t) &= 2c_{1}e^{-t} + 2c_{2}te^{-t} \\
y(t) &= c_{1}e^{-t} + c_{2}e^{-t}(2 + t)
\end{align*}
En este caso nos interesa el caso límite $t \rightarrow \infty$. Muestra explícitamente que
$$\lim_{t \to \infty} x(t) = \lim_{t \to \infty} y(t) = 0$$
Este resultado nos indica que las trayectorias del sistema tienden al origen. Para valores grandes de $t$ las funciones $x(t)$ y $y(t)$ se pueden aproximar por
\begin{align*}
x(t) &\approx 2c_{2}te^{-t} \\
y(t) &\approx c_{2}te^{-t}
\end{align*}
Es decir, la tangente de las trayectorias tienden hacia la recta paralela al vector propio $\mathbf{K}_{1}$, esto lo podemos ver si escribimos a $y$ en función de $x$, dicha función es
$$y(x) \approx \dfrac{x}{2}$$
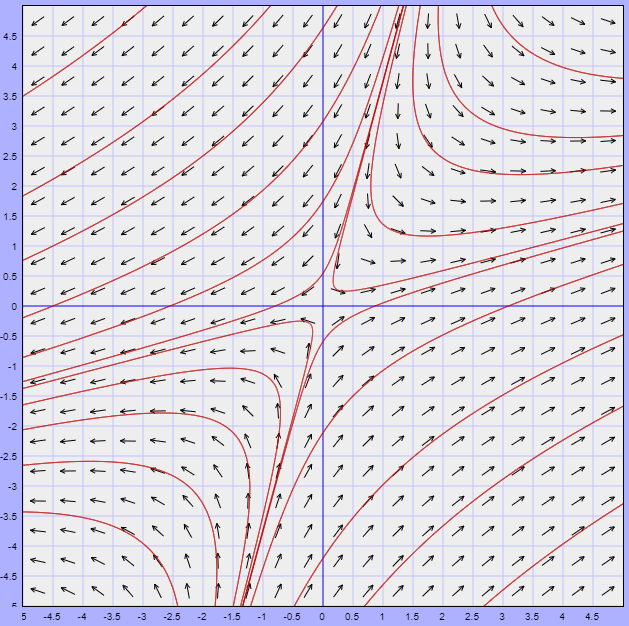
El plano fase, indicando algunas trayectorias y al único vector propio, se muestra a continuación.
El punto de equilibrio $Y_{0} = (0, 0)$ es un atractor.
El campo vectorial lo obtenemos de la función vectorial
$$F(x, y) = \left( -\dfrac{3}{2}x + y, -\dfrac{1}{4}x -\dfrac{1}{2}y \right)$$
Dicho campo y algunas trayectorias se muestran a continuación.
$\square$
Hemos concluido con el caso en el que los valores propios son repetidos. Para concluir con esta sección, en la siguiente entrada revisaremos el último caso en el que puede haber valores propios nulos.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Resolver los siguientes sistemas lineales y hacer un análisis cualitativo de las soluciones.
- $\mathbf{Y}^{\prime} \begin{pmatrix}
-5 & 0 \\ 0 & -5
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} \begin{pmatrix}
3 & -4 \\ 1 & -1
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} \begin{pmatrix}
-3 & 5/2 \\ -5/2 & 2
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} \begin{pmatrix}
200 & 0 \\ 0 & 200
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} \begin{pmatrix}
5/4 & 3/4 \\ -3/4 & -1/4
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} \begin{pmatrix}
1 & -4 \\ 4 & -7
\end{pmatrix} \mathbf{Y}$
Más adelante…
Estamos por concluir con el estudio cualitativo de los sistemas lineales homogéneos compuestos por dos ecuaciones diferenciales de primer orden con coeficientes constantes. En la siguiente entrada revisaremos el último caso en el que uno o ambos valores propios son nulos.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios complejos
- Siguiente entrada del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios nulos
- Video relacionado al tema: Plano fase para sistemas lineales con valores propios repetidos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»