Cálculo Diferencial e Integral I: Introducción. Repaso: Teoría de Conjuntos (Parte 1)

Por Karen González Cárdenas

2 respuestas

Introducción

Probablemente en el bachillerato ya habrás tomado algún curso de matemáticas en el que te presentaron varios de los conceptos íntimamente relacionados con el cálculo. Por lo que has oído hablar de números reales, funciones, derivadas – por citar algunos-, pero en algún momento te has preguntado: ¿De dónde salió todo eso?, ¿Por qué podemos asegurar lo que nos enseñan nuestros profesores o leemos en los libros de texto?

En esta entrada veremos un poco sobre la motivación histórica del cálculo y a lo largo de todo el curso haciendo uso de la herramienta de la demostración buscaremos dar respuesta a la segunda pregunta planteada.

Así, ¡comenzamos!

Veloz cómo una tortuga

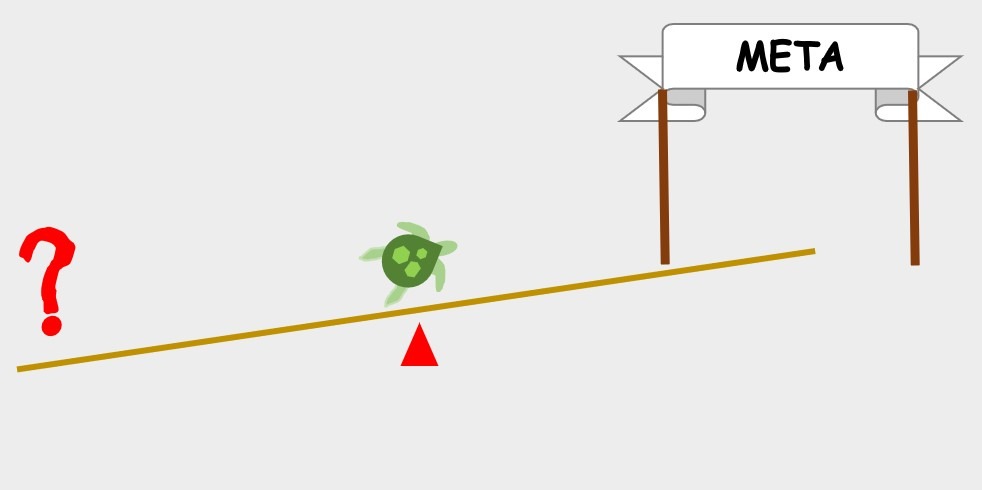
Imagina que un grupo de amigos te retan a una carrera contra una tortuga. Te dicen que, si lograras pasar por delante de ella y llegar primero a la meta, ganas un auto del año.

Sabiendo que la tortuga es extremadamente lenta en su caminar, decides darle ventaja para hacer la apuesta más interesante. Cuando ella se inicia su recorrido en el punto marcado en la imagen, finalmente comienzas a avanzar, en ese momento todos se percatan que no logras alcanzarla. ¿Cómo es esto posible?

Si nos detenemos un momento para observar lo que está pasando notamos lo siguiente:

  1. Para cuando llegas al punto donde la tortuga inició el recorrido, ella ya ha avanzado una pequeña distancia.
  2. Para cuando tú llegas al nuevo punto en el que se encuentra la tortuga, ella ya se ha movido un poco más hacia adelante.
  3. Este proceso continúa infinitamente, con la tortuga siempre moviéndose un poco más adelante.

Debido a que hay un número infinito de estos pasos, nunca rebasarás realmente a la tortuga. Por lo que haberle dado ventaja al final no parece haber sido una buena elección.

Esta idea fue expuesta por el filósofo griego Zenón de Elea en una de sus paradojas, conocida como Aquiles y la tortuga. Su planteamiento desconcertó a los intelectuales de la época. Observamos que este problema tiene como punto de preocupación, no sólo para los filósofos, sino también para los matemáticos: el problema del movimiento. Por lo tanto, podemos considerar como uno de los propósitos del Cálculo el establecer un modelo del movimiento. Veremos más adelante que el conocimiento de los números y las funciones reales se vuelve elemental para dicha tarea.

Observación: No se está considerando la variable de la velocidad en el planteamiento del movimiento recién mencionado. De este modo, cuestionarnos si es posible que Aquiles logre alcanzar a la tortuga al aumentar su velocidad queda descartado.

Una historia de amor

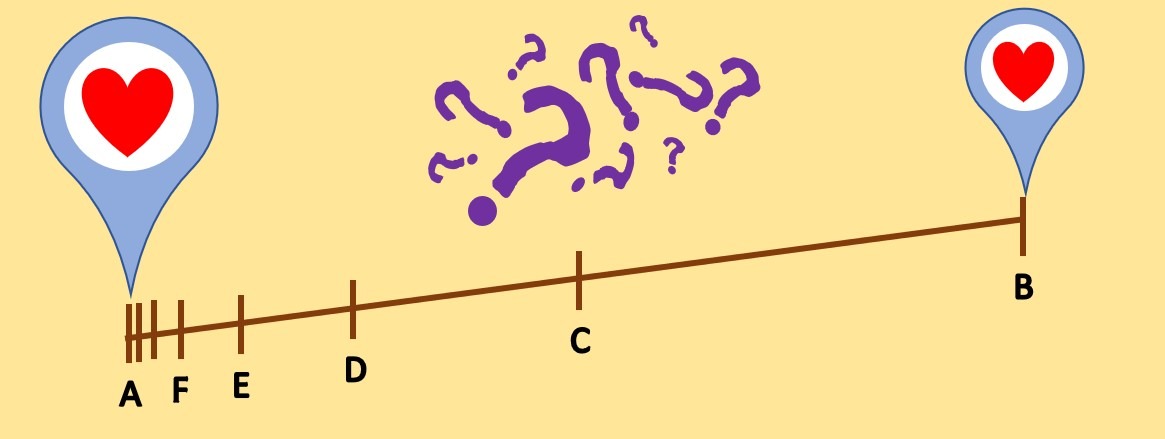
Un par de enamorados desean verse. Uno de ellos se encuentra en el punto $A$ de la ciudad y el otro en el punto $B$. Cuando el enamorado del punto A se dispone a ponerse en marcha para llegar al punto $B$, un hombre en la calle le pregunta: ¿estás seguro de que puedes desplazarte al punto $B$?

Perplejo el enamorado que se encuentra en el punto $A$ responde: “No entiendo su pregunta, ¿por qué no podría?”

El hombre sonriendo le plantea lo siguiente: “Mira, para que puedas llegar a $B$ primero deberás pasar por el punto $C$ que se encuentra a la mitad de la distancia entre $A$ y $B$. Pero… también para llegar a $C$ debes pasar por el punto $D$ que se encuentra a la mitad de la distancia entre $A$ y $C$, ¿no?

Y si te lo piensas bien así será sucesivamente, pasarás una vez por cada punto que se encuentre a la mitad de la distancia de cualesquiera dos. Ahora dime ¿en algún momento podrás moverte de tu posición $A$? ”

Desconcertado, el enamorado $A$ se detiene a pensar sobre lo sucedido.

  • ¿Qué respuesta le darías? ¿Llegarán a reunirse los enamorados bajo estas condiciones? Plantea una posible explicación, dicho ejercicio será parte de la tarea moral de esta primera parte.

Ya que hemos visto un par de paradojas interesantes, comenzaremos con un repaso de los conceptos básicos de Teoría de Conjuntos que se usarán a lo largo de todo el curso.

Repaso: Conceptos básicos de Teoría de Conjuntos.

En Matemáticas usaremos el concepto de «conjunto» para referirnos a una colección de objetos que serán considerados como una sola entidad. En la vida cotidiana algunos ejemplos serían:

  • Rebaño de ovejas
  • Equipo de fútbol
  • Estudiantes de la Facultad de Ciencias

Y utilizaremos el concepto de «elemento de un conjunto» para referirnos a cualquier objeto o entidad que pertenece a dicho conjunto. Aplicando dicha definición a un equipo de fútbol, el jugador que es portero del equipo sería un elemento del equipo de fútbol.

Cuestiones de notación

Usaremos las letras mayúsculas $A,B,C,…,X,Y,Z$ para referirnos a conjuntos, y las letras minúsculas $a,b,c,…,x,y,z$ para referirnos a los elementos.

Pertenencia

Utilizaremos el símbolo $\in$ para referirnos a la pertenencia de un elemento a un conjunto. Así, si tenemos lo siguiente:

$x\in A \text{,}$

esto se leería como $x$ pertenece al conjunto $A$, o $x$ es un elemento del conjunto $A$.

Si quisiéramos decir que $x$ no pertenece al conjunto $A$, o $x$ no es un elemento del conjunto $A$ usaríamos el símbolo $\notin$ y tendríamos:

$x\notin A \text{.}$

Denotando conjuntos

En algunas ocasiones encontraremos a los conjuntos escritos de la siguiente manera:

\[ A=\left\{0,1, 2, 3, 4\right\}\text{.} \]

Sin embargo, en muchas ocasiones no resultará práctico escribir todos los elementos del conjunto que queremos denotar. Por lo que se usará una notación diferente llamada «por comprensión». Utilizando el ejemplo anterior tendríamos lo siguiente:

\[ A=\left\{x\mid 0\leqslant x \leqslant 4 , x\in \mathbb{N} \right\} \text{;}\]

esto se leería como «el conjunto de los primeros cinco números naturales» o «el conjunto de los números naturales mayores o iguales que cero y menores o iguales a cuatro». Comúnmente esta última notación será la más utilizada tanto en libros de texto como en los cursos.

Como un breve recordatorio, los números naturales son un conjunto de números utilizados para contar objetos o representar una cantidad de cosas y se denotan usualmente con el símbolo $\mathbb{N}$.

Subconjuntos

Ahora veremos una relación muy especial que nos permitirá crear nuevos conjuntos a partir de uno dado. Si tenemos el siguiente conjunto:

\[ B=\left\{0,1, 2, 3, a, b, c, d\right\} \text{,}\]

y decidimos tomar los elementos $0,3,b,c$ del conjunto $B$, vemos que podemos formar un conjunto C cuyos elementos sean los previamente seleccionados de modo que:

\[ C=\left\{0, 3, b, c \right\} \text{.}\]

Así diremos que $C$ es un subconjunto de $B$.

Usaremos el símbolo $\subseteq$ para representar la contención de conjuntos. Así presentamos la siguiente definición:

Definición (Subconjunto): Consideremos $A$ y $B$ conjuntos. Diremos que $A$ es un subconjunto de $B$:

$A \subseteq B$

si se cumple que todo elemento de $A$ pertenece también a $B$, en otras palabras, si todo elemento de $A$ también es un elemento de $B$.

NOTA.- $A \subseteq B$ también se puede leer como: «$A$ está contenido en $B$» o «$B$ contiene a $A$»

Definición (Igualdad de conjuntos): Consideremos $A$ y $B$ conjuntos. Diremos que $A$ es igual a $B$:

$A = B$

si y sólo si se cumple que: $A \subseteq B$ y $B \subseteq A$.

Esta definición nos resultará de utilidad al realizar demostraciones sobre la igualdad entre conjuntos.

Más adelante

En esta primera entrada hemos visto la notación utilizada en Teoría de Conjuntos, el significado de pertenencia a un conjunto, que es un subconjunto y la definición de igualdad entre conjuntos. En la siguiente entrada veremos las operaciones fundamentales entre conjuntos, donde lo antes visto será de suma importancia.

Tarea moral

  1. Da una posible explicación al planteamiento de la paradoja «Una historia de amor».
  2. Dados los siguientes conjuntos $A$ y $B$. Responde si los enunciados escritos a continuación son verdaderos o falsos, argumenta tu respuesta.

\[ A=\left\{5,7,9, b, h, k, j\right\} \]

\[ B=\left\{5,7,9, h, k, j\right\} \]

  • $A \subseteq B$
  • $B \subseteq A$
  • Si tenemos $C=\left\{5,7,9, h, k, j\right\}$ entonces $C \subseteq B$.
  • $\left\{5,7\right\}\in A$
  • $\left\{5,7,9,h,k,j\right\}\in B$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Moderna I: Operación binaria asociativa y conmutativa

Por Cecilia del Carmen Villatoro Ramos

3 respuestas

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior definimos el concepto de operación binaria, en esta entrada veremos dos tipos más específicos de operaciones binarias: las operaciones binarias asociativas y las operaciones conmutativas. Éstas nos interesan ya que hacen que las operaciones sean más sencillas de manejar.

Nuevas definiciones

Definición. Una operación binaria $*$ en un conjunto $\mathcal{S}$ es asociativa si, para todos $a, b, c \in \mathcal{S}$

$(a*b)*c = a*(b*c)$.

Definición. Una operación binaria $*$ en un conjunto $\mathcal{S}$ es conmutativa si, para todos $a,b \in \mathcal{S}$

$a*b=b*a$.

Ejemplos de operaciones binarias asociativas y conmutativas

Repasemos los ejemplos vistos en la entrada anterior. Ahora los analizaremos con mayor profundidad.

  • Consideremos $\mathcal{S} := \mathbb{R}$ con la operación $a*b=ab-2$. Entonces $*$ no es asociativa.

Demostración. Sean $a,b,c \in \mathbb{R}$.

Si sustituimos los valores de acuerdo a la forma en que está definida $*$, por un lado obtenemos

$\begin{align}(a * b)*c = (ab-2)c -2 = (ab)c -2c-2\end{align}$

y por otro,

$\begin{align}a*(b*c) = a*(bc -2) = a(bc-2)-2 = a(bc)-2a-2. \end{align}$

Observamos que $(1)$ y $(2)$ en general son distintos. Por lo tanto $*$ no es asociativa.

Ejemplo. Si hacemos la operación con $1, 2, 3$ obtenemos:

$(1*2)*3 = 0 * 3 = -2$

$1*(2*3)= 1 *4 = +2$

Así, claramente no es asociativa.

$\blacksquare$

Sin embargo, sí es conmutativa.

Demostración. Por la conmutatividad de la multiplicación de reales,

$a*b = ab-2 = ba-2 = b*a \qquad \forall a,b \in \mathbb{R}$.

$\blacksquare$

  • Consideremos ahora el conjunto $\mathcal{S} := \mathbb{R}^+$ (los reales positivos), con la operación $a*b=\frac{a}{b}$. Entonces $*$ no es asociativa.

Demostración. Sean $a,b,c \in \mathbb{R}^+$.

Si sustituimos de acuerdo a la definición de nuestra operación binaria, obtenemos

$(a*b)*c = \frac{a}{b}*c =\frac{\frac{a}{b}}{c} = \frac{a}{bc}$

por otro lado,

$a*(b*c)= a* \frac{b}{c} = \frac{a}{\frac{b}{c}} = \frac{ac}{b}$.

En general, $(a*b)*c \neq a*(b*c)$, por lo que esta operación binaria no es asociativa.

$\blacksquare$

Ejemplo. Tomemos $3,4$ y $5$:

$(3*4)*5 = \frac{3}{4} * 5 = \frac{\frac{3}{4}}{5} = \frac{3}{20}$.

$3*(4*5) = 3* \frac{4}{5} = \frac{3}{\frac{4}{5}} = \frac{15}{4}$.

Claramente, $$\frac{3}{20} \neq \frac{15}{4}.$$

$\blacksquare$

Esta operación tampoco es conmutativa.

Demostración. Sean $a,b \in \mathbb{R}^+$.

Sustituyendo nuestra definición, en general tenemos que,

$a*b = \frac{a}{b} \neq \frac{b}{a} = b*a$.

Por lo tanto, nuestra operación binaria no es conmutativa.

$\blacksquare$

Ejemplo. Un ejemplo sencillo y claro,

$1*2 = \frac{1}{2} \neq 2 = 2*1$.

$\blacksquare$

  • En $\mathcal{S} := \mathbb{Z}^+$, $a*b = \text{máx} \{a,b\}$ es asociativa y conmutativa.
  • En $\mathcal{S} := \mathbb{Z}^+$, $a*b = a$ es asociativa y no conmutativa.
  • En $\mathcal{S} := \mathcal{M}_{2\times 2}(\mathbb{Z})$, $A*B = A + B$ es asociativa y conmutativa.
  • En $\mathcal{S}:= \{f \; | \; f: \mathbb{R} \to \mathbb{R} \}$, $f*g := f\circ g$ es asociativa pero no conmutativa.
  • En $\mathcal{S}:= S_3$, $f*g = f\circ g$. Es asociativa pero no conmutativa.

Ejemplo con tablas

En esta sección analizaremos algunas operaciones binarias definidas con tablas. El hecho de que una función sea conmutativa se ve reflejado en la tabla. Cuando la operación es conmutativa, si nos fijamos en la línea diagonal que divide a la tabla (la diagonal principal), podemos observar que la tabla es simétrica con respecto a la diagonal.

Demostrar la asociatividad a partir de la tabla es un poco más complicado. Se tendrían que escoger todas las distintas combinaciones de tres elementos del conjunto, lo que lo haría muy largo, incluso para conjuntos pequeños. Por eso conviene definir la operación de otra manera. En los siguientes ejemplos encontrarás la función definida de ambas maneras, con la tabla y con una regla de correspondencia.

  • En $\mathcal{S} = \{2,4,6\}$, la operación $a*b = \text{máx}\{a,b\}$ se vería como
$*$$2$$4$$6$
$2$$2$$4$$6$
$4$$4$$4$$6$
$6$$6$$6$$6$

La tabla es simétrica con respecto a la diagonal principal, por lo tanto esta operación sí es conmutativa. Queda como ejercicio demostrar que es asociativa.

  • En $\mathcal{S} = \{2,4,6\}$, la operación $a*b = a$ se vería como
$*$$2$$4$$6$
$2$$2$$2$$2$
$4$$4$$4$$4$
$6$$6$$6$$6$

De la misma manera, si nos fijamos en la diagonal principal, observamos que esta operación no es conmutativa. Pero, será tu trabajo demostrar que sí es asociativa.

  • En $\mathcal{S} = \{1, -1\}$, la operación $a*b = ab$ se vería como
$*$$1$$-1$
$1$$1$$-1$
$-1$$-1$$1$

A diferencia de los anteriores dos ejemplos, esta operación sí es conmutativa y también asociativa.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra o da contraejemplos de las propiedades (conmutatividad y asociatividad) que quedaron pendientes en los ejemplos.
  2. Con ayuda de las tablas, verifica las propiedades de conmutatividad y asociatividad que quedaron pendientes en los ejemplos correspondientes.
  3. Para el conjunto $\mathcal{S}:= \{\bigstar, \blacktriangledown, \blacklozenge, \clubsuit \}$, define
    • una operacion binaria conmutativa (pero no asociativa),
    • una operación asociativa (pero no conmutativa),
    • una operación asociativa y conmutativa,
    • una operación que no sea ni asociativa ni conmutativa.
  4. De los ejemplos que hiciste en la tarea moral anterior, determina si son conmutativas, asociativas o ambas.
  5. Del ejercicio 5 de la tarea moral anterior, determina si las operaciones binarias son conmutativas, asociativas, ambas o ninguna de las dos.

Más adelante…

Ahora sí, ya estás listo para que comencemos con los grupos. En la siguiente entrada comenzaremos a definirlos y a dar algunos ejemplos. Verás que las operaciones binarias tienen un papel importante a la hora de definir esta estructura algebraica.

Entradas relacionadas

Álgebra Moderna I: Operación binaria

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Bienvenido al curso de Álgebra Moderna I. Antes de comenzar de lleno con el tema principal del curso, los grupos, es necesario sentar ciertas bases, así que en esta primera entrada comenzaremos con la definición de una operación binaria.

El objetivo de una operación binaria, como dice su nombre, es tomar dos elementos de un conjunto, operarlos y obtener un resultado que también pertenezca al mismo. La suma (+) y la multiplicación (•) de números reales son operaciones binarias que conocemos desde hace tiempo. Además de ellas, veremos ejemplos de varias operaciones binarias definidas en diversos conjuntos, no sólo en los reales.

¿Qué es una Operación Binaria?

Como mencionamos en la introducción, la operación binaria es una función que toma dos elementos de un conjunto y devuelve un elemento del mismo. Formalmente escrito, quedaría de la siguiente manera:

Definición. Una operación binaria en un conjunto $\mathcal{S}$ es una función $\mu : \mathcal{S} \times \mathcal{S} \to \mathcal{S}$, es decir una forma de asignar a cada par ordenado $(a,b) \in \mathcal{S} \times \mathcal{S}$ un elemento $\mu (a,b) \in \mathcal{S}$.

Sin embargo, normalmente no trabajamos la notación de función. Así que hacemos la siguiente aclaración:

Notación. Nuestra operación binaria $\mu$ será denotada por $*$ y al elemento asignado a la pareja $(a,b)$. En lugar de ser denotado por $\mu (a,b)$ será denotado por $a*b$, más adelante será denotada simplemente por $ab$ o por $a+b$.

Además, necesitamos las siguientes observaciones para que nuestra función sea una operación binaria:

Observación 1. A cada par de elementos en $\mathcal{S}$ se le asigna exactamente un elemento de $\mathcal{S}$, es decir, $*$ es una función bien definida.

Observación 2. Para cada par de elementos en $\mathcal{S}$ el elemento debe estar en $\mathcal{S}$, es decir, $*$ es una operación cerrada en $\mathcal{S}$.

Ejemplos de operaciones binarias

Para ilustrar los ejemplos, tomaremos el símbolo $:=$ como una asignación de valor, y lo usaremos para definir y al símbolo $=$ como la igualdad usual, que indica eso, una igualdad entre dos valores.

  1. En $\mathcal{S} := \mathbb{R}$, podemos definir la siguiente operación binaria, $a*b := ab – 2$, es decir, la multiplicación de ambos números, menos dos unidades.
  2. En $\mathcal{S} := \mathbb{R}^+$, observemos que es posible tomar la operación $a*b := \frac{a}{b}$ como la división usual. Es importante considerar el conjunto $\mathcal{S}$ en el que estamos trabajando. Por ejemplo, esta operación no se podría considerar en $\mathbb{Z}^+$ porque no podemos asegurar que siempre nos dé un entero, por lo tanto no sería una operación binaria.
  3. Ahora, si tomamos $\mathcal{S} := \mathbb{Z}^+$ y definimos $a*b := \text{máx}{\{a,b\}}$, es decir, una operación binaria no tiene que ser siempre aritmética.
  4. En $\mathcal{S} := \mathbb{Z}^+$, podemos definir $a*b = a$, es decir, la operación asigna a cada par de números el primero de los dos.
  5. También podemos trabajar con matrices, por ejemplo $\mathcal{S} := \mathcal{M}_{2\times2}(\mathbb{Z})$ (el conjunto de matrices $2\times 2$ con entradas enteras), definida como $A*B := A + B$, es decir, la suma de matrices.
  6. Si pensamos en funciones, podemos considerar $\mathcal{S}:=\{f \;| f:\mathbb{R} \to \mathbb{R}\}$ y definir la composición de funciones, $f*g:= f\circ g$. Como todas las funciones comparten dominio y codominio, tiene sentido componer. Recordemos que esa notación se lee de derecha a izquierda, es decir, primero se aplica $g$ y luego $f$.
  7. En $\mathcal{S}:= S_3$, con $S_3 := \{f | f: \{1,2,3\} \to \{1,2,3\}, f \text{ es biyectiva}\}$, también podemos considerar $f*g := f\circ g$ y sería una operación binaria en el conjunto.

Para este último ejemplo, recordemos que como el dominio de $f$ es finito podemos denotar a $f$ como una matriz de la forma,

$f = \begin{pmatrix} 1 & 2 & 3\\ f(1) & f(2) & f(3) \end{pmatrix}.$

Ejemplo:

Si $f = \begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix}$ y $g = \begin{pmatrix} 1 & 2 & 3\\ 3 & 1 & 2 \end{pmatrix}$, entonces la composición $f \circ g = \begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix}$. Puesto que $g$ manda el $1$ al $3$ y $f$ manda el $3$ al $1$, $g$ manda el $2$ al $1$ y $f$ manda el $1$ al $2$ y $g$ manda el $3$ al $2$ y $f$ manda el $2$ al $3$.

$\blacksquare$

De modo más general, si $f$ es una función cuyo dominio es un conjunto finito con $n$ elementos $a_1,a_2,\dots, a_n,$ la regla de correspondencia de $f$ se puede describir con el arreglo

$f = \begin{pmatrix} a_1 & a_2 & \dots & a_n\\ f(a_1) & f(a_2)&\dots & f(a_n) \end{pmatrix}.$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Como calentamiento, piensa por qué ocurren las dos observaciones dadas.
  2. Investiga cómo se pueden definir operaciones binarias con tablas.
  3. De los ejemplos dados, busca conjuntos en donde la operación binaria deje de serlo por no cumplir con la cerradura.
  4. Da cinco ejemplos de conjuntos y operaciones binarias sobre ellos.
  5. Determina si las siguientes operaciones son binarias o no y en caso de no serlo, ¿qué le cambiarías al conjunto para que lo sea?
    • En $\mathcal{S} = \mathbb{R}^+$, $a*b = ab-2$.
    • En $\mathcal{S} = \mathcal{M}_{2\times2}(\mathbb{Z})$, $A*B = A^{-1}B$.
    • En $\mathcal{S} = \mathbb{Z}\setminus \{-1\}$, $a*b = 1 + ab$.
    • En $\mathcal{S} = \mathbb{Z}_5$, $a*b = ab(\text{mód } 7)$.

Más adelante…

Con el fin de trabajar con operaciones que sean más manejables, continuaremos expandiendo nuestro concepto de operación binaria agregándole las propiedades de conmutatividad y asociatividad.

Entradas relacionadas

Álgebra Lineal II: Introducción al teorema de Cayley-Hamilton

Por Julio Sampietro

1 respuesta

Introducción

En esta entrada introducimos el teorema de Cayley-Hamilton, otro de los teoremas importantes del curso. Intuitivamente este teorema nos dice que «el polinomio característico anula al operador lineal». Es decir, si $P(\lambda)$ es el polinomio característico de una transformación lineal $T$, entonces $P(T)=0$.

Algunos ejemplos

Damos unos cuantos ejemplos para que entendamos que está pasando.

Ejemplo 1. Sea $A\in M_2(\mathbb{R})$ la matriz dada por

\begin{align*}
A=\begin{pmatrix} 0 & -1\\ 1 & 0
\end{pmatrix}.
\end{align*}

Calculemos su polinomio característico

\begin{align*}
\chi_A(X)=\det \begin{pmatrix} X & 1\\ -1 & X\end{pmatrix}=X^2+1.
\end{align*}

Así, si evaluamos al polinomio $\chi_A$ en la matriz $A$ tenemos que calcular

\begin{align*}
\chi_A(A)= A^2+I_2.
\end{align*}

Por un lado

\begin{align*}
A^2=\begin{pmatrix} 0 & 1\\ -1 & 0\end{pmatrix}\cdot \begin{pmatrix} 0 & 1 \\ -1 & 0\end{pmatrix}=\begin{pmatrix} -1 &0 \\ 0 & -1\end{pmatrix}=-I_2.
\end{align*}

Luego

\begin{align*}
\chi_A(A)=A^2+I_2= -I_2+I_2=O_2.
\end{align*}

Es decir, ¡$\chi_A(A)$ es la matriz cero!

$\triangle$

Ejemplo 2. Calculemos el polinomio característico de la matriz $A\in M_3(\mathbb{R})$ dónde $A$ está dada por

\begin{align*}
A=\begin{pmatrix}
0 & -1 & -2\\ 0 & 3 &4\\ 0 & 0 & -5.
\end{pmatrix}
\end{align*}

Notamos que $A$ es una matriz triangular superior. Por una entrada anterior sabemos que el polinomio característico es solo el producto de los monomios $(X-a_{ii})$. Es decir

\begin{align*}
\chi_A(X)=(X-0)(X-3)(X-(-5))= X(X-3)(X+5).
\end{align*}

Enseguida, evaluemos $\chi_A(A)$. Recordamos que esto quiere decir que tenemos que calcular

\begin{align*}
\chi_A(A)=A(A-3I_3)(A+5I_3).
\end{align*}

Por un lado

\begin{align*}
A-3I_3=\begin{pmatrix}
-3 & -1 & -2\\ 0 & 0 & 4\\ 0 & 0 & -8
\end{pmatrix},
\end{align*}

y por otro

\begin{align*}
A+5I_3=\begin{pmatrix}
5 & -1 & -2\\ 0 & 8 & 4\\ 0 & 0 &0
\end{pmatrix}.
\end{align*}

Así

\begin{align*}
(A-3I_3)(A+5I_3)&=\begin{pmatrix}
-3 & -1 & -2\\ 0 & 0 & 4\\ 0 & 0 & -8
\end{pmatrix}\cdot \begin{pmatrix}
5 & -1 & -2\\ 0 & 8 & 4\\ 0 & 0 &0
\end{pmatrix}\\ &=\begin{pmatrix} -15 & -5 & -2\\ 0 &0 &0 \\ 0 & 0 &0\end{pmatrix}.
\end{align*}

Finalmente

\begin{align*}
A(A-I_3)(A+5I_3)=\begin{pmatrix}
0 & -1 & -2\\ 0 & 3 &4\\ 0 & 0 & -5.
\end{pmatrix}\cdot \begin{pmatrix} -15 & -5 & -2\\ 0 &0 &0 \\ 0 & 0 &0\end{pmatrix}=O_3.
\end{align*}

Una vez más $\chi_A(A)=0$.

$\triangle$

El teorema

Los ejemplos anteriores sirven de calentamiento para enunciar el teorema de Cayley-Hamilton, que dice exactamente lo que sospechamos.

Teorema (de Cayley-Hamilton). Para cualquier matriz $A\in M_n(F)$ se cumple

\begin{align*}
\chi_A(A)=O_n.
\end{align*}

En otras palabras, si $\chi_A(X)=X^n+a_{n-1}X^{n-1}+\dots+a_0$ entonces

\begin{align*}
A^{n}+a_{n-1}A^{n-1}+\dots+a_0 I_n=O_n.
\end{align*}

Demostraremos este teorema en la próxima entrada. Uno podría sospechar que la demostración consiste en simplemente sustituir $A$ en la expresión de $\chi_A$ como sigue

\begin{align*}
\chi_A(A)= \det(AI_n-A)=\det(0)=0.
\end{align*}

Sin embargo, esta ‘prueba’ no es correcta, ya que estamos multiplicando a $A$ con $I_n$ como si fueran matrices, mientras que la expresión de $\chi_A$ se refiere a escalares. Más aún, observa como el resultado de la expresión que anotamos es el escalar cero, mientras que sabemos que $\chi_A(A)$ debería ser la matriz cero.

Concluimos esta sección con una breve aplicación del teorema de Cayley-Hamilton.

Proposición. El polinomio mínimo de una matriz $A\in M_n(F)$ divide al polinomio característico.

Demostración. Por el teorema de Cayley-Hamilton, $\chi_A(A)=0$. Luego por definición del polinomio mínimo se sigue que $\mu_A(X)$ divide a $\chi_A(X)$.

$\square$

Más adelante…

En la próxima entrada demostraremos el teorema de Cayley-Hamilton, y luego pasaremos a dar aplicaciones de este.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso. Sin embargo, sirven de ayuda para repasar los conceptos vistos en esta entrada.

  1. En una entrada anterior calculamos el polinomio característico de una matriz nilpotente. Explica por qué el teorema de Cayley-Hamilton es compatible con dicho cálculo. De otra manera, verifica el teorema de Cayley-Hamilton en ese caso particular.
  2. Sea $A\in M_3(\mathbb{R})$ tal que $\operatorname{Tr}(A)=\operatorname{Tr}(A^2)=0$. Usa el teorema de Cayley-Hamilton para demostrar que existe un $\alpha\in \mathbb{R}$ tal que $A^3=\alpha I_3$.
  3. Calcula el polinomio característico de $A\in M_2(\mathbb{C})$ donde
    \begin{align*}
    A=\begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}.
    \end{align*}
    Es decir, $A$ es la misma matriz que en el ejemplo pero pensada como una matriz compleja. Verifica que $\chi_A(A)=O_2$.
  4. Verifica que $\chi_A(A)=O_3$ con
    \begin{align*}
    A= \begin{pmatrix} 1 & 0 & -1\\ 1 & 1 & 1 \\ 0 & 2 & 1\end{pmatrix}\in M_3(\mathbb{R}).
    \end{align*}
  5. Sea $A\in M_n(\mathbb{R})$ una matriz tal que $A$ y $3A$ son similares. Demuestra que $A^n=O_n$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Geometría Analítica I: Hipérbolas

Por Héctor Morales

2 respuestas

Introducción

En las entradas anteriores definimos un círculo y establecimos algunas de sus propiedades; esto nos llevó naturalmente a estudiar las elipses: una de las tres figuras geométricas que podemos observar al hacer «cortes» en diferentes secciones de un cono. Al igual que para las circunferencias, discutimos detalladamente los elementos que componen a una elipse, estudiamos sus propiedades y hablamos, de manera general, sobre las aplicaciones que pueden tener en diferentes campos como en física o ingeniería.

La segunda de las secciones cónicas que vamos a estudiar en esta unidad son las hipérbolas. Decimos que será la segunda, pues recordemos que una circunferencia es una elipse; una en la cual el eje mayor y el eje menor tienen el mismo tamaño. Al igual que para las elipses, la motivación para estudiar analíticamente las hipérbolas, nace de observar fenómenos naturales. Probablemente ya has visto antes una hipérbola, y tal vez tengas dificultades pensando en qué momento de tu vida cotidiana has visto la misma figura; para motivarnos a estudiar la hipérbola hablaremos de una de sus aplicaciones: sistemas de navegación.

En el sistema de navegación LORAN se utiliza la propiedad de la definición de la hipérbola que nos dice que «la diferencia de las distancias de los puntos de la hipérbola a los focos es constante»; es este tipo de sistema de navegación, una estación radioemisora maestra y otra estación radioemisora secundaria emiten señales que pueden ser recibidas por un barco en altamar (ver figura). Puesto que un barco que monitoreé las dos señales estará probablemente más cerca de una de las estaciones, habrá una diferencia entra las distancias recorridas por las dos señales, lo cual se registrará como una pequeña diferencia de tiempo entre las señales. En tanto la diferencia de tiempo permanezca constante, la diferencia entre las dos distancias también será constante. Si el barco sigue la trayectoria correspondiente a una diferencia fija de tiempo, esta trayectoria será una hipérbola cuyos focos están localizados en las posiciones de las dos estaciones.

Esquema del sistema de navegación LORAN: una de las aplicaciones de la hipérbola a la ingeniería.

Como pudimos ver, las hipérbolas son extensamente usadas para resolver problemas importantes; entonces es importante encontrar una expresión analítica que nos permita extraer toda su información geométrica. Esta expresión analítica, saldrá naturalmente cuando veamos cómo podemos definir una hipérbola.

Definición de Hipérbola

Ya que hemos discutido brevemente por qué queremos tener una expresión analítica de la hipérbola, pasemos a definirla de una forma más formal. La hipérbola está definida como el lugar geométrico de los puntos cuya diferencia (em valor absoluto) de sus distancias a dos puntos fijos $\mathbf{p}$ y $\mathbf{q}$, llamados focos, es constante. Entonces, una hipérbola $\mathcal{H}$ está definida por la ecuación

\begin{equation}
|d(\mathbf{x}, \mathbf{p})-d(\mathbf{x}, \mathbf{q})|=2 a.
\end{equation}

donde $a>0$, y además $2 a<d(\mathbf{p}, \mathbf{q})=: 2 c$. A continuación puedes ver la figura que define a este conjunto de puntos, sometidos a la condición de la definición. Como ya te habrás dado cuenta, la definición de la hipérbola es muy parecida a la definición de la elipse. A lo largo de esta entrada y de la siguiente veremos que a pesar de ser figuras muy distintas comparten varios elementos y características.

Hipérbola como conjunto de puntos que cumplen la ecuación 1.

Así como hicimos para la elipse, queremos llegar a una ecuación canónica que sea «sencilla» y que nos permite leer toda la información geométrica de la figura. Si tomamos como focos a $\mathbf{p}=(c, 0)$ y a $\mathbf{q}=(-c, 0)$; ver la siguiente figura, esta ecuación toma la forma

\begin{equation}
\left|\sqrt{(x-c)^{2}+y^{2}}-\sqrt{(x+c)^{2}+y^{2}}\right|=2 a.
\end{equation}

y veremos a continuación que es equivalente a

\begin{equation}
\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1
\end{equation}

donde $b>0$ está definida por $a^{2}+b^{2}=c^{2}$. A esta última ecuación se le llama la ecuación canónica de la hipérbola.

Hipérbola vertical centrada en el orgien

Como las ecuaciones anteriores involucraban un valor absoluto, entonces se tienen dos posibilidad que corresponden a las dos ramas de la hipérbola. En una de ellas la distancia a uno de los focos es mayor y en la otra se invierten los papeles. De la ecuación $2$ se tienen dos posibilidades:

\begin{equation}
\sqrt{(x-c)^{2}+y^{2}}=2 a+\sqrt{(x+c)^{2}+y^{2}}
\end{equation}

\begin{equation}
\sqrt{(x+c)^{2}+y^{2}}=2 a+\sqrt{(x-c)^{2}+y^{2}}
\end{equation}

la primera corresponde a la rama donde $x<0$ y la segunda a $x>0$. Como hicimos en el caso de la elipse vamos a llegar a la ecuación canónica desarrollando todos los pasos. Partiendo de la definición y de la fórmula de distancia:

$$
d_{2}-d_{1}=\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a.
$$

Ahora, simplificando la expresión:

$$
\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=2 a.
$$

Si movemos uno de los radicales al lado opuesto:

$$
\sqrt{(x+c)^{2}+y^{2}}=2 a+\sqrt{(x-c)^{2}+y^{2}}.
$$

Luego, elevando al cuadrado ambos lados:

$$
(x+c)^{2}+y^{2}=\left(2 a+\sqrt{(x-c)^{2}+y^{2}}\right)^{2}.
$$

Después, expandimos los cuadrados:

$$
x^{2}+2 c x+c^{2}+y^{2}=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}+(x-c)^{2}+y^{2}.
$$

Ahora, si expandimos el cuadrado restante:

$$
x^{2}+2 c x+c^{2}+y^{2}=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}+x^{2}-2 c x+c^{2}+y^{2}.
$$

En la ecuación anterior combinamos los términos y separamos al radical:

$$
2 c x=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}-2 c x
$$

$$
4 c x-4 a^{2}=4 a \sqrt{(x-c)^{2}+y^{2}}
$$

Dividiendo entre $4$ y elevando al cuadrado ambos lados:

$$
c x-a^{2}=a \sqrt{(x-c)^{2}+y^{2}}
$$

$$
\left(c x-a^{2}\right)^{2}=a^{2}\left[\sqrt{(x-c)^{2}+y^{2}}\right]^{2}
$$

Finalmente, expandiendo de nuevo el cuadrado y agrupando términos semejantes llegamos a que,

$$
c^{2} x^{2}-2 a^{2} c x+a^{4}=a^{2}\left(x^{2}-2 c x+c^{2}+y^{2}\right)
$$

$$
c^{2} x^{2}-2 a^{2} c x+a^{4}=a^{2} x^{2}-2 a^{2} c x+a^{2} c^{2}+a^{2} y^{2}
$$

$$
a^{4}+c^{2} x^{2}=a^{2} x^{2}+a^{2} c^{2}+a^{2} y^{2}
$$

$$
c^{2} x^{2}-a^{2} x^{2}-a^{2} y^{2}=a^{2} c^{2}-a^{4}
$$

$$
x^{2}\left(c^{2}-a^{2}\right)-a^{2} y^{2}=a^{2}\left(c^{2}-a^{2}\right)
$$

$$
x^{2} b^{2}-a^{2} y^{2}=a^{2} b^{2}
$$

$$
\frac{x^{2} b^{2}}{a^{2} b^{2}}-\frac{a^{2} y^{2}}{a^{2} b^{2}}=\frac{a^{2} b^{2}}{a^{2} b^{2}}
$$

$$
\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1
$$

Como ya mencionamos, esta última ecuación es la ecuación canónica de la hipérbola.

Como conclusión de este primer acercamiento a las hipérbolas, prueba el siguiente recuadro interactivo de GeoGebra. Identifica los elementos básicos de la hipérbola y dibuja algunas variando parámetros. Observa cómo variando los diferentes elementos de la ecuación cambia la forma de la hipérbola.

Más adelante…

En esta entrada nos familiarizamos con la idea elemental de la hipérbola. Todavía nos queda mucho que estudiar acerca de esta sección cónica. En la siguiente entrada nombraremos cada uno de sus elementos, presentaremos algunas propiedades métricas y discutiremos su propiedad focal. Al igual que como hicimos para las elipses, tocaremos brevemente el tema de excentricidad y luego realizaremos algunos ejercicios sobre hipérbolas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • A partir de la definición de hipérbola, determine la ecuación de la que tiene sus focos en $(6,0)$ y $(-6,0)$ si $2a=8$.
  • A partir de su definición, muestre que la ecuación de una hipérbola cuyos focos están en $F_{1}(a,a)$ y $F_{2}(-a,a)$ y para la cual se cumple que $$|\mathbf{PF}_{1}| – |\mathbf{PF}_{2}| = \pm 2a$$ para todo punto $P(x,y)$ de la curva es $xy=\frac{1}{2}a^{2}$.
  • Dada la siguiente ecuación, determina si se trata de una hipérbola. En caso de que sí, escríbela en su forma canónica:

$$
25 x^{2}-16 y^{2}=400
$$

Entradas relacionadas