Introducción
En las entradas anteriores definimos un círculo y establecimos algunas de sus propiedades; esto nos llevó naturalmente a estudiar las elipses: una de las tres figuras geométricas que podemos observar al hacer «cortes» en diferentes secciones de un cono. Al igual que para las circunferencias, discutimos detalladamente los elementos que componen a una elipse, estudiamos sus propiedades y hablamos, de manera general, sobre las aplicaciones que pueden tener en diferentes campos como en física o ingeniería.
La segunda de las secciones cónicas que vamos a estudiar en esta unidad son las hipérbolas. Decimos que será la segunda, pues recordemos que una circunferencia es una elipse; una en la cual el eje mayor y el eje menor tienen el mismo tamaño. Al igual que para las elipses, la motivación para estudiar analíticamente las hipérbolas, nace de observar fenómenos naturales. Probablemente ya has visto antes una hipérbola, y tal vez tengas dificultades pensando en qué momento de tu vida cotidiana has visto la misma figura; para motivarnos a estudiar la hipérbola hablaremos de una de sus aplicaciones: sistemas de navegación.
En el sistema de navegación LORAN se utiliza la propiedad de la definición de la hipérbola que nos dice que «la diferencia de las distancias de los puntos de la hipérbola a los focos es constante»; es este tipo de sistema de navegación, una estación radioemisora maestra y otra estación radioemisora secundaria emiten señales que pueden ser recibidas por un barco en altamar (ver figura). Puesto que un barco que monitoreé las dos señales estará probablemente más cerca de una de las estaciones, habrá una diferencia entra las distancias recorridas por las dos señales, lo cual se registrará como una pequeña diferencia de tiempo entre las señales. En tanto la diferencia de tiempo permanezca constante, la diferencia entre las dos distancias también será constante. Si el barco sigue la trayectoria correspondiente a una diferencia fija de tiempo, esta trayectoria será una hipérbola cuyos focos están localizados en las posiciones de las dos estaciones.
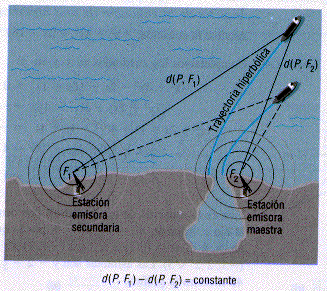
Como pudimos ver, las hipérbolas son extensamente usadas para resolver problemas importantes; entonces es importante encontrar una expresión analítica que nos permita extraer toda su información geométrica. Esta expresión analítica, saldrá naturalmente cuando veamos cómo podemos definir una hipérbola.
Definición de Hipérbola
Ya que hemos discutido brevemente por qué queremos tener una expresión analítica de la hipérbola, pasemos a definirla de una forma más formal. La hipérbola está definida como el lugar geométrico de los puntos cuya diferencia (em valor absoluto) de sus distancias a dos puntos fijos $\mathbf{p}$ y $\mathbf{q}$, llamados focos, es constante. Entonces, una hipérbola $\mathcal{H}$ está definida por la ecuación
\begin{equation}
|d(\mathbf{x}, \mathbf{p})-d(\mathbf{x}, \mathbf{q})|=2 a.
\end{equation}
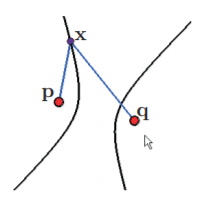
donde $a>0$, y además $2 a<d(\mathbf{p}, \mathbf{q})=: 2 c$. A continuación puedes ver la figura que define a este conjunto de puntos, sometidos a la condición de la definición. Como ya te habrás dado cuenta, la definición de la hipérbola es muy parecida a la definición de la elipse. A lo largo de esta entrada y de la siguiente veremos que a pesar de ser figuras muy distintas comparten varios elementos y características.
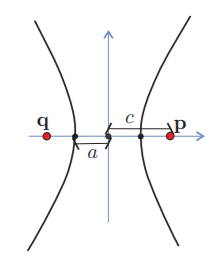
Así como hicimos para la elipse, queremos llegar a una ecuación canónica que sea «sencilla» y que nos permite leer toda la información geométrica de la figura. Si tomamos como focos a $\mathbf{p}=(c, 0)$ y a $\mathbf{q}=(-c, 0)$; ver la siguiente figura, esta ecuación toma la forma
\begin{equation}
\left|\sqrt{(x-c)^{2}+y^{2}}-\sqrt{(x+c)^{2}+y^{2}}\right|=2 a.
\end{equation}
y veremos a continuación que es equivalente a
\begin{equation}
\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1
\end{equation}
donde $b>0$ está definida por $a^{2}+b^{2}=c^{2}$. A esta última ecuación se le llama la ecuación canónica de la hipérbola.
Como las ecuaciones anteriores involucraban un valor absoluto, entonces se tienen dos posibilidad que corresponden a las dos ramas de la hipérbola. En una de ellas la distancia a uno de los focos es mayor y en la otra se invierten los papeles. De la ecuación $2$ se tienen dos posibilidades:
\begin{equation}
\sqrt{(x-c)^{2}+y^{2}}=2 a+\sqrt{(x+c)^{2}+y^{2}}
\end{equation}
\begin{equation}
\sqrt{(x+c)^{2}+y^{2}}=2 a+\sqrt{(x-c)^{2}+y^{2}}
\end{equation}
la primera corresponde a la rama donde $x<0$ y la segunda a $x>0$. Como hicimos en el caso de la elipse vamos a llegar a la ecuación canónica desarrollando todos los pasos. Partiendo de la definición y de la fórmula de distancia:
$$
d_{2}-d_{1}=\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a.
$$
Ahora, simplificando la expresión:
$$
\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=2 a.
$$
Si movemos uno de los radicales al lado opuesto:
$$
\sqrt{(x+c)^{2}+y^{2}}=2 a+\sqrt{(x-c)^{2}+y^{2}}.
$$
Luego, elevando al cuadrado ambos lados:
$$
(x+c)^{2}+y^{2}=\left(2 a+\sqrt{(x-c)^{2}+y^{2}}\right)^{2}.
$$
Después, expandimos los cuadrados:
$$
x^{2}+2 c x+c^{2}+y^{2}=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}+(x-c)^{2}+y^{2}.
$$
Ahora, si expandimos el cuadrado restante:
$$
x^{2}+2 c x+c^{2}+y^{2}=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}+x^{2}-2 c x+c^{2}+y^{2}.
$$
En la ecuación anterior combinamos los términos y separamos al radical:
$$
2 c x=4 a^{2}+4 a \sqrt{(x-c)^{2}+y^{2}}-2 c x
$$
$$
4 c x-4 a^{2}=4 a \sqrt{(x-c)^{2}+y^{2}}
$$
Dividiendo entre $4$ y elevando al cuadrado ambos lados:
$$
c x-a^{2}=a \sqrt{(x-c)^{2}+y^{2}}
$$
$$
\left(c x-a^{2}\right)^{2}=a^{2}\left[\sqrt{(x-c)^{2}+y^{2}}\right]^{2}
$$
Finalmente, expandiendo de nuevo el cuadrado y agrupando términos semejantes llegamos a que,
$$
c^{2} x^{2}-2 a^{2} c x+a^{4}=a^{2}\left(x^{2}-2 c x+c^{2}+y^{2}\right)
$$
$$
c^{2} x^{2}-2 a^{2} c x+a^{4}=a^{2} x^{2}-2 a^{2} c x+a^{2} c^{2}+a^{2} y^{2}
$$
$$
a^{4}+c^{2} x^{2}=a^{2} x^{2}+a^{2} c^{2}+a^{2} y^{2}
$$
$$
c^{2} x^{2}-a^{2} x^{2}-a^{2} y^{2}=a^{2} c^{2}-a^{4}
$$
$$
x^{2}\left(c^{2}-a^{2}\right)-a^{2} y^{2}=a^{2}\left(c^{2}-a^{2}\right)
$$
$$
x^{2} b^{2}-a^{2} y^{2}=a^{2} b^{2}
$$
$$
\frac{x^{2} b^{2}}{a^{2} b^{2}}-\frac{a^{2} y^{2}}{a^{2} b^{2}}=\frac{a^{2} b^{2}}{a^{2} b^{2}}
$$
$$
\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1
$$
Como ya mencionamos, esta última ecuación es la ecuación canónica de la hipérbola.
Como conclusión de este primer acercamiento a las hipérbolas, prueba el siguiente recuadro interactivo de GeoGebra. Identifica los elementos básicos de la hipérbola y dibuja algunas variando parámetros. Observa cómo variando los diferentes elementos de la ecuación cambia la forma de la hipérbola.
Más adelante…
En esta entrada nos familiarizamos con la idea elemental de la hipérbola. Todavía nos queda mucho que estudiar acerca de esta sección cónica. En la siguiente entrada nombraremos cada uno de sus elementos, presentaremos algunas propiedades métricas y discutiremos su propiedad focal. Al igual que como hicimos para las elipses, tocaremos brevemente el tema de excentricidad y luego realizaremos algunos ejercicios sobre hipérbolas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- A partir de la definición de hipérbola, determine la ecuación de la que tiene sus focos en $(6,0)$ y $(-6,0)$ si $2a=8$.
- A partir de su definición, muestre que la ecuación de una hipérbola cuyos focos están en $F_{1}(a,a)$ y $F_{2}(-a,a)$ y para la cual se cumple que $$|\mathbf{PF}_{1}| – |\mathbf{PF}_{2}| = \pm 2a$$ para todo punto $P(x,y)$ de la curva es $xy=\frac{1}{2}a^{2}$.
- Dada la siguiente ecuación, determina si se trata de una hipérbola. En caso de que sí, escríbela en su forma canónica:
$$
25 x^{2}-16 y^{2}=400
$$
Entradas relacionadas
- Ir a Geometría Analítica I
- Entrada anterior del curso: Problemas con elipses
- Siguiente entrada del curso: Propiedades de hipérbolas

Muy didactico, excelente trabajo, gracias
Gracias Jose.