Introducción

Probablemente en el bachillerato ya habrás tomado algún curso de matemáticas en el que te presentaron varios de los conceptos íntimamente relacionados con el cálculo. Por lo que has oído hablar de números reales, funciones, derivadas – por citar algunos-, pero en algún momento te has preguntado: ¿De dónde salió todo eso?, ¿Por qué podemos asegurar lo que nos enseñan nuestros profesores o leemos en los libros de texto?

En esta entrada veremos un poco sobre la motivación histórica del cálculo y a lo largo de todo el curso haciendo uso de la herramienta de la demostración buscaremos dar respuesta a la segunda pregunta planteada.

Así, ¡comenzamos!

Veloz cómo una tortuga

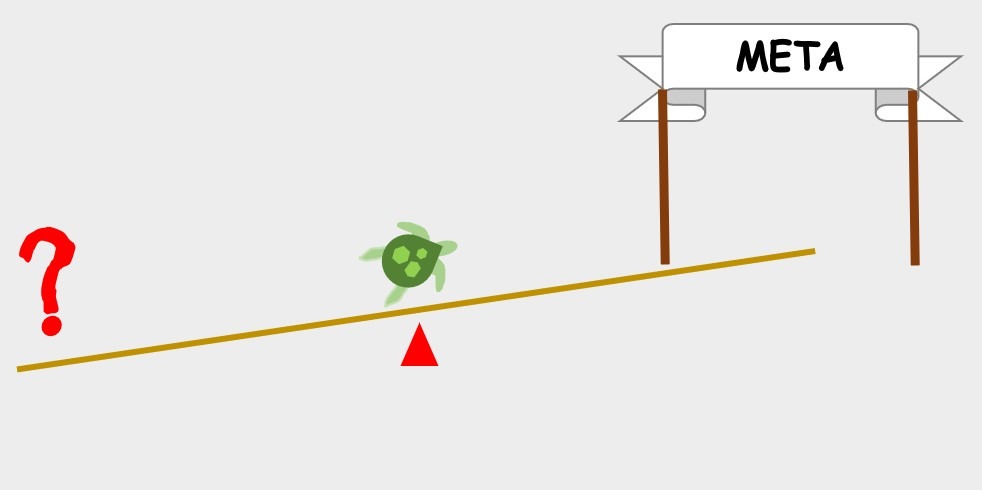
Imagina que un grupo de amigos te retan a una carrera contra una tortuga. Te dicen que, si lograras pasar por delante de ella y llegar primero a la meta, ganas un auto del año.

Sabiendo que la tortuga es extremadamente lenta en su caminar, decides darle ventaja para hacer la apuesta más interesante. Cuando ella se inicia su recorrido en el punto marcado en la imagen, finalmente comienzas a avanzar, en ese momento todos se percatan que no logras alcanzarla. ¿Cómo es esto posible?

Si nos detenemos un momento para observar lo que está pasando notamos lo siguiente:

1. Para cuando llegas al punto donde la tortuga inició el recorrido, ella ya ha avanzado una pequeña distancia.
2. Para cuando tú llegas al nuevo punto en el que se encuentra la tortuga, ella ya se ha movido un poco más hacia adelante.
3. Este proceso continúa infinitamente, con la tortuga siempre moviéndose un poco más adelante.

Debido a que hay un número infinito de estos pasos, nunca rebasarás realmente a la tortuga. Por lo que haberle dado ventaja al final no parece haber sido una buena elección.

Esta idea fue expuesta por el filósofo griego Zenón de Elea en una de sus paradojas, conocida como Aquiles y la tortuga. Su planteamiento desconcertó a los intelectuales de la época. Observamos que este problema tiene como punto de preocupación, no sólo para los filósofos, sino también para los matemáticos: el problema del movimiento. Por lo tanto, podemos considerar como uno de los propósitos del Cálculo el establecer un modelo del movimiento. Veremos más adelante que el conocimiento de los números y las funciones reales se vuelve elemental para dicha tarea.

Observación: No se está considerando la variable de la velocidad en el planteamiento del movimiento recién mencionado. De este modo, cuestionarnos si es posible que Aquiles logre alcanzar a la tortuga al aumentar su velocidad queda descartado.

Una historia de amor

Un par de enamorados desean verse. Uno de ellos se encuentra en el punto $A$ de la ciudad y el otro en el punto $B$. Cuando el enamorado del punto A se dispone a ponerse en marcha para llegar al punto $B$, un hombre en la calle le pregunta: ¿estás seguro de que puedes desplazarte al punto $B$?

Perplejo el enamorado que se encuentra en el punto $A$ responde: “No entiendo su pregunta, ¿por qué no podría?”

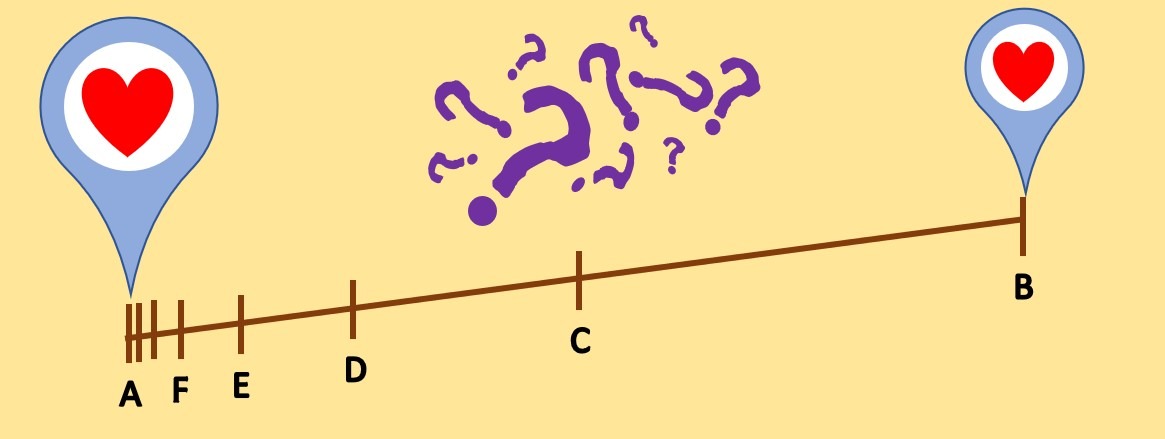
El hombre sonriendo le plantea lo siguiente: “Mira, para que puedas llegar a $B$ primero deberás pasar por el punto $C$ que se encuentra a la mitad de la distancia entre $A$ y $B$. Pero… también para llegar a $C$ debes pasar por el punto $D$ que se encuentra a la mitad de la distancia entre $A$ y $C$, ¿no?

Y si te lo piensas bien así será sucesivamente, pasarás una vez por cada punto que se encuentre a la mitad de la distancia de cualesquiera dos. Ahora dime ¿en algún momento podrás moverte de tu posición $A$? ”

Desconcertado, el enamorado $A$ se detiene a pensar sobre lo sucedido.

• ¿Qué respuesta le darías? ¿Llegarán a reunirse los enamorados bajo estas condiciones? Plantea una posible explicación, dicho ejercicio será parte de la tarea moral de esta primera parte.

Ya que hemos visto un par de paradojas interesantes, comenzaremos con un repaso de los conceptos básicos de Teoría de Conjuntos que se usarán a lo largo de todo el curso.

Repaso: Conceptos básicos de Teoría de Conjuntos.

En Matemáticas usaremos el concepto de «conjunto» para referirnos a una colección de objetos que serán considerados como una sola entidad. En la vida cotidiana algunos ejemplos serían:

Pertenencia

Utilizaremos el símbolo $\in$ para referirnos a la pertenencia de un elemento a un conjunto. Así, si tenemos lo siguiente:

$x\in A\text{,}$

esto se leería como $x$ pertenece al conjunto $A$, o $x$ es un elemento del conjunto $A$.

Si quisiéramos decir que $x$ no pertenece al conjunto $A$, o $x$ no es un elemento del conjunto $A$ usaríamos el símbolo $\notin$ y tendríamos:

$x\notin A\text{.}$

Denotando conjuntos

En algunas ocasiones encontraremos a los conjuntos escritos de la siguiente manera:

Sin embargo, en muchas ocasiones no resultará práctico escribir todos los elementos del conjunto que queremos denotar. Por lo que se usará una notación diferente llamada «por comprensión». Utilizando el ejemplo anterior tendríamos lo siguiente:

$$A=\{x\mid 0⩽x⩽4,x\in \mathbb{N}\}\text{;}$$

esto se leería como «el conjunto de los primeros cinco números naturales» o «el conjunto de los números naturales mayores o iguales que cero y menores o iguales a cuatro». Comúnmente esta última notación será la más utilizada tanto en libros de texto como en los cursos.

Como un breve recordatorio, los números naturales son un conjunto de números utilizados para contar objetos o representar una cantidad de cosas y se denotan usualmente con el símbolo $\mathbb{N}$.

Subconjuntos

Ahora veremos una relación muy especial que nos permitirá crear nuevos conjuntos a partir de uno dado. Si tenemos el siguiente conjunto:

$$B=\{0,1,2,3,a,b,c,d\}\text{,}$$

y decidimos tomar los elementos $0,3,b,c$ del conjunto $B$, vemos que podemos formar un conjunto C cuyos elementos sean los previamente seleccionados de modo que:

$$C=\{0,3,b,c\}\text{.}$$

Así diremos que $C$ es un subconjunto de $B$.

Usaremos el símbolo $\subseteq$ para representar la contención de conjuntos. Así presentamos la siguiente definición:

Definición (Subconjunto): Consideremos $A$ y $B$ conjuntos. Diremos que $A$ es un subconjunto de $B$:

$A\subseteq B$

si se cumple que todo elemento de $A$ pertenece también a $B$, en otras palabras, si todo elemento de $A$ también es un elemento de $B$.

NOTA.- $A\subseteq B$ también se puede leer como: «$A$ está contenido en $B$» o «$B$ contiene a $A$»

Definición (Igualdad de conjuntos): Consideremos $A$ y $B$ conjuntos. Diremos que $A$ es igual a $B$:

$A=B$

si y sólo si se cumple que: $A\subseteq B$ y $B\subseteq A$.

Esta definición nos resultará de utilidad al realizar demostraciones sobre la igualdad entre conjuntos.

Más adelante

En esta primera entrada hemos visto la notación utilizada en Teoría de Conjuntos, el significado de pertenencia a un conjunto, que es un subconjunto y la definición de igualdad entre conjuntos. En la siguiente entrada veremos las operaciones fundamentales entre conjuntos, donde lo antes visto será de suma importancia.

Tarea moral

1. Da una posible explicación al planteamiento de la paradoja «Una historia de amor».
2. Dados los siguientes conjuntos $A$ y $B$. Responde si los enunciados escritos a continuación son verdaderos o falsos, argumenta tu respuesta.

$$A=\{5,7,9,b,h,k,j\}$$

$$B=\{5,7,9,h,k,j\}$$

• $A\subseteq B$
• $B\subseteq A$
• Si tenemos $C=\{5,7,9,h,k,j\}$ entonces $C\subseteq B$.
• $\{5,7\}\in A$
• $\{5,7,9,h,k,j\}\in B$

Entradas relacionadas

• Ir a: Cálculo Diferencial e Integral I
• Entrada siguiente del curso: Cálculo Diferencial e Integral I: Repaso. Teoría de Conjuntos. (Parte 2)

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»