Archivo de la etiqueta: valor medio

Cálculo Diferencial e Integral II: Teorema del valor medio para la integral

Por Moisés Morales Déciga

Deja un comentario

Introducción

En una entrada anterior, presentamos un ejemplo de integración por punto medio que sirve como introducción al tema del teorema del valor medio para la integral. En dicho ejemplo, aproximamos la integral mediante sumas de áreas de rectángulos cuyas bases eran todas iguales, y cuya altura estaba dada por la evaluación de una función en el punto medio de cada intervalo.

Esta manera de aproximar una integral usando algún punto arbitrario dentro de cada intervalo de una partición, y haciendo la suma de Riemann correspondiente, será el punto de partida para entender primero a la integral como un promedio, y luego para llevar ese entendimiento más allá y enunciar el teorema del valor medio para la integral. Lo que nos dirá este teorema es que cuando una integral de una función continua exista, entonces dicha integral siempre puede calcularse como la longitud del intervalo de integración, por la evaluación de la función en algún punto del intervalo.

A continuación formalizamos estas ideas.

Función promedio e intuición del teorema del valor medio

Quizás recuerdes la siguiente definición de tu educación básica.

Definición. Sean $z_1,\ldots,z_n$ números reales. Su promedio o media aritmética es el número

$$\frac{z_1 + z_2 + … + z_n}{n}.$$

De manera similar, si tomamos $x_1,\ldots,x_n$ números en un cierto intervalo $[a,b]$ y $f:[a,b]\to \mathbb{R}$, entonces podemos considerar a los valores $f(x_1),\ldots,f(x_n)$ y obtener su promedio:

$$\frac{f(x_1) + f(x_2) + … + f(x_n)}{n} .$$

A esto le llamamos el valor promedio de la función en $x_1,\ldots,x_n$.

Pensemos que tomamos una partición en $n$ partes del intervalo $[a,b]$. La longitud de cada celda sería $\Delta x_i = (b-a)/n$. Si tomamos a los puntos $x_1,\ldots,x_n$, uno en cada celda de dicha partición, entonces tendríamos que

\begin{align*}
\frac{f(x_1) + f(x_2) + … + f(x_n)}{n}&=\frac{b-a}{b-a} \sum_{i=1} ^n \frac{f(x_i)}{n}\\
&=\frac{1}{b-a} \sum_{i=1}^n f(x_i) \Delta x_i.
\end{align*}

A la derecha nos queda una suma de Riemann. Si la función fuera integrable en $[a,b]$, dicha suma convergería a $\frac{1}{b-a}\int_a^b f(x)\, dx$ conforme $n\to \infty$ (como recordatorio, revisa la entrada de definición de la Integral). Y el lado izquierdo, conforme $n$ crece, se vuelve el promedio de más y más puntos distribuidos homogéneamente en $[a,b]$. De aquí sale la siguiente intuición: «la integral entre $b-a$ es el valor promedio de la función en todo el intervalo».

Esta intuición es buena y conviene formalizarla con un nombre apropiado.

Definición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función acotada e integrable en un intervalo $[a,b]$, con $a<b$ reales. Definimos el promedio de $f$ en $[a,b]$ como el número $$\frac{1}{b-a}\int_a^b f(x)\, dx.$$

Observa que podemos poner a esta expresión como un cociente de integrales:

$$\frac{1}{b-a} \int \limits_{a}^{b} f(x) \ dx = \frac{ \int \limits_{a}^{b} f(x) \ dx }{ \int \limits_{a}^{b} 1 \ dx }.$$

Teorema del valor medio para la integral

El teorema del valor medio establece una relación muy importante entre una función continua y promedio en cierto intervalo $[a,b]$.

Teorema. Sea $f:\mathbb{R}\to \mathbb{R}$ una función que es continua en el intervalo $[a,b]$, con $a\leq b$ reales. Entonces, siempre existe $\xi\in[a,b]$ tal que

$$ \int \limits_{a}^{b} f(x) dx = f(\xi)(b-a).$$

Si $b>a$, podemos dividir entre $b-a$ y esto quiere decir que siempre podemos encontrar un valor $\xi\in [a,b]$ tal que $f(\xi)$ es igual al promedio de $f$ en $[a,b]$.

Demostración. Si $a=b$, entonces no hay nada que hacer, pues en ambos lados de la igualdad tenemos cero. Así, sean $a<b$ números reales y $f:\mathbb{R}\to \mathbb{R}$ función continua dentro del intervalo $[a,b]$.

Las funciones continuas tienen valor máximo y mínimo en intervalos cerrados y acotados. Así, existen $x_0$ y $y_0$ en $[a,b]$ tales que $f(x_0) = m$ es el mínimo de la función en el intervalo y, $f(y_0) = M$ es el máximo de la función en el intervalo. Como las funciones constantes son integrables y la integral respeta desigualdades, tenemos que:

\begin{align*}
m(b \ – \ a) &= f(x_0) (b \ – \ a)\\
&=\int_a^b f(x_0)\, dx\\
&\leq \int_a^b f(x)\, dx\\
&\leq \int_a^b f(y_0)\, dx\\
&=f(y_0) (b-a)\\
&=M (b-a).
\end{align*}

Nos importa recuperar de esta cadena de desigualdades que $$m(b-a)\leq \int_a^b f(x)\, dx \leq M(b-a),$$ y por lo tanto $$m\leq \frac{1}{b-a} \int_a^b f(x)\, dx \leq M.$$

De esta manera, $\frac{1}{b-a} \int_a^b f(x)$ es un valor entre $f(x_0)$ y $f(y_0)$. Pero por el teorema del valor intermedio, si una función continua toma dos valores, entonces toma cualquier valor entre ellos. Así, existe $\xi$ entre $x_0$ y $y_0$ tal que $$f(\xi)=\frac{1}{b-a} \int_a^b f(x)\, dx.$$

Multiplicando por $b-a$, obtenemos la igualdad deseada.

$ \square$

Para entender un poco mejor el teorema del valor medio para la integral, veamos un ejemplo.

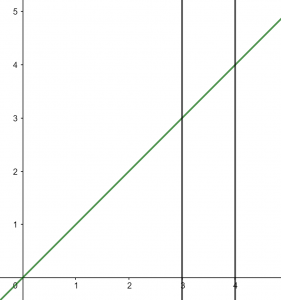
Ejemplo. Veamos el teorema del valor medio en acción para la función $f(x)=x$ en el intervalo $[3,4]$.

Ya habíamos encontrado el valor de esta integral en la entrada «Definición de la Integral Definida». Dicho valor fue $\frac{7}{2}=3.5$.

Lo que nos diría el teorema del valor medio es que podemos encontrar un punto $\xi \in[3,4]$ tal que Sustituyendo en la expresión encontrada por el teorema, se tiene lo siguiente.

$$f(\xi)(4 \ – \ 3) = \int \limits_{3}^{4} f(x) dx=3.5,$$

es decir, tal que $f(\xi)=3.5$. Y en efecto, dicho punto es justamente $3.5$, pues $f(3.5)=3.5$. Notemos que, tal como se quería, tenemos que $3.5\in [3,4]$. Por lo tanto, el punto $\xi = 3.5 $ dentro del intervalo $[3,4]$ es tal que al evaluarlo en la función, da por resultado el promedio de $f$ en $[3,4]$.

$\triangle$

Teorema del valor medio generalizado para la integral

Hay otra versión del teorema del valor medio que generaliza la noción de promedio. Quizás en tu educación básica cursaste una materia en donde el $30\%$ de tu calificación eran tareas, el $20\%$ era participaciones y el $50\%$ el examen. En este caso, si sacaste $x,y,z$ en las tareas, participaciones y examen respectivamente, entonces tu calificación final era $0.3 x + 0.2 y + 0.5 z$. Este tipo de promedios en donde distintos números tienen distinto valor quedan reflejados en la siguiente definición.

Definición. Sean $z_1,\ldots,z_n$ números reales y $p_1,\ldots,p_n$ números positivos. La media aritmética ponderada con dichos pesos es el número real $$\frac{p_1z_1+p_2z_2+\ldots+p_nz_n}{p_1+p_2+\ldots+p_n}.$$

El promedio se recupera eligiendo todos los pesos $p_i$ iguales a $1$, es decir, dando la misma ponderación para todos los valores que tenemos dentro del conjunto, independientemente del valor que hayan tenido. Las medias aritméticas son importantes pues aparecen en las aplicaciones. Por ejemplo, en física podemos pensar que los $p_i$ son pesos de partículas localizadas en los puntos $z_i$. En este caso la media aritmética ponderada representará el centro de gravedad de dichos objetos.

Estas ideas pueden llevarse al contexto continuo. Se pueden pensar en las ideas del teorema del valor medio, pero donde ahora en cada punto ponderaremos de acuerdo a una función peso. Esto hará que ahora distintos puntos tengan distinta preferencia, y que a su vez ya no se tenga una media aritmética, sino una media aritmética ponderada.

Definición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función integrable en $[a,b]$ y sea $p:\mathbb{R}\to \mathbb{R}$ una función integrable en $[a,b]$ y no negativa, con integral positiva. Definimos el promedio ponderado de $f$ como el número

$$\frac{\int_a^b f(x) p(x) \, dx}{\int_a^b p(x)\, dx}.$$

Se puede demostrar el siguiente teorema, que generaliza al teorema del valor medio para la integral.

Teorema. Sea $f:\mathbb{R}\to \mathbb{R}$ una función continua en $[a,b]$ y sea $p:\mathbb{R}\to \mathbb{R}$ una función continua en $[a,b]$ y no negativa, con integral positiva. Entonces existe un valor $\xi\in [a,b]$ tal que:

$$\int \limits_{a}^{b} f(x) \ p(x) \ dx = f(\xi) \ \int \limits_{a}^{b} p(x) \ dx .$$

Observación. Si $p(x)$ es la función constante $1$, recuperamos el teorema del valor medio para la integral.

Ya tienes todas las herramientas para probar esta generalización. ¡Te espera en los problemas!

Más adelante…

A partir de la definición de la integral mediante sumas se obtienen teoremas y propiedades que nos permiten simplificar el cálculo de la integral y tener herramientas para resolver problemas mediante diferentes métodos.

Este teorema nos permite calcular la integral a partir del punto medio del intervalo, simplificando el proceso ya que no es necesario determinar el ínfimo o el supremo de cada partición.

Un poco después veremos algunas aplicaciones de este teorema. Será de suma importancia cuando enunciemos y mostremos los teoremas fundamentales del cálculo.

Tarea moral

  1. Encuentra el valor promedio la función dada, en el intervalo dado. Luego, encuentra un valor $\xi$ en el intervalo dado tal que $f(\xi)$ sea la integral que encontraste.
    • $f(x)=1 + x^2$ en $[-1,2]$.
    • $f(x)=\sqrt x$ en el intervalo $[0,4]$.
    • $f(x)=1+2x-x^2$ en el intervalo $[-2,2]$.
  2. Determina el valor promedio ponderado de las siguientes funciones, usando la función ponderación dada.
    • $f(x)=1+x^2$ en $[-1,2]$, con función ponderación $p(x)=x+1$.
    • $f(x)=4x^2 – 2x$ en $[1,4]$, con función ponderación $p(x)=3$.
    • $f(x)=(x-3)^2$ en en $[2,5]$, con función ponderación $p(x)=x-2$.
  3. Demuestra el teorema del valor medio generalizado para la integral.
  4. El teorema del valor medio es falso en general si la función no es continua. Considera la siguiente función $$f(x)=\begin{cases} 0 & \text{si $x\in [0,1]$}\\ 1 & \text{si $x\in[1,3].$}\end{cases}$$
    • Demuestra que esta función es integrable en $[0,3]$.
    • Encuentra explícitamente el valor de esa integral mediante la definición.
    • Muestra que no existe ningún $\xi\in [0,3]$ tal que $f(\xi)=\frac{1}{3-0} \int_a^b f(x)\, dx.$
  5. Sea $f:\mathbb{R}\to\mathbb{R}$ una función continua y tal que $f(x)\geq 3$ para todo $x$ en cierto intervalo $[a,b]$. Demuestra que si el promedio de $f$ en $[a,b]$ es $3$, entonces $f(x)=3$ para todo $x\in [a,b]$. ¿Fue importante que el número fuera $3$? Enuncia y demuestra una generalización.

Entradas relacionadas

Seminario de Resolución de Problemas: Problemas de cálculo variados

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En las entradas anteriores ya tratamos varios temas de cálculo y cómo se combinan con heurísticas para resolver problemas de cálculo. Veremos ahora otros problemas para repasar las técnicas que hemos aprendido hasta ahora y explorar algunas nuevas ideas.

Los primeros dos ejemplos son del libro Problem Solving through Problems de Loren Larson. Los últimos dos son de un concurso universitario: la Competencia Iberoamericana Interuniversitaria de Matemáticas.

El método del factor de integración

Para resolver problemas de cálculo, también es útil tener algunas ideas de ecuaciones diferenciales. Un método muy útil en la resolución de problemas es el método de factor de integración, que ayuda a resolver ecuaciones diferenciales de la forma $$y’+a(x)y=b(x).$$

La idea para resolver esta ecuación diferencial en $y$ (es decir, despejar a $y$ en términos de $a$ y $b$) es multiplicar ambos lados de la ecuación por $I(x)=e^{\int a(x)\, dx$ y observar que por regla de la cadena, la regla del producto y el teorema fundamental del cálculo, tenemos la ecuación diferencial equivalente $$(yI(x))’ =I(x)b(x).$$

De aquí, podemos integrar de ambos lados en un intervalo $[c,x]$. Por el teorema fundamental del cálculo, existe una constante $C$ tal que $$yI(x)=\int_{c}^x I(t) b(t)\, dt + C,$$ y ya de aquí podemos despejar $$y=I(x)^{-1}\left( \int_{c}^x I(t) b(t)\, dt + C\right).$$

A $I(x)$ se le conoce como el factor de integración.

Problema. Sea $f:(0,\infty)\to \mathbb{R}$ una función diferenciable y supongamos que $$\lim_{x\to \infty} f(x)+f'(x) = 0.$$ Muestra que $$\lim_{x\to 0} f(x) = 0.$$

Sugerencia pre-solución. Define $g(x)=f(x)+f'(x)$ y usando el método de integración «despeja» a $f$ en términos de $g$.

Solución. Definamos $g(x)=f(x)+f'(x)$. La hipótesis dice que $\lim_{x\to 0} g(x) = 0$, así que para obtener información de $f$ en términos de $g$, podemos usar el método de factor de integración. Por la discusión antes de este párrafo, tenemos que $$f(x)=e^{-x}\int_a^x e^t g(t) \,dt + Ce^{-x}.$$

Tomemos un $\epsilon>0$. Como $g(x)\to 0$ cuando $x\to \infty$, podemos tomar un $a$ tal que $|g(x)|<\epsilon$ para todo $x>a$. Usando desigualdad del triángulo en sumas e integrales, tenemos que para $x>a$
\begin{align*}
|f(x)|&\leq e^{-x}\left|\int_a^x e^t g(t)\right|+|Ce^{-x}|\\
&\leq e^{-x}\int_a^x e^t|g(t)|\, dt + |C|e^{-x}\\
&\leq \epsilon e^{-x}\int e^t\, dt + |C|e^{-x}\\
&=\epsilon e^{-x}(e^x-e^a)+|C|e^{-x}\\
&=\epsilon(1-e^{a-x})+|C|e^{-x}
\end{align*}

Tenemos que $\lim_{x\to \infty} e^{a-x} = 0$ y que $\lim_{x\to \infty} e^{-x}=0$, de modo que si $x$ es suficientemente grande, la expresión anterior nos dice $|f(x)|<2\epsilon$. En otras palabras, $f(x)\to 0$ cuando $x\to \infty$, como queríamos.

$\square$

Una integral con doble derivada

Problema. Sea $f:[0,1]\to \mathbb{R}$ una función dos veces diferenciable que cumple $f(0)=f(1)=0$ y tal que $f(x)>0$ para $x$ en $(0,1)$. Muestra que $$\int_0^1 \left| \frac{f»(x)}{f(x)} \, dx \right| > 4.$$

Sugerencia pre-solución. Tenemos ya varias técnicas para evaluar o estimar integrales. Si con un método llegas a una pared, intenta usar otro método. Necesitarás el teorema del valor extremo, el teorema del valor medio y el teorema fundamental del cálculo.

Solución. Por el teorema del valor extremo, existe un valor $c$ en $(0,1)$ tal que $y=f(c)$ es un máximo de $f$. Por el teorema del valor medio, existen puntos $a$ en $(0,c)$ y $b$ en $(c,1)$ tales que $$f'(a)=\frac{f(c)-f(0)}{c}=\frac{y}{c}$$ y $$f'(b)=\frac{f(1)-f(c)}{1-c}=\frac{-y}{1-c}.$$

Usando que $f$ alcanza su máximo $y$ en $c$

\begin{align*}
\int_0^1 \left| \frac{f»(x)}{f(x)} \, dx \right|&\geq \int_a^b \left| \frac{f»(x)}{f(x)} \, dx \right| \\
&\geq \frac{1}{y} \int_a^b \left| f»(x) \, dx \right|,
\end{align*}

de modo que aplicando el teorema fundamental del cálculo a la última integral, obtenemos que

\begin{align*}
\int_0^1 \left| \frac{f»(x)}{f(x)} \, dx \right| &\geq \frac{1}{y} \int_0^1 \frac{1}{y}|f'(b)-f'(a)|\\
&=\frac{1}{y} \left|\frac{-y}{1-c}-\frac{y}{c}\right|\\
&=\left|\frac{1}{c(1-c)}\right|.
\end{align*}

Para terminar, notamos que la función $h(x)=x(1-x)$ es diferenciable en $(0,1)$ y continua en $[0,1]$, de modo que alcanza su máximo en $0$, en $1$ o en donde la derivada $h'(x)=1-2x$ es $0$, es decir, en $1/2$. Tenemos que $h(1/2)=1/4$ y que $h(0)=h(1)=0$, de modo que el máximo es $1/4$. Con esto, concluimos que $$\left|\frac{1}{c(1-c)}\right| \geq 4,$$ de donde se completa la cadena de desigualdades que queremos.

$\square$

En el problema anterior usamos el teorema del valor medio como paso intermedio. Es recomendable que pienses qué hubiera pasado si nos hubiéramos saltado este paso y hubiéramos usado el mínimo directamente, sin limitarnos primero al intervalo $[a,b]$. En los problemas de cálculo a veces es muy importante el orden en el que se hacen las cosas.

Dos problemas de cálculo de competencias

Veamos ahora algunos problemas de cálculo que han aparecido en concursos a nivel universitario. El siguiente problema apareció en la Competencia Iberoamericana Interuniversitaria de Matemáticas, en 2015, como Problema 4.

Problema. Sea $f:\mathbb{R}\to \mathbb{R}$ una función continua y $\alpha$ un número real. Sabemos que $\lim_{x\to \infty} f(x) = \lim_{x\to -\infty} = \alpha$. Muestra que para cualquier real positivo $r$ existen reales $x$ y $y$ tales que $y-x=r$ y $f(x)=f(y)$.

Sugerencia pre-solución. Modifica el problema, construyendo una función que te ayude a resolverlo. Necesitarás el teorema del valor intermedio. También, una parte de la solución necesita que se use inducción.

Solución. Tomemos cualquier valor $r$ y consideremos la función $h(x)=f(x+r)-f(x)$. Como $f$ es continua, la función $h$ es continua. Si $h(x)>0$ para todo real, entonces podemos mostrar inductivamente que para cualesquiera enteros positivos $m$ y $n$ tenemos que $$f(x-mr)<f(x)<f(x+r)<f(x+nr).$$

Haciendo $n$ y $m$ ir a infinito, tendríamos que $$\alpha\leq f(x) < f(x+r) \leq \alpha,$$ lo cual es una contradicción.

Así, $h(x)$ toma valores menores o iguales a $0$. De modo similar, podemos mostrar que $h(x)$ toma valores mayores o iguales a $0$. Como $h$ es continua, por el teorema del valor intermedio debe tomar el valor $0$ para algún $c$, de modo que $f(c+r)-f(c)=h(c)=0$ y así, tomando $x=c$ y $y=c+r$ tenemos $y-x=r$ y $$f(y)=f(c+r)=f(c)=f(x).$$

$\square$

El siguiente problema apareció en la Competencia Iberoamericana Interuniversitaria de Matemáticas, en 2010, como Problema 4.

Problema. Sea $f:[0,1]\to [0,1]$ una función continua, creciente, diferenciable en $[0,1]$ y tal que $f'(x)<1$ en cada punto. La sucesión de conjuntos $A_1, A_2, \ldots$ se define recursivamente como $A_1=f([0,1])$ y para $n\geq 2$, $A_n=f(A_{n-1})$. Muestra que el diámetro de $A_n$ converge a $0$ conforme $n\to \infty$.

El diámetro de un conjunto $X$ es $\sup_{x,y \in X} |x-y|$.

Sugerencia pre-solución. Para una primer parte del problema que te ayudará a entender a los $A_i$, necesitarás el teorema del valor intermedio y el principio de inducción. Luego, necesitarás usar el teorema del valor medio y que las funciones continuas preservan límites de sucesiones convergentes.

Solución. Por conveniencia, nombramos $A_0=[0,1]$. Sea $d_n$ el diámetro de $A_n$. Tenemos $d_0=1$. Como $f$ es creciente, tenemos que $f(0)<f(1)$ y que no hay ningún valor fuera del intervalo $[f(0),f(1)]$ que se tome. Como $f$ es continua, se toman todos esos valores. Así, $A_1=[f(0),f(1)]$ y su diámetro es $d_1=f(1)-f(0)$. Inductivamente, podemos mostrar que $A_n= [f^n(0),f^n(1)]$ y que $d_n=f^{n}(1)-f^{n}(0)$.

Notemos que la sucesión $f^{n}(0)$ es creciente y acotada, de modo que converge a un real $a$. Como $f$ es contínua, tenemos que \begin{align*}f(a)&=f(\lim_{n\to \infty} f^{n}(0)) \\&= \lim_{n\to \infty} f^{n+1}(0) \\&= a.\end{align*} Análogamente, $f^n(1)$ converge a un real $b$ tal que $f(b)=b$. Como $f^n(0)\leq f^n(1)$, tenemos que $a\leq b$. Afirmamos que $a=b$. Si no, por el teorema del valor medio existiría un $c\in[a,b]$ tal que $$f'(c)=\frac{f(b)-f(a)}{b-a}=\frac{b-a}{b-a}=1,$$ contradiciendo la hipótesis de la cota de la derivada.

Esto muestra que $a=b$, y por lo tanto
\begin{align*}
\lim_{n\to \infty} d_n &= \lim_{n\to \infty} f^n(1)-f^n(0) \\
&=b-a\\
&= 0.
\end{align*}

$\square$

En este problema es muy importante primero mostrar que los extremos de los intervalos convergen a puntos fijos de $f$ y después usar el teorema del valor intermedio. Podría ser tentador usar el teorema del valor intermedio en cada intervalo $[f^n(0),f^n(1)]$, pero con ello no se llega al resultado deseado.

Más problemas

En todas estas entradas hemos platicado acerca de problemas de temas de cálculo. Se pueden encontrar muchos más problemas de este tema en el Capítulo 6 del libro Problem Solving through Problems de Loren Larson.

Además, puedes encontrar otros problemas resueltos en la sección de Material para practicar de este blog, que ayuda a prepararse para competencias internacionales de matemáticas a nivel universitario.