El problema

Les comparto un problema que se me ocurrió en las (muchas) horas que he pasado en el carro escuchando música, cuando vivía en la Ciudad de México. El estéreo del carro ordena las canciones alfabéticamente. Tiene un botón que permite «avanzar una canción». Pero a veces tarda mucho: si estoy escuchando «Adele – Hello», hay que apretar el botón muchas veces para llegar a «Shakira – Dónde están los ladrones».

En esas épocas descubrí una estrategia «intuitiva» para llegar más rápido a la canción. La idea es la siguiente: pasar temporalmente al modo de «canción aleatoria», apretar el botón unas cuantas veces para acercarme a la canción que quiero (en el ejemplo anterior, digamos que después de dos o tres veces el botón me lleva a «Paquita la del Barrio – Rata de dos Patas»), y de ahí quitar el aleatorio y avanzar normal. Eso, intuitivamente, siempre me ahorró muchos pasos. El problema consiste en encontrar la estrategia óptima, en donde se permiten mezclar pasos normales y aleatorios.

Para eso, voy a plantear un problema muy concreto. De aquí en adelante supondré que el lector sabe un poco de probabilidad. Pensemos que hay $2n$ canciones, numeradas de $1$ a $2n$. Estoy en la canción $n$ y quiero llegar a la canción $2n$. Pensemos que el estéreo tiene exactamente dos botones, el $A$ que avanza $1$ (y de $2n$ lleva a $1$), y el $B$ que lleva a una canción aleatoria (cualquiera de las canciones, incluida la actual, tiene probabilidad $1/2n$ de ser elegida). En cada paso se permite ver en qué canción estoy, y de ahí decidir apretar $A$ o $B$. ¿Cuál es la estrategia que en valor esperado tiene menos pasos? ¿Cuál es ese valor esperado?

En la imagen de aquí abajo se muestra un ejemplo de una forma de apretar los botones para $n=5$, con $2n=10$ canciones. Las flechas rojas corresponden a avanzar $1$ apretando el botón $A$. Las flechas azules corresponden a ir a un lugar aleatorio apretando el botón $B$. Se apretaron los botones en el orden $ABBAA$, de modo que se hicieron $5$ pasos.

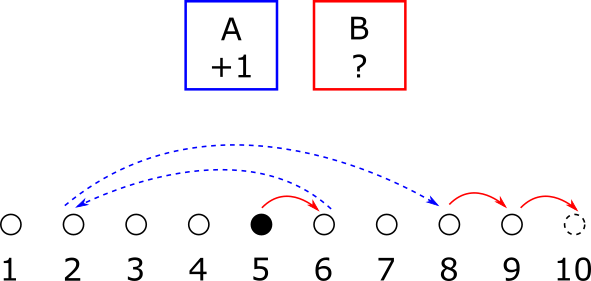
Ese es el enunciado del problema. De aquí en adelante empiezo a hablar de ideas para resolverlo, así que si quieres intentarlo, este es el momento correcto.

Primeras ideas

Notemos que la estrategia «siempre $A$, hasta llegar a $2n$» toma exactamente $n$ pasos siempre. La estrategia «siempre $B$» es para intentar atinarle, y en cada paso tiene probabilidad de éxito $1/2n$. Entonces, en esta segunda estrategia la cantidad de pasos requeridos es una variable aleatoria con distribución geométrica de parámetro $p=1/2n$, de modo que el número esperado de pasos es $1/p=2n$.

Sin embargo, suena a que la estrategia esbozada al inicio de esta entrada es intuitivamente mejor: usar el $B$ para acercarse y luego el $A$ para llegar.

La solución

Vamos a mostrar que la mejor estrategia en valor esperado es la siguiente: «apretar el botón $B$ hasta llegar aproximadamente al intervalo $[n-2\sqrt{n}, n]$, y de ahí apretar el botón $A$» hasta llegar a $n$.

El primer argumento es que en cada paso, lo que hace la estrategia sólo depende de en qué canción estamos. En efecto, el paso $A$ es determinista y el $B$ es una variable uniforme independiente de todo lo demás.

El segundo argumento es que, si en algún momento de la estrategia usamos el botón $A$, entonces después de ello nunca nos conviene usar el botón $B$. Lo probamos por contradicción: supongamos que por cualquier razón en la estrategia óptima tenemos que hacer un $AB$. El paso $A$ es determinista, y sabíamos exactamente a qué canción nos iba a llevar (a la siguiente). Pero hacer el paso $B$ en cualquier lugar que estemos es simétrico, pues nos lleva a una canción aleatoria. Si a priori sabíamos que íbamos a hacer un paso $B$, lo mejor es hacerlo lo antes posible. Así, la estrategia que substituye esos pasos $AB$ por $B$ se ahorra un paso, y no es óptima. Contradicción.

Ahora, afirmo lo siguiente. Si la estrategia óptima es apretar $A$ cuando estamos en la canción $j$, entonces también va a ser apretar $A$ cuando estemos en cualquier canción $k$ con $j\leq k < 2n$. Esto es debido al argumento anterior: al apretar $A$ llegamos a $j+1$, que por el párrafo de arriba, no le puede tocar $B$. Entonces le toca $A$. De ahí llegamos a $j+2$, que de nuevo no le puede tocar $B$. Y así sucesivamente (inductivamente), hasta llegar a $2n-1$.

Lo que acabamos de probar es que la estrategia óptima se ve de la siguiente manera para algún entero $k$: «Apretar $B$ hasta que lleguemos a alguno de los últimos $k$ elementos. De ahí, apretar $A$ hasta llegar a $2n$.» Nos falta determinar cuál es la mejor $k$ que podemos usar.

A estas alturas ya podemos calcular explícitamente el valor esperado de pasos en esta estrategia. El evento «llegar a alguno de los últimos $k$ elementos» tiene probabilidad $k/2n$ de ocurrir cada que se aprieta el botón $B$, así que la cantidad de veces que hay que apretar $B$ para ello es una variable aleatoria geométrica de valor esperado $2n/k$. Una vez que llegamos a los últimos $k$ elementos, caemos a cualquier elemento del intervalo $\{2n-k+1, 2n-k+2,\ldots,2n\}$ con la misma probabilidad, y respectivamente nos tomará $\{k-1, k-2,\ldots, 0\}$ pasos en llegar a $2n$, es decir, la cantidad de pasos que hacemos es una variable aleatoria uniforme discreta de media $(k-1)/2$.

Así, en total usamos $(2n/k) + (k-1)/2$ pasos para llegar. Queremos lograr que esta expresión sea lo más pequeña posible. Usando la desigualdad entre la media geométrica y la aritmética, notamos que $$\frac{2n}{k}+\frac{k-1}{2}=\frac{2n}{k}+\frac{k}{2}-\frac{1}{2} \geq 2\sqrt{n} – \frac{1}{2},$$ y que la igualdad se da si y sólo si $\frac{2n}{k}=\frac{k}{2}$, es decir, si y sólo si $k=2\sqrt{n}$. En este caso, la cantidad media de pasos que usamos es $2\sqrt{n}-\frac{1}{2}$.

Aquí arriba hicimos un poquito de trampa. En realidad $k=2\sqrt{n}$ tiene sentido para la estrategia sólo cuando $\sqrt{n}$ es un número entero. Sin embargo, por la convexidad de la función $
\frac{2n}{k}+\frac{k}{2}$ tenemos la garantía de que o bien $\lfloor
2\sqrt{n} \rfloor$ o bien $\lceil 2\sqrt{n} \rceil$ dan el máximo.

Conclusión y otros problemas

Está cool que hayamos bajado la cantidad de pasos que se necesitan de valor esperado de algo que era $n$ a algo que es del tamaño $2\sqrt{n}$. Para hacerse una idea de los pasos que se pueden ahorrar, toma una colección de $800$ canciones. Originalmente se necesitaban $400$ pasos $+1$ para ir de la mitad al final. Con la nueva estrategia se requieren como $40$.

Hacer esta estrategia en la vida real es un poco complicado pues los estéreos no muestran el número exacto de la canción en la que se está, además de que es difícil memorizar a qué canción le toca qué número. Pero a veces sí muestran el nombre de la canción y más o menos «se le puede aproximar».

Hay un par de variantes interesantes. Una es ¿qué sucede si además de tener botón $+1$ y aleatorio, también tenemos botón $-1$?. En esta variante la solución no cambia mucho, pero es bueno intentarla para repasar las ideas de la prueba.

La otra variante es la siguiente. La estrategia óptima, como está descrita arriba, tiene un problema: es posible que nunca termine, o que tome muchísimos pasos en terminar (esto será muy improbable y por eso el valor medio se compensa). Así, imaginemos que queremos la restricción adicional de que la estrategia que usemos nunca use más de, digamos, 4n pasos. En esta variante: ¿cuál es la estrategia óptima? ¿cuántos pasos toma?

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

• Una demostración del teorema de la función inversa
• Un ejemplo de aplicación del teorema de la función inversa
• Los teoremas fundamentales de los cuadraditos, o bien, una introducción amigable a los teoremas fundamentales del cálculo
• Un problema de probabilidad y escuchar música
• Mariposa de siete equivalencias de invertibilidad de matrices