Introducción
En una entrada anterior esbozamos las construcciones de los números racionales y los números reales. Es hora de construir los números complejos. Para ello, definiremos primero el conjunto, $\mathbb{C}$, sobre el que trabajaremos, después definiremos sus operaciones.
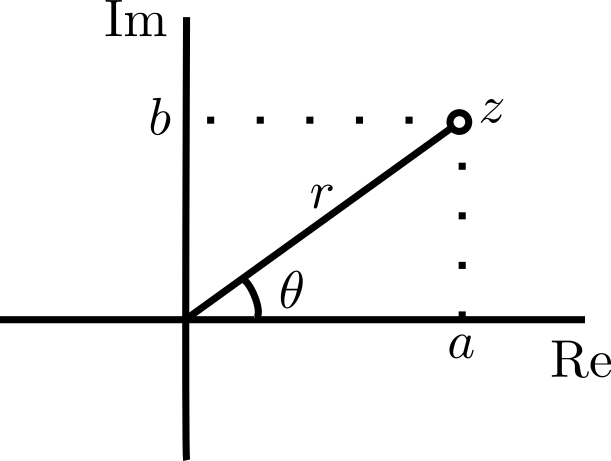
Una forma intuitiva de visualizar a $\mathbb{C}$ es tomar el conjunto de los números reales ($\mathbb{R}$) y en ellos introducir un nuevo elemento, $i$, el cual satisface que $i^2=-1$. Este es, realmente, un nuevo elemento, pues en $\mathbb{R}$ siempre se tiene que $x^2\geq 0$.
Una vez que introducimos a $i$, queremos que las operaciones de suma y producto estén definidas en $\mathbb{C}$ y que, además este conjunto, sea cerrado bajo estas operaciones. Es decir, es necesario que para cualquier número real $b$ se tenga $bi\in \mathbb{C}$ y que para cualesquiera números reales $a$ y $b$ tengamos, también, $a+bi\in \mathbb{C}$. Resulta que esto «es suficiente», en el sentido de que ya no hay que meter más números para que las operaciones estén bien definidas. Veamos como es esto, si tenemos los números de la forma $a+bi$ y $c+di$ con $a,b,c,d\in \mathbb{R}$ y los sumamos y multiplicamos como sigue: $$(a+bi)+(c+di)=(a+c)+(b+d)i$$, vemos que, la suma, «tiene la misma forma» (ya que $a+c$ y $b+d$ son números reales) así como su producto:
\begin{align*}
(a+bi)(c+di)&=ac+bci+adi+bdi^2\\
&=(ac-bd)+(ad+bc)i.
\end{align*}
Desde luego que lo anterior es soló una discusión informal. En las siguientes secciones veremos cómo formalizar estas ideas.
Los números complejos se comportan muy bien en términos algebraicos y en términos de análisis. En términos algebraicos, esto se comenzará a notar en la última parte del curso en donde veremos que cualquier polinomio tiene por lo menos una raíz compleja. En cursos posteriores, como el de álgebra lineal, verás otras de las propiedades algebraicas de los polinomios. Más adelante, si llevas un curso de variable compleja verás las bellas propiedades analíticas que tienen los números complejos.
El campo de los números complejos
La construcción del conjunto de números complejos es bastante sencilla. Para hacerla, simplemente consideraremos las parejas de números reales $$\mathbb{C}=\{(a,b): a,b\in \mathbb{R}\}.$$
Por el momento a cada $(a,b)$ lo puedes pensar de manera informal como el complejo $a+bi$. Lo interesante del conjunto de los números complejos no son sus elementos en sí, sino las siguientes operaciones que están definidas en él.
Definición. Para $(a,b)$ y $(c,d)$ en $\mathbb{C}$, definimos su suma como $$(a,b)+(c,d)=(a+c,b+d).$$
Recordemos que dentro del paréntesis se usa la suma de $\mathbb{R}$ ya que $a$, $b$, $c$ y $d$ son números reales.
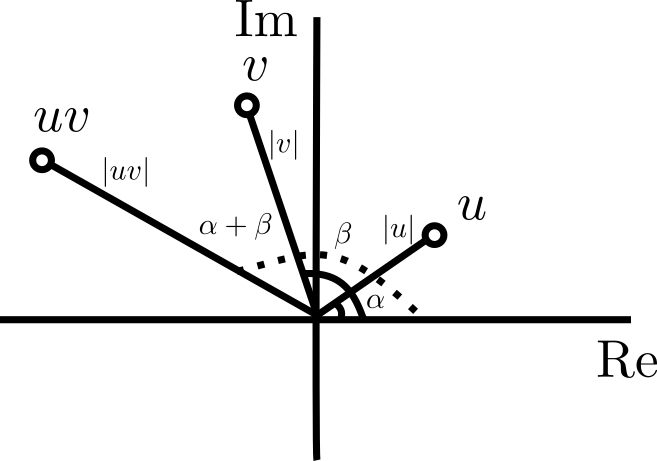
Definición. Para $(a,b)$ y $(c,d)$ en $\mathbb{C}$, definimos su producto como $$(a,b)(c,d)=(ac-bd,ad+bc).$$
Igualmente dentro del paréntesis se usan la suma y producto de $\mathbb{R}$. La definición de producto está motivada por la discusión que hicimos en la introducción.
Teorema. El conjunto $\mathbb{C}$, junto con las operaciones de suma y producto que definimos, es un campo.
Demostración. La suma es conmutativa y asociativa ya que cada entrada pertenece a $\mathbb{R}$ y en $\mathbb{R}$ la suma es conmutativa y asociativa. El neutro es $(0,0)$ pues $$(a,b)+(0,0)=(a+0,b+0)=(a,b)$$ y para $(a,b)$ su inverso aditivo es $(-a,-b)$.
Veamos ahora el producto. Probemos que es conmutativo. Para dos complejos $(a,b)$ y $(c,d)$ tenemos que $$(a,b)(c,d)=(ac-bd,ad+bc)$$ y que $$(c,d)(a,b)=(ca-db,cb+da).$$
Ambos resultados son iguales ya que cada entrada pertenece a $\mathbb{R}$ y la suma y el producto son conmutativos en $\mathbb{R}$.
Probemos que el producto es asociativo. Para ello tomemos tres complejos $(a,b)$, $(c,d)$ y $(e,f)$. Tenemos que
\begin{align*}
[(a,b)(c,d)](e,f)&=(ac-bd,ad+bc)(e,f)\\
&=(ace-bde-adf-bcf,acf-bdf+ade+bce),
\end{align*} y que
\begin{align*}
(a,b)[(c,d)(e,f)]&=(a,b)(ce-df,cf+de)\\
&=(ace-adf-bcf-bde,acf+ade+bce-bdf),
\end{align*}
Ambas expresiones son iguales ya que cada entrada pertenece a $\mathbb{R}$ y la suma es conmutativa en $\mathbb{R}$.
El complejo $(1,0)$ actúa como neutro multiplicativo, pues $$(a,b)(1,0)=(a\cdot 1 – b\cdot 0, a\cdot 0 + b\cdot 1)=(a,b).$$ Además, si tomamos un complejo $(a,b)\neq (0,0)$ y lo multiplicamos por $\left(\frac{a}{a^2+b^2},\frac{-b}{a^2+b^2}\right)$ obtenemos \begin{align*}
(a,b)\left(\frac{a}{a^2+b^2},\frac{-b}{a^2+b^2}\right)&= \left(\frac{a^2+b^2}{a^2+b^2}, \frac{-ab}{a^2+b^2}+\frac{ba}{a^2+b^2}\right)\\ &= (1,0),
\end{align*} lo cual muestra que tenemos inversos multiplicativos.
Sólo falta demostrar la propiedad distributiva. Su verificación se deja como tarea moral.
$\square$
La copia de los reales en los números complejos
Dentro de $\mathbb{C}$ hay una copia de los números reales. Esta consiste en asociarle, a cada número real $a$, el número complejo $\varphi(a)=(a,0)$. Esta asociación es claramente biyectiva. Además, si $a$ y $b$ son números reales, tenemos que $$(a,0)+(b,0)=(a+b,0)=\varphi(a+b)$$ y
\begin{align*}
(a,0)(b,0) &= (ab-0\cdot 0, a\cdot 0 + b\cdot 0)\\
&= (ab,0) = \varphi(ab).
\end{align*}
Además los neutros se van a neutros y los inversos a inversos. Esto muestra que $\varphi$ es una asociación biyectiva entre $\mathbb{R}$ y los complejos de la forma $(a,0)$ y que respeta la estructura de campo de $\mathbb{R}$.
Por otro lado, notemos que $$(0,1) (0,1)= (0\cdot 0 – 1\cdot 1, 0\cdot 1 + 1\cdot 0)= (-1, 0).$$
En otras palabras, al elevar el complejo $(0,1)$ al cuadrado obtenemos el número $(-1,0)$, que es precisamente $\varphi(-1)$.
Tras toda esta discusión, estamos justificados entonces en llamar simplemente $1$ al complejo $(1,0)$, en llamar $i$ al complejo $(0,1)$, y por lo tanto en llamar $a+bi$ al complejo $(a,b)$. A partir de aquí ya podemos olvidar la notación de parejas y tratar a los números complejos como lo discutimos en la introducción.
Operaciones en la notación $a+bi$
La notación $a+bi$ para números complejos es bastante práctica. Podemos trabajar con los complejos «igualito que en $\mathbb{R}$, pero, además, con la propiedad de que $i^2=-1$».
Como $i^4=(-1)^2=1$, tenemos que las potencias de $i$ se ciclan cada cuatro: $$1, i, i^2, i^3, i^4, i^5, i^6, \ldots$$ son $$1,i, -1, -i, 1, i,\ldots .$$ Ya mencionamos en la introducción que para complejos $a+bi$ y $c+di$ se tiene que $$(a+bi)+(c+di)=(a+c)+(b+d)i$$ y que $$(a+bi)(c+di)=(ac-bd)+(ad+bc)i,$$ de modo que cualquier composición de sumas y productos de números complejos se puede simplificar a la forma $x+yi$ con $x$ y $y$ reales.
Ejemplo. Simplifica la expresión $$(1+i)(1-i)+(2+i)(3-4i).$$ Solución. Haciendo el producto del primer sumando tenemos $(1+i)(1-i)=1^2-i^2=1-(-1)=2$. Haciendo el producto del segundo sumando tenemos \begin{align*}
(2+i)(3-4i)&=6+3i-8i-4i^2\\
&=6-5i+4\\
&=10-5i.
\end{align*}
De esta forma, el resultado de la operación es $$2+(10-5i)=12-5i.$$
$\triangle$
En complejos también podemos usar expresiones fraccionales, como $\frac{3+2i}{5-i}$. Si queremos pasar estas expresiones a la forma $x+yi$ con $x$ y $y$ reales, tenemos que pensar a $\frac{1}{5-i}$ como «el inverso multiplicativo de $5-i$», que como vimos en la demostración de que $\mathbb{C}$ es un campo, es $$\frac{5}{5^2+(-1)^2}+\frac{1}{5^2+(-1)^2}i=\frac{5}{26}+\frac{1}{26} i.$$ Una vez hecho esto, tenemos que \begin{align*}
\frac{3+2i}{5-i}&=(3+2i)\left( \frac{5}{26}+\frac{1}{26} i \right)\\
&=\frac{13}{26} + \frac{13}{26} i\\
&=\frac{1}{2}+\frac{1}{2} i.
\end{align*}
Otra forma de pensarlo es que a una expresión de la forma $\frac{a+bi}{c+di}$ la podemos simplificar «multiplicando arriba y abajo» por $c-di$. De esta forma, obtenemos
\begin{align*}
\frac{a+bi}{c+di} \cdot \frac{c-di}{c-di} = \left(\frac{ac+bd}{c^2+d^2}\right) + \left(\frac{bc-ad}{c^2+d^2}\right)i.
\end{align*}
Ambos métodos dan el mismo resultado.
Más adelante…
Al tomar un número complejo $z=a+bi$ y calcular su inverso, aparecen de manera natural las expresiones $a-bi$ y $a^2+b^2$. Estas expresiones son fundamentales.
- A $a-bi$ se le conoce como el conjugado de $z$, y se denota por $\overline{z}$.
- A $\sqrt{a^2+b^2}$ se le conoce como la norma de $z$ y se denota por $|z|$.
En la siguiente ocasión hablaremos de las propiedades de estas dos operaciones y cómo están relacionadas entre sí. Más adelante veremos su utilidad al resolver ecuaciones cuadráticas en los números complejos.
Si quieres, puedes revisar esta entrada sobre aplicaciones interesantes de los números complejos en la resolución de problemas. Tiene teoría que no hemos visto, pero te puede servir de motivación para aprender lo que veremos a continuación.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Demuestra que en los complejos se satisface la ley distributiva.
- Verifica que bajo la asociación $\varphi$ en efecto los neutros se van a los neutros y los inversos a inversos.
- Realiza la operación $(1+i)(2+i)(1+2i)(2+2i)$ y expresa el resultado de la forma $x+yi$ con $x$ y $y$ reales.
- Realiza la operación $$\frac{3+5i}{2+i}-\frac{1+2i}{4-3i}$$ y expresa el resultado de la forma $x+yi$ con $x$ y $y$ reales.
- Realiza la operación $$1+(1+i)+(1+i)^2+(1+i)^3+(1+i)^4$$ y expresa el resultado de la forma $x+yi$ con $x$ y $y$ reales.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Racionales y sus expansiones decimales
- Entrada siguiente del curso: Problemas de operaciones en complejos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»