Introducción
En la entrada anterior vimos lo que son las permutaciones de tamaño $r$ de una colección de $n$ objetos. Además, observamos que al momento de calcular la cantidad de permutaciones de ese tipo, se toman en cuenta los arreglos lineales que tienen los mismos objetos, pero ordenados de distinta manera. Por ejemplo, recuerda el problema de los $10$ estudiantes. Ahí, vimos que al momento de contar las permutaciones de tamaño $5$ de los $10$ estudiantes, se contabilizaban $\mathrm{BCEFI}$ y $\mathrm{CEFIB}$. Esto pues aunque tienen los mismos objetos, el orden en el que se encuentran es diferente.
Por otra parte, también puede interesarnos encontrar la cantidad de arreglos lineales en donde los elementos son distintos. Es decir, considerar a aquellos arreglos que tienen los mismos elementos como indistinguibles, incluso si se encuentran en un orden distinto. Esto es precisamente lo que haremos en esta entrada: desarrollar un concepto que nos permita contar nada más eso.
Motivación
Para comenzar, veamos un ejemplo clásico de conteo. Una baraja inglesa estándar está formada por $52$ cartas que comprenden $4$ palos: tréboles, diamantes, corazones y espadas. Cada palo tiene $13$ cartas: As, $2$, $3$, $4$, …, $9$, $10$, jota, reina y rey. Si se nos pide tomar tres cartas de una baraja inglesa, una después de otra y sin reemplazo (es decir, sin devolver las cartas que ya hemos tomado), entonces por el principio del producto hay
\[ 52 \cdot 51 \cdot 50 = \frac{52!}{49!} = P(52, 3) = 132{,}600 \]
posibles resultados. Por ejemplo, una de las posibles ternas de cartas que te pueden salir es $\color{red}{\mathrm{A}\heartsuit}$ (as de corazones), $9\clubsuit$ (nueve de tréboles), $\color{red}{\mathrm{K}\blacklozenge}$ (rey de diamantes). Pero, cuidado, recuerda que en el contexto de las permutaciones, «$\textcolor{red}{\mathrm{A}\heartsuit}\text{-}{9\clubsuit}\text{-}\textcolor{red}{\mathrm{K}\blacklozenge}$» se considera como un resultado distinto a «${9\clubsuit}\text{-}\textcolor{red}{\mathrm{A}\heartsuit}\text{-}\textcolor{red}{\mathrm{K}\blacklozenge}$» o «$\textcolor{red}{\mathrm{K}\blacklozenge}\text{-}\textcolor{red}{\mathrm{A}\heartsuit}\text{-}{9\clubsuit}$».
Sin embargo, observa que las cartas con las que terminas son las mismas sin importar el orden en el que las sacaste. Es decir, en tu mano estarán el as de corazones, el nueve de tréboles y el rey de diamantes sin importar el orden en el que se extraen. Por ello, podríamos considerar a todas las cadenas de cartas que tienen los mismos elementos como indistinguibles. Esto es, «$\textcolor{red}{\mathrm{A}\heartsuit} \text{-} {9\clubsuit} \text{-} \textcolor{red}{\mathrm{K}\blacklozenge}$», «$\textcolor{red}{\mathrm{A}\heartsuit} \text{-} \textcolor{red}{\mathrm{K}\blacklozenge} \text{-} {9\clubsuit}$», «${9\clubsuit} \text{-} \textcolor{red}{\mathrm{K}\blacklozenge} \text{-} \textcolor{red}{\mathrm{A}\heartsuit}$», «${9\clubsuit} \text{-} \textcolor{red}{\mathrm{A}\heartsuit} \text{-} \textcolor{red}{\mathrm{K}\blacklozenge}$», «$\textcolor{red}{\mathrm{K}\blacklozenge} \text{-} {9\clubsuit} \text{-} \textcolor{red}{\mathrm{A}\heartsuit}$» y «$\textcolor{red}{\mathrm{K}\blacklozenge} \text{-} \textcolor{red}{\mathrm{A}\heartsuit} \text{-} {9\clubsuit}$», las $6$ permutaciones posibles de las $3$ cartas, corresponden a una sola selección (sin orden) de cartas. En consecuencia, cada selección, o combinación, de $3$ cartas, sin tomar en cuenta el orden, corresponde a $3!$ permutaciones de $3$ cartas. En forma de ecuación, esto es:
\begin{align*} (3!)\cdot (\text{No. de combinaciones} \; &\text{de} \; \text{tamaño $3$ de una baraja de $52$}) \\ &= \text{No. de permutaciones de tamaño $3$ de una baraja de $52$} \\ &= P(52, 3) \\ &= \frac{52!}{49!}. \end{align*}
En conclusión, se pueden extraer, sin reemplazo, $3$ cartas sin reemplazo de una baraja inglesa estándar de $\frac{132{,}600}{3!} = 22{,}000$ maneras distintas.
Fórmula para el número de combinaciones sin repetición
Con la idea desarrollada en el ejemplo anterior, podemos presentar una fórmula para el cálculo del número de combinaciones de tamaño $r$ de una colección de $n$ objetos objetos.
Número de Combinaciones. Si tenemos $n$ objetos distintos, una combinación de $r$ de esos objetos, sin tomar en cuenta el orden, corresponde a $r!$ permutaciones de tamaño $r$ de los $n$ objetos. Por ello, el número de combinaciones de tamaño $r$ de una colección de $n$ objetos es
\[ C(n,r) = \frac{P(n,r)}{r!} = \frac{n!}{r!(n − r)!}, \]
para $n, r \in \mathbb{N}$ tales que $0 \leq r \leq n$.
Para denotar al número de combinaciones de tamaño $r$ de una colección de $n$ objetos también se utiliza el símbolo ${n \choose r}$, y en algunas ocasiones el símbolo $\mathrm{C}_{r}^{n}$.
Algunas observaciones importantes:
- ${n \choose k}$ es también conocido como coeficiente binomial.
- Para cualquier $n \geq 0$ se cumple que $C(n,0) = C(n,n) = 1$. Por un lado, el número de combinaciones de tamaño $0$ es $1$ porque sólo hay una combinación vacía. Por otro lado, el número de combinaciones de tamaño $n$ es $1$ porque la única combinación de tamaño $n$ es la colección misma.
- Para cualquier $n \geq 1$, $C(n,1) = C(n,n−1) = n$.
- En general, para cualesquiera $n, r \in \mathbb{N}$ tales que $0 \leq r \leq n$ se cumple que \[ C(n,r) = C(n, n−r). \]
- Cuando $n < r$, se tiene que $C(n,r) = 0$.
¡Observación importante! – Cuando te enfrentes a cualquier problema de conteo, la primera pregunta que debes de hacerte es: «¿importa el orden?» Cuando el orden sí es relevante, deberás pensar en términos de permutaciones y el principio del producto. Por otro lado, cuando el orden no es relevante, las combinaciones serán una parte importante para resolver el problema.
Ejemplos de problemas con combinaciones sin repetición
Ejemplo. Una primera aplicación interesante es la siguiente. Sean $n \in \mathbb{N}$ y $A$ un conjunto finito tal que $|A| = n$. En consecuencia, podemos escribir a $A$ como sigue:
\[ A = \{ a_{1}, a_{2}, \ldots, a_{n} \}. \]
Es decir, $A$ es una colección de $n$ objetos distintos. Para $r \leq n$, podemos preguntarnos: «¿cuántos subconjuntos de $A$ hay cuya cardinalidad es $r$?» Los conjuntos (en la teoría matemática) son colecciones de objetos en donde el orden en el que se escriben sus elementos no importa. Por ejemplo, se cumple que
\[ \{ a_{1}, a_{2} \} = \{ a_{2}, a_{1} \}. \]
Esto obedece al principio intuitivo que dice que «un conjunto está determinado por sus elementos». Por ello, un subconjunto de cardinalidad $r$ de $A$ es un ejemplo de una combinación de tamaño $r$ de los objetos en la colección $A$. Así, la cantidad de subconjuntos de cardinalidad $r$ de $A$ es simplemente $C(n,r) = {n \choose r}$.
Por ejemplo, para el conjunto $A = \{ 1, 2, 3, 4, 5 \}$, se cumple que $|A| = 5$. En consecuencia, hay $C(5,2) = {5 \choose 2} = \frac{5!}{(2!)(3!)} = 10$ subconjuntos de cardinalidad $2$ de $A$. Estos son:
\begin{align*} \{1,2\} &\qquad \{2,4\} \\ \{1,3\} &\qquad \{2,5\} \\ \{1,4\} &\qquad \{3,4\} \\ \{1,5\} &\qquad \{3,5\} \\ \{2,3\} &\qquad \{4,5\} \end{align*}
Ejemplo. En un curso de cálculo, la profesora se encuentra redactando el examen final que constará de $10$ preguntas a escoger.
- Primero, la profesora decide que las instrucciones digan que escojas cualesquiera $7$ de las $10$ preguntas. Como no importa el orden en el que las respondas, puedes responder el examen de \[ {10 \choose 7} = \frac{10!}{(7!)(3!)} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 120 \]maneras distintas.
- Sin embargo, la profesora se da cuenta de que quizás sus alumnos tendrán un sesgo por las primeras $5$ preguntas, que son más sencillas. Por ello, decide dividir el examen en dos secciones, cada una con $5$ preguntas. Además, el alumno deberá de escoger $3$ preguntas de la primera sección y $4$ preguntas de la segunda sección. Las $3$ preguntas de la primera sección se pueden escoger de ${5 \choose 3} = 10$ maneras, y las $4$ preguntas de la segunda sección pueden escogerse de ${5 \choose 4} = 5$ maneras. Así, por el principio del producto, el examen puede completarse de ${5 \choose 3}{5 \choose 4} = 10 \cdot 5 = 50$ maneras.
- Finalmente, la profesora decide restringir un poco menos las cosas para su grupo, y opta por lo siguiente: para resolver el examen, el alumno debe escoger $7$ preguntas tales que al menos $3$ de ellas vienen de la segunda sección. De esta manera, hay tres casos a considerar:
- Si el alumno escoge $3$ preguntas de la segunda sección y $4$ preguntas de la primera sección, por el principio del producto hay ${5 \choose 3}{5 \choose 4} = 10 \cdot 5 = 50$ maneras de hacerlo.
- Por otro lado, si el alumno decide escoger $4$ preguntas de la segunda sección y $3$ preguntas de la primera sección, puede hacerlo de ${5 \choose 4}{5 \choose 3} = 5 \cdot 10 = 50$ maneras.
- Si decide responder las $5$ preguntas de la segunda sección y $2$ de la primera sección, entonces por el principio del producto, hay ${5 \choose 5}{5 \choose 2} = 1 \dot 10 = 10$ maneras posibles de hacerlo.
Así, combinando los resultados de los tres casos, por el principio de la suma encontramos que el examen puede formar \[ {5 \choose 3}{5 \choose 4} + {5 \choose 4}{5 \choose 3} + {5 \choose 5}{5 \choose 2} = 50 + 50 + 10 = 110 \] combinaciones de $7$ preguntas donde cada combinación incluye al menos $3$ preguntas de la segunda sección.
¡Otra observación importante! – Hay problemas que requieren los conceptos de permutaciones y combinaciones para su resolución. Esto puede observarse en el siguiente ejemplo.
Ejemplo. El número de permutaciones de las letras en la palabra $\mathrm{CHACHALACA}$ es
\begin{align*} \frac{10!}{(4!)(3!)(2!)(1!)} = 12{,}600. \end{align*}
Ahora, ¿cuántas de estas permutaciones no tienen $\mathrm{C}$’s consecutivas? Sin considerar a las $\mathrm{C}$’s, el número de permutaciones de las letras que quedan ($\mathrm{HAHALAA}$) es
\begin{align*} \frac{7!}{(4!)(2!)(1!)} = 105. \end{align*}
Por ejemplo, una de estas $105$ permutaciones es la cadena de letras $\mathrm{LAHAAHA}$. Ahora, podemos acomodar esta permutación como sigue:
\begin{align*} \square \; \mathrm{L} \; \square \; \mathrm{A} \; \square \; \mathrm{H} \; \square \; \mathrm{A} \; \square \; \mathrm{A} \; \square \; \mathrm{H} \; \square \; \mathrm{A} \; \square \end{align*}
Observa que podemos poner las $3$ $\mathrm{C}$’s en cualesquiera de los $8$ espacios en blanco y se cumplirá que no hay $\mathrm{C}$’s consecutivas. Además, $3$ de esos $8$ espacios pueden escogerse de ${8 \choose 3} = 56$ maneras distintas. Esto se puede hacer para cada una de las $105$ permutaciones de las letras $\mathrm{HAHALAA}$, así que por el principio del producto se tienen $105 \cdot 56 = 5{,}880$ permutaciones de las letras en la palabra $\mathrm{CHACHALACA}$ que no tienen $\mathrm{C}$’s consecutivas.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Sea $X = \{2, 4, 6, 8 \}$. ¿Cuántos subconjuntos de cardinalidad $2$ de $X$ hay?
- ¿Cómo se relaciona el coeficiente multinomial (visto en la entrada pasada) con el coeficiente binomial? Para verlo, ¿qué pasa cuando sólo se tiene $2$ tipos de objetos en el coeficiente multinomial?
- Existen algunos ejercicios geométricos que pueden resolverse con las herramientas de esta entrada. Por ejemplo, considera los puntos $(2,1)$ y $(7,4)$ sobre una cuadrícula y conéctalos con un camino sobre esta, utilizando únicamente movimientos hacia la derecha y hacia arriba. Visualmente:
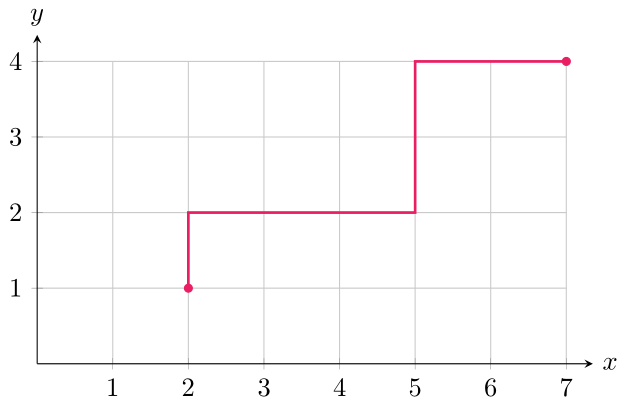
El anterior es un ejemplo de los muchos caminos posibles. ¿Cuántos caminos posibles existen entre estos dos puntos? Sugerencia: Considera a cada camino como una secuencia (o cadena) de pasos hacia la derecha ($\mathrm{D}$) y hacia arriba ($\mathrm{A}$). Así, el camino mostrado en la gráfica corresponde a la cadena $\mathrm{ADDDAADD}$.
Más adelante…
Con esto damos por terminada la parte del curso que corresponde a los principios de conteo. Sin embargo, hay otros resultados de conteo que no revisamos aquí, como las combinaciones con reemplazo. Por otro lado, es posible que los ejemplos aquí expuestos no sean suficientes para representar todas las complejidades de los problemas de conteo. Por ello, te recomendamos buscar la mayor cantidad de ejemplos de conteo y combinatoria posibles. En particular, puedes revisar el libro que utilizamos como base para esta parte del curso: Discrete And Combinatorial Mathematics: An Applied Introduction (5ta Edición) de Ralph P. Grimaldi, tiene una gran cantidad de ejemplos de todos los temas de conteo vistos (algunos de esos ejemplos los incluímos aquí).
En la siguiente entrada veremos otro de los enfoques más importantes en la historia de la probabilidad: la probabilidad clásica, que está basada en el cálculo de cardinalidades. Como con los enfoques pasados, este enfoque puede representarse de manera formal como una medida de probabilidad.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Principios de Conteo 2 – Permutaciones
- Siguiente entrada del curso: La Probabilidad Clásica

