Introducción
El propósito de esta entrada será conocer criterios para determinar cuándo el límite de una sucesión de funciones es una función continua. (El concepto de función continua se vio en la entrada Funciones continuas en espacios métricos).
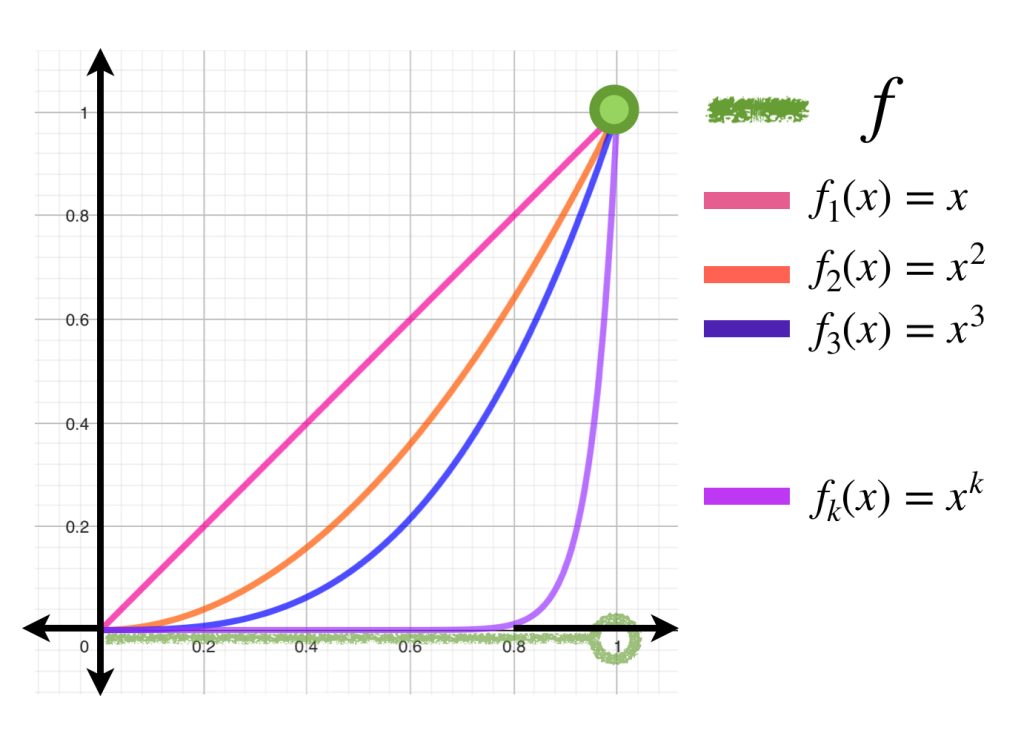
Nuestra intuición podría proponer que esto ocurre cuando todas las funciones de la sucesión son también continuas. No obstante, esto no basta cuando el límite de convergencia es puntual. Como ejemplo tomemos la sucesión de funciones continuas dada por:
$(x^n)_{n \in \mathbb{N}}$ donde para cada $n \in \mathbb{N}, \, x^n:[0,1] \to \mathbb{R}$
Queda como ejercicio al lector demostrar que $(x^n)_{n \in \mathbb{N}}$ converge puntualmente a la función:
\begin{equation*}
f(x) = \begin{cases}
0 & \text{si $0 \leq x < 1$} \\
1 & \text{si $x = 1$}
\end{cases}
\end{equation*}
Pero $f$ no es una función continua en $[0,1].$
¿Qué ocurre en los casos donde el límite es uniforme? A continuación mostraremos que bajo esa situación, la función a la que la sucesión converge sí es continua. Pero antes hagamos una aclaración sobre la notación a usar:
En la entrada anterior (Convergencia puntual y convergencia uniforme) las funciones suelen definirse como funciones de $A$ en $X$ $(f:A \to X),$ donde $A$ se considera como un conjunto cualquiera (que no necesariamente es un espacio métrico y por tanto la distancia de los puntos en el dominio no es relevante), y $X$ es un espacio métrico con distancia indicada como $d$.
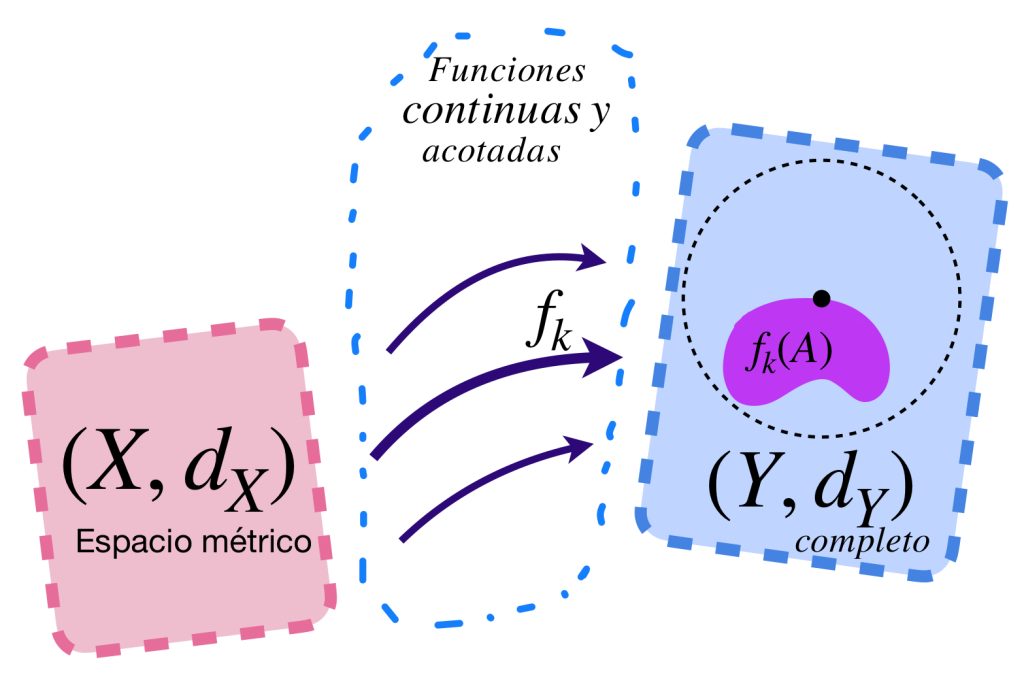
Ahora pasamos a tratar con funciones continuas, donde sí comparamos distancias entre puntos del dominio (la famosa distancia menor que $\delta$) y distancias en puntos del contradominio (la famosa distancia menor que $\varepsilon$). Así, las funciones de esta entrada están definidas entre dos espacios métricos $(X,d_X)$ y $(Y,d_Y).$ Nota la importancia de señalar si la distancia a considerar es en $X$ o en $Y.$
Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Si $(f_n)_{n \in \mathbb{N}}$ con $f_n: X \to Y, \, n \in \mathbb{N} \, $ es una sucesión de funciones continuas que converge uniformemente a $f:X \to Y$ en $X$ entonces $f$ es continua.
Demostración:
Sea $\varepsilon > 0$ y $x_0 \in X.$ Buscamos probar que $f$ es continua en $x_0.$ Como $(f_n)_{n \in \mathbb{N}}$ converge uniformemente en $f$ entonces existe $N \in \mathbb{N}$ tal que para todo $k \geq N$ y para todo $x \in X, \, d_Y(f_k(x),f(x)) < \frac{\varepsilon}{3}.$
Por otro lado, como $f_N$ es continua, existe $\delta > 0$ tal que si $d_X(x,x_0)< \delta$ entonces $d_Y(f_N(x),f_N(x_0)) < \frac{\varepsilon}{3}.$
En consecuencia, si $d_X(x,x_0)< \delta$ se sigue que
\begin{align*}
d_Y(f(x),f(x_0)) & \leq d_Y(f(x),f_N(x)) + d_Y(f_N(x),f_N(x_0)) + d_Y(f_N(x_0),f(x_0)) \\
& < \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} \\
& = \varepsilon
\end{align*}
Lo cual demuestra que el límite uniforme de una sucesión de funciones continuas, es una función continua.
Es importante notar que esto no significa que toda sucesión de funciones continuas que converge en una función continua, lo hace de manera uniforme. Puede hacerlo solo de forma puntual. Veamos un ejemplo.
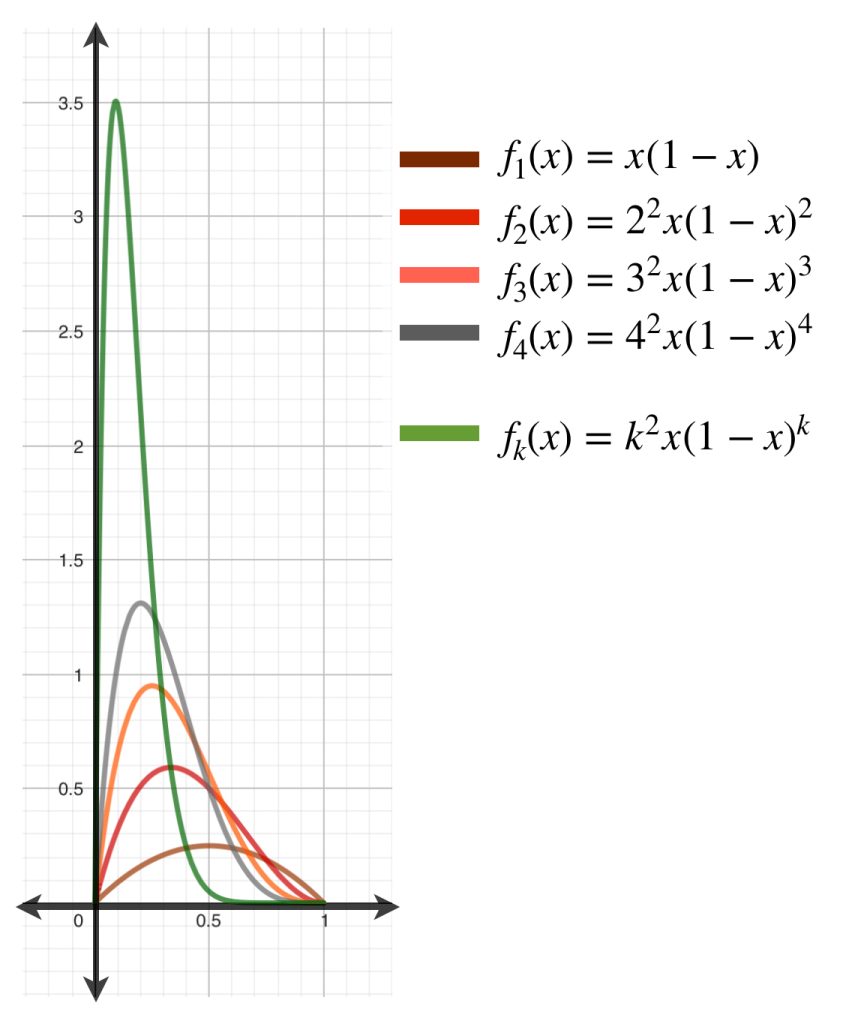
La sucesión de funciones continuas $(f_n)_{n \in \mathbb{N}}$ donde para cada $n \in \mathbb{N}, \, f_n:[0,1] \to \mathbb{R}$ se define como $f_n(x)= n^2x(1-x)^n,$ converge de forma puntual a la función $f(x)=0.$ Queda como ejercicio probar que la convergencia solo es puntual y no uniforme.
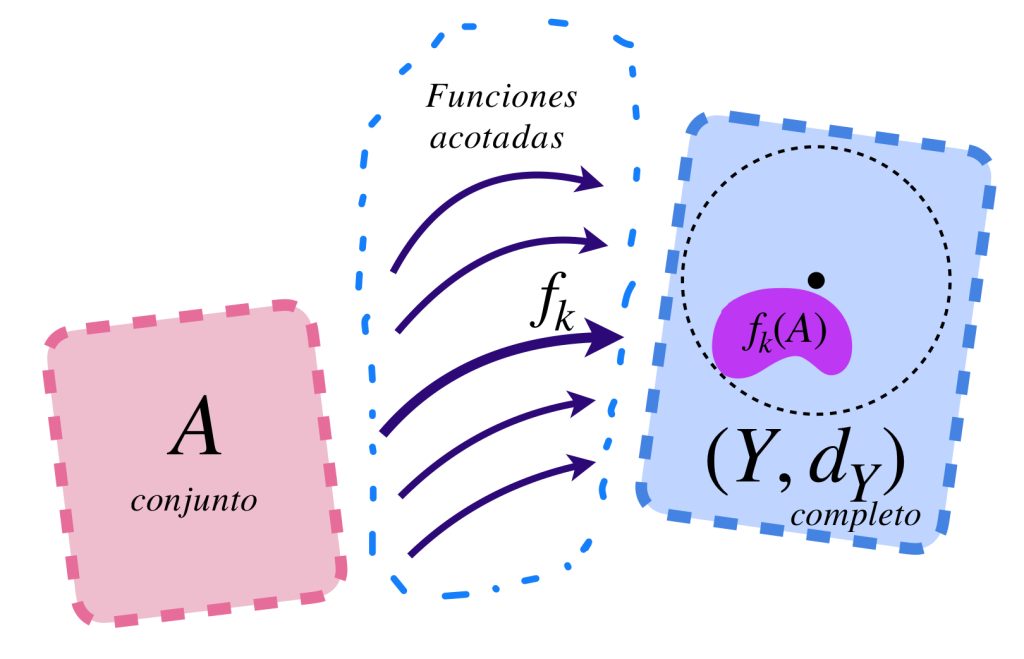
Ahora pensemos en funciones continuas y acotadas a través de la siguiente definición. (El concepto de función acotada se vio en Espacios de funciones).
Definición. El espacio métrico $\mathcal{C}_b^0(X,Y)$: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. El espacio de funciones continuas y acotadas de $X$ a $Y$ se define como:
$\mathcal{C}_b^0(X,Y):= \{f:X \to Y: f \text{ es continua y acotada } \}$
Y la métrica está dada por:
$$d_\infty(f,g)= \underset {x \in X}{sup} \, \, d_Y(f(x),g(x))$$
Donde $f,g \in \mathcal{C}_b^0(X,Y).$
Este espacio es cerrado en el espacio de funciones acotadas, de acuerdo con la siguiente:
Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Entonces $\mathcal{C}_b ^0(X,Y)$ es un subespacio cerrado de $\mathcal{B}(X,Y).$ (El espacio de funciones acotadas).
Demostración:
Buscamos probar que $\mathcal{C}_b ^0(X,Y)$ es igual a su cerradura. Sea $f \in \overline{\mathcal{C}_b ^0(X,Y)}.$ En la última proposición de la entrada Convergencia vimos que esto significa que existe una sucesión de funciones $(f_n)_{n \in \mathbb{N}}$ en $\mathcal{C}_b ^0(X,Y)$ que convergen a $f$ en $\mathcal{B}(X,Y).$ En la entrada anterior vimos que esto implica que $f$ es límite uniforme de $(f_n)_{n \in \mathbb{N}}. \, $ La proposición anterior nos permite concluir que $f$ es continua, es decir $f \in \mathcal{C}_b ^0(X,Y),$ probando así que $\mathcal{C}_b ^0(X,Y)$ es cerrado en $\mathcal{B}(X,Y).$
Ahora veamos la siguiente:
Proposición: Sea $Y$ un espacio métrico completo. Se cumple que:
- Si $A$ es un conjunto entonces $\mathcal{B}(A,Y)$ es completo.
- Si $X$ un espacio métrico entonces $\mathcal{C}^0_b(X,Y)$ es completo.
Demostración:
Para probar que $\mathcal{B}(A,Y)$ es completo toma $(f_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $\mathcal{B}(A,Y).$ Veamos que es convergente.
Sea $\varepsilon >0.$ Por definición, existe $N \in \mathbb{N}$ tal que $\forall \, l,m \geq N, \, d_\infty(f_l,f_m) < \varepsilon.$ Así, para cada $a \in A$ se cumple que $d_Y(f_l(a),f_m(a)) \leq d_\infty(f_l,f_m) < \varepsilon$ de modo que $(f_n)_{n \in \mathbb{N}}$ es uniformemente de Cauchy. De acuerdo con el Criterio de convergencia uniforme de Cauchy visto en la entrada anterior esto significa que $(f_n)_{n \in \mathbb{N}}$ converge uniformemente en $A$ y por tanto converge en el espacio métrico de funciones $\mathcal{B}(A,Y).$
Para probar que $\mathcal{C}^0_b(X,Y)$ es completo partimos de la proposición anterior donde concluimos que es subespacio cerrado de $\mathcal{B}(A,Y)$ que ya sabemos es completo. A partir de una proposición vista en Espacios métricos completos se sigue que $\mathcal{C}^0_b(X,Y)$ es completo.
Si $Y$ es un espacio de Banach entonces está provisto de una norma $\norm{\cdot}$ que induce una métrica bajo la cual $Y$ es completo.
Al final se te pedirá probar que el conjunto $\mathcal{B}(A,Y)$ es un espacio vectorial normado con
$\norm{f}_\infty = \underset {a \in A}{sup} \, \norm{f(a)}$
En esta situación, las proposiciones se plantean de la siguiente manera:
- Si $A$ es un conjunto entonces $\mathcal{B}(A,Y)$ es de Banach.
- Si $X$ un espacio métrico entonces $\mathcal{C}^0_b(X,Y)$ es de Banach.
Unos resultados que requieren el concepto de compacidad
En entradas posteriores hablaremos del concepto de espacios métricos compactos. En la sección Funciones en espacios topológicos compactos verás que toda función continua en un compacto es acotada. Ese resultado en suma con la proposición anterior, permite concluir que si $A$ es compacto y $X$ es completo entonces $\mathcal{C}^0(A,X)=\{\phi:A \to X :\phi \text{ es continua } \}$ es un espacio completo.
Ahora presentamos condiciones que aseguran la convergencia uniforme de una sucesión de funciones continuas en un espacio compacto a partir de la monotonía. Es decir:
Proposición: Sea $A$ un espacio métrico compacto, $(f_n)_{n \in \mathbb{N}}$ una sucesión de funciones continuas con $f_n:A \to \mathbb{R}, n \in \mathbb{N}$ tal que $(f_n)$ converge puntualmente a una función continua $f$. Si para cada $x \in A$ y $n \in \mathbb{N} \, f_n(x) \geq f_{n+1}(x),$ entonces $(f_n)$ converge a $f$ uniformemente en $A.$
Demostración:
Podrá consultarse en la entrada Compacidad en espacios métricos.
Más adelante…
Continuaremos analizando resultados de convergencia uniforme, ahora en funciones diferenciables. ¿Será diferenciable también la función límite? ¿Será convergente también la sucesión de derivadas? ¿Coincide el límite de derivadas con la derivada de la función límite?
Tarea moral
- Demuestra que $(x^n)_{n \in \mathbb{N}}$ con $x^n:[0,1] \to \mathbb{R}$ converge puntualmente a la función:
\begin{equation*}
f(x) = \begin{cases}
0 & \text{si $0 \leq x < 1$} \\
1 & \text{si $x = 1$}
\end{cases}
\end{equation*}
Pero $f$ no es una función continua en $[0,1].$ - Demuestra que la sucesión de funciones continuas $(f_n)_{n \in \mathbb{N}}$ donde para cada $n \in \mathbb{N}, \, f_n:[0,1] \to \mathbb{R}$ se define como $f_n(x)= n^2x(1-x)^n,$ converge de forma puntual a la función $f(x)=0$ pero el límite no es uniforme.
- Sea $A$ un conjunto, y $(Y, \norm{\cdot})$ un espacio normado. Prueba que $\mathcal{B}(A,Y)$ es un espacio vectorial con las operaciones
$(f+g)(x):= f(x) + g(x)$
$(\lambda f)(x):= \lambda f(x)$
Y que $\norm{f}_\infty = \underset {a \in A}{sup} \, \norm{f(a)}$
es una norma en $\mathcal{B}(A,Y).$