$\textcolor{Red}{\textbf{Extremos Restringidos (Multiplicadores de Lagrange)}}$

Supongase que se quieren hallar los valores extremos (máximo ó mínimo) de una función $f(x,y)$ sujeta a la restircción $x^2+y^2=1$; esto es, que $(x,y)$ está en el circulo unitario. Con mayor generalidad, podemos necesitar maximizar o minimizar $f(x,y)$ sujeta a la condición adicional de que $(x,y)$ también satisfaga una ecuación $g(x,y)=c$ donde $g$ es alguna función y $c$ es una constante. En el ejemplo $g(x,y)=x^2+y^2$ y $c=1$]. El conjunto de dichas $(x,y)$ es un conjunto de nivel de $g$.

En general, sean $f:u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ y $g: u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ funciones $C^1$ dadas, y sea $S$ el conjunto de nivel de $g$ con valor $c$. Recordar que el conjunto de nivel son los puntos $x\in
\mathbb{R}^n$ con $g(x)=c$] Cuando $f$ se restringe a $S$, de nuevo tenemos el concepto de máximos locales o mínimos locales de $f$ (extremos locales), y un máximo (valor mayor) o un minimo absoluto (valor menor) debe ser un extremo local.

$\textbf{Teorema.- Método de los multiplicadores de lagrange.}$ Sean $f:u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ y $g: u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ funciones $C^1$ con valores reales dados. Sean $x_0 \in u$ y $g(x_0)=c$, y sea $S$ el conjunto de nivel de $g$ con valor $c$. Suponer $\nabla g(x_0)\neq 0$.
Si $f|_s$ (f restringida a s) tiene un máximo o un mínimo local en $S$, en $x_0$, entonces existe un número real $\lambda$ tal que $\nabla f(x_0)=\lambda\nabla g(x_0)$.

$Demostrción$ Para $n=3$ el espacio tangente o plano tangente de $S$ en $x_0$ es el
espacio ortogonal a $\nabla g(x_0)$ y para $n$ arbitraria podemos dar la misma definición de espacio tangente de $S$ en $x_0$. Esta definición se puede motivar al considerar tangentes a trayectorias $c(t)$ que estan en $s$, como sigue: si $c(t)$ es una trayectoria en $S$ y $c(0)=x_0$, entonces $c'(0)$ es un vector tangente a $S$ en $x_0$, pero $$\frac{dg(c(t))}{dt}=\frac{d}{dt}(c)=0$$
Por otro lado usando regla de la cadena
$$\left.\frac{d}{dt}g(c(t))\right|_{t=0}=\nabla g(x_0)\cdot c'(0)$$
de manera que $\nabla g(x_0)\cdot c'(0)=0$, esto es, $c'(0)$ es ortogonal a $\nabla g(x_0)$.

Si $f|s$ tiene un máximo en $x_0$, entonces $f(c(t))$ tiene un máximo en $t=0$. Por cálculo de una variable, $\displaystyle\left.\frac{df(c(t))}{dt}\right|{t=0}=0$. Entonces por regla de la cadena $$0=\displaystyle\left.\frac{df(c(t))}{dt}\right|_{t=0}=\nabla f(x_0)\cdot c'(0)$$
Asi, $\nabla f(x_0)$ es perpendicular a la tangente de toda curva en $S$ y entonces tambien es perpendicular al espacio tangente completo de $S$ en $x_0$. Como el espacio perpendicular a este espacio tangente es una recta, $\nabla f(x_0)$ y $\nabla
g(x_0)$ son paralelos. Como $\nabla g(x_0)\neq 0$, se deduce que $\nabla f(x_0)$ es multiplo de $\nabla g(x_0)$.

$\textbf{Corolario.}$ Si $f$ al restringirse a una superficie $S$, tiene un máximo o un mínimo local en $x_0$, entonces $\nabla f(x_0)$ es perpendicular a $S$ en $x_0$.La geometria de los valores extremos restringidos.

$\textbf{Ejemplo.}$ Sea $S\subset\mathbb{R}^2$ la recta que pasa por $(-1,0)$ inclinada a $45^{o}$, y sea $f:\mathbb{R}^2 \rightarrow \mathbb{R}$ daa asi $f(x,y)=x^2+y^2$. Hallar los extremos de $f|_s$.

$Solución.$ Aqui $S=\left\{(x,y) | y-x-1=0 \right\}$ y por lo tanto hacemos $g(x,y)=-y-x-1$ y $c=0$. Tenemos $\nabla g(x,y)=-i+j \neq 0$. Los extremos relativos de $f|_s$ deben hallarse entre los puntos en que $\nabla f$ es ortogonal a $S$, esto es, inclinada a $-45^{o}$. Pero $\nabla f (x,y)=(2x.2y)$, que tiene la pendiente deseada sólo cuando $x=-y$, o cuando $(x,y)$ está sobre la recta L, que pasa por el origen inlinada a $-45^{o}$. Esto puede suceder en el conjunto $S$ sólo para el unico punto en
el que se intersecan L y S. Al referirnos a las curvas de nivel de $f$ se indica que este punto $(-\frac{1}{1},\frac{1}{2})$ es un mínimo relativo de $f|_s$ (Pero no de $f$).

$\textbf{Ejemplo.}$ Sea $f:\mathbb{R}^2\rightarrow \mathbb{R}$ dada asi $f(x,y)=x^2-y^2$ y sea $S$ el círculo de radio 1 alrededor del origen. Hallar los extremos de $f|_s$.

$Solución.$ El conjunto $S$ es la curva de nivel para $g$ con valor $t$. Donde $g:\mathbb{R}^2\rightarrow \mathbb{R}$, $(x,y) \rightarrow x^2+y^2$. La condición de que $\nabla f=\lambda \nabla g$ en $x_0$, es decir que $\nabla f$ y $\nabla g$ son pararlelos en $x_0$, es la misma que las curvas de nivel sean tangentes en $x_0$. Asi los puntos extremos de $f |_s$ son $(0,\pm 1)$ y $(\pm1,0)$. Evaluando $f$ hallamos que $(0,\pm 1)$ son mínimos y $(\pm1,0)$ son máximos. Usando Multiplicadores de
lagrange $\nabla f(x,y)=(2x,2y)$ y $\nabla g(x,y)=(2x,2y)$\ $\therefore$ \quad $(2x,-2y)=\lambda(2x,2y)$ cuya solución es $(0,\pm 1)$, $(\pm1,0)$.

$\textbf{Ejemplo.}$ Maximizar la función $f(x,y,z)=x+z$ sujeta a la restricción $x^2+y^2+z^2=1$

$Solución.$ Buscamos $\lambda$ y $(x,y,z)$ tales que $1=2x\lambda$, $0=2y\lambda$ y $1=2z\lambda$ $x^2+y^2+z^2=1$ la solución es $(\frac{1}{\sqrt{2}},0,\frac{1} {\sqrt{2}})$, $(-\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}})$ comprobando los valores de $f$ en estos puntos podemos ver que el primer punto produce el máximo de $f$ y el segundo el mínimo.

$\textbf{Ejemplo.}$ Hallar los puntos extremos de $f(x,y,z)=x+y+z$ sujeto a las dos condiciones $x^2+y^2=2$ y $x+z=1$

$Solución.$ Aquí hay dos restricciones $g_1=(x,y,z)=x^2+y^2-2=0$ $g_2(x,y,z)=x+z-1=0$ asi, debemos encontrar $x,y,z,\lambda_1$ y $\lambda_2$ tales que $$\nabla f(x,y,z)=\lambda_1 \nabla g (x,y,z)+ \lambda_2 \nabla g_2(x,y,z)$$
$$g_1(x,y,z)=0 \quad y \quad g_2(x,y,z)=0$$
Calculando gradientes e igualando componentes, obtenemos

$\begin{eqnarray}
1=\lambda_1\cdot 2x+\lambda_2\cdot 1\\
1=\lambda_1 2y+\lambda_2\cdot 0\\
1=\lambda_1\cdot 0 + \lambda_2\cdot 1\\
x^2+y^2=2\\
x+z=1
\end{eqnarray}$

De (3) $\lambda_2=1$ y asi $2x\lambda_1=0$, $2y\lambda_1=1$.

Como la segunda implica $\lambda_1\neq 0$ $x=0$. Asi $y=\pm\sqrt{2}$ y $z=1$. Entonces los extremos deseados son $(0,\pm\sqrt{2},1)$.

Por inspección $(0,\sqrt{2},1)$ da un máximo relativo y $(0,-\sqrt{2},1)$ un mínimo relativo.

La condición $x+z=1$ implica que $z$ tambien está acotada. Se deduce que el conjunto de restricciones $S$ es cerrada y acotada,

Por lo tanto $f$ tiene un máximo y un mínimo en $S$ que se deben alcanzar en $(0,\sqrt{2},1)$ y $(0,-\sqrt{2},1)$ respectivamente.

Extremos Locales parte 2 pequeño

Para el caso de funciones $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ tenemos que recordando un poco de la expresión de taylor
$$f(x,y)=f(x_{0},y_{0})+\left(\frac{\partial f}{\partial x}\right){p}(x-x_{0})+\left(\frac{\partial f}{\partial y}\right){p}(y-y_{0})+\left(\frac{\partial f}{\partial z}\right){p}(z-z_{0})+$$

$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}{p}(x-x_{0})^{2}+2\frac{\partial^{2}f}{\partial x \partial
y}{p}(x-x_{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}{p}(y-y_{0})^{2}+2\frac{\partial^{2}f}{\partial
x\partial z}{p}(z-z_{0})(x-x_{0})+2\frac{\partial^{2}f}{\partial
y\partial z}{p}(z-z_{0})(y-y_{0})\right)}$$
$$\textcolor{Red}{+\frac{\partial^{2}f}{\partial
z^{2}}{p}(z-z_{0})}$$

Haciendo $x-x_{0}=h_{1},y-y_{0}=h_{2},z-z_{0}=h_{3}$ podemos escribir el término rojo de la siguiente manera
$$\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}\right)$$

y también se puede ver como producto de matrices
$$\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial y\partial x}&\frac{\partial^{2}f}{\partial z\partial x}\\\frac{\partial^{2}f}{\partial x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial y\partial z}&\frac{\partial^{2}f}{\partial z^{2}}\end{matrix}\right){p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

Si $(x_{0},y_{0},z_{0})$ es un punto critico de la función entonces en la expresión de Taylor
$$f(x,y)=f(x_{0},y_{0})+\left(\frac{\partial f}{\partial
x}\right){p}(x-x_{0})+\left(\frac{\partial f}{\partial
y}\right){p}(y-y_{0})+\left(\frac{\partial f}{\partial
z}\right){p}(z-z_{0})$$
$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}{p}(x-x_{0})^{2}+2\frac{\partial^{2}f}{\partial x \partial
y}{p}(x-x_{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}{p}(y-y{0})^{2}+2\frac{\partial^{2}f}{\partial
x\partial z}{p}(z-z{0})(x-x_{0})+2\frac{\partial^{2}f}{\partial
y\partial z}{p}(z-z_{0})(y-y_{0})\right)}$$
$$\textcolor{Red}{+\frac{\partial^{2}f}{\partial
z^{2}}{p}(z-z_{0})(x-x_{0})}$$

El término
$$\frac{\partial f}{\partial x}{p}(x-x_{0})+\frac{\partial f}{\partial y}{p}(y-y_{0})+\frac{\partial f}{\partial z}{p}(z-z_{0})=0$$
y por lo tanto
$$f(x,y)-f(x_{0},y_{0})=\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial
y\partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right){p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$
vamos a determinar el signo de la forma
$$Q(h)=\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial
y\partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right){p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

vamos a trabajar sin el término $\displaystyle{\frac{1}{2!}}$ que no afectara al signo de la expresión, tenemos entonces

$$Q(h)=(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial
y\partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right){p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)=\textcolor{Red}{\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$

$$=\textcolor{Red}{\frac{\partial^{2}f}{\partial x^{2}}\left(h_{1}+\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}\right)^{2}+\left(\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}\right)h_{2}^{2}}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$

$$=\textcolor{Red}{\frac{\partial^{2}f}{\partial x^{2}}\left(h_{1}+\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}\right)^{2}+\left(\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}\right)h_{2}^{2}}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$

hacemos $\displaystyle{b_{1}=\frac{\partial^{2}f}{\partial x^{2}},h_{1}’=\left(h_{1}+\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}\right),b_{2}=\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}},~~h_{2}’=h_{2}}$ y obtenemos
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
que podemos escribir

$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}\left(h_{1}+\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}-\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}\right)h_{3}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}\left(h_{1}’-\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}’\right)h_{3}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{1}’h_{3}+\left(2\frac{\partial^{2}f}{\partial y\partial z}-\frac{2\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}\right)h_{2}’h_{3}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
hacemos

$$2b_{23}=2\frac{\partial^{2}f}{\partial y\partial z}-\frac{2\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}$$y obtenemos
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{1}’h_{3}+2b_{23}h_{2}’h_{3}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
que se puede escribir

$$=b_{1}\left(h_{1}’^{2}+2\frac{\frac{\partial^{2}f}{\partial x\partial z}}{b_{1}}h_{1}’h_{3}+\left(\frac{\frac{\partial^{2}f}{\partial x\partial z}h_{3}}{b_{1}}\right)^{2}\right)+b_{2}\left(h_{2}’^{2}+2\frac{b_{23}}{b_{2}}h_{2}’h_{3}+\left(\frac{b_{23}}{b_{2}}h_{3}\right)^{2}\right)+\left(\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}\right)h_{3}^{2}$$
hacemos
$$b_{3}=\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}$$
y obtenemos

$$=b_{1}\left(h_{1}’^{2}+2\frac{\frac{\partial^{2}f}{\partial x\partial z}}{b_{1}}h_{1}’h_{3}+\left(\frac{\frac{\partial^{2}f}{\partial x\partial z}h_{3}}{b_{1}}\right)^{2}\right)+b_{2}\left(h_{2}’^{2}+2\frac{b_{23}}{b_{2}}h_{2}’h_{3}+\left(\frac{b_{23}}{b_{2}}h_{3}\right)^{2}\right)+b_{3}h_{3}^{2}$$
$$=b_{1}\left(h_{1}’+\frac{\frac{\partial^{2}f}{\partial x\partial z}}{b_{1}}h_{3}\right)^{2}+b_{2}\left(h_{2}’+\frac{b_{23}}{b_{2}}h_{3}\right)^{2}+b_{3}h_{3}^{2}$$
esta última expresión será positiva si y solo si $b_{1}>0~~b_{2}>0$ y $b_{3}>0$ en clases pasadas vimos los dos primeros, veamos ahora que $$b_{3}=\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}>0$$
tenemos entonces que

$$\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}=\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{\frac{\partial^{2}f}{\partial z^{2}}}-\frac{\left(\frac{\partial^{2}f}{\partial y\partial z}-\frac{2\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}\right)^{2}}{\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}}$$

$$=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}-\frac{\frac{\left(\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\left(\frac{\partial^{2}f}{\partial x^{2}}\right)^{2}}}{\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}}=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}-\frac{\left(\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)\frac{\partial^{2}f}{\partial x^{2}}}$$

$$=\frac{\left(\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}\right)\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)-\left(\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)}$$

$$=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}-\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}+\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}-\left(\frac{\partial^{2}f}{\partial y\partial z}\right)^{2}\left(\frac{\partial^{2}f}{\partial x^{2}}\right)^{2}-}{\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)}$$

$$\frac{2\left(\frac{\partial^{2}f}{\partial x^{2}}\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)-\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)}$$
$$=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial z^{2}}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}-\frac{\partial^{2}f}{\partial y^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}-\left(\frac{\partial^{2}f}{\partial y\partial z}\right)^{2}\frac{\partial^{2}f}{\partial x^{2}}+2\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}$$
$$=\frac{\left|\begin{matrix}\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y\partial x}&\frac{\partial^{2}f}{\partial z\partial x}\\\frac{\partial^{2}f}{\partial x\partial y}&\frac{\partial^{2}f}{\partial y^{2}}&\frac{\partial^{2}f}{\partial z\partial y}\\\frac{\partial^{2}f}{\partial x\partial z}&\frac{\partial^{2}f}{\partial y\partial z}&\frac{\partial^{2}f}{\partial z^{2}}\end{matrix}\right|}{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}$$

por lo tanto
$$b_{3}>0~\Leftrightarrow~\left|\begin{matrix}\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y\partial x}&\frac{\partial^{2}f}{\partial z\partial x}\\\frac{\partial^{2}f}{\partial x\partial y}&\frac{\partial^{2}f}{\partial y^{2}}&\frac{\partial^{2}f}{\partial z\partial y}\\\frac{\partial^{2}f}{\partial x\partial z}&\frac{\partial^{2}f}{\partial y\partial z}&\frac{\partial^{2}f}{\partial z^{2}}\end{matrix}\right|>0$$

Definición 1. La forma $Q(x)=xAx^{t}$, que tiene asociada la matriz A (respecto a la base canónica de $\mathbb{R}^{n}$) se dice:
$\textcolor{Red}{\textbf{Definida positiva}}$, si $Q(x)>0~\forall x \in~\mathbb{R}^{n}$
La forma $Q(x)=xAx^{t}$, que tiene asociada la matriz A (respecto a la base canónica de $\mathbb{R}^{n}$) se dice:
$\textcolor{Red}{\textbf{Definida negativa}}$, si $Q(x)<0~ \forall x \in~\mathbb{R}^{n}$

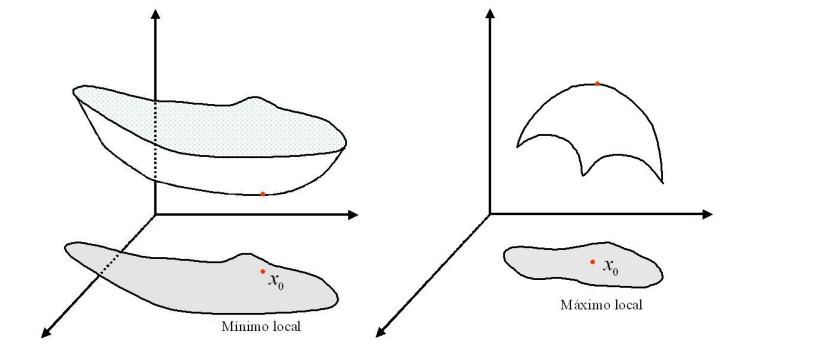
Definición 2. Si la forma $Q(x)=xAx^{t}$ es definida positiva, entonces f tiene un mínimo local en en x.
Si la forma $Q(x)=xAx^{t}$ es definida negativa, entonces f tiene un máximo local en en x.

Hay criterios similares para una matriz simetrica $A$ de $n\times n$ y consideramos las $n$ submatrices cuadradas a lo largo de la diagonal, $A$ es definida positiva si y solo si los determinantes de estas submatrices diagonales son todos mayores que cero. Para $A$ definida negativa los signos deberan alternarse $<0$ y $>0$. En casi de que los determinantes de las submatrices diagonales sean todos diferentes de cero pero que la matrix no sea definida positiva o negativa, el punto crítico es tipo silla. Y por lo tanto el punto no es máximo ni mínimo. Asi tenemos el siguiente resultado.

Definición 3. Dada una matriz cuadrada $A=a_{ij}j=1,…,ni=1,…,n$ se consideran las submatrices angulares $A_{k}k=1,…,n$ definidas como $$A_{1} (a_{11})~A_{2}=\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{matrix}\right)~~A_{3}=\left(\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{matrix}\right),\cdots,A_{n}=A$$
se define $\det A_{k}=\triangle_{k}$

Definición 4. Se tiene entonces que que la forma $Q(x)=xAX^{t}$ es definida positiva si y solo si todos los dterminantes $\triangle_{k}~~k=1,…,n$ son números positivos.

Definición 5. La forma $Q(x)=xAX^{t}$ es definida negativa si y solo si los dterminantes $\triangle_{k}k=1,…,n$ tienen signos alternados comenzando por $\triangle_{1}<0,\triangle_{2}>0,…$ respectivamente.

Ejemplo. Consideremos la función $f:\mathbb{R}^3\rightarrow
\mathbb{R}$ $f(x,y,z)=\sin x +\sin y + \sin z -\sin(x+y+z)$, el punto $P=\left(\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}\right)$ es
un punto crítico de $f$ y en ese punto la matriz hessiana de

$f$ es $$H(p)=\left[
\begin{array}{ccc}
-2 & -1 & -1 \\
-1 & -2 & -1 \\
-1 & -1 & -2 \
\end{array}
\right]
$$
los determinantes de las submatrices angulares son
$$\Delta_1=det(-2)\qquad \quad $$ $$\Delta_2=det \left[
\begin{array}{cc}
-2 & -1 \\
-1 & -2 \
\end{array}
\right]$$

$$\Delta_3=det H(p)=-4$$ puesto que son signos alternantes con $\Delta t< 0$ concluimos que la funcion $f$ tiene en $\left(\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}\right)$ un máximo local. Este máximo local vale $f\left(\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}\right)=4$

Introducción

Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor.

Definición 1. Si $f:u\subset \mathbb{R}^n \rightarrow \mathbb{R}$ es una función escalar, dado un punto $x_0 \in u$ se llama mínimo local de $f$ si existe una vecindad $v$ de $x_0$ tal que $\forall x \in v$, $f(x)> f(x_0)$. De manera análoga, $x_0 \in u$ es un máximo local si existe una vecindad $v$ de $x_0$ tal que $f(x)< f(x_0)$ $\forall \quad x \in v$. El punto $x_0 \in u$ es un extremo local o relativo, si es un mínimo local o máximo local.

Un punto $x_0$ es un punto crítico de $f$ si $Df(x_0)=0$.

Un punto crítico que no es un extremo local se llama punto silla.

Teorema 1. $\textcolor{Red}{\textbf{Criterio de la primera derivada}}$ Si $u \in \mathbb{R}$ es abierto, la función $f:u\subset \mathbb{R}^n \rightarrow \mathbb{R}$ es diferenciable y $x_0 \in u$ es un extremo local entonces $\nabla f(x_0)=0$, esto es $x_0$ es un punto crítico de $f$.

Demostración. Supongamos que $t$ alcanza su máximo local en $x_0$. Entonces para cualquier $h \in \mathbb{R}^n$ la función $g(t)=f(x_0+th)$ tiene un máximo local en $t=0$. Asi, del cálculo de una variable $g'(0)=0$ ya que como $g(0)$ es máximo local, $g(t)\leq g(0)$ para $t > 0$ pequeño
$$\therefore \quad g'(0)=\displaystyle\lim_{t \rightarrow t_0^+}\frac{g(t)-g(0)}{t}=0$$
Análogamente para $t< 0$ pequeño tomamos
$$g'(0)=\displaystyle\lim_{t \rightarrow t_0^-}\frac{g(t)-g(0)}{t}=0$$
Ahora por regla de la cadena $$g'(0)=\frac{\partial f}{\partial x_{1}}(x_{0})h_{1}+\frac{\partial f}{\partial x_{2}}(x_{0})h_{2}+\cdots+\frac{\partial f}{\partial x_{n}}(x_{0})h_{0}=\nabla f(x_{0})\cdot h$$
Así $\nabla f(x_{0})\cdot h=0 \quad \forall \: h$ de modo que $\nabla f(x_{0})=0$. En resumen si $x_0$ es un extremo local, entonces $\displaystyle\frac{\partial f}{\partial x_i}(x_0)=0 \quad \forall~i=1,\ldots,n$. En otras palabras $\nabla f(x_0)=0$. $\square$

Ejemplo. Hallar los máximos y mínimos de la función $f:\mathbb{R}^2 \rightarrow \mathbb{R}$, definida por $$f(x,y)=x^2+y^2-2x-6y+14$$

Solución. Debemos identificar los puntos críticos de $f$ resolviendo $\displaystyle{\frac{\partial f}{\partial x}=0}$, $\displaystyle{\frac{\partial f}{\partial y}=0}$ para $x,y$, $$2x-2=0~~~2y-6=0$$ De modo que el punto crítico es $(1,3)$. Como $$f(x,y)=\left(x^{2}-2x+1\right)+\left(y^{2}-6y+9\right)+4=\left(x-1\right)^{2}+\left(y-3\right)^{2}+4$$ tenemos que $f(x,y)\geq 4$ por lo tanto en $(1,3)$ $f$ alcanza un mínimo relativo.

Ejemplo. Considerar la función $f:\mathbb{R}^2 \rightarrow \mathbb{R}$,
$f(x,y)=4-x^2-y^2$ entonces $\displaystyle{\frac{\partial f}{\partial x}=-2x}$, $\displaystyle{\frac{\partial f}{\partial y}=-2y}$. $f$ solo tiene un punto crítico en el origen, donde el valor de $f$ es 4. Como $$f(x,y)=4-(x^{2}+y^{2})$$
tenemos que $f(x,y)\leq 4$ por lo tanto en $(0,0)$ $f$ alcanza un máximo relativo.

Ejemplo. En el siguiente ejemplo mostramos que no todo punto critico es un valor extremo\Sea $f(x,y)=x^{2}y+y^{2}x$ tenemos que sus puntos criticos son
$$\frac{\partial f}{\partial x}=2xy+y^{2}~\frac{\partial f}{\partial y}=2xy+x^{2}=0$$ por lo tanto $$\left(\begin{matrix}2xy+y^{2}=0\\2xy+x^{2}=0\end{matrix}\right)\Leftrightarrow\left(\begin{matrix}x=y\\x=-y\end{matrix}\right)$$ tomando $x=-y$ tenemos que $$2xy+y^{2}=0~\Rightarrow~-2y^{2}+y^{2}=0~\Rightarrow~y^{2}=0\Rightarrow~y=0~\Rightarrow~x=0$$ tomando $x=y$ tenemos que $$2xy+y^{2}=0~\Rightarrow~2y^{2}+y^{2}=0~\Rightarrow~-3y^{2}=0\Rightarrow~y=0~\Rightarrow~x=0$$ por lo tanto $(0,0)$ es el único punto critico.\Ahora bien para $f(x,y)$ tomamos $x=y$ $$f(x,x)=2x^{3}$$ la cual es ($<0$ si $x<0$) y ($>0$ si $x>0$) por lo tanto el punto critico $(0,0)$ no es ni máximo ni mínimo local de f \Ahora bien para $f(x,y)$ tomamos $x=-y$ $$f(x,-x)=0~\forall x$$
por lo tanto el punto critico $(0,0)$ no es ni máximo ni mínimo local de $f$

Requerimos un criterio que dependa de la segunda derivada para que un punto sea extremo relativo. En el caso particular $n=1$ el criterio es $f»(x)>0$ y $f»(x)<0$ para máximo o mínimo respectivamente para el contexto de varias variables usaremos el hessiano el cual esta definido por

$$Hf(x_0)h=\frac{1}{2}\sum_{i,j=1}^{n}\frac{\partial^2t}{\partial x_i\partial
x_j}(x_0|_{x_ix_j}).$$

Recordando un poco de la expresión de taylor$$f(x,y)=f(x_{0},y_{0})+\left(\frac{\partial f}{\partial x}\right){p}(x-x{0})+\left(\frac{\partial f}{\partial y}\right){p}(y-y{0})+\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial x^{2}}{p}(x-x{0})^{2}+2\frac{\partial^{2}f}{\partial y \partial x}{p}(x-x{0})(y-y_{0})+\frac{\partial^{2}f}{\partial y^{2}}{p}(y-y{0})^{2}\right)}$$

Teorema 2. Sea $B=\left[
\begin{array}{cc}
a & b \\
b & c \
\end{array}
\right]
$ y $H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a & b \\
b & c \
\end{array}
\right]\left(
\begin{array}{c}
h_1 \\
h_2 \
\end{array}
\right)
$ entonces $H(h)$ es definida positiva si y solo si $a>0$ y $ac-b^2>0$.

Demostración. Tenemos $$H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a h_1& bh_2 \\
b h_1& ch_2 \
\end{array}
\right]=\frac{1}{2}(ah_1^2+2bh_1h_2+ch_1^2)$$
si completamos el cuadrado
$$H(h)=\frac{1}{2}a\left(h_1+\frac{b}{a}h_2\right)^2+\frac{1}{2}\left(c-\frac{b^2}{a}\right)h_2^2$$
supongamos que $h$ es definida positiva. Haciendo $h_2=0$ vemos que $a>0$. Haciendo $h_1=-\frac{b}{a}h_2$ $c-\frac{b^2}{a}>0$ ó $ac-b^2>0$ De manera analoga $H(h)$ es definida negativa si y solo si $a<0$ y $ac-b^2>0$. $\square$

Criterio del máximo y del mínimo para funciones de dos variables Sea $f(x,y)$ de clase
$C^3$ en un conjunto abierto $u$ de $\mathbb{R}^2$. Un punto $x_0,y_0$ es un mínimo local (Estricto) de $f$ si se cumple las siguientes tres condiciones:

I) $\frac{\partial f}{\partial x}(x_0,y_0)=\frac{\partial f}{\partial y}(x_0,y_0)$

II) $\frac{\partial^2 f}{\partial x^2}(x_0,y_0)> 0$

III ) $\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right)-\left(\frac{\partial^2 f}{\partial x \partial y}\right)^2> 0$ en $(x_0,y_0)$ (Discriminante)

Si en II) tenemos $<0$ en lugar de $>0$ sin cambiar III) hay un máximo local

Ejemplo. Sea $f:\mathbb{R}^2\rightarrow\mathbb{R}$ la función dada por
$$f(x,y)=2(x-1)^2+3(y-2)^2$$ tenemos entonces que $\frac{\partial f}{\partial x}=4(x-1)$ $\frac{\partial f}{\partial y}=6(y-2)$ por lo tanto $\frac{\partial f}{\partial x}=0$ $\Rightarrow \quad x=1$

$\frac{\partial f}{\partial y}=0$ $\Rightarrow$ $y=2$

por lo tanto $x_0=(1,2)$ es un punto critico

$\displaystyle{\frac{\partial^{2} f}{\partial x^{2}}}=4$, $\displaystyle{\frac{\partial^{2} f}{\partial y^{2}}}=6$, $\displaystyle{\frac{\partial^{2} f}{\partial x\partial y}}=0$, $\displaystyle{\frac{\partial^{2} f}{\partial y\partial x}}=0$

$H(1,2)=\left|\begin{array}{cc}
4 & 0 \\
0 & 6 \
\end{array}
\right|=24> 0 \forall \:(x,y) \in
B_{\epsilon}(1,2)$
podemos decir que $f$ tiene un mínimo relativo en $(1,2)$

Funciones de $\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ (parte dos)

Ejemplo. Encontrar el dominio y la imagen de la región $\displaystyle{R=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq x\leq1,~0\leq y\leq1\right\}}$ para la función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$ dada por $$\displaystyle{f(x,y)=\left(x^{2}-y^{2},2xy\right)}$$

Solución. En este caso $$f_{1}=\left(x^{2}-y^{2}\right)~\Rightarrow~Dom_{f_{1}}=\mathbb{R}^{2}$$
$$f_{2}=\left(2xy\right)~\Rightarrow~Dom_{f_{2}}=\mathbb{R}^{2}$$
por lo tanto
$$Dom_{f}=Dom_{f_{1}}\bigcap Dom_{f_{}}=\mathbb{R}^{2}\bigcap \mathbb{R}^{2}=\mathbb{R}^{2}$$
Para la imagen de la región $\displaystyle{R=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq x\leq1,~0\leq y\leq1\right\}}$ procedemos de la siguiente manera:
Definimos los siguientes conjuntos que limitan la región

$$A_{1}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq x\leq 1,~y=0\right\}$$
$$A_{2}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq y\leq 1,~x=1\right\}$$
$$A_{3}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq x\leq 1,~y=1\right\}$$
$$A_{1}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq y\leq 1,~x=0\right\}$$

ahora procedemos a encontrar las imagenes de cada uno de los conjuntos definidos

Para $A_{1}$ se tiene
$$A_{1}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq x\leq 1,~y=0\right\}f(x,y)=\left(x^{2}-y^{2},2xy\right)=(x’,y’)$$ $$x’=x^{2}-y^{2}~\underbrace{\Rightarrow}_{y=0}~x’=x^{2}~y~si~0\leq x\leq\leq1~\Rightarrow~0\leq x^{2}\leq 1~\Rightarrow~0\leq x’\leq 1$$
$$y’=2xy\underbrace{\Rightarrow}_{y=0}y’=0$$ por lo tanto $$f(A_{1})=\left\{(x’,y’)\in\mathbb{R}^{2}~|~0\leq x’\leq 1~,~y’=0\right\}$$ Para $A_{2}$ se tiene $$A_{2}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq y\leq 1,~x=1\right\}f(x,y)=\left(x^{2}-y^{2},2xy\right)=(x’,y’)$$
$$x’=x^{2}-y^{2}~\underbrace{\Rightarrow}_{x=1}~x’=1-y^{2}~\Rightarrow~y=\sqrt{1-x’}$$ $$y’=2xy\underbrace{\Rightarrow}_{x=1}y’=2y~\Rightarrow~y’=2\sqrt{1-x’}~\Rightarrow~y’^{2}=4(1-x’)$$
por lo tanto
$$f(A_{2})=\left\{(x’,y’)\in\mathbb{R}^{2}~|~y’^{2}=4(1-x’),~0\leq y’\leq 2 \right\}$$
Para $A_{3}$ se tiene
$$A_{3}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq x\leq 1,~y=1\right\}f(x,y)=\left(x^{2}-y^{2},2xy\right)=(x’,y’)$$
$$x’=x^{2}-y^{2}~\underbrace{\Rightarrow}_{y=1}~x’=x^{2}-1~\Rightarrow~x’+1=x^{2}~\Rightarrow~x=\sqrt{x’+1}$$ $$y’=2xy\underbrace{\Rightarrow}_{y=1}y’=2x~\Rightarrow~y’=2\sqrt{x’+1}~\Rightarrow~y’^{2}=4(x’+1)$$
por lo tanto
$$f(A_{3})=\left\{(x’,y’)\in\mathbb{R}^{2}~|~y’^{2}=4(x’+1),~0\leq y’\leq 2 \right\}$$
Para $A_{4}$ se tiene
$$A_{4}=\left\{(x,y)\in \mathbb{R}^{2}~|~0\leq y\leq 1,~x=0\right\}f(x,y)=\left(x^{2}-y^{2},2xy\right)=(x’,y’)$$
$$x’=x^{2}-y^{2}~\underbrace{\Rightarrow}_{x=0}~x’=-y^{2}ysi0\leq y\leq1~\Rightarrow~0\leq y^{2}\leq 1~\Rightarrow~-1\leq y^{2}\leq 0$$ $$y’=2xy\underbrace{\Rightarrow}_{x=0}y’=0$$
por lo tanto
$$f(A_{4})=\left\{(x’,y’)\in\mathbb{R}^{2}~|~-1\leq x’\leq 0~,~y’=0\right\}$$

Operaciones con Funciones de $\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$

Definición 1. Sean $f,g:A\subset \mathbb{R}^{n}\rightarrow\mathbb{R}^{m},\alpha\in\mathbb{R}y~~h:D\subset\mathbb{R}^{m}\rightarrow\mathbb{R}^{k}$. Definimos

1. La suma de f y g que denotamos por f+g como
   $$(f+g)(x)=f(x)+g(x),~~~x\in A$$
2. El producto del escalar $\alpha$ por la función f que denotamos $\alpha f$ como
   $$(\alpha f)(x)=\alpha f(x),~~~x\in A$$
3. El producto punto de f por g que denotamos $f\cdot g$ como
   $$(f\cdot g)(x)=f(x)\cdot g(x),~~~x\in A$$
4. Si $m=3$ el producto cruz de f por g que denotamos $f\times g$ como
   $$(f\times g)(x)=f(x)\times g(x),~~~x\in A$$
5. Si $m=1$ el cociente de f por g que denotamos $\displaystyle{\frac{f}{g}}$ como
   $$\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)},~~~x\in A$$
6. La composición de h con f, que denotamos como $h\circ f$ como
   $$(h\circ f)(x)=h(f(x))para~cada~~\left\{x\in A~|~f(x)\in D\right\}$$

Gráficas de Funciones de $\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$

Definición 2. Dada la función $f (f_{1},…,f_{m}):A\subset\mathbb{R}^{n}\rightarrow
\mathbb{R}^{m}$, definimos su gráfica como el subconjunto
$$g_{f}={(x_{1},…,x_{n},f_{1}(x_{1},…,x_{n}),f_{2}(x_{1},…,x_{n}),…,f_{m}(x_{1},…,x_{n}))\in\mathbb{R}^{n+m}|(x_{1},…,x_{n})\in A}$$

{Límite de Funciones de $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$

Definición 3. $\textcolor{Red}{\textbf{Por sucesiones}}$ Sean $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ y $x_{0}\in A’$. Decimos que f tiene límite en $x_{0}$ y que su límite es $\ell\in\mathbb{R}^{m}$, si para toda sucesión ${x_{k}}$ contenida en $A-{x_{0}}$ que converge a $x_{0}$ se tiene que la sucesión ${f(x_{k})}$ converge a $\ell$. En este caso escribimos
$$\lim_{x\rightarrow x_{0}}f(x)=\ell$$
y decimos que $\ell$ es el límite de f en $x_{0}$.

Definición 4. $\textcolor{Red}{(\epsilon-\delta)}$ Sea $f:A\subset\mathbb{R}^{n} \rightarrow
\mathbb{R}^{m}$, y sea $x_{0}$ un punto de acumulación de A.
Se dice que $\ell\in\mathbb{R}^{m}$ es el límite de $f$ en
$x_{0}$, y se denota por:\ $$\displaystyle\lim_{x\rightarrow
x_{0}}f(x)=\ell$$ Si dado $\forall~\epsilon > 0$, existe $\delta > 0$ tal
que $$|f(x)-\ell|<\epsilon~cuando~0<|x-x_{0}|<\delta$$

Continuidad de Funciones de Varias Variables

Definición 5. Sean $f:\Omega\subset\mathbb{R}^n\rightarrow\mathbb{R}^m$ y
$x_0\in\Omega$. Se dice que $f$ es continua en $x_0$ si dado $\epsilon>0$, $\exists$ $\delta>0$ tal que $|f(x)-f(x_0)|<\epsilon$ siempre que $x\in\Omega$ y $0<|x-x_0|<\delta$

Definición 6. Se dice que un subconjunto $V\subset\mathbb{R}^{n}$ es un entorno del punto $x$, si exite $\epsilon>0$ tal que $B(x,\epsilon)\subset V.$

Definición 7. Sean $f:\Omega\subset\mathbb{R}^n\rightarrow\mathbb{R}^m$ y $x_0\in\Omega$. Se dice que $f$ es continua en $x_0$ cuando $\forall$ entorno V de $f(x_{0})$ existe un entorno U de $x_{0}$ tal que $f(U)\subset V$ es decir para cualquier $x\in U$ se cunple $f(x)\in V$

Proposición 1. Una función $f:D\subset\mathbb{R}^{n}\rightarrow \mathbb{R}^m$ es continua si y solo si
$$f^{-1}(v)=\left\{x\in D\mid f(x)\in v\right\}$$
es un abierto (contenido en $D$) para cada abierto $v\subset\mathbb{R}^m$.

Demostración. $\textcolor{Red}{\Rightarrow}$ Sea $v$ un abierto en $\mathbb{R}^m$ y sea $\overline{x}\in f^{-1}(v)$; tenemos por definición $f(\overline{x})\in v$. Como $v$ es un
conjunto abierto $\exists\ \ r>0$ tal que $B(f(\overline{x}),r)\subset v$ como $f$ es continua $\exists$ $\rho>0$ tal que $f(B(x,\rho))\subset B(f(x),r)$ pero esto significa que $B(x,\rho)\subset f^{-1}(B(f(x),r))\subset f^{-1}(v)$ por lo que cada punto $x\in f^{-1}(v)$ es punto interior lo que prueba que $v$ es abierto.
$\textcolor{Red}{\Leftarrow}$ Supongamos que $f^{-1}(v)$ es un abierto, para cada conjunto abierto $v\subset\mathbb{R}^{m}$\Sea $\epsilon>0$ y $x\in\mathbb{R}^{n}$, hacemos:
$B(f(x),\epsilon)=V$ por lo que$f^{-1}(V)$ es abierto, esto quiere decir que $\exists~\delta>0$ tal que $B(x,\delta)\subset f^{-1}(V)$ esto implica $f(B(x,\delta))\subset V$ esto es $f(B(x,\delta))\subset B(f(x),\epsilon)$ esto muestra que $f$ es continua en $x$.

Proposición 2.

(1) $$f^{-1}(v)=\left\{x\in D\mid f(x)\in v\right\}$$
es un abierto (contenido en $D$) para cada abierto
$v\subset\mathbb{R}^m$.
(2) $$f^{-1}(v)=\left\{x\in D\mid f(x)\in v\right\}$$
es un cerradoo (contenido en $D$) para cada cerradoo
$v\subset\mathbb{R}^m$.

Vamos a probar que $\textcolor{Red}{1\Rightarrow 2}$

Demostración. Si $V=\overline{V}\subset\mathbb{R}^{m}$, consideremos el conjunto $V^{c}$ el cual es abierto y por hipotesis $f^{-1}(V^{c})$ es abierto, pero
$$f^{-1}(V^{c})=\left(f^{-1}(V)\right)^{c}$$
por lo que $\left(f^{-1}(V)\right)^{c}$ es abierto, en consecuencia $f^{-1}(V)$ es cerrado\
Vamos a probar que \textcolor{Red}{$2\Rightarrow 1$}
Si $V=int(V)\subset\mathbb{R}^{m}$ entonces $V^{c}$ es cerrado y por hipotesis $f^{-1}(V^{c})$ es cerrado, pero
$$f^{-1}(V^{c})=\left(f^{-1}(V)\right)^{c}$$
por lo que $\left(f^{-1}(V)\right)^{c}$ es cerradoo, en consecuencia $f^{-1}(V)$ es abierto $\square$

Teorema de la Función Inversa (sistema $f_{i}:\mathbb{R}^{n}\rightarrow\mathbb{R}$)

Teorema 1. Sea $U\subset\mathbb{R}^{n}$ un abierto y sean
$$\begin{matrix}
f_{1}:U\rightarrow\mathbb{R} \\
\vdots \\
f_{n}:U\rightarrow\mathbb{R}
\end{matrix}$$
con derivadas parciales continuas. Considerar las ecuaciones
$$\begin{array}{c}
f_1(x_1,x_2,…,x_n)= y_1\\
f_2(x_1,x_2,…,x_n)= y_2\\
\vdots\\
f_n(x_1,x_2,…,x_n)= y_n
\end{array}$$ Tratamos de resolver las n-ecuaciones para $x_1,x_2,… x_n$como funciones de $y_1,y_2,… y_n$.
La condición de existencia para la solución en una vecindad del punto $x_0$ es que el determinante de la matriz $Df(x_0)$ y $f=(f_1,f_2,… f_n)$ sean distintos de cero.

La condición de existencia para la solución en una vecindad del punto $x_0$ es que el determinante de la matriz $Df(x_0)$ y $f=(f_i,f_2,… f_n)$ sean distintos de cero. Explicitamente:

$[\left. \begin{array}{c}
\displaystyle\frac{\partial(f_1,f_2,…,f_n)}{\partial(x_1,x_2,…,x_n)}
\end{array}\right|_{x=x_0}= J(f)(x_0)= \left| \begin{array}{ccc}
\displaystyle\frac{\partial f_1}{\partial x_1}(x_0)&\ldots&\displaystyle\frac{\partial f_1}{\partial x_1}(x_0)\\
\vdots & & \vdots\\
\displaystyle\frac{\partial f_n}{\partial x_1}(x_0)&\ldots&\displaystyle\frac{\partial f_n}{\partial x_n}(x_0)
\end{array}\right| \neq 0
]$

entonces el sistema anterior se puede resolver de manera ‘unica como $x=g(y)$ para $x$ cerca de $x_{0}$ y y cerca de $y_{0}$ $\square$

Nota. La cuestión de existencia se responde por medio del teorema general de la función implícita aplicado a las funciones $y_i-f_i(x_1,x_2,…,x_n)$ con las incognitas $x_1,x_2,…,x_n$.

Ejemplo. El problema de factorizar un polinomio $x^{n}+a_{n-1}x^{n-1}+\cdots+a_{0}$ en factores lineales es, en cierto sentido un problema de función inversa. Los coeficientes $a_{i}$ son funciones conocidas de las n raices $r_{j}$. ¿Se podran expresar las raices como funciones de los coeficientes en alguna región?. Con $n=3$ , aplicar el teorema de la función inversa a este problema y enunciar la conclusión acerca de la posibilidad de hacer lo planteado.

Solución. Para el caso n=3 tenemos que podemos factorizar el polinomio de la siguiente forma
$$x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=(x-r_{1})(x-r_{2})(x-r_{3})$$
desarrolando el lado derecho tenemos que
$$(x-r_{1})(x-r_{2})(x-r_{3})=x^{3}-r_{3}x^{2}-r_{2}x^{2}+r_{2}r_{3}x-r_{1}x^{2}+xr_{1}r_{3}+r_{1}r_{2}x-r_{1}r_{2}r_{3}$$
que se puede escribir
$$x^{3}+x^{2}(-r_{3}-r_{2}-r_{1})+x(r_{2}r_{3}+r_{1}r_{3}+r_{1}r_{2})-r_{1}r_{2}r_{3}$$
igualando las expresiones
$$x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=x^{3}+x^{2}(-r_{3}-r_{2}-r_{1})+x(r_{2}r_{3}+r_{1}r_{3}+r_{1}r_{2})-r_{1}r_{2}r_{3}$$
por lo tanto igualando coeficientes
$$\begin{matrix}a_{0}=-r_{1}r_{2}r_{2}\\a_{1}=r_{2}r_{3}+r_{1}r_{3}+r_{1}r_{2}\\a_{2}=-r_{1}-r_{2}-r_{3}\end{matrix}$$

Al sistema anterior le aplicamos el teorema de la función implicita para comprobar si las raices se pueden expresar en términos de los coeficientes, para ello calculamos el determinante de jacobiano del sistema que en este caso es

$$J=\left(\begin{matrix}\frac{\partial a_{0}}{\partial r_{1}}&\frac{\partial a_{0}}{\partial r_{2}}&\frac{\partial a_{0}}{\partial r_{3}}\\\frac{\partial a_{1}}{\partial r_{1}}&\frac{\partial a_{1}}{\partial r_{2}}&\frac{\partial a_{2}}{\partial r_{3}}\\\frac{\partial a_{2}}{\partial r_{1}}&\frac{\partial a_{2}}{\partial r_{2}}&\frac{\partial a_{3}}{\partial r_{3}}\end{matrix}\right)=\left(\begin{matrix}-r_{2}r_{3}&-r_{1}r_{3}&-r_{1}r_{2}\\r_{3}+r_{2}&r_{3}+r_{1}&r_{2}+r_{1}\\-1&-1&-1\end{matrix}\right)$$

de esta manera el determinante del jacobiano es
$$\det\left(\begin{matrix}-r_{1}r_{3}&-r_{1}r_{3}&-r_{1}r_{2}\\r_{3}+r_{2}&r_{3}+r_{1}&r_{2}+r_{1}\\-1&-1&-1\end{matrix}\right)=\left|\begin{matrix}-r_{1}r_{3}&-r_{1}r_{3}&-r_{1}r_{2}\\r_{3}+r_{2}&r_{3}+r_{1}&r_{2}+r_{1}\\-1&-1&-1\end{matrix}\right|=$$
$$\textcolor{Green}{(-r_{2} r_{3})\times
\left|\begin{array}{cc}
r_{3}+r_{1} & r_{2}+r_{1} \\
-1 & -1\end{array}\right|}-\textcolor{Red}{(-r_{1}r_{3})\times
\left|\begin{array}{cc}
r_{3}+r_{2} & r_{2}+r_{1} \\
-1 &- 1\end{array}\right|}+\textcolor{Blue}{(-r_{1}r_{2})\times
\left|\begin{array}{cc}
r_{3}+r_{2} & r_{3}+r {1}\\ 3 & 1\end{array}\right|}=$$ $$\textcolor{Green}{(-r{2}r_{3})\times(r_{2}-r_{3})}+\textcolor{Red}{(r_{1}r_{3})\times(r_{1}-r_{3})}-\textcolor{Blue}{(r_{1}r_{2})\times(r_{1}-r_{2})}=-r_{2}r_{3}r_{2}+r_{2}r_{3}r_{3}+r_{1}r_{3}r_{1}-r_{1}r_{3}r_{3}-r_{1}r_{2}r_{1}+r_{1}r_{2}r_{2}$$

que se puede escribir
$$=r_{3}r_{1}r_{1}-r_{3}r_{1}r_{3}-r_{3}r_{2}r_{1}+r_{3}r_{2}r_{3}-r_{2}r_{1}r_{1}+r_{2}r_{1}r_{3}+r_{2}r_{2}r_{1}-r_{2}r_{2}r_{3}$$
$$=(r_{3}r_{1}-r_{3}r_{2}-r_{2}r_{1}+r_{2}r_{2})r_{1}-(r_{3}r_{1}-r_{3}r_{2}-r_{2}r_{1}+r_{2}r_{2})r_{3}=(r_{3}r_{1}-r_{3}r_{2}-r_{2}r_{1}+r_{2}r_{2})(r_{1}-r_{3})$$
$$=((r_{3}-r_{2})r_{1}-(r_{3}-r_{2})r_{2})(r_{1}-r_{3})=(r_{3}-r_{2})(r_{1}-r_{2})(r_{1}-r_{3})$$

Este último término no es cero si el polinomio tiene raices distintas. Así el teorema de la función inversa muestra que las raices se pueden hallar como funciones de los coeficientes en alguna vecindad de cualquier punto en el que las raices sean distintas. Esto es, si las rices $r_{1},~r_{2},~r_{3}$ de $x^{3}+a_{2}x^{2}+a_{1}x+a_{0}$ son todas diferentes, entonces hay vecindades V de $(r_{1},~r_{2},~r_{3})$ y $W$ de $(a_{0},~a_{1},~a_{2})$ tales que las raices en V son funciones de los coeficientes en $W$.

Funciones de $\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$

Definición 1. Una función f de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$ denotada $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$, es una relación que asigna a cada vector del espacio $\mathbb{R}^{n}$ un único vector del espacio $\mathbb{R}^{m}$\Si f es una función de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$, entonces f se expresa
$$f=(f_{1},f_{2},\cdots,f_{m})$$ en donde $f_{k}~~k=1,…,m$ es la k-ésima función componente y $f_{k}:\mathbb{R}^{n}\rightarrow \mathbb{R}$ $k=1,…,m$

Definición 2. Si $A\subset \mathbb{R}^{n}$, la imagen bajo la función f de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$ se denota $f(A)$, y se define
$$f(A)={f(x)\in \mathbb{R}^{m}~|~x\in A}$$

Definición 3. El dominio de una función f de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$ es la intersección de los dominios de las funciones componentes $f_{k}$ es decir
$$Dom_{f}=\bigcap_{k=1}^{m}Dom_{f_{k}}=Dom_{f_{1}}\bigcap Dom_{f_{2}}\bigcap Dom_{f_{3}}\bigcap\cdots \bigcap Dom_{f_{m}}$$

Ejemplo. Encontrar el dominio y la imagen de la recta $y=3x$ para la función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$ dada por $$\displaystyle{f(x,y)=\left(\frac{4x+2y}{5},\frac{2x+y}{5}\right)}$$
\item[Solución] En este caso $$f_{1}=\left(\frac{4x+2y}{5}\right)~\Rightarrow~Dom_{f_{1}}=\mathbb{R}^{2}$$
$$f_{2}=\left(\frac{2x+y}{5}\right)~\Rightarrow~Dom_{f_{2}}=\mathbb{R}^{2}$$
por lo tanto
$$Dom_{f}=Dom_{f_{1}}\bigcap Dom_{f_{}}=\mathbb{R}^{2}\bigcap \mathbb{R}^{2}=\mathbb{R}^{2}$$
Para la imagen de la recta $y=3x$ procedemos de la siguiente manera
$$f(x,y)=\left(\frac{4x+2y}{5},\frac{2x+y}{5}\right)=(x’,y’)~ \Rightarrow ~f(x,3x)=\left(\frac{4x+2(3x)}{5},\frac{2x+(3x)}{5}\right)=(x’,y’)~\Rightarrow~$$
$$x’=\frac{4x+2(3x)}{5}yy’=\frac{2x+(3x)}{5}~ \Rightarrow ~x’=2xyy’=x \Rightarrow y’=\frac{x’}{2}$$
por lo tanto la imagen de la recta $y=3x$ sera:
$$f(3x)=\left\{(x’,y’)\in\mathbb{R}^{2}~|~y’=\frac{x’}{2}\right\}$$

$\textbf{Definición 4.}$ Sean $f:A\subset\mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ y $D\subset\mathbb{R}^{m}$. Definimos la $\textbf{imagen inversa}$ de $D$ bajo $f$, que denotamos $f^{-1}(D)$, como el conjunto dado por:
$$f^{-1}(D)=\left\{\hat{x}\in A~|~f(\hat{x})\in D\right\}$$

Definición 5. Sean $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ y $D\subset\mathbb{R}^{m}$, $B\subset A$. Definimos la $\textbf{imagen directa}$ de $B$ bajo $f$, que denotamos $f(B)$, como el conjunto dado por:
$$f(B)=\left\{f(\hat{x})\in \mathbb{R}^{m}~|~\hat{x}\in B\right\}$$

Proposición 1. Sean $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$, $A_{\alpha},~B,C\subset A$ y $D_{\alpha},~D,~E\subset\mathbb{R}^{m}$, con $\alpha\in I$ I un conjunto de indices. Pruebe que:
$$\begin{matrix}
1.& D\subset E~\Rightarrow~f^{-1}(D)\subset f^{-1}(E) \\
2. & f^{-1}\left(\bigcup_{\alpha \in I}D_{\alpha}\right)=\bigcup_{\alpha\in I}f^{-1}(D_{\alpha})\
3.& f^{-1}\left(\bigcap_{\alpha \in I}D_{\alpha}\right)=\bigcap_{\alpha\in I}f^{-1}(D_{\alpha}) \\
4.&f^{-1}(D^{c})=(f^{-1}(D))^{c} \\
5.&B\subset C~\Rightarrow~f(B)\subset f(C)\\
6.&f\left(\bigcup_{\alpha\in I}A_{\alpha}\right)=\bigcup_{\alpha\in I}f(A_{\alpha}) \\
7.&f\left(\bigcap_{\alpha\in I}A_{\alpha}\right)\subset\bigcap_{\alpha\in I}f(A_{\alpha}) \\
8.&f(A)-f(B)\subset f(A-B) \\
9.&B\subset f^{-1}(f(B)) \\
10.&f(f^{-1})(D)\subset D
\end{matrix}$$

Demostración. $\textcolor{Blue}{(1). D\subset E~\Rightarrow~f^{-1}(D)\subset f^{-1}(E)}$
$$x\in f^{-1}(D)~\Rightarrow~f(x)\in D$$
$$~\underbrace{\Rightarrow}{D\subset E}~f(x)\in E$$ $$~\Rightarrow~x\in f^{-1}(E)$$ $\textcolor{Blue}{(2). f^{-1}\left(\bigcup{\alpha \in I}D_{\alpha}\right)=\bigcup_{\alpha\in I}f^{-1}(D_{\alpha})}$
$$x\in f^{-1}\left(\bigcup_{\alpha \in I}D_{\alpha}\right)~\Leftrightarrow~f(x)\in \bigcup_{\alpha \in I}D_{\alpha}$$
$$~\Leftrightarrow~f(x)\in D_{\alpha_{i}}p.a.~i\in I$$ $$~\Leftrightarrow~x\in f^{-1}(D_{\alpha_{i}})p.a.~i\in I$$
$$~\Leftrightarrow~x\in (\bigcup_{\alpha \in I}f^{-1}(D_{\alpha})$$
$\textcolor{Blue}{(3). f^{-1}\left(\bigcap_{\alpha \in I}D_{\alpha}\right)=\bigcap_{\alpha\in I}f^{-1}(D_{\alpha}) }$
$$x\in f^{-1}\left(\bigcap_{\alpha \in I}D_{\alpha}\right)~\Leftrightarrow~f(x)\in \bigcap_{\alpha \in I}D_{\alpha}$$
$$~\Leftrightarrow~f(x)\in D_{\alpha_{i}}\forall~i\in I$$ $$~\Leftrightarrow~x\in f^{-1}(D_{\alpha_{i}})\forall~i\in I$$
$$~\Leftrightarrow~x\in (\bigcap_{\alpha \in I}f^{-1}(D_{\alpha})$$
$\textcolor{Blue}{(4). f^{-1}(D^{c})=(f^{-1}(D))^{c} }$
$$x\in f^{-1}(D^{c})~\Leftrightarrow~f(x)\in D^{c}$$
$$~\Leftrightarrow~f(x)\notin D$$
$$~\Leftrightarrow~x\notin f^{-1}(D)$$
$$~\Leftrightarrow~x\in (f^{-1}(D))^{c}$$
$\textcolor{Blue}{(5). B\subset C~\Rightarrow~f(B)\subset f(C)}$
$$f(x)\in f(B)~\Rightarrow~x\in B$$
$$~\underbrace{\Rightarrow}{B\subset C}~x\in C$$ $$~\Rightarrow~f(x)\in f(C)$$ $\textcolor{Blue}{(6). f\left(\bigcup{\alpha\in I}A_{\alpha}\right)=\bigcup_{\alpha\in I}f(A_{\alpha})}$
$$f(x)\in f\left(\bigcup_{\alpha \in I}A_{\alpha}\right)~\Leftrightarrow~x\in \bigcup_{\alpha \in I}A_{\alpha}$$
$$~\Leftrightarrow~x\in A_{\alpha}p.a~\alpha\in~I$$ $$~\Leftrightarrow~f(x)\in~f(A_{\alpha})~p.a~\alpha\in~I$$ $$~\Leftrightarrow~f(x)\in \bigcup_{\alpha\in I}f(A_{\alpha})$$

$\textcolor{Blue}{(7). f\left(\bigcap_{\alpha\in I}A_{\alpha}\right)\subset\bigcap_{\alpha\in I}f(A_{\alpha})}$ $$f(x)\in f\left(\bigcap_{\alpha \in I}A_{\alpha}\right)~\Rightarrow~x\in \bigcap_{\alpha \in I}A_{\alpha}$$ $$~\Rightarrow~x\in A_{\alpha}\forall~\alpha\in~I$$
$$~\Rightarrow~f(x)\in~f(A_{\alpha})~\forall~\alpha\in~I$$
$$~\Rightarrow~f(x)\in \bigcap_{\alpha\in I}f(A_{\alpha})$$
$\textcolor{Blue}{(8). f\left(A\right)-f(B)\subset f(A-B)}$
$$f(A)-f(B)=f(A)\bigcap (f(B))^{c}$$
$$~ \Rightarrow ~f(x)\in f(A)-f(B)$$
$$~ \Rightarrow ~f(x)\in f(A)\bigcap (f(B))^{c}$$
$$~ \Rightarrow ~f(x)\in f(A)yf(x)\in (f(B))^{c}$$
$$~ \Rightarrow ~x\in Ayf(x)\notin f(B)$$
$$~ \Rightarrow x\in Ayx\notin B$$ $$~ \Rightarrow x\in Ayx\in B^{c}$$
$$~ \Rightarrow ~x\in A\bigcap B^{c}$$
$$~ \Rightarrow ~x\in A-B$$
$$~ \Rightarrow ~f(x)\in f(A-B)$$
$\textcolor{Blue}{(9). B\subset f^{-1}(f(B))}
$$x\in B~\Rightarrow~f(x)\in f(B)$$
$$~\Rightarrow~x\in f^{-1}(f(B))$$

$\textcolor{Blue}{(10).f(f^{-1}(D))\subset D}$
$$f(x)\in f(f^{-1}(D))~\Rightarrow~x\in f^{-1}(D)$$
$$~ \Rightarrow ~f(x)\in D$$ $\square$