Introducción
Este apartado considera algunos casos reales en los que podemos aplicar los conocimientos adquiridos a lo largo de éstas notas. Son ejemplos que nos permiten conocer qué tipo de inversiones nos convienen más, como lo es cuando queremos invertir en CETES, ante dicha situación podemos usar el conocimiento adquirido para determinar, el valor de uno de sus títulos, y poner en práctica de forma real, para conocer mejor cual es el manejo real de algunas una de las formulas, evidenciando la forma en la que se pueden utilizar de forma aplicada en alguna situación real.
Aplicación en CETES
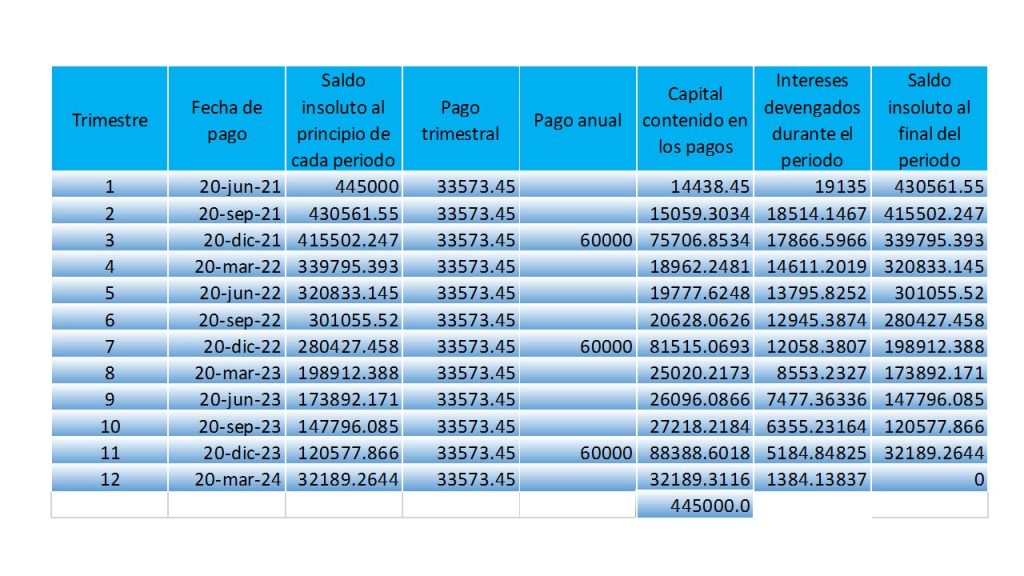
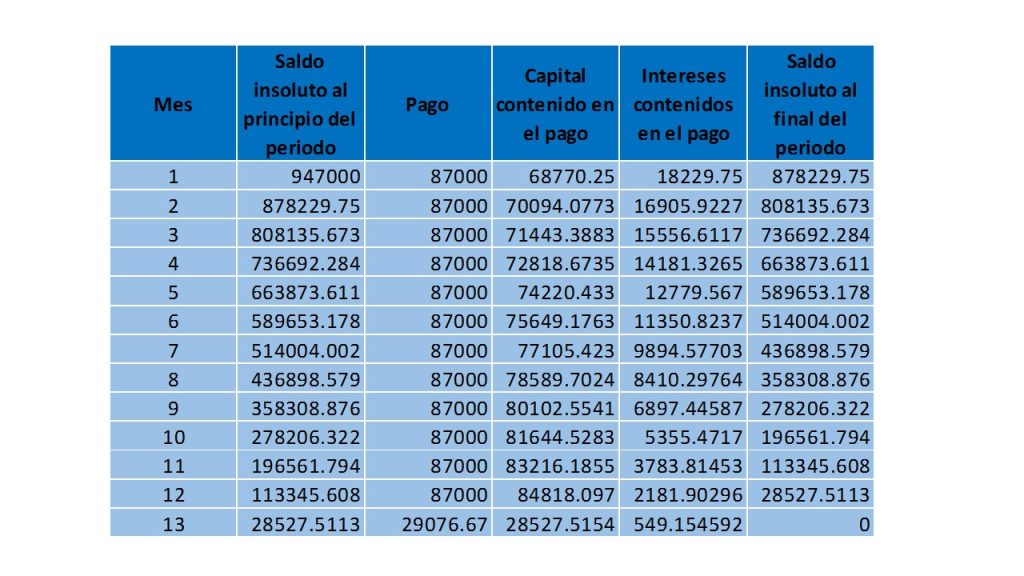
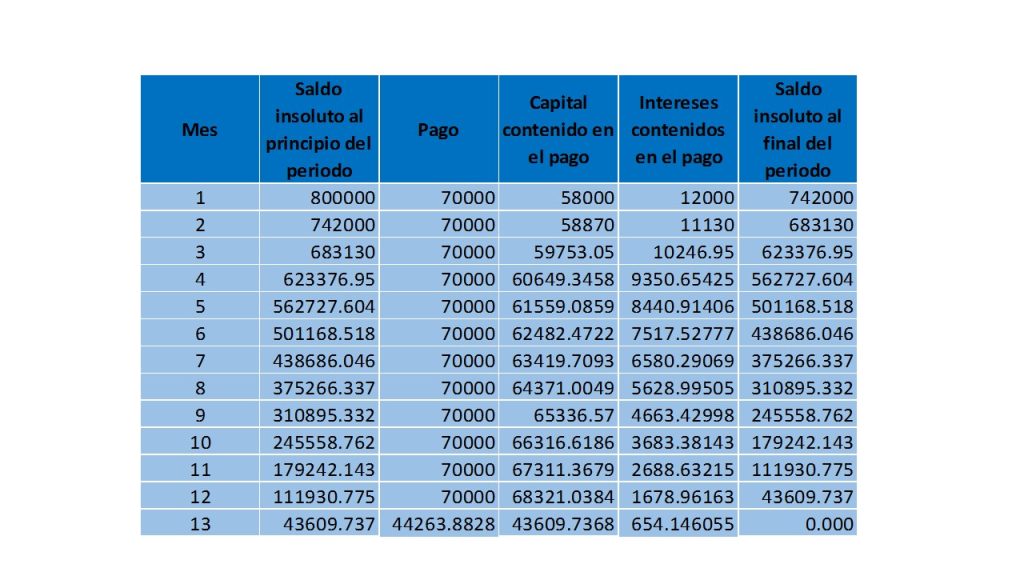
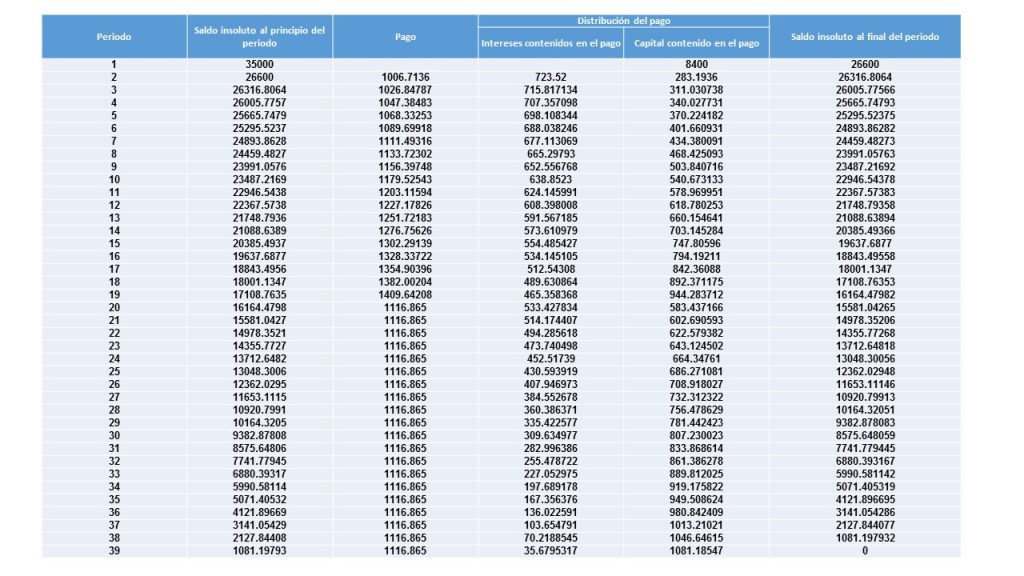
Como se estuvo exponiendo a lo largo del desarrollo de éstas notas, las matemáticas financieras son una poderosa herramienta, que nos sirve para determinar el valor del dinero a través del tiempo. Para realizar dicho análisis, vimos una cierta cantidad de conceptos que nos permitieron comprender mejor cómo funciona el mundo de las finanzas, aspectos que la afectan como lo es la inflación, partiendo desde el ejemplo más simple de interés compuesto, hasta llegar al punto de elaborar tablas de amortización, cálculo de valor de bonos, temas en los que se combinaban una enorme cantidad de conceptos para su construcción.
En este apartado, lo que se va a realizar es, mostrar algunos ejemplos con aplicaciones reales, de los conceptos que en éstas notas se estuvieron abordando, para que se pueda tener una mejor comprensión de la importancia del uso de las matemáticas financieras, en el mundo real.
Un ejemplo práctico del uso de las matemáticas financieras, en un caso real es el siguiente:
El precio de un CETE se puede calcular, conociendo su tasa de rendimiento, o su tasa de descuento, y se obtiene utilizando la siguiente ecuación1:
$$P=\frac{VN}{\left(1+\frac{i*t}{360}\right)}$$
donde:
P = Valor del CETE (redondeado a 7 decimales)
VN = Valor Nominal del título en pesos
i = Tasa de rendimiento
t = tiempo o plazo en días del CETE
Si $d$ es la tasa de descuento de un CETE se tiene que:
$$d=\frac{i}{\left(1+\frac{i*t}{360}\right)}$$
despejando $i$,
$$i=\frac{d}{\left(1-\frac{d*t}{360}\right)}$$
Al sustituir éste resultado en la primera ecuación se obtiene el precio de un CETE a partir de su tasa de descuento:
$$P=VN*\left(1-\frac{d*t}{360}\right)$$
Por lo que se tiene que el precio de un CETE está compuesto por el valor presente de su valor nominal.
Ejercicios resueltos
Ejercicio. El 31 de agosto del año 2000, un inversionista compra CETES con las siguientes características:
- Valor nominal: \$10 pesos
- Fecha de colocación: 31 de agosto del año 2020
- Fecha de vencimiento: 28 de septiembre del año 2020
- Días por vencer del título: 28 días
Suponiendo que está sujeto a una tasa de rendimiento anual del 15%, obtener el valor del CETE.
Solución
Para poder obtener el precio del CETE, se puede hacer por dos caminos, el primero sería calcular el valor presente, usando la tasa de rendimiento. Mientras que la segunda forma de obtenerlo es usando la tasa de descuento que proporcione este rendimiento.
Vamos a realizar utilizando la tasa de rendimiento que nos proporcionaron, calculando su valor presente, esto es:
$$P=\frac{10}{\left(1+\frac{0.15*28}{360}\right)}$$
$$=\frac{10}{1.01205555556}=9.8808805$$
El precio del CETE será de: \$9.8808805
Ahora usando la tasa de descuento, la forma de obtener el precio del CETE quedaría:
$$d=\frac{0.15}{\left(1+\frac{0.14*28}{360}\right)}$$
$$=\frac{0.15}{1.01205555556}=0.1532=15.32%$$
Con base en esta tasa de descuento (15.32%) se determina el precio al cual el inversionista tendrá que liquidar cada uno de los CETES que adquirió. Cabe señalar que es convención del mercado redondear a diezmilésimas las tasas de rendimiento y descuento, esto origina que el precio de un CETE calculado a partir del rendimiento difiera en algunos decimales del precio calculado a partir del descuento.*
$$P=10*\left(1-\frac{0.1532*28}{360}\right)$$
$$=10*(0.98808444)=9.8808444$$
Ejercicio. Supongamos ahora, el siguiente caso: un inversionista compra CETES con las siguientes características:
- Valor nominal: \$10 pesos
- Fecha de colocación: 24 de marzo de 2023
- Fecha de vencimiento: 23 de junio de 2023
- Duración del título: 91 días
- Tasa de rendimiento: 4.39%
Solución
**Se obtendrá el precio, usando la tasa de rendimiento, calculando el valor presente, es decir:
$$P=\frac{10}{\left(1+\frac{0.0439*91}{360}\right)}$$
$$=\frac{10}{1.011096944444}=9.8902485$$
El precio del CETE será de: \$9.8902485
Usando la tasa de descuento equivalente al 4.39% el procedimiento para obtener el precio del título es el siguiente:
$$d=\frac{0.0439}{\left(1+\frac{0.0439*91}{360}\right)}$$
$$=\frac{0.0439}{1.011096944444}=0.0434=4.34%$$
$$P=10*\left(1-\frac{0.434*91}{360}\right)$$
$$=10*(0.98902944)=9.8902944$$
Con base en esta tasa de descuento (4.34%) se determina el precio al cual el inversionista tendrá que liquidar cada uno de los CETES que adquirió. Cabe señalar que es convención del mercado redondear a diezmilésimas las tasas de rendimiento y descuento, esto origina que el precio de un CETE calculado a partir del rendimiento difiera en algunos decimales del precio calculado a partir
del descuento.2
Aplicación para calcular el Costo Anual Total (CAT)
Otra aplicación bastante útil, para la que nos sirve las Matemáticas financieras, es cuando nosotros contratamos una tarjeta de crédito, y deseamos saber el costo real que vamos a tener que pagar por la línea de crédito que no otorgan, dicho en otras palabras, deseamos saber cuánto dinero nos va a costar tener a nuestra disposición dichos recursos económicos.
Primero que nada, la definición del CAT, es una forma de poder medir el total de costos y gastos que se tienen que hacer, cuando algún banco nos otorga un crédito, en este caso particular, se va a analizar el caso de una tarjeta de crédito (lo que incluye intereses, comisiones, anualidad, comisiones por apertura, gastos de investigación, seguros, etc.). La importancia de conocer ésta herramienta, nos permite comparar y poder elegir cuál es la mejor opción de banco o institución financiera que nos ofrece la opción con un menor costo.
Para poder calcular el Costo Anual Total, de acuerdo con la circular 21/20093 emitida por el Banco de México, la metodología utilizada para calcular el CAT es la siguiente:
$$\sum_{j=1}^M\frac{A_j}{(1+i)^{t_j}}=\sum_{k=1}^N\frac{B_k}{(1+i)^{S_k}}$$
donde:
$i =$ CAT, expresado como decimal
$M =$ Número total de disposiciones de crédito
$j =$ Número consecutivo que identifica cada crédito
$A_j =$ Monto de la j-ésima disposición de crédito
$N =$ Número total de pagos
$k =$ Número consecutivo que identifica cada pago
$B_k =$ Monto del k-ésimo pago
$t_j =$ Intervalo de tiempo, expresado en años y fracciones de año, que transcurre entre la fecha en que surte efecto el contrato y la fecha j-ésima disposición del crédito
$s_k =$ Intervalo de tiempo, expresado en años y fracciones de año, que transcurre entra la fecha que surte efecto el contrato y la fecha del k-ésimo pago
$\sum =$ Símbolo utilizado para expresar la suma de las cantidades indicadas
Notemos que dentro de la ecuación que se acaba de presentar, se está usando el concepto de valor presente en la expresión $(1+i)^{t_j}$, aunque de forma general, la expresión para calcular el CAT, del lado izquierdo considerando la sumatoria, nos permite obtener la sumas del valor presente de las disposiciones del crédito.
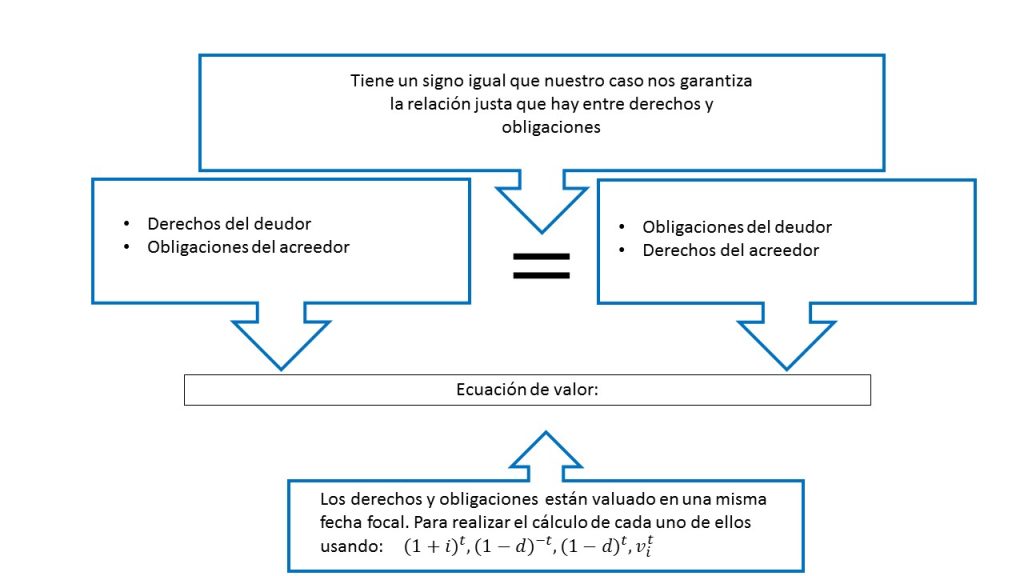
Por otra parte, el lado derecho de la fórmula para calcular el CAT, representa la suma del valor presente de los pagos que se realizaran para liquidar el crédito. Si hacemos un pequeño recordatorio, en general la fórmula que estamos usando, tanto el lado izquierdo como el derecho, ambas en conjunto son una ecuación de valor, concepto que también, fue abordado en su momento, para explicar cómo se realizan las operaciones financieras, es decir, los derechos que tiene el deudor, deben de ser iguales a los del prestamista o acreedor.
Ejercicios resueltos
Para mostrar la forma en que se utiliza la fórmula para calcular el CAT, se propone el siguiente ejemplo3:
Un banco otorga una tarjeta de crédito al señor Luis, por una línea de crédito disponible de \$15,000 pesos, cantidad que el decide gastar, inmediatamente después de haberla recibido. La cantidad de \$15 mil pesos es el valor de $A$ que es una disposición del crédito. Dicho crédito, el señor Luis, considera pagarlo dentro de 2 años, de forma mensual mediante pagos de \$962.33, sin embargo el banco le cobra una comisión por apertura de \$100 pesos.
Solución
Para encontrar le valor de CAT, se hace lo siguiente:
La disposición es $A=15,000$
La expresión anterior la igualamos con los pagos, y nos queda:
$$15000=\frac{100}{(1+i)^{\frac{0}{12}}}+\frac{962.33}{(1+i)^{\frac{1}{12}}}$$
$$+…+\frac{962.33}{(1+i)^{\frac{23}{12}}}+\frac{962.33}{(1+i)^{\frac{24}{12}}}$$
De donde despejando $i$ se obtiene que el Costo Anual Total es de .5736
Expresado como tasa de interés en porcentaje $i=57.4$.
Si a lo anterior, hacemos la sumatoria de cada uno de los pagos, junto con las comisiones, la cantidad total que deberá pagar por dicho crédito, con una tasa CAT del $57.4%$ es de $23,195.85$
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
- Información obtenida de https://www.banxico.org.mx/mercados/d/%7B0DE0044F-662D-09D2-C8B3-4F1A8E43655F%7D.pdf ↩︎
- información obtenida de: https://www.banxico.org.mx/elib/mercado-valores-gub-en/OEBPS/Rsc/anexo0201.pdf ↩︎
- Información obtenida de: https://www.banxico.org.mx/marco-normativo/normativa-emitida-por-el-banco-de-mexico/circular-21-2009/%7B29285862-EDE0-567A-BAFB-D261406641A3%7D.pdf ↩︎