Archivo del Autor: Elsa Fernanda Torres Feria

Geometría analítica I: Aplicaciones a geometría del triángulo

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

En esta entrada usaremos la forma normal de la recta para demostrar dos teoremas conocidos como teoremas de concurrencia de líneas.

Medianas y baricentro

Cerremos la entrada con la enunciación y la demostración del siguiente teorema.

Teorema. Dado un triángulo PQR, sus tres medianas concurren en un punto que divide al segmento dentro del triángulo (de cada mediana) en proporción 1:2.

Demostración.

Para empezar la demostración, construimos un triángulo PQR.

Para construir las medianas, primero localizamos los puntos medios de cada segmento (A, B, C) cuyas coordenadas baricéntricas están dadas por

\begin{align*}
A&=\frac{1}{2}P + \frac{1}{2}Q \\
B&=\frac{1}{2}Q + \frac{1}{2}R \\
C&=\frac{1}{2}R + \frac{1}{2}P \\
\end{align*}

Ya que queremos que se encuentren justo en el punto medio de cada segmento.

Al trazar la mediana del segmento $PQ$ tenemos lo siguiente

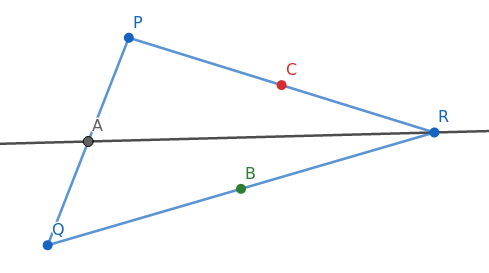
La manera en la que procederemos a partir de ahora, es que localizaremos el punto en el segmento de cada mediana que lo divide en proporción 1:2 esperando llegar a que los tres puntos son el mismo.

Comencemos con el punto $G$ que divide al segmento $AR$ en proporción 1:2, esto es que $G$ sea:

$G=\frac{1}{3}R+\frac{2}{3}A $

AL sustituir el valor de $A$, tenemos como resultado
\begin{align*}
G&=\frac{1}{3}R+\frac{2}{3}\left( \frac{1}{2}P + \frac{1}{2}Q \right) \\
&= \frac{1}{3}R+\frac{1}{3}P+\frac{1}{3}Q \\
\end{align*}

Lo que puede ser replicado para cada segmento. Para el $BP$ se tiene

\begin{align*}
G’ &=\frac{1}{3}P+\frac{2}{3}B \\
&=\frac{1}{3}P+\frac{2}{3} \left( \frac{1}{2}Q + \frac{1}{2}R \right) \\
&= \frac{1}{3}P+\frac{1}{3}Q+\frac{1}{3}R \\
&= \frac{1}{3}R+\frac{1}{3}P+\frac{1}{3}Q \\
\end{align*}

Y para el $CQ$

\begin{align*}
G»&=\frac{1}{3}Q+\frac{2}{3}C \\
&=\frac{1}{3}Q+\frac{2}{3} \left( \frac{1}{2}R + \frac{1}{2}P \right) \\
&= \frac{1}{3}Q+\frac{1}{3}R+\frac{1}{3}P \\
&= \frac{1}{3}R+\frac{1}{3}P+\frac{1}{3}Q \\
\end{align*}

$\therefore$ $G=G’=G»$

Acabamos de demostrar que los puntos que dividen a cada mediana en una proporción 1:2 son el mismo para cada una, por lo que las tres medianas concurren en este punto.

$\square$

A este punto $G$ se le conoce como el baricentro del triángulo, y podrás imaginar después de que discutimos la idea física de estas coordenadas, que $G$ corresponde al centro de masa o punto de equilibrio del triángulo.

Utiliza el siguiente interactivo para asegurarte de que esto es válido con cualquier triángulo, puedes mover los puntos P,Q y R y aún existirá el punto $G$ de intersección de las 3 medianas. Si te da curiosidad, puedes usar la herramienta de distancia de GeoGebra para medir la longitud de cada segmento de la mediana y verificar que efectivamente, está en una relación 1:2 con respecto al punto $G$.

Teoremas de concurrencia

Para poder realizar las demostraciones, definiremos a la altura de un triángulo como la recta que pasa por uno de sus vértices y es ortogonal al lado opuesto. Ahora, enunciemos y demostremos el primer teorema.

Teorema 1. Las alturas de un triángulo son concurrentes.

Demostración

Comencemos esta demostración con un interactivo que ilustre un triángulo y sus alturas.

Las rectas verdes son las alturas del triángulo y en el interactivo es bastante evidente que concurren en un punto y que esto pasa para cualquier triángulo (para comprobarlo puedes mover con tu cursor los vértices para modificar el triángulo). Sin embargo en este curso de geometría analítica, queremos demostrarlo de manera algebraica.

Para esta demostración algebraica, notemos que los vértices del triángulo son $A$, $B$, y $C$ y las alturas asociadas a cada vértice son $a$, $b$ y $c$ respectivamente. Escribamos la forma normal de cada una de estas rectas (alturas). Para $a$ tenemos

$a$ : $(C-B) \cdot x = (C-B) \cdot A$

pues la recta $a$ es ortogonal al lado del triángulo que pasa por los vértices $C$ y $B$, por lo que este lado tiene dirección $(C-B)$ y pasa por el punto $A$. De manera análoga, sabemos que $b$ es perpendicular a la recta que pasa por $A$ y $C$ con dirección $A-C$ y pasa también por el punto $B$, así

$b$ : $(A-C) \cdot x = (A-C) \cdot B$

Y de la misma forma para $c$ tenemos

$c$ : $(B-A) \cdot x = (B-A) \cdot C$

Nota que si sumamos las dos primeras ecuaciones, obtendremos la ecuación negativa de $c$:

\begin{align*}
(C-B) \cdot x + (A-C) \cdot x &= (C-B) \cdot A + (A-C) \cdot B \\
(C-B + A-C) \cdot x & = C \cdot A – B \cdot A + A \cdot B – C \cdot B\\
(-B+A) \cdot x & = C \cdot A – A \cdot B + A \cdot B – C \cdot B\\
(-B+A) \cdot x & = C \cdot A – C \cdot B \\
(-B+A) \cdot x & =(A – B) \cdot C
\end{align*}

Esto es importante, pues si tomamos un elemento en la intersección de las alturas $a$ y $b$ ($x \in a \cap b$), entonces también está en la suma y está última nos da como resultado el negativo de la ecuación de la recta $c$, por lo tanto $x \in c$.

De manera análoga, si sumamos $b$ y $c$ obtenemos

$(B-C) \cdot x = (B- C) \cdot A$

que corresponde a la ecuación negativa de $a$, por lo que si $x \in b \cap c$, entonces $x$ está en la suma de las ecuaciones y por tanto está en $a$.

Para completar la demostración, deberíamos realizar el mismo procedimiento al sumar las ecuaciones de $c$ y $a$ y confirmar que un punto en su intersección está en $b$.

$\therefore$ si dos de las alturas se intersectan, entonces la tercera recta también y en el mismo punto.

$square$

Teorema 2.

Demuestra que las tres mediatrices de un triángulo son concurrentes.

Demostración

Para comenzar la demostración, recordemos que la mediatriz de un segmento es la recta que es ortogonal a este y pasa por su punto medio.

De nuevo, es claro que las tres mediatrices del triángulo con vértices $D$, $E$ y $F$ concurren en un punto. Denominamos a los puntos medios de cada lado como $a$, $b$ y $c$, que es por donde pasan las mediatrices.

Ahora, para comenzar la parte algebraica de la demostración, definamos en su forma normal la primera miediatriz $i$. Siguiendo la idea de la demostración pasada, $i$ es ortogonal a $(E-F)$ y pasa por el punto $a$ por lo que

$i$ : $(E-F) \cdot x = (E-F) \cdot a$

De la misma manera, $j$ es ortogonal a $(D-E)$ y pasa por $b$, así

$j$ : $(D-E) \cdot x = (D-E) \cdot b$

Y para $k$ tenemos

$k$ : $(F-D) \cdot x = (F-D) \cdot c

Sigamos la intuición de la demostración anterior y sumemos las expresiones de $i$ y $j$

\begin{align*}
(E-F) \cdot x + (D-E) \cdot x &= (E-F) \cdot a + (D-E) \cdot b \\
E \cdot x – F \cdot x + D \cdot x – E \cdot x &= E \cdot a – F \cdot a + D \cdot b – E \cdot b \\
D \cdot x- F \cdot x &=E \cdot a – F \cdot a + D \cdot b – E \cdot b
\end{align*}

Para seguir avanzando con nuestra demostración, debemos recordar que $a,$, $b$ y $c$ son los puntos medios de cada lado del triángulo, por lo que podemos expresarlos en términos de los vértices de la siguiente manera

$a=\frac{F+E}{2}$, $b=\frac{E+D}{2}$ Y $c=\frac{D+F}{2}$

Con esto en mente, podemos sustituir $a$ y $b$ en la ecuación anterior y desarrollar

$D \cdot x- F \cdot x = E \cdot \left( \frac{F+E}{2} \right) – F \cdot \left( \frac{F+E}{2} \right) + D \cdot \left( \frac{E+D}{2} \right) – E \cdot \left( \frac{E+D}{2} \right) $

Al realizar todo el desarrollo obtenemos que

$D \cdot x- F \cdot x = \frac{1}{2}( D \cdot D – F \cdot F)$

Ahora, en la demostración pasada queríamos llegar a algún múltiplo de $k$ para demostrar que las 3 rectas se intersectaban, siguiendo con esa lógica, desarrollemos el lado derecho de $k$ tomando en cuenta a $c$ como punto medio de un lado

\begin{align*}
(F-D) \cdot c &= (F-D) \cdot \frac{D+F}{2} \\
&= \frac{1}{2} (F-D) \cdot (D+F) \\
&= \frac{1}{2}(F \cdot D + F \¢dot F – D \cdot D – F \cdot D) \\
&= \frac{1}{2}(F \cdot F – D \cdot D)
\end{align*}

Que es justamente el negativo de lo que obtuvimos arriba, por lo que al sumar las expresiones de $i$ y $j$ obtenemos el negativo de la expresión de $k$. Así, si un punto $x$ está en $ i \cap j$, entonces está en la suma y por lo tanto está en $k$.

El procedimiento es análogo para cada uno de los casos faltantes.

$\square$

Para concluir esta entrada, denotaremos al punto en el que concurren las mediatrices como circuncentro.

Más adelante…

En las próximas entradas discutiremos la forma normal de un elemento geométrico en el espacio $\mathbb{R}^3$ que no será la recta y hablaremos de la norma de un vector, que de cierta manera apareció en nuestras demostraciones pero no lo hemos discutido con formalidad hasta ahora.

Tarea moral

  • Completa los casos faltantes en la demostración del primer teorema.
  • Completa los casos faltantes en la demostración del segundo teorema.
  • Encuentra el circuncentro del triángulo que tiene como vértices los puntos $(5,3)$, $(2,-1)$ y $(8,0)$.

Geometría analítica I: Rectas en forma normal y sus intersecciones

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

En esta nueva entrada analizaremos una nueva forma de la recta, la normal. Se discutió la idea de esta al final de la entrada anterior. Además, como es algo nuevo para nosotros, será conveniente explorar la intersección de rectas partiendo de esta nueva forma.

Ecuación normal de la recta

Iniciemos esta entrada con la definición y un ejemplo de esta nueva ecuación de la recta.

Definición. Una recta en forma normal consiste de tomar un vector $q \in \mathbb{R}^2$, un escalar $c \in \mathbb{R}$ y considerar el conjunto

$l=\{ x \in \mathbb{R}^2 : x \cdot q = c \}$

Ejemplo: Encuentra la forma normal de la recta $l=\{ (2,-1) + r (3,5) : r \in \mathbb{R} \}$.

Por la última proposición vista en la entrada anterior, debemos escribir el conjunto de los vectores $x$ tales que el producto interior con $q$ ortogonal nos de $p \cdot q ^{\perp}$, cuyo resultado es un escalar. Así, obtenemos

\begin{align*}
l&=\{ x \in \mathbb{R}^2 : x \cdot (3,5)^{\perp} = (3,5)^{\perp} \cdot (2,-1) \} \\
&=\{ x \in \mathbb{R}^2 : x \cdot (-5,3) = (-5,3) \cdot (2,-1) \} \\
&=\{ x \in \mathbb{R}^2 : x \cdot (-5,3) = (-5)(2)+3(-1)=-13 \} \\
\end{align*}

Si definimos a $x=(x_1,x_2)$ tal que $x_1, x_2 \in \mathbb{R}$, entonces $(x_1,x_2) \cdot (-5,3)=-5x_1+3x_2$. Así, la forma normal de la recta $l$ está dada por

$l=\{ x_1, x_2 \in \mathbb{R} : -5x_1+3x_2=-13\}$

$\square$

Recordatorio. Hasta ahora hemos hablado de rectas en su forma paramétrica, rectas en su forma baricéntrica y en esta entrada rectas en su forma normal. Es importante resaltar que el término recta es un «espacio geométrico» en el espacio, y al hablar de forma paramétrica, baricéntrica o normal, sólo nos referimos a su expresión algebraica.

Intersección de rectas en su forma normal

Para desarrollar de manera más completa este tema, hablemos de la intersección de rectas cuando están expresadas en su forma normal. Sean las rectas

$l_1=\{ x \in \mathbb{R}^2 : p \cdot x = e\}$

$l_2=\{ x \in \mathbb{R}^2 : q \cdot x = f \}$

donde $c$ y $d$ son números reales, qué debemos hacer para saber primero si se intersectan estas rectas y si pasa,cuál es el punto de intersección.

Aquí, podemos recurrir a lo que vimos en la entrada anterior a cerca del compadre ortogonal. Por como definimos la forma normal de la recta anteriormente, sabemos que $p$ es un vector perpendicular a $l_1$, por lo que el vector director de esta recta es un multiplo de $p^{\perp}$. De la misma manera, la dirección de $l_2$ es un múltiplo de $q^{\perp}$.

El caso más sencillo es cuando la intersección de las rectas es vacía, esto es que sean paralelas, lo cual implicaría que $p^{\perp} \parallel q^{\perp}$ y por lo tanto $p \parallel q$. Además puede pasar que $l_1$ y $l_2$ sean la misma recta, esto sí y sólo si $c=rd$.

El caso que falta es la intersección de las rectas. Para encontrar este punto de intersección, comencemos desarrollando los productos puntos que definen las rectas para así obtener un sistema lineal de ecuaciones. Sea $x=(x,y)$, $p=(a,b)$ y $q=(c,d)$, tenemos que

\begin{cases}
p \cdot x = ax+by=e \\
q \cdot x = cx+dy=f
\end{cases}

Recordemos por lo visto en una entrada anterior que un sistema de ecuaciones así tiene solución única cuando $ad-bc \neq 0$.

Podemos reescribir este sistema de ecuaciones pensando en una igualdad de vectores, es decir entrada a entrada

$x(a,c)+y(b,d)=(e,f)$

Si desarrollas las operaciones e igualas las entradas, verás que es lo mismo que nuestro sistema; sin embargo al escribirlo de esta forma tenemos herramientas que pueden facilitar la solución del sistema. En el camino que exploramos con anterioridad para la solución, eliminábamos cierto término para poder despejar una de las variables… Si ahora queremos eliminar digamos el término con $x$, podemos multiplicar la ecuación vectorial por el vector $(a,c)^{\perp}=(-c,a)$, ya que su producto interior con $(a,c)$ es cero

\begin{align*}
x(a,c) \cdot (-c,a) + y(b,d) \cdot (-c,a)&=(e,f) \cdot (-c,a) \\
\Rightarrow y (b,d) \cdot (-c,a)&=(e,f) \cdot (-c,a) \\
\Rightarrow y (da-bc)&=fa-ec
\end{align*}
Si despejamos a $y$, tenemos

$y=\frac{fa-ec}{da-bc}$

De manera análoga, podemos hacer producto punto con $(b,d)^{\perp}=(-d,b)$ para obtener a $x$

$x=\frac{bf-ed}{bc-ad}$

Recapitulemos para poder concluir. Por como definimos a los vectores usados en este desarrollo, $ax+by=e$ corresponde a la recta en forma normal $l_1$

$l_1=\{ (x,y) \in \mathbb{R}^2 : (a,b) \cdot (x,y) = e\}$

mientras que $cx+dy=f$ está asociada a $l_2$ en su forma normal

$l_2={ (x,y) \in \mathbb{R}^2 : (c,d) \cdot (x,y) = f}$

Como estamos en el caso en el que $l_1$ no es paralela a $l_2$, entonces $(a,b)$ no es paralelo a $(c,d)$, por lo que $ad-bc \neq 0$ y el sistema tiene una única solución ( el punto de intersección):

$(x,y)=\left( \frac{bf-ed}{bc-ad} ,\frac{fa-ec}{da-bc} \right)$

Para $n > 2$

Cerremos está entrada hablando de un plano en su forma normal.

Definición. Un plano en forma normal en $\mathbb{R}^3$ consiste de tomar un vector $q \in \mathbb{R}^3$, un escalar $c \in \mathbb{R}$ y considerar el conjunto

$\Pi=\{ x \in \mathbb{R}^3 : x \cdot q =c \}$

Más adelante…

Todo lo que vamos desarrollando nos es de utilidad más adelante, y esta entrada no será la excepción. Sobre todo cuando hablemos en la siguiente entrada de los teoremas de concurrencia, ya que usaremos la forma normal de la recta para demostrarlos.

Tarea moral

  • Encuentra la forma normal de las siguientes rectas
    • $\{ (1,-1)+t(2,3) : t \in \mathbb{R} \}$
    • ${ (-5,-0)+(6s,-4s) : s \in \mathbb{R} }$
  • Encuentra la forma normal de la recta que pasa por los puntos
    • $(1,-3)$ y $(3,4)$
    • $(2,-4)$ y $(9,5)$
  • Encuentra la intersección de las rectas de los ejercicios anteriores.

Geometría Analítica I: Producto interior y el ortogonal canónico

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

Continuando la conexión con la geometría Euclidiana con la que empezamos, hay un concepto en la geometría analítica que se conecta con la noción de ángulo, la de distancia y la de norma en la primera geometría mencionada, el producto interior. Dentro del contenido de esta entrada esta su definición en una dimensión de $2$ o mayor, ejemplos y sus propiedades. También, se discute el concepto del vector ortogonal canónico, que en conjunción con el producto interior, sirve como herramienta para detectar ciertas características de rectas y vectores.

Producto interior

Abramos esta entrada con la definición de este nuevo concepto.

Definición. Si tenemos dos vectores $u=(u_1,u_2)$ y $v=(v_1,v_2)$ en $\mathbb{R}^2$, el producto interior (o producto punto) en $\mathbb{R}^2$ de $u$ con $v$, está dado por

$u\cdot v := (u_1,u_2) \cdot (v_1,v_2) = u_1v_1 +u_2 v_2$

Esta definición se puede expresar en dimensiones mayores.

Definición. Si tenemos dos vectores $u=(u_1,u_2, \dots, u_n)$ y $v=(v_1,v_2, \dots, v_n)$ en $\mathbb{R}^n$, el producto interior (o producto punto) en $\mathbb{R}^n$ de $u_1$ con $u_2$, está definido como

\begin{align*}
u\cdot v : &= (u_1,u_2, \dots, u_n) \cdot (v_1,v_2, \dots, v_n) \\
&= u_1v_1 +u_2 v_2+u_3 v_3 + \dots + u_n v_n \\
&= \sum _{j=1} ^{n} u_j v_j
\end{align*}

Es importante notar que el resultado del producto interior (que es una operación vectorial), es un escalar.

Ejemplos:

1. Sean los vectores $(5,3)$ y $(2,-4)$ en $\mathbb{R}^2$, el producto interior de estos es

\begin{align*}
(5,3) \cdot (2,-4)&=5(2)+3(-4)\\
&=10-12\\
&=-2
\end{align*}

2. Sean los vectores $(-3,1,-1)$ y $(-6,2,-3)$ en $\mathbb{R}^3$, el producto interior de estos es

\begin{align*}
(-3,1,-1) \cdot (-6,2,-3)&=-3(-6)+1(2)+(-1)(-3)\\
&=18+2+3\\
&=23
\end{align*}

3. Sean los vectores $(1,0,-5,2,0,1)$ y $(0,-6,0,0,2,0)$ en $\mathbb{R}^6$, el resultado de su producto interior es cero, verifica.

Ahora que hemos definido una nueva operación, nos gustaría demostrar algunas propiedades asociadas a esta.

Teorema. Para todos los vectores $u,v,w \in \mathbb{R}^n$ y para todo número $t \in \mathbb{R}$ se cumple que

  1. $u \cdot v = v \cdot u$
  2. $u \cdot (tv)=t(u\cdot v)$
  3. $u \cdot (v + w)= u \cdot v + u \cdot w$
  4. $u \cdot u \geq 0$
  5. $u \cdot u =0 \Leftrightarrow u=(0,0)$

La primera propiedad nos dice que el producto interior es conmutativo; la siguiente que la operación saca escalares; la tercera expresa que esta abre sumas; la cuarta que al hacer el producto interior de un vector consigo mismo, el resultado es siempre mayor o igual a cero la última que la igualdad a cero sólo sucede cuando el vector $u$ es el vector cero.

Demostración

Haremos la demostración para vectores en $\mathbb{R}^2$, (el caso para dimensión $n$ es análogo) y usaremos los axiomas de los números reales.

Para empezar definamos los vectores $u=(u_1,u_2)$, $v=(v_1,v_2)$ y $w=(w_1,w_2)$ en $\mathbb{R}^2$

1. P. D. $u \cdot v = v \cdot u$. Comencemos con la definición y desarrollemos a partir de ella

\begin{align*}
u \cdot v &=(u_1,u_2) \cdot (v_1,v_2)\\
&=u_1v_1+u_2v_2 \\
&=v_1u_1+v_2u_2 \\
&=(v_1,v_2) \cdot (u_1,u_2)\\
&=v \cdot u
\end{align*}

$\therefore$ $u\cdot v= v \cdot u$

2. P.D. $u \cdot (tv)=t(u\cdot v)$

\begin{align*}
u \cdot (tv)&=(u_1,u_2) \cdot t(v_1,v_2) \\
&= (u_1,u_2) \cdot (tv_1,tv_2) \\
&= u_1(tv_1)+u_2(tv_2)\\
&= t(u_1v_1+u_2v_2) \\
&=t(u_1,u_2) \cdot (v_1,v_2)\\
&= t (u \cdot v)
\end{align*}

$\therefore u \cdot (tv)=t(u\cdot v)$

3. P.D. $u \cdot (v + w)= u \cdot v + u \cdot w$

\begin{align*}
u \cdot (v + w)&=(u_1,u_2) \cdot ((v_1,v_2) + (w_1,w_2)) \\
&= (u_1,u_2) \cdot (v_1+w_1,v_2+w_2) \\
&=u_1(v_1+w_1)+u_2(v_2+w_2) \\
&=u_1v_1+u_1w_1+u_2v_2+u_2w_2 \\
&=u_1v_1+u_2v_2+u_1w_1+u_2w_2 \\
&=(u_1v_1+u_2v_2)+(u_1w_1+u_2w_2) \\
&=((u_1,u_2)\cdot(v_1,v_2)) + ((u_1,u_2) \cdot (w_1,w_2)) \\
&= u \cdot v + u \cdot w
\end{align*}

$\therefore$ $u \cdot (v + w)= u \cdot v + u \cdot w$

4 y 5. P.D. $u \cdot u \geq 0$ y $u \cdot u =0 \Leftrightarrow u=(0,0)$

\begin{align*}
u \cdot u&=(u_1,u_2) \cdot (u_1,u_2) \\
&= u_1u_1+u_2u_2\\
&= u_1^2 + u_2^2 \geq 0
\end{align*}

La última relación se da ya que es una suma de números al cuadrado y cada término por sí sólo es mayor o igual a cero.

Resulta que si $u_1 \neq 0$ ó $u_2 \neq 0$, entonces $u_1^2 + u_2^2 > 0$, por lo que el único caso en el que se da la igualdad a cero es cuando $u=(0,0)$.

$\therefore$ $u \cdot u \geq 0$ y $u \cdot u =0 \Leftrightarrow u=(0,0)$

$\square$

Lo usado en esta demostración se restringe a los axiomas de los reales y la definición del producto interior, por lo que aunque no haya mucha descripción, espero que te sea clara.

El ortogonal canónico

Definición. Sea $v=(x,y)$ un vector en $\mathbb{R}^2$, el vector ortogonal canónico a v es el vector

$v^{\perp}=(-y,x)$

Si te das cuenta, esta definición hace referencia a lo que sucede al aplicar el ortogonal a un vector. Además, esta definición define al ortogonal canónico, pero no significa que sea el único vector perpendicular (ortogonal) a $v$.

Antes de definir o probar más cosas relacionadas al ortogonal, hagamos algunas observaciones.

Observación: Si aplicamos 4 veces el ortogonal a un vector $v$, regresamos al mismo vector:


$v^{\perp}=(x,y)^{\perp}=(-y,x)$

$(-y,x)^{\perp}=(-x,-y)$

$(-x,-y)^{\perp}=(y,-x)$

$(y,-x)^{\perp}=(x,y)$

Observación: Para cualquier $v=(x,y) \in \mathbb{R}^2$, tenemos que

$v \cdot v^{\perp} =(a,b) \cdot (-b,a)=a(-b)+b(a)=-ab+ab=0$

Para continuar, usemos el producto interior para definir y probar ciertas cosas con relación al compadre ortogonal.

Definición. Diremos que dos vectores $u,v \in \mathbb{R}^2$ son perpendiculares (ortogonales) si $u \cdot v=0$.

Proposición. Sea $u \in \mathbb{R}^2$ \ ${ 0\}$. Entonces

$\{x \in \mathbb{R}^2 : x \cdot u =0\}=L_{u_{\perp}}:=\{ru^{\perp}: r \in \mathbb{R}\}$

Demostración

Como queremos comprobar una igualdad de conjuntos, hay que probar la doble contención. Comencemos con la contención $\supseteq$.

$\supseteq$ En esta contención, queremos demostrar que cualquier vector de la forma $ru^{\perp}$ es tal que

$(ru^{\perp}) \cdot u=0$

Tomemos un vector de la forma $ru^{\perp}$ con $r \in \mathbb{R}$ y notemos que gracias a la segunda propiedad del producto interior se cumple que

$(ru^{\perp}) \cdot u = r(u^{\perp} \cdot u)= r(0)=0 $

Esto es suficiente para la demostración de la primera contención, pues hemos probado que el producto interior de cualquier vector de la forma $ru^{\perp}$ con $u$ es cero.

$\subseteq$ Para esta contención, queremos demostrar que los vectores $x$ que cumplen $x \cdot u =0$, son de la forma $x=r u^{\perp}$. Para esto, tomemos un vector $x=(r,s)$ que cumpla la primera condición y expresemos al vector $u$ con sus coordenadas $u=(u_1,u_2)$. Al realizar el producto interior obtenemos

$x \cdot u=(r,s) \cdot (u_1,u_2)=ru_1+su_2=0 $

$\Rightarrow ru_1= -su_2 \cdots (a) $

Dado que $u \neq (0,0)$, al menos una de sus entradas es distinta de cero. Supongamos que $u_1 \neq 0$, entonces podemos despejar $r$

$r=\frac{-su_2}{u_1}$

Podemos sustituir este valor en $x$ y desarrollar para obtener

\begin{align*}
x=(r,s)&=\left( \frac{-su_2}{u_1},s \right)=s\left( \frac{-u_2}{u_1}, 1 \right) \\
&=s \left( \frac{-u_2}{u_1}, \frac{u_1}{u_1} \right) \\
&=\frac{s}{u_1} \left( -u_2, u_1 \right)
\end{align*}

Y ya está el primer caso, pues sabemos que $u^{\perp}=( -u_2, u_1)$.

Así, $x \in \mathbb{R}^2$ tal que $x \cdot u=0$, es de la forma $ru^{\perp}$, con r un escalar.

En el caso en el que $u_2 \neq 0$, tenemos algo análogo. A partir de $(a)$ podemos despejar $s$

$ ru_1= -su_2$

$s=\frac{-ru_1}{u_2}$

Al sustituir en $x$ y desarrollar obtendremos que

$x=\frac{r}{-u_2}(-u_2,u_1)$

$\square$

Aplicaciones del producto punto

Para cerrar esta entrada, usemos el producto interior para describir algunas características de las rectas y vectores.

Definición. Diremos que dos líneas $l_1$ y $l_2$ son perpendiculares si al escribirlas en forma paramétrica

$l_1=\{ p_1+rq_1 : r \in \mathbb{R} \}$

$l_2=\{ p_2+rq_2 : r \in \mathbb{R} \}$

se tiene que $q_1 \cdot q_2 =0$, esto es si sus vectores dirección son ortogonales.

Proposición. Dos vectores $u$ y $v$ son paralelos si y sólo si $u$ y $v^{\perp}$ son ortogonales, es decir si $u \cdot v^{\perp}=0$.

Demostración

Ida ($\Rightarrow$). Si $u$ y $v$ son paralelos, por definición $u=cv$ con $c \in \mathbb{R}$. Como queremos que $u$ y $v^{\perp}$ sean ortogonales, realicemos su producto interior y utilicemos las propiedades de este para desarrollar

\begin{align*}
u \cdot v^{\perp}&=(cv) \cdot v^{\perp} \\
&=c(v \cdot v^{\perp}) \\
&=c(0)=0
\end{align*}

Por lo que $u$ y $v^{\perp}$ son ortogonales.

Regreso ($\Leftarrow$). Si ahora suponemos que $u$ y $v^{\perp}$ son ortogonales, pasa que

$u \cdot v^{\perp}=0$

Pero por lo visto en la proposición de la sección anterior, esto sólo pasa cuando $u=c(v^{\perp})^{\perp}$ para algún $c \in \mathbb{R}$. Si $v=(v_1,v_2)$ esto se desarrolla como

\begin{align*}
u&=c(v^{\perp})^{\perp}=c(-v_2,v_1)^{\perp}\\
&=c(-v_1,-v_2)\\
&= -cv
\end{align*}

$\therefore$ por definición de paralelismo, $u$ y $v$ son paralelos.

$\square$

Otra cosa útil del producto punto, es que cualquier recta se puede escribir en términos de este. Precisemos esto en la siguiente proposición.

Proposición. Sea la recta $l$ en su forma paramétrica

$l=\{p+rq : r \in \mathbb{R}\}$

La recta $l$ se puede escribir usando el producto punto de la siguiente manera

$l=\{x \in \mathbb{R} ^2 : q^{\perp} \cdot x=q^{\perp} \cdot p \}$

Antes de adentrarnos en la demostración, hablemos un poco de qué significa esta proposición con ayuda del siguiente interactivo aclarando que $qT$ es el vector $q{^\perp}$.

Al definir $qT$ como el vector perpendicular a la recta, tenemos que $q$ es el vector director de esta; $p$ es el punto por el que pasa la recta y $x$ representa a los puntos en ella. Como $p$ y $qt$ son fijos, entonces $qT \cdot p$ es un número constante. Si tú mueves $x$ a lo largo de la recta, veras que el producto punto $qT \cdot x$ al cual denominamos como $a$ en GeoGebra, no varia.

Es así como expresamos la recta por medio del producto punto; el conjunto de todas los $x \in \mathbb{R}^2$ tal que el producto punto con $q^{\perp}$ ($qT$ en el interactivo) es igual a $q^{\perp} \cdot p$.

Con esto claro, procedamos a la demostración.

Demostración

Como queremos demostrar que $l$ en su forma paramétrica es el mismo conjunto que el descrito por el producto punto, tenemos que explorar las dos contenciones de los conjuntos.

$\supseteq$ Tomemos $x \in \mathbb{R}^2$ tal que $q^{\perp}\cdot x =q^{\perp}\cdot p$. De esta igualdad se tiene que

\begin{align*}
0 &= q^{\perp}\cdot x – q^{\perp}\cdot p\\
&=q^{\perp}\cdot (x-p)\\
& \Rightarrow q^{\perp}\cdot (x-p) =0
\end{align*}

Dada la última igualdad, sabemos (por la primera proposición de esta entrada) que $x-p$ debe ser un múltiplo de $(q^{\perp})^{\perp}=-q$ y por lo tanto un múltiplo de $q$; por lo que para algún $s \in \mathbb{R}$ se tiene que

\begin{align*}
x-p&=sq\\
\Rightarrow x&=p+sq
\end{align*}

$\subseteq$ Ahora partamos de un punto $x=p+rq \in$ $l$ y desarrollemos su producto punto con $q^{\perp}$ para finalizar esta demostración

\begin{align*}
q^{\perp} \cdot x &= q^{\perp} \cdot (p+rq)\\
&=(q^{\perp} \cdot p) + (q^{\perp} \cdot (rq)) \\
&= q^{\perp} \cdot p
\end{align*}

Donde la última igualdad se da gracias a que $q^{\perp} \cdot (rq)=r(q^{\perp} \cdot q)=0$.

$\therefore$ Partiendo la expresión paramétrica de la recta está contenida en la expresión con producto punto y viceversa y por lo tanto son el mismo conjunto (la misma recta).

$\square$

Más adelante…

El producto interior fungirá como herramienta para establecer las nociones de distancia y ángulo en las siguientes entradas y particularmente para definir la forma normal de la recta en la siguiente entrada.

Tarea moral

  • Completa los pocos pasos que omitimos en cada demostración o ejemplo.
  • Demuestra el teorema de las propiedades del producto interior para $n=3$.
  • Calcula el producto interior de los siguientes vectores:
    • $(4,-1)$ y $(7,2)$
    • $(-2,3,0)$ y $(4,-6,0)$
    • $(-2,3,0)$ y $(-2)(-2,3,0)$
    • $(5,0,-3,0,0)$ y $(0,4,0,-2,1)$
  • Usando la definición del producto interior, demuestra que dado $ u \in \mathbb{R}^2$ se tiene que

$u \cdot x =0$, $\forall x\in \mathbb{R}^2$

si y sólo si $u=(0,0)$.

  • Demuestra que para todos los vectores $ u \text{, }v \in \mathbb{R}^2$ y $\forall t \in \mathbb{R}$, se cumple que
    1. $(u+v)^{\perp}=u^{\perp}+v^{\perp}$
    2. $(tu^{\perp})=t(u^{\perp})$
    3. $u^{\perp} \cdot v^{\perp}=u \cdot v$
    4. $u^{\perp} \cdot v = -(u \cdot v^{\perp})$

Geometría Analítica I: Rectas paralelas e intersección de rectas

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

En entradas anteriores hemos definido las rectas en formas distintas y hemos realizado algunos ejercicios. El siguiente paso en nuestro curso es definir la noción de paralelismo y su relación con la intersección de rectas. Buscamos esto ya que no hay que olvidar que uno de nuestros objetivos más importantes es ver que desde nuestro modelo analítico podemos recuperar los postulados euclideanos.

Comenzaremos enunciando las nociones básicas de paralelismo. Luego hablaremos de intersección de rectas. De manera intuitiva, podemos imaginar que el punto de intersección de dos rectas es aquel que cumple con la ecuación de cada una al mismo tiempo ; esta idea será nuestra guía para desarrollar la teoría. Una vez que hayamos razonado este tema, volveremos para concluir la parte de paralelismo.

Paralelismo

Comencemos con la siguiente definición.

Definición. Dos rectas $l_1$ y $l_2$ $\in \mathbb{R}^2$ son paralelas si o bien son la misma, o bien no se intersectan, esto es que

$l_1 \cap l_2 = \emptyset,$

en donde $\emptyset$ denota al conjunto vacío. En símbolos, escribiremos $l_1 \parallel l_2$.

También es posible dar una definición de paralelismo para vectores.

Definición. Dados dos vectores $u,v \in \mathbb{R}^2$ distintos de $0$, decimos que $u$ es paralelo a $v$ si existe un número real $t$ tal que

$u=tv$

En símbolos, escribiremos $u \parallel v$.

Estas nociones parecen distintas, sin embargo hay un resultado crucial que las conecta: dos rectas serán paralelas si y sólo si al escribirlas en forma paramétrica tenemos que sus vectores dirección son paralelos. Aún no tenemos la teoría suficiente para demostrar este resultado por completo, pero ya podemos demostrar una parte.

Lema. Tomemos dos rectas con las siguientes expresiones en forma paramétrica:

$l=\{ p+rq : r \in \mathbb{R} \}$ y $m= \{ u+sv : r \in \mathbb{R} \}.$

Si $q$ y $v$ son paralelos, entonces las rectas son paralelas.

Demostración. Comencemos suponiendo que los vectores son paralelos por lo que debemos demostrar que $l\cap m =\emptyset$.

Si $q$ y $v$ son paralelos, entonces existe un $t \in \mathbb{R}$ tal que $q=tv$. Supongamos que la intersección de $l$ y $m$ es no vacía. Para ver que son paralelas debemos probar entonces que son la misma. Un punto en ambas nos daría la igualdad $$u+sv=p+rq$$ para algunos valores de $s$ y $r$.

Recordemos que por hipótesis $q=tv$, por lo que al sustituir este valor en la igualdad anterior tenemos $$u+sv=p+r(tv),$$ de donde $$u-p=rtv-sv.$$

Al despejar $p$ tenemos que

\begin{align*}
p&=u-rtv+sv \\
&=u-(rt-s)v
\end{align*}

Al sustituir $p$ y $q$ en la definición de la recta $l$ obtenemos que

\begin{align*}
l&=\{ ((u-v(rt-s))+r(tv) : r,s,t \in \mathbb{R} \} \\
&=\{ u-rtv+sv+rtv : r,s,t \in \mathbb{R} \} \\
&= \{ u+sv-rtv+rtv : r,s,t \in \mathbb{R} \} \\
&= \{ u+sv : s \in \mathbb{R} \}\\
&= m.
\end{align*}

De esta manera, obtenemos que $l=m$, como queríamos.

$\square$

Intersección de rectas

De manera intuitiva sabemos que dos rectas no paralelas se intersectan en un punto. En esta parte de la entrada, queremos encontrar ese punto.

Antes de estudiar el procedimiento general, realicemos un ejemplo para obtener una visión de lo que nos espera.

Ejemplo:

Tomemos dos rectas en su forma paramétrica dadas por

$l_1=\{ (2,-8)+r(7,-3) : r \in \mathbb{R} \}, \text{ } l_2={ (7,-4)+s(1,2) : s \in \mathbb{R} }$

Nuestro objetivo en este ejemplo es encontrar el punto $p$ en el cual $l_1$ y $l_2$ se intersectan, esto es el punto que cumpla ambas ecuaciones

\begin{align*}
(2,-8)+r(7,-3)&=p=(7,-4)+s(1,2) \\
\Rightarrow 2,-8)+r(7,-3)&=(7,-4)+s(1,2)
\end{align*}

Al juntar los términos que contienen un parámetro de un lado del igual y aquellos que son puntos definidos del otro y desarrollar obtenemos

\begin{align*}
(2,-8)-(7,-4)&=s(1,2)-r(7,-3) \\
\Leftrightarrow (2-7,-8+4)&=(s-7r,2s+3r) \\
\Leftrightarrow (-5,-4)&=(s-7r,2s+3r)
\end{align*}

Dado que son vectores que queremos sean iguales, entonces deben ser iguales entrada a entrada; por lo que tenemos un sistema de ecuaciones

\begin{cases}
-5=s-7r \dots (a)\\
-4=2s+3r \dots (b)
\end{cases}

Afortunadamente, ya sabemos como resolver sistemas de ecuaciones. En este caso en especial, podemos multiplicar la ecuación $a$ por $-2$ para obtener $10=-2s+14r$ y sumar este resultado a la ecuación $b$:

\begin{align*}
10&=-2s+14r\\
-4&=2s+3r \\
\hline
6&=17r
\end{align*}

$\Rightarrow r=\frac{6}{17}$

Ya que obtuvimos el valor de $r$, podemos sustituirlo en alguna de las ecuaciones principales para obtener $s$ y obtenemos su valor

$s=\frac{-43}{17}$

Usando cualquiera de los dos valores, encontramos que el punto de intersección es

$(2,-8+\frac{6}{17}(7,-3)\approx (4.4705,-9.0588)\approx (7,-4)+\frac{-43}{17}(1,2)$

Procedimiento general

Usemos como base el ejemplo pasado para establecer un procedimiento general para encontrar el punto de intersección de dos rectas.

Comencemos con las rectas

$l_1={ (p_1,p_2)+r(q_1,q_2) : r \in \mathbb{R} }, \text{ } l_2={ (u_1,u_2)+s(v_1,v_2) : s \in \mathbb{R} }$

Con base en el ejemplo, el siguiente paso es establecer un punto digamos $w$ que cumpla ambas ecuaciones

\begin{align*}
(p_1,p_2)+r(q_1,q_2)&=w=(u_1,u_2)+s(v_1,v_2) \\
(p_1,p_2)+r(q_1,q_2)&=(u_1,u_2)+s(v_1,v_2)
\end{align*}

Colocamos de un lado del igual los elementos que se multiplican por un parámetro y lo demás del otro lado y desarrollamos

\begin{align*}
r(q_1,q_2)-s(v_1,v_2)&=(u_1,u_2)-(p_1,p_2) \\
(rq_1-sv_1,rq_2-sv_2)&=(u_1-p_1,u_2-p_2)
\end{align*}

Como tenemos la igualdad de dos vectores, deben ser iguales entrada a entrada, esto es

\begin{cases}
rq_1-sv_1= u_1-p_1 \dots (a)\\
rq_2-sv_2= u_2-p_2 \dots (b)
\end{cases}

En este punto, debemos solucionar el sistema de ecuaciones de manera general, para lo cual multiplicaremos $(a)$ por $q_2$ y $(b)$ opr $q_1$ y restaremos las expresiones resultantes

\begin{align*}
rq_1q_2-sv_1q_2&=u_1q_2-p_1q_2 \\
rq_2q_1-sv_2q_1&=u_2q_1-p_2q_1\\
\hline
sv_2q_1-sv_1q_2&=u_1q_2-p_1q_2-u_2q_1+p_2q_1
\end{align*}
A partir de esta última expresión podemos despejar el parámetro $s$ para obtener

$s=\frac{u_1q_2-p_1q_2-u_2q_1+p_2q_1}{v_2q_1-v_1q_2}$

Notemos que $s$ se puede indefinir si $v_2q_1-v_1q_2=0$, esto es que

$v_2q_1=v_1q_2$

pero la única manera de que esto suceda es si $l_1 \parallel l_2$, que no es el caso que estamos tratando. Por lo tanto, el sistema siempre tiene solución. Así, el punto de intersección $w$ está dado por

\begin{align*}
w&=(u_1,u_2)+s(v_1,v_2) \\
&=(u_1,u_2)+\frac{u_1q_2-p_1q_2-u_2q_1+p_2q_1}{v_2q_1-v_1q_2}(v_1,v_2)
\end{align*}

Es posible encontrar el punto $w$ al encontrar el valor del parámetro $r$ y es de manera análoga a lo que acabamos de realizar.

Recapitulemos ligeramente lo que acaba de pasar, pues acabamos de demostrar la parte faltante del lema enunciado en la sección de paralelismo. Por lo descrito arriba, resulta que si las rectas son paralelas, entonces no hay un punto de intersección, esto es que el sistema de ecuaciones no tiene solución, pero esto pasa solamente si los vectores son paralelos.

$\square$

Podemos enunciar esto último como el lema que es el «regreso» del lema de la sección anterior.

Lema. Si los vectores directores de dos rectas en su forma paramétrica no son paralelos, entonces las rectas se intersectan en un único punto.

El quinto postulado

Concluyamos esta entrada con la demostración del quinto postulado.

Teorema. Dada una recta $l \in \mathbb{R}^2$ y un punto $P$ fuera de ella, siempre existe una única recta $m$ que pasa por $P$ y es paralela a $l$.

Demostración. Escribamos a la recta $l$ en forma paramétrica:

$l=\{ U+rV : r \in \mathbb{R} \}.$

Proponemos a la recta

$m=\{ P+rV : r \in \mathbb{R} \}.$

como una recta que pasa por $P$ y es paralela a $l$. Por como $m$ está definida, esta recta cumple que pasa por $P$ (tomando $r=0$). Además, sabemos que $1\dot V=V$, por lo que (por definición de vectores paralelos) $V$ es paralelo a $V$ y esto implica que $m$ es paralela a $l$ (por el lema).

De esta manera, logramos construir una recta por $P$ y paralela a $l$.

Para demostrar la unicidad, supongamos que hay otra recta $m’$ paralela a $l$ y que pasa por $P$. Como $m’$ es paralela a $l$ y $l$ es paralela a $m$, tenemos que $m’$ es paralela a $m$ (ver Tarea Moral). Dos rectas son paralelas o bien si no se intersectan, o bien si son iguales. Como $m’$ y $m$ tienen ambas al punto $P$ debe sucede lo segundo, es decir, que sean iguales.

$\square$

Más adelante…

En esta entrada tratamos la intersección de rectas en su forma paramétrica. Conforme avancemos en el curso, hablaremos de las rectas en otras formas a partir de las cuales también nos será posible encontrar su intersección. Hasta ahora hemos demostrado los postulados 1, 3 y 5. Necesitamos algunas definiciones y teoría adicional para poder demostrar los postulados 2 y 4.

Tarea moral

  • Demuestra que «ser paralela a» es una relación de equivalencia entre rectas. Demuestra que «ser paralelo a» es una relación de equivalencia entre vectores.
  • En el desarrollo general para encontrar la intersección de dos rectas, existe un caso en el que el sistema de ecuaciones no tiene solución, esto es cuando $v_2q_1-v_1q_2=0$. Justifica porqué este caso no es posible a partir de las hipótesis dadas.
  • Encuentra el parámetro $r$ en la sección antes mencionada, para encontrar a $w$ en términos de la otra recta.
  • Encuentra las intersecciones de cada pareja de las siguientes las rectas
    • $l_1=\{ (3,2)+t(2,0) : t \in \mathbb{R} \}$
    • $l_2=\{ (5,1)+s(-4,3) : s \in \mathbb{R} \}$
    • $l_3=\{ (-6,-1)+r(0,-7) : r \in \mathbb{R} \}$
  • Prueba que las rectas $l=\{(-1,5)+t(4,-2) : t \in \mathbb{R}\}$ y $m=\{ (0,2)+s(-20,10) : s \in \mathbb{R} \}$ son paralelas.

Geometría Analítica I: Aplicaciones a más dimensiones

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

Hasta ahora, describimos la recta de distintas maneras en el espacio $\mathbb{R}^2$. A partir de esto, es posible ampliar esas definiciones de recta al espacio $\mathbb{R}^n$, en especial a $\mathbb{R}^3$. Para este último caso, de manera escrita lo único que tendríamos que hacer sería establecer los puntos que definen a la recta dentro de $\mathbb{R}^3$; en la parte geométrica, estamos agregando una dimensión más al graficar, por lo que tenemos más opciones aún.

En esta entrada ampliaremos esas definiciones de recta al espacio vectorial $\mathbb{R}^3$ y el siguiente paso será definir el plano en este mismo espacio a partir de las definiciones mencionadas al inicio de este párrafo.

Rectas en $\mathbb{R}^3$

Comencemos esta entrada redefiniendo la recta en el espacio $\mathbb{R}^3$ a partir de las dos definiciones que tenemos de este elemento hasta ahora.

Definición. Una recta en forma paramétrica en $\mathbb{R}^3$ consiste de tomar un punto $P \in \mathbb{R}^3$ y otro punto (o vector) dirección $Q \in \mathbb{R}^3$ y considerar el conjunto

$L=\{ P+rQ : r \in \mathbb{R} \}$

Definición. Una recta en forma baricéntrica en $\mathbb{R}^3$ consta de tomar puntos distintos $P$ y $Q$ $\in \mathbb{R}^3$ y considerar al conjunto

$L=\{ rP+sQ : r,s \in \mathbb{R}, r+s=1 \}$

En el siguiente interactivo ponle Play a los delizadores para comprender mejor estas dos definiciones de recta en el espacio. Nota que $C$ es la definición paramétrica de la recta, cuyo parámetro es $a$; mientras que $F$ es la recta en forma baricéntrica que pasa por los puntos $A$ y $E$.

Si bien los deslizadores en este interactivo sólo corren de$-2$ a $2$, recuerda que tanto $a$ como $b$ $\in \mathbb{R}$.

En esta entrada comenzamos generalizando las definiciones de recta al espacio $\mathbb{R}^3. Por lo que (siguiendo esta lógica), el siguiente paso es plantear y trabajar la idea de un plano en el espacio.

Plano en forma paramétrica

Si el considerar un punto en $\mathbb{R}^3$ al cual se le suman múltiplos de un punto director (también en $\mathbb{R}^3$) obtenemos una recta en este espacio, ¿entonces qué necesitamos para describir un plano en el espacio?

Definición. Un plano en forma paramétrica en $\mathbb{R}^3$ consiste de tomar un punto $P \in \mathbb{R}^3$ y dos puntos dirección $Q, R \in \mathbb{R}^3$ y considerar el conjunto

$\Pi = \{ P+rQ+sR : r,s \in\mathbb{R} \}$

Para continuar, analicemos esta definición por partes con ayuda de lo que hemos descrito hasta ahora en esta entrada. Al tomar $r$ fijo en la parte de la definición dada por $rQ+sR$, obtenemos una recta que pasa por $rQ$ con dirección $R$; . De manera análoga, al tomar $s$ fijo, obtenemos una recta que para por $sR$ y tiene dirección $Q$.

Tomando a $Q=(-2,5,1)$ y a $R=(3,4,5)$ como ejemplo, usa los deslizadores en el siguiente interactivo para notar qué pasa cuando fusionas las dos ideas que acabamos de discutir, al establecer un punto $C=rQ+sR$ (con $r$ y $s$ en $\mathbb{R}$).

Ojalá hayas notado que al dejar correr ambos deslizadores, el rastro del punto $C$ describe un plano que claro pasa por $Q$ y $R$, pero pasa por otro punto definido más. Dentro del mismo interactivo, utiliza la herramienta Plano por tres puntos para definir el plano del que hablamos; deja correr los deslizadores y confirma con esto que el rastro de $C$ es este plano.

Para continuar con nuestro análisis, agreguemos la parte faltante al conjunto $\Pi$, el punto $P$. Ojalá recuerdes que en la descripción paramétrica de una recta, el punto que no tiene un parámetro multiplicando es el punto por el que pasa la recta, si ese punto no está, significa que la recta pasa por el origen. Esta idea se repite análogamente en el caso del plano.

En el análisis que acabamos de realizar, el plano descrito por $rQ+sR$, es el plano que tiene como dirección a $Q$ y a $R$ y además pasa por el origen. Al agregar $P$ a la expresión, lo que se obtiene es un plano paralelo al descrito anteriormente, pero esta vez pasa por $P$, es decir, a cada punto del plano $rQ+sR$ se le sumará el punto fijo $P$.

Plano en forma baricéntrica

Continuemos con la lógica que hemos seguido hasta ahora, con lo cual el siguiente paso es definir el plano en forma baricéntrica.

Definición. Un plano en forma baricéntrica en $\mathbb{R}^3$ consta de tomar los puntos $P$, $Q$, y $R$ y considerar el conjunto

$\Pi= \{ pP+qQ+rR : p,q,r \in \mathbb{R}$ y $p+q+r=1 \}$

Al definir el plano de esta manera, lo que debes imaginar es algo distinto a la primera definición que establecimos. Piensa a $\Pi$ como un plano que pasa por los puntos $P$, $Q$ y $R$.

El siguiente interactivo sólo es la ilustración de un plano en su forma baricéntrica.

Ahora que ya definimos de maneras distintas el plano en el espacio, lo más natural sería encontrar la equivalencia entre estas dos definiciones así como lo vimos al hablar de la recta, sólo que en este caso lo formalizaremos con una proposición.

Relación entre las expresiones de un plano

Proposición. Todo plano en forma paramétrica puede expresarse en forma baricéntrica y viceversa.

Lo que nos gustaría hacer para la demostración, sería mostrar que siempre se pueden encontrar $P’$, $Q’$ y $R’$ con los cuales se puede definir un plano en forma baricéntrica de tal manera que ese conjunto sea el mismo que el conjunto que define a un plano en forma paramétrica.

Demostración.

Parte 1: Partamos de un plano en su forma paramétrica al tomar $P,Q,R \in \mathbb{R}^3$ tal que

$\Pi=\{ P+rQ+sR :r,s \in \mathbb{R} \}$

En esta parte de la demostración, nuestro objetivo es encontrar tres puntos en $\Pi$ muy específicos con los cuales podemos describir el mismo plano pero en su forma baricéntrica.

Por lo anterior y yendo directo al grano, busquemos dos puntos en el plano. Si bien podemos escoger cualesquiera valores de $r$ y $s$ para determinar ciertos puntos en el plano, facilitaremos el álgebra al escoger casos particulares de valores para $r$ y $s$ y así obtener tres puntos «prácticos» en el plano que nos servirán para la forma baricéntrica de este. Los valores de los parámetros no serán tomados de manera aleatoria. Por lo que discutimos anteriormente, podemos definir ciertos puntos (en nuestra demostración $P$’, $Q$’ y $R$’) como combinaciones lineales puntuales de $P$, $Q$, $R$.

  1. El caso más sencillo es tomar $r=s=0$ y así obtener el punto $P$’$=P \in \Pi$.
  2. Si ahora $r=0$ y $s=1$, tenemos $R$’$=P+R$.
  3. Y si $r=1$ y $s=0$, obtenemos $Q$’$=P+Q$.

Ya que tenemos estos 3 puntos en $\Pi$, podemos definir el plano en su forma baricéntrica:

$\Pi$’$=\{pP$’$+qQ$’$+rR$’$ : p,q,r \in \mathbb{R}\}$

Para continuar, afirmamos que $\Pi=\Pi$’, y para comprobarlo, tenemos que checar que cada elemento en $\Pi$, está en $\Pi$’. La manera más sencilla de hacerlo, es tomar un elemento genérico de $\Pi$ (i.e. un elemento que «represente» a todos) y mostrar que está en $\Pi$’.

Tomemos un elemento de $\Pi$, es decir un vector de la forma $P+rQ+sR$.

Por Demostrar: Existen $a,b,c \in \mathbb{R}$, tales que $a+b+c=1$ y además

$P+rQ+sR=aP$’$+bQ$’$+cR$’

Encontremos entonces los valores de $a$,$b$, $c$.

Al sustituir los elementos primados, tenemos

\begin{align*}
P+rQ+sR&=aP+b(P+Q)+c(P+R) \\
&=aP+bP+bQ+cP+cR\\
&=(a+b+c)P+bQ+cR
\end{align*}

$\Rightarrow P+rQ+sR= (a+b+c)P+bQ+cR$

La igualdad nos lleva a un sistema de ecuaciones a partir del cual podremos obtener los valores de $a$, $b$, y $c$ para que esta se cumpla

\begin{align*}
a+b+c&=1 \\
b&=r \\
c&=s
\end{align*}

La primera condición ya cumple algo que queríamos y además, podemos despejar a $a=1-b-c$, que gracias a las otras igualdades que tenemos, conocemos su valor en términos de $r$ y $s$

$a=1-r-s$

Por lo que

$P+rQ+sR=(1-r-s)P+r(P+Q)+s(P+R)$

tal que $(1-r-s)+r+s=1$.

Hasta aquí, lo que hemos demostrado es que cualquier elemento en $\Pi$ lo podemos escribir como un elemento en $\Pi$’, esto es que $\Pi \subseteq Pi$’. Lo que sigue es realizar el camino contrario.

Ahora, lo que queremos es demostrar que $\Pi$’$\subseteq Pi$; para lo cual partiremos de un elemento en $\Pi$’ y buscaremos llegar a un elemento en $\Pi$.

Tomemos un elemento en $\Pi’$, esto es que es de la forma

$aP$’$+bQ$’$+cR$’$=aP+b(P+Q)+c(P+R)$

con $a+b+c=1$. Por medio de álgebra, queremos llegar a una expresión que represente un elemento de $\Pi$

\begin{align*}
aP+b(P+Q)+c(P+R) &= \\
&=aP+bP+bQ+cP+Cr \\
&=(a+b+c)P+bQ+cR \\
\end{align*}

Pero por hipótesis, $a+b+c=1$, por lo que

$=P+bQ+cR$

que efectivamente está en $\Pi$, pues es un elemento de la forma $P+rQ+sR$. Por lo que $\Pi$’ $\subseteq \Pi$.

$\therefore$ $\Pi \subseteq \Pi$’ y $\Pi$’ $\subseteq Pi$, entonces $\Pi=\Pi$’. Nota que concluimos esto partiendo de un plano en su forma paramétrica y al hacer el caso de la forma baricéntrica, utilizamos los puntos definidos a partir de la primera forma mencionada.

Parte 2. Para la parte 2, sólo te dare algunos consejos para que completes la demostración, pues es bastante parecida a lo que hicimos en la parte 1. Primero, tienes que partir del plano en su forma baricéntrica, es decir

$\Pi=\{ pP+qQ+rR : p+q+r=1 \text{ con }p,q,r \in \mathbb{R} \}$

Y buscar los puntos $P$’, $Q$’ y $R$’ tales que al tomar $P$’ como punto base y $Q$’ y $R$’ como direcciones, obtengas que $\Pi=\Pi’$.

Si realizas el procedimiento de la manera correcta, llegarás a que los puntos son :

\begin{align*}
P&=P’ \\
Q’&=Q-P \\
R’&=R-P
\end{align*}

Al completar esta segunda parte, entonces la demostración estará completa.

$\square$

Dimensiones mayores a 3

Para cerrar esta entrada, enunciaremos algunas definiciones que nos ayudarán en un futuro a definir cosas más complejas.

Definición. Sean $u_1$, $u_2$, $\dots$, $u_k$ puntos en $\mathbb{R}^n$. Sean $s_1$, $s_2$, $\dots$, $s_k$ números reales. A una expresión de la forma

$s_1u_2+s_2u_2+\dots+s_ku_k$

le llamamos una combinación lineal de $u_1$, $u_2$, $\dots$ $u_k$.

Ejemplo: Sea el espacio $\mathbb{R}^5$, una combinación lineal en este es

$-5(3,1,0,-2,7)+2(-3,6,8,1,9)+(-3)(3,9,0,-1,-2)$

Definición. A una combinación lineal en donde los coeficientes suman $1$, le llamamos una combinación afín. Esto es que

$s_1+s_2+\dots+s_k=1$

Ejemplo: La combinación del ejemplo anterior no es afín, pues

$-5+2+(-3)=-5+2-3=-8+2=-6 \neq 1$

Sin embargo, podemos obtener una combinación afín con los mismos vectores.

$-4(3,1,0,-2,7)+2(-3,6,8,1,9)+3(3,9,0,-1,-2)$

Es una combinación afín, pues

$-4+2+3=-4+5=1$

Definición. Al conjunto de todas las combinaciones lineales de ciertos vectores dados $u_1$, $u_2$, $\dots$ $u_k$ $\in \mathbb{R}^n$ se le conoce como el subespacio generado por $u_1$, $u_2$, $\dots$ $u_k$ y lo denotamos como

$\braket{u_1, u_2, \dots, u_k}$

esto es

$\braket{u_1, u_2, \dots, u_k}=\{ s_1u_2+s_2u_2+\dots+s_ku_k : s_1, \dots, s_k \in \mathbb{R} \}$

Veamos dos ejemplos de esta definición.

Ejemplo 1: Sea $v_1 \in \mathbb{R}^2$, $v_1 \neq 0$, el espacio generado por este vector es

$\braket{v_1}=\{ s_1v_1 : s_1 \in \mathbb{R} \}$

Ejemplo 2: Sea $v_1, v_2 \in \mathbb{R}^2$, $v_1 \neq 0$ y $v_2 \neq 0$, el espacio generado es

$\braket{v_1,v_2} = \{s_1v_1+s_2v_2 : s_1, s_2 \in \mathbb{R}\}$

Cerremos esta entrada con una última definición y su respectivo ejemplo.

Definición. Si $A$ es un subconjunto de $\mathbb{R}^n$y $p$ es un vector en $\mathbb{R}^n$, entonces el traslado de $A$ por el vector $p$ es el conjunto

$A+p=p+A= \{ x+p : x \in A \}$

Esta última definición nos es de utilidad para pasar de una recta o un plano que pasa por el origen a otro que pasa por cualquier punto $p$.

Ejemplo: Sea $\Pi=\{r(5,3,2)+s(-1,7,0): s,r \in mathbb{R}$ el plano que pasa por el origen y que tiene como vectores directores a $(5,3,2$ y $(-1,7,0)$. Entonces el traslado de $\Pi$ por $p=(-2,3,9)$ es el conjunto

\begin{align*}
p+\Pi&=\Pi+p=\Pi+(-2,3,9) \\
&=\{r(5,3,2)+s(-1,7,0)+(-2,3,9): s,r \in \mathbb{R}\}
\end{align*}

Más adelante

Con lo desarrollado en esta entrada seremos capaces de definir ciertos lugares geométricos ya no sólo en el plano, si no también en el espacio. Además, desarrollamos una intuición lógica para continuar construyendo lo que resta del curso.

Tarea moral

  • En el párrafo siguiente a la definición de un plano en el espacio:
    • ¿Cuál es el parámetro de la recta descrita al tomar $r$ fijo?
    • ¿Cuál es el parámetro de la recta descrita al tomar $s$ fijo?
  • Completa el interactivo de la sección Plano en el espacio al dibujar el plano definido por los puntos $Q$ y $R$ del interactivo y $P=(-3,2-6)$. Estarás en lo correcto si el plano que obtienes es paralelo al definido por $Q$, $R$ y el origen.
  • Completa la demostración de la proposición que trata la equivalencia entre las definiciones de plano en el espacio.
  • ¿Qué espacio geométrico define el primer ejemplo de subespacio generado? ¿y el ejemplo 2?
  • Da una expresión paramétrica para el plano que pasa por los puntos $P=(1,2,0)$, $Q=(1,0,1)$ y $R=(-1,0-2)$.