Archivo de la etiqueta: recta normal

Cálculo Diferencial e Integral I: Rectas tangente y normal a una curva

Por Karen González Cárdenas

Deja un comentario

Introducción

En la unidad anterior vimos la teoría relacionada a las funciones derivables. A lo largo de esta última parte del curso, veremos una serie de aplicaciones de la derivada en distintos ámbitos. Esperamos que te parezcan interesantes los ejemplos que aquí expondremos y la relación del Cálculo en problemáticas de otras áreas. Comenzaremos con obtener la recta tangente y normal de una función en un punto dado.

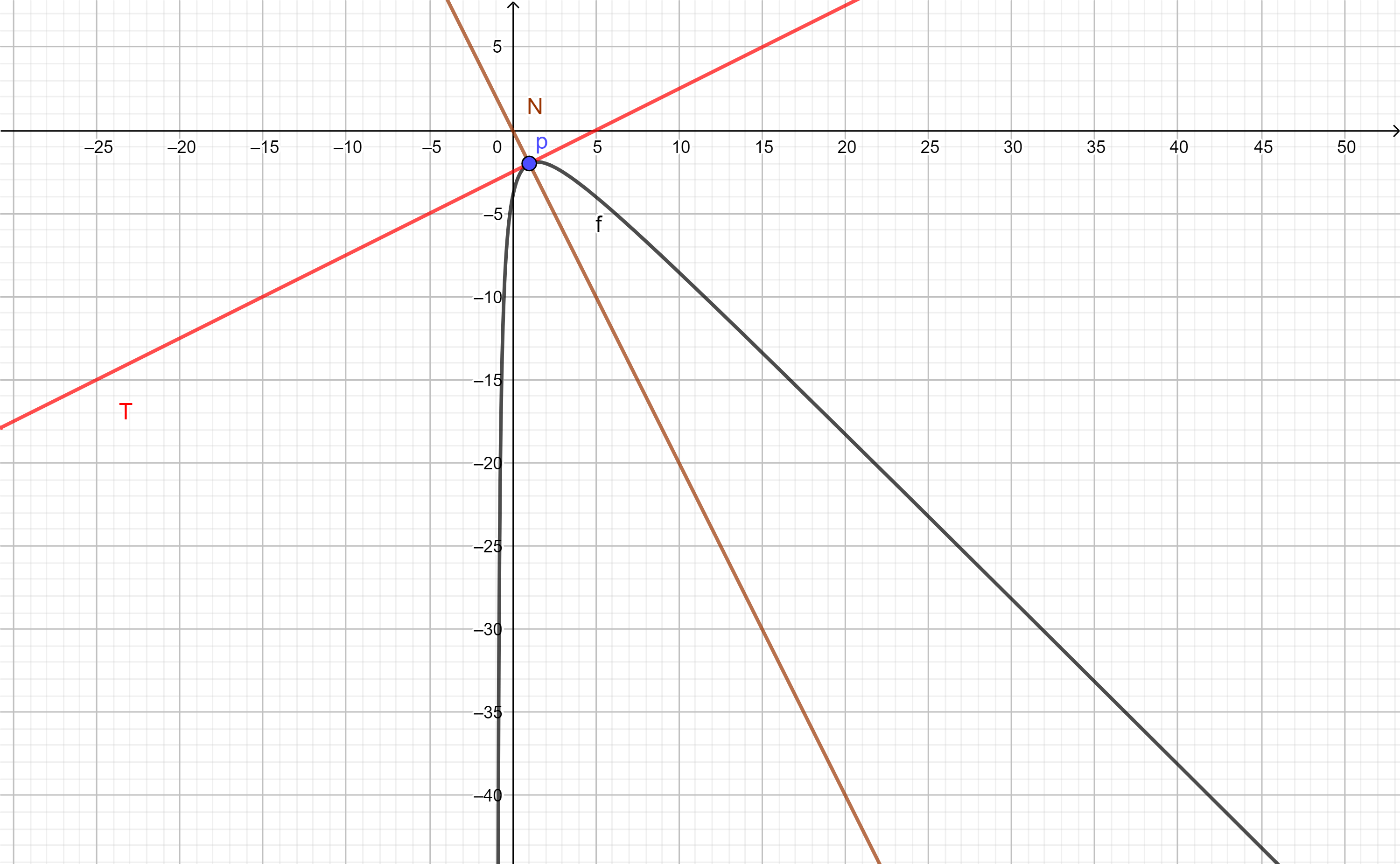
¿Qué dice la geometría?

Recordemos algunos conceptos geométricos para entrar en contexto:
Decimos que una recta $T$ es tangente si toca a una curva en un sólo punto. Y que una recta $N$ es normal si es perpendicular a la recta tangente en el punto de tangencia.

  • $T$ es la recta tangente en el punto $p$
  • $N$ es la recta normal en $p$

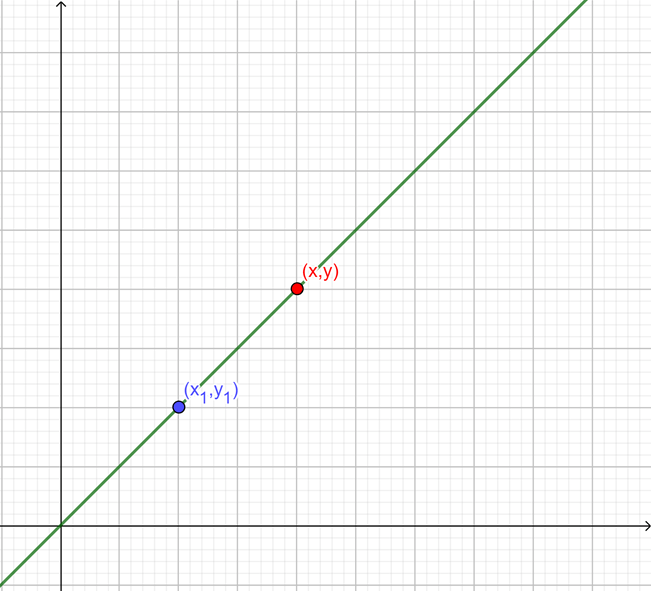
En los cursos de geometría probablemente te encontraste con la siguiente ecuación para definir a una recta:
$$y-y_1= m(x-x_1) $$
ésta es conocida como la forma punto-pendiente.


Vemos que gráficamente estamos considerando un punto $(x_1,y_1)$ sobre la recta y decimos que un punto cualquiera $(x,y)$ se encuentra también sobre la recta si cumple la igualdad anterior.

Recordando…

A principios de la unidad pasada vimos que una función $f$ es derivable en un punto $x_{0}$ si existe el siguiente límite:
$$\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}=f'(x_0).$$

Y que además la interpretación geométrica de dicho límite es justo la pendiente de la recta tangente a la gráfica de nuestra función $f$ en un $ (x_{0},f(x_{0}))$.
Con ayuda de este concepto y la definición vista en la sección anterior, vemos que la recta que pasa por el punto $ (x_{0},f(x_{0}))$ y que es tangente a la gráfica sería:
\begin{align*}
y-y_1&= m(x-x_1)\\
y-f(x_0)&=f'(x_0)(x-x_0)\\
y&=f'(x_0) (x-x_0) +f(x_0)
\end{align*}
donde $m=f'(x_0)$ y consideramos $(x_1,y_1)= (x_{0},f(x_{0})) $.

Definición de la recta tangente

Motivados por lo anterior tenemos la siguiente definición:
Definición (recta tangente): Sea $f$ una función derivable en un punto $x_0$. Definimos a la recta tangente a la gráfica de $f$ en el punto $(x_{0},f(x_{0}))$ como:
$$T(x)= f'(x_0) (x-x_0) +f(x_0).$$

Esta definición es la que estaremos usando en todos los ejercicios de esta entrada por lo que recomendamos tenerla presente. Pasaremos ahora a definir la recta normal a la gráfica de $f$ en el punto $(x_{0},f(x_{0}))$.

Definición de la recta normal

Como ya vimos que geométricamente la recta normal es perpendicular a la recta tangente, modificaremos la pendiente a la definición anterior tomando $m=-\frac{1}{f'(x_0)}$ con $f'(x_0) \neq 0$ :
Definición (recta normal): Tomando $f$ una función derivable en un punto $x_0$. Definimos a la recta normal a la gráfica de $f$ en el punto $(x_{0},f(x_{0}))$ con la ecuación:
$$N(x)= -\frac{1}{f'(x_0)}(x-x_0) +f(x_0).$$

Con ambas rectas definidas pasaremos a resolver algunos ejercicios.

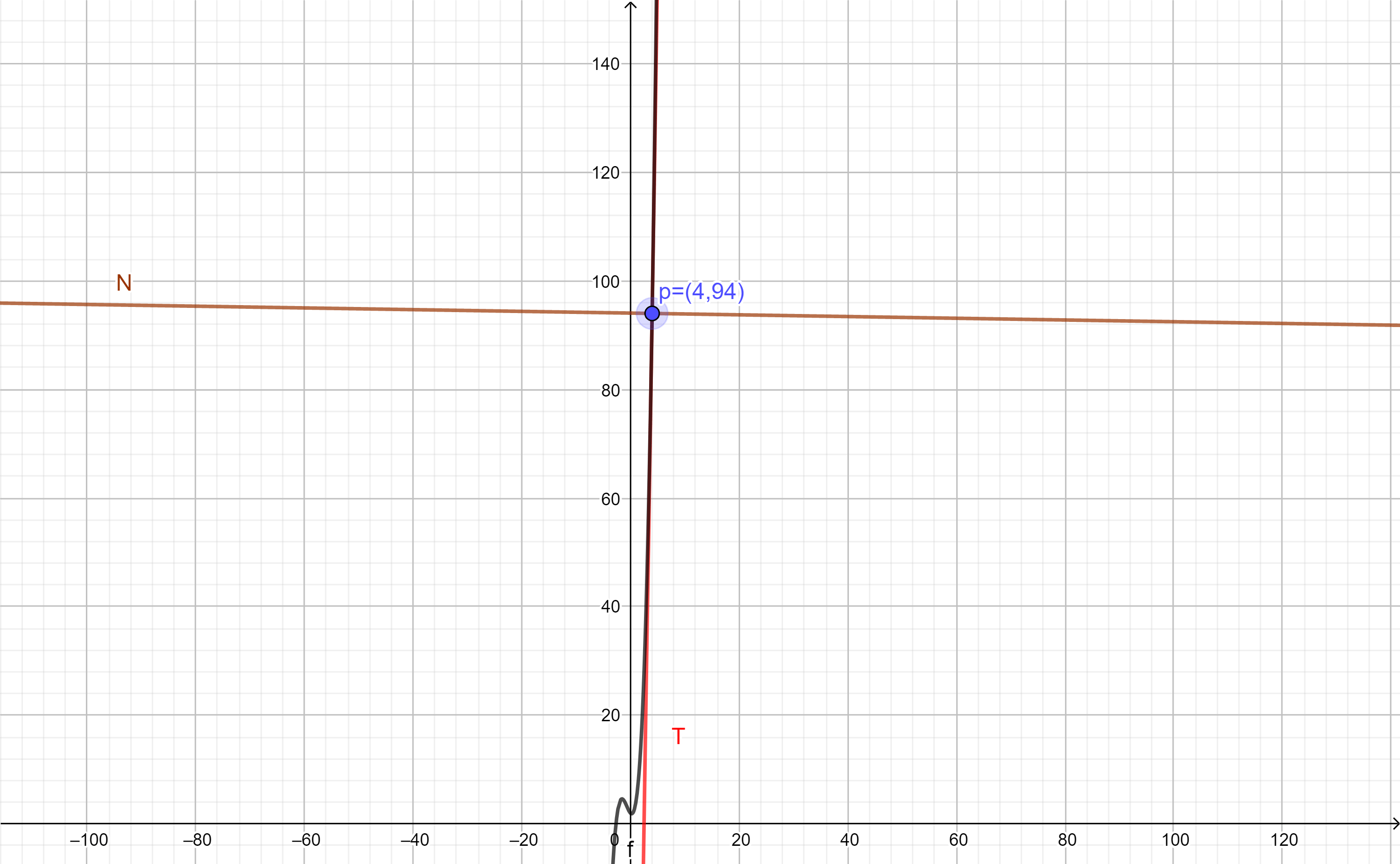
Ejemplo 1

Encuentra la recta tangente y normal de la función:
$$f(x)=x^{3}+2x^{2}-x+2$$
en el punto $(4,94)$.
Solución:
Comenzaremos por obtener la derivada de $f(x)$ haciendo uso de las reglas de derivación:
$$f'(x)=3x^{2}+4x-1.$$

Para obtener la pendiente en el punto indicado debemos sustituir $x=4$, así:
\begin{align*}
f'(4)&= 3(4)^{2}+4(4)-1\\
&=48+16-1\\
&=63
\end{align*}

Ahora comenzamos sustituyendo lo anterior en la definición de recta tangente:
\begin{align*}
T(x)&= 63 \cdot (x-4)+94\\
&=63x-252+94\\
&=63x-158
\end{align*}
$$\therefore T(x)= 63x-158 .$$

Finalmente sustituyendo en la definición de la recta normal:
\begin{align*}
N(x)&= -\frac{1}{63} \cdot (x-4)+94\\
&=-\frac{x}{63}+\frac{4}{63}+94\\
&=-\frac{x}{63} + \frac{5926}{63}
\end{align*}
$$\therefore N(x)= -\frac{x}{63} + \frac{5926}{63}.$$

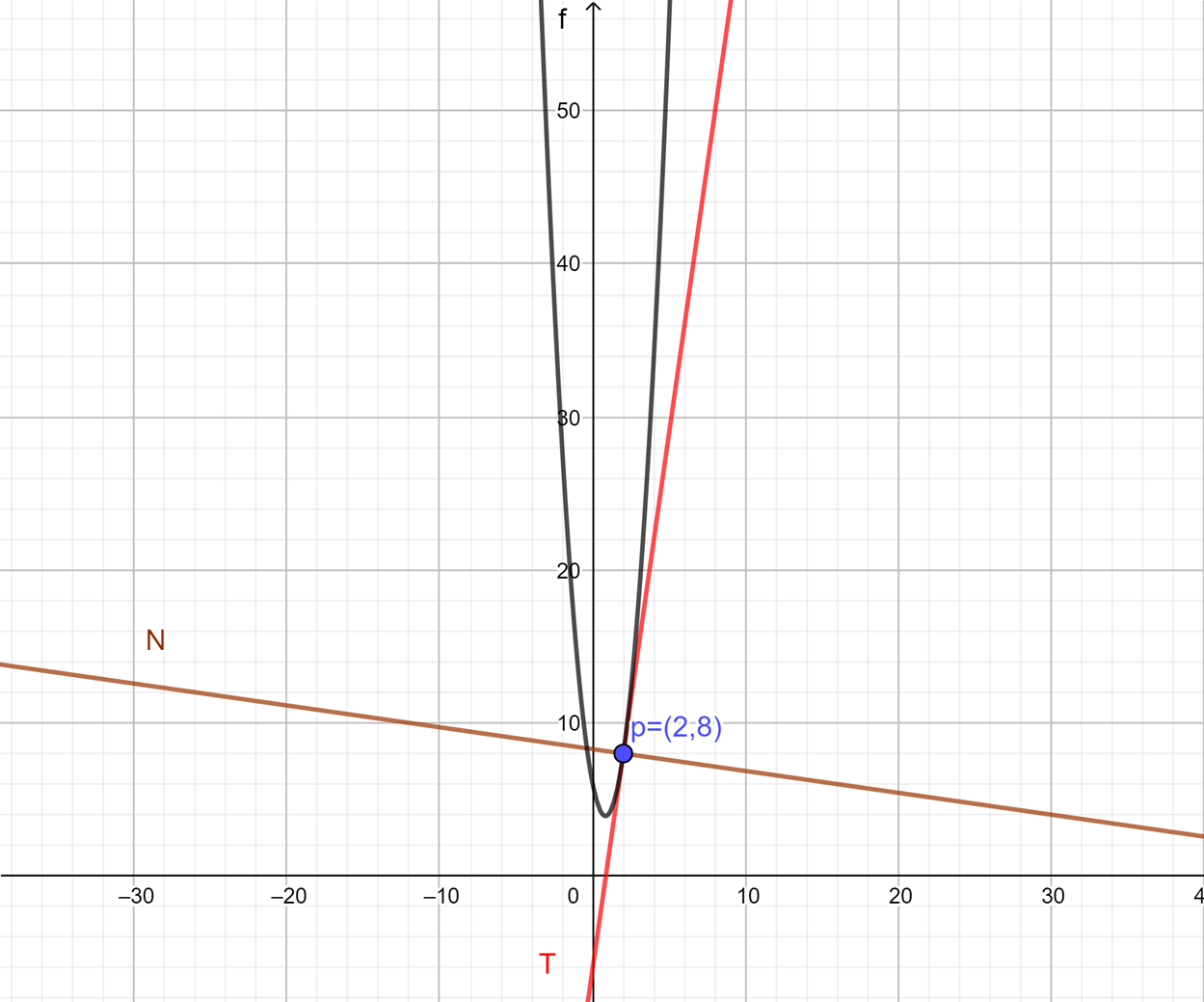
Ejemplo 2

Encuentra la recta tangente y normal con $x_0=2$ de la función:
$$f(x)=3x^{2}-5x+6.$$
Solución:
Comenzamos por sustituir $x_0=2$ para obtener el punto $p$ por donde pasarán ambas rectas:
\begin{align*}
f(2)&=3(2)^{2}-5(2)+6\\
&= 12-10+6\\
&=8
\end{align*}
$$\therefore p=(2,8).$$
Ahora pasemos a obtener la pendiente derivando la función y sustituyendo $x_0=2$:
$$f'(x)=6x-5 \Rightarrow f'(2)=6(2)-5=12-5=7.$$

Procedamos a sustituir en las definiciones para la tangente y la normal:
\begin{align*}
T(x)&= 7(x-2)+8 & N(x)&= -\frac{1}{7} (x-2)+8 \\
&= 7x-14+8 & &=-\frac{x}{7}+\frac{2}{7}+8\\
&= 7x-6 & &= -\frac{x}{7}+\frac{58}{7}
\end{align*}
Así concluimos que:
\begin{align*}
T(x)&= 7x-6 \\
N(x)&= -\frac{x}{7}+\frac{58}{7}
\end{align*}

Ejemplo 3

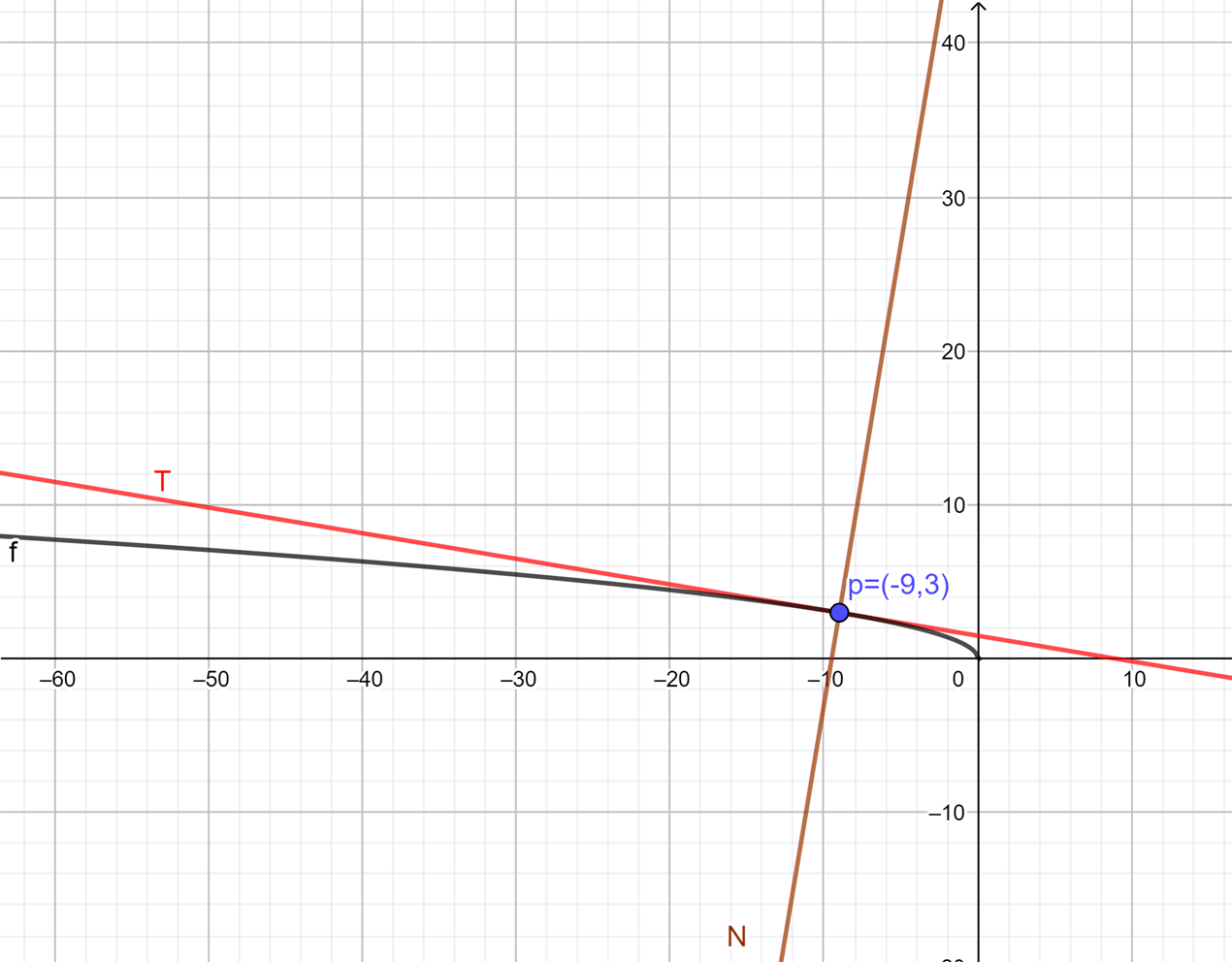
Hallar la recta tangente y normal de la función:
$$f(x)=\sqrt{-x}$$
en el punto $p=(-9,3)$.
Solución:
Procederemos a derivar la función haciendo uso de la Regla de la cadena:
\begin{align*}
f'(x)&= \frac{1}{2}(-x)^{\frac{1}{2}-1} \cdot (-1)\\
&=-\frac{1}{2}(-x)^{-\frac{1}{2}}\\
&=-\frac{1}{2\sqrt{-x}}
\end{align*}

Obtenemos la pendiente al sustituir $x_0=-9$:
\begin{align*}
f'(-9)&=-\frac{1}{2\sqrt{-(-9)}}\\
&=-\frac{1}{2\sqrt{9}}\\
&= -\frac{1}{6}
\end{align*}

Ahora hallamos la recta tangente y normal sustituyendo $f'(-9)= -\frac{1}{6}$:
\begin{align*}
T(x)&= -\frac{1}{6} (x-(-9))+3 & N(x)&=-\frac{1}{-\frac{1}{6}} (x-(-9))+3 \\
&= -\frac{1}{6}(x+9)+3 & &= 6 (x+9)+3 \\
&=-\frac{x}{6}-\frac{3}{2}+3 & &= 6x+54+3\\
&= -\frac{x}{6}+\frac{3}{2} & &=6x+57
\end{align*}

Por lo que finalmente tenemos:
\begin{align*}
T(x)&= -\frac{x}{6}+\frac{3}{2}\\
N(x) &=6x+57
\end{align*}

Más adelante

En la siguiente entrada veremos cómo encontrar máximos y mínimos de una función. Por lo tanto, definiremos dichos conceptos y probaremos algunos resultados que nos brindarán los criterios necesarios, haciendo uso de la derivada, para identificarlos.

Tarea moral

Encuentra la recta tangente y normal en cada uno de los incisos:

  • $f(x)=2x^{3}+3x^{2}+4x-2$ con $x_0=2$.
  • $f(x)=x^{3}-3x$ en $p=(2,2)$.
  • $f(x)=4x^{2}$ en $p=(2,16)$.
  • $f(x)=sen(\frac{\pi}{2}-x)$ en $p=\left(\frac{\pi}{3},\frac{1}{2} \right)$.
  • $f(x)=\frac{x+1}{x-1}$ en $p=(2,3)$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría analítica I: Rectas en forma normal y sus intersecciones

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

En esta nueva entrada analizaremos una nueva forma de la recta, la normal. Se discutió la idea de esta al final de la entrada anterior. Además, como es algo nuevo para nosotros, será conveniente explorar la intersección de rectas partiendo de esta nueva forma.

Ecuación normal de la recta

Iniciemos esta entrada con la definición y un ejemplo de esta nueva ecuación de la recta.

Definición. Una recta en forma normal consiste de tomar un vector $q \in \mathbb{R}^2$, un escalar $c \in \mathbb{R}$ y considerar el conjunto

$l=\{ x \in \mathbb{R}^2 : x \cdot q = c \}$

Ejemplo: Encuentra la forma normal de la recta $l=\{ (2,-1) + r (3,5) : r \in \mathbb{R} \}$.

Por la última proposición vista en la entrada anterior, debemos escribir el conjunto de los vectores $x$ tales que el producto interior con $q$ ortogonal nos de $p \cdot q ^{\perp}$, cuyo resultado es un escalar. Así, obtenemos

\begin{align*}
l&=\{ x \in \mathbb{R}^2 : x \cdot (3,5)^{\perp} = (3,5)^{\perp} \cdot (2,-1) \} \\
&=\{ x \in \mathbb{R}^2 : x \cdot (-5,3) = (-5,3) \cdot (2,-1) \} \\
&=\{ x \in \mathbb{R}^2 : x \cdot (-5,3) = (-5)(2)+3(-1)=-13 \} \\
\end{align*}

Si definimos a $x=(x_1,x_2)$ tal que $x_1, x_2 \in \mathbb{R}$, entonces $(x_1,x_2) \cdot (-5,3)=-5x_1+3x_2$. Así, la forma normal de la recta $l$ está dada por

$l=\{ x_1, x_2 \in \mathbb{R} : -5x_1+3x_2=-13\}$

$\square$

Recordatorio. Hasta ahora hemos hablado de rectas en su forma paramétrica, rectas en su forma baricéntrica y en esta entrada rectas en su forma normal. Es importante resaltar que el término recta es un «espacio geométrico» en el espacio, y al hablar de forma paramétrica, baricéntrica o normal, sólo nos referimos a su expresión algebraica.

Intersección de rectas en su forma normal

Para desarrollar de manera más completa este tema, hablemos de la intersección de rectas cuando están expresadas en su forma normal. Sean las rectas

$l_1=\{ x \in \mathbb{R}^2 : p \cdot x = e\}$

$l_2=\{ x \in \mathbb{R}^2 : q \cdot x = f \}$

donde $c$ y $d$ son números reales, qué debemos hacer para saber primero si se intersectan estas rectas y si pasa,cuál es el punto de intersección.

Aquí, podemos recurrir a lo que vimos en la entrada anterior a cerca del compadre ortogonal. Por como definimos la forma normal de la recta anteriormente, sabemos que $p$ es un vector perpendicular a $l_1$, por lo que el vector director de esta recta es un multiplo de $p^{\perp}$. De la misma manera, la dirección de $l_2$ es un múltiplo de $q^{\perp}$.

El caso más sencillo es cuando la intersección de las rectas es vacía, esto es que sean paralelas, lo cual implicaría que $p^{\perp} \parallel q^{\perp}$ y por lo tanto $p \parallel q$. Además puede pasar que $l_1$ y $l_2$ sean la misma recta, esto sí y sólo si $c=rd$.

El caso que falta es la intersección de las rectas. Para encontrar este punto de intersección, comencemos desarrollando los productos puntos que definen las rectas para así obtener un sistema lineal de ecuaciones. Sea $x=(x,y)$, $p=(a,b)$ y $q=(c,d)$, tenemos que

\begin{cases}
p \cdot x = ax+by=e \\
q \cdot x = cx+dy=f
\end{cases}

Recordemos por lo visto en una entrada anterior que un sistema de ecuaciones así tiene solución única cuando $ad-bc \neq 0$.

Podemos reescribir este sistema de ecuaciones pensando en una igualdad de vectores, es decir entrada a entrada

$x(a,c)+y(b,d)=(e,f)$

Si desarrollas las operaciones e igualas las entradas, verás que es lo mismo que nuestro sistema; sin embargo al escribirlo de esta forma tenemos herramientas que pueden facilitar la solución del sistema. En el camino que exploramos con anterioridad para la solución, eliminábamos cierto término para poder despejar una de las variables… Si ahora queremos eliminar digamos el término con $x$, podemos multiplicar la ecuación vectorial por el vector $(a,c)^{\perp}=(-c,a)$, ya que su producto interior con $(a,c)$ es cero

\begin{align*}
x(a,c) \cdot (-c,a) + y(b,d) \cdot (-c,a)&=(e,f) \cdot (-c,a) \\
\Rightarrow y (b,d) \cdot (-c,a)&=(e,f) \cdot (-c,a) \\
\Rightarrow y (da-bc)&=fa-ec
\end{align*}
Si despejamos a $y$, tenemos

$y=\frac{fa-ec}{da-bc}$

De manera análoga, podemos hacer producto punto con $(b,d)^{\perp}=(-d,b)$ para obtener a $x$

$x=\frac{bf-ed}{bc-ad}$

Recapitulemos para poder concluir. Por como definimos a los vectores usados en este desarrollo, $ax+by=e$ corresponde a la recta en forma normal $l_1$

$l_1=\{ (x,y) \in \mathbb{R}^2 : (a,b) \cdot (x,y) = e\}$

mientras que $cx+dy=f$ está asociada a $l_2$ en su forma normal

$l_2={ (x,y) \in \mathbb{R}^2 : (c,d) \cdot (x,y) = f}$

Como estamos en el caso en el que $l_1$ no es paralela a $l_2$, entonces $(a,b)$ no es paralelo a $(c,d)$, por lo que $ad-bc \neq 0$ y el sistema tiene una única solución ( el punto de intersección):

$(x,y)=\left( \frac{bf-ed}{bc-ad} ,\frac{fa-ec}{da-bc} \right)$

Para $n > 2$

Cerremos está entrada hablando de un plano en su forma normal.

Definición. Un plano en forma normal en $\mathbb{R}^3$ consiste de tomar un vector $q \in \mathbb{R}^3$, un escalar $c \in \mathbb{R}$ y considerar el conjunto

$\Pi=\{ x \in \mathbb{R}^3 : x \cdot q =c \}$

Más adelante…

Todo lo que vamos desarrollando nos es de utilidad más adelante, y esta entrada no será la excepción. Sobre todo cuando hablemos en la siguiente entrada de los teoremas de concurrencia, ya que usaremos la forma normal de la recta para demostrarlos.

Tarea moral

  • Encuentra la forma normal de las siguientes rectas
    • $\{ (1,-1)+t(2,3) : t \in \mathbb{R} \}$
    • ${ (-5,-0)+(6s,-4s) : s \in \mathbb{R} }$
  • Encuentra la forma normal de la recta que pasa por los puntos
    • $(1,-3)$ y $(3,4)$
    • $(2,-4)$ y $(9,5)$
  • Encuentra la intersección de las rectas de los ejercicios anteriores.