Archivo de la etiqueta: simediana

Geometría Moderna I: Punto simediano

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

El punto simediano es el punto en el que concurren las simedianas de un triángulo, es otro punto notable del triángulo, en esta entrada veremos algunas de sus propiedades.

Punto simediano

Teorema 1. Las tres simedianas de un triángulo son concurrentes, al punto de concurrencia se le conoce como punto simediano o punto de Lemoine a menudo denotado con la letra $K$.

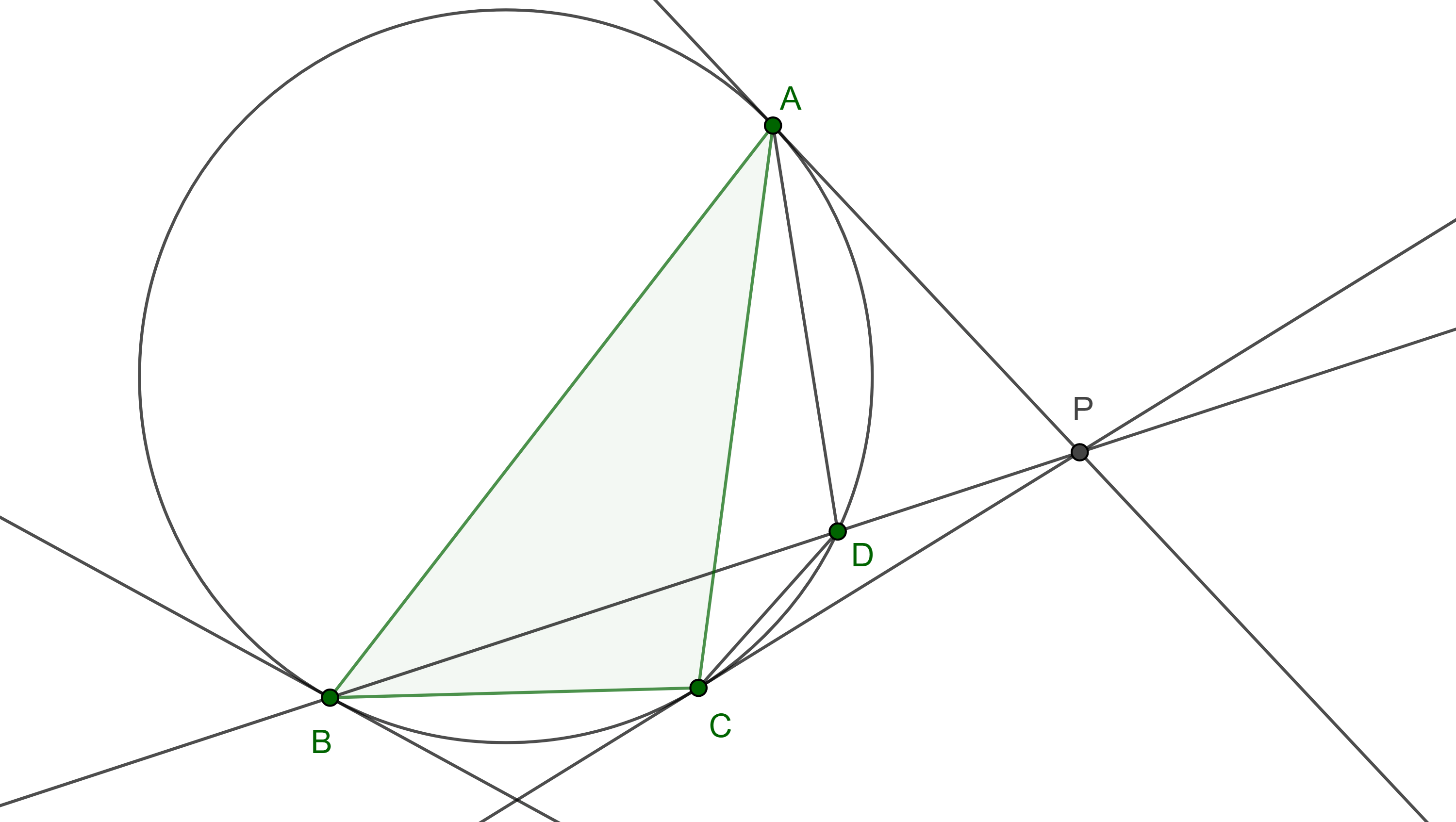
Demostración. En la entrada teorema de Menelao mostramos que un triángulo $\triangle ABC$ y su triangulo tangencial $\triangle K_aK_bK_c$, están en perspectiva desde una recta, conocida como eje de Lemoine.

Por el teorema de Desargues, $\triangle ABC$ y $\triangle K_aK_bK_c$ están en perspectiva desde un punto, es decir, $AK_a$, $BK_b$ y $CK_c$ concurren en un punto $K$.

Figura 1

Por el teorema 2 de la entrada anterior, dos exsimedianas (los lados del triángulo tangencial $\triangle K_aK_bK_c$) y una simediana, que pasan por vértices distintos de $\triangle ABC$ concurren en un punto exsimediano, es decir, $AK_a$, $BK_b$, $CK_c$ son las simedianas de $\triangle ABC$.

$\blacksquare$

Observación. Como el eje de Lemoine de $\triangle ABC$ es el eje de Gergonne de $\triangle K_aK_bK_c$, entonces el punto de Lemoine de $\triangle ABC$ es el punto de Gergonne de $\triangle K_aK_bK_c$, su triángulo tangencial.

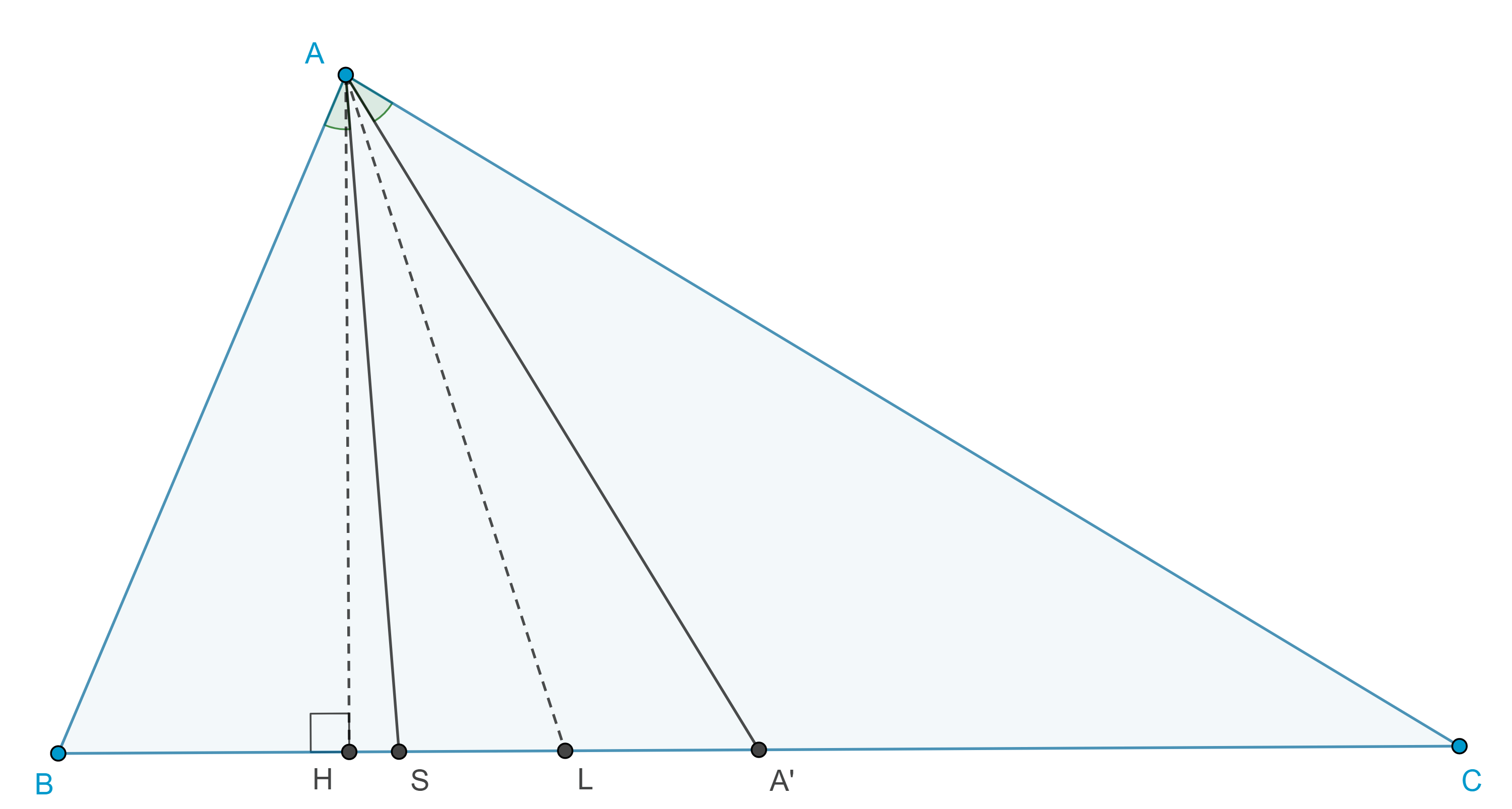
Corolario 1. Sea $S = AK \cap BC$ entonces $AKSK_a$ es una hilera armónica de puntos.

Demostración. Por el corolario de la entrada anterior $B(AK_bCK_a)$ es un haz armónico de rectas y como $AD$ es transversal entonces sus intersecciones con el haz forman una hilera armónica.

$\blacksquare$

Triángulo pedal del punto simediano

Definición. Dados un triángulo $\triangle ABC$ y un punto $P$, el triángulo pedal de $P$ respecto de $\triangle ABC$, es aquel cuyos vértices son las proyecciones de $P$ en los lados de $\triangle ABC$. Por ejemplo, el triángulo órtico es el triángulo pedal del ortocentro.

Teorema 2, de Lemoine. El punto simediano es el único punto del plano que es el centroide de su propio triángulo pedal.

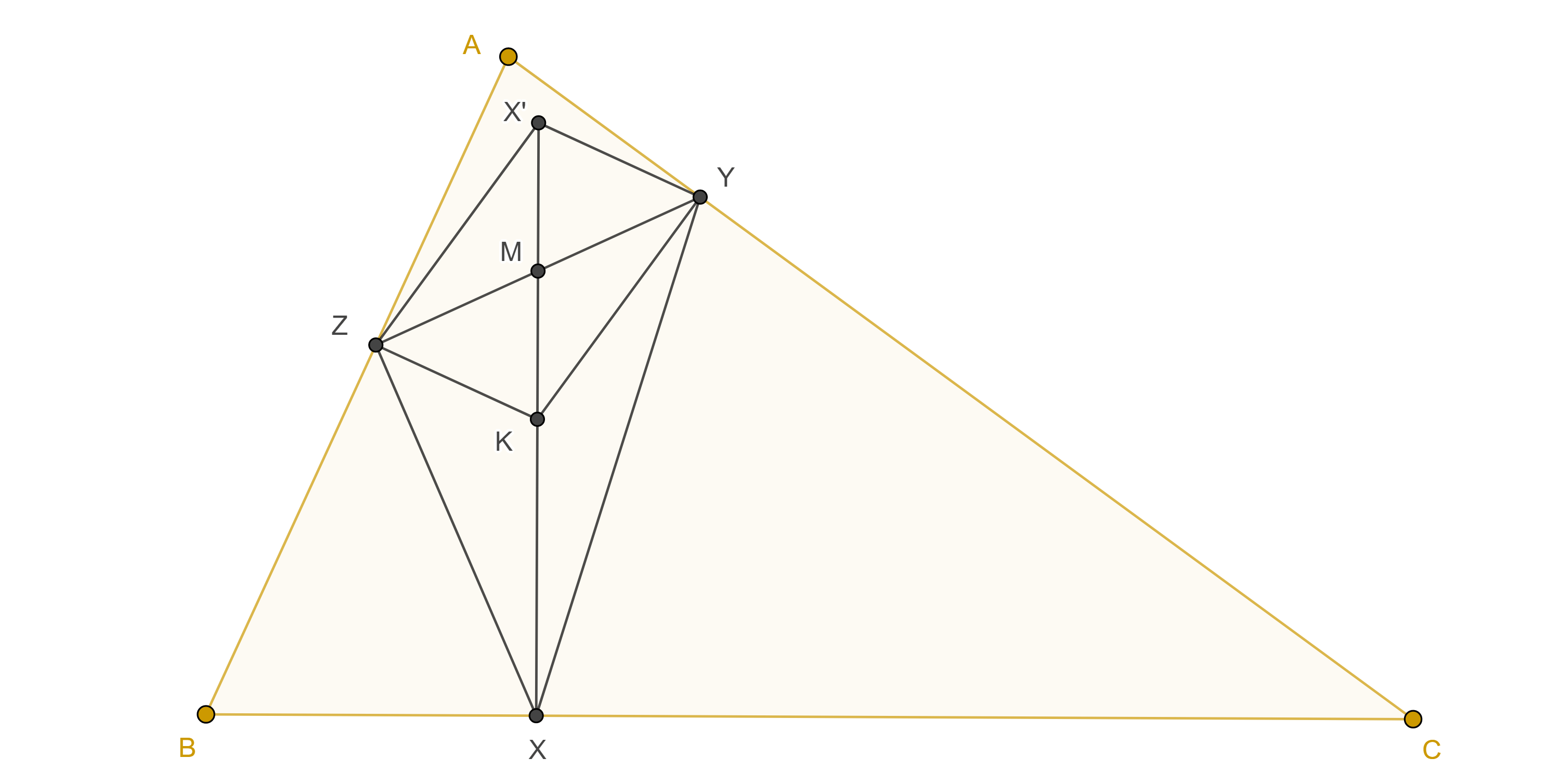
Demostración. Sean $\triangle ABC$ y $K$ su punto simediano, considera $X$, $Y$ y $Z$ las proyecciones de $K$ en $BC$, $CA$ y $AB$ respectivamente, sea $X’ \in KX$ tal que $YX’ \parallel KZ$.

Figura 2

Entonces $\triangle ABC \sim \triangle YX’K$, pues sus respectivos lados son perpendiculares, esto es
$\dfrac{AB}{AC} = \dfrac{YX’}{YK}$.

Pero $\dfrac{AB}{AC} = \dfrac{KZ}{KY}$ pues $K$ esta en la $A$-simediana, por lo tanto $KZ = YX’$.

En consecuencia, $\square X’ZKY$ es un paralelogramo y por lo tanto $KX’$ biseca a $YZ$.

Como resultado tenemos que $XK$ es mediana de $\triangle XYZ$.

De manera análoga vemos que $YK$, $ZK$ son medianas de $\triangle XYZ$, por lo tanto, $K$ es el centroide de su triangulo pedal.

$\blacksquare$

Recíprocamente, supongamos que $K$ es el centroide de su triángulo pedal $\triangle XYZ$ respecto a $\triangle ABC$, con $X \in BC$, $Y \in CA$, $Z \in AB$, sea $M$ el punto medio de $YZ$, extendemos $KM$ hasta un punto $X’$ tal que $KM = MX’$.

Como $YZ$ y $KX’$ se bisecan entonces $\square X’ZKY$ es un paralelogramo, entonces $YX’ = KZ$ y $YX’ \parallel KZ$.

Ya que los lados de $\triangle YX’K$ son perpendiculares a los lados de $\triangle ABC$, entonces son semejantes, esto es
$\dfrac{AB}{AC} = \dfrac{YX’}{YK} = \dfrac{KZ}{KY}$.

Por lo tanto, $K$ está en la $A$-simediana, igualmente vemos que $K$ pertenece a las $B$ y $C$-simedianas.

En consecuencia, $K$ es el punto simediano de $\triangle ABC$.

$\blacksquare$

Conjugado isotómico del punto simediano

Teorema 3. Las rectas que unen el punto medio del lado de un triángulo con el punto medio de la altura perpendicular a ese lado concurren en el punto simediano del triángulo.

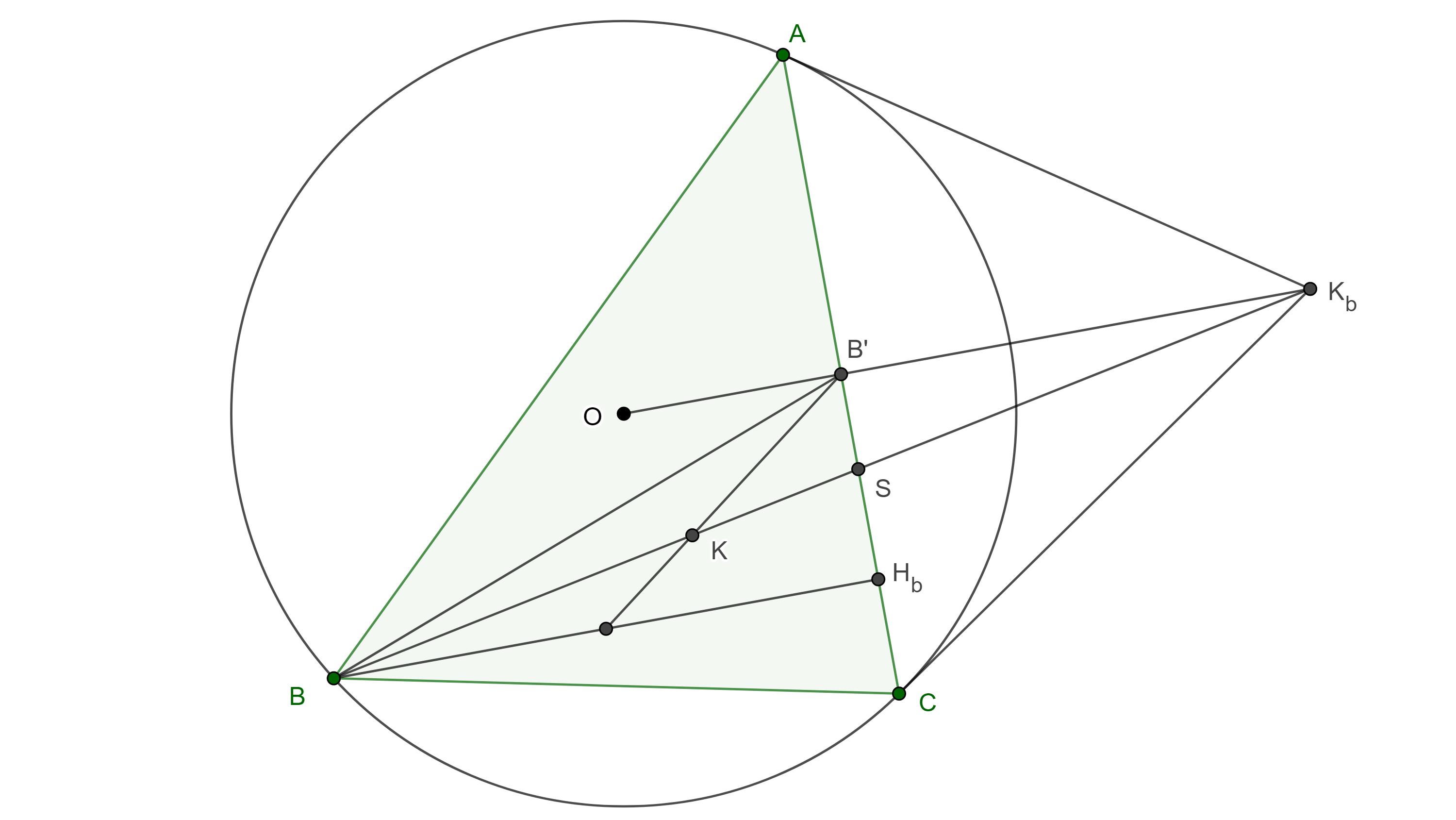
Demostración. Sean $\triangle ABC$, $K$ el punto simediano, $K_b$ el punto exsimediano opuesto al vértice $B$, $S = BK_b  \cap CA$.

Figura 3

Por el corolario 1, $BKSK_b$ es una hilera armónica, por lo tanto, $B’(BKSK_b)$ es un haz armónico, donde $B’$ es el punto medio de $CA$.

Considera $O$ el circuncentro de $\triangle ABC$ y $H_b$ el pie de la altura por $B$, notemos que $O$, $B’$ y $K_b$ son colineales, por lo tanto, $B’K_b$ es perpendicular a $CA$ y así $BH_b \parallel B’K_b$.

Como $BH_b$ es paralela a una de las rectas del haz armónico, entonces las otras tres rectas del haz dividen a $BH_b$ en dos segmentos iguales, es decir $B’K$ biseca a $BH_b$.

Igualmente vemos que $A’K$ y $C’K$ bisecan a $AH_a$ y $CH_c$ respectivamente, y de esto concluimos la concurrencia de las rectas mencionadas.

$\blacksquare$

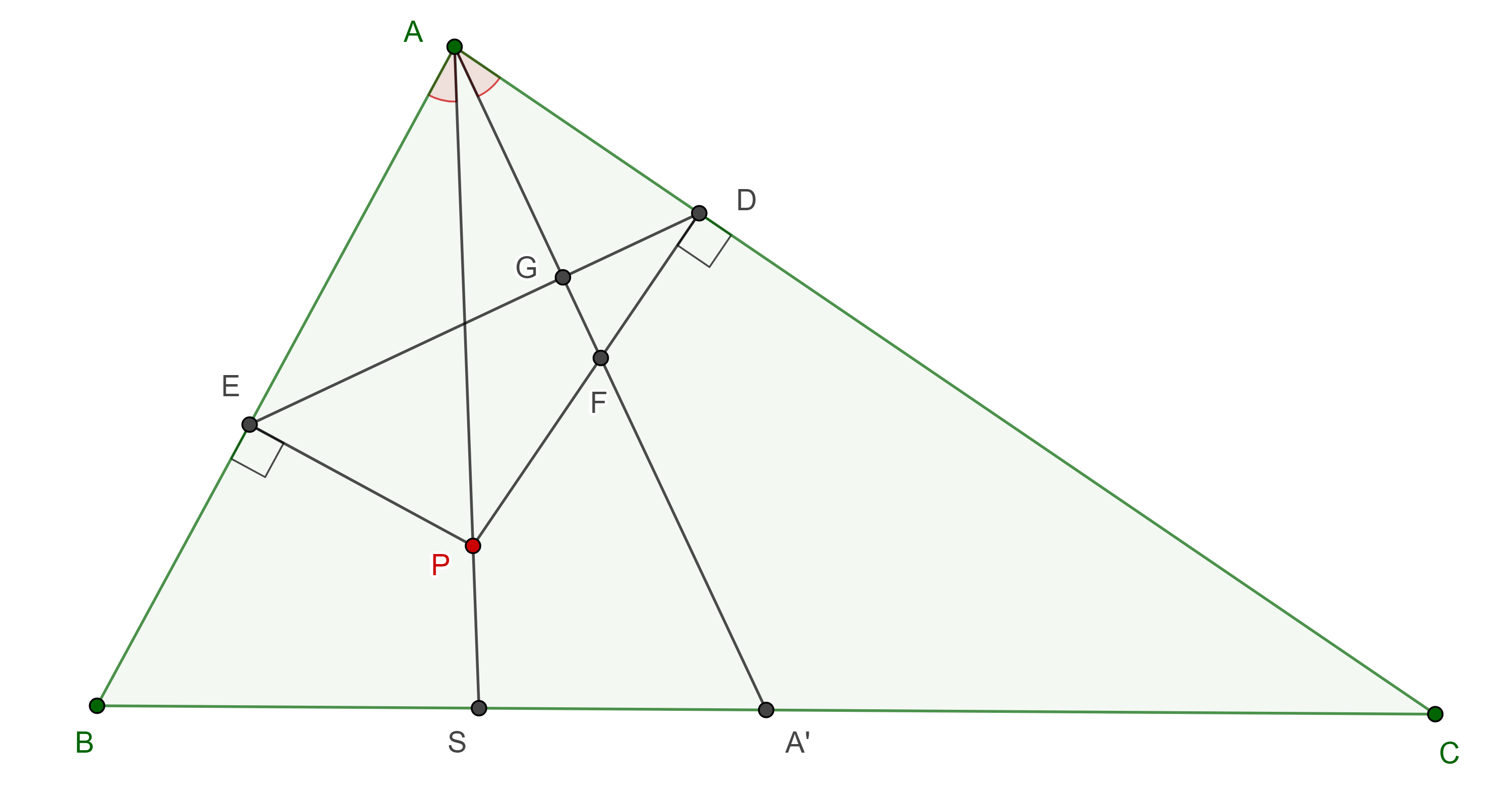
Proposición 1. El ortocentro de un triángulo y el punto simediano de su triángulo anticomplementario son conjugados isotómicos respecto del triángulo original.

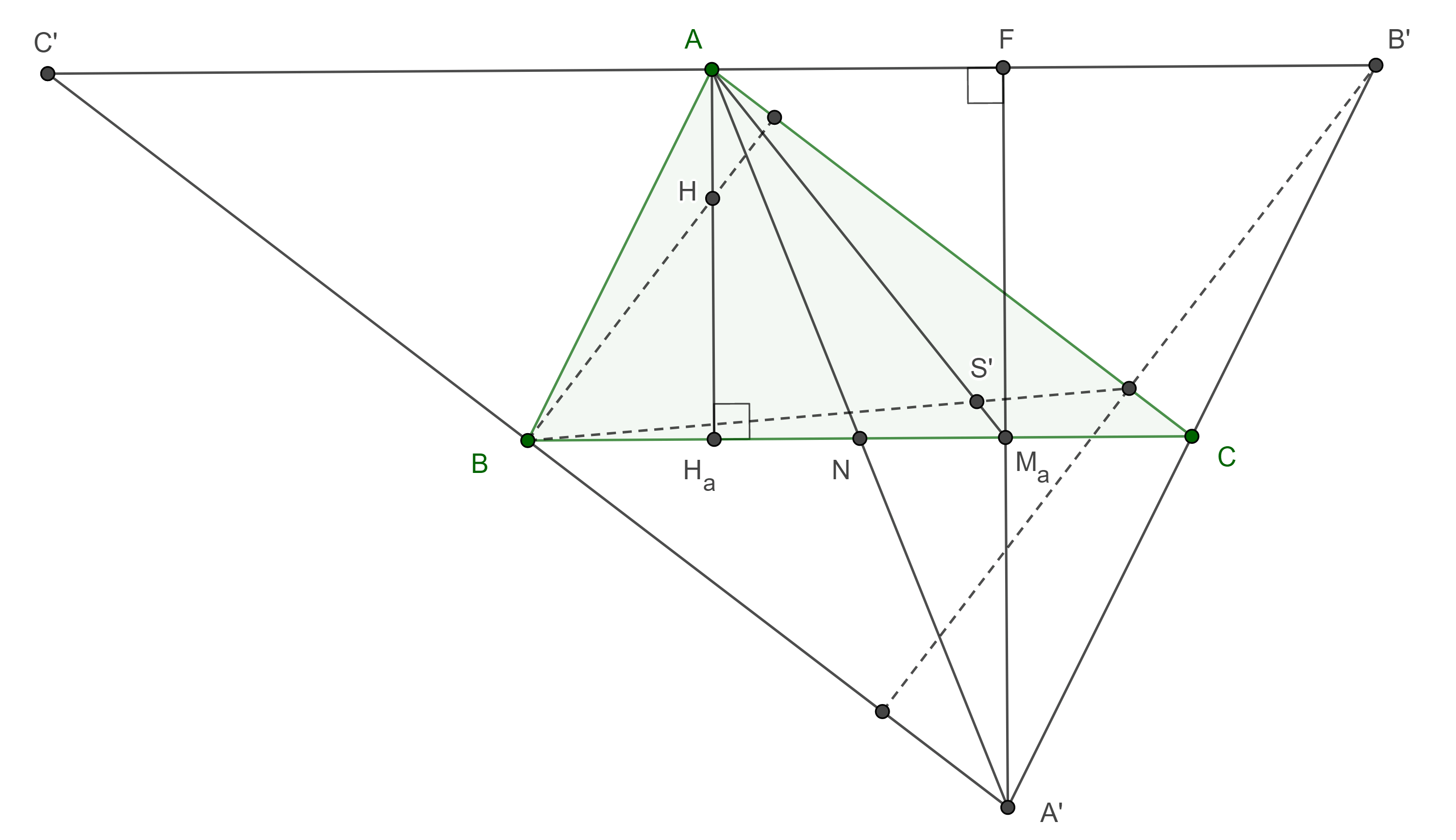
Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo anticomplementario.

Como $AB$ y $AC$ son segmentos medios de $\triangle A’B’C’$, entonces $\square ABA’C$ es un paralelogramo, por lo tanto, $\triangle ABC$ y $\triangle A’CB$ son congruentes, además $AA’$ y $BC$ se intersecan en su punto medio $N$.

Figura 4

Sean $H_a$, $M_a$ los pies de las alturas desde $A$ y $A’$ respectivamente en $BC$, como $\triangle ABC \cong \triangle A’CB$, entonces $AH_a = M_aA’$.

Por criterio de congruencia ALA, $\triangle AH_aN \cong \triangle A’M_aN$, por lo que $H_aN = NM_a$, es decir, el punto medio de $H_a$ y $M_a$ coincide con el punto medio de $BC$,

Por lo tanto, $H_a$ y $M_a$ son puntos isotómicos respecto de $\triangle ABC$.

Sea $F$ el pie de la altura por $A’$ en $\triangle A’B’C’$, como $\square AH_aM_aF$ es un rectángulo entonces $M_aA’ = AH_a = FM_a$, y así $M_a$ es el punto medio de la altura $A’F$.

Por lo tanto, el segmento $AM_a$ une los puntos medios de un lado y una altura de $\triangle A’B’C’$.

De manera análoga vemos que los pies de las alturas en $\triangle ABC$, $H_b$, $H_c$ son isotómicos a los puntos medios de las alturas en $\triangle A’B’C’$, $M_b$, $M_c$, respectivamente.

Como las alturas de $\triangle ABC$ concurren en el ortocentro $H$ y, por el teorema 3, los segmentos $AM_a$, $BM_b$, $CM_c$ concurren en el punto simediano $S’$ de $\triangle A’B’C’$, entonces estos puntos son conjugados isotómicos respecto de $\triangle ABC$.

$\blacksquare$

Construcción de un triángulo dado su punto simediano

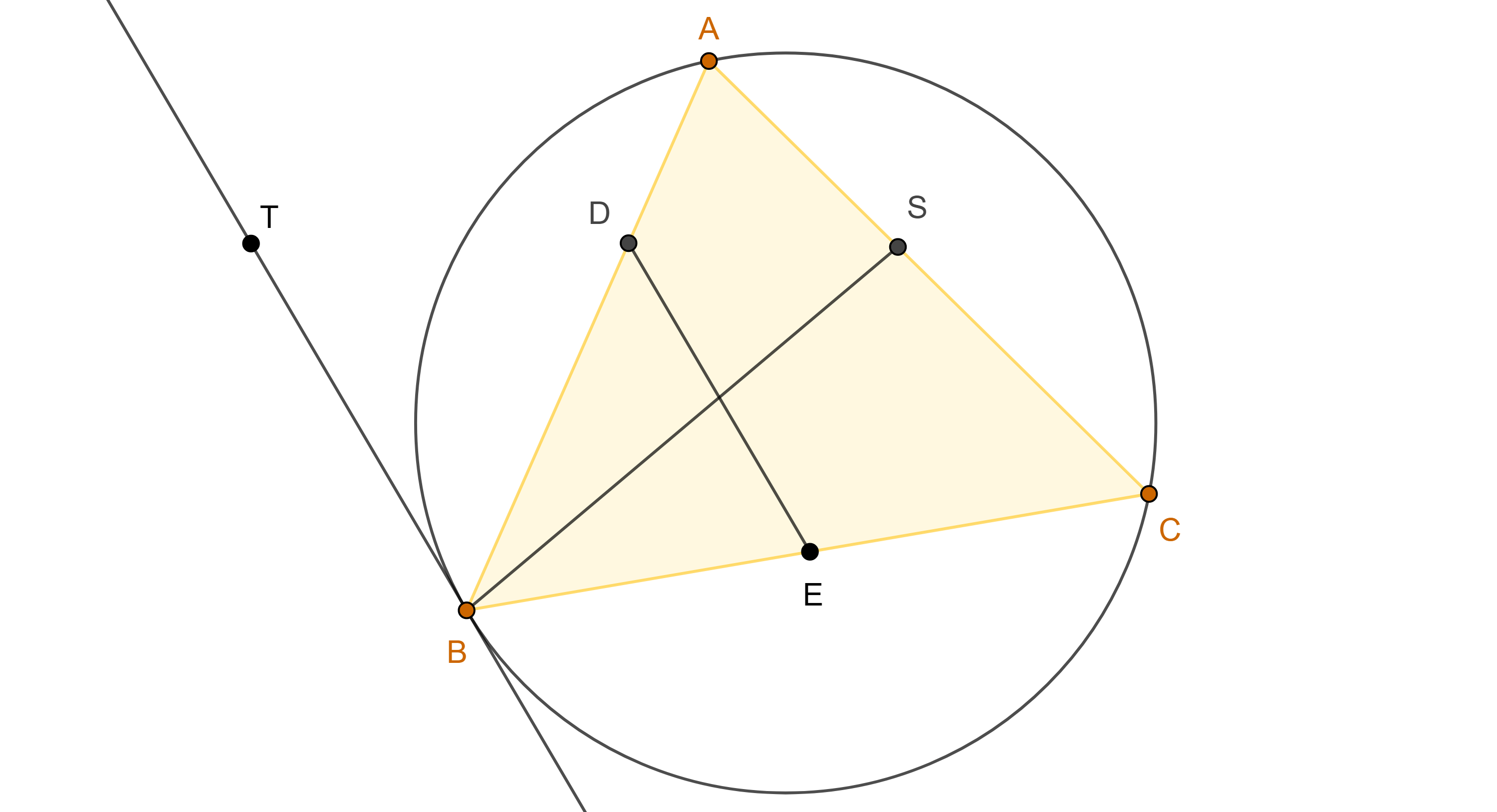
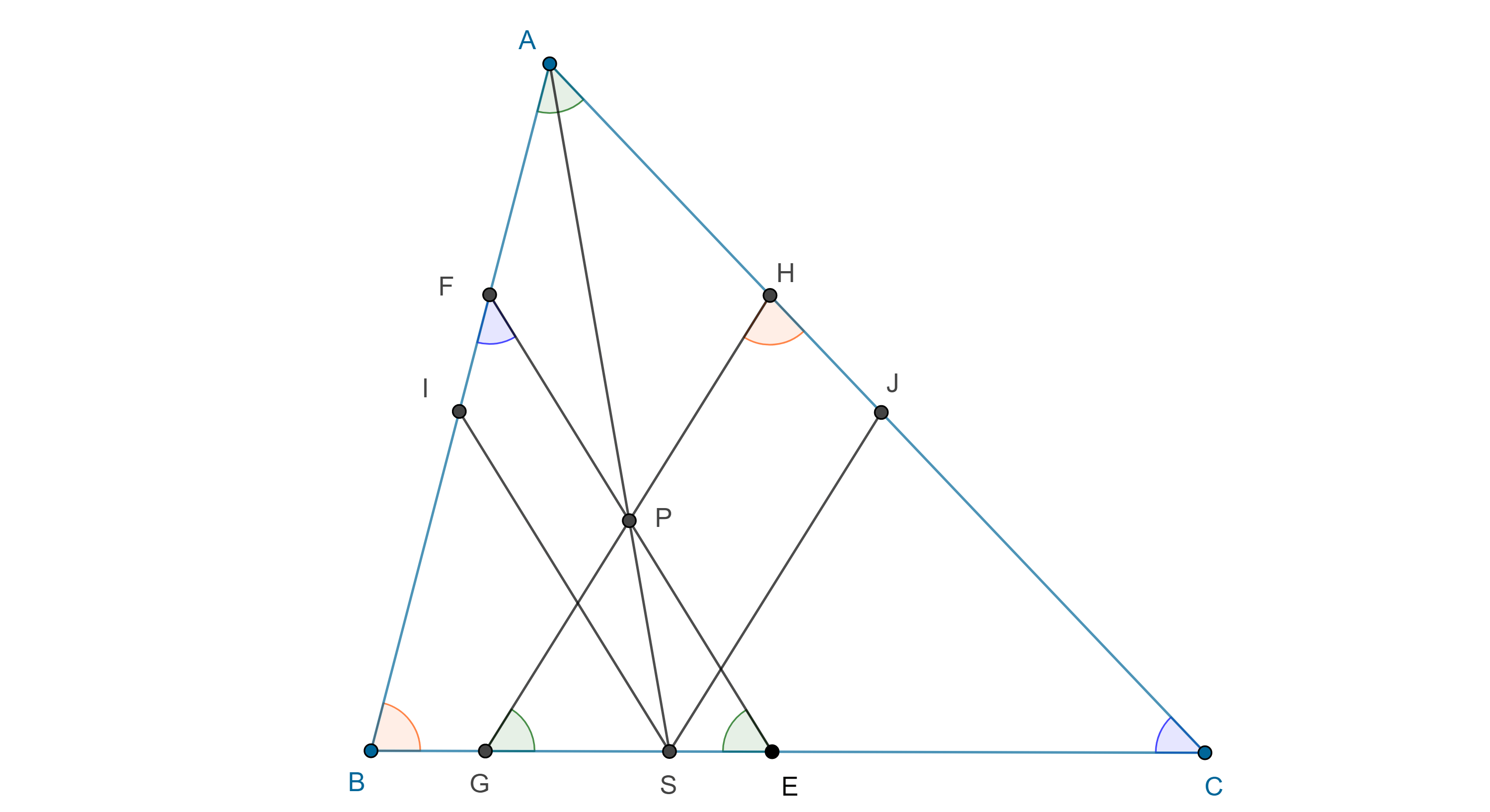
Problema. Construye un triángulo dados dos vértices $B$, $C$, y su punto simediano $K$.

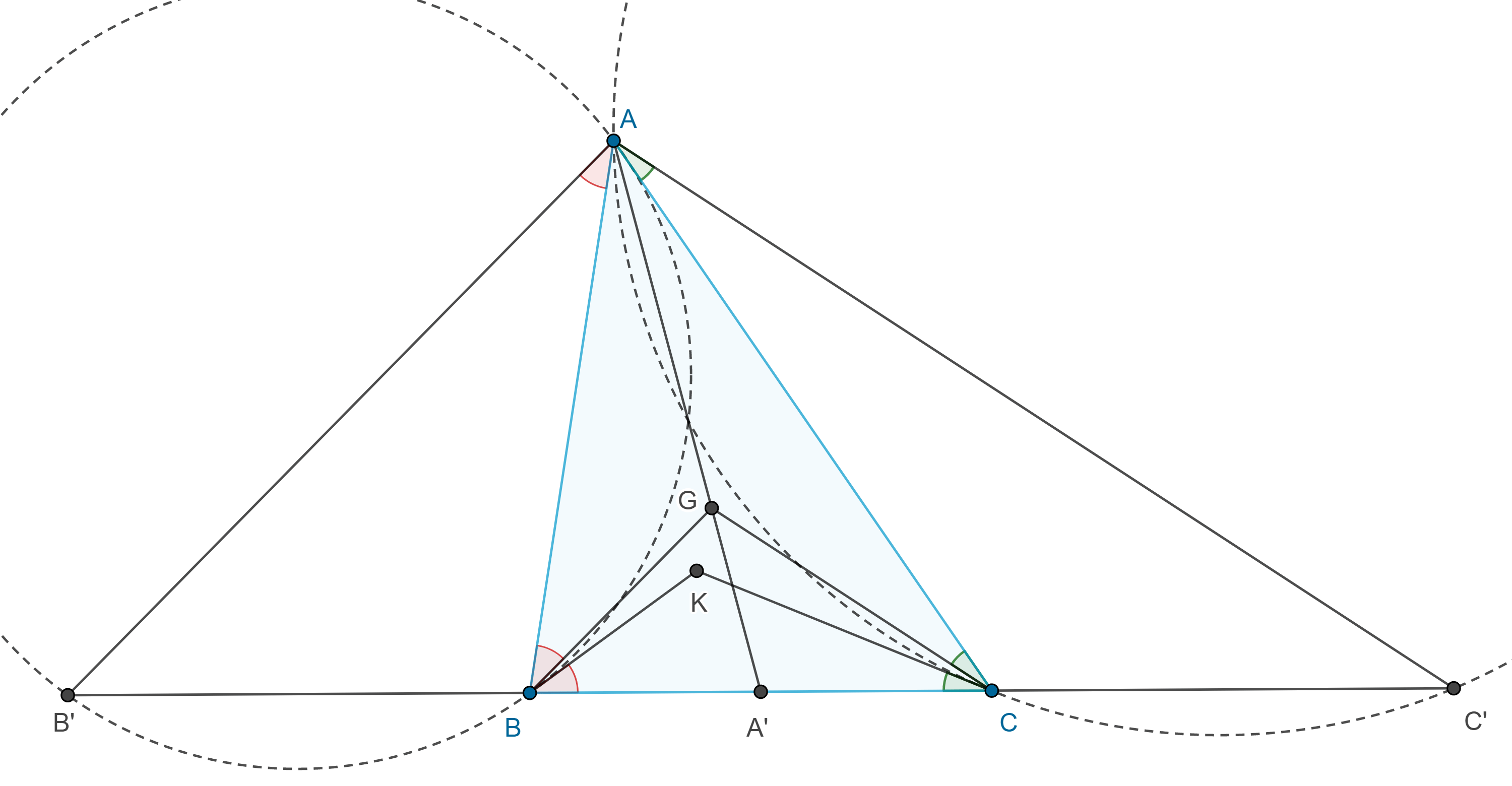
Solución. Supongamos que $\triangle ABC$ es el triángulo requerido y consideremos $G$ y $A’$ el centroide y el punto medio de $BC$ respectivamente.

Sean $B’$, $C’ \in BC$, tales que $B’A \parallel BG$ y $AC’ \parallel GC$.

Figura 5

Por el teorema de Tales tenemos
$\dfrac{1}{2} = \dfrac{A’G}{GA} = \dfrac{A’B}{BB’} = \dfrac{A’C}{CC’}$.

Por lo tanto, $BB’ = CC’ = 2A’B = BC$, así que $B’$ y $C’$ pueden ser construidos teniendo $B$ y $C$.

Por otro lado, como $B’A \parallel BG$ y $AC’ \parallel GC$ y tomando en cuenta que $K$ esta en las reflexiones de $BG$ y $CG$ respecto de las bisectrices de $\angle B$ y $\angle C$ respectivamente, tenemos lo siguiente:

$\angle B’AB = \angle GBA = \angle KBC$ y $\angle CAC’ = \angle ACG = \angle KCB$.

Y estos ángulos son conocidos.

Entonces $B’B$ y $CC’$ subtienden ángulos conocidos en $A$, por lo que podemos trazar los arcos de circunferencia que son el lugar geométrico de los puntos que subtienden estos ángulos.

Así que de la intersección de estos dos arcos resultara en el vértice faltante.

Notemos que los arcos pueden tener dos intersecciones, ser tangentes o no intersecarse, por lo tanto, existen dos, una o cero soluciones.

$\blacksquare$

Distancia del punto simediano a los lados del triángulo

Proposición 2. El punto simediano de un triángulo es el único punto dentro del triángulo cuyas distancias a los lados del triángulo son proporcionales a los respectivos lados.

Demostración. Sean $\triangle ABC$ y $K$ su punto simediano, considera $X$, $Y$ y $Z$ las proyecciones de $K$ en $BC$, $CA$ y $AB$ respectivamente, denotemos $BC = a$, $CA = b$, $AB = c$.

Figura 6

Dado que $K$ está en las tres simedianas del triángulo, por el teorema 4 de la entrada anterior, las razones de sus distancias a los lados del triángulo son proporcionales a estos:

$\begin{equation} \dfrac{KZ}{KY} = \dfrac{c}{b}, \end{equation}$
$\begin{equation} \dfrac{KY}{KX} = \dfrac{b}{a}, \end{equation}$
$ \begin{equation} \dfrac{KX}{KZ} = \dfrac{a}{c}. \end{equation}$

Por $(1)$, $(2)$ y $(3)$
$\dfrac{KX}{a} = \dfrac{KY}{b} = \dfrac{KZ}{c} = q$.

Por lo tanto,
$KZ = \dfrac{cKY}{b} = cq$,
$KY = \dfrac{b KX}{a} = bq$,
$KX = \dfrac{a KZ}{c} = aq$.

La unicidad se da por que solo los puntos en las simedianas cumplen esa propiedad y solo $K$ se encuentra en las tres simedianas.

$\blacksquare$

Corolario. 2 $KX = a \dfrac{2(ABC)}{a^2 + b^2 + c^2}$.

Demostración. Calculamos el área de $\triangle ABC$ en función de áreas menores (figura 6).

$(\triangle ABC) = (\triangle KBC) + (\triangle KCA) + (\triangle KAB) $
$= \dfrac{1}{2}(aKX + bKY + cKZ)$
$= \dfrac{q}{2}(a^2 + b^2 + c^2)$.

Por lo tanto, $KX = aq = a \dfrac{2(ABC)}{a^2 + b^2 + c^2}$.

$\blacksquare$

Teorema 4. La suma de los cuadrados de las distancias de un punto a los lados de un triángulo dado, es mínima si el punto es el punto simediano del triángulo.

Demostración. Sean $a$, $b$, $c$, $x$, $y$, $z$ seis números reales entonces la siguiente igualdad es cierta:

 $(a^2 + b^2 + c^2)(x^2 + y^2 + z^2) = (ax + by + cz)^2 + (ay – bx)^2 + (az – cx)^2 + (bz – cy)^2$.

Para comprobarlo solo hace falta realizar los productos.

Podemos pensar estas cantidades como los lados de un triángulo $\triangle ABC$, $BC = a$, $CA = b$, $AB = c$, y $x$, $y$, $z$, las distancias de un punto $K$, a los lados de $\triangle ABC$.

Notemos $ax + by + cz$ representa al menos dos veces el área del triángulo $\triangle ABC$, $2(\triangle ABC)$, que junto con $(a^2 + b^2 + c^2)$ son constantes.

Como las cantidades $(ay – bx)^2$, $(az – cx)^2$, $(bz – cy)^2$ son mayores o iguales a cero, entonces el mínimo se alcanza si se satisfacen las siguientes igualdades:
$\begin{equation} (ay – bx)^2 = (az – cx)^2 = (bz – cy)^2 = 0, \end{equation}$
$\begin{equation} ax + by + cz = 2(\triangle ABC). \end{equation}$

Por otra parte, por las ecuaciones $(1)$, $(2)$ y $(3)$ sabemos que el punto simediano cumple $(4)$ y por el corolario 2 cumple $(5)$, también podemos calcular directamente,

$KX^2 + KY^2 + KZ^2 = \dfrac{(2(\triangle ABC))^2}{a^2 + b^2 + c^2}$.

Por lo tanto, si $K$ es el punto simediano de $\triangle ABC$, se alcanza el mínimo.

$\blacksquare$

Más adelante…

En la próxima entrada veremos otra propiedad del punto simediano, o punto de Lemoine, que amerita su propia entrada, se trata de un conjunto de circunferencias asociadas a este punto.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Si $K$ es el punto simediano de $\triangle ABC$, sea $X$ la proyección de $K$ en $BC$, muestra que la reflexión de $X$ respecto de $K$ esta en la mediana que pasa por $A$.
  2.  Encuentra el punto simediano de un triángulo rectángulo.
  3. Sobre los lados de un triángulo $\triangle ABC$ construye cuadrados externamente, muestra que los lados (de los cuadrados) opuestos a los lados de $\triangle ABC$ se intersecan formando un triángulo homotético a $\triangle ABC$, con centro de homotecia el punto simediano de $\triangle ABC$.
  4. Si las simedianas de $\triangle ABC$ intersecan a su circuncírculo en $D$, $E$ y $F$ muestra que $\triangle ABC$ y $\triangle DEF$ tienen el mismo punto simediano.
  5. $i)$ Muestra que las distancias a los lados de un triángulo desde sus puntos exsimedianos son proporcionales a las longitudes de los lados del triángulo,
    $ii)$ calcula dichas distancias.
  6. Prueba que de entre todos los triángulos inscritos en un triángulo dado, el triángulo pedal del punto simediano, es el que tiene la propiedad de que la suma de los cuadrados de sus lados es mínima.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 252-257.
  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 129-145.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 215-218.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Simediana

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

La simediana es un tipo especial de ceviana relacionada con la mediana de un triángulo, veremos algunas caracterizaciones y propiedades.

Simediana, primera caracterización

Definición 1. Una simediana de un triángulo es la reflexión de una mediana respecto de la bisectriz interna que pasa por el mismo vértice. Un triángulo tiene tres simedianas.

Notación. Denotaremos a la intersección de una simediana con el lado opuesto como $S$.

Teorema 1. Una ceviana de un triángulo divide internamente al lado opuesto en la razón de los cuadrados de los lados adyacentes si y solo si es simediana.

Demostración. Sean $AA’$ la mediana y $AS$ la simediana en un triángulo $\triangle ABC$.

Sea $H$ el pie de la altura por $A$, calculamos las áreas de los triángulos $\triangle BAS$, $\triangle BAA’$, $\triangle SAC$ y $\triangle A’AC$.

Figura 1

$\begin{equation} (\triangle BAS) = \dfrac{BS \times AH}{2} = \dfrac{BA \times AS \sin \angle BAS}{2}, \end{equation}$
$\begin{equation} (\triangle BAA’) = \dfrac{BA’ \times AH}{2} = \dfrac{BA \times AA’ \sin \angle BAA’}{2}, \end{equation}$
$ \begin{equation} (\triangle SAC) = \dfrac{SC \times AH}{2} = \dfrac{SA \times AC \sin \angle SAC}{2}, \end{equation}$
$\begin{equation} (\triangle A’AC) = \dfrac{A’C \times AH}{2} = \dfrac{AA’ \times AC \sin \angle A’AC}{2}. \end{equation}$

Sea $L$ la intersección de la bisectriz de $A$ con $BC$, entonces
$\begin{equation} \angle BAS = \angle BAL – \angle SAL = \angle LAC – \angle LAA’ = \angle A’AC, \end{equation}$
$\angle BAA’ = \angle BAL + \angle LAA’ = \angle LAC + \angle SAL = \angle SAC.$

Haciendo el cociente de $(1)$ con $(4)$ y de $(2)$ con $(3)$ obtenemos
$\dfrac{BS}{A’C} = \dfrac{BA \times AS}{AA’ \times AC}$,
$\dfrac{BA’}{SC} = \dfrac{BA \times AA’}{SA \times AC}$.

Multiplicando estas dos ecuaciones obtenemos el resultado esperado
$\dfrac{BS}{SC} = \dfrac{BA^2}{AC^2}$.

El reciproco también es cierto, pues el punto $S$ que divide a $BC$ en la razón $\dfrac{BA^2}{AC^2}$, es único.

$\blacksquare$

Exsimediana

Definición 2. Las tangentes al circuncírculo de un triángulo por sus vértices se conocen como simedianas externas o exsimedianas.

Corolario. La simediana y la exsimediana que pasan por el mismo vértice de un triángulo son conjugadas armónicas respecto de los lados del triángulo que forman dicho vértice.

Demostración. En la entrada teorema de Menelao mostramos que la exsimediana de un triángulo divide externamente al lado opuesto en la razón de los cuadrados de los lados que pasan por el mismo vértice.

El resultado se sigue del hecho de que el conjugado armónico es único y el teorema 1.

$\blacksquare$

Teorema 2. Una simediana y las exsimedianas que pasan por vértices distintos son concurrentes, al punto de concurrencia se le conoce como punto exsimediano.

Demostración. En $\triangle ABC$, $AP$ y $CP$ son tangentes al circuncírculo $\Gamma$ de $\triangle ABC$ en $A$ y en $C$ respectivamente y se cortan en $P$ (figura 2).

Figura 2

Sea $D = BP \cap \Gamma$, $D \neq B$, por la proposición 5 de la entrada anterior, $\square ABCD$ es un cuadrilátero armónico.

Entonces, por el teorema 2 de la entrada anterior, el Haz $B(BCDA)$ es armónico, es decir, la tangente a $\Gamma$ en $B$, y $BD$ son conjugadas armónicas respecto de $BA$ y $BC$.

Como el conjugado armónico es único, $BP$ es simediana de $\triangle ABC$, por el corolario anterior.

$\blacksquare$

Antiparalelas (1)

Teorema 3. La $B$-simediana de un triángulo $\triangle ABC$ es el lugar geométrico de los puntos que bisecan a las antiparalelas de $AC$ respecto a $AB$ y $BC$.

Demostración. Sean $D \in AB$ y $E \in BC$ tales que $AC$ y $DE$ son antiparalelas respecto a $AB$ y $BC$, entonces $\square ADEC$ es cíclico.

Figura 3

Por lo tanto, $\angle ACE$ y $\angle EDA$ son suplementarios, en consecuencia, $\angle ACB = \angle ACE = \angle BDE$.

Sea $TB$ tangente al circuncírculo de $\triangle ABC$ en $B$, entonces $\angle ABT = \angle ACB$ pues abarcan el mismo arco, por lo tanto, la $B$-exsimediana y $DE$ son paralelas.

Sea $BS$ una ceviana de $\triangle ABC$, entonces por la proposición 2 de la entrada anterior $BS$ biseca a $DE$ si y solo si el haz $B(TCSA)$ es armónico.

En consecuencia, como el conjugado armónico de $BT$ respecto de $BC$ y $BA$ es la $B$-simediana, $BS$ biseca a $DE$ si y solo si $BS$ es simediana de $\triangle ABC$.

$\blacksquare$

Antiparalelas (2)

Proposición. 1 Si dos antiparalelas a dos de los lados de un triángulo tienen la misma longitud, entonces estas se intersecan en la simediana relativa al tercer lado, el reciproco también es cierto.

Demostración. Sean $\triangle ABC$, $E$, $G \in BC$, $F \in AB$ y $H \in CA$, tales que $EF$, $AC$ son antiparalelas respecto a $AB$ y $BC$; $AB$, $GH$ son antiparalelas respecto a $BC$ y $CA$, y $EF = GH$.

Figura 4

Como $\square AFEC$ y $\square ABGH$ son cíclicos, entonces, $\angle FEB = \angle BAC = \angle CGH$, por lo tanto $PG = PE$.

Sea $P = EF \cap GH$, dado que $FE = GH$ entonces $FP = HP$.

Si $S = AP \cap BC$, considera $I \in AB$, $J \in CA$, tales que $IS \parallel FE$ y $JS \parallel GH$, entonces $\triangle ASI \sim \triangle APF$ y $\triangle ASJ \sim \triangle APH$.

Por lo tanto, $\dfrac{SI}{PF} = \dfrac{AS}{AP} = \dfrac{SJ}{PH}$, como $PF = PH$ entonces $SI = SJ$.

Por otro lado $\triangle SBI \sim \triangle ABC \sim \triangle SJC$, esto es
$\dfrac{SB}{SI} = \dfrac{AB}{AC}$ y $\dfrac{SJ}{SC} = \dfrac{AB}{AC}$.

Como resultado de multiplicar estas dos ecuaciones obtenemos
$\dfrac{BS}{SC} = \dfrac{AB^2}{AC^2}$.

Por el teorema 1, esto implica que $AS$ es la $A$-simediana de $\triangle ABC$.

Notemos que el reciproco también es cierto, esto es, si dos antiparalelas a dos de los lados de un triángulo se intersecan en la simediana relativa al tercer lado, entonces estas tienen la misma longitud.

Esto lo podemos ver tomando la prueba anterior en sentido contrario.

$\blacksquare$

Otra caracterización importante

Teorema 4. Una simediana es el lugar geométrico de los puntos (dentro de los ángulos internos del triángulo o sus ángulos opuestos por el vértice) tales que la razón de sus distancias a los lados adyacentes a la simediana, es igual a la razón entre esos lados.

Demostración. Sean $\triangle ABC$, $A’$ el punto medio de $BC$ y $P \in AA’$, considera las proyecciones $P_c$, $P_b$ de $P$ en $AB$ y $AC$ respectivamente y $A’_c$, $A’_b$, las correspondientes de $A’$.

Figura 5

Como $\triangle APP_c \sim \triangle AA’A’_c$ y $\triangle APP_b \sim \triangle AA’A’_b$ entonces
$\dfrac{PP_c}{A’A’_c} = \dfrac{AP}{AA’} = \dfrac{PP_b}{A’A’_b}$.

Tomando en cuenta que los triángulos $\triangle ABA’$ y $\triangle AA’C$ tienen la misma altura desde $A$, tenemos lo siguiente:
$\dfrac{AC}{AB} = \dfrac{PP_c}{PP_b} = \dfrac{A’A’_c}{A’A’_b}$
$\Leftrightarrow AC \times A’A’_b = AB \times A’A’_c$
$\Leftrightarrow (\triangle AA’C) = (\triangle AA’B)$
$ \Leftrightarrow A’C = BA’$.

Por lo tanto, la mediana de un triángulo es el lugar geométrico de los puntos tales que la razón de sus distancias a los lados adyacentes a la mediana es el inverso de la razón entre dichos lados.

Denotamos la distancia de un punto $P$ a una recta $l$ como $d(P, l)$.

Para $P \in AA’$ considera $P’ \in AS$ su reflexión respecto de la bisectriz de $\angle BAC$, entonces

$\dfrac{d(P’, AB)}{d(P’, AC)} = \dfrac{d(P, AC)}{d(P’, AB)} = \dfrac{AB}{AC}$.

$\blacksquare$

Proposición 2. La recta que une las proyecciones de un punto en la simediana (mediana) de un triángulo, sobre los lados adyacentes, es perpendicular a la mediana (simediana) que pasa por el mismo vértice.

Demostración. En un triángulo $\triangle ABC$ sean $AA’$ la mediana y $AS$ la simediana, considera $P \in AS$ y $D$, $E$, las proyecciones de $P$ en $CA$ y $AB$ respectivamente.

Figura 6

Como $\angle PEA + \angle ADP = \pi$ entonces $\square AEPD$ es cíclico, así que $\angle EAP = \angle EDP$, por la ecuación $(5)$, $\angle EAP = \angle A’AD$.

Sean $F = PD \cap AA’$ y $G = DE \cap AA’$, en los triángulos $\triangle ADF$ y $\triangle DGF$, $\angle FAD = \angle GDF$ y $\angle DFG$ es un ángulo común, por lo tanto son semejantes.

Como $PD \perp AC$ entonces $DE \perp AA’$.

El caso para la mediana es análogo.

$\blacksquare$

Más adelante…

Así como las medianas de un triángulo son concurrentes, las simedianas también son concurrentes, pero dicho punto tiene propiedades importantes por si mismo, y de eso hablaremos en la próxima entrada.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que las segundas intersecciones de una mediana y su correspondiente simediana con el circuncírculo del triángulo, determinan una recta paralela al lado del triángulo relativo a la mediana considerada.
  2.  Sea $\triangle ABC$ un triángulo acutángulo, $D$ y $A’$ las proyecciones de $A$ y $O$, el circuncírculo de $\triangle ABC$, en $BC$ respectivamente, sean $E = BO \cap AD$, $F = CO \cap AD$ y considera $P$ el segundo punto en común entre los circuncírculos de $\triangle ABE$ y $\triangle AFC$, demuestra que $AP$ es la $A$-simediana de $\triangle ABC$.
  3. Sea $P$ un punto dentro de un triángulo isósceles $\triangle ABC$ con $AB = AC$, tal que $\angle PBC = \angle ACP$, si $A’$ es el punto medio de $BC$, muestra que $\angle BPA’$ y $\angle CPA$ son suplementarios.
  4. Sean $\triangle ABC$, $D \in AB$ y $E \in CA$ tal que $DE \parallel BC$, considera $P = BE \cap CD$, los circuncírculos de $\triangle BDP$ y $\triangle CEP$ se intersecan en $P$ y $Q$, muestra que $\angle BAQ = \angle PAC$.
  5. La $A$-simediana $AS$ y la $A$-meidnana $AA’$ de un triángulo $\triangle ABC$ intersecan otra vez a su circuncírculo en $S’$ y $L$ respectivamente, prueba que la rectas de Simson de $S’$ y $L$ son perpendiculares a $AA’$ y a $AS$ respectivamente.
  6. Muestra que las exsimedianas de un triángulo tienen la misma propiedad que se señala en el teorema 4 respecto a las simedianas, pero esta vez para los puntos dentro de los ángulos externos del triángulo.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 247-252.
  • Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 86-92.
  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 129-145.
  • Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 66-70.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»