relación inversa archivos

Introducción

En esta entrada retomaremos el tema de relaciones que vimos anteriormente. Esta vez definiremos una nueva relación a partir de dos relaciones: la composición. Veremos si la composición de dos relaciones tiene propiedades como la conmutatividad o la asociatividad.

Definamos la composición

Definición. Sean $R_{1}$ y $R_{2}$ relaciones de $A$ en $B$ y de $C$ en $D$ respectivamente. Definimos a la composición de $R_{1}$ con $R_{2}$ como el siguiente conjunto:

$R_{2} \circ R_{1} = {(a, c) : \exists b ((a, b) \in R_{1} y (b, c) \in R_{2})}$ .

En otros símbolos, si $a, b, c$ son elementos tales que $a R_{1} b$ y $b R_{2} c$ , entonces se cumplirá que $a (R_{2} \circ R_{1}) c$ .

Ejemplo.

Sean $X = {0, 1}$ y $Y = {1, 2}$ y $Z = {1, 2, 3, 4}$ conjuntos. Sean $R_{1}$ y $R_{2}$ relaciones de $X$ en $Y$ y de $Y$ en $Z$ definidas como sigue:

$R_{1} = {(0, 1), (0, 2)} y R_{2} = {(1, 3), (1, 4)}$ .

Podemos hacer diagramas de ambas relaciones en una misma figura como sigue:

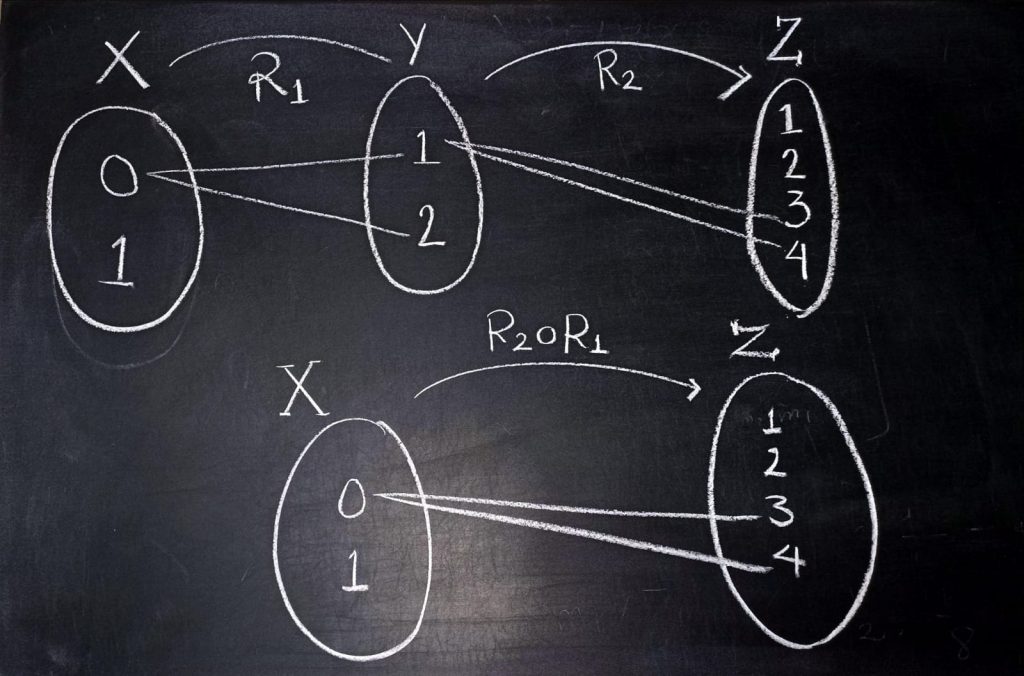
Luego, la composición de $R_{2} \circ R_{1}$ resulta ser el siguiente conjunto:

$R_{2} \circ R_{1} = {(0, 3), (0, 4)}$ .

Para leerlo en el diagrama, podemos ver que hay un «camino» de $0$ a $3$ que usa las flechas de $0$ a $1$ , y de $1$ a $3$ . También hay un «camino» de $0$ a $4$ que usa las flechas de $0$ a $1$ , y de $1$ a $4$ .

Además de notarlo en el diagrama, podemos verificar mediante la definición. La pareja $(0, 3)$ está pues $1 \in Y$ tal que $(0, 1) \in R_{1}$ y $(1, 3) \in R_{2}$ . Por su parte, la pareja $(0, 4)$ está pues existe $1 \in Y$ tal que $(0, 1) \in R_{1}$ y $(1, 4) \in R_{2}$ .

Algunos resultados

A continuación hablaremos de algunos resultados de la composición, la relación inversa y la relación identidad.

Proposición. Si $R$ es una relación en $A$ , entonces $R \circ I d_{A} = R$ .

Demostración.

Sea $R$ una relación en $A$ . Veamos que $R \circ I d_{A} = R$ .

$\subseteq$ ] Sea $(x, z) \in R \circ I d_{A}$ , entonces existe $y$ tal que $(x, y) \in I d_{A}$ y $(y, z) \in R$ .
Luego, como $(x, y) \in I d_{A}$ se sigue que $x = y$ y así $(y, z) = (x, z) \in R$ .

$\supseteq$ ] Sea $(a, c) \in R$ . Como $a, c \in A$ , se sigue que $(a, a) \in I d_{A}$ . Por lo que existe $a$ tal que $(a, a) \in I d_{A}$ y $(a, c) \in R$ . Por lo tanto, $(a, c) \in R \circ I d_{A}$ .

Por lo tanto, $R \circ I d_{A} = R$ .

Proposición. Si $R$ es una relación de $A$ en $B$ , entonces $I d_{I m R} \subseteq R \circ R^{- 1}$ .

Demostración.

Sea $y \in I m (R)$ . Como $y \in I m R$ existe $a \in A$ tal que $(a, y) \in R$ , y por definición de relación inversa tenemos que $(y, a) \in R^{- 1}$ .

Encontramos $a \in A$ tal que $(y, a) \in R^{- 1}$ y $(a, y) \in R$ , esto es $(y, y) \in R \circ R^{- 1}$ . Así, $I d_{I m R} \subseteq R \circ R^{- 1}$ .

Propiedades de la composición

Hemos dicho hasta ahora que la composición es una operación entre dos conjuntos que son relaciones. Por ello, podemos preguntarnos qué pasa con la conmutatividad y la asociatividad de dicha operación.

En general, no es cierto que $R_{1} \circ R_{2} = R_{2} \circ R_{1}$ , es decir, la composición no es conmutativa.

Ejemplo.

Consideremos $X = {1, 2}$ . Sean $R_{1} = {(1, 1), (1, 2)}$ y $R_{2} = {(1, 2), (2, 1)}$ relaciones en $X$ .

Por un lado tenemos que

$R_{1} \circ R_{2} = {(2, 1), (2, 2)}$

y por otro lado

$R_{2} \circ R_{1} = {(1, 2), (1, 1)}$ .

De modo que $R_{1} \circ R_{2} \neq R_{2} \circ R_{1}$ .

El segundo resultado que tenemos es que la asociatividad siempre se cumple.

Proposición. Si $R_{1}$ , $R_{2}$ y $R_{3}$ son relaciones, entonces, $(R_{3} \circ R_{2}) \circ R_{1} = R_{3} \circ (R_{2} \circ R_{1})$ .

Demostración.

Sean $R_{1}$ , $R_{2}$ y $R_{3}$ relaciones. Si $(x, z) \in (R_{3} \circ R_{2}) \circ R_{1}$ , existe $y$ tal que $(x, y) \in R_{1}$ y $(y, z) \in R_{3} \circ R_{2}$ . Luego, como $(y, z) \in R_{3} \circ R_{2}$ , existe $w$ tal que $(y, w) \in R_{2}$ y $(w, z) \in R_{3}$ . Así, dado que $(x, y) \in R_{1}$ y $(y, w) \in R_{2}$ , $(x, w) \in R_{2} \circ R_{1}$ , y como $(w, z) \in R_{3}$ entonces $(x, z) \in R_{3} \circ (R_{2} \circ R_{1})$ . Por tanto, $(R_{3} \circ R_{2}) \circ R_{1} \subseteq R_{3} \circ (R_{2} \circ R_{1})$ .
Ahora, si $(x, z) \in R_{3} \circ (R_{2} \circ R_{1})$ , existe $w$ tal que $(x, w) \in R_{2} \circ R_{1}$ y $(w, z) \in R_{3}$ . Luego, existe $y$ tal que $(x, y) \in R_{1}$ y $(y, w) \in R_{2}$ y, por tanto, $(x, y) \in R_{1}$ y $(y, z) \in R_{3} \circ R_{2}$ , por lo que $(x, z) \in (R_{3} \circ R_{2}) \circ R_{1}$ . En consecuencia, $R_{3} \circ (R_{2} \circ R_{1}) \subseteq (R_{3} \circ R_{2}) \circ R_{1}$ .

Por lo tanto, $(R_{3} \circ R_{2}) \circ R_{1} = R_{3} \circ (R_{2} \circ R_{1})$ .

Hemos probado que la composición de relaciones es asociativa y a su vez concluimos que en general no conmuta.

Tarea moral

Demuestra que si $R$ es una relación arbitraria, $R \circ \emptyset = \emptyset = \emptyset \circ R$ .
Prueba que si $R$ es una relación en $A$ , entonces $R = I d_{A} \circ R$ .
Si $R$ y $S$ son relaciones, entonces $S \circ R \subseteq d o m (R) \times i m (S)$ .
Sean $A = {1, 2, 3}$ , $B = {1, 2}$ y $C = {1, 2, 3, 4}$ . Sean $R_{1} = {(1, 2), (3, 1)}$ y $R_{2} = {(1, 4), (2, 1), (2, 3)}$ relaciones de $A$ en $B$ y de $B$ en $C$ respectivamente. Calcula $R_{2} \circ R_{1}$ .

Más adelante…

Ya hemos hablado de relaciones en general, y de cómo componerlas. A partir de ahora comenzaremos a pedirle más propiedades a nuestras relaciones para que se conviertan en algunos tipos de relaciones muy especiales: funciones, relaciones de equivalencia, órdenes, etc. Comenzaremos a hacer esto en la siguiente entrada, en donde veremos qué se le debe pedir a una relación para que sea una función. Así, todas las funciones son relaciones, sin embargo, no toda relación será función.

Entradas relacionadas

Entrada relacionada: Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición
Ir a Teoría de los Conjuntos I
Entrada anterior: Teoría de los Conjuntos I: Relaciones
Siguiente entrada: Teoría de los Conjuntos I: Funciones

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Introducción

En esta nueva entrada veremos el concepto de relación, para lo cual es necesario tener fresco el concepto de producto cartesiano. Así mismo, definiremos nuevos conjuntos a partir de una relación, como lo son el dominio, la imagen de una relación, la imagen de un conjunto bajo una relación y el concepto de relación inversa. Concluiremos esta entrada definiendo a la imagen inversa de un conjunto bajo una relación.

Relación

Definición. Sean $A$ y $B$ conjuntos. Una relación $R$ de $A$ en $B$ es un subconjunto de $A \times B$ . A $A$ le llamamos el dominio de la relación y a $B$ el codominio.

Si $A = B$ diremos que $R$ es una relación en $A$ .

Ejemplo 1.

Sea $A = {\emptyset, {\emptyset}}$ y $B = {\emptyset, {{\emptyset}}}$ y definimos $R$ como:

$R = {(\emptyset, \emptyset), (\emptyset, {{\emptyset}})}$ .

Dado que $A \times B = {(\emptyset, \emptyset), (\emptyset, {{\emptyset}}), ({\emptyset}, \emptyset), ({\emptyset}, {{\emptyset}})}$ y $R \subseteq A \times B$ decimos que $R$ es una relación de $A$ en $B$ .

Ejemplo 2.

Sea $A = {1, 2}$ y $B = {1, 2, 3}$ . Definimos $S = {(1, 1), (1, 2), (1, 3)}$ . Tenemos que $S$ es una relación de $A$ en $B$ . En efecto, esto sucede pues $S = {(1, 1), (1, 2), (1, 3)} \subseteq A \times B$ , ya que $A \times B = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3)}$ .

Podemos representar a $S$ mediante el siguiente diagrama. Del lado izquierdo hemos puesto al dominio $A$ . Del lado derecho al codominio $B$ . Para cada pareja $(a, b)$ de la relación, hemos puesto una flecha de $a$ a $b$ .

Definición. Si $(x, y) \in R$ con $R$ relación, decimos que $x$ está relacionado con $y$ mediante $R$ (o simplemente que $x$ está relacionado con $y$ si por el contexto es claro quién es $y$ ) y lo denotaremos como $x R y$ .

Si retomamos el Ejemplo 1 podemos decir que $\emptyset R \emptyset$ y $\emptyset R {{\emptyset}}$ .

A partir del Ejemplo 2 podemos decir que $1 S 1$ , $1 S 2$ y $1 S 3$ .

Relaciones relevantes

A continuación hablaremos de algunos ejemplos de relaciones que nos serán de utilidad más adelante.

Relación vacía.
Si $R = \emptyset$ , entonces $R$ será llamada la relación vacía. Esto tiene sentido pues $\emptyset \subseteq A \times B$ para cualesquiera $A$ y $B$ conjuntos.
Relación identidad.
Sea $A$ un conjunto cualquiera. Definimos la relación identidad en $A$ como:
$I d_{A} = {(a, a) : a \in A} .$
Notamos que $I d_{A} \subseteq A \times A$ pues para cualquier $(x, y) \in I d_{A}$ se tiene que $x = y$ con $x, y \in A$ , lo que significa que $(x, y) \in A \times A$ .
Relación de pertenencia.
Sea $A$ un conjunto. Definimos a la relación de pertenencia en $A$ como el siguiente conjunto:
$\in_{A} = {(a, b) : a \in A, b \in A, a \in b} .$
Relación de contención.
Sea $A$ un conjunto. Definimos a la relación de contención en $A$ como el siguiente conjunto:
$\subseteq_{A} = {(a, b) : a \in A, b \in A, a \subseteq b} .$

Dominio de una relación

Ya que hemos definido el concepto de relación de $A$ en $B$ , a continuación definiremos al dominio de una relación.

Definición. Sea $R$ una relación de $A$ en $B$ . Definimos el dominio de la relación como:

$dom (R) = {x \in A : \exists y \in B ((x, y) \in R)}$ .

Ejemplo.

Sean $A = B = {1, 2}$ . Definimos $R = {(1, 2), (1, 1), (2, 2)} \subseteq A \times B$ . Tenemos que $dom (R) = {1, 2}$ pues para $1 \in A$ existe, digamos, $1 \in B$ tal que $(1, 1) \in R$ y para $2 \in A$ existe $2 \in B$ tal que $(2, 2) \in R$ .

Imagen de una relación

A continuación vamos a definir lo análogo al dominio activo, pero para el codominio. Le daremos un nombre al subconjunto de elementos del codominio que sí participan en la relación.

Definición. Sea $R$ una relación de $A$ en $B$ . Definimos la imagen de $R$ como el conjunto

$im (R) = {y \in B : \exists x \in A ((x, y) \in R)}$ .

Ejemplo.

Sean $A = B = {1, 2}$ . Definimos $R = {(1, 2), (2, 2)} \subseteq A \times B$ .

Tenemos que $im (R) = {2}$ pues para $2 \in B$ existe, digamos $2 \in A$ tal que $(2, 2) \in R$ . Sin embargo, $1 \notin im (R)$ pues $R$ no tiene ninguna pareja de la forma $(x, 1)$ con $x \in A$ .

Imagen de un conjunto bajo una relación

A veces queremos preguntarnos por los elementos del codominio que participan en la relación, pero sólamente con ciertos elementos del dominio. La siguiente definición establece esto.

Definición. Sea $R$ una relación de $A$ en $B$ . Sea $C \subseteq A$ . Definimos a la imagen de $C$ bajo $R$ como el el conjunto

$R [C] = {y \in B : \exists x \in C (x R y)}$ .

Ejemplo.

Sean $A = {1, 2}$ y $B = {1, 2, 3, 4}$ conjuntos. Sea $R = {(1, 1), (1, 3), (2, 1), (2, 2), (2, 4)}$ , la cual es una relación de $A$ en $B$ . Tomemos $C = {1} \subseteq A$ . Tenemos que

$R [C] = {y \in {1, 2, 3, 4} : \exists x \in {1} (x R y)} = {1, 3}$ .

Relación inversa

Para cerrar esta entrada, introduciremos un concepto más: el de relación inversa.

Definición. Sean $A$ y $B$ conjuntos. Sea $R$ una relación de $A$ en $B$ . Definimos la relación inversa de $R$ como la relación $R^{- 1}$ de $B$ en $A$ definida como sigue:

$R^{- 1} = {(b, a) : (a, b) \in R}$ .

Notemos que la relación inversa intercambia el orden de las entradas de las parejas ordenadas que son elementos de la relación $R$ .

Ejemplo.

Sea $A = {\emptyset}$ y $B = {\emptyset, {\emptyset}}$ y definimos $R$ como:

$R = {(\emptyset, \emptyset), (\emptyset, {\emptyset})} .$

Tenemos que

$R^{- 1} = {(\emptyset, \emptyset), ({\emptyset}, \emptyset)} .$

En efecto, como $(\emptyset, \emptyset) \in R$ tendremos que $(\emptyset, \emptyset) \in R^{- 1}$ y como $({\emptyset}, \emptyset) \in R$ tendremos que $(\emptyset, {\emptyset}) \in R^{- 1}$ .

Proposición. Sea $R$ una relación. Se cumple que $(R^{- 1})^{- 1} = R$ .

Demostración.

Tenemos que

$\begin{aligned} (R^{- 1})^{- 1} & = {(x, y) : (y, x) \in R^{- 1}} \\ = {(x, y) : (x, y) \in R} \\ = R . \end{aligned}$

Imagen inversa de un conjunto bajo una relación

Definición. Sea $R$ una relación de $A$ en $B$ . Sea $C \subseteq B$ . Definimos a la imagen inversa de $C$ bajo $R$ como el el conjunto

$R^{- 1} [C] = {x \in A : \exists y \in C (x R y)}$ .

Ejemplo.

Sean $A = {1, 2}$ y $B = {1, 2, 3, 4}$ conjuntos. Si $R = {(1, 1), (1, 3), (2, 1), (2, 2), (2, 4)}$ es una relación de $A$ en $B$ , entonces $R^{- 1} = {(1, 1), (1, 2), (2, 2), (3, 1), (4, 2)}$ . Tomemos $C = {1} \subseteq B$ . Tenemos que

$R^{- 1} [C] = {x \in {1, 2} : \exists y \in {1} (x R y)} = {1, 2}$ .

Tarea moral

La siguiente lista de ejercicios te permitira reforzar los conceptos de relación, dominio activo e imagen.

Si $R$ es la relación vacía, encuentra el dominio y la imagen de $R$ .
Para $R$ es la relación identidad de $A$ , encuentra el dominio y la imagen de $R$ .
Sea $R = {(1, 2), (3, 4)}$ una relación de $A = {1, 2, 3}$ en $B = {1, 2, 3, 4}$ . Encuentra el dominio y la imagen de $R$ . Además, escribe al conjunto $R^{- 1}$ .
Si $R$ es la relación identidad de $A$ , describe quién es $R^{- 1}$ .

Más adelante…

En la siguiente entrada continuaremos con el tema de relaciones. Esta vez trataremos el tema de composición de relaciones. Definiremos a la composición de relaciones como una relación que se construye a partir de al menos dos relaciones cuyos dominios y codominios tienen ciertas propiedades en común.

Entradas relacionadas

Entradas relacionadas:
Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición
Álgebra Superior I: Tipos de relaciones en conjuntos
Ir a: Teoría de los Conjuntos I
Entrada anterior: Teoría de los Conjuntos I: Propiedades del producto cartesiano
Siguiente entrada: Teoría de los Conjuntos I: Composición de relaciones

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: relación inversa

Teoría de los Conjuntos I: Composición de relaciones

Introducción

Definamos la composición

Algunos resultados

Propiedades de la composición

Tarea moral

Más adelante…

Entradas relacionadas

Agradecimientos

Teoría de los Conjuntos I: Relaciones

Introducción

Relación

Relaciones relevantes

Dominio de una relación

Imagen de una relación

Imagen de un conjunto bajo una relación

Relación inversa

Imagen inversa de un conjunto bajo una relación

Tarea moral

Más adelante…

Entradas relacionadas

Agradecimientos