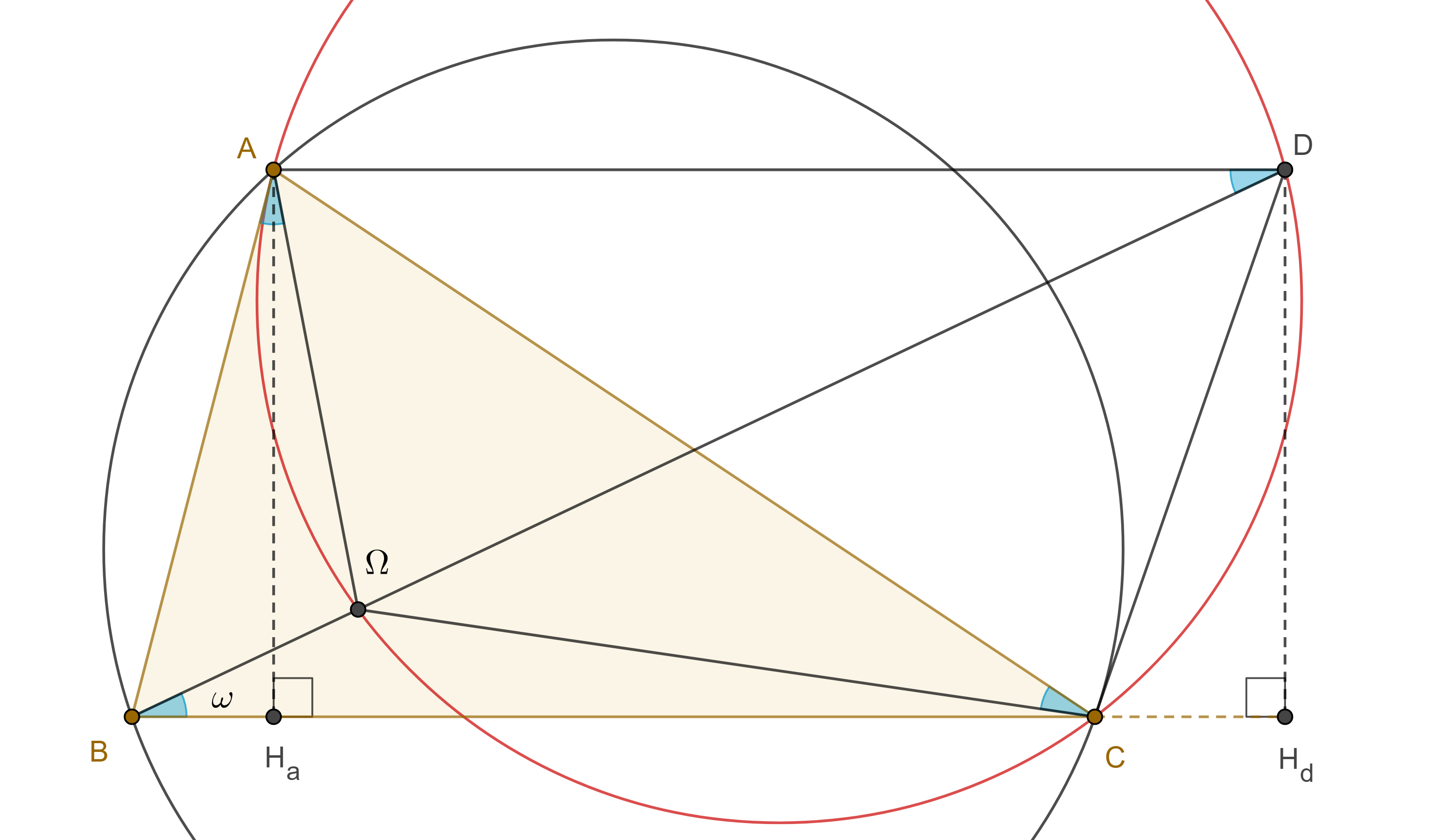Archivo de la etiqueta: puntos de Brocard

Geometría Moderna I: Circunferencia de Brocard

Por Rubén Alexander Ocampo Arellano

Introducción

Con esta entrada concluimos la unidad tres y en general temas relacionados con el triángulo, hablaremos de la circunferencia de Brocard y el primer triángulo de Brocard, veremos como se relacionan con los puntos de Brocard.

Circunferencia de Brocard

Definición. La circunferencia $Γ (K O)$ que tiene como diámetro el segmento que une el punto simediano $K$ y el circuncentro $O$ de un triángulo se conoce como circunferencia de Brocard.

El triángulo cuyos vértices son las segundas intersecciones de las mediatrices de un triángulo con su circunferencia de Brocard es el primer triángulo de Brocard.

Observación. Recordemos que el centro de la primera circunferencia de Lemoine es el punto medio entre el punto simediano y el circuncentro de un triángulo, por lo tanto, la circunferencia de Brocard y la primera circunferencia de Lemoine son concéntricas.

Teorema 1. Los puntos de Brocard están en la circunferencia de Brocard.

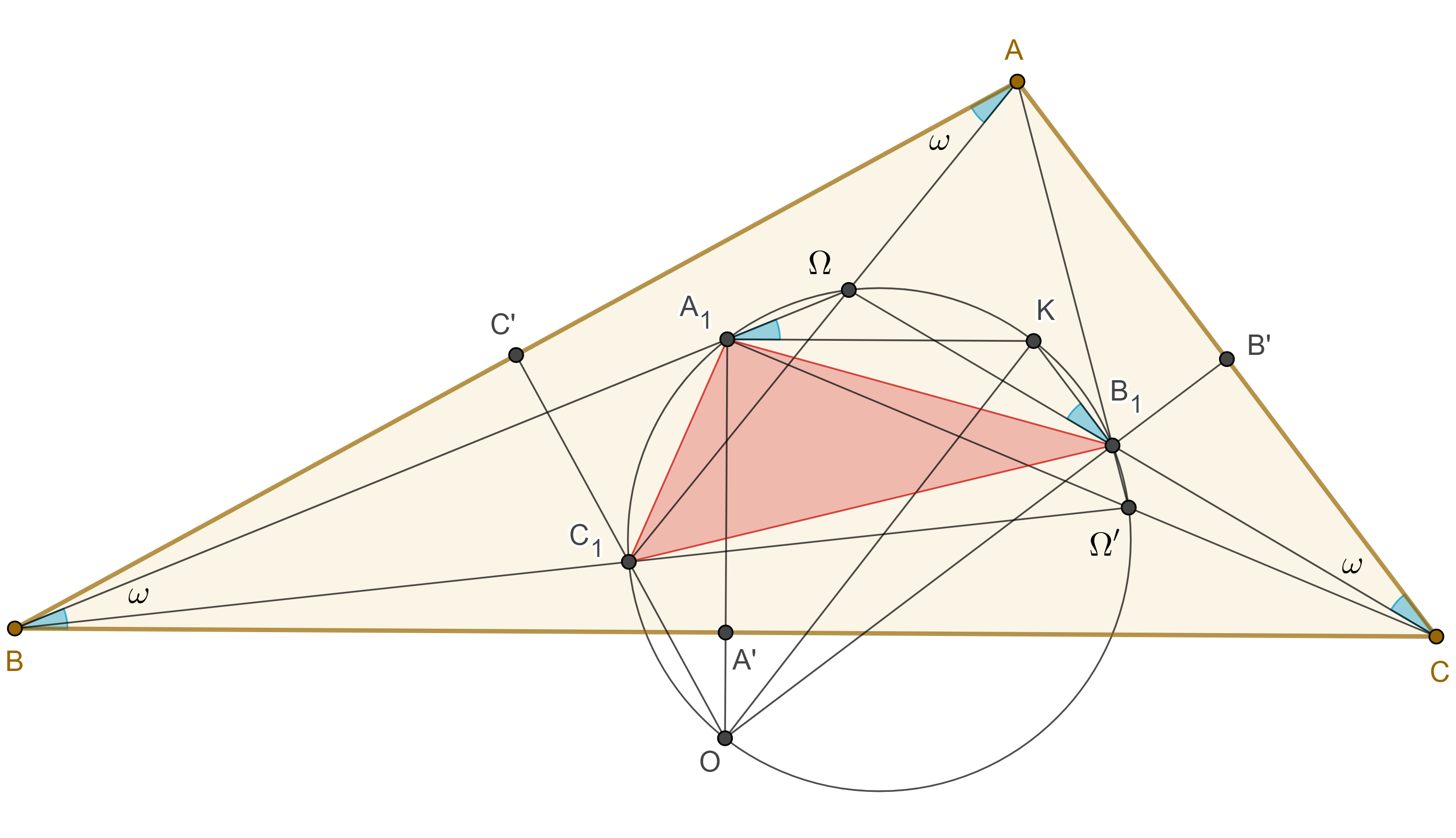
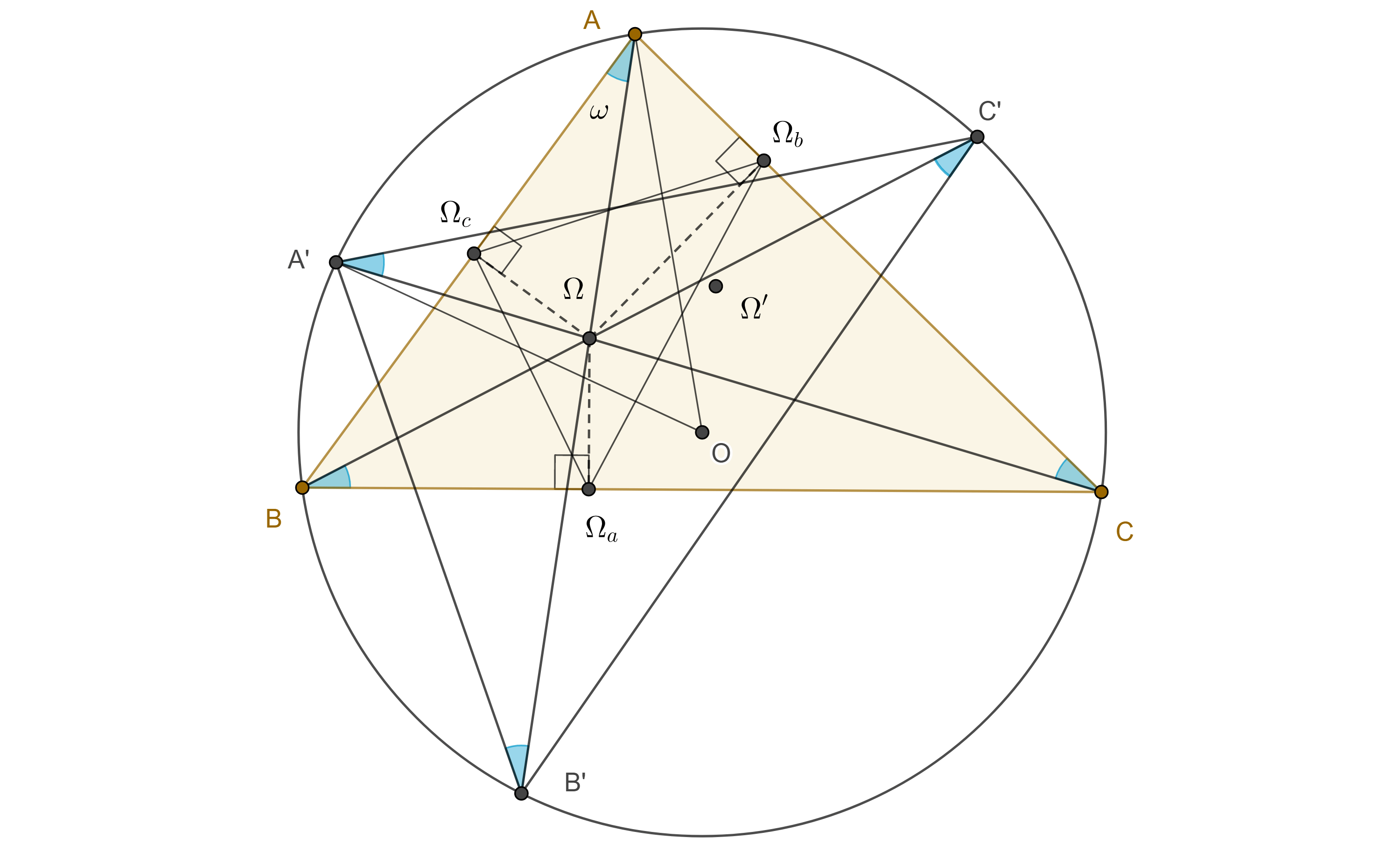
Demostración. En $△ A B C$ sea $Ω$ el primer punto de Brocard, $K$ el punto simediano, $O$ el circuncentro y $A^{'}$ , $B^{'}$ , $C^{'}$ , los puntos medios de $B C$ , $C A$ y $A B$ respectivamente.

Recordemos que las distancias de $K$ a los lados del triángulo son proporciónales a estos,
$d (K, B C) = a \frac{2 (△ A B C)}{a^{2} + b^{2} + c^{2}}$

En un ejercicio de la entrada anterior se pide mostrar que
$\frac{1}{\tan ω} = \cot ω = \frac{a^{2} + b^{2} + c^{2}}{4 (△ A B C)}$ .

Donde $ω$ es el ángulo de Brocard y $a$ , $b$ , $c$ los lados de $△ A B C$ .

Por lo tanto, $d (K, B C) = \frac{a}{2} \tan ω$ .

Sea $A_{1} = O A^{'} \cap B Ω$ , en $△ A_{1} B A^{'}$ , $A^{'} A_{1} = \frac{a}{2} \tan ω$ .

Esto implica que $A_{1} K ∥ B C$ , como $O A_{1}$ es mediatriz de $B C$ entonces $∠ O A_{1} K = \frac{π}{2}$ , y por lo tanto $A_{1} \in Γ (K O)$ .

De manera similar si consideramos $B_{1}$ la intersección del rayo $C Ω$ con la mediatriz de $C A$ , podemos ver $B_{1} K ∥ C A$ y que $B_{1} \in Γ (K O)$ .

Como $A_{1} K ∥ B C$ y $B_{1} K ∥ C A$ entonces $∠ K A_{1} Ω = ω = ∠ K B_{1} Ω$ .

En consecuencia, el cuadrilátero $Ω A_{1} B_{1} K$ es cíclico, pero el circuncírculo de $△ A_{1} B_{1} K$ , es la circunferencia de Brocard.

Por lo tanto, el primer punto de Brocard $Ω$ , está en la circunferencia de Brocard.

Sea $Ω^{'}$ el segundo punto de Brocard, como $A_{1}$ y $B_{1}$ están en las mediatrices de $B C$ y $C A$ entonces $△ A_{1} B C$ y $△ B_{1} C A$ son isósceles y $∠ A_{1} C B = ∠ B_{1} A C = ∠ Ω^{'} C B = ∠ Ω^{'} A C = ω$ .

Esto implica que $C A_{1}$ y $A B_{1}$ se intersecan en $Ω^{'}$ .

Ya que $A_{1} K ∥ B C$ y $B_{1} K ∥ C A$ , entonces, $∠ Ω^{'} A_{1} K = ω$ y $∠ K B_{1} Ω^{'} = π - ω$ .

Esto implica que $A_{1} Ω B_{1} K$ es cíclico, y así el segundo punto de Brocard está en la circunferencia de Brocard.

Corolario 1. Un triángulo y su primer triángulo de Brocard están en perspectiva desde los puntos de Brocard.

Demostración. En el teorema anterior vimos que $B A_{1}$ y $C B_{1}$ se intersecan en el primer punto de Brocard, de manera similar se puede ver que $A$ , $C_{1}$ y $Ω$ son colineales.

También mostramos que $C A_{1} \cap A B_{1} = Ω^{'}$ , de manera análoga podemos ver que $B C_{1}$ pasa por $Ω^{'}$ .

Por lo tanto $Ω$ y $Ω^{'}$ son centros de perspectiva de $△ A B C$ y $△ A_{1} B_{1} C_{1}$ .

Corolario 2. $△ A B C$ y su primer triángulo de Brocard son semejantes.

Demostración. Como $B_{1} K ∥ C A$ , $A_{1} K ∥ B C$ y tomando en cuenta que $A_{1} C_{1} B_{1} K$ es cíclico entonces $∠ A C B = π - ∠ A_{1} K B_{1} = ∠ B_{1} C_{1} A_{1}$ .

De manera similar vemos que $∠ A = ∠ A_{1}$ y $∠ B = ∠ B_{1}$ .

Conjugado isotómico del punto simediano

En la entrada triángulos en perspectiva vimos que si dos triángulos tienen dos centros de perspectiva entonces existe un tercero, en la siguiente proposición describimos este punto.

Proposición 1. El tercer centro de perspectiva entre un triángulo y su triángulo de Brocard es el conjugado isotómico del punto simediano respecto del triángulo original.

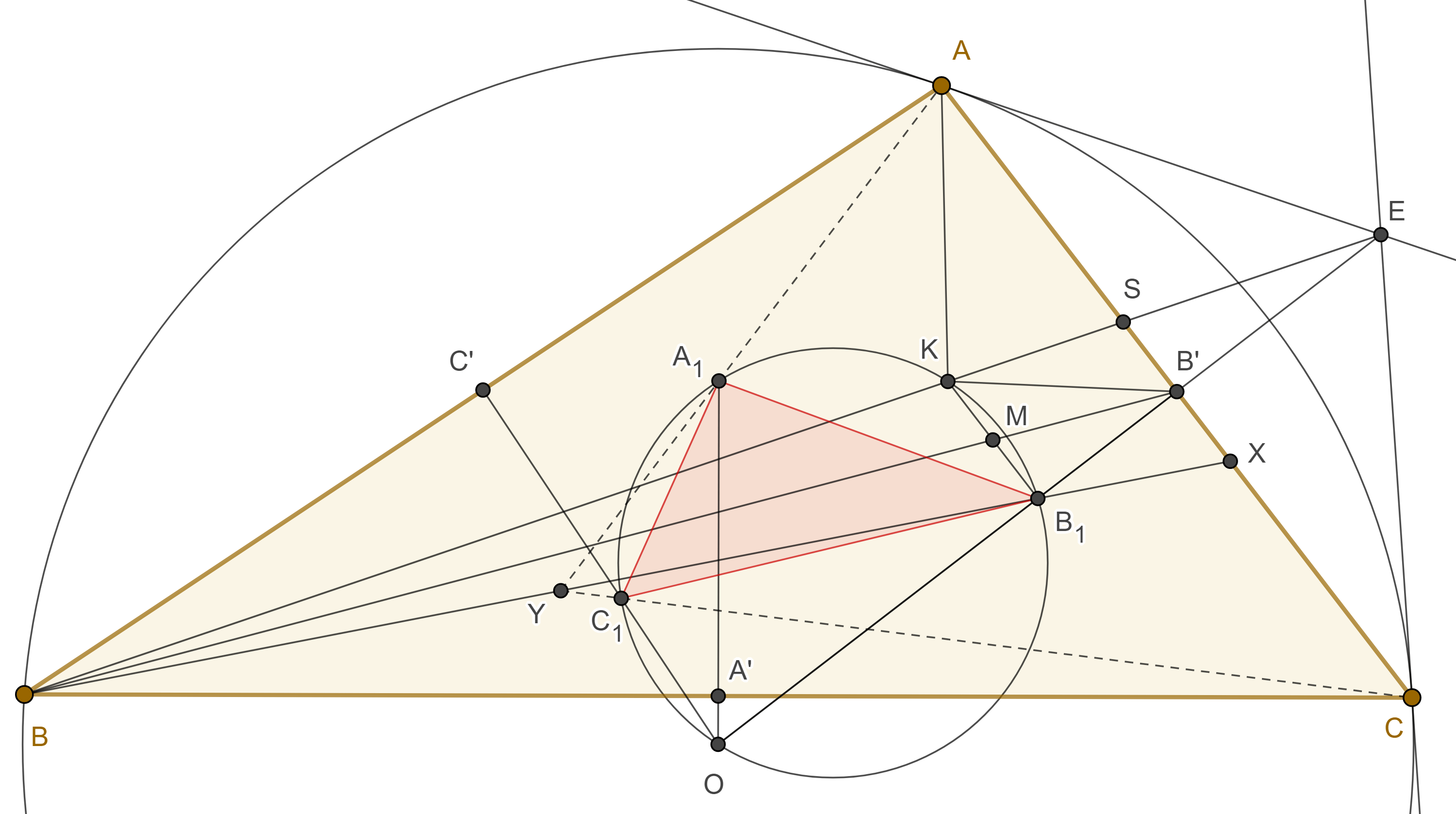
Demostración. Bajo la misma notación del teorema anterior, Recordemos que la $A$ -simediana y la $A$ -exsimediana son conjugadas armónicas respecto de $A B$ , $A C$ .

También sabemos que $B K$ y la $A$ -exsimediana se intersecan en un punto exsimediano, es decir el punto de intersección de las tangentes por $A$ y $C$ al circuncírculo de $△ A B C$ .

Sea $S = B K \cap A C$ , entonces la hilera $B K S E$ es armónica, así, el haz $B^{'} (B K S E)$ es armónico.

Tomando en cuenta que $O B_{1} B^{'} E$ es una recta.

En el teorema anterior vimos que $B_{1} K ∥ A C$ , entonces las otras tres rectas del haz bisecan a $B_{1} K$ , es decir $B B^{'}$ biseca a $B_{1} K$ .

Sea $X = B B_{1} \cap A C$ , como $△ B B_{1} K$ y $△ B X S$ son semejantes entonces $B^{'}$ es el punto medio entre $X$ y $S$ .

Por lo tanto, $B K$ , $B B_{1}$ , son rectas isotómicas, es decir, unen puntos isotómicos con el vértice opuesto.

Igualmente vemos que $A K$ , $A A_{1}$ y $C K$ , $C C_{1}$ son rectas isotómicas, como las simedianas concurren en $K$ , entonces, $A A_{1}$ , $B B_{1}$ , $C C_{1}$ concurren en u punto $Y$ .

Centroide del triángulo de Brocard

Teorema 2. El centroide de un triángulo y el centroide de su primer triángulo de Brocard coinciden.

Demostración. Nuevamente emplearemos la notación del teorema 1.

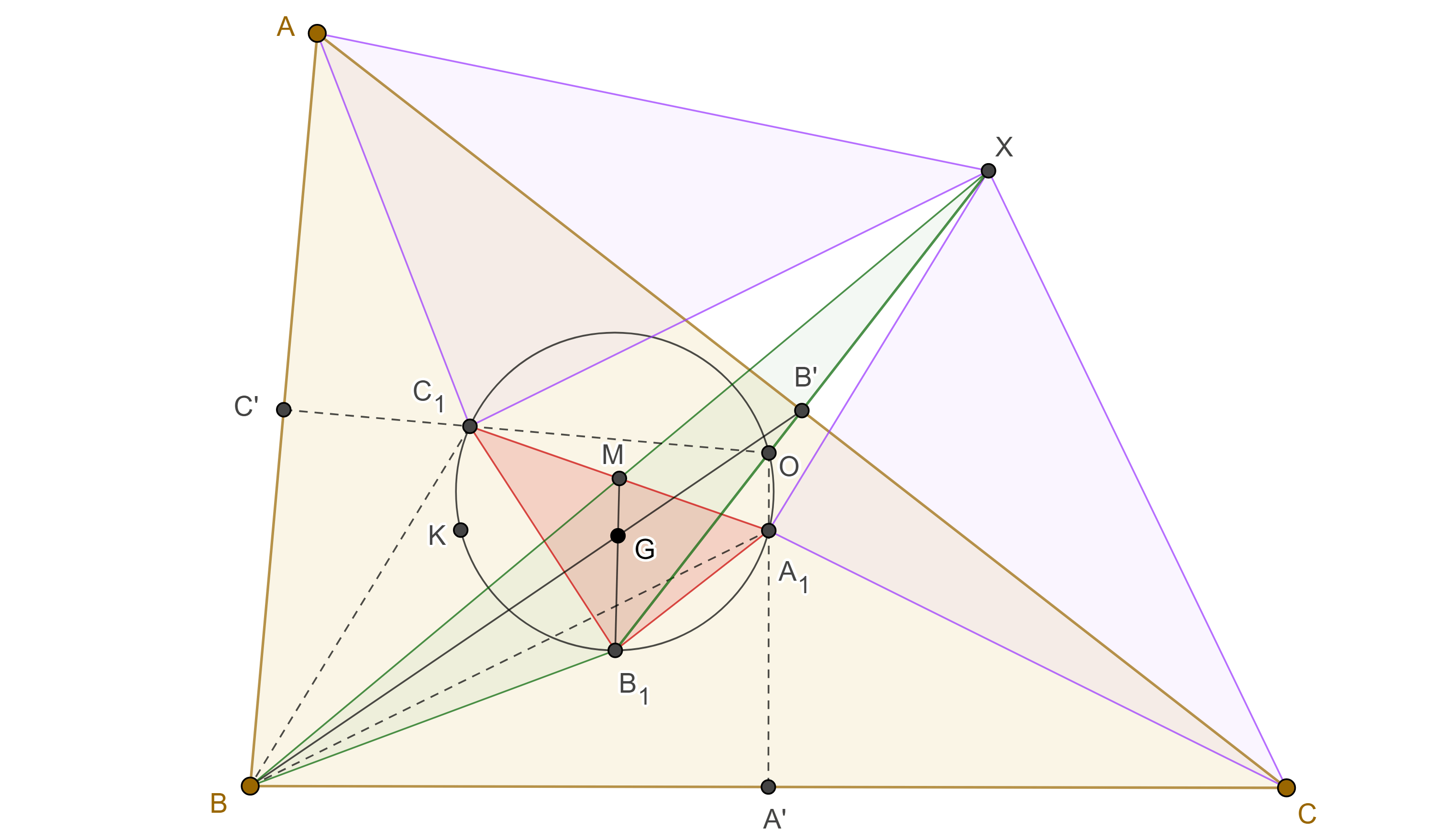
$A_{1}$ , $B_{1}$ y $C_{1}$ están en las mediatrices de $B C$ , $C A$ y $A B$ entonces $△ A_{1} B C$ , $△ B_{1} C A$ , $△ C_{1} A B$ son isósceles, además son semejantes, pues $∠ A_{1} B C = ∠ B_{1} C A = ∠ C_{1} A B = ω$ , por lo tanto,

$\frac{A C_{1}}{A B_{1}} = \frac{A B}{C A}$ y $\frac{C A_{1}}{C B_{1}} = \frac{B C}{C A}$ .

Sea $X$ la reflexión de $B_{1}$ respecto de $C A$ , entonces
$∠ C_{1} A X = ∠ C_{1} A C + ∠ C A X$
$= ∠ C_{1} A C + ∠ B_{1} A C = ∠ C_{1} A C + ω$
$= ∠ A$ ,

además $\frac{A C_{1}}{A X} = \frac{A C_{1}}{A B_{1}} = \frac{A B}{C A}$ .

Por criterio de semejanza LAL, $△ A B C \sim △ A C_{1} X$ , igualmente podemos ver que $△ A B C \sim △ X A_{1} C$ .

Por lo tanto, $△ A C_{1} X \sim △ X A_{1} C$ , pero $A X = A B_{1} = B_{1} C = C X$ , así que $△ A C_{1} X$ y $△ X A_{1} C$ son congruentes.

En consecuencia, $C_{1} X = A_{1} C = A_{1} B$ y $X A_{1} = A C_{1} = C_{1} B$ , esto implica que $C_{1} B A_{1} X$ es un paralelogramo y por lo tanto $A_{1} C_{1}$ y $B X$ se cortan en su punto medio $M$ .

En $△ B_{1} B X$ , $B_{1} M$ y $B B^{'}$ son medianas, donde $B^{'}$ es el punto medio de $B_{1} X$ y $C A$ , por lo tanto, su intersección $G$ , triseca a ambas medianas de $△ B_{1} B X$ .

Pero el centroide de $△ A B C$ y de $△ A_{1} B_{1} C_{1}$ es el único punto con esa propiedad, por lo tanto, su centroide es el mismo.

Concurrencia en el centro de los nueve puntos.

Proposición 3. Las perpendiculares a los lados de un triángulo desde los puntos medios de su primer triángulo de Brocard concurren en el centro de los nueve puntos.

Demostración. Sean $△ A B C$ y $△ A_{1} B_{1} C_{1}$ su primer triángulo de Brocard, $D$ , $E$ , $F$ , los puntos medios de $B_{1} C_{1}$ , $C_{1} A_{1}$ , $A_{1} B_{1}$ respectivamente.

Notemos que las perpendiculares por $D$ , $E$ , $F$ , a $B C$ , $C A$ , $A B$ , respectivamente, son paralelas a $O A_{1}$ , $O B_{1}$ , $O C_{1}$ respectivamente, donde $O$ es el circuncentro de $△ A B C$ .

Como $△ A_{1} B_{1} C_{1}$ y $△ D E F$ , están en homotecia desde $G$ , el centroide de $△ A_{1} B_{1} C_{1}$ , y razón $\frac{- 1}{2}$ , entonces los tres pares de rectas paralelas son pares de rectas homotéticas, pues pasan por puntos homólogos.

Como $O A_{1}$ , $O B_{1}$ , $O C_{1}$ , concurren en $O$ entonces sus correspondientes rectas homotéticas concurren en el correspondiente punto homólogo, $O^{'}$ .

Entonces $O$ , $G$ y $O^{'}$ son colineales en ese orden y $\frac{O G}{2} = G O^{'}$ .

Como $G$ también es el centroide de $△ A B C$ entonces $O^{'}$ es el centro de los nueve puntos de $△ A B C$ .

Punto de Steiner

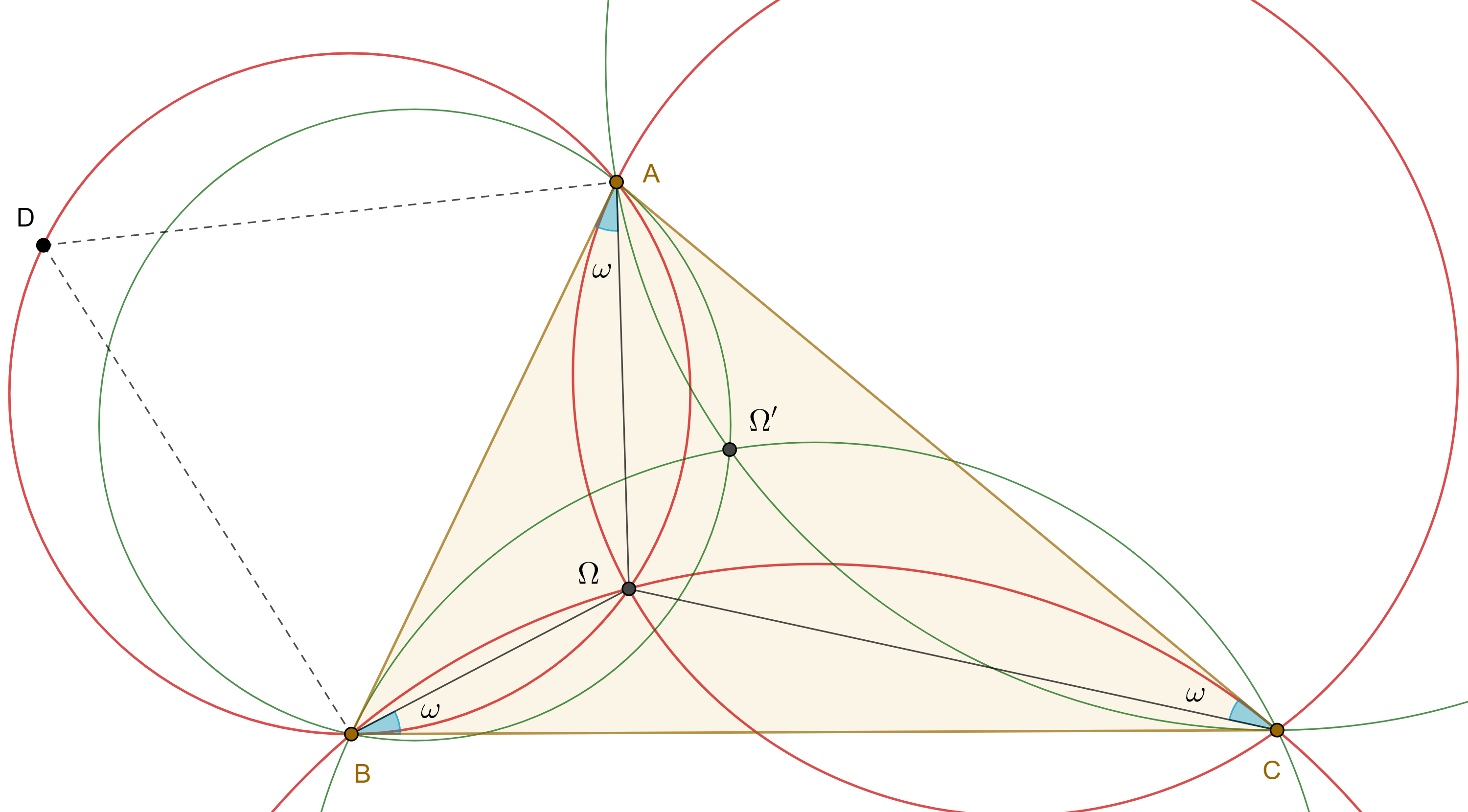
Proposición 4. Las rectas paralelas (perpendiculares) por los vértices de un triángulo a los respectivos lados de su primer triángulo de Brocard concurren en el circuncírculo del triángulo original, el punto de concurrencia se conoce como punto de Steiner (Tarry).

Demostración. Si $△ A_{1} B_{1} C_{1}$ es el primer triángulo de Brocard de $△ A B C$ , sea $S$ la intersección de la paralela a $A_{1} C_{1}$ por $B$ y la paralela a $A_{1} B_{1}$ por $C$ .

$∠ B S C = ∠ C_{1} A_{1} B_{1} = ∠ B A C$ , por lo tanto, $S$ se encuentra en el arco $\overset{⌢}{A B}$ .

De manera análoga vemos que $C S$ y la paralela a $B_{1} C_{1}$ por $A$ se intersecan en el circuncírculo de $△ A B C$ .

Por lo tanto, las paralelas concurren en $S$ .

Considera $T$ el punto diametralmente opuesto a $S$ , entonces $A T ⊥ A S \Rightarrow A T ⊥ B_{1} C_{1}$ .

De manera similar vemos que $B T ⊥ A_{1} C_{1}$ y $C T ⊥ A_{1} B_{1}$ .

Por lo tanto, las perpendiculares concurren en el circuncírculo de $△ A B C$ .

Más adelante…

Con la siguiente entrada comenzaremos la última unidad en la que hablaremos sobre cuadriláteros, mostraremos algunos teoremas que establecen propiedades análogas a la de los triángulos, como, cuando un cuadrilátero tiene un incírculo o la formula de Euler que mide la distancia entre el incentro y el circuncentro pero esta vez para cuadriláteros.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Construye un triángulo, dado su primer triángulo de Brocard.
Muestra que la recta que une los vértices de un triángulo con los correspondientes vértices de su primer triángulo de Brocard dividen a los lados opuestos del triángulo original en el inverso de la razón de los cuadrados de los lados adyacentes.
Prueba que la reflexión del punto simediano respecto del centro de los nueve puntos de un triángulo es el centro de la circunferencia de Brocard de su triángulo anticomplementario.
Muestra que el punto simediano y el circuncentro de un triángulo son el punto de Steiner y el punto de Tarry de su primer triángulo de Brocard.
El triángulo cuyos vértices son las segundas intersecciones de las simedianas de un triángulo con su circunferencia de Brocard es el segundo triángulo de Brocard, demuestra que:
$i)$ los vértices del segundo triángulo de Brocard son los puntos medios de las cuerdas del circuncírculo de su triángulo de referencia determinadas por sus simedianas,
$i i)$ las circunferencias del grupo directo e indirecto que son tangentes a los lados de un mismo ángulo de un triángulo se intersecan en los vértices de su segundo triángulo de Brocard.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Puntos de Brocard.
Siguiente entrada del curso: Teoremas de Varignon y Van Aubel.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 279-284.
Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 277-282.
Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 73-75.
Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 106-124.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Puntos de Brocard

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada hablaremos sobre un par de puntos conjugados isogonales del triángulo, los puntos de Brocard, que surgen de una construcción particular de circunferencias tangentes a los lados del triángulo.

Puntos de Brocard

Definición y notación. Dado un triángulo $△ A B C$ , considera $Γ (B C)$ la circunferencia tangente a $B C$ en $B$ que pasa por $A$ , $Γ (C A)$ la circunferencia tangente a $C A$ en $C$ que pasa por $B$ , $Γ (A B)$ la circunferencia tangente a $A B$ en $A$ que pasa por $C$ . Llamaremos a este conjunto de circunferencias, grupo directo de circunferencias.

De manera análoga, la circunferencia $Γ (C B)$ tangente a $B C$ en $C$ que pasa por $A$ , la circunferencia $Γ (A C)$ tangente a $C A$ en $A$ que pasa por $B$ y la circunferencia $Γ (B A)$ tangente a $A B$ en $B$ que pasa por $C$ , seran referidas como grupo indirecto de circunferencias.

Teorema 1. Las tres circunferencias del grupo directo (indirecto) asociado a un triángulo tienen un punto en común, al punto de concurrencia $Ω$ $(Ω^{'})$ se le conoce como primer (segundo) punto de Brocard.

Demostración. Sean $△ A B C$ y $Ω = Γ (B C) \cap Γ (C A)$ , considera $D \in \overset{⌢}{A B}$ arco de $Γ (B C)$ , recorrido en ese sentido.

Como $∠ C B A$ es un ángulo semiinscrito de $Γ (B C)$ entonces $∠ B D A = ∠ C B A$ , por lo tanto, $∠ A Ω B = π - ∠ B$ .

De manera análoga vemos que $∠ B Ω C = π - ∠ C$ .

En consecuencia,
$∠ C Ω A = 2 π - (∠ A Ω B) - (∠ B Ω C)$
$= 2 π - (π - ∠ B) - (π - ∠ C) = ∠ B + ∠ C$
$= π - ∠ A$ .

Por otra parte, como $∠ B A C$ es un ángulo semiinscrito de $Γ (A B)$ , entonces todos los puntos en el arco $\overset{⌢}{C A}$ , recorrido en ese sentido, subtienden un ángulo $∠ A$ con la cuerda $C A$ , por lo tanto, el arco $\overset{⌢}{A C}$ es el lugar geométrico de los puntos que subtienden con la cuerda $C A$ un ángulo igual a $π - ∠ A$ .

En conclusión $Ω \in Γ (A B)$ .

La demostración es análoga para el caso del grupo indirecto.

Corolario 1. Los dos puntos de Brocard son los únicos puntos dentro de un triángulo $△ A B C$ que tienen la siguiente propiedad:
$i)$ $∠ B A Ω = ∠ C B Ω = ∠ A C Ω$ ,
$i i)$ $∠ Ω^{'} A C = ∠ Ω^{'} C B = ∠ Ω^{'} B A$ .

Demostración. $i)$ $∠ B A Ω$ y $∠ C B Ω$ son ángulos inscrito y semiinscrito respectivamente de $Γ (B C)$ que abarcan el mismo arco, por lo tanto son iguales.

De manera análoga vemos que $∠ C B Ω = ∠ A C Ω$ .

Por otro lado supongamos que existe un punto $F$ dentro de $△ A B C$ tal que $∠ B A F = ∠ C B F = ∠ A C F$ , considera el circuncírculo de $△ A B F$ , como $∠ C B F$ es igual al ángulo inscrito $∠ B A F$ , entonces $B C$ debe ser tangente al circuncírculo de $△ A B F$ en $B$ , por lo tanto, $F \in Γ (B C)$ .

De manera análoga vemos que $F \in Γ (C A)$ y $F \in Γ (A B)$ por lo tanto $F$ coincide con $Ω$ .

$i i)$ Se muestra de manera similar.

Ángulo de Brocard

Corolario 2. Los puntos de Brocard son puntos conjugados isogonales.

Demostración. Si $X$ es el conjugado isogonal de $Ω$ entonces (figura 1)
$∠ B A Ω = ∠ X A C$ ,
$∠ C B Ω = ∠ X B A$ ,
$∠ A C Ω = ∠ X C B$ .

Pero $∠ B A Ω = ∠ C B Ω = ∠ A C Ω = ω$ , por lo tanto, el conjugado isogonal de $Ω$ respecto a $△ A B C$ cumple que $∠ X A C = ∠ X B A = ∠ X C B$ .

Como $Ω^{'}$ es el único punto que tiene esa propiedad dentro de $△ A B C$ entonces $X = Ω^{'}$ .

Definición 2. Los segmentos $A Ω$ , $A Ω^{'}$ ; $B Ω$ , $B Ω^{'}$ ; $C Ω$ , $C Ω^{'}$ , se conocen como rayos de Brocard y el ángulo $∠ B A Ω = ∠ Ω^{'} A C = ω$ se conoce como ángulo de Brocard.

Definición 3. Los lados del triángulo anticomplementario de un triángulo dado (las rectas paralelas a los lados de un triángulo por los vértices opuestos), se llaman exmedianas del triángulo dado.

Teorema 2. Una exsimediana, una exmediana y un rayo de Brocard, cada una por un vértice distinto de un triángulo dado, son concurrentes.

Demostración. En $△ A B C$ sea $B Ω$ el rayo de Brocard que pasa por el primer punto de Brocard y $D$ la intersección de este rayo con la exmediana por $A$ .

Como $A D ∥ B C$ entonces $∠ C A D = ∠ C$ y $∠ A D B = ∠ C B Ω = ω = ∠ A C Ω$ , por lo tanto, $A Ω C D$ está inscrito en $Γ (A B)$ .

Por el corolario 1, $∠ C Ω A = ∠ B + ∠ C$ , esto implica que $∠ A D C = ∠ A$ , por lo tanto, $∠ D C A = ∠ B$ .

Como resultado $C D$ es exsimediana de $△ A B C$ , es decir, es tangente al circuncírculo de $△ A B C$ en $C$ .

Corolario 3. El ángulo de Brocard $ω$ de un triángulo $△ A B C$ satisface la siguiente igualdad $\cot ω = \cot ∠ A + \cot ∠ B + \cot ∠ C$

Demostración. En la figura anterior sean $H_{a}$ , $H_{d}$ las proyecciones de $A$ y $D$ en $B C$ , como $∠ D C A = ∠ B$ entonces $∠ H_{d} C D = ∠ A$ , por lo tanto,
$\cot ω = \frac{B H_{d}}{D H_{d}}$
$= \frac{B H_{a}}{D H_{d}} + \frac{H_{a} C}{D H_{d}} + \frac{C H_{d}}{D H_{d}}$
$= \frac{B H_{a}}{A H_{a}} + \frac{H_{a} C}{A H_{a}} + \frac{C H_{d}}{D H_{d}}$
$= \cot ∠ B + \cot ∠ C + \cot ∠ A$ .

Construcción de un triángulo dado su ángulo de Brocard

Problema. Construye un triángulo, dados un lado, un ángulo y $ω$ , su ángulo de Brocard.

Solución. Sea $∠ B^{'} A C^{'}$ el ángulo dado, en $A C^{'}$ tomamos un punto $C$ arbitrario, sobre $C A$ y con vértice en $C$ abrimos un ángulo igual a $ω$ en el sentido contrario al de las manecillas del reloj, hacemos lo mismo pero esta vez sobre $A B$ en y vértice en $A$ .

La intersección de los segundos lados de los ángulos construidos será $Ω$ , el primer punto de Brocard, ahora sobre $Ω C$ construimos el lugar geométrico de los puntos que subtienden un ángulo igual a $ω$ con los puntos $Ω$ y $C$ , el cual es un arco de circunferencia.

Este arco puede intersecar a $A B^{'}$ en dos puntos $B$ y $B^{″}$ , entonces obtenemos $△ A B C$ y $△ A C B^{″}$ , sin embargo, estos dos triángulos son semejantes, si este arco no interseca a $A B$ entonces no hay solución.

$△ A B C$ es semejante al triangulo requerido, el cual puede ser construido a partir del lado dado.

Triángulo circunscrito de ceva de los puntos de Brocard

Teorema 3.
$i)$ Los rayos de Brocard intersecan otra vez al circuncírculo del triángulo, en tres puntos que forman un triángulo congruente con el triángulo original,
$i i)$ este triángulo puede ser obtenido rotando el triángulo original un ángulo igual a dos veces su ángulo de Brocard con centro en el circuncentro,
$i i i)$ el primer (segundo) punto de Brocard del triángulo original es el segundo (primer) punto de Brocard del triángulo rotado.

Demostración. Sea $Ω$ el punto positivo de Brocard de $△ A B C$ , consideremos $B^{'}$ , $C^{'}$ , $A^{'}$ las segundas intersecciones de $A Ω$ , $B Ω$ , $C Ω$ con el circuncírculo de $△ A B C$ .

Entonces,
$∠ B^{'} A^{'} C^{'} = ∠ B^{'} A^{'} C + ∠ C A^{'} C^{'} = ∠ B^{'} A C + ∠ C B C^{'} = ∠ B^{'} A C + ω = ∠ B A C$ .

Igualmente vemos que $∠ B = ∠ B^{'}$ y $∠ C^{'} = ∠ C$ .

Como $△ A B C$ y $△ A^{'} B^{'} C^{'}$ son semejantes y están inscritos en el mismo circulo, entonces son congruentes.

Por otro lado, $∠ A O A^{'} = 2 ∠ A C A^{'} = 2 ω$ .

Finalmente $∠ Ω A^{'} C^{'} = ∠ C A^{'} C^{'} = ∠ C B C^{'} = ω$ .

Similarmente, $∠ Ω C^{'} B^{'} = ω = ∠ Ω B^{'} A^{'}$ .

Por lo tanto $Ω$ es el segundo punto de Brocard de $△ A^{'} B^{'} C^{'}$ .

Corolario 4. Los dos puntos de Brocard de un triángulo son equidistantes del circuncentro del triángulo.

Demostración. Si partimos esta vez del triángulo $△ A^{'} B^{'} C^{'}$ y hacemos una rotación un ángulo igual a $2 ω$ con centro en $O$ en el sentido de las manecillas del reloj, entonces su segundo punto de Brocard coincidirá con el segundo punto de Brocard de $△ A B C$ .

Ya que el segundo punto de Brocard de $△ A^{'} B^{'} C^{'}$ , es el primer punto de Brocard de $△ A B C$ , entonces estos puntos son equidistantes a $O$ .

Triángulo pedal de los puntos de Brocard

Corolario 5. El triángulo pedal del primer (segundo) punto de Brocard es semejante a su triángulo de referencia, además el primer (segundo) punto de Brocard es el mismo para ambos triángulos.

Demostración. En la figura anterior, sean $Ω_{a}$ , $Ω_{b}$ , $Ω_{c}$ , las proyecciones de $Ω$ en $B C$ , $C A$ , $A B$ , respectivamente.

En la entrada anterior mostramos que para cualquier punto $ω$ , su triángulo pedal $△ Ω_{a} Ω_{b} Ω_{c}$ , es semejante a su triángulo circunscrito de Ceva respecto de $△ B^{'} C^{'} A^{'}$ .

Por el teorema anterior, $△ A B C ≅ △ A^{'} B^{'} C^{'}$ , por lo tanto $△ Ω_{c} Ω_{a} Ω_{b} \sim △ A B C$ .

Por otro lado, como $Ω_{c} B Ω_{a} Ω$ es cíclico entonces
$∠ Ω Ω_{c} Ω_{a} = ∠ Ω B Ω_{a} = ω$ .

Igualmente vemos que $∠ Ω Ω_{a} Ω_{b} = ω = ∠ Ω Ω_{b} Ω_{c}$ .

La prueba es análoga para el caso del segundo punto de Brocard.

Corolario 6. Los triángulos pedales de los dos puntos de Brocard de un triángulo son congruentes.

Demostración. Como los dos puntos de Brocard de un triángulo son conjugados isogonales, entonces sus triangulo pedales tienen el mismo circuncírculo y como son semejantes, entonces son congruentes.

Más adelante…

Continuando con el tema de geometría de Brocard, en la siguiente entrada hablaremos de la circunferencia de Brocard, veremos que los puntos de Brocard están en esta circunferencia y que estos permiten la construcción de un triángulo que es semejante y esta en perspectiva con el triángulo original.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Prueba que $\cot ω = \frac{a^{2} + b^{2} + c^{2}}{4 (△ A B C)}$ .
Muestra que el valor del ángulo de Brocard $ω$ de un triángulo es a lo mas $\frac{π}{6}$ .
Muestra que los triángulos antipedales de los puntos de Brocard son semejantes a su triangulo de referencia.
Construye un triángulo dados dos lados indefinidos y un punto de Brocard.
Muestra que un rayo de Brocard, una mediana y una simediana, cada uno por un vértice distinto de un triángulo, son concurrentes.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Rectas isogonales.
Siguiente entrada del curso: Circunferencia de Brocard.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 274-278.
Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 263-270.
Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 99-106.
Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 71-73.
Aref, M. y Wernick, W., Problems and Solutions in Euclidean Geometry. New York: Dover, 2010, pp 188-191.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: puntos de Brocard

Geometría Moderna I: Circunferencia de Brocard

Introducción

Circunferencia de Brocard

Conjugado isotómico del punto simediano

Centroide del triángulo de Brocard

Concurrencia en el centro de los nueve puntos.

Punto de Steiner

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Geometría Moderna I: Puntos de Brocard

Introducción

Puntos de Brocard

Ángulo de Brocard

Construcción de un triángulo dado su ángulo de Brocard

Triángulo circunscrito de ceva de los puntos de Brocard

Triángulo pedal de los puntos de Brocard

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos