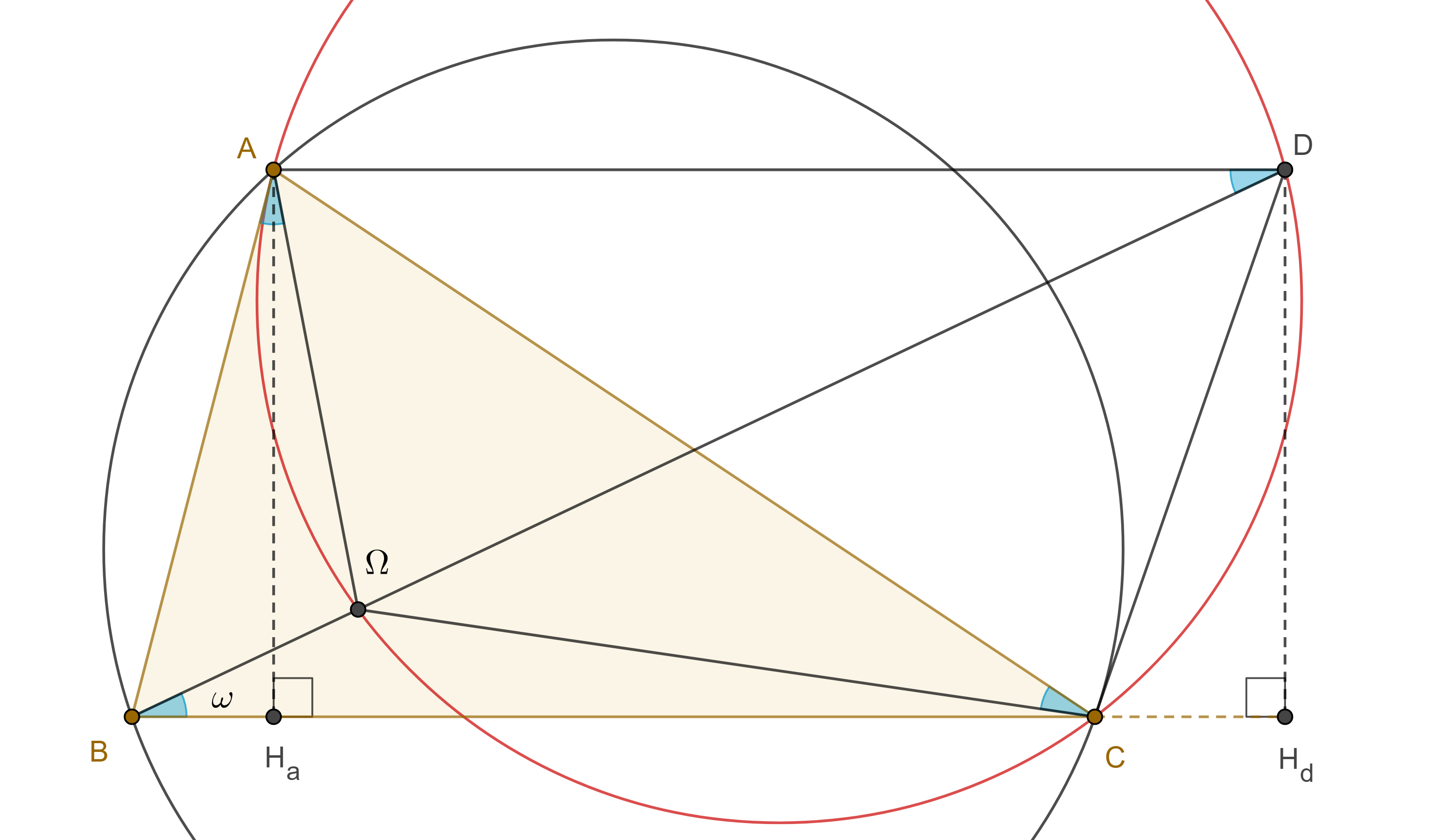Introducción
En esta entrada hablaremos sobre un par de puntos conjugados isogonales del triángulo, los puntos de Brocard, que surgen de una construcción particular de circunferencias tangentes a los lados del triángulo.
Puntos de Brocard
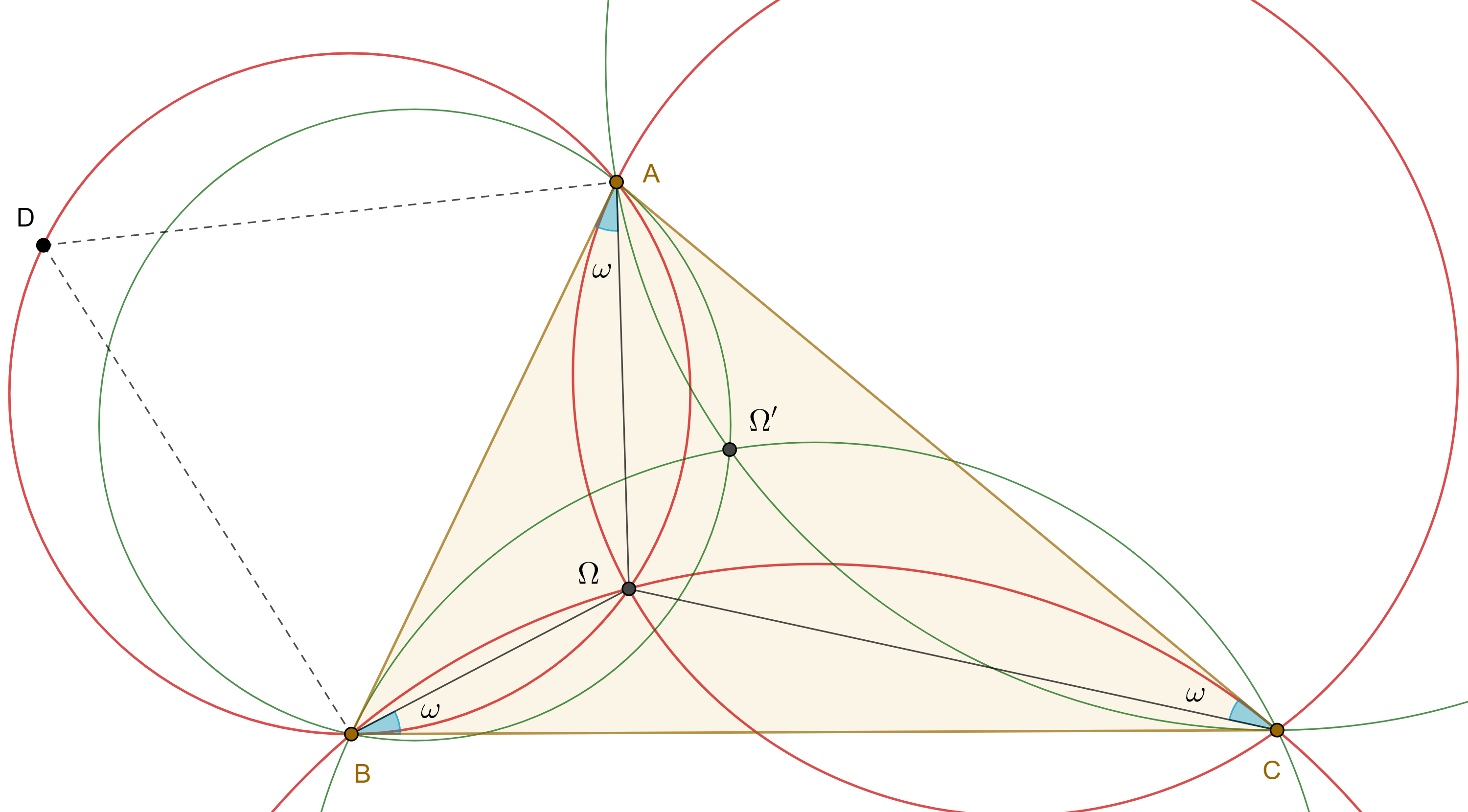
Definición y notación. Dado un triángulo $\triangle ABC$, considera $\Gamma(BC)$ la circunferencia tangente a $BC$ en $B$ que pasa por $A$, $\Gamma(CA)$ la circunferencia tangente a $CA$ en $C$ que pasa por $B$, $\Gamma(AB)$ la circunferencia tangente a $AB$ en $A$ que pasa por $C$. Llamaremos a este conjunto de circunferencias, grupo directo de circunferencias.
De manera análoga, la circunferencia $\Gamma(CB)$ tangente a $BC$ en $C$ que pasa por $A$, la circunferencia $\Gamma(AC)$ tangente a $CA$ en $A$ que pasa por $B$ y la circunferencia $\Gamma(BA)$ tangente a $AB$ en $B$ que pasa por $C$, seran referidas como grupo indirecto de circunferencias.
Teorema 1. Las tres circunferencias del grupo directo (indirecto) asociado a un triángulo tienen un punto en común, al punto de concurrencia $\Omega$ $(\Omega’)$ se le conoce como primer (segundo) punto de Brocard.
Demostración. Sean $\triangle ABC$ y $\Omega = \Gamma(BC) \cap \Gamma(CA)$, considera $D \in \overset{\LARGE{\frown}}{AB}$ arco de $\Gamma(BC)$, recorrido en ese sentido.
Como $\angle CBA$ es un ángulo semiinscrito de $\Gamma(BC)$ entonces $\angle BDA = \angle CBA$, por lo tanto, $\angle A\Omega B = \pi – \angle B$.
De manera análoga vemos que $\angle B\Omega C = \pi – \angle C$.
En consecuencia,
$\angle C\Omega A = 2\pi – (\angle A\Omega B) – (\angle B\Omega C) $
$= 2\pi – (\pi – \angle B) – (\pi – \angle C) = \angle B + \angle C $
$= \pi – \angle A$.
Por otra parte, como $\angle BAC$ es un ángulo semiinscrito de $\Gamma(AB)$, entonces todos los puntos en el arco $\overset{\LARGE{\frown}}{CA}$, recorrido en ese sentido, subtienden un ángulo $\angle A$ con la cuerda $CA$, por lo tanto, el arco $\overset{\LARGE{\frown}}{AC}$ es el lugar geométrico de los puntos que subtienden con la cuerda $CA$ un ángulo igual a $\pi – \angle A$.
En conclusión $\Omega \in \Gamma(AB)$.
La demostración es análoga para el caso del grupo indirecto.
$\blacksquare$
Corolario 1. Los dos puntos de Brocard son los únicos puntos dentro de un triángulo $\triangle ABC$ que tienen la siguiente propiedad:
$i)$ $\angle BA\Omega = \angle CB\Omega = \angle AC\Omega $,
$ii)$ $\angle \Omega’ AC = \angle \Omega’ CB = \angle \Omega’ BA$.
Demostración. $i)$ $\angle BA\Omega$ y $\angle CB\Omega$ son ángulos inscrito y semiinscrito respectivamente de $\Gamma(BC)$ que abarcan el mismo arco, por lo tanto son iguales.
De manera análoga vemos que $\angle CB\Omega = \angle AC\Omega$.
Por otro lado supongamos que existe un punto $F$ dentro de $\triangle ABC$ tal que $\angle BAF = \angle CBF = \angle ACF$, considera el circuncírculo de $\triangle ABF$, como $\angle CBF$ es igual al ángulo inscrito $\angle BAF$, entonces $BC$ debe ser tangente al circuncírculo de $\triangle ABF$ en $B$, por lo tanto, $F \in \Gamma(BC)$.
De manera análoga vemos que $F \in \Gamma(CA)$ y $F \in \Gamma(AB)$ por lo tanto $F$ coincide con $\Omega$.
$ii)$ Se muestra de manera similar.
$\blacksquare$
Ángulo de Brocard
Corolario 2. Los puntos de Brocard son puntos conjugados isogonales.
Demostración. Si $X$ es el conjugado isogonal de $\Omega$ entonces (figura 1)
$\angle BA\Omega = \angle XAC$,
$\angle CB\Omega = \angle XBA$,
$ \angle AC\Omega = \angle XCB$.
Pero $\angle BA\Omega = \angle CB\Omega = \angle AC\Omega = \omega$, por lo tanto, el conjugado isogonal de $\Omega$ respecto a $\triangle ABC$ cumple que $\angle XAC = \angle XBA = \angle XCB$.
Como $\Omega’$ es el único punto que tiene esa propiedad dentro de $\triangle ABC$ entonces $X = \Omega’$.
$\blacksquare$
Definición 2. Los segmentos $A\Omega$, $A\Omega’$; $B\Omega$, $B\Omega’$; $C\Omega$, $C\Omega’$, se conocen como rayos de Brocard y el ángulo $\angle BA\Omega = \angle \Omega’AC = \omega$ se conoce como ángulo de Brocard.
Definición 3. Los lados del triángulo anticomplementario de un triángulo dado (las rectas paralelas a los lados de un triángulo por los vértices opuestos), se llaman exmedianas del triángulo dado.
Teorema 2. Una exsimediana, una exmediana y un rayo de Brocard, cada una por un vértice distinto de un triángulo dado, son concurrentes.
Demostración. En $\triangle ABC$ sea $B\Omega$ el rayo de Brocard que pasa por el primer punto de Brocard y $D$ la intersección de este rayo con la exmediana por $A$.
Como $AD \parallel BC$ entonces $\angle CAD = \angle C$ y $\angle ADB = \angle CB\Omega = \omega = \angle AC\Omega$, por lo tanto, $\square A\Omega CD$ está inscrito en $\Gamma(AB)$.
Por el corolario 1, $\angle C\Omega A = \angle B + \angle C$, esto implica que $\angle ADC = \angle A$, por lo tanto, $\angle DCA = \angle B$.
Como resultado $CD$ es exsimediana de $\triangle ABC$, es decir, es tangente al circuncírculo de $\triangle ABC$ en $C$.
$\blacksquare$
Corolario 3. El ángulo de Brocard $\omega$ de un triángulo $\triangle ABC$ satisface la siguiente igualdad $\cot \omega = \cot \angle A + \cot \angle B + \cot \angle C$
Demostración. En la figura anterior sean $H_a$, $H_d$ las proyecciones de $A$ y $D$ en $BC$, como $\angle DCA = \angle B$ entonces $\angle H_dCD = \angle A$, por lo tanto,
$\cot \omega = \dfrac{BH_d}{DH_d}$
$= \dfrac{BH_a}{DH_d} + \dfrac{H_aC}{DH_d} + \dfrac{CH_d}{DH_d}$
$= \dfrac{BH_a}{AH_a} + \dfrac{H_aC}{AH_a} + \dfrac{CH_d}{DH_d}$
$ = \cot \angle B + \cot \angle C + \cot \angle A$.
$\blacksquare$
Construcción de un triángulo dado su ángulo de Brocard
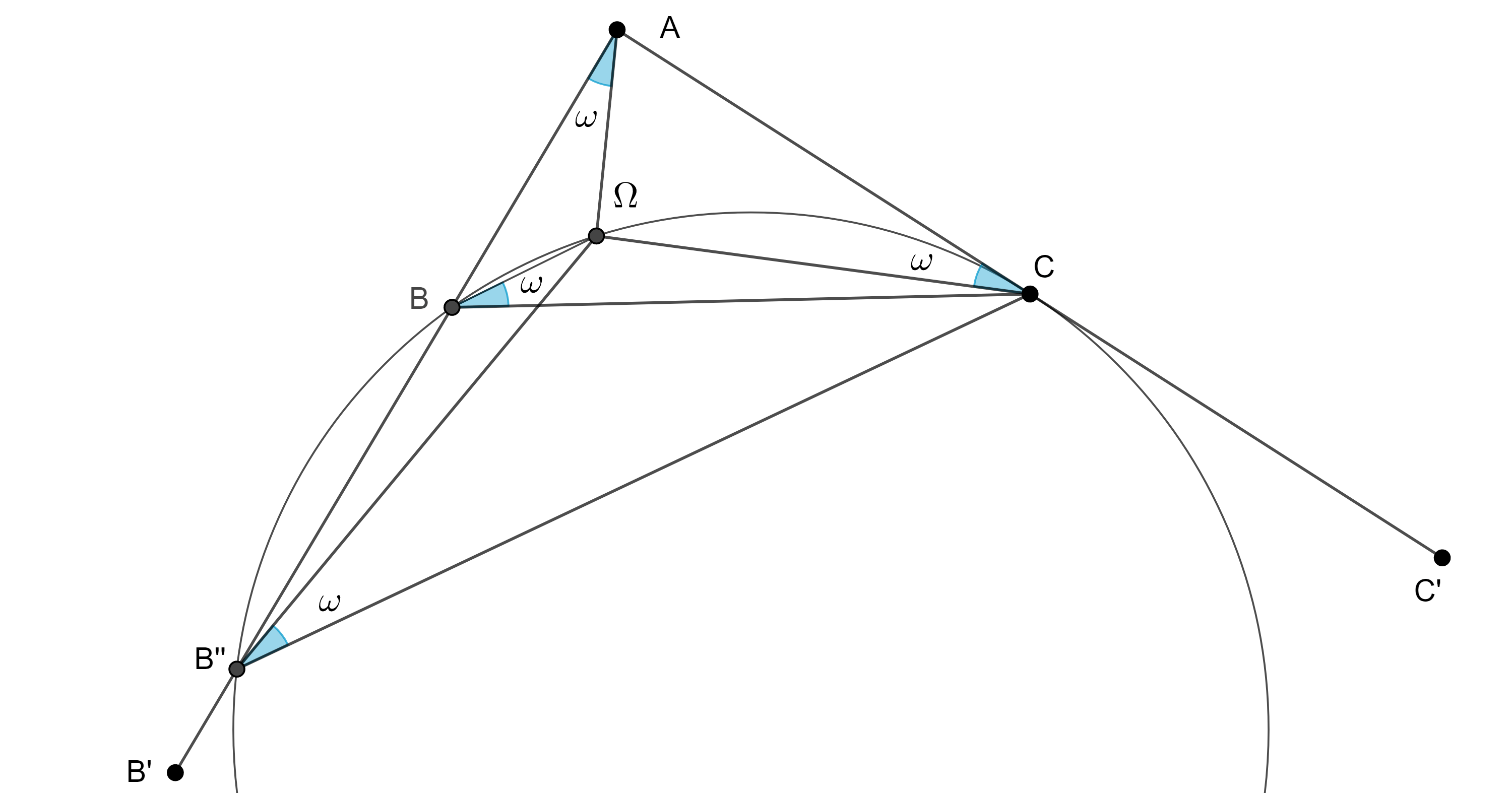
Problema. Construye un triángulo, dados un lado, un ángulo y $\omega$, su ángulo de Brocard.
Solución. Sea $\angle B’AC’$ el ángulo dado, en $AC’$ tomamos un punto $C$ arbitrario, sobre $CA$ y con vértice en $C$ abrimos un ángulo igual a $\omega$ en el sentido contrario al de las manecillas del reloj, hacemos lo mismo pero esta vez sobre $AB$ en y vértice en $A$.
La intersección de los segundos lados de los ángulos construidos será $\Omega$, el primer punto de Brocard, ahora sobre $\Omega C$ construimos el lugar geométrico de los puntos que subtienden un ángulo igual a $\omega$ con los puntos $\Omega$ y $C$, el cual es un arco de circunferencia.
Este arco puede intersecar a $AB’$ en dos puntos $B$ y $B’’$, entonces obtenemos $\triangle ABC$ y $\triangle ACB’’$, sin embargo, estos dos triángulos son semejantes, si este arco no interseca a $AB$ entonces no hay solución.
$\triangle ABC$ es semejante al triangulo requerido, el cual puede ser construido a partir del lado dado.
$\blacksquare$
Triángulo circunscrito de ceva de los puntos de Brocard
Teorema 3.
$i)$ Los rayos de Brocard intersecan otra vez al circuncírculo del triángulo, en tres puntos que forman un triángulo congruente con el triángulo original,
$ii)$ este triángulo puede ser obtenido rotando el triángulo original un ángulo igual a dos veces su ángulo de Brocard con centro en el circuncentro,
$iii)$ el primer (segundo) punto de Brocard del triángulo original es el segundo (primer) punto de Brocard del triángulo rotado.
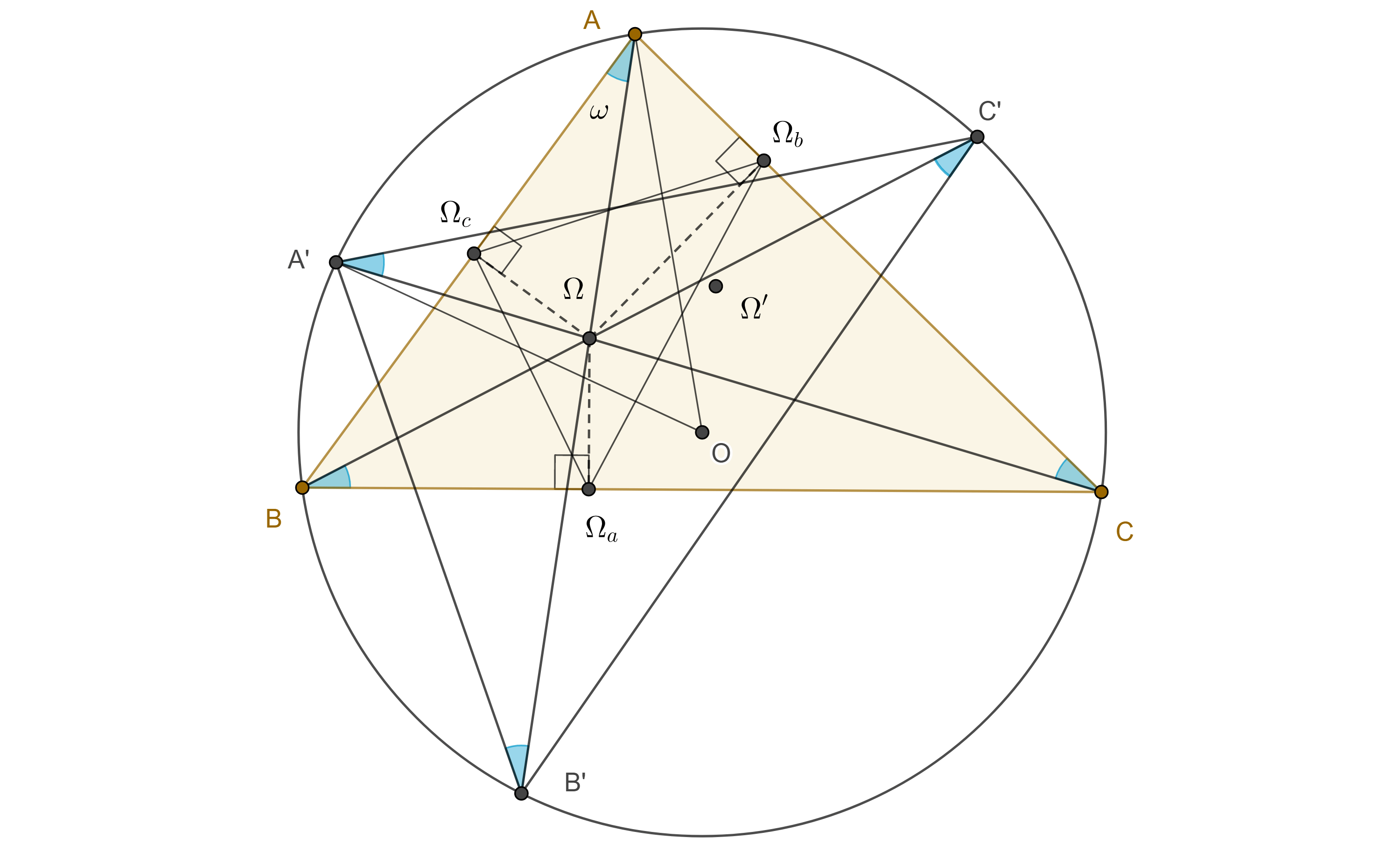
Demostración. Sea $\Omega$ el punto positivo de Brocard de $\triangle ABC$, consideremos $B’$, $C’$, $A’$ las segundas intersecciones de $A\Omega$, $B\Omega$, $C\Omega$ con el circuncírculo de $\triangle ABC$.
Entonces,
$\angle B’A’C’ = \angle B’A’C + \angle CA’C’ = \angle B’AC + \angle CBC’ = \angle B’AC + \omega = \angle BAC$.
Igualmente vemos que $\angle B = \angle B’$ y $\angle C’ = \angle C$.
Como $\triangle ABC$ y $\triangle A’B’C’$ son semejantes y están inscritos en el mismo circulo, entonces son congruentes.
Por otro lado, $\angle AOA’ = 2 \angle ACA’ = 2 \omega$.
Finalmente $\angle \Omega A’C’ = \angle CA’C’ = \angle CBC’ = \omega$.
Similarmente, $\angle \Omega C’B’ = \omega = \angle \Omega B’A’$.
Por lo tanto $\Omega$ es el segundo punto de Brocard de $\triangle A’B’C’$.
$\blacksquare$
Corolario 4. Los dos puntos de Brocard de un triángulo son equidistantes del circuncentro del triángulo.
Demostración. Si partimos esta vez del triángulo $\triangle A’B’C’$ y hacemos una rotación un ángulo igual a $2\omega$ con centro en $O$ en el sentido de las manecillas del reloj, entonces su segundo punto de Brocard coincidirá con el segundo punto de Brocard de $\triangle ABC$.
Ya que el segundo punto de Brocard de $\triangle A’B’C’$, es el primer punto de Brocard de $\triangle ABC$, entonces estos puntos son equidistantes a $O$.
$\blacksquare$
Triángulo pedal de los puntos de Brocard
Corolario 5. El triángulo pedal del primer (segundo) punto de Brocard es semejante a su triángulo de referencia, además el primer (segundo) punto de Brocard es el mismo para ambos triángulos.
Demostración. En la figura anterior, sean $\Omega_a$, $\Omega_b$, $\Omega_c$, las proyecciones de $\Omega$ en $BC$, $CA$, $AB$, respectivamente.
En la entrada anterior mostramos que para cualquier punto $\omega$, su triángulo pedal $\triangle \Omega_a\Omega_b\Omega_c$, es semejante a su triángulo circunscrito de Ceva respecto de $\triangle B’C’A’$.
Por el teorema anterior, $\triangle ABC \cong \triangle A’B’C’$, por lo tanto $\triangle \Omega_c\Omega_a\Omega_b \sim \triangle ABC$.
Por otro lado, como $\square \Omega_cB\Omega_a\Omega$ es cíclico entonces
$\angle \Omega\Omega_c\Omega_a = \angle \Omega B\Omega_a = \omega$.
Igualmente vemos que $\angle \Omega\Omega_a\Omega_b = \omega = \angle \Omega\Omega_b\Omega_c$.
La prueba es análoga para el caso del segundo punto de Brocard.
$\blacksquare$
Corolario 6. Los triángulos pedales de los dos puntos de Brocard de un triángulo son congruentes.
Demostración. Como los dos puntos de Brocard de un triángulo son conjugados isogonales, entonces sus triangulo pedales tienen el mismo circuncírculo y como son semejantes, entonces son congruentes.
$\blacksquare$
Más adelante…
Continuando con el tema de geometría de Brocard, en la siguiente entrada hablaremos de la circunferencia de Brocard, veremos que los puntos de Brocard están en esta circunferencia y que estos permiten la construcción de un triángulo que es semejante y esta en perspectiva con el triángulo original.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que $\cot \omega = \dfrac{a^2 + b^2 + c^2}{4(\triangle ABC)}$.
- Muestra que el valor del ángulo de Brocard $\omega$ de un triángulo es a lo mas $\dfrac{\pi}{6}$.
- Muestra que los triángulos antipedales de los puntos de Brocard son semejantes a su triangulo de referencia.
- Construye un triángulo dados dos lados indefinidos y un punto de Brocard.
- Muestra que un rayo de Brocard, una mediana y una simediana, cada uno por un vértice distinto de un triángulo, son concurrentes.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Rectas isogonales.
- Siguiente entrada del curso: Circunferencia de Brocard.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 274-278.
- Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 263-270.
- Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 99-106.
- Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 71-73.
- Aref, M. y Wernick, W., Problems and Solutions in Euclidean Geometry. New York: Dover, 2010, pp 188-191.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»