Archivo de la etiqueta: límite de una función

Cálculo Diferencial e Integral I: Límite de una función a través de sucesiones

Por Juan Manuel Naranjo Jurado

2 respuestas

Introducción

Alternativamente a la definición épsilon-delta revisada en la entrada anterior, se puede estudiar el límite de una función a través de límites de sucesiones; este enfoque tiene varias bondades en el sentido de que podremos hacer un amplio uso de las propiedades demostradas anteriormente para el límite de una sucesión. En esta entrada nos enfocaremos en probar un teorema que nos indica la equivalencia entre ambas formas de concebir el límite de una función.

Negación de la definición del límite de una función

Veamos primero qué significa que el límite de una función no exista, es decir, revisaremos la negación del concepto dado en la entrada anterior, para ello retomemos la definición de límite de una función:

Definición. Decimos que $f$ tiende hacia el límite $L$ en $x_0$ si para todo $\varepsilon > 0$ existe algún $\delta > 0$ tal que, para todo $x$, si $0<|x-x_0|< \delta$, entonces $|f(x)-L|< \varepsilon.$

De esta forma, si no se cumple la definición anterior, entonces tenemos lo siguiente: $f$ no tiende hacia el límite $L$ en $x_0$ si existe algún $\varepsilon > 0$, tal que para todo $\delta > 0$, hay algún $x$ que satisface $0 < |x-x_0| < \delta$, pero $|f(x)-L| \geq \varepsilon.$

Criterio de sucesiones para límites

Es momento de revisar un teorema que será particularmente útil para demostrar las propiedades del límite de una función. Este teorema nos indica que una función $f$ tiende al límite $L$ en $x_0$ si y solo si para toda sucesión $\{ a_n \}$ en el dominio de $f$ que converja a $x_0$ se tiene que la sucesión generada por $\{f(a_n) \}$ converge a $L.$

Teorema. Sean $A \subset \mathbb{R}$, $f:A \rightarrow \mathbb{R}$ y $x_0$ un punto de acumulación de $A$. Los siguientes enunciados son equivalentes.

  1. $$\lim_{x \to x_0} f(x) = L.$$
  2. Para toda sucesión $\{ a_n \}$ en $A$ que converge a $x_0$ tal que $a_n \neq x_0$ para todo $n\in \mathbb{N}$, la sucesión $\{f(a_n)\}$ converge a $L.$

Demostración.

$1) \Rightarrow 2)]$ Sea $\varepsilon >0$. Supongamos que $$\lim_{x \to x_0} f(x) = L.$$
Y sea $\{ a_n \}$ una sucesión en $A$ que converge a $x_0$ tal que $a_n \neq x_0$ para todo $n\in \mathbb{N}$.

Por hipótesis $f$ converge a $L$ en $x_0$, entonces existe $\delta > 0$ tal que si
$0<|x-x_0|<\delta$, entonces $|f(x)-L| < \varepsilon.$

Además, como la sucesión $\{a_n\}$ converge a $x_0$, para el valor $\delta > 0$ dado, existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$ entonces $0<|a_n- x_0| < \delta$ y por hipótesis de la convergencia de $f$ a $L$ en $x_0$, podemos concluir que $|f(a_n)-L| < \varepsilon$. Así la sucesión $\{f(a_n)\}$ converge a $L$, es decir,
$$\lim_{n \to \infty} f(a_n) = L.$$


$1) \Leftarrow 2)]$ Procederemos a hacer esta implicación por contrapositiva, es decir, demostraremos que si no sucede $1)$, entonces tampoco sucede $2).$

Supongamos que $1)$ no se cumple, es decir, existe algún $\varepsilon_0 > 0$, tal que para todo $\delta > 0$, hay al menos un real $x$ que cumple $0<|x-x_0| < \delta$, pero $|f(x)-L| \geq \varepsilon_0$. Así, consideremos justo ese valor de $\varepsilon_0.$ Notemos que para todo natural $n \in \mathbb{N}$, si consideramos $\delta=\frac{1}{n}$, entonces existe al menos un término $a_n$ en $A$ tal que $0<|a_n-x_0| < \frac{1}{n}$, pero $|f(a_n)-L| \geq \varepsilon_0.$

Tomemos la sucesión generada por $\{a_n\}$, se tiene que la sucesión $\{ a_n \}$ converge a $x_0$ y $a_n \neq x_0$ para todo $n \in \mathbb{N}$, pero la sucesión $\{f(a_n)\}$ no converge a $L$. Así, si no se cumple $1)$, entonces tampoco $2)$. Por lo anterior, podemos concluir que $2) \Rightarrow 1).$

$\square$

Límite de una función a través de sucesiones

Ahora nos enfocaremos en hacer uso del teorema anterior. En el momento de hacer las demostraciones correspondientes, debemos tener presente que una vez que expresamos el límite de una función en términos del límite de una sucesión, podemos hacer uso de las propiedades del mismo.

Ejemplo 1. Sea $A =\mathbb{R} \backslash \{ 1 \}$. Consideremos la función $f: A \to \mathbb{R}$ con $f(x) = \frac{x^3-x^2+x-1}{x-1}$. Prueba que $$\lim_{x \to 1} f(x) = 2.$$

Demostración.

Primero notemos que
\begin{align*}
f(x) & = \frac{x^3-x^2+x-1}{x-1} \\ \\
& = \frac{(x-1)(x^2+1)}{x-1} \\ \\
& = x^2+1.
\end{align*}

$$\therefore f(x) = x^2+1.$$

Sea $\{a_n\}$ una sucesión en $\mathbb{R}$ tal que

  • $\lim\limits_{n \to \infty} a_n = 1.$
  • Para todo $n \in \mathbb{N}$, $a_n \neq 1.$
  • Para todo $n \in \mathbb{N}$, $a_n \in A.$

Entonces tenemos que

\begin{align*}
\lim_{x \to 1} f(x) & = \lim_{n \to \infty} f(a_n) \\ \\
& = \lim_{n \to \infty} (a_n^2+1) \\ \\
& = \lim_{n \to \infty} a_n^2 + \lim_{n \to \infty} 1 \tag{1} \\ \\
& = 1+1 \\ \\
& = 2.
\end{align*}

$$\therefore \lim_{x \to 1} \frac{x^3-x^2+x-1}{x-1} = 2.$$

$\square$

Es importante resaltar que aún no hemos probado ninguna propiedad del límite de una función, por lo que el criterio de sucesiones para límites es lo que nos permite emplear las propiedades que conocemos respecto a sus operaciones aritméticas y así realizar el paso $(1)$ en el ejemplo anterior.

Ejemplo 2. Sea $A = [0, \infty)$. Consideremos la función $f: A \to \mathbb{R}$ con $f (x) = \sqrt{x}$. Demuestra que $$\lim_{x \to 2} f(x) = \sqrt{2}.$$

Sea $\{a_n\}$ una sucesión en $\mathbb{R}$ tal que

  • $\lim\limits_{n \to \infty} a_n = 2.$
  • Para todo $n \in \mathbb{N}$, $a_n \neq 2.$
  • Para todo $n \in \mathbb{N}$, $a_n \in A.$

Sabemos que si $\{a_n\}$ converge a $2$, entonces $\{ \sqrt{a_n} \}$ converge a $\sqrt{2}$. Así, tenemos que

\begin{align*}
\lim_{x \to 2} f(x) & = \lim_{n \to \infty} f(a_n) \\
& = \lim_{n \to \infty} \sqrt{a_n} \\
& = \sqrt{2}.
\end{align*}

$$\therefore \lim_{x \to 2} \sqrt{x} = \sqrt{2}.$$

$\square$

Ejemplo 3. Sea $A =\mathbb{R} \backslash \{ 0 \}$. Consideremos la función $f: A \to \mathbb{R}$ con $f (x)= \frac{(3+x)^2-9}{x}$. Prueba que $$\lim_{x \to 0} f(x) = 6.$$

Demostración.

Primero notemos que

\begin{align*}
f (x) & = \frac{(3+x)^2-9}{x} \\ \\
& = \frac{9+6 x+x^2-9}{x} \\ \\
& = \frac{6x+x^2}{x} \\ \\
& = 6+x.
\end{align*}

$$\therefore f(x) = 6+x.$$

Sea $\{a_n\}$ una sucesión en $\mathbb{R}$ tal que

  • $\lim\limits_{n \to \infty} a_n = 0.$
  • Para todo $n \in \mathbb{N}$, $a_n \neq 0.$
  • Para todo $n \in \mathbb{N}$, $a_n \in A.$

\begin{align*}
\lim_{x \to 0} f(x) & = \lim_{n \to \infty} f(a_n) \\ \\
& = \lim_{n \to \infty} (6+a_n) \\ \\ 
& = 6.
\end{align*}

$$\therefore \lim_{x \to 0} \frac{(3+x)^2-9}{x} = 6.$$

$\square$

Hasta este momento, solo hemos hecho uso del criterio de sucesiones para límites para probar la existencia de los mismos. Sin embargo, es posible usarlo también para el caso en el que tal límite no existe. Derivado directamente del teorema anterior se tiene que:

  • Si existen dos sucesiones $\{ a_n \}$, $\{b_n\}$ en el dominio de $f$, ambas convergentes a $x_0$, tal que $a_n$, $b_n \neq x_0$ para todo $n \in \mathbb{N}$, pero $\lim\limits_{n \to \infty} f(a_n) \neq \lim\limits_{n \to \infty} f(b_n)$ entonces no existe el límite de $f$ en $x_0.$

Veremos ahora un ejemplo donde el límite no existe.

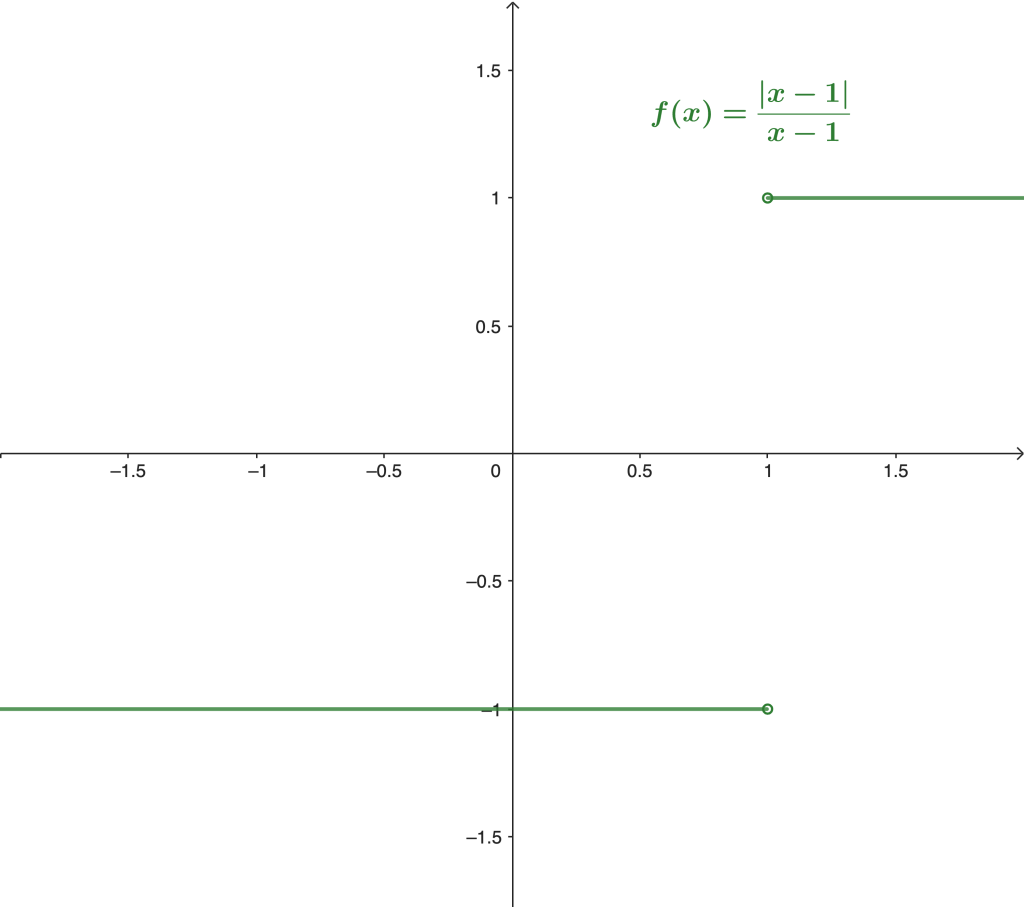
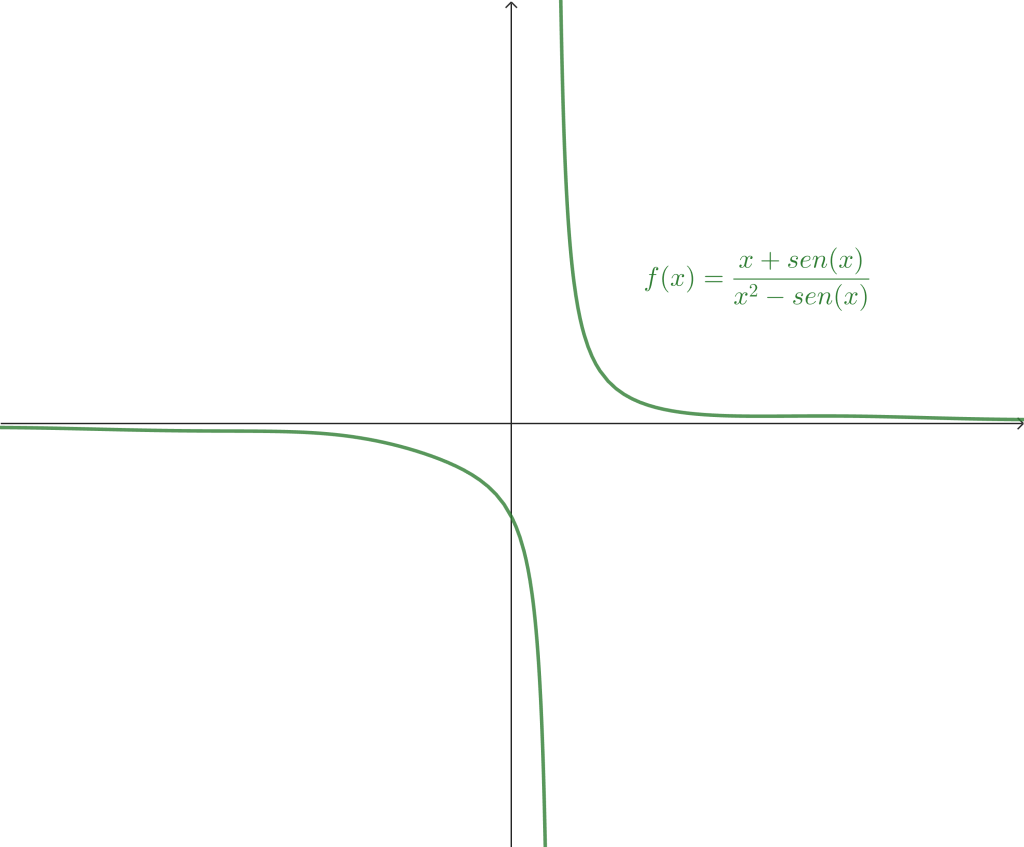
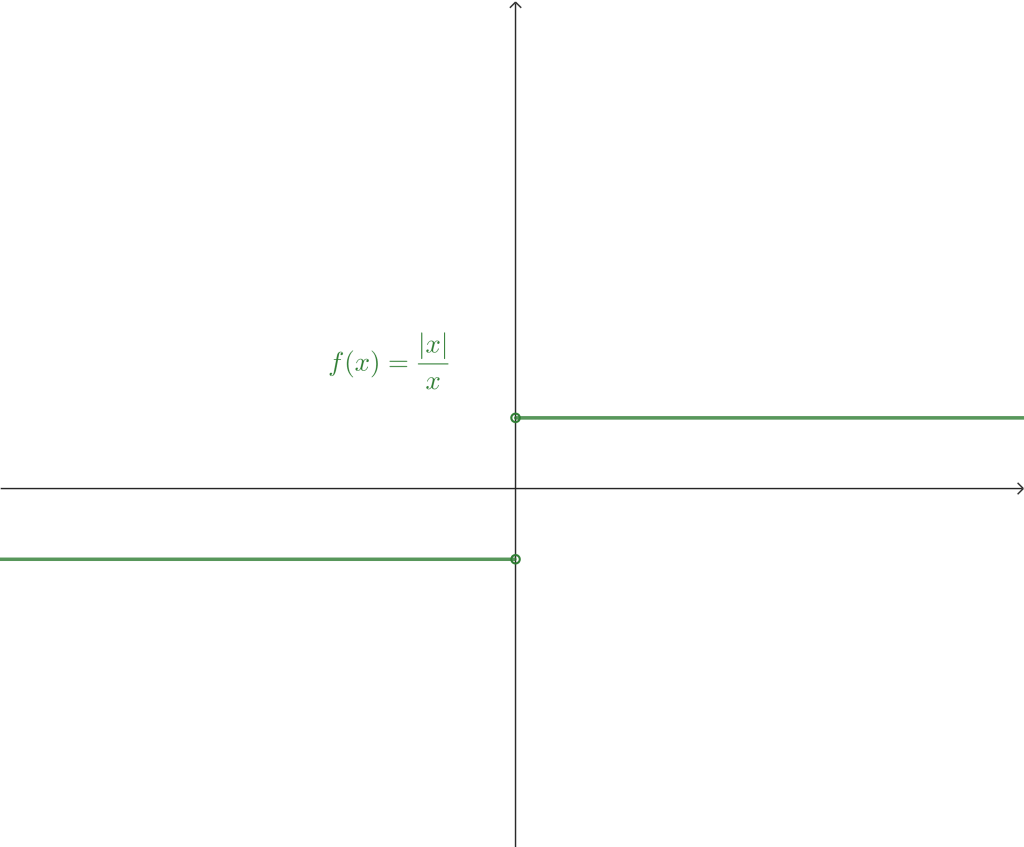
Ejemplo 4. Sea $A =\mathbb{R} \backslash \{ 1 \}$. Consideremos la función $f: A \to \mathbb{R}$ con $f(x) = \frac{|x-1|}{x-1}$. Prueba que el límite

$$\lim_{x \to 1} f(x)$$

no existe.

Demostración.

Veamos primero la gráfica de la función:

Podemos observar que es conveniente tomar una sucesión que se aproxime a $x_0 = 1$ por la derecha y otra que se aproxime por la izquierda. Sean $\{a_n\}$, $\{b_n\}$ dos sucesiones en el dominio de $f$ definidas de la siguiente forma:

$$a_n = 1 + \frac{1}{n} \quad \text{y} \quad b_n = 1 – \frac{1}{n}.$$

Se sigue que

$$ \lim_{n \to \infty} a_n = 1 \quad \text{y} \quad \lim_{n \to \infty} b_n = 1.$$

Además, $a_n \neq 1$, $b_n \neq 1$ para todo $n \in \mathbb{N}$.

Se tiene que

\begin{align*}
\lim_{n \to \infty} f(a_n) & = \lim_{n \to \infty} \frac{|a_n-1|}{a_n-1} \\ \\
& = \lim_{n \to \infty} \frac{ |1 + \frac{1}{n} – 1|}{1 + \frac{1}{n} -1} \\ \\
& = \lim_{n \to \infty} \frac{ |\frac{1}{n}|}{ \frac{1}{n} } \\ \\
& = \lim_{n \to \infty} \frac{ \frac{1}{n} }{ \frac{1}{n} } \\ \\
& = 1.
\end{align*}

$$\therefore \lim_{n \to \infty} f(a_n) = 1 \tag{1}.$$

Por otro lado,

\begin{align*}
\lim_{n \to \infty} f(b_n) & = \lim_{n \to \infty} \frac{|b_n-1|}{b_n-1} \\ \\
& = \lim_{n \to \infty} \frac{ |1 – \frac{1}{n} – 1|}{1 – \frac{1}{n} -1} \\ \\
& = \lim_{n \to \infty} \frac{ |- \frac{1}{n}|}{- \frac{1}{n} } \\ \\
& = \lim_{n \to \infty} \frac{ \frac{1}{n} }{ – \frac{1}{n} } \\ \\
& = – 1.
\end{align*}

$$\therefore \lim_{n \to \infty} f(b_n) = -1. \tag{2}$$

De $(1)$ y $(2)$, se tiene que

\begin{gather*}
\lim_{n \to \infty} f(a_n) \neq \lim_{n \to \infty} f(b_n). \\ \\
\therefore \lim_{x \to 1} \frac{|x-1|}{x-1} \text{ no existe.}
\end{gather*}

$\square$

Más adelante…

En las siguientes entradas veremos propiedades específicas que nos ayudarán a calcular el límite de una función; y, como podrás imaginar, varias de estas propiedades son un símil a las revisadas para las sucesiones convergentes.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

A través del criterio de sucesiones para límite, prueba si existen o no los siguientes límites:

  • $$\lim_{x \to 0} \frac{x}{x+1}.$$
  • $$\lim_{x \to 0} x \cdot |x|.$$
  • $$\lim_{x \to 7} \frac{x^2-5x+10}{2-x}.$$
  • $$\lim_{x \to 0} \frac{x}{|x|}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral: Límites de funciones trigonométricas

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En las entradas anteriores nos enfocamos en desarrollar el concepto de límite y revisamos diversos tipos de funciones, sin embargo, evitamos un tipo particular: las funciones trigonométricas. En esta entrada centraremos nuestra atención en la revisión de estos límites haciendo uso de toda la teoría revisada hasta este punto.

Límite de funciones trigonométricas cuando $x$ tiende a $x_0$

En los primeros ejemplos podrás visualizar la gráfica de la función con la finalidad de tener cierta intuición respecto a los límites, pero, en caso de requerirlo, puedes repasar las funciones trigonométricas.

Ejemplo 1. Prueba que $$\lim_{x \to 0} sen(x) = sen(0).$$

Demostración.

Para probar este límite, procederemos a calcular los límites laterales.

Sea $x \in (0, \pi / 2 )$. Usaremos que $0 < sen(x) < x$ si $x \in (0, \pi / 2 )$.

Además, $$\lim_{x \to 0} = 0 \qquad \text{y} \qquad \lim_{x \to 0} x = 0.$$

Por el teorema del sándwich, podemos concluir que $$\lim_{x \to 0^+} sen(x) = 0 = sen(0). \tag{1}$$

Si $x \in (- \pi / 2, 0)$, entonces $-x \in (0, \pi /2)$. De esta forma, se obtiene que

$$ 0 < sen(-x) < -x.$$

Como $sen(-x) = -sen(x)$, se sigue que $$0 < -sen(x) < -x.$$

Por lo tanto $$ x < sen(x) < 0$$

Nuevamente por el teorema del sándwich, se sigue que $$\lim_{x \to 0^-} sen(x) = 0 = sen(0). \tag{2}$$

De $(1)$ y $(2)$ se concluye que $$\lim_{x \to 0} sen(x) = sen(0).$$

$\square$

Ejemplo 2. Prueba que $$\lim_{x \to 0} cos(x) = cos(0).$$

Demostración.

Como $$ cos^2(x)+sen^2(x) = 1,$$ se sigue que $$|cos(x)| = \sqrt{1-sen^2(x)}.$$

Consideremos $x \in (-\pi/2, \pi/2)$, entonces $cos(x) > 0$, y de la expresión anterior se sigue que $$cos(x) = \sqrt{1-sen^2(x)}.$$

De esta manera, se tiene que

\begin{align*}
\lim_{x \to 0} cos(x) & = \lim_{x \to 0} \sqrt{1-sen^2(x)} \\
& = \sqrt{1-0} \\
& = 1 \\
& = cos(0).
\end{align*}

Por lo tanto

$$\lim_{x \to 0} cos(x) = cos(0).$$

$\square$

Ejemplo 3. Prueba que el siguiente límite no existe $$\lim_{x \to 0} sen \left( \frac{1}{x} \right).$$

Demostración.

Notemos que por la relación entre el límite de una función y el de una sucesión, basta dar dos sucesiones $\{a_n\}$, $\{b_n\}$ tal que converjan a $x_0 = 0$ y $a_n$, $b_n \neq 0$ para todo $n \in \mathbb{N}$, pero que las sucesiones obtenidas de evaluar la función en los términos de ambas sucesiones, $\{f(a_n)\}$, $\{f(b_n)\}$ converjan a valores distintos.

Definimos $f(x) = sen(\frac{1}{x})$ y consideremos las sucesiones $a_n = (\pi n) ^{-1} \quad$ y $b_n = (\frac{1}{2} \pi + 2 \pi n)^{-1},$ donde $a_n$, $b_n \neq 0$ para todo $n \in \mathbb{N}.$

Veamos que
\begin{align*}
\lim_{n \to \infty} a_n = & \lim_{n \to \infty} (\pi n) ^{-1} \\
= & \lim_{n \to \infty} \frac{1}{\pi n} \\
= & 0.
\end{align*}
$$\therefore \lim_{n \to \infty} a_n = 0.$$
Además,
\begin{align*}
\lim_{n \to \infty} b_n = & \lim_{n \to \infty} \left( \frac{1}{2} \pi + 2 \pi n \right)^{-1}\\ \\
= & \lim_{n \to \infty} \frac{1}{\frac{1}{2} \pi + 2 \pi n} \\ \\
= & \lim_{n \to \infty} \frac{1}{\frac{\pi + 4 \pi n}{2}} \\ \\
= & \lim_{n \to \infty} \frac{2}{\pi + 4 \pi n} \\ \\
= & 0.
\end{align*}
$$\therefore \lim_{n \to \infty} b_n = 0.$$
Es decir, las sucesiones $\{a_n\}$ y $\{b_n\}$ tienden a cero. Y notemos que $f(a_n) = sen(n \pi ) = 0$ y $f(b_n) = sen(\frac{1}{2} \pi + 2 \pi n) = 1$ para todo $n \in \mathbb{N}.$

De esta forma $$\lim_{n \to \infty} f(a_n) \neq \lim_{n \to \infty} f(b_n).$$
Por tanto, podemos concluir que el límite no existe.

$\square$

Ejemplo 4. Prueba que $$\lim_{x \to 0} x sen \left( \frac{1}{x} \right) = 0.$$

Demostración.

Haremos la demostración de este límite mediante la definición épsilon-delta.

Sea $\varepsilon > 0$. Consideremos $\delta = \varepsilon.$
Si $0<|x-0| < \delta$, entonces
\begin{gather*}
& |x| < \delta = \varepsilon. \\
\Rightarrow & |x|< \varepsilon.
\end{gather*}
Además, sabemos que $-1 < sen \left( \frac{1}{x} \right) < 1$ para cualquier $x \neq 0.$ Entonces

\begin{align*}
|f(x)-0| = & \left|x sen \left( \frac{1}{x} \right) \right| \\
= & |x|\left|sen \left( \frac{1}{x} \right) \right| \\
\leq & \delta \cdot 1 \\
= & \varepsilon.
\end{align*}
$$\therefore \lim_{x \to 0} x sen \left( \frac{1}{x} \right) = 0.$$

$\square$

El siguiente ejemplo es un límite que nos ayudará en diversas ocasiones, así que vale la pena ponerle particular atención.

Ejemplo 5. Prueba que $$\lim_{x \to 0 } \frac{sen(x)}{x} = 1.$$

Demostración.

Como nos interesa revisar qué sucede cuando $x \to 0$. Podemos considerar que $x \in (-\frac{\pi}{2}, \frac{\pi}{2})$ con $x\neq 0.$

De esta forma, se tiene que

  • Área $\triangle ABC = \frac{sen(x)cos(x)}{2}$.
  • Área del sector circular $ADC = \frac{xr^2}{2} = \frac{x}{2}$.
  • Área $\triangle ADE = \frac{1 \cdot tan(x)}{2} = \frac{sen(x)}{2cos(x)}$.

Podemos notar que Área $\triangle ABC <$ Área del sector circular $ADC <$Área $\triangle ADE$.

Como $x \in (-\frac{\pi}{2}, \frac{\pi}{2})$ con $x\neq 0$, entonces $sen(x) \neq 0$ y $cos(x) \neq 0$. Así, se sigue que

\begin{gather*}
\frac{sen(x)cos(x)}{2} < \frac{x}{2} < \frac{sen(x)}{2cos(x)}.
\end{gather*}

De donde se obtiene que $$cos(x) < \frac{x}{sen(x)} < \frac{1}{cos(x)}.$$

Y se sigue que $$ cos(x) < \frac{x}{sen(x)} \qquad \text{ y } \qquad \frac{x}{sen(x)} < \frac{1}{cos(x)}.$$

Es decir, $$ \frac{sen(x)}{x} < \frac{1}{cos(x)} \qquad \text{ y } \qquad cos(x) < \frac{sen(x)}{x}. $$

$$ \therefore cos(x) < \frac{sen(x)}{x} < \frac{1}{cos(x)}.$$

Además, $\lim\limits_{x \to 0} cos(x) = 1$ y $\lim\limits_{x \to 0} \frac{1}{cos(x)} = 1$. Por el teorema del del sándwich se concluye que

$$\lim_{x \to 0 } \frac{sen(x)}{x} = 1.$$

$\square$

Ejemplo 6. Determina el siguiente límite $$\lim_{x \to 0} \frac{1-cos(x) }{x}.$$

Si $0< |x| < \pi$, entonces

\begin{align*}
\frac{1-cos(x)}{x} = & \frac{1-cos(x)}{x} \cdot \frac{1+cos(x)}{1+cos(x)} \\ \\
= & \frac{1-cos^2(x)}{x (1+cos(x) )} \\ \\
= & \frac{sen^2(x)}{x(1+cos(x))} \\ \\
= & \frac{sen(x)}{x} \frac{sen(x)}{1+cos(x)}.
\end{align*}

Así,
\begin{align*}
\lim_{x \to 0} \frac{1-cos(x) }{x} = & \lim_{x \to 0}\frac{sen(x)}{x} \cdot \frac{sen(x)}{1+cos(x)} \\
= & \lim_{x \to 0} \frac{sen(x)}{x} \cdot \lim_{x \to 0} \frac{sen(x)}{1+cos(x)} \\
= & 1 \cdot \frac{0}{2} \\
= & 0.
\end{align*}

$$\therefore \lim_{x \to 0} \frac{1-cos(x) }{x} = 0.$$

Ejemplo 7. Calcula el siguiente límite $$\lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)}.$$

\begin{align*}
\lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)} = & \lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)} \cdot \frac{\frac{1}{x}}{\frac{1}{x}} \\ \\
= & \lim_{x \to 0} \frac{1+\frac{sen(x)}{x}}{x-\frac{sen(x)}{x}} \\ \\
= & \frac{1+1}{0-1} \\ \\
= & -2.
\end{align*}
$$\therefore \lim_{x \to 0} \frac{x+sen(x)}{x^2-sen(x)} = -2.$$

Ejemplo 8. Calcula $$\lim_{x \to 0} \frac{sec(x) -1}{x}.$$

\begin{align*}
\lim_{x \to 0} \frac{sec(x) -1}{x} = & \lim_{x \to 0} \frac{\frac{1}{cos(x)} -1}{x} \\ \\
= & \lim_{x \to 0} \frac{\frac{1- cos(x)}{cos(x)}}{x} \\ \\
= & \lim_{x \to 0} \frac{1- cos(x)}{x cos(x)} \\ \\
= & \lim_{x \to 0} \frac{1}{cos(x)} \frac{1- cos(x)}{x} \\ \\
= & 1 \cdot 0 \\ \\
= & 0.
\end{align*}
$$\therefore \lim_{x \to 0} \frac{sec(x) -1}{x} = 0.$$

Límite de funciones trigonométricas cuando $x$ tiende a infinito

Ahora procederemos a revisar algunos ejemplos de funciones trigonométricas cuando $x \to \infty$, o bien, cuando $x \to – \infty.$

Ejemplo 9. Calcula el límite $$\lim_{x \to \infty} \frac{sen(x)}{x}.$$

Sabemos que $-1 \leq sen(x) \leq 1.$ De esta forma, si $x \neq 0$, se tiene que $$ -\frac{1}{x} \leq \frac{sen(x)}{x} \leq \frac{1}{x}.$$

Además, $$ \lim_{x \to \infty} -\frac{1}{x} = 0 = \lim_{x \to \infty} \frac{1}{x}.$$

Por el teorema del sándwich, se concluye que
$$ \lim_{x \to \infty} sen(x) = 0.$$

Ejemplo 10. Calcula el límite $$\lim_{x \to \infty} \frac{x sen(x)}{x^2+5}.$$
\begin{align*}
\lim_{x \to \infty} \frac{x sen(x)}{x^2+5} = & \lim_{x \to \infty} \frac{x sen(x)}{x^2+5} \cdot \frac{\frac{1}{x^2}}{\frac{1}{x^2}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{x sen(x)}{x^2}}{\frac{x^2+5}{x^2}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{sen(x)}{x}}{1+\frac{5}{x^2}} \\ \\
= & \frac{0}{1} \text{, por lo visto en el ejemplo anterior }\\ \\
= & 0.
\end{align*}
$$\therefore \lim_{x \to \infty} \frac{x sen(x)}{x^2+5} = 0.$$

Ejemplo 11. Determina si existe el siguiente límite $$\lim_{x \to \infty} \frac{x^2(1+sen^2(x))}{(x+sen(x))^2}.$$

El límite no existe. Considera las sucesiones generadas por $a_n = \pi n \quad$ y $\quad b_n = \frac{1}{2} \pi + 2 \pi n \quad$ donde $a_n$, $b_n \rightarrow \infty$ cuando $n \rightarrow \infty.$ Notemos que
\begin{align*}
\lim_{n \to \infty} f(a_n) = & \lim_{n \to \infty} \frac{(\pi n)^2(1+sen^2(\pi n))}{(\pi n+sen(\pi n))^2} \\ \\
= & \lim_{n \to \infty} \frac{(\pi n)^2(1+0)}{(\pi n+0)^2} \\ \\
= & \lim_{n \to \infty} \frac{(\pi n)^2}{(\pi n)^2} \\ \\
= & \lim_{n \to \infty} 1 \\ \\
= & 1.
\end{align*}
$$ \therefore \lim_{n \to \infty} f(a_n) = 1.$$
Por otro lado,
\begin{align*}
\lim_{n \to \infty} f(b_n) = & \lim_{n \to \infty} \frac{(\frac{1}{2} \pi + 2 \pi n)^2(1+sen^2(\frac{1}{2} \pi + 2 \pi n))}{(\frac{1}{2} \pi + 2 \pi n+sen(\frac{1}{2} \pi + 2 \pi n))^2} \\ \\
= & \lim_{n \to \infty} \frac{(\frac{1}{2} \pi + 2 \pi n)^2(1+1)}{(\frac{1}{2} \pi + 2 \pi n+1)^2} \\ \\
= & \lim_{n \to \infty} \frac{2(\frac{1}{2} \pi + 2 \pi n)^2}{(\frac{1}{2} \pi + 2 \pi n+1)^2} \\ \\
= & 2.
\end{align*}
$$ \therefore \lim_{n \to \infty} f(b_n) = 2.$$

Como $$\lim_{n \to \infty} f(a_n) \neq \lim_{n \to \infty} f(b_n).$$
Podemos concluir que el límite $\lim_\limits{x \to \infty} \frac{x^2(1+sen^2(x))}{(x+sen(x))^2}$ no existe.

Ejemplo 12. Determina el siguiente límite $$\lim_{x \to -\infty} \frac{3x^2-sen(5x)}{x^2+2}.$$

Recordemos que $-1 < sen(5x) < 1$, de donde se sigue que $-1 < -sen(5x) < 1$, así
\begin{gather*}
& 3x^2-1 < 3x^2-sen(5x) < 3x^2+1.
\end{gather*}

Se sigue que
\begin{gather*}
\frac{3x^2-1}{x^2+2} < \frac{3x^2-sen(5x)}{x^2+2} < \frac{3x^2+1}{x^2+2} \text{, pues } x^2+2 >0.
\end{gather*}

Y notemos que

\begin{align*}
\lim_{x \to -\infty} \frac{3x^2+1}{x^2+2} = & \lim_{x \to -\infty} \frac{\frac{3x^2+1}{x^2}}{\frac{x^2+2}{x^2}} \\ \\
= & \lim_{x \to -\infty} \frac{3+\frac{1}{x^2}}{1+\frac{2}{x^2}} \\ \\
= & \frac{3}{1} \\ \\
=& 3.
\end{align*}

De forma similar, se obtiene que $$\lim_{x \to -\infty} \frac{3x^2-1}{x^2+2}= 3.$$

Por lo que se tiene que $$\lim_{x \to -\infty} \frac{3x^2+1}{x^2+2} = 3 = \lim_{x \to -\infty} \frac{3x^2-1}{x^2+2}.$$ Usando el teorema del sándwich podemos concluir que
$$\lim_{x \to -\infty} \frac{3x^2-sen(5x)}{x^2+2} = 3.$$


Más adelante…

En la siguiente entrada revisaremos el concepto de asíntotas con lo que nos será posible analizar un comportamiento particular que llegan a tener las funciones, el cual es aproximarse a una recta en determinado momento; y, con esto, estaremos finalizando la unidad referente al límite de una función.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Halla los siguientes límites, justifica en caso de no alguno no exista.

  • $$\lim_{x \to 0} \frac{x^2 (3+sen(x))}{(x+sen(x))^2}.$$
  • $$\lim_{x \to 1} \frac{sen(x^2-1)}{x-1}.$$
  • $$\lim_{x \to \infty} x^2 sen \left(\frac{1}{x} \right).$$
  • $$\lim_{x \to \infty} \frac{x + sen^3(x)}{5x+6}.$$
  • $$\lim_{x \to 0} \frac{tan^2(x)+2x}{x + x^2}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Límites en el infinito

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Previamente se revisó el concepto de límite de una función, así como el de límites laterales. En la revisión de estos temas nos habíamos enfocado en revisar el límite de una función $f$ en un punto $x_0$. Ahora ampliaremos el concepto estudiando $f$ para el caso cuando $x$ tiende a infinito.

Límite en el infinito

La intuición detrás de la definición de límite en el infinito es que $f$ tiene límite $L$ cuando $x$ tiende a infinito si para valores lo suficientemente grandes de $x$ nos acercamos arbitrariamente a $L.$

Definición. Sea $f: A \rightarrow \mathbb{R}$. Decimos que $f$ tiende al límite $L \in \mathbb{R}$ cuando $x$ tiende a infinito si para cualquier $\varepsilon > 0$ existe $M \in \mathbb{R}$, tal que para cualquier $x>M$, se tiene que $|f(x)-L|<\varepsilon$ y lo denotamos $$\lim_{x \to \infty} f(x) = L.$$

Ejemplo 1. Prueba que $$\lim_{x \to \infty} \frac{1}{x} = 0.$$
Demostración.

Sea $\varepsilon > 0$ y tomemos $M = \frac{1}{\varepsilon}$. De esta forma, para todo $x > M$ se tiene que $x > \frac{1}{\varepsilon}$, y por lo tanto $-\varepsilon < 0 <\frac{1}{x} < \varepsilon$, es decir, $|\frac{1}{x}-0|< \varepsilon.$
$$\therefore \lim_{x \to \infty} \frac{1}{x} = 0.$$

$\square$

Podemos observar que la definición es bastante natural una vez hemos entendido el concepto de límite, por lo cual procederemos directamente a revisar algunas de sus propiedades.

Propiedades de los límites en el infinito

Al igual que la definición revisada para el límite de una función en un punto, el límite de una función cuando $x$ tiende a infinito también es único.

Proposición. El límite de una función cuando $x$ tiende a infinito es único, es decir, si $f$ tiende a $L$ cuando $x \rightarrow \infty$ y $f$ tiende a $L’$ cuando $x \rightarrow \infty$, entonces $L = L’.$

La demostración es muy similar a la realizada en la entrada de definición formal del límite, por lo cual se omitirá, pero de ser necesario puedes realizarla para repasar los conceptos.

Análogamente a las entradas anteriores, tenemos una relación entre el límite al infinito de una función y el límite de una sucesión.

Teorema. Sea $f: A \rightarrow \mathbb{R}$. Los siguientes enunciados son equivalentes.

  1. $$\lim_{x \to \infty} f(x) = L.$$
  2. Para cualquier sucesión $\{a_n\}$ en $A$ que diverge a infinito se tiene que la sucesión $\{f(a_n)\}$ converge a $L.$

Notemos que para que el límite en el infinito tenga sentido, se debe cumplir que $(a, \infty) \subset A$ para algún $a \in \mathbb{R}.$

Demostración.

$1) \Rightarrow 2)]$ Sea $\varepsilon >0$. Supongamos que $$\lim_{x \to \infty} f(x) = L.$$
Y sea $\{ a_n \}$ en $A$ que diverge a infinito.

Por hipótesis $f$ tiende a $L$ cuando $x$ tiende a infinito, entonces existe $M \in \mathbb{R}$ tal que si $x > M$ se tiene que $|f(x)-L| < \varepsilon.$

Además, como $\{a_n\}$ diverge a infinito, entonces para $M$ existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$ se tiene que $a_n > M.$ Por lo tanto, $|f(a_n)-L| < \varepsilon.$
$$\therefore \lim_{n \to \infty} f(a_n) = L.$$


$1) \Leftarrow 2)]$ Realizaremos esta demostración por contrapositiva, es decir, probaremos que si $$\lim\limits_{x \to \infty} f(x) \neq L,$$

entonces existe $\{a_n\}$ en $A$ tal que $$\lim\limits_{n \to \infty} a_n = \infty \qquad \text{ y } \qquad \lim\limits_{n \to \infty} f(a_n) \neq L.$$

Supongamos que $\lim\limits_{x \to \infty} f(x) \neq L$. Entonces existe $\varepsilon > 0$ tal que para todo $M_n > a$ existe $x’_n > M_n$ tal que $|f(x’_n) -L| \geq \varepsilon.$

De esta forma, es posible generar la sucesión $\{ x’_n \}$ en $A.$ Primero veremos que esta sucesión diverge a infinito.

Sea $\alpha \in \mathbb{R}$. Entonces existe $M_{n_0} \in \mathbb{R}$ tal que $M_{n_0} > \alpha$. Además, $x’_{n_0} > M_{n_0} > \alpha$, y por lo tanto para todo $n \geq n_0$ se sigue que $x’_n > M_n \geq M_{n_0} > \alpha$. Es decir, $x’_n > \alpha$ para todo $n \geq n_0$.

$$\therefore \lim_{n \to \infty} x’_n = \infty.$$

Además, se tiene que $|f(x’_n)-L| \geq \varepsilon$ para todo $n \in \mathbb{N}$.

Consideremos $\{a_n\} = \{x’_n\}$, entonces

$$\lim\limits_{n \to \infty} a_n = \infty \qquad \text{ y } \qquad \lim\limits_{n \to \infty} f(a_n) \neq L.$$

Por lo tanto, concluimos que $2) \Rightarrow 1)$

$\square$

Después de este teorema, nuevamente logramos obtener las mismas propiedades que conocemos del límite de una sucesión.

Proposición. Sean $f: A \rightarrow \mathbb{R}$, $g: A \rightarrow \mathbb{R}$ con $A \subset \mathbb{R}$ tal que $(a, \infty) \subset A$ para algún $a \in \mathbb{R}$. Si además

$$\lim_{x \to \infty} f(x) = L \quad \text{ y } \quad \lim_{x \to \infty} g(x) = T$$

entonces

  1. $$\lim_{x \to \infty} c \cdot f(x) = cL.$$
  2. $$\lim_{x \to \infty} (f+g)(x) = L+T.$$
  3. $$\lim_{x \to \infty} (f-g)(x) = L-T.$$
  4. $$\lim_{x \to \infty} (f \cdot g)(x) = LT.$$
  5. Si $T \neq 0$ y $g(x) \neq 0$ para $x > a$, entonces $$\lim_{x \to \infty} \frac{f}{g}(x) = \frac{L}{T}.$$

Ahora veremos una proposición que nos será útil para el cálculo de límites.

Proposición. Para todo $k \in \mathbb{N}$ se tiene que $$\lim_{x \to \infty} \frac{1}{x^k} = 0.$$

Demostración.

Procederemos a realizar esta demostración mediante inducción.
Caso base: $k = 1$.
En el ejemplo anterior se probó mediante la definición que $$\lim_{x \to \infty} \frac{1}{x^1} = \lim_{x \to \infty} \frac{1}{x} = 0.$$
Hipótesis de inducción: $$\lim_{x \to \infty} \frac{1}{x^k} = 0.$$
Ahora veamos que también se cumple para $k+1$.

\begin{align*}
\lim_{x \to \infty} \frac{1}{x^{k+1}} = & \lim_{x \to \infty} \frac{1}{x^k} \cdot \frac{1}{x^1} \\ \\
= & \lim_{x \to \infty} \frac{1}{x^k} \lim_{x \to \infty} \frac{1}{x^1} \\ \\
= & 0 \cdot 0 = 0.
\end{align*}

\begin{gather*}
\therefore \lim_{x \to \infty} \frac{1}{x^{k+1}} = 0. \\ \\
\therefore \lim_{x \to \infty} \frac{1}{x^k} = 0 \text{, } \forall k \in \mathbb{N}.
\end{gather*}

$\square$

Revisaremos un par de ejemplos donde aplicaremos las propiedades enunciadas.

Ejemplo 2. Determina $$\lim_{x \to \infty} \frac{8x+5}{x^3+10}.$$

Notemos que
\begin{align*}
\lim_{x \to \infty} \frac{8x+5}{x^3+10} = & \lim_{x \to \infty} \frac{8x+5}{x^3+10} \cdot \frac{\frac{1}{x^3}}{\frac{1}{x^3}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{8x}{x^3} + \frac{5}{x^3}}{\frac{x^3}{x^3}+\frac{10}{x^3}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{8}{x^2} + \frac{5}{x^3}}{1+\frac{10}{x^3}} \\ \\
= & \frac{\lim\limits_{x \to \infty} \frac{8}{x^2} + \frac{5}{x^3}}{\lim\limits_{x \to \infty} 1+\frac{10}{x^3}} \\ \\
= & \frac{0 + 0}{1+0} \\ \\
= & \frac{0}{1} \\ \\
= & 0.
\end{align*}
$$\therefore \lim_{x \to \infty} \frac{8x+5}{x^3+10} = 0.$$

Ejemplo 3. Calcula el siguiente límite $$\lim_{x \to \infty} \frac{1}{\sqrt{x^2-2x}-x}.$$

Como consideraremos que $x \rightarrow \infty$, podemos suponer, particularmente, que $x>0$, entonces

\begin{align*}
\frac{1}{\sqrt{x^2-2x}-x} = & \frac{1}{\sqrt{x^2-2x}-x} \cdot \frac{\sqrt{x^2-2x}+x}{\sqrt{x^2-2x}+x} \\ \\
= & \frac{\sqrt{x^2-2x}+x}{\left( \sqrt{x^2-2x} \right)^2 – x^2}\\ \\
= & \frac{\sqrt{x^2-2x}+x}{x^2-2x – x^2} \\ \\
= & \frac{\sqrt{x^2-2x}+x}{-2x} \\ \\
= & -\frac{\sqrt{x^2-2x}}{2x} – \frac{x}{2x} \\ \\
= & -\frac{\sqrt{x^2-2x}}{\sqrt{4x^2}} – \frac{1}{2} \text{, como $x$ es positivo, $\sqrt{4x^2} = |2x| = 2x$ } \\ \\
= & -\sqrt{\frac{x^2-2x}{4x^2}} – \frac{1}{2} \\ \\
= & -\sqrt{\frac{x^2}{4x^2} – \frac{2x}{4x^2}} – \frac{1}{2} \\ \\
= & -\sqrt{\frac{1}{4} – \frac{1}{2x}} – \frac{1}{2}.
\end{align*}
$$\Rightarrow \frac{1}{\sqrt{x^2-2x}-x} = -\sqrt{\frac{1}{4} – \frac{1}{2x}} – \frac{1}{2}.$$

Entonces tenemos que
\begin{align*}
\lim_{x \to \infty} \frac{1}{\sqrt{x^2-2x}-x} = & \lim_{x \to \infty} \left( -\sqrt{\frac{1}{4} – \frac{1}{2x}} – \frac{1}{2} \right) \\
= & -\sqrt{\frac{1}{4} – 0} – \frac{1}{2} \\
= & -\frac{1}{2} -\frac{1}{2} \\
= & -1.
\end{align*}
$$\therefore \lim_{x \to \infty} \frac{1}{\sqrt{x^2-2x}-x} = -1.$$

A continuación enunciaremos el teorema del sándwich para este tipo de límites.

Proposición. Sean $f$, $g$, $h: A \rightarrow \mathbb{R}$ con $A \subset \mathbb{R}$ tal que $(a, \infty) \subset A$ para algún $a \in \mathbb{R}$. Si existe $M_1 \in \mathbb{R}$ tal que para todo $x >M_1$ se tiene que $$f(x) \leq g(x) \leq h(x) \quad \text{ y } \quad \lim_{x \to \infty} f(x) = L = \lim_{x \to \infty} h(x).$$

Entonces $$ \lim_{x \to \infty} g(x) = L.$$

Nuevamente, omitiremos la demostración pues es análoga a la revisada en una entrada anterior.

Extensión del límite en el infinito

Así como tenemos el límite en el infinito, existe una definición análoga que considera el límite de una función cuando $x$ tiende a $- \infty$.

Definición. Sean $A \subseteq \mathbb{R}$ y $f: A \rightarrow \mathbb{R}$. Decimos que $f$ tiende al límite $L \in \mathbb{R}$ cuando $x$ tiende a $- \infty$ si para cualquier $\varepsilon > 0$ existe $m \in \mathbb{R}$, tal que para cualquier $x<m$, se tiene que $|f(x)-L|<\varepsilon$ y lo denotamos $$\lim_{x \to -\infty} f(x) = L.$$

La definición nos indica que $f$ tiene límite $L$ cuando $x$ tiende a $-\infty$ si para valores lo suficientemente pequeños de $x$ nos acercamos arbitrariamente a $L$.

Esta extensión de límite tiene propiedades análogas revisadas en esta entrada.

Más adelante…

En la siguiente entrada revisaremos una nueva variante del límite de una función: los límites infinitos. Es decir, veremos el caso donde el límite de una función es infinito.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Demostrar que si $f: A \rightarrow \mathbb{R}$ es tal que $$\lim_{x \to \infty} x f(x) = L$$ con $L \in \mathbb{R}$, entonces $$\lim_{x \to \infty} f(x) = 0.$$
  • Sean $f$ y $g$ dos funciones definidas en $(a, \infty)$ tales que $$\lim_{x \to \infty} f(x) = L \quad \text{ y } \quad \lim_{x \to \infty} g(x) = \infty.$$
    Entonces se tiene que $$\lim_{x \to \infty} f(g(x)) = L.$$
  • Prueba que $$\lim_{x \to \infty} f(x) = \lim_{x \to -\infty} f(-x).$$
  • Prueba que $$\lim_{x \to 0^-} f(\frac{1}{x}) = \lim_{x \to -\infty} f(x).$$
  • Calcula los siguientes límites
    $i$) $$\lim_{x \to \infty} \frac{\sqrt{x+1}}{x} \text{, definido para } x >0.$$
    $ii$) $$\lim_{x \to \infty} \frac{\sqrt{x}-x}{\sqrt{x}+x} \text{, definido para } x >0.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Límites laterales

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En las entradas anteriores hemos trabajado con la definición de límite y revisamos sus propiedades. En esta ocasión, daremos la definición de límite por la derecha y límite por la izquierda, que en conjunto son llamados límites laterales. De igual forma, revisaremos algunos ejemplos y su relación con la definición vista anteriormente.

Límites laterales

Las definiciones que veremos a continuación se basan en restringir la forma en que nos acercamos a $x_0.$ El límite por la derecha se enfoca en acercarnos por la derecha, es decir, pediremos que $x > x_0,$ lo cual se traducirá en que debe cumplirse que $0<x-x_0 < \delta$. Por otro lado, para el límite por la izquierda debe cumplirse que $x < x_0,$ de esta forma se tendrá que $0<x_0-x< \delta.$ Primero daremos la definición de límite por la derecha.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la derecha de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x-x_0<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la derecha, lo denotamos $$\lim_{x \to x_0+} f(x) = L.$$

Análogamente, tenemos la definición de límite por la izquierda.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la izquierda de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x_0 – x<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la izquierda, lo denotamos $$\lim_{x \to x_0-} f(x) = L.$$

Propiedades de los límites laterales

De forma similar al teorema que vimos para los límites, existe una relación entre el límite lateral de una función y el límite de una sucesión, basta agregar a los supuestos la condición de que la sucesión sea mayor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la derecha y que sea menor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la izquierda.

Teorema. Sea $A \subset \mathbb{R}.$ Definimos la función $f:A \rightarrow \mathbb{R}.$ Entonces, dado un $x_0,$ los siguientes enunciados son equivalentes.

  1. $$\lim_{x \to x_0+} f(x) = L.$$
  2. Para toda sucesión $\{ a_n \}$ en $A$ que converge a $x_0$ y tal que $a_n > x_0$ para todo $n\in \mathbb{N},$ la sucesión $\{f(a_n)\}$ converge a $L.$

El teorema de límite por la izquierda es similar al anterior. Además, la demostración es totalmente análoga a la revisada en una entrada anterior por lo cual quedará como tarea moral. También recordemos que este teorema nos ayuda a determinar las propiedades que tienen los límites laterales debido a la herencia que nos brinda el límite de una sucesión; es gracias a ello que podremos hacer uso de tales propiedades en los siguientes ejemplos.

Ejemplo 1. Sea $f: \mathbb{R} \rightarrow \mathbb{R},$ definida de la siguiente forma

$$f(x) =
\begin{cases}
x^3+1 & \quad \text{si } x<-1 \\
x^2+1& \quad \text{si } x \geq -1. \\
\end{cases}
$$

Determina los límites laterales en $x_0 = -1.$

Primero mostraremos la gráfica de la función:

Calculando el límite por la izquierda, tenemos
$$\lim_{x \to -1^-} f(x) = \lim_{x \to -1^-} x^3+1 = 0.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to -1^+} f(x) = \lim_{x \to -1^+} x^2+1= 2.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 0 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 2.$$

Ejemplo 2. Sea $f: \mathbb{R} \setminus \{0 \} \rightarrow \mathbb{R}.$ Calcula los límites laterales en $x_0 = 0$ de

$$f(x) = \frac{|x|}{x}.$$

La gráfica de la función es la siguiente:

Calculando el límite por la izquierda, tenemos
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} \frac{|x|}{x} \\
= & \lim_{x \to 0^-} \frac{-x}{x} \text{, pues $x$ < 0} \\
= & \lim_{x \to 0^-} -1 \\
= & -1.
\end{align*}
Por otro lado, el límite por la derecha
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} \frac{|x|}{x} \\
= & \lim_{x \to 0^+} \frac{x}{x} \text{, pues $x$ > 0} \\
= & \lim_{x \to 0^+} 1 \\
= & 1.
\end{align*}
Por lo tanto
$$\lim_{x \to 0^-} f(x) = -1 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 1.$$

De los ejemplos revisados, el primero tiene la propiedad de que sus límites laterales son iguales mientras que para el segundo y el tercero tales límites son distintos en $x_0.$

Relación entre el límite de una función y sus límites laterales

Parece inmediato inferir que, considerando un punto $x_0$ dado, si los límites por la izquierda y por la derecha existen y son iguales, entonces el límite de la función sí existe en tal punto. De la misma manera, resulta natural que si el límite existe, entonces los límites laterales también existen y son iguales. Probaremos esta equivalencia, pero para hacerlo, primero demostraremos la siguiente proposición.

Proposición. Sean $x,$ $x_0$ en $\mathbb{R}$ y $\delta >0.$ Entonces $0<|x-x_0|< \delta$ si y solo si $0<x-x_0<\delta \quad$ ó $\quad 0<x_0-x<\delta.$

Demostración.
Supongamos que $0<|x-x_0|< \delta$.

Caso 1: $x-x_0 > 0$.
Entonces $|x-x_0| = x-x_0$, así
\begin{gather*}
0<|x-x_0|< \delta \Leftrightarrow 0< x-x_0 < \delta.
\end{gather*}

Caso 2: $x- x_0 < 0$.
Entonces $|x-x_0| = x_0-x$, así
\begin{gather*}
0<|x-x_0| < \delta \Leftrightarrow 0< x_0-x < \delta.
\end{gather*}

$$\therefore 0<|x-x_0|< \delta \Leftrightarrow 0<x-x_0<\delta \quad \text{ ó } \quad 0<x_0-x<\delta.$$

$\square$

Teorema. El límite de una función $f$ en el punto $x_0$ existe y es igual a $L$ si y solo si los límites laterales existen y son iguales a $L$, es decir

$$\lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

Demostración.

$\Rightarrow]$ Supongamos que $$\lim_{x \to x_0} f(x) = L.$$
Sea $\varepsilon > 0$. Como $f$ converge a $L$ en $x_0$, existe $\delta > 0$ tal que si $0<|x-x_0|< \delta$ se tiene que $|f(x)-L| < \varepsilon.$

Si $0<x-x_0 < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^+} f(x) = L.
\end{gather*}

Si $0<x_0-x < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^-} f(x) = L.
\end{gather*}

$\Leftarrow]$ Supongamos que $$\lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x)$$
Sea $\varepsilon > 0.$

Como $\lim\limits_{x \to x_0^+} f(x) = L$, existe $\delta_1$ tal que si $0<x-x_0<\delta_1$ entonces $|f(x)-L| < \varepsilon.$

Como $\lim\limits_{x \to x_0^-} f(x) = L$, existe $\delta_2$ tal que si $0<x_0-x<\delta_2$ entonces $|f(x)-L| < \varepsilon.$

Consideremos $\delta = min \{ \delta_1, \delta_2\}.$ Por la proposición, si $0<|x-x_0|< \delta$, entonces $0<x-x_0<\delta$ ó $0<x_0-x<\delta.$

Para el primer caso, tenemos que $0<x-x_0<\delta \leq \delta_1$, entonces $|f(x)-L| < \varepsilon.$
Para el segundo caso, se tiene que $0<x_0-x<\delta \leq \delta_2$, entonces $|f(x)-L| < \varepsilon.$

Por lo tanto $$\lim_{x \to x_0} f(x) = L.$$

$$\therefore \lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

$\square$

Observación. Ya que hemos demostrado este teorema, podemos notar que si los límites laterales de una función son distintos en un punto $x_0$, entonces no existe el límite de la función en tal punto.

Finalizaremos esta entrada revisando los siguientes ejemplos.

Ejemplo 3. Determina si existe el límite en $x_0 = 0$ para la siguiente función $$f(x) = x \sqrt{\frac{1}{4x^2}-16}.$$

Veamos primero qué sucede con el límite por la izquierda
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^-} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ \sqrt{4x^2} } \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ 2|x|} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ -2x} \text{, pues $x$ < 0} \\ \\
= & \lim_{x \to 0^-} – \frac{\sqrt{1-64x^2} }{2} \\ \\
= & – \frac{1}{2}.
\end{align*}

De forma similar, tenemos que
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^+} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^+} \frac{ x \sqrt{1-64x^2} }{ 2x} \text{, pues $x$ > 0} \\ \\
= & \lim_{x \to 0^+} \frac{\sqrt{1-64x^2} }{2} \\ \\
= & \frac{1}{2}.
\end{align*}
$$\therefore \lim_{x \to 0^-} f(x) = -\frac{1}{2} \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = \frac{1}{2}.$$

Como los límites laterales son distintos, podemos concluir que el límite de la función $f$ no existe en el punto $x_0 = 0.$

Ejemplo 4. Sea $f: \mathbb{R} \rightarrow \mathbb{R}$, definida de la siguiente forma
$$f(x) =
\begin{cases}
x^2 & \quad \text{si } x<5 \\
2x+15 & \quad \text{si } x \geq 5. \\
\end{cases}
$$
Determina si el límite existe en $x_0 = 5.$

Iniciemos calculando el límite por la izquierda.
$$\lim_{x \to 5^-} f(x) = \lim_{x \to 5^-} x^2 = 25.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to 5^+} f(x) = \lim_{x \to 5^+} 2x+15 = 25.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 25 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 25.$$

Como los límites laterales existen y son iguales, podemos concluir que
$$\lim_{x \to 0} f(x) = 25.$$

Más adelante…

¿Qué sucede cuando en lugar de acercarnos a un punto en particular $x_0$, hacemos que $x$ crezca indefinidamente? Esto y otras ampliaciones del concepto del límite serán revisadas en la siguiente entrada con lo cual estaremos listos para calcular todo tipo de límites y, con ello, podremos conocer el comportamiento que toman las funciones tanto en un punto específico como «en el infinito».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Demuestra que
    $i$) $\lim_\limits{x \to 0^+} f(x) = \lim_\limits{x \to 0^-} f(-x).$
    $ii$) $\lim_\limits{x \to 0} f(|x|) = \lim_\limits{x \to 0^+} f(x).$
  • Usando la definición épsilon-delta de límite por la derecha, prueba que $\lim_{x \to 8^+} \sqrt{x-8} = 0.$
  • Calcula el límite en $x_0 = 5$ de la función
    $$f(x) =
    \begin{cases}
    \frac{x^2-12x+35}{x-5} & \quad \text{si } x < 5 \\
    \frac{x-5}{1- \sqrt{x-4} } & \quad \text{si } x \geq 5.
    \end{cases}
    $$
  • Usando límites laterales, determina si existe $$\lim_{x \to 0} \frac{3x + |x|}{7x-5|x|}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Teoremas sobre el límite de una función

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Después de haber revisado algunos ejemplos de límite de funciones, estamos listos para conocer y demostrar algunas de las propiedades; para este fin, usaremos la relación existente entre el límite de una función y el de una sucesión demostrada en la entrada anterior.

Teoremas sobre el límite de una función

Considerando el criterio de sucesiones para límites visto anteriormente, es natural que haya una gran cantidad de propiedades que se hereden del límite de sucesiones. A continuación revisaremos algunas de ellas y podremos aprovechar la relación de ambos conceptos para hacer la demostración de las mismas.

Teorema. Sean $f: A \rightarrow \mathbb{R}$ y $g: A \rightarrow \mathbb{R}$ dos funciones y sea $c \in \mathbb{R}$. Si $$\lim_{x \to x_0} f(x) = L \quad \text{ y } \quad \lim_{x \to x_0} g(x) = M.$$
Entonces

  1. $$\lim_{x \to x_0} c \cdot f(x) = cL.$$
  2. $$\lim_{x \to x_0} (f+g)(x) = L+M.$$
  3. $$\lim_{x \to x_0} (f-g)(x) = L-M.$$
  4. $$\lim_{x \to x_0} (f \cdot g)(x) = L\cdot M.$$
  5. Si además $M \neq 0$, entonces $$\lim_{x \to x_0} \left( \frac{f}{g} \right) (x) = \frac{L}{M}.$$

Demostración

Daremos la demostración del inciso 4 y la demostración de los demás es análoga.

Sea $\{ a_n \}$ una sucesión en $A$ que converge a $x_0$ tal que $a_n \neq x_0$ para todo $n\in \mathbb{N}$, por el teorema anterior tenemos que
$$\lim_{n \to \infty} f(a_n) = L \quad \text{ y } \quad \lim_{n \to \infty} g(a_n) = M.$$

De esta forma podemos usar las propiedades de convergencia de una sucesión, así

$$\lim_{n \to \infty} (f \cdot g)(a_n) = \lim_{n \to \infty} \left( f(a_n) \cdot g(a_n) \right) = \lim_{n \to \infty} f(a_n) \cdot \lim_{n \to \infty} g(a_n) = L \cdot M.$$
Por el teorema revisado, podemos concluir que $$\lim_{x \to x_0} (f \cdot g)(x) = L \cdot M.$$

$\square$

Observación. Particularmente podemos generalizar los puntos 2 y 4, de tal forma que si $f_1, f_2, \dots, f_n$ son funciones definidas de $A$ a $\mathbb{R}$ cada una con límite $L_1, L_2, \dots L_n$ en $x_0$. Entonces

\begin{gather*}
\lim_{x \to x_0} (f_1 + f_2 + \ldots + f_n) (x) = L_1 + L_2 + \ldots + L_n \\
\text{ y } \\
\lim_{x \to x_0} (f_1 \cdot f_2 \cdot \ldots \cdot f_n)(x) = L_1 \cdot L_2 \cdot \ldots \cdot L_n.
\end{gather*}

Revisaremos un par de ejemplos donde aplicaremos las propiedades anteriores.

Ejemplo 1. Calcula $$\lim_{x \to 2} \frac{5x-12}{2x + 10}.$$
\begin{align*}
\lim_{x \to 2} \frac{5x-12}{2x + 10} =& \frac{ \lim_\limits{x \to 2} ( 5x-12 ) }{ \lim_\limits{x \to 2} (2x + 10) } \text{, por el punto 5 del teorema anterior} \\ \\
= & \frac{ \lim_\limits{x \to 2} 5x – \lim_\limits{x \to 2} 12 }{ \lim_\limits{x \to 2} 2x + \lim_\limits{x \to 2} 10 } \text{, por los puntos 2 y 3 del teorema anterior} \\ \\
= & \frac{10-12}{4+10} \\ \\
= & – \frac{1}{7}.
\end{align*}
$$\therefore \lim_{x \to 2} \frac{5x-12}{2x + 10} = – \frac{1}{7}.$$

Ejemplo 2. Calcula $$\lim_{x \to 5} \frac{x^3+3}{8x^2 + 7}.$$
\begin{align*}
\lim_{x \to 5} \frac{x^3+3}{8x^2 + 7} = & \frac{\lim_\limits{x \to 5} (x^3+3)}{ \lim_\limits{x \to 5} (8x^2 + 7)} \text{, por el punto 5 del teorema anterior} \\ \\
= & \frac{\lim_\limits{x \to 5} x^3+ \lim_\limits{x \to 5} 3}{ \lim_\limits{x \to 5} 8x^2 + \lim_\limits{x \to 5} 7} \text{, por el punto 2 del teorema anterior} \\ \\
= & \frac{125+ 3}{200 + 7} \\ \\
= & \frac{128}{207}.
\end{align*}
$$\therefore \lim_{x \to 5} \frac{x^3+3}{8x^2 + 7} = \frac{128}{207}.$$

En los ejemplos anteriores se hizo énfasis en las propiedades que nos permitieron calcular el límite con la finalidad de mostrar claramente cómo se emplean, sin embargo, esto no será necesario y, de hecho, no se hará tal hincapié de ahora en adelante.

A continuación probaremos el teorema del sándwich para el límite de una función.

Teorema. Sean $f$, $g$, $h : A \rightarrow \mathbb{R}$ y sea $x_0 \in A$. Si

$$f(x) \leq g(x) \leq h(x) \text{, para todo } x \in A, x \neq x_0,$$

y si $$\lim_{x \to x_0} f(x) = L \quad \text{ y } \quad \lim_{x \to x_0} h(x) = L.$$

Entonces

$$\lim_{x \to x_0} g(x) = L.$$
Demostración

Sea $\varepsilon > 0 $, como $f$ y $h$ tienen como límite a $L$ en $x_0$, entonces existen $\delta_1$, $\delta_2$ tales que

\begin{gather*}
0<|x-x_0|< \delta_1, \quad \text{entonces} \quad |f(x)-L|< \varepsilon \\
\text{ y } \\
0<|x-x_0|< \delta_2, \quad \text{entonces} \quad |h(x)-L| < \varepsilon.
\end{gather*}

Consideremos $\delta = min\{ \delta_1, \delta_2 \}$, si $0<|x-x_0|< \delta$, se cumple que

\begin{gather*}
-\varepsilon < f(x)-L < \varepsilon \quad \Leftrightarrow \quad L-\varepsilon < f(x) < L + \varepsilon \\
\text{ y } \\
-\varepsilon < h(x)-L < \varepsilon \quad \Leftrightarrow \quad L-\varepsilon < h(x) < L + \varepsilon.
\end{gather*}

Además, por hipótesis se tiene que $f(x) \leq g(x) \leq h(x)$, entonces

\begin{gather*}
L-\varepsilon < f(x) \leq g(x) \quad \text{ y } \quad g(x) \leq h(x) < L + \varepsilon.
\end{gather*}
Se sigue que
\begin{gather*}
L-\varepsilon < g(x) < L + \varepsilon. \\ \\
\Leftrightarrow -\varepsilon < g(x) – L< \varepsilon. \\ \\
\therefore |g(x) – L| < \varepsilon. \\ \\
\therefore \lim_{x \to x_0} g(x) = L.
\end{gather*}

$\square$

A continuación veremos un ejemplo donde podemos aplicar el teorema del sándwich.

Ejemplo 3. Encuentra el siguiente límite: $$\lim_{x_0 \to 0} x^2 e^{sen(\frac{1}{x})}.$$
Sabemos que

\begin{gather*}
– 1 \leq sen(\frac{1}{x}) \leq 1 \text{, para todo } x \neq 0.
\end{gather*}
Dado que la función exponencial no altera la relación de orden, entonces tenemos
\begin{gather*}
e^{- 1} \leq e^{sen(\frac{1}{x})} \leq e^{ 1}.
\end{gather*}
Se sigue que
\begin{gather*}
x^2 e^{- 1} \leq x^2 e^{sen(\frac{1}{x})} \leq x^2 e^{ 1}.
\end{gather*}

La función original $g(x) = x^2 e^{sen(\frac{1}{x})}$ está acotada por $f(x) = x^2 e^{- 1}$ y $h(x) = x^2 e^{1}$. Tal como se muestra en la siguiente gráfica:

Notemos que
$$\lim_{x \to 0} x^2 e^{- 1} = 0 \quad \text{ y } \quad \lim_{x \to 0} x^2 e^{1} = 0.$$
Por el teorema del sándwich podemos concluir que $$\lim_{x_0 \to 0} x^2 e^{sen(\frac{1}{x})} = 0.$$

En esta entrada revisamos algunas de las propiedades que tiene el límite de una función haciendo uso del límite de sucesiones, pero vale la pena destacar que también se pudo recorrer este tramo del camino usando la definición épsilon-delta y te invitamos a realizar el ejercicio de demostrar algunas de las propiedades haciendo uso de tal definición con la finalidad de tener un dominio mayor del concepto.

Más adelante…

Extenderemos la noción de límite de una función definiendo una nueva clase de límites: los límites laterales. Veremos la definición de límite por la derecha y límite por la izquierda que son definiciones menos exigentes y las cuales nos permiten tener un análisis más detallado para aquellas funciones donde el límite no existe.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Prueba que si $$\lim_{x \to x_0} f(x) = L \text{, entonces } \lim_{x \to x_0} |f(x)| = |L|.$$
  • Calcula el límite $$\lim_{x \to 0} \frac{(x+1)^2-1}{x}.$$
  • Calcula el límite $$\lim_{x \to 0} \frac{\sqrt{x}-1}{x-1}.$$
  • Calcula el límite $$\lim_{x \to 0} x^2 cos \left( \frac{1}{x^2} \right).$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»