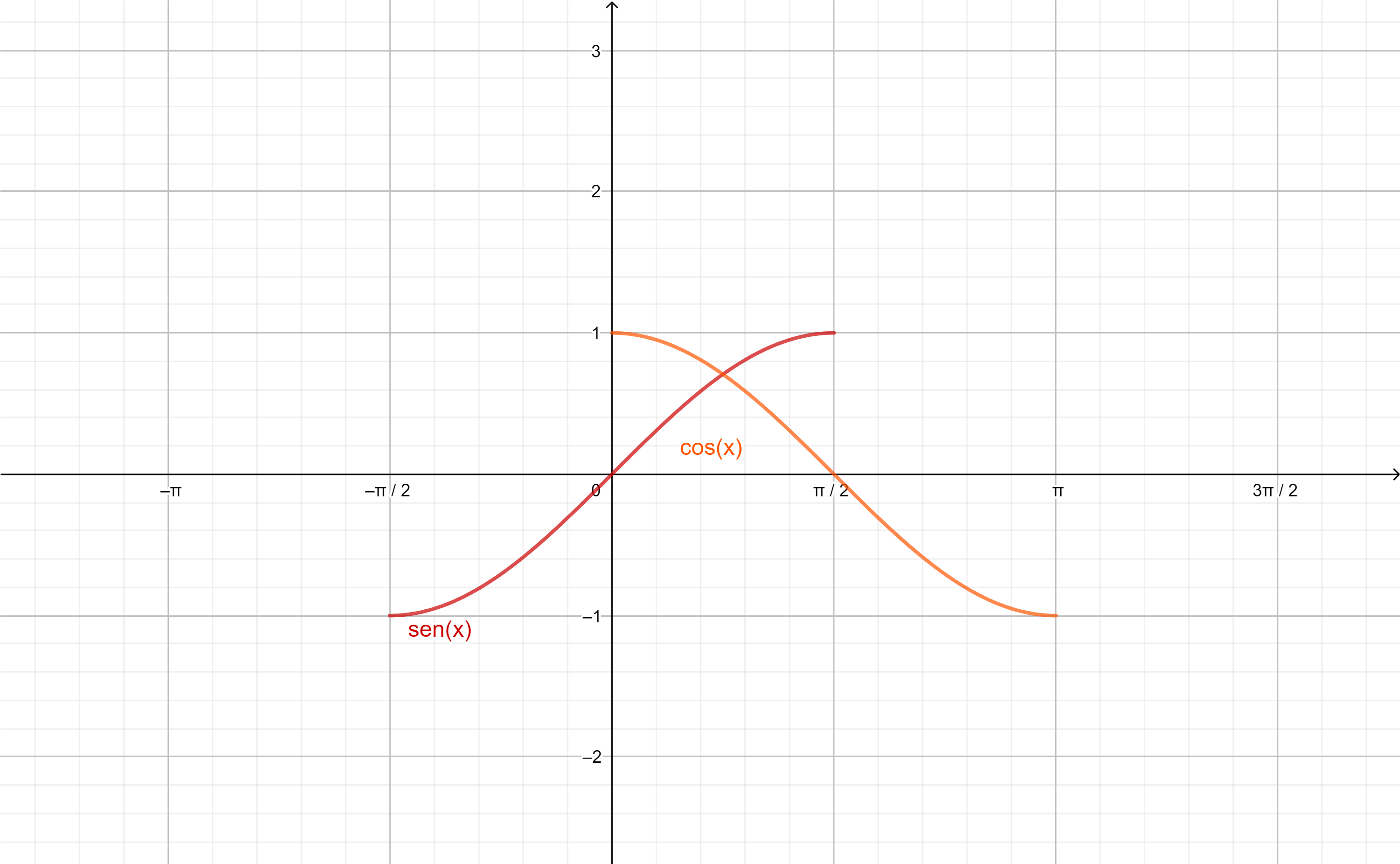Archivo de la etiqueta: funciones

Cálculo Diferencial e Integral I: Funciones trigonométricas (Parte 1)

Por Karen González Cárdenas

Deja un comentario

Introducción

De las clases en el bachillerato recordarás las siguientes definiciones, utilizando el triángulo rectángulo de la imagen siguiente:


\begin{align*}
sen\theta&=\frac{\text{cat op}}{\text{hip}}=\frac{b}{c} & csc\theta&=\frac{\text{hip}}{\text{cat op}}=\frac{c}{b}\\
cos\theta&=\frac{\text{cat ad}}{\text{hip}}=\frac{a}{c} & sec\theta&=\frac{\text{hip}}{\text{cat ad}}=\frac{c}{a}\\
tan\theta&=\frac{\text{cat op}}{\text{cat ad}}=\frac{b}{a} & cot\theta&=\frac{\text{cat ad}}{\text{cat op}}=\frac{a}{b}\\
\end{align*}
donde:
cat op = cateto opuesto ; cat ad = cateto adyacente e hip= hipotenusa.

También recordemos que tenemos la siguiente equivalencia:

$360°$ es equivalente a $2\pi$.

A lo largo de esta entrada veremos las principales características de este conjunto de funciones, sus gráficas y algunas identidades trigonométricas.

Identidades trigonométricas Pitagóricas

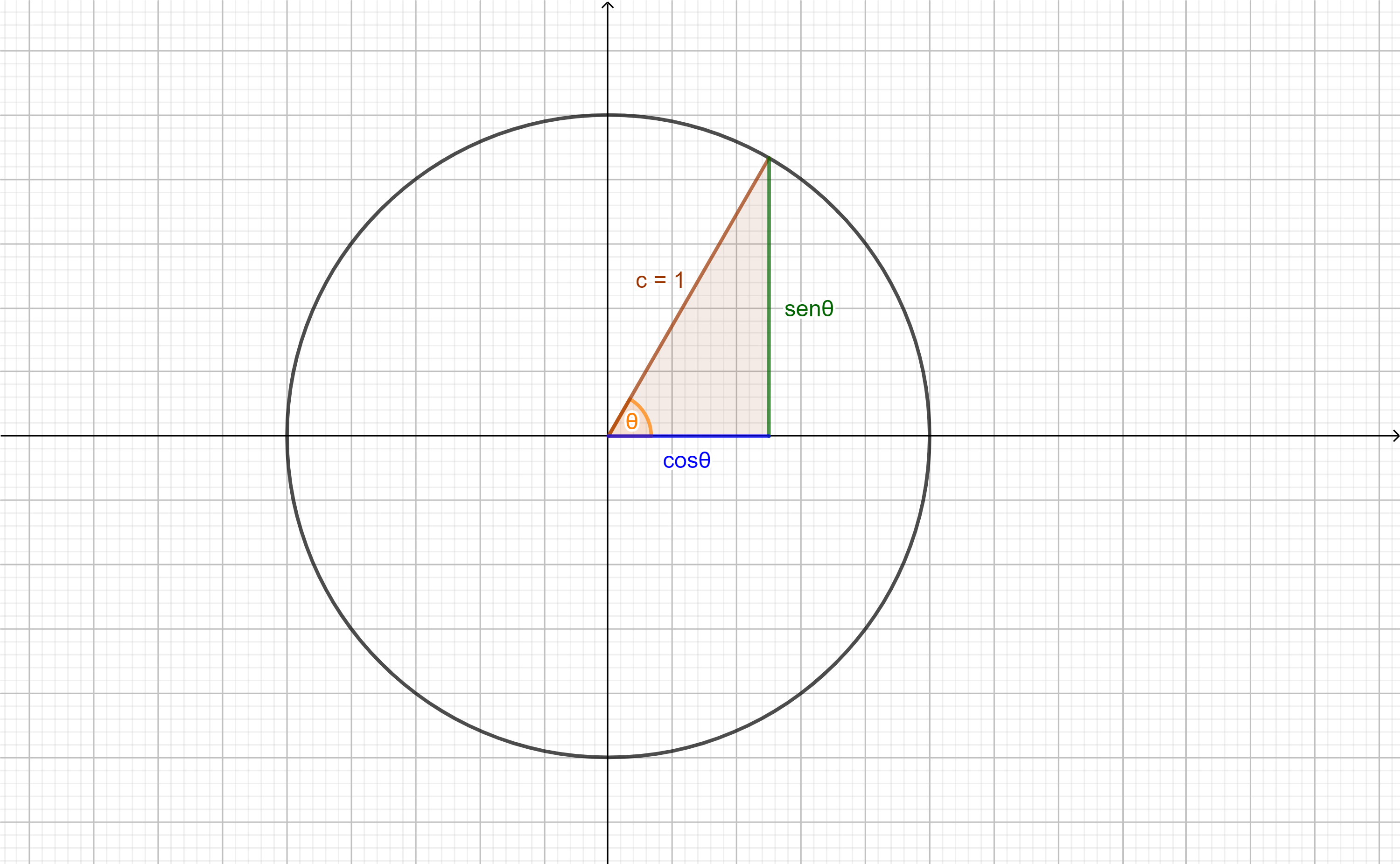
Si tomamos a la circunferencia unitaria y un triángulo rectángulo como en la imagen:

Observamos que al sustituir el valor hip $=1$ en las definiciones anteriores para el $sen\theta$ y el $cos\theta$ tenemos:
\begin{align*}
sen\theta&=\frac{\text{cat op}}{\text{1}} & cos\theta&=\frac{\text{cat ad}}{\text{1}}\\
&= \text{cat op} & &=\text{cat ad}\\
&= b & &=a\
\end{align*}


Dadas las igualdades obtenidas e hip$=1$ al sustituir para el resto de las funciones tenemos:
\begin{align*}
tan\theta &= \frac{sen\theta}{cos\theta} & cot\theta &=\frac{cos\theta}{sen\theta}\\
sec\theta &=\frac{1}{cos\theta} & csc\theta&=\frac{1}{sen\theta}
\end{align*}

Recordemos el conocido Teorema de Pitágoras que nos da una relación entre los catetos y la hipotenusa de un triángulo rectángulo:
$$a^{2}+b^{2}=c^{2}.$$

Si lo aplicamos al triángulo rectángulo obtenido en la imagen anterior donde:
\begin{align*}
a&= cos\theta & b&=sen\theta & c&=1
\end{align*}
entonces tenemos la siguiente igualdad:
\begin{equation}
cos^{2}\theta + sen^{2}\theta =1.
\end{equation}
Si dividimos $(1)$ entre $cos^{2}\theta$ obtenemos:
\begin{equation*}
\frac{cos^{2}\theta}{ cos^{2}\theta}+ \frac{sen^{2}\theta}{cos^{2}\theta} =\frac{1}{cos^{2}\theta}.
\end{equation*}
Que simplificando sería:
\begin{equation}
1+ tan^{2}\theta=sec^{2}\theta.
\end{equation}

Ahora bien si decidimos dividir $(1)$ entre $sen^{2}\theta$:
\begin{equation*}
\frac{cos^{2}\theta}{sen^{2}\theta} + \frac{sen^{2}\theta}{sen^{2}\theta} =\frac{1}{sen^{2}\theta}.
\end{equation*}
Que finalmente sería:
\begin{equation}
cot^{2}\theta +1= csc^{2}\theta.
\end{equation}

Las igualdades $(1)$, $(2)$ y $(3)$ son llamadas Identidades Pitagóricas:
\begin{align*}
cos^{2}\theta + sen^{2}\theta &=1,\\
1+ tan^{2}\theta &=sec^{2}\theta,\\
cot^{2}\theta +1&= csc^{2}\theta.\\
\end{align*}

Otras identidades trigonométricas


Otras identidades trigonométricas que son de utilidad son las de suma de ángulos:
\begin{align*}
cos( \alpha + \beta)&=cos(\alpha) cos(\beta) – sen(\alpha) sen(\beta),\\
sen(\alpha + \beta)&= cos(\alpha) sen(\beta) + cos(\beta) sen(\alpha).
\end{align*}
Para la resta de ángulos tendríamos un par similar:
\begin{align*}
cos( \alpha -\beta)&=cos(\alpha) cos(\beta) + sen(\alpha) sen(\beta),\\
sen(\alpha – \beta)&= cos(\alpha) sen(\beta) – cos(\beta) sen(\alpha).
\end{align*}
Ahora veremos cómo obtener las identidades para los ángulos dobles:
\begin{align*}
cos(2\alpha)&= cos(\alpha + \alpha)\\
&= cos(\alpha) cos(\alpha) – sen(\alpha) sen(\alpha)\\
&= cos^{2}\alpha – sen^{2}\alpha
\end{align*}
Por lo tanto tendríamos para el coseno de $2\alpha$:
\begin{equation}
cos(2\alpha)=cos^{2}\alpha – sen^{2}\alpha.
\end{equation}
Si procedemos análogamente para el seno de $2\alpha$:
\begin{align*}
sen(2\alpha)&= sen(\alpha + \alpha)\\
&= cos(\alpha) sen(\alpha) + cos(\alpha) sen(\alpha)\\
&= 2sen(\alpha) cos(\alpha)
\end{align*}
Así concluimos que:
\begin{equation}
sen(2\alpha)=2sen(\alpha) cos(\alpha).
\end{equation}
También tenemos un par de identidades que relacionadas con el $sen^{2}\theta$ y el $cos^{2}\theta$:
\begin{align*}
sen^{2}\theta &= \frac{1}{2}(1-cos(2\theta)), & cos^{2}\theta& =\frac{1}{2}(1+ cos(2\theta)).\\
\end{align*}
Se dejará como ejercicios en la Tarea moral obtener este par de igualdades.

Simetrías

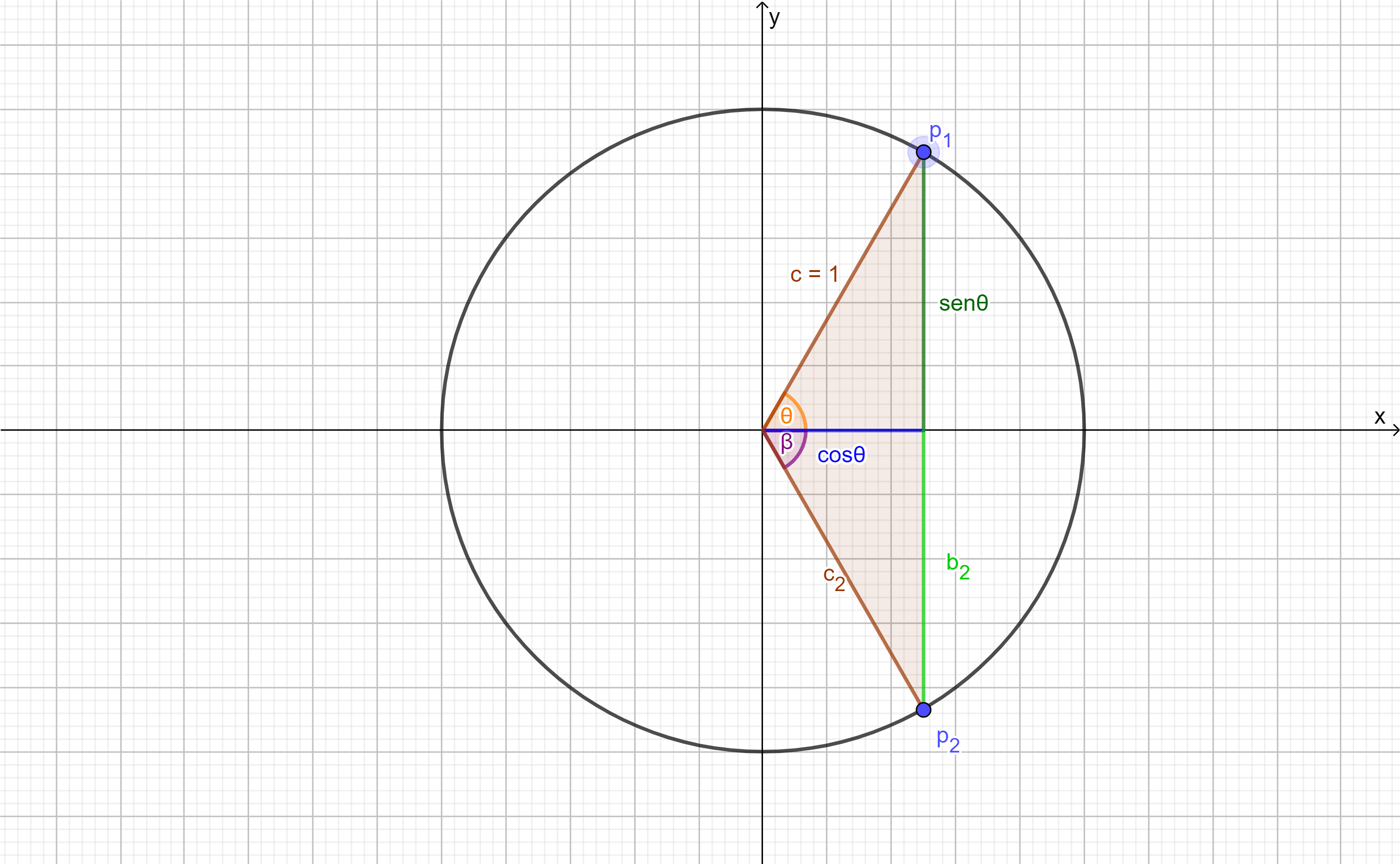
Retomando la imagen anterior, si ahora reflejamos al triángulo respecto al eje $x$, tenemos lo siguiente:

donde observamos los siguiente:
\begin{align*}
\beta &= – \theta & c_{2}&=1 & b_{2}=sen(-\theta)\\
\end{align*}

Así al considerar a los puntos $p_{1}$ y $p_{2}$ tenemos que estarían definidos de la siguiente manera:
\begin{align*}
p_{1}&=(cos(\theta), sen(\theta)) & p_{2}&=(cos(-\theta), sen(-\theta))\\
\end{align*}
Resaltamos para $p_{2}$ que:
$$p_{2}=(cos(-\theta), sen(-\theta))=(cos(\theta), -sen(\theta)).$$
de esta igualdad podemos determinar si las funciones seno y coseno son pares o impares, este ejercicio formará parte de la Tarea moral.

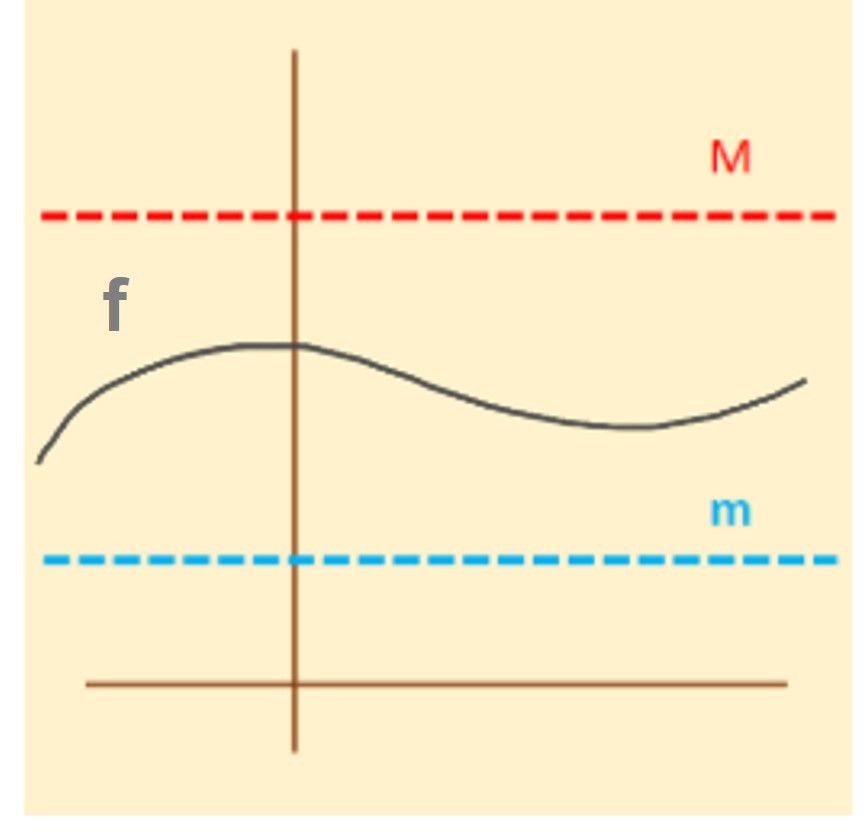
Función periódica

Definición (función periódica): Decimos que una función $f$ es periódica si existe $N \in \r$ tal que para todo $x \in D_{f}$ cumple que:
$$f(x)=f(x+ N)$$
y $|N|$ se llama periodo de $f$.
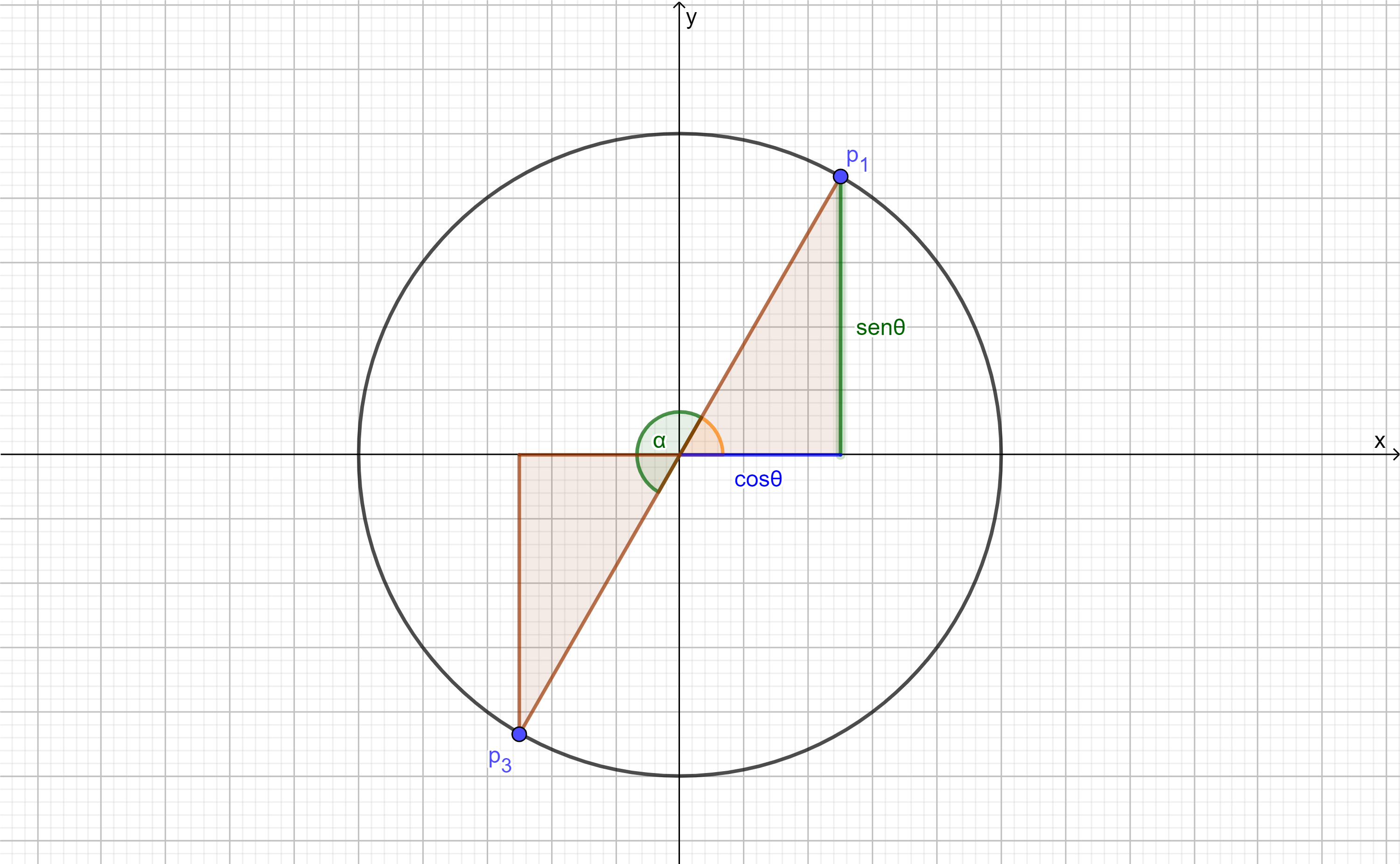
En la siguiente imagen observamos que $\alpha = \pi$ por lo que tendríamos que el nuevo triángulo agregado es en realidad el original rotado:

Así tendríamos la siguiente definición para los puntos $p_{1}$ y $p_{3}$:

\begin{align*}
p_{1}&=(cos(\theta), sen(\theta)) & p_{3}&=(cos(\theta + \pi), sen(\theta+ \pi))\\
\end{align*}

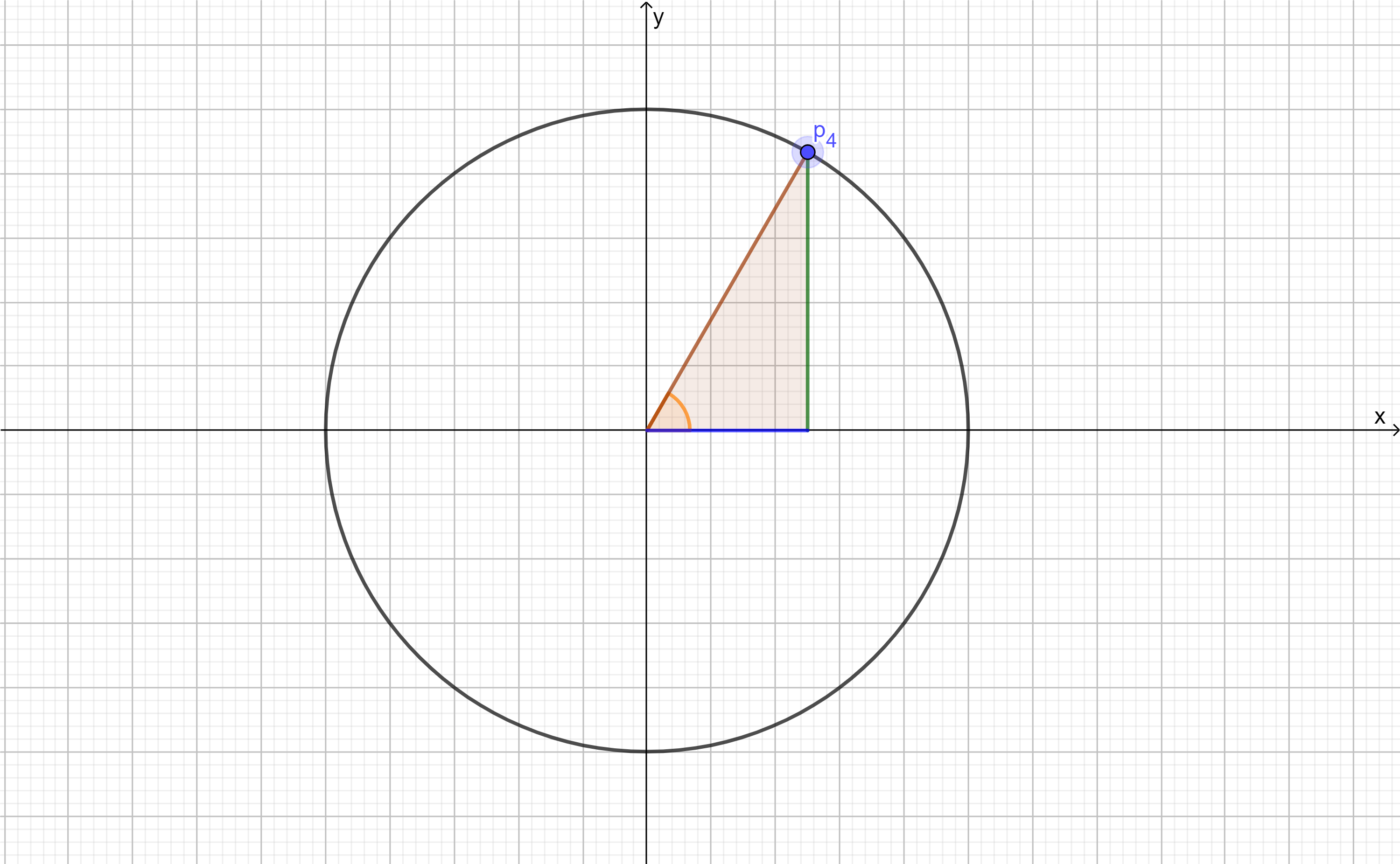
Si rotamos el triángulo ahora $\alpha = 2\pi$ tenemos que $p_{4}$ estaría definido como:
$$p_{4}=(cos(\theta + 2\pi), sen(\theta+ 2\pi)).$$


¡Y observamos que obtenemos el triángulo original! Consecuentemente tenemos las siguientes igualdades:
\begin{align*}
sen(\theta)&=sen(\theta+2\pi),\\
cos(\theta)&=cos(\theta+ 2\pi).
\end{align*}
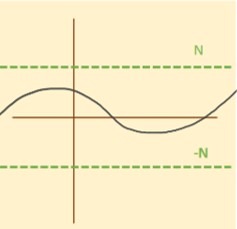
Aplicando la definición decimos que las funciones seno y coseno son periódicas con periodo $N=2\pi$.
En las gráficas de las funciones observamos el comportamiento anterior, cada $2 \pi$ se comienzan a repetir los valores:

Observación: Vemos que para todo $x \in \r$ ocurre:
$$-1 \leq sen(x) \leq 1$$
$$-1 \leq cos(x) \leq 1$$
por lo que las funciones seno y coseno son acotadas.

Consideraremos sus ramas principales definidas en los siguientes dominios donde cada uno de las funciones cumple ser inyectiva :
\begin{align*}
sen: \left[-\frac{\pi}{2}, \frac{\pi}{2} \right] \rightarrow [-1,1]
\end{align*}

\begin{align*}
cos: [0, \pi] \rightarrow [-1,1]
\end{align*}

Más adelante

En la próxima entrada, continuaremos con las definiciones de las funciones tangente, cotangente, secante y cosecante. Por lo tanto, realizaremos un análisis similar al dado para las funciones seno y coseno.

Tarea moral

  • Obtener las siguientes identidades trigonométricas:
    • $$sen^{2}\theta = \frac{1}{2}(1-cos(2\theta)).$$
    • $$cos^{2}\theta =\frac{1}{2}(1+ cos(2\theta)).$$
    • $$tan(\alpha + \beta)=\frac{tan(\alpha) + tan(\beta)}{-tan(\alpha)tan(\beta)}.$$
      Sugerencia.-Considera la igualdad:
      $$tan\theta=\frac{sen\theta}{cos\theta}$$
  • Determina si las siguientes funciones son pares, impares o ninguna de las opciones anteriores:
    • $sen(\theta).$
    • $cos(\theta).$
  • Obtén la gráfica de las siguientes funciones:
    • $f(x)=sen(x+\frac{\pi}{2}).$
    • $f(x)=-2cos(x)+1.$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Funciones polinomiales y racionales. Análisis geométrico de funciones

Por Karen González Cárdenas

Deja un comentario

Introducción

Quizás en algunos de tus cursos anteriores te presentaron funciones parecidas a las siguientes:
\begin{align*}
f(x)&= 4x^{2}-3x+1, & t(x)&=\frac{x^{2}+2x+5}{x^{3}+3}, & k(x)&= x^{3}\text{.}\\
\end{align*}
Todas pertenecen al conjunto de las funciones algebraicas. A lo largo de esta entrada, veremos las definiciones formales para cada una y comenzaremos a realizar un análisis geométrico con este conjunto de funciones.

Funciones polinomiales

Definición (función polinomial): Sea $f$ una función. Decimos que $f$ es una función polinomial si está definida como:
$$p(x)=a_{n}x^{n}+ a_{n-1}x^{n-1}+ \ldots + a_{0}$$
donde $ n \in \mathbb{N}\cup \left\{0 \right\}$ y los coeficientes $a_{i} \in \r$.

Definición (grado de una función polinomial): Llamamos grado de p(x) a la potencia mayor de $x$ con un coeficiente $a_{i} \neq 0$.
Ejemplos:

  • $g(x)= 120x^{10}+34x^{6}+14$
    el grado de $g(x)$ es $10$
  • $h(x)= \pi x^{3}+ 2\pi x^{2}+x$
    el grado de $h(x)$ es $3$

Una observación importante es que las funciones del tipo $f(x)=x^{n}$ con $n\in \mathbb{N}$, mejor conocidas como potencias de $x$, son un caso particular de las funciones polinomiales.

Funciones racionales

Definición (función racional): Consideremos $g$ una función. Diremos que $g$ es una función racional si está definida como el cociente de dos polinomios:
$$g(x)=\frac{a_{n}x^{n}+ a_{n-1}x^{n-1}+ \ldots + a_{0}}{b_{n}x^{n}+ b_{n-1}x^{n-1}+ \ldots + b_{0}}$$
donde $ n \in \mathbb{N}\cup \left\{0 \right\}$, los coeficientes $a_{i}, b_{i} \in \r$ y $b_{n}x^{n}+ b_{n-1}x^{n-1}+ \ldots + b_{0} \neq 0$.

Ejemplos:

  • $$h(x)=\frac{x^{2}-1}{x+3}$$
  • $$g(x)=\frac{x}{x^{3}+1}$$

Análisis geométrico

En numerosas ocasiones tendremos la necesidad de realizar un bosquejo de la gráfica de una función. Para ello nos basaremos en la gráfica de una función conocida previamente y la siguiente serie de elementos donde consideremos a $f(x)$ una función en los reales y a $\alpha$ una constante:
Traslaciones

  • Para $h(x)= f(x)+ \alpha$ con $\alpha >0$ tenemos que la gráfica de $h$ es la gráfica de $f$ trasladada verticalmente $\alpha$ unidades hacia arriba (sobre el eje $y$).
  • Y para $h(x)= f(x)- \alpha$ con $\alpha >0$ la gráfica de $h$ es la gráfica de $f$ trasladada verticalmente $\alpha$ unidades hacia abajo (sobre el eje $y$).
  • Ahora si $h(x)= f(x-c)$ con $\alpha >0$ entonces la gráfica de $h$ sería la gráfica de $f$ trasladada horizontalmente $\alpha$ unidades hacia la derecha (sobre el eje $x$).
  • En cambio si $h(x)= f(x+c)$ con $\alpha >0$ entonces la gráfica de $h$ sería la gráfica de $f$ trasladada horizontalmente $\alpha$ unidades hacia la izquierda (sobre el eje $x$).

Consideremos los siguientes ejemplos para $f(x)= x^{2}$:

Ampliaciones y reducciones

  • Si $g(x)= f(\alpha x)$ con $\alpha >1$ su gráfica sería la gráfica de $f$ comprimida horizontalmente (sobre el eje $x$).
  • Para $g(x)= f(\alpha x)$ con $0<\alpha <1$ su gráfica sería la gráfica de $f$ expandida horizontalmente (sobre el eje $x$).
  • Y para $g(x)= f(\alpha x)$ con $\alpha <-1$ su gráfica sería la gráfica de $f$ comprimida horizontalmente (sobre el eje $x$) y reflejada respecto del eje $y$.
  • Finalizamos con $g(x)= f(\alpha x)$ con $-1<\alpha <0$ su gráfica sería la gráfica de $f$ expandida horizontalmente (sobre el eje $x$) y reflejada respecto del eje $y$.

Observación: Si $\alpha=1$ vemos que $f((1)x)=f(x)$ por lo que no hay cambios.

  • Ahora bien si $g(x)= \alpha f(x)$ donde $\alpha >1$ la gráfica de $g$ es la gráfica de $f$ expandida verticalmente (sobre el eje $y$).
  • Cuando $g(x)= \alpha f(x)$ donde $0<\alpha <1$ la gráfica de $g$ es la gráfica de $f$ comprimida verticalmente (sobre el eje $y$).
  • Si $g(x)= \alpha f(x)$ donde $-1<\alpha $ la gráfica de $g$ es la gráfica de $f$ expandida verticalmente (sobre el eje $y$) y reflejada respecto del eje $x$.
  • Para $g(x)= \alpha f(x)$ donde $-1<\alpha <0$ la gráfica de $g$ es la gráfica de $f$ comprimida verticalmente (sobre el eje $y$) y reflejada respecto del eje $x$.

Observación: Para $\alpha =1$ tenemos que $(1)(f(x))=f(x)$.

Hablemos sobre la función inversa

Recordemos que si tenemos $f: A \rightarrow B$ una función esto significa que:
$$Graf(f)= \left\{(x, f(x)): x \in A \right\}\quad\text{.}$$

Ahora si consideramos a $f$ una función invertible, vemos que para $f^{-1}: B \rightarrow A$ ocurre:
$$Graf(f^{-1})= \left\{(f(x), x): f(x) \in B \right\}\quad \text{.}$$
Esto nos permite observar que un punto $(y,x) \in Graf(f^{-1})$ es la reflexión ortogonal del punto $(x,y) \in Graf(f)$ respecto a la función identidad.

De este modo podemos obtener la gráfica de $f^{-1}$ reflejando ortogonalmente la gráfica de $f$ respecto a la identidad.

En este ejemplo tomamos la función $f(x)=x^{2}$ en el dominio donde cumple ser biyectiva por lo que su función inversa sería $h(x)= \sqrt{x}$:

En la sección de Tarea moral encontrarás algunos ejercicios que te ayudarán a poner en práctica lo desarrollado en esta entrada.

Más adelante

En la siguiente entrada, comenzaremos a revisar el conjunto de las funciones trigonométricas. Veremos sus definiciones, algunas identidades trigonométricas que serán de utilidad y sus gráficas.

Tarea moral

Realiza las gráficas de las siguientes funciones dado que $f(x)=x^{3}$:

  • $f(x)+4$
  • $f(x-3)+2$
  • $f^{-1}(x)$
  • $f(2x)$
  • $2f(x)$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Funciones crecientes y decrecientes. Funciones acotadas

Por Karen González Cárdenas

Deja un comentario

Introducción

Continuando ahora con las funciones crecientes y decrecientes, veremos qué condiciones se deben cumplir para determinar si una función crece o decrece en un intervalo. De igual manera, veremos cuándo una función es no creciente o no decreciente para finalizar con la definición de función acotada.

Definición de función creciente y decreciente

Definición: Sea $f: A \rightarrow B$ una función.

  • Decimos que $f$ es una función creciente si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ tales que
    $$x_{1}< x_{2} \Rightarrow f(x_{1})<f(x_{2})\quad\text{.}$$
  • Decimos que $f$ es una función decreciente si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ tales que
    $$x_{1}< x_{2} \Rightarrow f(x_{2})<f(x_{1})\quad\text{.}$$

Definición de función no creciente y no decreciente

Definición: Consideremos a la función $f: A \rightarrow B$.

  • Llamamos a $f$ una función no creciente (que decrece o permanece igual) si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ que cumplen
    $$x_{1}< x_{2} \Rightarrow f(x_{2})\leq f(x_{1})\quad\text{.}$$
  • Llamamos a $f$ una función no decreciente (que crece o permanece igual) si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ que cumplen
    $$x_{1}< x_{2} \Rightarrow f(x_{1})\leq f(x_{2})\quad\text{.}$$

Ejemplo 1

Veamos que para la función definida como:
$$f(x)=x^{2}$$

Tenemos las siguientes observaciones:

  1. Es creciente en el intervalo $[0, \infty)$.
  2. Es decreciente en el intervalo $(- \infty,0)$.

Demostración:

  1. Sea $0 \leq x_{1} < x_{2}$ así se sigue que:
    \begin{align*}
    &\Rightarrow x_{1}^{2} < x_{2}^{2}\\
    &\Rightarrow f(x_{1}) < f(x_{2})
    \end{align*}
    $\therefore f$ es creciente en $[0, \infty)$.
  2. Ahora tomemos $x_{1} < x_{2} < 0$
    \begin{align*}
    &\Rightarrow 0< -x_{2} <-x_{1}\tag{ Multiplicando por $-1$}\\
    &\Rightarrow f(-x_{2})<f(-x_{1})\tag{por 1.}\\
    &\Rightarrow (-x_{2})^{2} <(-x_{1})^{2}\\
    &\Rightarrow x_{2}^{2} < x_{1}^{2}\\
    &\Rightarrow f(x_{2})<f(x_{1})
    \end{align*}
    $\therefore f$ es decreciente en $(- \infty,0)$.

$\square$

Ejemplo 2

Para la función $g(x)= x^{2}-5x+2$ probaremos que es creciente en el intervalo $[0,\infty)$.

Tomemos $x_{1}, x_{2} \in [0,\infty)$ tales que $x_{1} < x_{2}$. Queremos demostrar que $g(x_{1})<g(x_{2})$ por lo que desarrollamos lo siguiente:
\begin{align*}
x_{1} < x_{2} &\Rightarrow x_{1} – 5 < x_{2}-5 \tag{restando $-5$}\\
&\Rightarrow x_{1}(x_{1} – 5) <x_{2}( x_{2}-5) \tag{multiplicando por $x_{1}$ y $x_{2}$}\\
&\Rightarrow x_{1}^{2} – 5x_{1} < x_{2}^{2}-5x_{2}\\
&\Rightarrow x_{1}^{2} – 5x_{1}+2 < x_{2}^{2}-5x_{2}+2 \tag{sumado $2$}\\
&\Rightarrow g(x_{1})<g(x_{2})
\end{align*}
Así concluimos que $g$ es creciente en el intervalo $[0,\infty)$.

$\square$

Algunos teoremas

Teorema: Sean $f,g: D \subseteq \r \rightarrow \r$ si $f$ y $g$ son crecientes en $D$ tales que
$f(x)>0$ y $g(x) >0$ para todo $x \in D \Rightarrow fg$ es creciente en D.
Demostración:
Tomemos $x_{1}, x_{2} \in D$ tales que $x_{1}<x_{2}$. Queremos probar que:
$$(fg)(x_{1})< (fg)(x_{2})\quad\text{.}$$
Es decir, queremos ver que se cumple la siguiente desigualdad:
$$f(x_{1})g(x_{1})< f(x_{2})g(x_{2})\quad\text{.}$$
Observemos que por hipótesis tenemos que se cumplen para todo $x \in D$ las siguientes desigualdades:

  1. $f(x)>0 \quad$ y $\quad g(x)>0$.
  2. $f(x_{1}) < f(x_{2})$ ya que $f$ es creciente.
  3. $g(x_{1}) < g(x_{2})$ ya que $g$ es creciente.

De los puntos 2 y 3 al realizar el producto obtenemos:
$$f(x_{1})g(x_{1})< f(x_{2})g(x_{2})\quad\text{.}$$

$\square$

Teorema: Si tenemos una función $f$ tal que:

  1. $f$ par y creciente en el intervalo $[0, \infty) \Rightarrow f$ es decreciente en $(-\infty, 0)$.
  2. $f$ par y decreciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
  3. $f$ impar y creciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
  4. $f$ impar y decreciente en el intervalo $[0, \infty) \Rightarrow f$ es decreciente en $(-\infty, 0)$.

La demostración de los puntos 1,2 y 3 se dejarán como ejercicios para el lector en la Tarea moral de esta entrada.

Demostración del punto 4:

Queremos probar que $f$ es decreciente en $(-\infty, 0)$.
Tenemos por hipótesis que $f$ es una función impar, así por definición:
$$f(-x)=-f(x)\quad\text{.}$$
Ahora si tomamos $0< x_{1}<x_{2}$ ocurre que:
\begin{align*}
f(-x_{1})&= -f(x_{1}) & f(-x_{2})&= -f(x_{2})\\
\end{align*}
Vemos que si multiplicamos por $-1$ las igualdades anteriores tenemos la siguiente equivalencia:
\begin{align}
-f(-x_{1})&= f(x_{1}) & -f(-x_{2})&= f(x_{2})\\
\end{align}

Como $f$ es una función decreciente en $[0, \infty)$ para $x_{1}$ y $x_{2}$ se sigue:
$$f(x_{2})< f(x_{1})\quad\text{.}$$
Aplicando $(1)$ tendríamos la siguiente desigualdad:
$$-f(-x_{2})< -f(-x_{1})\quad\text{.}$$
donde $-x_{1},-x_{2} \in (-\infty,0)$.

$\square$

Definición de función acotada

Definición: Sea $f: A \rightarrow B$. Decimos que:

  • $f$ está acotada superiormente $\Leftrightarrow$ existe $M \in \r$ tal que $f(x) \leq M$ para todo $x \in A$.
La gráfica de $f$ queda por debajo del valor $M$.
  • $f$ está acotada inferiormente $\Leftrightarrow$ existe $m \in \r$ tal que $m \leq f(x)$ para todo $x \in A$.
La gráfica de $f$ queda por arriba del valor $m$.
  • $f$ está acotada $\Leftrightarrow$ existe $m, M \in \r$ tal que $m \leq f(x) \leq M$ para todo $x \in A$.
La gráfica de $f$ queda entre los valores de $M$ y $m$.
  • Una equivalencia para la última definición sería:
    $f$ está acotada $\Leftrightarrow$ existe $N \in \r$ tal que $|f(x)| \leq N$ para todo $x \in A$.
La gráfica de $f$ queda entre los valores de $N$ y $-N$.
  • $f$ no está acotada $\Leftrightarrow$ para toda $M >0$ existe $x_{M} \in A$ tal que $|f(x_{M})|>M$.

Ejemplo 1

Si tenemos la función $f: \r^{+} \rightarrow \r$ definida como:
$$f(x)=\sqrt{x}\quad\text{.}$$

Probaremos que $f$ no es acotada en su dominio.
Demostración: Consideremos a $M>0$ y a $x_{M}=(M+1)^{2}$ donde $x_{M} \in D_{f}$. Así al evaluar la función en $x_{M}$ tenemos:
\begin{align*}
f(x_{M})&=f((M+1)^{2})\\
&=\sqrt{(M+1)^{2}}\\
&= M+1
\end{align*}
aquí observamos siempre ocurre que: $M+1>M$
$\therefore f$ es no acotada en su dominio.

$\square$

Ejemplo 2

Ahora si consideramos la función $g: (0, \infty) \rightarrow \r^{+}$ definida como:
\begin{equation*}
g(x)=\frac{1}{\sqrt[3]{x^{2}}} \quad\text{.}
\end{equation*}

Veremos ahora que $g$ no es acotada en su dominio.
Demostración: Sea $N>0$ y a $x_{N} \in D_{g}$ definida como:
\begin{equation*}
x_{N}= \frac{1}{(N+1)^{\frac{3}{2}}}\quad\text{.}
\end{equation*}
Al tomar $g(x_{N})$ tenemos:
\begin{align*}
g(x_{N})&=g\left(\frac{1}{(N+1)^{\frac{3}{2}}}\right)\\
&=\frac{1}{\left(\frac{1}{(N+1)^{\frac{3}{2}}}\right)^{\frac{2}{3}}}\\
&=\frac{1}{\frac{1}{N+1}}\\
&=N+1
\end{align*}
donde $N+1>N$ por lo que conluimos que $g$ es no acotada en su dominio.

$\square$

Más adelante

En la siguiente entrada, veremos un conjunto de funciones muy particular: las funciones polinomiales. Adicionalmente, revisaremos las funciones racionales. Para ambos tipos de funciones, examinaremos su definición y algunos ejemplos.

Tarea moral

  • Dada la función $f(x)=x^{3}$. Demuestra que:
    • $f$ es creciente en $[0, \infty)$.
    • $f$ es creciente en $(-\infty,0)$.
  • Demuestra los puntos 1, 2 y 3 del Teorema:
    • $f$ par y creciente en el intervalo $[0, \infty) \Rightarrow f$ es decreciente en $(-\infty, 0)$.
    • $f$ par y decreciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
    • $f$ impar y creciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
  • Demuestra que la función $h: (0,1) \rightarrow \r$ definida como:
    $$h(x)=\frac{1}{x^{3}}$$
    no es acotada en su dominio.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Funciones pares e impares

Por Karen González Cárdenas

2 respuestas

Introducción

Ahora veremos cuales son las características que debe cumplir una función para ser par o impar. Veremos geométricamente qué ocurre con estas funciones. De igual manera, veremos qué ocurre al realizar operaciones entre ellas.

Definición de función par

Definición: Decimos que $f: A \rightarrow B$ una función es par si y sólo si para todo $x \in A$ ocurre que:
$$f(x)=f(-x)\quad\text{.}$$

Ejemplo

La función $f(x)=x^{2}$ cumple ser par ya que:
$$f(-x)=(-x)^{2}=x^{2}=f(x)$$
para todo $x \in \r$.
De su gráfica observamos que $f$ se refleja respecto al eje $y$:

Definición de función impar

Definición: Decimos que $f: A \rightarrow B$ una función es impar si y sólo si para todo $x \in A$ ocurre que:
$$f(-x)= – f(x)\quad\text{.}$$

Ejemplo

La función $g(x)=x$ cumple ser impar ya que:
$$g(-x)=(-x) = – (x) = -g(x)$$
para todo $x \in \r$.
De su gráfica observamos que $f$ se refleja respecto al origen:

Un teorema importante

Teorema: Cualquier función $f: \r \rightarrow \r$ puede expresarse como la suma de una función par e impar, es decir,
$$f(x)= P(x)+ I(x)$$
para toda $x \in \r$, donde $P(x)$ e $I(x)$ son únicas.
Demostración: Consideremos las funciones $P(x)$ par e $I(x)$ impar como sigue:
\begin{align*}
P(x)&=\frac{f(x)+f(-x)}{2} & I(x)&=\frac{f(x)-f(-x)}{2}
\end{align*}

Vemos que al realizar la suma obtenemos:
\begin{align*}
P(x)+I(x) &= \frac{f(x)+f(-x)}{2} + \frac{f(x)-f(-x)}{2}\\
&= \frac{f(x)+f(-x)+f(x)-f(-x)}{2}\\
&= \frac{2f(x)}{2}\\
&= f(x)
\end{align*}

Ahora nos falta ver qué $P(x)$ e $I(x)$ son únicas. Como ya sabemos que $f(x)= P(x)+ I(x)$ tenemos lo siguiente:
\begin{align}
f(x)&=P(x)+I(x)\\
f(-x)&=P(x)-I(x)\\
\end{align}
Así sumando $(1)$ y $(2)$ obtenemos:
\begin{align*}
f(x)+f(-x) &= 2 P(x)\\
P(x) &= \frac{f(x)+f(-x)}{2}
\end{align*}
Ahora restando $(1)$ y $(2)$ obtenemos:
\begin{align*}
f(x)-f(-x) &= 2 I(x)\\
I(x) &= \frac{f(x)-f(-x)}{2}
\end{align*}
Dado que tenemos la igualdad $f(x)= P(x)+ I(x)$ concluimos que $P(x)$ e $I(x)$ son únicas.

$\square$

Ejercicio

Consideremos las funciones $f,g: \r \rightarrow \r$. ¿Cómo es $f+g$, $fg$ y $f \circ g$ si:

  1. $f$ y $g$ son pares
  2. $f$ y $g$ son impares
  3. $f$ es par y $g$ es impar
  4. $f$ es impar y $g$ es par

es par, impar o no necesariamente alguna de las anteriores?

En la suma de funciones


1. Si $f$ y $g$ son pares $\Rightarrow f+g$ es par.
Demostración:
Vemos que al desarrollar:
\begin{align*}
(f+g)(-x)&= f(-x)+g(-x)\tag{ definición de $f+g$}\\
&= f(x)+g(x)\tag{ por $f$ y $g$ pares}\\
&= (f+g)(x)\tag{ definición de $f+g$}\\
\end{align*}
3. Si $f$ es par y $g$ es impar $\Rightarrow f+g$ no necesariamente es par o impar.
Consideremos $f(x)= x^{2}$ y $g(x)=x$. Luego si $x=1$ entonces:
\begin{align*}
(f+g)(-1)&= f(-1)+g(-1) & (f+g)(1)&= f(1)+g(1)\\
&= 1-1 & &= 1+1\\
&= 0 & &=2
\end{align*}
$\therefore (f+g)(-1) \neq (f+g)(1)$
$\therefore f+g$ no es par.

Además veamos que $-(f+g)(1)=-2$ por lo que:
$$-(f+g)(1) \neq (f+g)(-1)$$
$\therefore f+g$ tampoco es impar.

En el producto de funciones


1. Si $f$ y $g$ son pares $\Rightarrow fg$ es par.
Demostración:
Si tomamos $fg(-x)$ observamos lo siguiente:
\begin{align*}
(fg)(-x)&= f(-x)g(-x) \tag{definción de $fg$}\\
&= f(x)g(x) \tag{por$f$ y $g$ pares}\\
&= (fg)(x)
\end{align*}
$\therefore fg$ es par.

2. Si $f$ y $g$ son impares $\Rightarrow fg$ es par.
Demostración:
Comenzando con $fg(-x)$ y desarrollando tenemos:
\begin{align*}
(fg)(-x)&= f(-x)g(-x) \tag{definción de $fg$}\\
&= (-f(x))(-g(x)) \tag{por$f$ y $g$ impares}\\
&=f(x)g(x)\\
&= (fg)(x)
\end{align*}
$\therefore fg$ es par.

En la composición de funciones


3. Si $f$ es par y $g$ es impar $\Rightarrow f \circ g$ es par.
Demostración:
Realizando la composición $(f \circ g)(-x)$:
\begin{align*}
(f \circ g)(-x)&=f(g(-x)) \tag{definción de $f \circ g$}\\
&= f(-g(x)) \tag{ por $g$ impar}\\
&= f(g(x)) \tag{por $f$ par}\\
&=(f \circ g)(x)
\end{align*}
$\therefore f \circ g$ es par.

4.Si $f$ es impar y $g$ es par $\Rightarrow f \circ g$ es par.
Demostración:
Procediendo análogamente al punto anterior:
\begin{align*}
(f \circ g)(-x)&=f(g(-x)) \tag{definción de $f \circ g$}\\
&= f(g(x)) \tag{ por $g$ par}\\
&=(f \circ g)(x)
\end{align*}
$\therefore f \circ g$ es par.

Los puntos faltantes se dejarán como ejercicios de Tarea moral, para resolverlos se debe proceder como en los incisos anteriores según sea el caso.

Más adelante

En la siguiente entrada, continuaremos con las funciones crecientes y decrecientes. Veremos qué características debe cumplir una función para poder determinar si crece o decrece en un intervalo. También exploraremos qué significa ser una función acotada y algunas pruebas relacionadas con este concepto.

Tarea moral

  • Prueba que las funciones $P(x)$ e $I(x)$ cumplen con ser par e impar respectivamente:
    \begin{align*}
    P(x)&=\frac{f(x)+f(-x)}{2} & I(x)&=\frac{f(x)-f(-x)}{2}
    \end{align*}
  • Demuestra que la función constante cero es la única que cumple ser par e impar.
  • Exprese a las siguientes funciones como suma de una función par y una impar:
    • $f(x)= x^{2}-4x+2$
    • \begin{multline*}h(x)=\frac{1}{1+x^{2}}\end{multline*}
  • Termina los puntos faltantes del ejercicio anterior:
    • Para $f+g$ cuando $f$ y $g$ son impares

    • Para $f+g$ cuando $f$ es impar y $g$ es par.

    • Para $fg$ cuando $f$ es par y $g$ es impar

    • Para $fg$ cuando $f$ es impar y $g$ es par

    • Para $f \circ g$ cuando $f$ y $g$ son pares

    • Para $f \circ g$ cuando $f$ y $g$ son impares

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Suma, producto, cociente y composición de funciones

Por Karen González Cárdenas

Deja un comentario

Introducción

Ya que hemos visto el concepto de función, en esta entrada veremos cómo están definidas las operaciones de suma, producto y cociente. De igual modo, definiremos la composición entre un par de funciones. Para dejar más claras dichas operaciones, daremos ejemplos.

Operaciones de funciones

Definición (operaciones): Sean $f: D_{f}\subseteq \r \rightarrow \r$, $\quad g: D_{g}\subseteq \r \rightarrow \r$. Definimos las siguientes operaciones como:

  • $f+g: D_{f} \cap D_{g} \subseteq \r \rightarrow \r$
    $$(f+g)(x)= f(x)+g(x)\quad \text{.}$$
  • $\alpha f: D_{f}\subseteq \r \rightarrow \r \quad$ y $\quad \alpha \in \r$
    $$(\alpha f)(x)= \alpha f(x)\quad \text{.}$$
  • $fg: D_{f} \cap D_{g} \subseteq \r \rightarrow \r$
    $$(fg)(x)= f(x)g(x)\quad \text{.}$$
  • $\begin{multline*} \frac{f}{g}: D_{f/g} \subseteq \r \rightarrow \r \end{multline*}$
    \begin{equation*}
    \left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\quad \text{.}
    \end{equation*}
    donde $D_{f/g}=D_{f} \cap (D_{g} – \left\{x \in D_{g}: g(x)=0 \right\})$

Notación: Cuando escribamos $f-g$ hacemos referencia a:
$$f-g=f+ (-g) \quad \text{.}$$

Ejemplos

Consideremos a las siguientes funciones:
\begin{align*}
f: \r – \left\{-1\right\} &\rightarrow \r & g: \r &\rightarrow \r & h: \r &\rightarrow \r^{+}
\end{align*}
\begin{align*}
f(x)&= \frac{1}{x+1}& g(x)&= x^{3}+3 & h(x)&=x^{2}+2x+1
\end{align*}
Notación: Usamos $\r^{+}$ para referirnos al conjunto de los números reales positivos.

Realizaremos las siguientes operaciones para ejemplificar lo visto anteriormente:

  • $$(f+g)(x)= f(x)+g(x)= \frac{1}{x+1} + x^{3}+3$$
    con $D_{f+g}=D_{f} \cap D_{g}= \r \cap (\r- \left\{-1\right\})= \r- \left\{-1\right\}$
  • $$(fg)(x)= f(x)g(x)=\left(\frac{1}{x+1}\right)(x^{3}+3)=\frac{x^{3}+3}{x+1}$$
    con $D_{fg}=D_{f} \cap D_{g}= \r \cap (\r- \left\{-1\right\})= \r- \left\{-1\right\}$
  • Si $\alpha = – 4$:
    $$(\alpha g)(x)= \alpha g(x)= -4(x^{3}+3)=-4x^{3}-12$$
    con $D_{\alpha g}= D_{g}= \r$
  • $$\left(\frac{g}{h}\right)(x)=\frac{g(x)}{h(x)}=\frac{x^{3}+3}{x^{2}+2x+1}$$
    como $D_{g/h}=D_{g} \cap (D_{h} – \left\{x \in D_{h}: h(x)=0 \right\})$
    Observemos que $x^{2}+2x+1 = (x+1)^{2}$ por lo que $(x+1)^{2}=0$ cuando $x=-1$.
    Así el dominio sería:
    $$D_{g/h}=\r \cap (\r- \left\{-1 \right\})= \r – \left\{-1\right\}$$
  • $$(h-g)(x)=h(x)-g(x)=x^{2}+2x+1-(x^{3}+3)=x^{2}+2x+1-x^{3}-3$$
    con $D_{h-g}= D_{h} \cap D_{g}= \r \cap \r= \r$

Composición de funciones

Definición (composición): Consideremos a las funciones $g: A \rightarrow B$ y $f: B \rightarrow C$ definimos a la composición de $g$ seguida de $f$ como:

$$f \circ g: A \rightarrow C$$
$$f \circ g(x)= f(g(x)),$$
observamos que la composición sólo está definida si $Im_g \subseteq D_f$, por lo que $g(x) \in B$.
En el siguiente diagrama podemos ver más claramente cómo funciona la composición $f \circ g$:

PASO 1

Primero tomamos $x \in A$ a la cual le aplicamos la función $g$ para así obtener $g(x) \in B$.

PASO 2

Ahora tomamos a $g(x) \in B$ para aplicarle la función $f$ y finalmente obtener $f(g(x)) \in C$.

DIAGRAMA PARA $f \circ g$

Así la composición de $f \circ g$ se vería como en el diagrama anterior.

Observación: La composición no es conmutativa, es decir, ocurre que:
$$f \circ g \neq g \circ f\quad \text{.}$$

Ejemplos

Retomando las funciones:
\begin{align*}
f(x)&= \frac{1}{x+1}& g(x)&= x^{3}+3 & h(x)&=x^{2}+2x+1
\end{align*}

Realicemos las siguientes composiciones de funciones para tener más claro cómo funciona lo antes explicado:

  • Ejemplo 1:
    \begin{align*}
    (g \circ f)(x)&= g(f(x))\\
    &= g\left(\frac{1}{x+1} \right)\\
    &= \left( \frac{1}{x+1} \right)^{3} +3\\
    &= \frac{1}{(x+1)^{3}}+3
    \end{align*}
    Así tenemos que la composición obtenida es:
    \begin{equation*}
    (g \circ f)(x)=\frac{1}{(x+1)^{3}}+3
    \end{equation*}
  • Ejemplo 2:
    \begin{align*}
    (f \circ h)(x)&= f(h(x))\\
    &= f((x^{2}+2x+1))\\
    &= \frac{1}{(x^{2}+2x+1)+1}\\
    &=\frac{1}{x^{2}+2x+2}
    \end{align*}
    Por lo que la composición quedaría como:
    \begin{equation*}
    (f \circ h)(x) = \frac{1}{x^{2}+2x+2}
    \end{equation*}

Más adelante

Ahora que ya hemos definido las operaciones entre funciones y la composición, en la siguiente entrada veremos qué características debe cumplir una función para poder determinar si es inyectiva, sobreyectiva o biyectiva. Del mismo modo, examinaremos el concepto de función inversa, donde haremos uso de la composición de funciones y algunas condiciones.

Tarea moral

  • Si tenemos a las funciones $f : \r \rightarrow \r$ y $g : \r \rightarrow \r^{+}$ definidas como siguen:
    $$ f(x) = x-8$$
    $$g(x)= x^{4}$$
    Realiza las siguientes operaciones:
    • $f + g$
    • $f – g$
    • $fg$
    • $\frac{g}{f}$
    • $g \circ f$
  • Da una función $f$ y una función $g$ que ejemplifiquen que la composición no es conmutativa:
    $$f \circ g \neq g \circ f\quad \text{.}$$
  • Demuestra que la composición es asociativa, es decir,
    $$f\circ (g \circ h)= (f\circ g) \circ h\quad \text{.}$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»