Archivo de la etiqueta: Ecuaciones Diferenciales

Ecuaciones Diferenciales I – Videos: Sistemas hamiltonianos

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En anteriores entradas, hemos estudiado sistemas no lineales de ecuaciones de primer orden. Hemos visto la dificultad de conocer el comportamiento completo de las curvas solución en el plano fase, debido a que el campo vectorial asociado al sistema puede ser muy complejo. Afortunadamente logramos conocer el comportamiento de las soluciones cercanas a los puntos de equilibrio, gracias a la linealización del sistema, siempre y cuando los puntos de equilibrio fueran hiperbólicos. También estudiamos el método de las nulclinas para esbozar el plano fase de manera completa, pero como ya mencionamos, este método está sujeto a la complejidad del campo vectorial del sistema.

En esta entrada estudiaremos un tipo de sistema cuyo plano fase es relativamente sencillo de estudiar. Estos sistemas son los llamados sistemas hamiltonianos, que son de la forma $$\begin{array}{rcl} \dot{x} & = & \frac{\partial{H}}{\partial{y}} \\ \dot{y} & = & -\frac{\partial{H}}{\partial{x}} \end{array}$$ para cierta función $H:\mathbb{R}^{2} \rightarrow \mathbb{R}.$

Veremos algunas propiedades importantes que satisfacen tanto el sistema hamiltoniano como la función $H$, que llamaremos función hamiltoniana. La más importante será la que nos afirma que las curvas solución del plano fase serán las curvas de nivel de la función hamiltoniana. Así, para los sistemas hamiltonianos el problema de estudiar cualitativamente las curvas solución en el plano fase será equivalente a conocer las curvas de nivel de la función hamiltoniana.

Por supuesto, veremos las condiciones bajo las cuáles un sistema es hamiltoniano, y en caso de que lo sea, desarrollaremos un método para encontrar la función hamiltoniana que define al sistema.

¡Vamos a comenzar!

Sistemas hamiltonianos

En el primer video definimos a los sistemas hamiltonianos, y vemos las principales propiedades que cumplen dichos sistemas, y la función hamiltoniana que los define. Establecemos la condición que debe satisfacer un sistema de ecuaciones para que este sea hamiltoniano, y en caso de serlo, estudiamos una forma de hallar a la función hamiltoniana.

En el segundo video aplicamos todo el conocimiento adquirido en el primer video para estudiar un par de sistemas hamiltonianos y esbozar su plano fase.

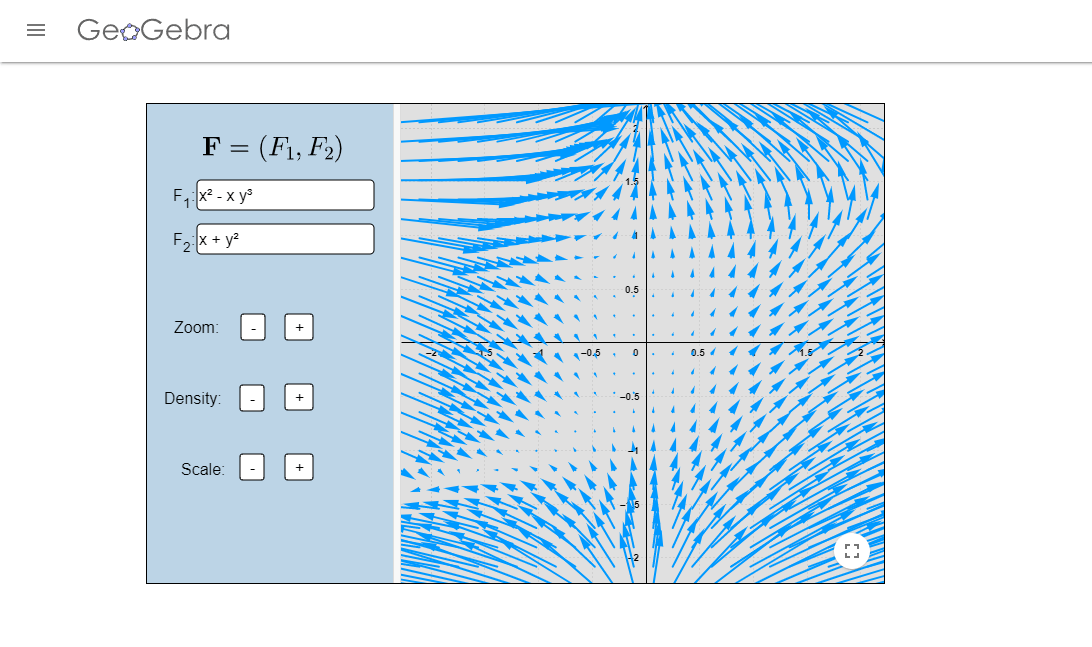
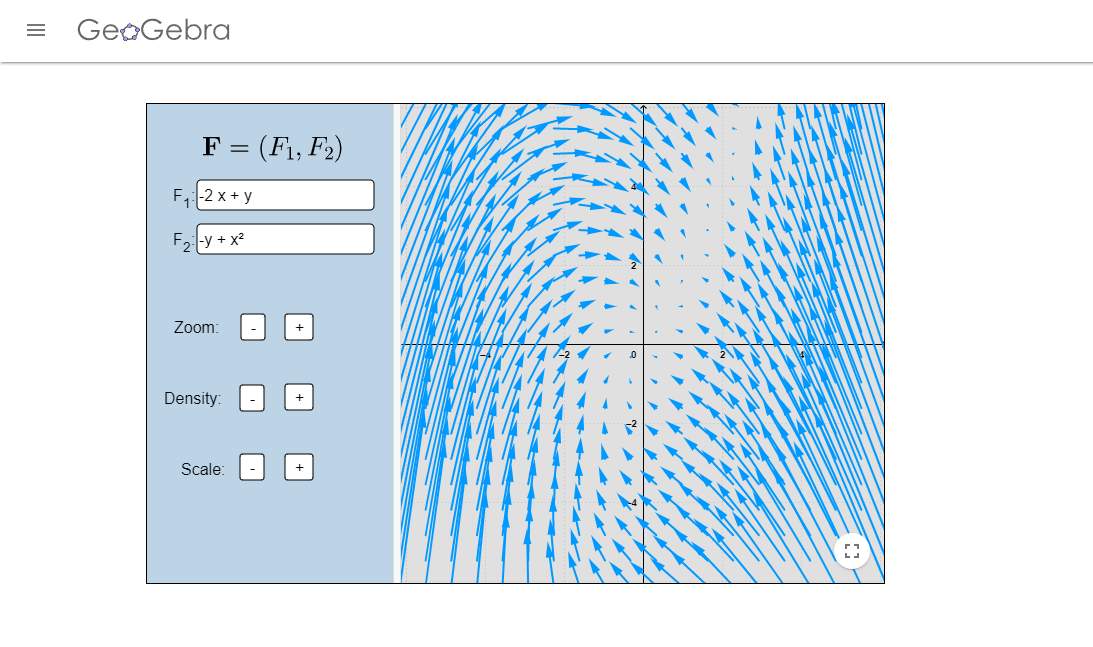
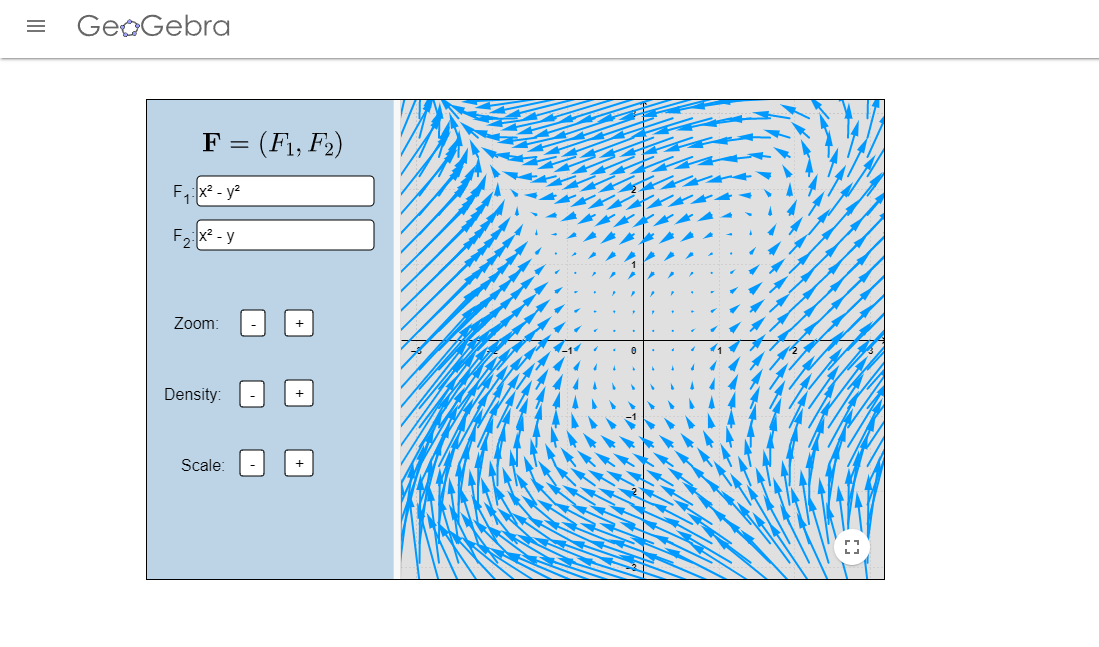
Los campos vectoriales que aparecen en los videos fueron realizados en el siguiente enlace.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Verifica si el sistema $$\begin{array}{rcl} \dot{x} & = & x+\sin{y} \\ \dot{y} & = & -y \end{array}$$ es hamiltoniano. En caso de serlo, encuentra una función hamiltoniana y esboza el plano fase del sistema.
  • Haz lo mismo que en el ejercicio anterior para el sistema de ecuaciones $$\begin{array}{rcl} \dot{x} & = & -\sin^{2}{x}\sin{y} \\ \dot{y} & = & -2\sin{x}\cos{x}\cos{y}. \end{array}$$
  • Demuestra que el sistema $$\begin{array}{rcl} \dot{x} & = & x\cos{xy} \\ \dot{y} & = & -y\cos{xy} \end{array}$$ es hamiltoniano. Encuentra una función hamiltoniana, verifica que es una cantidad conservada para el sistema y esboza el plano fase.
  • Considera el sistema lineal de ecuaciones $$\dot{\textbf{X}}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\textbf{X}.$$ Establece condiciones para las constantes $a,b,c,d$ de tal forma que el sistema sea hamiltoniano.
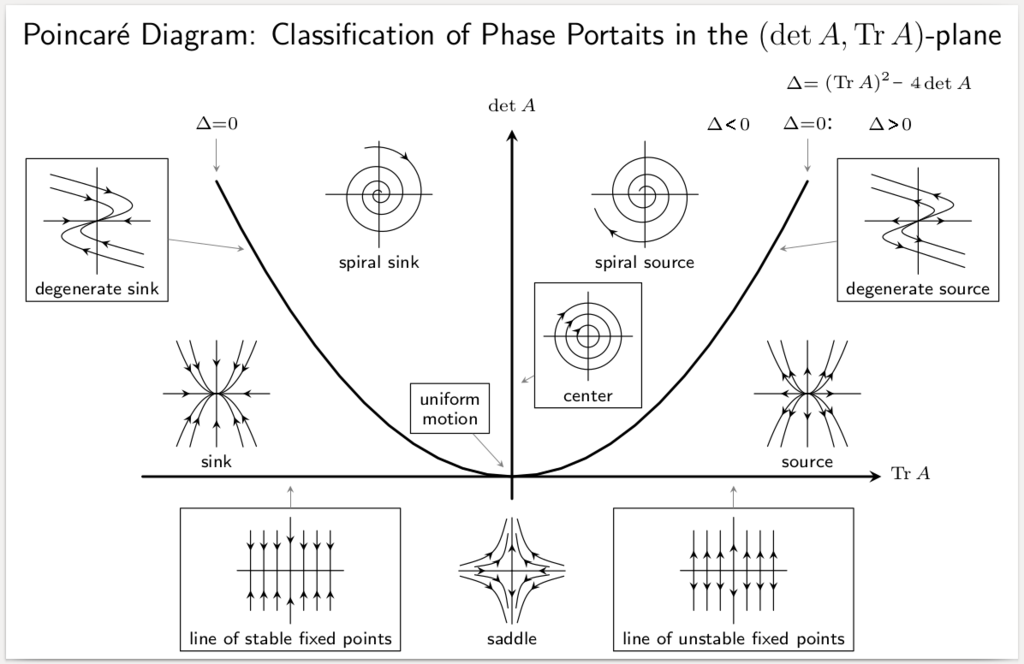
  • Prueba que si un sistema es hamiltoniano, entonces los puntos de equilibrio del sistema linealizado son únicamente puntos silla o centros.
  • Considera el sistema de ecuaciones de la forma $$\begin{array}{rcl} \dot{x} & = & F_{1}(y) \\ \dot{y} & = & F_{2}(x). \end{array}$$ Demuestra que este sistema es hamiltoniano y encuentra una función hamiltoniana.

Más adelante

Hemos terminado el análisis de los sistemas hamiltonianos. Lamentablemente, no todos los sistemas lo son, y de hecho, casi ninguno lo es. En la siguiente entrada comenzaremos abordando nuevamente el modelo del péndulo, pero ahora agregaremos fricción, por lo que el sistema dejará de ser hamiltoniano. Estudiaremos los problemas que se presentan, posteriormente definiremos un función similar a la función hamiltoniana, la cual es la llamada función de Lyapunov y veremos algunas propiedades interesantes

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Sistemas de ecuaciones no lineales. Las nulclinas y el plano fase

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En la entrada anterior comenzamos el estudio cualitativo a los sistemas de ecuaciones no lineales de primer orden. A través de algunos ejemplos vimos la complejidad de los planos fase para dichos sistemas, por lo que no es posible clasificar a dichos planos y a sus puntos de equilibrio como lo hicimos en el caso lineal, y tratar de interpretarlos de manera completa también es muy complicado.

Un paso importante que dimos fue estudiar las curvas solución cercanas a los puntos de equilibrio del sistema. Por medio de la matriz jacobiana del campo vectorial asociado, es decir la matriz $$\textbf{DF}(x,y)=\begin{pmatrix} \frac{\partial{F_{1}}}{\partial{x}}(x_{0},y_{0}) & \frac{\partial{F_{1}}}{\partial{y}}(x_{0},y_{0}) \\ \frac{\partial{F_{2}}}{\partial{x}}(x_{0},y_{0}) & \frac{\partial{F_{1}}}{\partial{y}}(x_{0},y_{0}) \end{pmatrix}$$ logramos linealizar el sistema y gracias a el Teorema de Hartman – Grobman, logramos hallar el comportamiento de las soluciones cerca de los puntos de equilibrio, siempre y cuando los valores propios del sistema lineal tuvieran parte real no nula. En tal caso, las soluciones se comportan de una manera similar a las soluciones del sistema lineal que obtuvimos mediante la linealización. Nuestro objetivo sigue siendo tratar de entender el plano fase completo de un sistema no lineal.

En esta entrada vamos a estudiar uno de los métodos que nos puede ayudar a resolver este problema. Dado un sistema de ecuaciones $$\dot{\textbf{X}}=\textbf{F}(\textbf{X})=(F_{1}(\textbf{X}),…,F_{n}(\textbf{X}))$$ vamos a definir la $x_{i}$-nulclina como el conjunto de puntos tales que la función $F_{i}$ se anula. Para sistemas de dos ecuaciones vamos a definir la $x$-nulclina y la $y$-nulclina. Veremos cómo se comporta el campo vectorial sobre estos conjuntos, y dado que podemos dibujar en el plano las curvas que los representan (ya que son las curvas de nivel dadas por $F_{1}(x,y)=0$ y $F_{2}(x,y)=0$), estas curvas van a separar al plano en distintas regiones. Lo que haremos será estudiar el campo vectorial, y por tanto el comportamiento de las soluciones sobre cada una de estas regiones. Al final podremos hacer un esbozo del plano fase para el sistema no lineal.

Las nulclinas y el plano fase

En el primer video definimos de forma general las nulclinas de un sistema de ecuaciones $$\dot{\textbf{X}}=\textbf{F}(\textbf{X})=(F_{1}(\textbf{X}),…,F_{n}(\textbf{X})).$$ Como siempre, nos restringimos al caso de sistemas de dos ecuaciones para destacar los aspectos más importantes de la $x$-nulclina y la $y$-nulclina.

En el segundo video aplicamos el método de las nulclinas para esbozar el plano fase de dos sistemas de ecuaciones no lineales.

Los campos vectoriales que aparecen en los videos fueron realizados en el siguiente enlace.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Considera el sistema $$\begin{array}{rcl} \dot{x} & = & F_{1}(x,y) \\ \dot{y} & = & F_{2}(x,y) \end{array}.$$ Muestra que el conjunto de puntos de equilibrio del sistema es la intersección de la $x$-nulclina y la $y$-nulclina.
  • Para el sistema $$\begin{array}{rcl} \dot{x} & = & x^{2}-x \\ \dot{y} & = & x^{2}-y \end{array}$$ determina las nulclinas, dibújalas en el plano, y con ayuda de estas esboza el plano fase del sistema.
  • Utilizando el método de las nulclinas, esboza el plano fase para el sistema $$\begin{array}{rcl} \dot{x} & = & y \\ \dot{y} & = & x-x^{2} \end{array}.$$
  • Haz lo mismo que en el ejercicio anterior para el sistema $$\begin{array}{rcl} \dot{x} & = & 2x^{2}+xy-2x \\ \dot{y} & = & y^{2}-y \end{array}.$$
  • Considera el sistema de Volterra – Lotka $$\begin{array}{rcl} \dot{x} & = & x(10-x-y) \\ \dot{y} & = & y(30-2x-y) \end{array}$$ el cual modela una interacción del tipo depredador – presa. Mediante el método de las nulclinas esboza el plano fase del sistema e interpreta su significado respecto a la interacción de las dos especies en competencia. (Recuerda que el número de especies es no negativa, así que enfócate únicamente en el primer cuadrante del plano).

Más adelante

Hemos logrado conocer el plano fase completo de algunos sistemas no lineales a través del método de las nulclinas. Sin embargo, este método está sujeto a la forma del campo vectorial asociado al sistema. Entre más complejo sea el campo, más difícil será encontrar las nulclinas y hacer el estudio del plano fase.

En la próxima entrada veremos un tipo de sistemas en particular, que tienen un plano fase que podremos estudiar por completo mediante las curvas de nivel de una función que va a definir al sistema. Estos son los sistemas hamiltonianos, y la función que los define será llamada función hamiltoniana.

¡Hasta la próxima!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Sistemas de ecuaciones no lineales. Linealización de puntos de equilibrio

Por Eduardo Vera Rosales

2 respuestas

Introducción

En entradas anteriores hemos estudiado a detalle sistemas de dos ecuaciones lineales homogéneas con coeficientes constantes de la forma $$\dot{\textbf{X}}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$. Resolvimos tales sistemas de manera analítica, hallando su solución general, y también estudiamos el comportamiento de las curvas solución en el plano fase. Vimos que los valores propios asociados al sistema determinan la estabilidad de los puntos de equilibrio y la forma del plano fase. Finalmente, en la entrada anterior clasificamos las formas de los planos fase y los puntos de equilibrio, según la traza y el determinante de la matriz asociada al sistema.

Ahora que tenemos esta información a nuestra disposición, podemos estudiar sistemas de ecuaciones no lineales. Como en el caso lineal, nos enfocaremos en sistemas autónomos, donde la variable independiente $t$ no aparece explícitamente en el sistema. Lo primero que haremos será analizar algunos sistemas y sus campos vectoriales asociados, los cuales van a sugerir soluciones que ya no tienen un comportamiento conocido o fácil de interpretar como en los sistemas lineales. Necesitaremos nuevos métodos para conocer el plano fase por completo.

De tu curso de Cálculo de varias variables, sabes que la mejor aproximación lineal a una función $\textbf{F}:\mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ en un punto $(x_{0},y_{0})$ está dada por la matriz jacobiana evaluada en dicho punto. En nuestro caso, tenemos que $$\textbf{F}(x,y)=(F_{1}(x,y).F_{2}(x,y))$$ entonces la matriz jacobiana se convierte en $$\textbf{DF}(x_{0},y_{0})= \begin{pmatrix} \frac{\partial{F_{1}}}{\partial{x}}(x_{0},y_{0}) & \frac{\partial{F_{1}}}{\partial{y}}(x_{0},y_{0}) \\ \frac{\partial{F_{2}}}{\partial{x}}(x_{0},y_{0}) & \frac{\partial{F_{1}}}{\partial{y}}(x_{0},y_{0}) \end{pmatrix}.$$ Esta matriz tendrá coeficientes constantes, y al sistema $$\dot{\textbf{X}}=\textbf{DF}(x_{0},y_{0})\textbf{X}$$ ya sabemos analizarlo.

El teorema de Hartman – Grobman nos garantizará que las soluciones al sistema no lineal cercanas al punto de equilibrio se comportarán de una manera similar a las curvas del plano fase del sistema lineal obtenido por la linealización. Con este método, podremos conocer una parte del plano fase.

Sistemas de ecuaciones no lineales. Linealización de puntos de equilibrio

En el primer video revisamos tres ejemplos de sistemas de ecuaciones no lineales, estudiamos sus planos fase a través del campo vectorial asociado y vemos las dificultades que se presentan. Posteriormente linealizamos un sistema de ecuaciones cerca de sus puntos de equilibrio mediante la matriz jacobiana del campo asociado. Finalmente enunciamos el teorema de Hartman – Grobman.

En el segundo video linealizamos dos sistemas de ecuaciones no lineales, y estudiamos el comportamiento de las curvas solución cerca de los puntos de equilibrio.

El péndulo simple

Estudiamos el sistema de ecuaciones asociado al movimiento simple de un péndulo. Linealizamos los puntos de equilibrio, estudiamos el plano fase y por último, interpretamos las curvas solución del plano fase.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Construye un sistema de dos ecuaciones no lineal tal que $(0,0)$ sea el único punto de equilibrio, y tal que las soluciones cerca del origen se comporten como espirales. Justifica tu respuesta.
  • Prueba que el sistema $$\begin{array}{rcl} \dot{x} & = & x^{2}-xy^{3} \\ \dot{y} & = & x+y^{2} \end{array}$$ tiene dos puntos de equilibrio. Linealiza cerca de los puntos de equilibrio y determina el comportamiento de las soluciones cercanas, siempre y cuando esto sea posible.
Campo vectorial del ejercicio 1
Campo vectorial del ejercicio 1
  • Determina los puntos de equilibrio y el comportamiento de las soluciones cerca de estos, del sistema $$\begin{array}{rcl} \dot{x} & = & -2x+y \\ \dot{y} & = & x^{2}-y. \end{array}$$
Campo vectorial del ejercicio 2
Campo vectorial del ejercicio 2
  • Calcula los puntos de equilibrio del sistema $$\begin{array}{rcl} \dot{x} & = & x^{2}-y^{2} \\ \dot{y} & = & x^{2}-y. \end{array}$$ Determina el comportamiento de los puntos de equilibrio, cuando esto sea posible.
Campo vectorial del ejercicio 3
Campo vectorial del ejercicio 3
  • Encuentra los puntos de equilibrio y el comportamiento de las soluciones cerca de estos, para el sistema $$\begin{array}{rcl} \dot{x} & = & \sin{x} \\ \dot{y} & = & \cos{y} \end{array}$$ cuando sea posible.

Más adelante

Hemos avanzado un poco en nuestro propósito de estudiar el plano fase de sistemas de dos ecuaciones no lineales. Al obtener la linealización de los puntos de equilibrio conocemos, al menos, el comportamiento de las curvas solución cerca de estos.

En la siguiente entrada estudiaremos el método de las nulclinas, que nos permitirá conocer más aspectos del plano fase a un sistema no lineal, no solamente cerca de los puntos de equilibrio, sino que además nos permitirá conocer el comportamiento de soluciones lejanas. Las nulclinas son los conjuntos de puntos donde las funciones coordenadas $\textbf{F}_{i}$ del campo vectorial asociado al sistema se anulan. En el caso de sistemas de dos ecuaciones, las nulclinas dividirán el plano $x(t)-y(t)$ en regiones. Estudiaremos el comportamiento de las soluciones en cada región y podremos tener un mejor conocimiento del plano fase entero.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: El plano traza – determinante

Por Eduardo Vera Rosales

Deja un comentario

Introducción

Antes de finalizar con el estudio cualitativo a sistemas de ecuaciones de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$, vamos a clasificar la estabilidad del punto de equilibrio, y por tanto el plano fase, en un diagrama que resume toda la información que estudiamos en las últimas entradas. Este diagrama es llamado plano traza – determinante. En esta entrada veremos cómo interpretar dicho diagrama.

Vimos que el plano fase y la estabilidad de los puntos de equilibrio depende de la forma de los valores propios asociados. Es fácil observar que los valores propios del sistema son las soluciones a la ecuación $$\det{(\textbf{A}-\lambda\textbf{Id})}=\lambda^{2}-(a+d)\lambda+(ad-bc)=0.$$ Notemos que podemos reescribir la ecuación anterior en términos de dos propiedades de la matriz asociada $\textbf{A}$: su traza y su determinante. En efecto, resulta que $$ \lambda^{2}-(a+d)\lambda+(ad-bc)=\lambda^{2}-\lambda\mathrm{tr}{A}+\det{A}.$$ Entonces los valores propios están dados por la fórmula $$\lambda=\frac{\mathrm{tr}{A}\pm\sqrt{\mathrm{tr}{A}^{2}-4\det{A}}}{2}$$ Así, el plano fase y la estabilidad de los puntos de equilibrio dependerán de la traza y el determinante de la matriz asociada. Analizaremos la forma de los valores propios según la última fórmula.

La información obtenida se podrá resumir en el plano traza – determinante, que puedes observar en la siguiente imagen (tomada del siguiente sitio) que nos indica la forma del plano fase, según los valores de la traza y el determinante.

Plano traza determinante
Plano traza – determinante. Imagen tomada de https://es.m.wikipedia.org/wiki/Archivo:Stability_Diagram.png

El plano traza – determinante

Clasificamos la naturaleza del plano fase y la estabilidad de los puntos de equilibrio del sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ según la traza y el determinante de la matriz asociada. Englobamos toda la información obtenida en el plano traza – determinante.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Considera el sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ Muestra que los valores propios del sistema $\lambda_{1}, \lambda_{2}$ satisfacen las identidades $$\lambda_{1}+\lambda_{2}=\mathrm{tr}{A}$$ $$\lambda_{1}\lambda_{2}=\det{A}.$$ Recuerda considerar los casos cuando los valores propios son distintos o iguales.

Clasifica el plano fase y puntos de equilibrio de los siguientes sistemas de ecuaciones, calculando únicamente la traza y el determinante de la matriz asociada:

  • $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 15 & -1 \\ -60 & 4 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$
  • $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} \pi & 0 \\ e & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$
  • Considera el sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & a+2 \\ a-2 & a \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ Determina la forma del plano fase y la estabilidad del punto de equilibrio según la traza y el determinante de la matriz asociada, y el valor $a$.
  • Para el ejercicio anterior, identifica la región del plano traza – determinante donde los planos fase tienen comportamientos similares.
  • Realiza el mismo análisis de los dos ejercicios anteriores para el sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & a+b \\ a-b & a \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$ para cualquier valor de $a$ y $b$.

Más adelante

Con todo el conocimiento adquirido acerca de sistemas de ecuaciones lineales, es momento de estudiar, al menos de manera cualitativa, sistemas de ecuaciones no lineales. En la próxima entrada daremos una breve introducción a tales sistemas.

Además, veremos que es posible linealizar este tipo de sistemas para obtener un sistema de ecuaciones lineales equivalente que nos brinde la información cualitativa de las soluciones al sistema no lineal. Así, podremos dibujar el plano fase de un sistema no lineal, sin conocer explícitamente las soluciones a dicho sistema.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Plano fase para sistemas lineales con cero como valor propio

Por Eduardo Vera Rosales

Deja un comentario

Introducción

Vamos a finalizar esta serie de entradas referentes al plano fase de sistemas de dos ecuaciones lineales homogéneas con coeficientes constantes de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ estudiando el caso cuando el sistema tiene al menos un cero como valor propio.

En las entradas anteriores revisamos los casos cuando los valores propios son reales distintos y no nulos, son complejos o se repiten, por lo que el caso que revisaremos en esta entrada es el último por estudiar. En todos los casos anteriores el punto de equilibrio es único y se encuentra en el punto $(0,0)$ del plano fase. Sin embargo, cuando el cero es un valor propio de la matriz asociada al sistema resultará que no habrá un único punto equilibrio, sino que tendremos una infinidad de dichos puntos. Es por eso que dejamos este caso al final.

Veremos cómo se distribuyen los puntos de equilibrio en el plano fase. Finalmente las curvas solución serán muy fáciles de dibujar según el análisis que realizaremos de la solución general al sistema, que será de la forma $$\textbf{X}(t)=c_{1}\begin{pmatrix} u_{1} \\ u_{2} \end{pmatrix}+c_{2}e^{\lambda_{2} t}\begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}$$ donde $(u_{1},u_{2})$ es un vector propio asociado al valor propio $\lambda_{1}=0$ y $(v_{1},v_{2})$ es un vector propio asociado al valor propio $\lambda_{2} \neq 0$ (si $\lambda_{2}=0$ la solución general se simplifica aún más y es igualmente sencillo hacer el análisis del plano fase).

Dicho lo anterior, vamos a comenzar.

Plano fase para sistemas con cero como valor propio

En el primer video analizamos el plano fase para un sistema de ecuaciones de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuando este tiene a cero como un valor propio asociado.

En el segundo video dibujamos el plano fase de algunos sistemas en particular que tienen al menos un valor propio igual a cero.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Encuentra todas las matrices de tamaño $2 \times 2$ diagonalizables cuyo único valor propio es cero.
  • Encuentra todos los sistemas de ecuaciones lineales homogéneos con coeficientes constantes cuyo campo vectorial se ve de la siguiente manera:
Campo vectorial 1 cero valor propio
Campo vectorial. Elaboración propia.
  • En el segundo video dibujamos los planos fase de los siguientes sistemas $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} -1 & 1 \\ 1 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$ $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 2 \\ 0 & 0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ ¿Qué puedes decir acerca de los puntos de equilibrio en cada caso? ¿Son estables, asintóticamente estables, inestables, o ninguno de los tres?
  • Encuentra la solución general del siguiente sistema y dibuja su plano fase: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 2 \\ 0 & 5 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Resuelve el siguiente sistema y dibuja su plano fase: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 5 & 0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Encuentra la solución general y dibuja el plano fase del siguiente sistema: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 4 & 6 \\ -2 & -3 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$

Más adelante

Hemos terminado de estudiar el plano fase para sistemas de dos ecuaciones lineales homogéneas con coeficientes constantes. Determinamos el comportamiento de las soluciones en el plano y la estabilidad de los puntos de equilibrio en función de los valores propios del sistema.

Estamos a punto de comenzar a estudiar sistemas no lineales, al menos de manera cualitativa (ya que estos sistemas no los sabemos resolver analíticamente). Pero antes vamos a hacer un resumen de todo el análisis realizado recientemente en un dibujo que clasifica las formas del plano fase según dos características de la matriz asociada al sistema: la traza (que es la suma de los elementos en la diagonal) y su determinante.

¡Hasta la próxima!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»