Introducción

Antes de finalizar con el estudio cualitativo a sistemas de ecuaciones de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$, vamos a clasificar la estabilidad del punto de equilibrio, y por tanto el plano fase, en un diagrama que resume toda la información que estudiamos en las últimas entradas. Este diagrama es llamado plano traza – determinante. En esta entrada veremos cómo interpretar dicho diagrama.

Vimos que el plano fase y la estabilidad de los puntos de equilibrio depende de la forma de los valores propios asociados. Es fácil observar que los valores propios del sistema son las soluciones a la ecuación $$\det{(\textbf{A}-\lambda\textbf{Id})}=\lambda^{2}-(a+d)\lambda+(ad-bc)=0.$$ Notemos que podemos reescribir la ecuación anterior en términos de dos propiedades de la matriz asociada $\textbf{A}$: su traza y su determinante. En efecto, resulta que $$ \lambda^{2}-(a+d)\lambda+(ad-bc)=\lambda^{2}-\lambda\mathrm{tr}{A}+\det{A}.$$ Entonces los valores propios están dados por la fórmula $$\lambda=\frac{\mathrm{tr}{A}\pm\sqrt{\mathrm{tr}{A}^{2}-4\det{A}}}{2}$$ Así, el plano fase y la estabilidad de los puntos de equilibrio dependerán de la traza y el determinante de la matriz asociada. Analizaremos la forma de los valores propios según la última fórmula.

La información obtenida se podrá resumir en el plano traza – determinante, que puedes observar en la siguiente imagen (tomada del siguiente sitio) que nos indica la forma del plano fase, según los valores de la traza y el determinante.

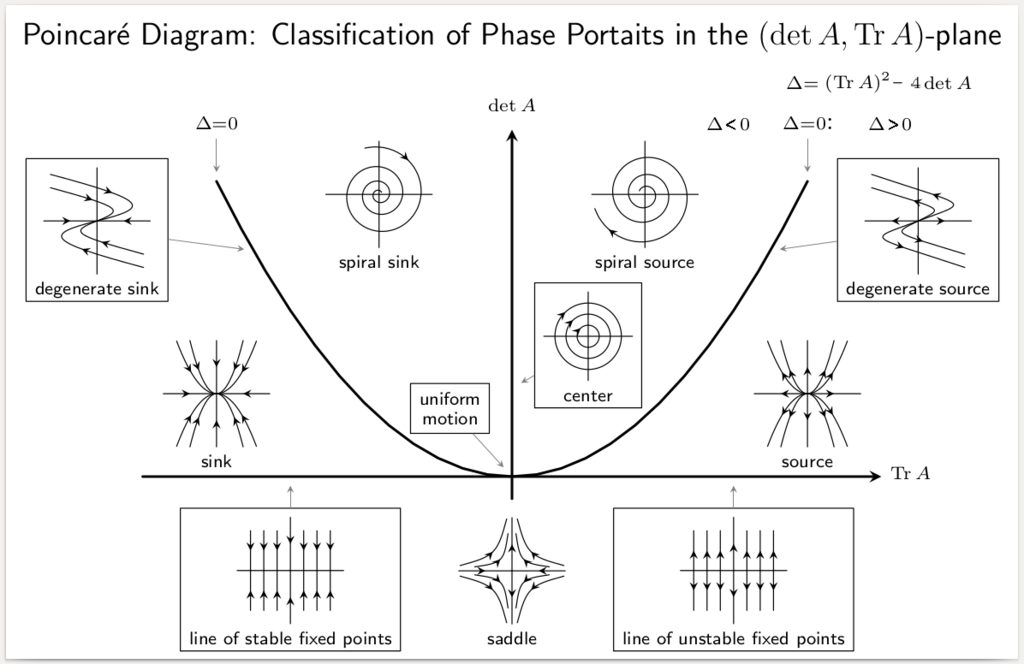
El plano traza – determinante

Clasificamos la naturaleza del plano fase y la estabilidad de los puntos de equilibrio del sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ según la traza y el determinante de la matriz asociada. Englobamos toda la información obtenida en el plano traza – determinante.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

• Considera el sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ Muestra que los valores propios del sistema $\lambda_{1}, \lambda_{2}$ satisfacen las identidades $$\lambda_{1}+\lambda_{2}=\mathrm{tr}{A}$$ $$\lambda_{1}\lambda_{2}=\det{A}.$$ Recuerda considerar los casos cuando los valores propios son distintos o iguales.

Clasifica el plano fase y puntos de equilibrio de los siguientes sistemas de ecuaciones, calculando únicamente la traza y el determinante de la matriz asociada:

• $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 15 & -1 \\ -60 & 4 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$

• $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} \pi & 0 \\ e & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$

• Considera el sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & a+2 \\ a-2 & a \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ Determina la forma del plano fase y la estabilidad del punto de equilibrio según la traza y el determinante de la matriz asociada, y el valor $a$.

• Para el ejercicio anterior, identifica la región del plano traza – determinante donde los planos fase tienen comportamientos similares.

• Realiza el mismo análisis de los dos ejercicios anteriores para el sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & a+b \\ a-b & a \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$ para cualquier valor de $a$ y $b$.

Más adelante

Con todo el conocimiento adquirido acerca de sistemas de ecuaciones lineales, es momento de estudiar, al menos de manera cualitativa, sistemas de ecuaciones no lineales. En la próxima entrada daremos una breve introducción a tales sistemas.

Además, veremos que es posible linealizar este tipo de sistemas para obtener un sistema de ecuaciones lineales equivalente que nos brinde la información cualitativa de las soluciones al sistema no lineal. Así, podremos dibujar el plano fase de un sistema no lineal, sin conocer explícitamente las soluciones a dicho sistema.

Entradas relacionadas

• Ir a Ecuaciones Diferenciales I
• Entrada anterior del curso: Plano fase para sistemas lineales con cero como valor propio
• Siguiente entrada del curso: Sistemas de ecuaciones no lineales. Linealización de los puntos de equilibrio

• Notas escritas relacionadas con el tema: El plano Traza – Determinante

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»