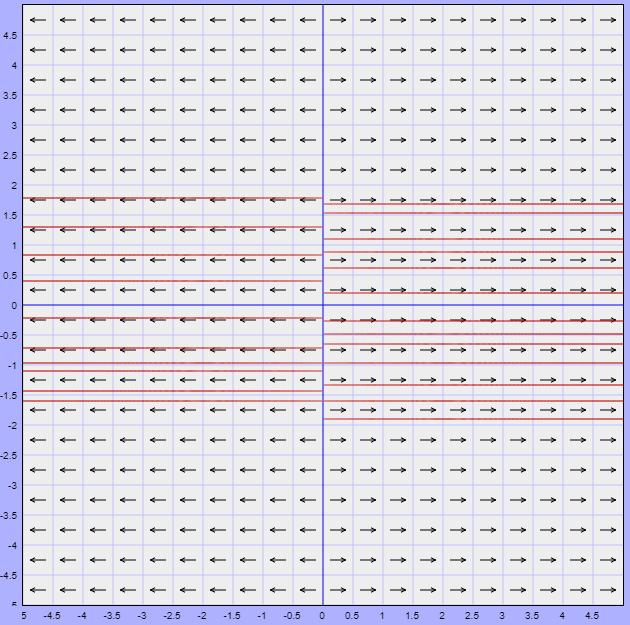
Algún matemático dijo que el verdadero placer no reside
en el descubrimiento de la verdad, sino en su búsqueda.
– Tolstoy
Introducción
Hemos comenzado con el estudio cualitativo de los sistemas no lineales. Hasta este momento sólo somos capaces de predecir el comportamiento de las soluciones de un sistema no lineal alrededor de los puntos de equilibrio. Vimos que para hacerlo debemos encontrar el sistema lineal cuyas soluciones mejor se aproximen a las del sistema no lineal, a tal proceso se le conoce como linearización.
Nuestro propósito es esbozar de manera general el plano fase de un sistema no lineal, o al menos describir las trayectorias en zonas lejanas a los puntos de equilibrio.
En esta entrada veremos como hacer una descripción más general del plano fase a través de un método geométrico.
Nulclinas
\begin{align*}
x^{\prime} &= F_{1}(x, y) \\
y^{\prime} &= F_{2}(x, y) \label{1} \tag{1}
\end{align*}Se define la nulclina $x$ como el conjunto de puntos $(x, y)$, tales que $F_{1}(x, y) = 0$. De forma similar, se define la nulclina $y$ como el conjunto de puntos $(x, y)$, tales que $F_{2}(x, y) = 0$
Una observación de la definición anterior es que las nulclinas corresponden a las curvas de nivel de las funciones $F_{1}$ y $F_{2}$
\begin{align*}
F_{1}(x, y) &= c \\
F_{2}(x, y) &= c \label{2} \tag{2}
\end{align*}
en el caso en el que $c = 0$.
Ejemplo: Determinar las nulclinas del siguiente sistema no lineal.
\begin{align*}
x^{\prime} &= x(2 -x -y) \\
y^{\prime} &= y(y -x)
\end{align*}
Solución: De este sistema no lineal vemos que
\begin{align*}
F_{1}(x, y) &= x(2 -x -y) \\
F_{2}(x, y) &= y(y -x)
\end{align*}
Para obtener la nulclina $x$ (o nulclinas $x$) hacemos $F_{1}(x, y) = 0$, es decir
$$x(2 -x -y) = 0$$
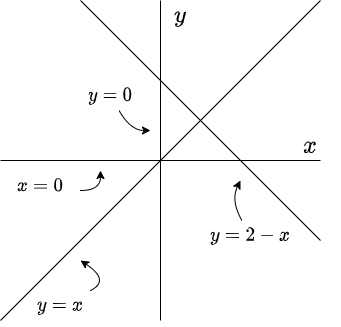
de donde $x = 0$ o $2 -x -y = 0$. Una primer nulclina $x$ corresponde al eje $y$ del plano fase ya que $x = 0$. De la segunda expresión se obtiene la función $y(x) =2 -x$, la cual corresponde a una recta con pendiente negativa. Dicha recta es una segunda nulclina $x$.
Para obtener las nulclinas $y$ hacemos $F_{2}(x, y) = 0$, es decir,
$$y(y -x) = 0$$
de donde $y = 0$ o $y -x = 0$. En este caso una nulclina $y$ corresponde al eje $x$ del plano fase ya que $y = 0$, mientras que la segunda nulclina corresponde a la recta definida por la función $y(x) =x$.
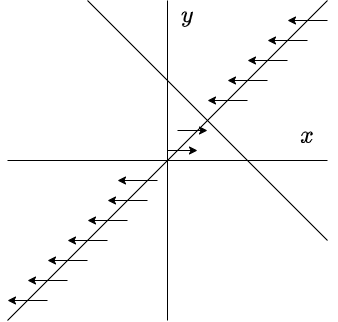
Por lo tanto, las rectas $x = 0$ (eje $y$), $y = 0$ (eje $x$), $y(x) =x$ y $y(x) =2 -x$ son las nulclinas del sistema no lineal. A continuación se muestran las nulclinas en el plano fase (o plano $XY$).
$\square$
¿Y de qué nos sirven las nulclinas?. Consideremos la función vectorial
$$F(x, y) = (F_{1}(x, y), F_{2}(x, y)) \label{3} \tag{3}$$
De acuerdo a la definición de nulclinas notamos enseguida que, en general, el campo vectorial sobre una nulclina siempre será vertical (apuntará hacia arriba o hacia abajo) o será horizontal (apuntará hacia la izquierda o a la derecha) dependiendo de qué componente de la función vectorial (\ref{3}) sea cero.
Supongamos que los puntos $(x_{0}, y_{0})$ pertenecen a la nulclina $x$, entonces, por definición, se cumple
$$F(x_{0}, y_{0}) = (0, F_{2}(x_{0}, y_{0})) \label{4} \tag{4}$$
en este caso el campo vectorial en el punto $(x_{0}, y_{0})$ será vertical ya que no hay componente horizontal y apuntará hacia arriba si $F_{2}(x_{0}, y_{0}) > 0$ o hacia abajo si $F_{2}(x_{0}, y_{0}) < 0$.
De forma similar, si los puntos $(x_{0}, y_{0})$ pertenecen a la nulclina $y$, entonces se cumple
$$F(x_{0}, y_{0}) = (F_{1}(x_{0}, y_{0}), 0) \label{5} \tag{5}$$
es decir, el campo vectorial será horizontal a lo largo de la nulclina $y$. Apuntará a la izquierda si $F_{1}(x_{0}, y_{0}) < 0$ o a la derecha si $F_{2}(x_{0}, y_{0}) > 0$.
Notemos otro hecho importante. Por definición, un punto de equilibrio satisface que
$$F(x_{0}, y_{0}) = (0, 0) \label{6} \tag{6}$$
es decir,
\begin{align*}
F_{1}(x_{0}, y_{0}) &= 0 \\
F_{2}(x_{0}, y_{0}) &= 0 \label{7} \tag{7}
\end{align*}
Eso significa que existe un punto $(x_{0}, y_{0})$ que esta tanto en la nulclina $x$ como en la nulclina $y$, en otras palabras, las intersecciones entre nulclinas corresponden a los puntos de equilibrio del sistema no lineal.
Ejemplo: Determinar los puntos de equilibrio así como la dirección del campo vectorial sobre las nulclinas del sistema no lineal del ejemplo anterior.
Solución: El sistema que teníamos era
\begin{align*}
x^{\prime} &= x(2 -x -y) \\
y^{\prime} &= y(y -x)
\end{align*}
La función vectorial $F$ es
$$F(x, y) = (x(2 -x -y), y(y -x))$$
Comencemos por determinar los puntos de equilibrio, dichos puntos se obtienen de resolver el sistema
\begin{align*}
x(2 -x -y) &= 0 \\
y(y -x) &= 0
\end{align*}
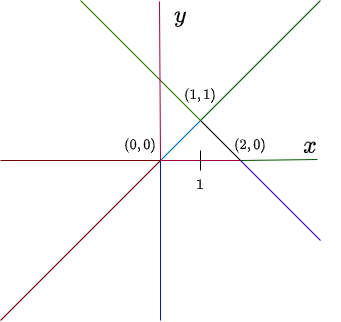
De la primer ecuación tenemos $x = 0$ o $2 -x -y = 0$, de la segunda relación se obtiene $y = 2 -x$. Por otro lado, de la segunda ecuación tenemos $y = 0$ o $y -x = 0$. Sustituyendo $x = 0$, entonces $y = 0$, por lo tanto, un punto de equilibrio es el origen $Y_{0} = (0, 0)$.
Si sustituimos $y = 2-x$ en $y -x = 0$ se tiene
$$(2 -x) -x = 2 -2x = 0$$
de donde $x = 1$, así $y = 2 -1 =1$, por tanto, otro punto de equilibrio es $Y_{1} = (1, 1)$.
Finalmente si $y = 0$, entonces $x = 2$, así el punto $Y_{2} = (2, 0)$ es otro punto de equilibrio.
Recordemos que las nulclinas del sistema están definidas por las rectas $x = 0$, $y = 0$, $y = x$ y $y = 2 -x$. Verifica que los puntos de equilibrio
$$Y_{0} = (0, 0), \hspace{1cm} Y_{1} = (1, 1) \hspace{1cm} y \hspace{1cm} Y_{2} = (2, 0)$$
efectivamente corresponden a los puntos de intersección entre las nulclinas del sistema.
¿Por qué el punto $(0, 2)$ no es un punto de equilibrio si es también la intersección de dos nulclinas?.
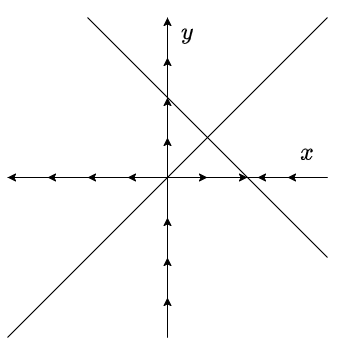
Ahora veamos que dirección tiene el campo vectorial sobre cada nulclina.
Lo primero que debemos notar es que cada nulclina está definida en intervalos.
- El eje $y$ (nulclina $x = 0$) se debe estudiar en los intervalos $y \in (-\infty, 0), (0, \infty)$.
- El eje $x$ (nulclina $y = 0$) se debe estudiar en los intervalos $x \in (-\infty, 0), (0, 2), (2, \infty)$.
- La nulclina definida por $y(x) = x$ se debe estudiar en los intervalos en los que $x \in (-\infty, 0), (0, 1), (1, \infty)$.
- Finalmente, la nulclina definida por $y(x) = 2 -x$ se debe estudiar en los intervalos $x \in (-\infty, 1), (1, 2), (2, \infty)$.
Determinemos la dirección de los vectores en cada intervalo de cada nulclina apoyándonos de la función vectorial
$$F(x, y) = (x(2 -x -y), y(y -x))$$
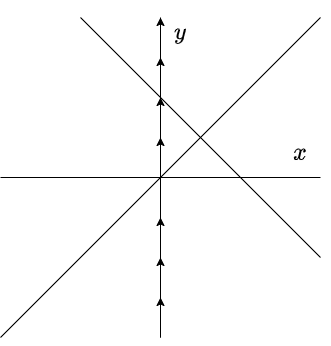
Comencemos por la nulclina $x$ definida por $x = 0$. Si $x = 0$, entonces
$$F(0, y) = (0, y^{2})$$
como $y^{2} > 0$ en todo momento, es decir para $y \in (-\infty, 0)$ y $y \in (0, \infty)$, entonces el campo vectorial sera vertical apuntando hacia arriba.
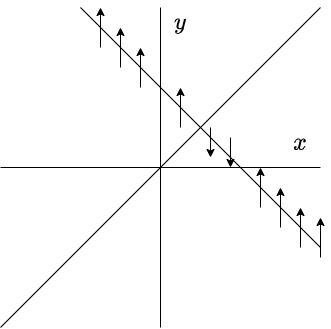
Para el caso de la nulclina $y$ definida por $y = 0$, se tiene
$$F(x, 0) = (2x -x^{2}, 0)$$
Comencemos con $x \in (-\infty, 0)$. Si $x < 0$, entonces $2x < 0$ y claro está que $-x^{2} < 0$, por tanto, en dicho intervalo $2x -x^{2} < 0$, esto significa que el campo vectorial será horizontal señalando hacia la izquierda.
Si $x \in (0, 2)$, entonces $x > 0$, o bien $2x > 0$ y $-x^{2} < 0$, es sencillo notar que dentro del intervalo que estamos considerando se cumple que $2x -x^{2} > 0$, por tanto, el campo apuntará a la derecha
Finamente, si $x \in (2, \infty)$, es claro que $2x -x^{2} < 0$, así que el campo volverá a apuntar hacia la izquierda.
Consideremos ahora la nulclina $y$ definida por $y = x$, en este caso el campo vectorial esta dado por
$$F(y, y) = (2y -2y^{2}, 0)$$
o bien,
$$F(x, x) = (2x -2x^{2}, 0)$$
En el intervalo $x \in (-\infty, 0)$, se cumple que $x < 0$, $2x < 0$ y claro es que $-2x^{2} < 0$, así en dicho intervalo $2x -2x^{2} < 0$, por lo tanto, el campo vectorial es horizontal y apunta hacia la izquierda.
Si $x \in (0,1)$, entonces $2x -2x^{2} > 0$, el campo apuntará a la derecha y finalmente volverá a apuntar a la izquierda para $x \in (1, \infty )$, ya que $2x -2x^{2} < 0$.
Finalmente, para la nulclina $x$ definida por $y = 2 -x$, se tiene
$$F(x, 2 -x) = (0, 2x^{2} -6x + 4)$$
Es posible verificar que si $x \in (-\infty, 1)$, entonces
$$2x^{2} -6x + 4 > 0$$
Si $x \in (1, 2)$, entonces
$$2x^{2} -6x + 4 < 0$$
y si $x \in (2, \infty)$ se cumple que
$$2x^{2} -6 + 4 > 0$$
Por lo tanto, el campo vectorial apuntará hacia arriba, luego hacia abajo y después nuevamente hacia arriba, respectivamente.
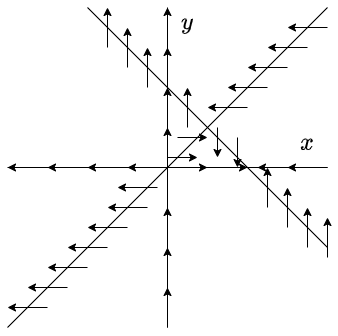
Por lo tanto, el campo vectorial sobre cada nulclina se ve de la siguiente forma.
$\square$
Recordemos que el campo vectorial es tangente a las trayectorias del sistema y la dirección indica la evolución de dichas trayectorias conforme $t \rightarrow \infty$, de manera que ahora tenemos una idea, aunque puede ser un poco vaga, de como se puede ir viendo el plano fase del sistema.
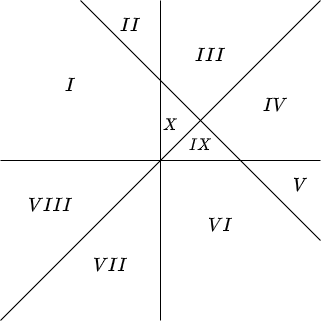
Una última observación que hacemos es que las curvas que representan a las nulclinas dividen al plano en varias regiones. En el ejemplo anterior se forman 10 regiones distintas las cuales se muestran en la siguiente figura.
Esto nos permitirá esbozar el campo vectorial sobre cada región y con ello podremos trazar trayectorias obteniendo así una representación más general del plano fase de un sistema no lineal.
Ejemplo: Intentar esbozar el plano fase del sistema no lineal estudiado.
\begin{align*}
x^{\prime} &= x(2 -x -y) \\
y^{\prime} &= y(y -x)
\end{align*}
Solución: Hasta este momento conocemos los puntos de equilibrio del sistema, las nulclinas y la dirección del campo vectorial sobre cada una de ellas.
Lo que se puede hacer es determinar un vector aleatorio sobre cada una de las regiones limitadas por las nulclinas del sistema y en base a él aproximar una solución apoyándose también de los vectores ubicados sobre las nulclinas. En el segundo video de la sección de videos de este curso puedes encontrar el desarrollo de este método.
Debido a que a nosotros nos resulta más difícil dibujar algunas trayectorias, lo que haremos es utilizar nuestra herramienta de costumbre para visualizar el campo vectorial del sistema.
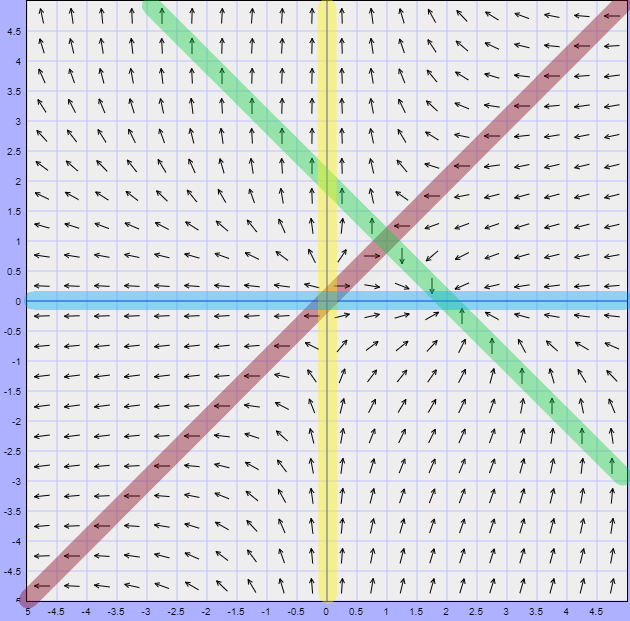
En esta figura visualizamos el campo vectorial del sistema, así como sobre las nulclinas.
Lo primero que se puede hacer es linealizar el sistema con respecto a cada uno de los puntos de equilibrio. Recordemos que la función vectorial $F$ es
$$F(x, y) = (x(2 -x -y), y(y -x))$$
de manera que
\begin{align*}
F_{1}(x, y) &= x(2 -x -y) \\
F_{2}(x, y) &= y(y -x)
\end{align*}
Las derivadas parciales son
$$\dfrac{\partial F_{1}}{\partial x} = 2 -2x -y, \hspace{1cm} \dfrac{\partial F_{1}}{\partial y} = -x, \hspace{1cm} \dfrac{\partial F_{2}}{\partial x} = -y, \hspace{1cm} \dfrac{\partial F_{2}}{\partial y} = 2y -x$$
Por lo tanto, la matriz Jacobiana es
$$\mathbf{J}(x, y) = \begin{pmatrix}
2 -2x -y & -x \\ -y & 2y -x
\end{pmatrix}$$
Los puntos de equilibrio son $(0, 0), (1, 1)$ y $(2, 0)$, evaluando cada punto en la matriz Jacobiana se obtienen las siguientes matrices.
$$\mathbf{J}(0, 0) = \begin{pmatrix}
2 & 0 \\ 0 & 0
\end{pmatrix}, \hspace{1cm} \mathbf{J}(1, 1) = \begin{pmatrix}
-1 & -1 \\ -1 & 1
\end{pmatrix}, \hspace{1cm} \mathbf{J}(2, 0) = \begin{pmatrix}
-2 & -2 \\ 0 & -2
\end{pmatrix}$$
Por lo tanto, los sistemas lineales que se aproximan a la descripción de las trayectorias del sistema no lineal alrededor de los puntos de equilibrio son:
- $Y_{0} = (0, 0)$:
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
2 & 0 \\ 0 & 0
\end{pmatrix}\mathbf{Y}$$
- $Y_{1} = (1, 1)$:
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-1 & -1 \\ -1 & 1
\end{pmatrix}\mathbf{Y}$$
- $Y_{2} = (2, 0)$:
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-2 & -2 \\ 0 & -2
\end{pmatrix}\mathbf{Y}$$
Con el conocimiento de la forma de las trayectorias alrededor de los puntos de equilibrio y con la dirección del campo vectorial sobre algunos puntos del plano fase, entre ellos sobre las nulclinas, es que podemos esbozar completamente el plano fase del sistema no lineal.
En este caso, el plano fase correspondiente al sistema no lineal estudiado es
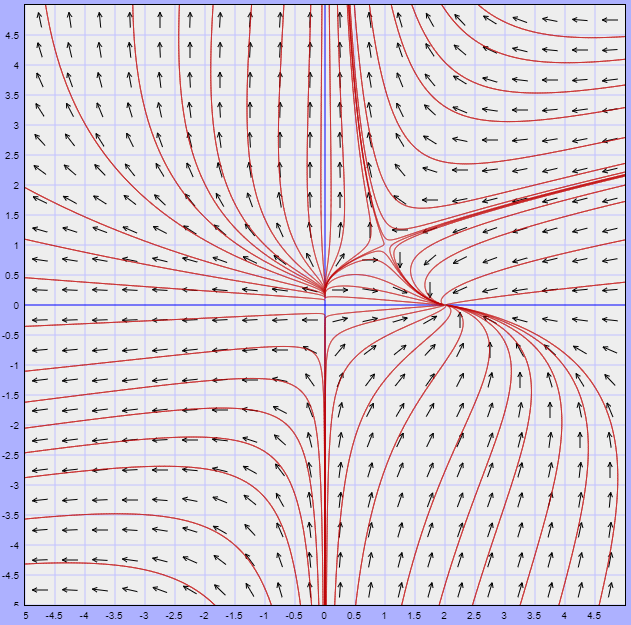
El flujo de las trayectorias es algo que ya intuíamos al considerar toda la información que estuvimos desarrollando sobre el sistema a lo largo de la entrada.
$\square$
Con esto concluimos el estudio cualitativo de algunos sistemas no lineales sencillos.
En la siguiente entrada estudiaremos un comportamiento interesante que presentan las trayectorias de algunos sistemas no lineales y cuya descripción se establece en el conocido teorema de Poincaré – Bendixon.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Hacer un bosquejo del plano fase de los siguientes sistemas no lineales siguiendo el método desarrollado a lo largo de la unidad.
(Recuerda que el propósito es esbozar el plano fase a mano, una vez que concluyas puede comparar tu resultado con el obtenido usando una computadora.)
- $x^{\prime} = x(2 -x -y)$
$y^{\prime} = y(y -x^{2})$
- $x^{\prime} = x(x -1)$
$y^{\prime} = y(x^{2} -y)$
- $x^{\prime} = xy -2y$
$y^{\prime} = x^{2} + y$
- Intentar hacer un bosquejo del plano fase del siguiente sistema no lineal.
- $x^{\prime} = y$
$y^{\prime} = -x + (1 -x^{2} -2y^{2})y$
¿Qué se observa de este sistema no lineal?.
¿Hay alguna dificultad en esbozar el plano fase?.
Más adelante…
Ahora somos capaces de hacer un estudio cualitativo de algunos sistemas no lineales, sin embargo existen situaciones en las que un sistema no lineal presenta un comportamiento interesante en el que las trayectorias tienden a una curva cerrada conocida como ciclo límite. En la siguiente y última entrada del curso estudiaremos la descripción de estos sistemas y enunciaremos el teorema de Poincaré – Bendixson en el plano.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Linealización de los puntos de equilibrio de sistemas no lineales
- Siguiente entrada del curso: Teorema de Poincaré – Bendixon en el plano
- Video relacionado al tema: Sistemas de ecuaciones no lineales. Las nulclinas y el plano fase
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»